任务二平面汇交、力偶系
合集下载
理论力学作业二
平面汇交力系与平面力偶系作业1．四力作用于一点，其方向如图所示。
已知各力的大小为：F1=50N，F2=80N，F3=60N，F4=100N。
求力系的合力。
2．一均质球重P=1000N，放在两个相交的光滑斜面之间如图示。
如斜面AB的倾角ϕ =45º，而斜面BC的倾角θ =60º。
求两斜面的约束力F D和F E的大小。
3．以吊斗运物过河，吊斗系用小车C挂在钢丝绳AB上，如图所示。
如欲将小车拉向左岸，则利用一跨过滑车A而绕在绞盘D上的绳索C AD；如欲将小车拉向右岸，则可利用一跨过滑车B而绕在铰盘E上的绳索C BE。
A、B两点在同一水平线上，距离AB=100m，钢索ACB长102m，吊斗重5kN。
如略去钢索和绳子的重量以及小车C沿钢索的摩擦，求当AC=20m时绳子C AD和钢索A C B的张力。
4．均质杆AB长l，置于销子C与铅垂面间，如图所示。
不计摩擦力，求平衡时杆与铅垂线间的夹角θ。
5．三个相同的光滑圆柱放置如图示，求圆柱不至于倒塌时θ 角的最小值。
6．杆AB以铰链A及弯杆BC支持，杆AB上作用一力偶，其力偶矩大小为M，顺时针转向，如图所示。
所有杆件的重量不计，求铰链A与C的约束力。
7．图示机构中杆AB 上有一导槽，套在CD 杆的销子E 上，在AB 和CD 杆上各有一力偶作用，如图所示。
己知M 1=1000N ·m ，不计杆重及摩擦。
求机构在图示位置平衡时力偶矩M 2的大小。
8．水平杆AB 由铰链A 与连杆CD 支持于铅垂转轴EF 上，在AB 杆的一端作用有一力偶（F ，F ′）其矩的大小为M 。
设所有杆件的重量不计，求CD 杆的内力及轴承E 与F 处的约束力。
平面汇交力系和平面力偶系
平面汇交力系和平面力偶系
平面汇交力系和平面力偶系是平面力学中的两个重要概念。
平面汇交力系是指各力的作用线在同一平面内且汇交于一点的力系。
在平面汇交力系中，力的大小和方向可以通过力的矢量表示。
平面汇交力系的合成可以通过力的多边形法则来进行，即将各个力按照首尾相接的顺序连接起来，形成一个封闭的多边形，合力则为这个多边形的封闭矢量。
平面力偶系是指由若干个力偶组成的力系，其中力偶是由大小相等、方向相反且不共线的两个力组成的力矩对。
在平面力偶系中，力偶的作用效果是产生旋转，而不是平移。
平面力偶系的合成可以通过力偶矩的代数和来进行。
平面汇交力系和平面力偶系在工程和物理学中有广泛的应用。
在结构分析、机械设计和力学问题中，常常需要考虑和分析平面汇交力系和平面力偶系的作用效果。
总的来说，平面汇交力系和平面力偶系是平面力学中的重要概念，它们的合成和平衡条件对于理解和解决平面力学问题至关重要。
第二章-1 平面汇交力系与平面力偶系
第二章-1 平面汇交力系与平面力偶系一、判别题（正确和是用√，错误和否×，填入括号内。
）2-1 平面汇交力系平衡的充分与必要的几何条件是：力多边形自行封闭。
（√）2-2 力在某一固定面上的投影是一个代数量。
（×）2-3 两个力F1、F2大小相等，则它们在同一轴上的投影也相等。
（×）2-4 一个力不可能分解为一个力偶；一个力偶也不可能合成一个力。
（√）2-5 力偶无合力、不能用一个力来等袒代替，也不能用一个力来平衡；（√）2-6 力偶无合力，也就是说力偶的合力等于零。
（×）2-7 力偶矩和力对点之矩本质上是二样的，讲的是一回事。
（×）2-8 力偶的作用效果取决于力偶矩的大小和转向。
（√）2-9 只要两力偶的力偶矩代数值相等，就是等效力偶。
（√）2-10 力偶中的两个力对同平面内任一点之矩的代数和等于力偶矩。
（√）2-11 力偶只能用力偶来平衡。
（√）2-12 平面力偶系可简化为一个合力偶。
（√）2-13 力偶可任意改变力的大小和力偶臂的长短。
（×）2-14 力偶的两力在其作用面内任意轴上的投影的代数和都等于零。
（√）2-15 若两个力F1、F2在同一轴上的投影相等，则这两个力相等，即F1 = F2。
（×）2-16 若两个力F1、F2大小相等，则在同一轴Ox上投影相等，即F1x = F2x。
（×）2-17 若两个力F1、F2大小、方向、作用点完全相同，则这两个力在任一轴上的投影相等。
（√）2-18 若两个力大小相等、方向相反，则在任一轴Ox上的投影大小相等。
（√）2-19 若两个力平行，则它们在任一轴上的投影相等。
（×）2-20 若两个力在某轴上的投影均为零，则该两力平行。
（√）2-21 图示为分别作用在刚体上A、B、C、D点的4个共面力，它们所构成的力多边形自行封闭且为平行四边形。
由于力多边形自行封闭，所以是平衡的。
平面汇交力系与平面力偶系精品PPT课件
四块相同的均质板，各重P，长2b，叠放如图示。 在板I右端点A挂着重物B，其重2P。欲使各板都平衡， 求每块板可伸出的最大距离。
3P
P
N3
4P
P
N4
P 2P
求图示结构AB杆与AC杆所受的力，已知F力位于AD 的中点E且垂直AD。
FA FAB
A FA
FAC
45 o 45 o
F
FA
FD
450
F
B
C
D
W3
F
W2
W1
塔吊及所受荷载如图。自重P=200kN，中心 通过塔基中心。起重量W=25kN，距右轨B为 15m.平衡物重Q，距左轨A为6m，在不考虑风 荷载时， 求： （1）满载时，为了保证塔
身不至于倾覆，Q至 少应多大？ （2）空载时，Q又应该不 超过多大，才不至于 使塔身向另一侧倾覆？
如图示，一钢筋混凝土梁BC置于砖墙上，挑出1.5m， 顶端C作用一集中力P=1kN，梁自重q=1.2kN/m，取 抗倾覆安全系数κ=1.5，试求BA段的长度a。
的力矩。
抗倾覆力矩（Mk）：抵抗结构或构件倾覆
的力矩。
K=抗倾覆安全系数
K MK Mq
规范规定：钢筋砼构件的抗倾覆安全系数 K≥1.5
带有雨蓬的钢筋混凝土门顶过梁，尺寸如图示，梁 和板的长度均为4m。设在此梁上的砖砌至3m高时， 便欲将雨篷下的木支撑拆除。试验算此时雨蓬会不 会绕A点倾覆。已知钢筋混凝土容重为25kN／m3 ， 砖砌体容重为19kN/m3 ，验算时应考虑雨蓬最外边 缘B上作用有施工荷载F=1kN。
3 如果力F通过矩心O，则mo(F)=0，此时力对物体
的作用效应为移动。
4 互成平衡的二力对同一点之矩的代数和等于零。
第2章平面汇交力系与平面力偶系
FBA
FBC
FAB
A
' F' FBA BC
B B
B
P
C
F2 F1
C
FCB
解：
y
FBA F2
600
300
（1） 取滑轮为研究对象，将其视为 一个几何点。受力如图所示。
其中 F1= F2 =P = 20 kN （2）选取图示坐标系。列方程
B
FBC
F1
x
X 0, Y 0,
FBA F1cos600 F2cos300 0 FBC F1cos300 F2cos600 0
解：（1）取碾子为研究对 象。 画受力图。
F
F
O B
O B
FB
P
P
A FA
A
（2）根据力系平衡的几何条件，作封闭的力多边形。
按比例，先画已知力，各力矢首位相接。
FB
a.从图中按比例量得
FA=11.4 kN , FB=10 kN 5 kN
FA
0
P
b.也可由几何关系计算
Rh cos 0.866 R
即：若作用在刚体上 {F1 , F2 ,, Fn } {FR }
则：
M O ( FR ) MO (Fi )
i 1
n
在古代，人们没有大型的 起重工具，只能依靠人力和畜力 。在建造宏伟的建筑物时，为了 将巨大的石柱竖立起来，可能采 用了右图所示的方法。其中起关 键作用的是用木材作成的 A 字形 支架。试从力学角度说明采用此 项措施的必要性。
P
解： 取梁为研究对象。 画受力图。
注意：这里所设力 FA 的方向与 实际方向相反。
解：取横梁为研究对象。画受力图。 建立图示直角坐标系。 由平面汇交力系的平衡条件列方程
FBC
FAB
A
' F' FBA BC
B B
B
P
C
F2 F1
C
FCB
解：
y
FBA F2
600
300
（1） 取滑轮为研究对象，将其视为 一个几何点。受力如图所示。
其中 F1= F2 =P = 20 kN （2）选取图示坐标系。列方程
B
FBC
F1
x
X 0, Y 0,
FBA F1cos600 F2cos300 0 FBC F1cos300 F2cos600 0
解：（1）取碾子为研究对 象。 画受力图。
F
F
O B
O B
FB
P
P
A FA
A
（2）根据力系平衡的几何条件，作封闭的力多边形。
按比例，先画已知力，各力矢首位相接。
FB
a.从图中按比例量得
FA=11.4 kN , FB=10 kN 5 kN
FA
0
P
b.也可由几何关系计算
Rh cos 0.866 R
即：若作用在刚体上 {F1 , F2 ,, Fn } {FR }
则：
M O ( FR ) MO (Fi )
i 1
n
在古代，人们没有大型的 起重工具，只能依靠人力和畜力 。在建造宏伟的建筑物时，为了 将巨大的石柱竖立起来，可能采 用了右图所示的方法。其中起关 键作用的是用木材作成的 A 字形 支架。试从力学角度说明采用此 项措施的必要性。
P
解： 取梁为研究对象。 画受力图。
注意：这里所设力 FA 的方向与 实际方向相反。
解：取横梁为研究对象。画受力图。 建立图示直角坐标系。 由平面汇交力系的平衡条件列方程
第二章平面汇交力系与平面力偶系
F
Fr
静
力 已 知 : F , l1, l2 , α . 求: MO(F)
学
—
平
面
汇 交
MO (F) = F d
力 系
d=?
、
力
偶
系 解: MO (F) = MO (F cosα) +MO(F sin α)
静 力 例：三角形分布载荷作用在水平梁上，如图示。 学 最大载荷强度为 q，梁长l。试求该力系的合力。
—
平
面 汇
NC 2 2a − M = 0
交 力 系
NA
=
NC
=
M 2 2a
、
力
偶
系
NC
NA
静 力 例：已知力偶矩 M1 =10 N⋅ m,求系统在图示位置平衡时 学 的力偶矩 M 2 的大小，不计构件自重及摩擦。α = 45 °
—
平
面
汇
交
力
系
、
力
偶 系
(a)M 2 = M 1,
(b)M 2 = 2M 1
系 、
MO(FR) = MO(F1)+MO(F2)+
+MO(Fn)
力 =∑MO(F)
偶 系
当平面汇交力系处于平衡状态时合力为零, 则各力对任意点之矩的代数和也为零.
静
力 学
例：如图圆柱直齿轮受啮合力的作用。设F=1400N, α=20。，压力角齿轮的节圆（啮合圆）半径
r=60mm，试计算力对轴心O的力矩。
求压榨机对工件与地面的压力，以及AB杆所受的力。
—
平
面 解： 取活塞BD为研究对象并受力分
汇 交
析如图。建立坐标，由平面汇 交力系的平衡方程有：
理论力学第二章平面汇交力系与平面力偶系
FR FRx 2 FRy 2
合力作用点：为该力系的汇交点
2-2 平面汇交力系合成与平衡的解析法
(2)平面汇交力系平衡的充要条件： 各力在两个坐标轴上投影的代数和分别等于零。 ——平面汇交力系的平衡方程
X0,
Y
i 1
n
i
0
只可求解两个未知量
[ 例1 ] 系统如图，不计杆、轮自重，忽略滑轮大小， 已知： P=20kN； 求：系统平衡时，杆AB、BC受力。
解：AB、BC杆为二力杆，
取滑轮B（或点B），画受力图。 用解析法，建图示坐标系
Fix 0
FBA F1 cos 60 F2 cos 30 0
Fiy 0
FBC F1 cos 30 F2 cos 60 0
F1 F2 P
解得： FBC
27.32kN
②应用合力矩定理
mO ( F ) Fx l F y l ctg
m o (Q ) Q l
[例P28 2-4，习题P38 2-10]
[例2]水平梁AB受按三角型分布的载荷作用，如图所示。 载荷的最大值为q，梁长l ,试求合力作用线的位置。
解：在距A端x 的微段dx上， 作用力的大小为q’dx,其中 q’ 为该处的载荷强度。由图可知 ，q’=xq/l。，因此分布载荷合 力的大小为： l
2-2 平面汇交力系合成与平衡的解析法
二、平面汇交力系合成的解析法：
各分力在x轴和在y轴投影的代数 和 等于合力在对应轴上的投影。
FR x X 1 X 2 X 4
X
FR y Y1 Y2 Y3 Y4
Y
i
i
合力作用点：为该力系的汇交点
2-2 平面汇交力系合成与平衡的解析法
(2)平面汇交力系平衡的充要条件： 各力在两个坐标轴上投影的代数和分别等于零。 ——平面汇交力系的平衡方程
X0,
Y
i 1
n
i
0
只可求解两个未知量
[ 例1 ] 系统如图，不计杆、轮自重，忽略滑轮大小， 已知： P=20kN； 求：系统平衡时，杆AB、BC受力。
解：AB、BC杆为二力杆，
取滑轮B（或点B），画受力图。 用解析法，建图示坐标系
Fix 0
FBA F1 cos 60 F2 cos 30 0
Fiy 0
FBC F1 cos 30 F2 cos 60 0
F1 F2 P
解得： FBC
27.32kN
②应用合力矩定理
mO ( F ) Fx l F y l ctg
m o (Q ) Q l
[例P28 2-4，习题P38 2-10]
[例2]水平梁AB受按三角型分布的载荷作用，如图所示。 载荷的最大值为q，梁长l ,试求合力作用线的位置。
解：在距A端x 的微段dx上， 作用力的大小为q’dx,其中 q’ 为该处的载荷强度。由图可知 ，q’=xq/l。，因此分布载荷合 力的大小为： l
2-2 平面汇交力系合成与平衡的解析法
二、平面汇交力系合成的解析法：
各分力在x轴和在y轴投影的代数 和 等于合力在对应轴上的投影。
FR x X 1 X 2 X 4
X
FR y Y1 Y2 Y3 Y4
Y
i
i
工程力学ppt 2平面汇交力系和平面力偶系
FR F1 F2 Fn Fi
i 1
(2-1)
a
b 图2.1
c
● 2.1.2 平面汇交力系合成的几何法
由力多边形法则知，平面汇交力系的合成结果为一合力，显然， 平面汇交力系平衡的必要和充分条件是该力系的合力等于零。如 果用矢量形式表示，即
FR
F
i 1
n
i
0
（2-2）
由力的合成的几何法可知，平面汇交力系的合力是由力多边形 的封闭边来表示的。在平衡的情形下合力为零，也就是力多边形 中最后一力终点与第一个力的起点重合，此时的力多边形称为封 闭的力多边形。于是得到如下结论：平面汇交力系平衡的必要和 充分条件是力多边形自行封闭。这就是平面汇交力系平衡的几何 条件。 运用平面汇交力系平衡的几何条件求解问题时，需要首先按比 例画出封闭的力多边形，然后用尺和量角器在图上量得所要求的 未知量；也可根据图形的几何关系，用三角公式计算出所要求的 未知量，这种解题方法称为几何法。
FA 22.4kN，FC 28.3kN
根据作用力和反作用力的关系，作用于杆DC在端C的力FC与 FC 的大小相等，方向相反，由此可知杆DC是受压杆，如图2.3(b)所 示。
应该指出，封闭的力的多边形也可以根据三角几何关系，作成 如图2.3(d)所示的力三角形，同样可求得力 FA 和 FC ，且结果相 同。 通过以上例题，可知用几何法求解平衡问题的主要步骤如下： (1) 选取研究对象。根据题意，分析已知量与待求量，选取恰 当的平衡物体作为研究对象，并画出分离体简图。 (2) 分析研究对象的受力情况，正确地画出其相应的受力图。 在研究对象上，画出其所受的全部外力。若某个约束反力的作用 线不能根据约束特性直接确定，而物体又只受三个力作用时，则 可根据三力平衡汇交的条件来确定未知力的作用线方位。 (3) 作封闭的力多边形图，求解未知量。可以应用比例尺直接 量出待求的未知量，也可以根据几何三角关系计算出来。
i 1
(2-1)
a
b 图2.1
c
● 2.1.2 平面汇交力系合成的几何法
由力多边形法则知，平面汇交力系的合成结果为一合力，显然， 平面汇交力系平衡的必要和充分条件是该力系的合力等于零。如 果用矢量形式表示，即
FR
F
i 1
n
i
0
（2-2）
由力的合成的几何法可知，平面汇交力系的合力是由力多边形 的封闭边来表示的。在平衡的情形下合力为零，也就是力多边形 中最后一力终点与第一个力的起点重合，此时的力多边形称为封 闭的力多边形。于是得到如下结论：平面汇交力系平衡的必要和 充分条件是力多边形自行封闭。这就是平面汇交力系平衡的几何 条件。 运用平面汇交力系平衡的几何条件求解问题时，需要首先按比 例画出封闭的力多边形，然后用尺和量角器在图上量得所要求的 未知量；也可根据图形的几何关系，用三角公式计算出所要求的 未知量，这种解题方法称为几何法。
FA 22.4kN，FC 28.3kN
根据作用力和反作用力的关系，作用于杆DC在端C的力FC与 FC 的大小相等，方向相反，由此可知杆DC是受压杆，如图2.3(b)所 示。
应该指出，封闭的力的多边形也可以根据三角几何关系，作成 如图2.3(d)所示的力三角形，同样可求得力 FA 和 FC ，且结果相 同。 通过以上例题，可知用几何法求解平衡问题的主要步骤如下： (1) 选取研究对象。根据题意，分析已知量与待求量，选取恰 当的平衡物体作为研究对象，并画出分离体简图。 (2) 分析研究对象的受力情况，正确地画出其相应的受力图。 在研究对象上，画出其所受的全部外力。若某个约束反力的作用 线不能根据约束特性直接确定，而物体又只受三个力作用时，则 可根据三力平衡汇交的条件来确定未知力的作用线方位。 (3) 作封闭的力多边形图，求解未知量。可以应用比例尺直接 量出待求的未知量，也可以根据几何三角关系计算出来。
第2章 平面汇交力系与平面力偶理论
且在同一平面内，由平面力偶系的合成理论．其合力偶矩为
式中，负号表示合力偶的转向为顺时针方向转动。
欲求作用在A、B处的水平力，应以工件为研究对象，受力分析如图 2—13所示，由于工件在水平面内受四个力偶和两个螺栓的水平反力 的作用下而平衡。因为力偶只能与力偶平衡，故两个螺栓的水平反 力N一和jv”必然组成一个力偶。由平面力偶系的平衡方程
二、平面汇交力系合成与平衡的解析法
根据合力投影定理，可计算出合力R的投影Rx和Ry
合力R与x轴正向间的夹角为
平面汇交力系平衡的充要条件是该力系的合力R等于0，则有
上式成立，必须同时满足
平面汇交力系解析法平衡的必要与充分条件是：力系中所有 各力在两个坐标轴上投影的代数和分别等于零。
例2-2 图2-5(a)所示圆柱体A重Q，在中心上系着两条绳AB和 AC，并分别经过滑轮B和C，两端分别挂重为P和2P的重物，试 求平衡时绳AC和水平线所构成的角α及D处的约束反力。 解 选圆柱为研究对象，取分离体画受
（2）作用在同一平面内的两个力偶，只要它的力偶矩的大 小相等、转向相同，则该两个力偶彼此等效。这就是平面力 偶的等效定理。
定理的推论
(1)力偶可以在其作用面内任意移动，而不影响它对 刚体的作用效应。 (2)只要保持力偶矩大小和转向不变，可以任意改变 力偶中力的大小和相应力偶臂的长短。而不改变它 对刚体的作用效应 上述推论表明，在研究同一平面内有关力偶问题时， 只需考虑力偶矩的代数值，而不必研究其中力的大 小和力偶臂的长短。
从而解得
所以
例 图a 所示结构中，各构件自重不计。在构件AB 上作用1力 偶矩为M 的力偶，求支座A 和C 的约束力。
解（1）BC为二力杆： F c= −F B（图c） （2）研究对象AB，受力如图b 所示， F AFB' 构成力偶， 则
式中，负号表示合力偶的转向为顺时针方向转动。
欲求作用在A、B处的水平力，应以工件为研究对象，受力分析如图 2—13所示，由于工件在水平面内受四个力偶和两个螺栓的水平反力 的作用下而平衡。因为力偶只能与力偶平衡，故两个螺栓的水平反 力N一和jv”必然组成一个力偶。由平面力偶系的平衡方程
二、平面汇交力系合成与平衡的解析法
根据合力投影定理，可计算出合力R的投影Rx和Ry
合力R与x轴正向间的夹角为
平面汇交力系平衡的充要条件是该力系的合力R等于0，则有
上式成立，必须同时满足
平面汇交力系解析法平衡的必要与充分条件是：力系中所有 各力在两个坐标轴上投影的代数和分别等于零。
例2-2 图2-5(a)所示圆柱体A重Q，在中心上系着两条绳AB和 AC，并分别经过滑轮B和C，两端分别挂重为P和2P的重物，试 求平衡时绳AC和水平线所构成的角α及D处的约束反力。 解 选圆柱为研究对象，取分离体画受
（2）作用在同一平面内的两个力偶，只要它的力偶矩的大 小相等、转向相同，则该两个力偶彼此等效。这就是平面力 偶的等效定理。
定理的推论
(1)力偶可以在其作用面内任意移动，而不影响它对 刚体的作用效应。 (2)只要保持力偶矩大小和转向不变，可以任意改变 力偶中力的大小和相应力偶臂的长短。而不改变它 对刚体的作用效应 上述推论表明，在研究同一平面内有关力偶问题时， 只需考虑力偶矩的代数值，而不必研究其中力的大 小和力偶臂的长短。
从而解得
所以
例 图a 所示结构中，各构件自重不计。在构件AB 上作用1力 偶矩为M 的力偶，求支座A 和C 的约束力。
解（1）BC为二力杆： F c= −F B（图c） （2）研究对象AB，受力如图b 所示， F AFB' 构成力偶， 则
2汇交力系、力偶系平衡
摇杆 FA
A
例2-6
30 ;
解：取轮，由力偶只能由力偶平衡的性质，画受力图。
M1
O
M1
FO
销子
M 0
解得
M1 FA r sin 0 M1 2 FO FA 8 kN 0 r sin 0.5 sin 30
例2-6
解得 FO FA 8kN
FA
A
力的投影
y
F
投影
x
投影
Fy Fy Fx Fx
y F
分力
F1
Fy Fx
y
F
分力
Fy
x
Fx
x
2）合矢量投影定理
合矢量在轴上的投影等于
y F1
各分矢量在同一轴上投影的代数和。
y
F2 j O
Fn i F3 x Fy j O
b
FR
Fx Fxi
x
i
Fy Fyi
Fx
合力大小 FR Fx 2 Fy 2 ( Fxi )2 ( Fyi )2 Fx Fy 合力方向 cos FR , i） （ cos FR , j） （ FR FR
F'= F''=F
B F''
d
F A B
d
B
d
F
A
F B A
M
F'
M
A
附加力偶矩：M=MB(F)=±Fd
2. 平面任意力系向作用面内一点简化 主矢和主矩 各力向矩心平移
矩心 Fn
F1 O
平面汇交力系 平面力偶系
Fn F1 Fi
Fi
A
例2-6
30 ;
解：取轮，由力偶只能由力偶平衡的性质，画受力图。
M1
O
M1
FO
销子
M 0
解得
M1 FA r sin 0 M1 2 FO FA 8 kN 0 r sin 0.5 sin 30
例2-6
解得 FO FA 8kN
FA
A
力的投影
y
F
投影
x
投影
Fy Fy Fx Fx
y F
分力
F1
Fy Fx
y
F
分力
Fy
x
Fx
x
2）合矢量投影定理
合矢量在轴上的投影等于
y F1
各分矢量在同一轴上投影的代数和。
y
F2 j O
Fn i F3 x Fy j O
b
FR
Fx Fxi
x
i
Fy Fyi
Fx
合力大小 FR Fx 2 Fy 2 ( Fxi )2 ( Fyi )2 Fx Fy 合力方向 cos FR , i） （ cos FR , j） （ FR FR
F'= F''=F
B F''
d
F A B
d
B
d
F
A
F B A
M
F'
M
A
附加力偶矩：M=MB(F)=±Fd
2. 平面任意力系向作用面内一点简化 主矢和主矩 各力向矩心平移
矩心 Fn
F1 O
平面汇交力系 平面力偶系
Fn F1 Fi
Fi
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
卷扬机：卷扬机是通过转动卷筒，将缠绕在卷筒上的钢丝产生 牵引力的起重设备。那么起重物大小的计算怎么进行呢？这里 涉及到的是平面力偶系的知识。
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
解决任务的方法:
1、了解平面汇交力系合成的几何法和解析法。
3、了解平面力偶系合成的解析法。
4、熟练掌握平面汇交力系和平面力偶系平衡的解析条件。
F3
F4
F5 F6 x
F1x F1 cos 45 141.4 N , F1 y F1 sin 45 141.4 N F2 x F2 cos60 100N , F2 y F2 sin 60 173.2 N F3 x F3 cos30 173.2 N , F3 y F3 sin 30 100N F4 x F4 cos60 100N , F4 y F4 sin 60 173.2 N F5 x 0, F5 y 200N F6 x 200N , F6 y 0
B
60
A
30
C
G
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
解：如图建立直角坐标系，以A滑轮（带销钉）为研究对象 进行受力分析，建立平衡方程
y
F
FAC
x
x
0, 0,
FAC sin 30 T FAB cos30 0
T FAB
F
y
FAC cos30 FAB sin 30 G 0
G
FAB= -7.32kN， FAC=27.32kN
负值说明真实受力方向与假设方向相反。可判断AB杆受 压，AC杆受压。（思考：坐标轴怎么设定可以使求解过 程更加简单？）
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
课堂思考题
1、力沿轴Ox、Oy的分力和力在两轴上的投影有何区别？分别以两坐标轴 垂直和不垂直举例说明。
引
平面力系
言
平面汇交力系 平面力偶系 平面一般力系(平面任意力系)
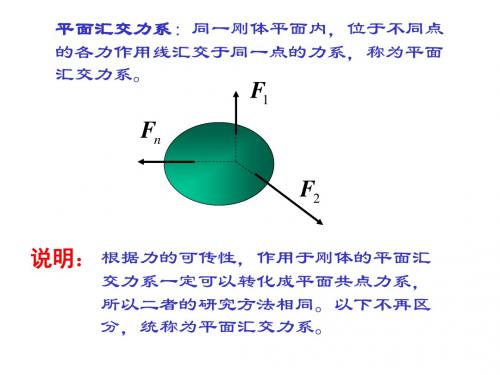
平面汇交力系： 各力的作用线都在同一平 面内且汇交于一点的力系。
O B
A
C G
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
模块1 平面汇交力系合成与平衡的几何法
一、合成的几何法 1.两个共点力的合成
F1
A
FR
FR
FR F1 F2
F1
80mm
解：如图建立坐标系，则
F2
B x
F1 X Y 0 100
2
F2 30 40
F3 50 0
2
Σ 80 140
A
60mm
C
F3
FR
Y tg X
X Y
161.2 N
7 (是合力F与坐标轴x轴之间的夹角） 4
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
二、合力投影定理
由图可看出，各分力在x 轴和在y 轴投影的和分别为：
FR x X1 X 2 X 4 X i
FR y Y1 Y2 Y3 Y4 Y i
FR x X i
FR y Yi
合力投影定理：合力在任一轴上的投影，等于各分力在同一 轴上投影的代数和。
按合力矩定理 把力F沿着切向和径向进行正交分解，分力为
Ft 和Fr。
Ft
MO (F ) MO (Ft ) MO (Fr ) M O (Ft )
Fr
F cos r 78.93 N m
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
三、平面力偶及其性质 力偶：大小相等，方向相反，作用线不重合的一对平行力组 成的力系叫力偶，力偶对刚体只产生转动效应。
三、平面汇交力系平衡的解析法
从前述可知：平面汇交力系平衡的必要与充分条件是该力系 的合力为零。
X 0 Y 0
i i
FR ( X i ) 2 ( Yi ) 2 0
为平衡的充要条件，也叫平衡方程。只能建立两 个独立的平衡方程，因此只能求出两个未知量。
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系） 1、选择合适的研究对象，进行受力分析。
一、力对点的矩
F
工程实例
测力矩扳手
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
力对点之矩（简称 力矩）：用来衡量力F使刚体绕某点O产生转 动效应的量度。其中O点为矩心，矩心O到力F作用线的垂直距 离称为力臂，则力F对O点之矩的大小为力的大小与力臂的乘积 ，力矩在平面内的转动方向用正负号区分。
O G
FOA 57.74kN , FOB 28.87kN
G
求出的力均为正值，说明图中假定的力的指向与实际 指向一致，可判定OA杆为拉杆，OB杆为压杆。
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
例：起重架可借绕过滑轮A的绳索将重力的大小G=20KN的物 体吊起，滑轮A用不计自重的杆AB和AC支撑，不计滑轮的自 重、尺寸和轴承处的摩擦。求系统平衡时杆AB、AC所受力。
比较力在给定不同坐标轴上的投影和分力的区别。
分力 分力 投影
在正交坐标系中，力在投影轴上的投影大小等于力沿两坐标轴的分力的 大小，在非正交坐标系中两者大小不相等。
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
例：求各力在x轴和y轴上的投影。已知Fi=200N。
y F1
45°
F2
60°
30° 30°
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
任务引入：平面汇交力系和平面力偶系研究物体在受到相关力
系作用下的平衡条件，为平面任意力系的讨论奠定基础。下列这 些实例都是本部分任务要涉及的问题。
简易起重机：工程中类 似问题很常见，往往需 要求解起重物的大小。 如不考虑滑轮尺寸，面 对的就是一个简单的平 面汇交力系。那么，平 面汇交力系的平衡条件 是什么样的呢？
【例】 如图所示，一圆柱直齿轮受啮合力F的作用。设F＝ 1400N，压力角 20，齿轮节圆的半径r＝60mm。试计 算啮合力F对轴心O的力矩。 解：计算力F对点O的矩，直接按力矩定义
MO (F ) F d Fr cos 1 400 N 60 103 m cos 20 78.93 N m
与假设相反（柔索、光滑支撑类约束必须判断约束力的真实方向）。
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
[例 ]
铆接薄板在孔心A、B和C处受三力作用，如图所示
F1=100N，沿铅直方向； F3=50N，沿水平方向，并通过点A； F2=50N，力的作用线也通过A，尺寸如图。求此力系的合力。 y
M O (F ) F d
+
-
① M O (F ) 是一个与矩心位 置有关的代数量。 ② M O (F )是影响转动的独立因素。 ③ 单位N m或kN m。
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
二、合力矩定理 定理：具有合力的平面力系，则该平面力系的合力对平面 内任一点的矩，等于所有各分力对同一点之矩的代数和。
M O ( FR ) M O ( Fi )
i 1
n
力对点之矩解决了单个力对物体转动效应的度量，但有时 力臂不易直接求出，采用力矩定义计算力矩较困难。此时 可应用合力矩定理求得力对点之矩。 实际上合力矩定理不但适用于平面汇交力系，也适用于有 合力的任何力系。
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
A
F1 F2
F2
改变作图的顺序，结果不变。
由力的平行四边形法则作，也可用力的三角形来作。
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
2. 任意个共点力的合成
F2 F1
F3
F4
FR
为力多边形
FR F1 F2 F3 F4
平面汇交力系的合力等于各分力的矢量和，合力的作用线通 过各力的汇交点。
熟练处理与平面汇交力系和力偶系有关的工程问题。
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
模块1 模块2
平面汇交力系合成和平衡的几何法 平面汇交力系合成和平衡的解析法
模块3
模块4
力矩 力偶的概念及其性质
平面力偶系的合成与平衡
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
解题步骤：
2、建立参考直角坐标系，列平衡方程。 3、求出待求未知量。
解题技巧及说明：
1、对几何法只作了解，熟练掌握解析法。 2、投影轴常选择与未知力垂直，最好使每个方程中只有一个未知数。 3、受力分析时力方向不能判定的，用两个正交分量来表示，两个正交分量 的指向事先假设。如果方位能判定，指向不能判定的，指向可以事先假设。 4、解析法解题时，力的方向如果是任意设的，如果求出负值说明力方向
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
合力的大小： FR 方向： 作用线：
2 2 ( X ) ( Y ) F Rx F Ry i i 2 2
t g
FR y FR x
∴ tg
1
FR y FR x
tg
1
Y X
i i
通过该平面汇交力系的汇交点
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
简易压缩机：工程上对简易压缩机带给被压对象的压力往往 需要进行求解。
成都纺专 工程力学（项目一：任务二 平面汇交力系和力偶系）
液压式夹紧机构：工程上有各种各样的夹紧机构，夹紧机构带给 物体的夹紧力有多大，必须进行计算。