数值分析方法第六章
《数值分析》第六章答案

习题61.求解初值问题y x y +=' )10(≤≤x 1)0(=y取步长2.0=h ,分别用Euler 公式与改进Euler 公式计算,并与准确解xe x y 21+-=相比较。
解: 1) 应用Euler 具体形式为 )(1i i i i y x h x y ++=+,其中i x i 2.0= 10=y 计算结果列于下表i i x i y )(i x y i i y x y -)( 1 0.2 1.200000 1.242806 0.042806 2 0.4 1.480000 1.583649 0.103649 3 0.6 1.856000 2.044238 0.188238 4 0.8 2.347200 2.651082 0.303882 5 1.0 2.976640 3.436564 0.4599242) 用改进的Euler 公式进行计算,具体形式如下: 10=y)()(1i i i D i y x h y y ++=+ )()(11)(1D i i i C i y x h y y +++++= )(21)(1)(11c i D i i y y y ++++= 4,3,2,1,0=i计算结果列表如下i i x i y )(1D i y + )(1c i y + i i y x y -)( 0 0.0 1.000000 1.200000 1.280000 0.000000 1 0.2 1.240000 1.528000 1.625600 0.002860 2 0.4 1.576800 1.972160 2.091232 0.006849 3 0.6 2.031696 2.558635 2.703303 0.012542 4 0.8 2.630669 3.316803 3.494030 0.020413 5 1.0 3.405417 0.0311473. 对初值问题1)0(=-='y y y)0(>x ,证明用梯形公式所求得的近似值为ii hh y ih y )22()(+-=≈ ),2,1,0( =i并证明当0→h 时,它收敛于准确解ix e y -=,其中ih x i =为固定点。
数值分析课后参考答案06

第六章习题解答1、设函数01(),(),,()n x x x φφφ 在[,]a b 上带权()x ρ正交,试证明{}()nj j x φ=是线性无关组。
证明:设0()nj jj l x φ==∑,两端与01()(,,,)kx k n φ= 作内积,由()jx φ的正交性可知,200(),()((),())((),())()()n n b k j j j k j k k k k k a j j x l x l x x l x x l x x dx φφφφφφρφ==⎛⎫==== ⎪⎝⎭∑∑⎰, 于是有001(,,,)k l k n == ,即{}()nj j x φ=是线性无关组。
2、试确定系数,a b 的值使22(()cos )ax b x dx π+-⎰达到最小。
解:定义02,[,]f g C π∈上的内积为20fgdx π⎰,取011(),()x x x ϕϕ==,()s x ax b =+,()cos f x x =,则法方程为0001010111(,)(,)(,)(,)(,)(,)f a f b ϕϕϕϕϕϕϕϕϕϕ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 其中()2000112,dx ππϕϕ=⨯=⎰,()2201018,xdx ππϕϕ=⨯=⎰,()3211024,x xdx ππϕϕ=⨯=⎰,()2001,cos f xdx πϕ==⎰,()21012,cos f x xdx ππϕ==-⎰,于是方程组为22312812824a b πππππ⎛⎫⎛⎫ ⎪⎛⎫ ⎪ ⎪= ⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭,解之得1158506644.,.a b ==-。
3、已知函数11()(,)f x x =∈-,试用二类Chebyshev 多项式()n U x 构造此函数的二次最佳平方逼近元。
解:法一、取20121(),(),(),x x x x x ϕϕϕ===()()()00112222235,,,,,ϕϕϕϕϕϕ===,()()()011202203,,,,ϕϕϕϕϕϕ===,同时由二类Chebyshev 多项式的性质知 ()()()11101211028,,,,,f f f x ππϕϕϕ---======⎰⎰⎰于是可得法方程为0122203220003220835c c c ππ⎛⎫⎛⎫⎪ ⎪⎛⎫ ⎪ ⎪ ⎪⎪= ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭ ⎪⎝⎭,解之得0121.0308,0,0.7363c c c ===-, 于是()f x 的二次最佳逼近元是2001122() 1.03080.7363x c c c x ϕϕϕϕ=++=-法一、二类Chebyshev 多项式2012()1,()2,()41U x U x x U x x ===-,取内积权函数()()x f x ρ==,于是11200114(,)(1)3f U fU dx x dx ρ--==-=⎰⎰,1121111(,)2(1)0f U fU dx x x dx ρ--==-=⎰⎰,112222114(,)(41)(1)15f U fU dx x x dx ρ--==--=-⎰⎰ 由()n U x 正交性及(,)2n n U U π=可得0000(,)8(,)3f U c U U π==,1111(,)0(,)f U c U U ==,2222(,)8(,)15f U c U U π==-, 于是()f x 的二次最佳逼近元为001122()x c U c U c U ϕ=++=21632515x ππ- 4、设012{(),(),()}L x L x L x 是定义于[0,)+∞上关于权函数()xx eρ-=的首项系数为1的正交多项式组,若已知01()1,()1L x L x x ==-,试求出二次多项式2()L x 。
数值分析第六章课件

a(1) 1n
x1
b(1) 1
a(1) 21
a(1) 22
a(1) 2n
x2
b(1) 2
.
a(1) m1
a(1) m2
a(1) mn
xn
b(1) m
将(2.1)记为A(1)x=b(1),其中
a(1) 11
a(1) 12
a(1) 1n
a11
a12
a1n
A(1)
a(1) 21
5.2 高斯消去法
本节介绍高斯消去法(逐次消去法)及消去法和 矩阵三角分解之间的关系. 虽然高斯消去法是一种 古老的求解线性方程组的方法(早在公元前250年 我国就掌握了解方程组的消去法),但由它改进、 变形得到的选主元素消去法、三角分解法仍然是目 前计算机上常用的有效方法.我们在中学学过消去 法,高斯消去法就是它的标准化的、适合在计算机 上自动计算的一种方法.
有的问题的数学模型中虽不直接表现为含线性方 程组,但它的数值解法中将问题“离散化”或“线性 化”为线性方程组.因此线性方程组的求解是数值分 析课程中最基本的内容之一.
关于线性方程组的解法一般有两大类:
1. 直接法 经过有限次的算术运算,可以求得方程组的精确解( 假定计算过程没有舍入误差).如线性代数课程中提到 的克莱姆算法就是一种直接法.但该法对高阶方程组 计算量太大,不是一种实用的算法.
下面讨论求解一般线性方程组的高斯消去法.由
a11 x1 a12 x2 a1n xn b1 a21 x1 a22 x2 a2n xn b2
am1 x1 am2 x2 amn xn bm
a(1) 11
a(1) 21
x1 x1
a(1) 12
x2
数值分析第六章_ppt课件

12 j i n n
% | D l = l ( e ) a | = e , j = 1 , 2 , L , n j| j
1 n
E 设 10,n 20 , 则 101 .若 在 A 的上三角位置,则特征值并无扰动.
湘潭大学数学与计算科学学院 上一页 下一页 8
定理3 设 A 为 n阶实对称矩阵,其特征值
为 1 2 n,则
n x 0
1 x 0
m i n R ( x ) m i n ( A x , x )
m a x R ( x ) m a x ( A x , , x )
通过求它的根来求矩阵的特征值,实际计算中并不采用。
数值方法 基本思想: 直接从矩阵A 或者对A 做一系列的 相似变换后得到的具有更简单形式的矩阵入手,
设计迭代过程;最后求得A 的近似特征值和相应
的特征向量.
湘潭大学数学与计算科学学院
上一页
下一页
4
特征值的估计及扰动问题
1、特征值的估计
D ( A ) { z c :| z a | | a | }, i 1 , 2 , ,n i ii ij i
为矩阵 A关于向量 x 的Rayleigh(雷利)商.
A 为 n 阶实对称矩阵,则其特征值皆为实数,
记做
1 2
, n
并且存在规范正交特征向量系满足:
Au u ,i 1 , 2 , , n , ( u , u ) ,i , j 1 , 2 , , n i i i i j ij
3 4
湘潭大学数学与计算科学学院
上一页
下一页
7
实对称矩阵的极大-极小定理:
数值分析Newton法

迭代法。
© 2009, Henan Polytechnic University §3 Newton法
2 2
第六章 方程求根
6.3.1 牛顿迭代法 基本思想:将非线性方程f(x)=0 线性化
f ( ) 2 f ( x ) f ( x0 ) f ( x0 )( x x0 ) ( x x ) 0 Newton 2 迭代公式 f ( x ) 0 0 f ( x ) f ( x0 ) f ( x0 )( x x0 ) x x0 f ( x0 ) f ( x0 ) x1 x0 作为第一次近似值 f ( x0 ) f ( xk ) 重复上述过程 xk 1 xk f ( xk )
x* x
x 2 x 1 x0
牛顿法也称为切线法
© 2009, Henan Polytechnic University §3 Newton法
f ( x1 ) x2 x1 f ( x1 )
4 4
第六章 方程求根
6.3.3 牛顿法的收敛性与收敛速度 (局部收敛性定理)设 f (x)C2[a, b],若 x* 为 f (x) 在[a, b]上的根,且 f (x*) 0,则存在 x* 的 邻域 U ( x ) 使得任取初始值 x0 U ( x ), Newton 法产生的序列{ xk } 收敛到 x*,且满足
2
则由Newton迭代公式
xn c 1 c x n 1 x n ( xn ) 2 xn 2 xn
选取初始值 x0 c即可
© 2009, Henan Polytechnic University §3 Newton法
x0 c可以吗?
1212
第六章 方程求根
《数值分析》第六章
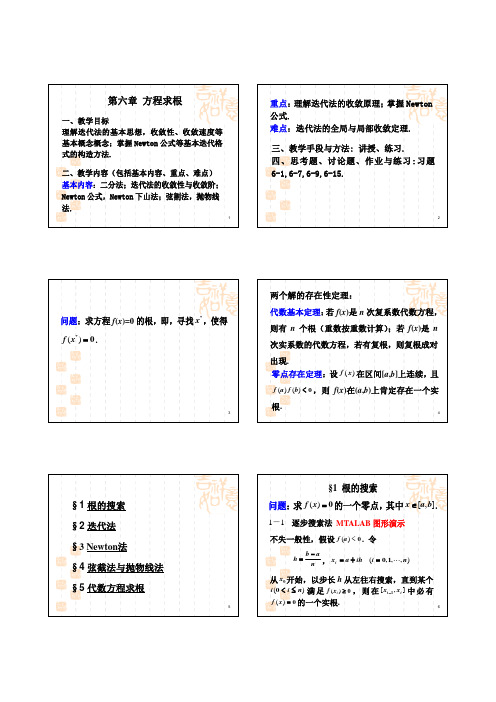
有局部收敛性.
证 明 . 由 连 续 函 数 的 性 质 , 存 在 x* 的 邻 域
Δ : x − x* ≤ δ
,使 ∀x ∈ Δ 成立 ϕ '( x) ≤ L < 1 ,此外,
对于任意 x ∈ Δ ,总有 ϕ ( x) ∈ R ,这是因为
15 16
迭代法不一定收敛. 对同一个问题,不同的迭代法, 可能有的收敛,有的不收敛. 如下例.
Th 1 假定函数 ϕ (x) 满足: 1 对任意 x ∈ [a, b] 有, ϕ ( x) ∈ [a, b] (即,映像入内)
∀x ∈ [a, b] , ϕ '( x ) ≤ L < 1 2 存在非负数 L < 1 使得, (压 缩映射)
k → ∞ 时成立下列渐近关系式
= xk − x * 当
求根 x * 的邻近连续,并且满足:
ϕ '( x* ) = ϕ ''( x* ) = L = ϕ ( p −1) ( x * ) = 0 , ϕ ( p ) ( x * ) ≠ 0
ek +1 → C ( C ≠ 0) e kp
则称该迭代过程是 p 阶收敛的. 特别地, p = 1 时称为线性收敛,
*
* *
* * 假设 x , y ∈ [a, b] 是任意的两个根,因为
xk = x * . 故 lim k →∞
x* − y* = ϕ ( x* ) − ϕ ( y* ) = ϕ '(ξ )( x* − y* ) ≤ L x* − y*
* * 故 x = y , 即, x = ϕ ( x ) 在[a,b]上有唯一的根.
数值分析(李庆扬)第六章资料
(n1) B (n) g
若收敛
x x { (k)} * ,则
x* Bx* g
n 0,1,2,
即
(I B)x* g D1Ax* D1b
Ax* b
故如果序列收敛, 则收敛到解.B 称迭代矩阵.
例:用Jacobi迭代法求解 1x01x1 10xx2222xx337823 x1 x2 5x3 42
k
k
即x是方程组Ax b的解。
引入误差向量
(k 1) x(k 1) x
所以 lim x(k) x 等价于 lim (k) 0
k
k
由
x(k 1) Mx (k ) g
x Mx g
则可得
(k 1) M (k )
(k ) M (k 1) M k (0)
问题是在什么条件下
满足
x(k1) Bx(k) g (k 0,1, 2, )
此过程所给出的迭代法称为Jacobi迭代法,又称简单
迭代法。
Jacobid迭代的矩阵形式
0
B
b21
b12
0
b1n 1
b2n
0
0 1
0 1
0
b21
b 12 1
b1n b 2n
b b
n1
n2
0
0
0
1
, n).
0 b12 b13 若记 B b21 0 b23
bn1 bn2 bn3
b1n1 b1n
g1
b2n1
b2
n
g
g
2
bnn1 0
gn
则方程组可简记为 x Bx g
选初值向量x(0)代入 x(1) , x(1) Bx(0) g,代入x(1)
数值分析第六章_数值插值方法
M n1 (n 1)!
n1 ( x)
说明:
n=1时,
R1 ( x)
1 2
f
( )2 (x)
1 2
f
( )(x
x0 )(x
x1)
n=2时,
( [x0 , x1])
R2 (x)
1 6
f
( )(x
x0 )(x
x1)(x
x2 )
( [x0 , x2 ])
,
x1,
Hale Waihona Puke xn)1
x1
x12
x1n
n
( xi
ni j1
xj)
1 xn xn2 xnn
因 xi x j (i j) 故上式不为0。
据Cramer法则,方程组解存在且唯一。 故Pn (x)存在且唯一。虽然直接求解上述方程组 可求得插值多项式,但繁琐复杂,一般不用。
得关于a0,a1,…,an的n+1阶线性方程组
a0 a1x0 a0 a1x1
an x0n an x1n
y0 y1
a0 a1xn an xnn yn
其系数行列式是Vandermonde行列式
1 x0 x02 x0n
V
( x0
jk jk
(j,k=0,1)
称l0 (x)及l1 (x)为线性插值基函数。
2. 抛物插值:n=2情形
假定插值节点为x0, x1, x2 ,求二次插值多项式 L2 (x),使 L2(xj)=yj (j=0,1,2) y= L2 (x)的几何意义就是过 (x0, y0),(x1, y1) , (x2, y2)三点的抛物线。 采用基函数方法,设
数值分析第六章插值法
P( x) an x an1 x
n
n1
a1 x a0
是函数 y f ( x) 在区间[a, b]上的n+1个互异的节点 x i (i=0,1,2,…,n )上的插值多项式,则求插值多项式P(x) 的问题就归结为求它的系数 a i(i=0,1,2,…,n )。
,现要求用线性函数 p( x) ax b 近似地代替f(x)。选 择参数a和b, 使 p( xi ) f ( xi )(i 0,1)。称这样的线性函数 P(x)为f(x)的线性插值函数 。
线性插值的几何意义:用
通过点
A( x0 , f ( x0 ))
和 B( x1 , f ( x1 ))
由插值条件: p( xi ) f ( xi ) (i=0,1,2,…,n),可得
a n x0 n a n 1 x0 n 1 a1 x0 a 0 f ( x0 ) n n 1 a n x1 a n 1 x1 a1 x1 a 0 f ( x1 ) a x n a x n 1 a x a f ( x ) n 1 n 1 n 0 n n n
拉格朗日插值多项式
两个插值点可求出一次插值多项式,而三 个插值点可求出二次插值多项式。插值点增加到n+1 个时,也就是通过n+1个不同的已知点 ( xi , yi )(i 0,1,, n) ,来构造一个次数为n的代数多项式P(x)。与推导线性插 值的基函数类似,先构造一个特殊n次多项式 li ( x) 的插 值问题,使其在各节点 x i 上满足
n
例6.2 已知y=f(x)的函数表 X 1 y 1
3 2
求线性插值多项式, 并计算x=1.5 的值 解: 由线性插值多项式公式得 x x0 x x1 p( x) y0 y1 x 0 x1 x1 x 0
东南大学_数值分析_第六章_常微分方程数值解法
第六章 常微分方程数值解法——RK 4法、AB 4法******(学号) *****(姓名)上机题目要求见教材P307,23题。
一、算法原理题目要求采用RK 4法和AB 4法求解最简单的常微分方程初值问题(,),()y f x y a x by a η'=≤≤⎧⎨=⎩ (1)为求解式(1),采用离散化方法,就是寻求解)(x y 在区间],[b a 上的一系列点<<<<<n x x x x 321上的近似值 ,,,,21n y y y 。
记1(1,2,)i i i h x x i -=-=表示相邻两个节点的间距,称为步长。
求微分方程数值解的主要问题:(1) 如何将微分方程(,)y f x y '=离散化,并建立求其数值解的递推公式; (2) 递推公式的局部截断误差、数值数n y 与精确解)(n x y 的误差估计; (3) 递推公式的稳定性与收敛性. a) Runge-Kutta 方法基本思想:通过在1[,]i i x x +多预报几个点求斜率,并将其加权平均作为k *的近似值,以此构造更高精度的计算公式。
如果每步计算四次函数 的值,完全类似的,可以导出局部截断误差为)(5h O 的四阶Runge-Kutta 公式(RK 4):1123412132431(22),6(,),(,),221(,),22(,).n n n n n n n n n n y y k k k k k f x y h h k f x y k h k f x h y k k f x h y hk +⎧=++++⎪⎪=⎪⎪⎪=++⎨⎪⎪=++⎪⎪=++⎪⎩ (2)b) Adams 显式公式Runge-Kutta 方法是单步法,计算1+n y 时,只用到n y , 而已知信息1-n y 、2-n y 等没有被直接利用。
可以设想如果充分利用已知信息1-n y ,2-n y ,…来计算1+n y ,那么不但有可能提高精度,而且大大减少了计算量,这就是构造所谓线性多步法的基本思想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中心差商
f ( x0 h) f ( x0 h) f ' ( x0 ) 2h
由Taylor展开
h2 h3 f ( x0 h) f ( x0 ) hf '( x0 ) f ''( x0 ) f '''(1 ), x0 1 x0 h 2! 3! h2 h3 f ( x0 h) f ( x0 ) hf '( x0 ) f ''( x0 ) f '''( 2 ), x0 h 2 x0 2! 3!
[ x0 , x2 ]
16
类似地,可以得到n=2的带余项的二阶三点公式
1 h 2 (4) f ( x0 ) h 2 [ f ( x0 ) 2 f ( x1 ) f (x2 )] [hf (1 ) 6 f ( 2 )] 1 h 2 (4) f ( ) f ( x1 ) 2 [ f ( x0 ) 2 f ( x1 ) f (x2 )] h 12 1 h 2 (4) f ( 2 )] f ( x2 ) 2 [ f ( x0 ) 2 f ( x1 ) f ( x2 )] [hf (1 ) h 6
26
数值积分雏形 数格子
例:计算 R1 R R2 的 颗粒数量(分数)
分布密度,f
F
R2 R1
f ( R)dR
F
R1
R2
颗粒尺寸,R
原始方法:曲线下面面积所占方格数目
27
定积分的计算
当 f (x) 是闭区间上的连续函数时,如何 计算下列定积分?
I ( f ) f ( x)dx
23
例 用不同的方法求函数f(x)的数值导数,并在同一个坐标系中 做出f'(x)的图像。 程序如下: f=inline('sqrt(x.^3+2*x.^2-x+12)+(x+5).^(1/6)+5*x+2'); g=inline('(3*x.^2+4*x-1)./sqrt(x.^3+2*x.^2x+12)/2+1/6./(x+5).^(5/6)+5'); x=-3:0.01:3; p=polyfit(x,f(x),5); %用5次多项式p拟合f(x) dp=polyder(p); %对拟合多项式p求导数dp dpx=polyval(dp,x); %求dp在假设点的函数值 dx=diff(f([x,3.01]))/0.01; %直接对f(x)求数值导数 gx=g(x); %求函数f的导函数g在假设点的导数 plot(x,dpx,x,dx,'.',x,gx,'-'); %作图
7
向后差商
f ( x0 ) f ( x0 h) f ' ( x0 ) h
由Taylor展开
h2 f ( x0 h) f ( x0 ) hf ' ( x0 ) f ' ' ( ), x0 x0 h 2!
误差
f ( x0 ) f ( x0 h) h R( x) f ' ( x0 ) f ' ' ( ) O(h) h 2!
试计算美国20世纪的年增长率
若记t时刻的人口为 x(t ),则人口的增长率为
dx dt r (t ) x(t )
dx 如何求 dt
2
在实际问题中,往往会遇到某函数f(x)是用表格 表示的,用通常的导数定义无法求导,因此要寻求其他 方法近似求导。常用的数值微分方法有: 一. 运用差商求数值微分 二. 运用插值函数求数值微分 三. 运用样条插值函数求数值微分
10
插值型求导公式
主要方法:插值多项式,讨论函数f(x)导数的近似值求法。
定义:若函数f(x)在节点 xi (i 1,2,, n 1) 处的函数 值已知,作f(x)的n次插值多项式 Pn ( x) ,并用 Pn ( x) 近似代 替f(x),即
f ( x) Pn ( x)
由于Pn ( x) 是多项式,容易求其导数,故对应于f(x) 的每一个插值多项式 Pn ( x) ,建立一个数值微分公式
f ( x) Pn( x)
这样建立起来的数值微分公式,称为插值型数值微分公式。 11
带有余项的数值微分公式
即使 Pn ( x) 与f(x)的函数值处处相差甚微,但两个 函数的导数在某些点上的值仍可能有很大的差异 所以要对误差进行分析
n1 ( x) df (n1) ( ) f ( n1) ( ) 1 ( x) f ( x) Pn( x) n (n 1)! (n 1)! dx
10
0
1
2
annealing time t, 1000 s
5
10
20
50
100
13
如果只计算结点处的导数值
f ( xi ) Pn( xi )
数值微分公式的余项为
f ( ) 1 ( xi ) f ( xi ) Pn( xi ) n (n 1)!
( n 1)
14
带余项的两点数值微分公式
22
例 设x由[0,2π]间均匀分布的10个点组成,求sinx的 1~3阶差分。
命令如下: X=linspace(0,2*pi,10); Y=sin(X); DY=diff(Y); %计算Y的一阶差分 D2Y=diff(Y,2); %计算Y的二阶差分,也可用命令diff(DY) 计算 D3Y=diff(Y,3); %计算Y的三阶差分,也可用diff(D2Y)或 diff(DY,2)
xi 1 0.02k (k 0,1,,100)
处的近似值。
20
21
MATLAB中的数值微分
数值微分的实现
在MATLAB中,没有直接提供求数值导数的函数,只有
计算向前差分的函数diff,其调用格式为:
DX=diff(X):计算向量X的向前差分, DX(i)=X(i+1)-X(i),i=1,2,…,n-1。 DX=diff(X,n):计算X的n阶向前差分。 diff(X,2)=diff(diff(X))。
Chapter 5 数值微分与数值积分
§1 数值微分
先看一个实例: 已知20世纪美国人口的统计数据为(单位:百万)
年份 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 人口 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 251.4
a b
积分中值定理
I ( f ) f ( x)dx (b a) f ( )
a
28
b
上述公式的几何意义
f ( ) 的矩形面积恰好等于 所求曲边梯形的面积 I ( f ) 。 y
当h充分小时 , 可用差商来逼近导数
5
差商公式
f ( a h) f ( a ) 向前差商近似计算: f (a ) h
f ( a ) f ( a h) 向后差商近似计算: f (a ) h
f ( a h) f ( a h) 中心差商近似计算: f (a) 2h
误差
f ( x0 h) f ( x0 h) R( x) f ' ( x0 ) 2h h2 h2 [ f ' ' ' (1 ) f ' ' ' ( 2 )] f ' ' ' ( ) O(h 2 ) 12 6
9
分析
1、步长过大则截断误差显著,但如果步长太小又会导 致舍入误差的增长。 2、在实际计算时,在保证截断误差满足精度要求的前 提下选取尽可能大的步长 3、事先给出一个合适的步长往往是很困难的。通常在 在变步长的过程中实现步长的自动选择。
其中 在x0 , x1 ,, xn 之间,上式第一项是 f ( xi ) 的近 似值。
12
300
Seebeck Coefficient a, ) A B exp( 30
250 200
误差放大 !!!
150 20
da dt
100 50 0
da dt
注意
S "( xi ) M i
19
1 例: 利用函数 f ( x) 2 在节点 1 25 x
S’(-1)=0.0740, S’(1)=-0.0740
xi 1 0.1i (i 0,1, ,20) 上的函数值和边界条件
构造三次样条插值函数S(x),并用它来计算f(x)和 f’(x)在下列点
(n=1)
x x0 x x1 p1 ( x) f ( x0 ) f ( x1 ) x0 x1 x1 x0
f ( x1 ) f ( x0 ) f ( x0 ) h f ( x1 ) f ( x0 ) f ( x1 ) h f ( x1 ) f ( x0 ) h f ( x0 ) f ( ) h 2 , [ x0 , x1 ] f ( x1 ) f ( x0 ) h f ( x1 ) f ( ) h 2
15
类似地,可以得到n=2的带余项的三点公式
1 h2 f ( x0 ) 2h [3 f ( x0 ) 4 f ( x1 ) f (x2 )] 3 f ( ) 1 h2 f ( x1 ) [ f ( x0 ) f ( x2 )] f ( ) 2h 6 1 h2 f ( x2 ) [ f ( x0 ) 4 f ( x1 ) 3 f ( x2 )] f ( ) 2h 3
四. 运用数值积分求数值微分
