导数与微分的笔记
专转本微分知识点总结

专转本微分知识点总结微分学具有广泛的应用,包括物理学、工程学、经济学等领域。
微分学可以帮助研究者分析和解决各种实际问题,例如研究函数的最大值和最小值、曲线的形状、速度和加速度等。
本文将从导数、微分、微分方程等方面总结微分学的知识点,帮助读者更加深入地了解微分学的概念和应用。
一、导数导数是微分学中最基本的概念之一,它描述了函数在某一点的变化率。
设函数y=f(x),如果这个函数在点x0处的导数存在,则称这个导数是函数f(x)在点x0处的导数,记作f'(x0)。
导数的几何意义是切线的斜率,即函数在某一点的局部变化率。
在代数上,导数可以通过极限的概念来定义。
如果函数f(x)在点x0处的导数存在,则它的导数可以表示为:f'(x0) = lim(h→0) (f(x0+h)-f(x0))/h导数的计算方法包括基本导数法则、和差积商法则、复合函数的导数等。
导数的应用包括判别函数的增减性、求曲线的凹凸性、求函数的极值点等。
例如,判别函数f(x)=x^2在点x0=1处的增减性,可以通过求导数f’(x)=2x然后分析函数的正负性来判别。
导数还可以用来研究曲线的切线和法线,通过切线和法线求斜率和法线方程,可以更加深入地研究函数曲线的性质。
二、微分微分是导数的一种应用,它是函数在某一点的局部线性近似。
设函数y=f(x),如果这个函数在点x0处的导数存在,则在点x0处的微分可以表示为:dy = f'(x0)dx微分的几何意义是切线的增量,即函数在某一点的局部线性近似。
在代数上,微分可以通过导数来计算,例如如果函数f(x)的导数是f’(x),则它的微分可以表示为:dy = f’(x0)(x-x0)微分的应用包括利用微分近似计算函数的增量,例如通过微分近似计算曲线上某一点的函数值,可以帮助研究者更加灵活地分析函数的性质。
另外,微分还可以用来求函数的极值点,通过求导后令导数等于零的方法求出函数的极值点,进而帮助研究者研究函数的最大值和最小值。
第2章导数与微分总结
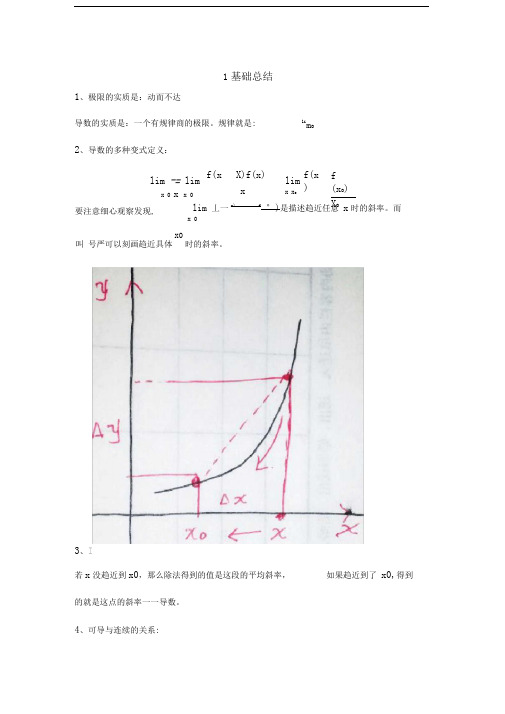
1、极限的实质是:动而不达导数的实质是:一个有规律商的极限。
规律就是:2、导数的多种变式定义:lim 丄一x)f°)是描述趋近任意 x 时的斜率。
而x 03、I若x 没趋近到x0,那么除法得到的值是这段的平均斜率, 如果趋近到了 x0,得到的就是这点的斜率一一导数。
4、可导与连续的关系:1基础总结lim -= limx 0 x x 0 f(x X)f(x)xlim x x o f(x )f (x o )X o叫 号严可以刻画趋近具体x0时的斜率。
lim o要注意细心观察发现,导数的实质是定义在某点的左右极限。
既然定义在了某点上,该点自然存在,而 且还得等于左右极限。
因此,可导一定是连续的。
反之,如果连续,不一定可导。
不多说。
同理,如果不连续,肯定某点要么无定义,要么定义点跳跃跑了,肯定 极限有可能存在,但是导数绝不会存在。
同理要注意左右导数的问题。
如果存在左或者右导数,那么在左侧该点一定是存 在的。
如:f(x) x,x 0这个函数,在0点就不存在左导数,只存在右导数。
为什么嫩?看定义:万不要以为导数是一种简单的极限,极限是可以在某点无定义的,而导数却是该 点必须存在! 由此引发了一些容易误判的血案: 例如:A 旦主^謎IC m F 左电鼓 pg 总生戟乞f ( x) f (x)-中的f(x))至u 底是神马。
比如求上图limf(x x) f(x)x 0xlimf(X X)f(0)。
x 0定义里面需要用到f(0)啊!因此,千中 iimf (x)论) x 1x x 0,这个f(x0)千万要等于2/3,而不是1 !定义解决时候一定要注意问。
X X o由此也可以知道,f (x)2x 3, x 1这个函数是不存在导数的,也不存在左导数,3只存在右导数。
5、反函数的导数与原函数的关系:注意,求反函数时候不要换元。
因为换了元虽然对自身来讲函数形式不变, 与原函数融合运算时候就算是换了一个不是自己反函数的一个函数进行运算 果显然是错误的。
全微分知识点笔记总结

全微分知识点笔记总结一、导数与全微分基本概念1. 导数的概念导数是微积分学中非常重要的概念,它描述了一个函数在某一点的变化率。
如果函数y=f(x)在某一点x0处可导,那么它的导数f'(x0)定义为f'(x0)=lim(x→x0) (f(x)-f(x0))/(x-x0)导数可以理解为函数在某一点的斜率,也可以理解为函数在某一点的瞬时变化率。
2. 全微分的概念全微分也是微积分学中的一个重要概念,它描述了函数在某一点的微小变化。
如果函数y=f(x)在某一点x0处可导,那么它的全微分dy可以定义为dy = f'(x0)dx全微分可以理解为函数在某一点微小变化的量,它是函数的局部变化率与自变量的微小变化量的乘积。
二、全微分的计算1. 一元函数的全微分对于一元函数y=f(x),如果它在某一点x0处可导,那么它的全微分可以通过导数来计算,全微分dy=f'(x0)dx。
这个公式可以准确地描述函数在x0处微小变化的量。
2. 多元函数的全微分对于多元函数z=f(x,y),如果它在某一点(x0,y0)处可导,那么它的全微分可以通过偏导数来计算。
全微分dz在点(x0,y0)处的计算公式为dz = ∂f/∂x|_(x0,y0)dx + ∂f/∂y|_(x0,y0)dy这个公式可以描述多元函数在某一点微小变化的量,其中∂f/∂x和∂f/∂y分别是函数在各自自变量上的偏导数。
三、全微分的物理意义1. 全微分的物理意义全微分可以用来描述函数在某一点微小增量的变化。
在物理学中,全微分可以用来描述物体在某一点的微小位移、速度、加速度等物理量的变化。
这就是全微分的物理意义。
2. 全微分与微分量的关系在物理学中,微分量描述了一个物体在某一点的微小变化量,而全微分描述了函数在某一点的微小变化量。
它们之间存在着密切的关系,可以相互换算,因此在物理学中也可以用全微分来描述物体的微小变化。
四、全微分的应用1. 全微分在最优化问题中的应用在最优化问题中,全微分可以用来描述函数的微小变化量。
同济大学数学系《高等数学》(第7版)(上册)教材包含 笔记 课后习题 考研真题 导数与微分(圣才出品

区间 Ix={x|x=f(y),y∈Iy}内也可导,且
f 1 x
f
1
y
或
dy dx
1 dx
dy
3.复合函数的求导法则
如果 u=g(x)在点 x 可导,而 y=f(u)在点 u=g(x)可导,则复合函数 y=f[g(x)]
在点 x 可导,且其导数为
dy f ug x或 dy dy du
dx
dx du dx
u nv
nu n1v
nn
1
u
n2 v
...
n
n
1... n
k
1
u
nk
v
k
... uv
n
2!
k!
或
uv n n Cnkunkvk k 0
四、隐函数及由参数方程所确定的函数的导数
1.隐函数的导数
(1)隐函数 F(x,y)=0 导数的求法
把函数方程两边分别对 x 求导,然后化简得到 dy/dx 的结果。
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 2 章 导数与微分
2.1 复习笔记
一、导数概念
1.导数
(1)导数与导函数
①导数的定义
f
x0
lim
x0
y x
lim
x0
f
x0
x
x
f
x0
(2)单侧导数
①左导数
f ( x0
)
lim
h0
f
x0 h
h
f
x0
②右导数
(1)参数方程的一阶导数公式
dy dx
dy dt dt dx
高阶导数与高阶微分学习笔记

则有(sin x)(k1) (sin(x k )) cos(x k ) sin(x k 1 )
2
2
2
依数学归纳法知结论成立
类似有: (cosx)(n) cos(x n ),n 1,2,
2
例4 求y ln(1 x)的n阶导数
解: (ln(x 1)) 1 (1 x)1, 1 x
x3ex 90x2ex 2610xex 24360ex
教材上还有例6,是通过找递推关系式来求解。
二 高阶微分
1 概念 若y f (x)的微分函数 dy关于x可微,则称y f (x)关于x二阶可微,
其微分称为二阶微分,记作: d 2 y, d 2 f (x), 类似地有d n y, d n f (x) 若记(dx)n dxn,则有:
y(30) (x3ex )(30)
x3 (ex )(30) C310 (x3 )(ex )(29) C320 (x3 )(ex )(28) C330 (x3 )(ex )(27)
x3(1)30 ex 30(3x2 )(1)29 ex 30 29 (6x)(1)28 ex 21
30 29 28 6 (1)27 ex 3 21
2
2
sin x
分析:正弦函数的导数是4阶一个轮回,而其本身就是一个周期函数,函 数值一个周期重复一次,因此可考虑利用其周期来处理。
猜想其n阶导数为:
(sin x)(n) sin(x n )
2
下面用数学归纳法进行证明:
(1)n 1时结论显然成立
(2)假设n k时结论成立,即有(sin x)(k) sin(x k )
高阶导数与高阶微分学习笔记
一、高阶导数 二、高阶微分
一、高阶导数
1 二阶导数的定义
大一上册高数知识点笔记

大一上册高数知识点笔记一、微分学1. 函数与极限在微分学中,一个重要的概念是函数和极限。
一个函数可以看作是一种映射关系,将一个自变量的取值映射到一个因变量的取值。
而极限则描述了一个函数在某一点附近的变化趋势。
2. 导数与微分导数描述了函数在某一点处的变化率,可以看作是函数曲线在该点处的切线斜率。
微分则是导数的微小变化,用于描述函数在某一点处的局部线性逼近。
3. 高阶导数与泰勒展开高阶导数描述了函数变化的更高阶特性,可以通过多次求导得到。
而泰勒展开则是一种将函数在某一点附近展开为幂级数的方法,用于近似计算函数的值。
二、积分学1. 定积分与不定积分积分描述了函数曲线下某一区间的面积,可以看作是导数的逆运算。
定积分是计算函数在一定区间上的积分值,而不定积分则是求出一个与原函数的导数关系的函数。
2. 牛顿—莱布尼兹公式牛顿—莱布尼兹公式是计算定积分的重要方法,它将函数在两个端点处的值与积分结果联系起来。
3. 曲线长度与旋转体的体积利用定积分,我们可以计算曲线的长度以及旋转体的体积。
曲线长度的计算是将曲线分割成无数小段,在每一小段上计算微小长度,然后将这些微小长度相加。
旋转体的体积计算则是将曲线围绕某个轴旋转,然后计算旋转体的体积。
三、微分方程1. 一阶微分方程一阶微分方程是描述未知函数的导数与自变量之间关系的方程。
常见的一阶微分方程有可分离变量方程、一阶线性方程和可降阶方程等。
2. 高阶微分方程高阶微分方程是描述未知函数的高阶导数与自变量之间关系的方程。
常见的高阶微分方程有常系数线性齐次方程、常系数线性非齐次方程和欧拉方程等。
3. 解微分方程的方法解微分方程的方法有常数变易法、待定系数法、特征方程法和变量可分离法等。
不同类型的微分方程需要采用不同的解法。
四、多元函数微积分1. 多元函数的极限与连续性多元函数的极限与单变量函数的极限类似,描述了函数在某一点附近的变化趋势。
多元函数的连续性则表明函数在某一点处存在极限,并且其极限与函数值相等。
高等数学笔记(含数一内容)

隐函数求导
参数方程确定的函数求导
分段函数求导
先讨论关键点是否连续,确定连续后再判断函数各个部分是否可导。
求函数高阶导
一般使用数学归纳法解决。
微分
可微
定义:设y=f(x) (x∈D),x₀∈D。若∆y=A∆x+৹(∆x),则称f(x)在x=x₀处可微。
性质
可微一定可导,可导一定可微(充要条件)
若∆y=A∆x+৹(∆x),则A=f'(x₀),即dy∣₍x=x₀₎=f'(x₀)dx
二阶线性微分方程解的结构 齐+齐=齐 齐 + 非齐 = 非齐 非齐 + 非齐 = 齐 (拆解性质)对于方程**,若f(x)=f1(x)+f2(x)(即可拆成两部分),则分别构造两个二阶非齐次线性微分方程,且φ1(x),φ2(x)分别为它们的特解,则 有原方程特解为:
y=φ1(x)+φ2(x) (系数和的特点)设φ1(x),φ2(x),...,φn(x),为方程**的解,则通解的组合形式为y=k1φ1(x)+k2φ2(x)+...+knφn(x) 若y为方程*的通解,则k1+k2+...+kn=0(系数和为0) 若y为方程**的通解,则k1+k2+...+kn=1(系数和为1) (二阶常系数线性微分方程通解形式推导定理)
函数f(x)∈ c【a,b】的性质(函数在区间内恒连续)
性质1:∃最大值 M 和最小值 m (最值); 性质2:∃M₀>0,使得∣f(x)∣≤M₀(有界);
性质3: ∀η ∈【m,M】,∃ξ∈【a,b】,使得f(ξ)=η(介值定理);
性质4:若 f(a)*f(b)<0,则∃c∈(a,b),使得f(c)=0(零点定理)。 连续函数的运算
微分知识点总结

微分知识点总结一、微分的基本概念1. 导数的定义在微分的讨论中,导数是一个非常核心的概念。
在数学中,导数表示了函数在某一点的变化率,也可以理解成函数曲线在该点的切线斜率。
设函数y=f(x),在点x0处的导数定义为:\[ f'(x_0)=lim_{\Delta x\to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \]2. 微分的概念微分是导数的一个相关概念,它主要研究了函数在某一点的局部线性变化。
设函数y=f(x),在点x0处的微分dy定义为:\[ dy=f'(x_0)dx \]3. 微分形式微分dy=f'(x)dx这个等式称为微分形式,它表示了函数在某一点的微分。
在微分形式中,导数f'(x)表示了函数在该点的变化率,dx表示自变量x的变化量,dy表示因变量y的对应变化量。
4. 微分的几何意义从几何学的角度来看,微分表示了函数曲线在某一点处的切线斜率。
也就是说,微分可以帮助我们理解函数在某一点的局部变化规律,对于研究函数的极值、凹凸性、临界点等性质非常重要。
二、微分的性质1. 微分的线性性质设函数y=f(x),g(x)分别在点x0处可导,常数a、b,则:\[ d(af(x)+bg(x))=af'(x)dx+bf'(x)dx \]这个性质表示了微分在加法、乘法和数乘方面的线性性质,这对于微分的运算和计算是非常重要的。
2. 链式法则如果函数y=f(u),u=g(x)都分别在对应的点可导,那么复合函数y=f(g(x))在x0的微分为:\[ dy=f'(u)g'(x)dx \]链式法则是微分中的一个重要性质,它描述了复合函数的微分计算规则。
对于求解复合函数的微分非常有用。
3. 高阶微分高阶微分指的是对微分的多次计算,设函数y=f(x),它的一阶微分为dy=f'(x)dx,二阶微分为d2y=f''(x)dx2,以此类推。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导数与微分的笔记
导数和微分是微积分中非常重要的概念,以下是关于导数和微分的笔记:
一、导数
1. 定义:导数是函数在某一点处的变化率,即函数在该点处切线的斜率。
2. 求导公式:对于常见的函数,如幂函数、指数函数、对数函数、三角函数等,有相应的求导公式。
3. 导数的几何意义:导数表示函数在某一点处的切线斜率。
4. 导数的物理意义:导数可以用来描述物理量的变化率,如速度、加速度等。
二、微分
1. 定义:微分是函数在某一点处的微小变化量,可以用导数来表示。
2. 微分公式:对于常见的函数,如幂函数、指数函数、对数函数、三角函数等,有相应的微分公式。
3. 微分的几何意义:微分表示函数在某一点处切线的纵坐标的增量。
4. 微分的应用:微分可以用来近似计算函数在某一点处的取值,也可以用来求函数的极值和拐点等。
三、导数和微分的关系
导数和微分是密切相关的概念,导数是微分的商,微分是导数的线性主部。
在求导的过程中,我们实际上是在求函数的微分,并将其除以自变量的微分,得到导数。
