电工技术的课件第二章
合集下载
电工电子技术基础第二章直流电路分析 ppt课件

结点数 N=4 支路数 B=6
(取其中三个方程)
PPT课件
6
b
列电压方程
I2
abda :
I1
I6
E4 I6R6 I4 R4 I1R1
a I3 I4
R6
c
I5 bcdb :
0 I2R2 I5R5 I6R6
+E3
d R3
adca : I4R4 I5R5 E3 E4 I3R3
对每个结点有
I 0
3. 列写B-(N-1)个KVL电压
方程 对每个回路有
E U
4. 解联立方程组
PPT课件
5
I1 a
b I2
I6
R6
I3 I4
d
+E3
R3
列电流方程
结点a: I3 I4 I1
c 结点b: I1 I6 I2
I5
结点c: I2 I5 I3
结点d: I4 I6 I5
基本思路
对于包含B条支路N个节点的电路,若假 设任一节点作为参考节点,则其余N-1个节点 对于参考节点的电压称为节点电压。节点电压 是一组独立完备的电压变量。以节点电压作为 未知变量并按一定规则列写电路方程的方法称 为节点电压法。一旦解得各节点电压,根据 KVL可解出电路中所有的支路电压,再由电路 各元件的VCR关系可进一步求得各支路电流。
3、会用叠加定理、戴维宁定理求解复杂电路中的电压、电流、功率等。
PPT课件
1
对于简单电路,通过串、并联关系即可 求解。如:
R
R
R
+ E 2R 2R 2R 2R
-
PPT课件
+
电工学电工技术第二章ppt课件

U R1 R2 (3)等效电阻的倒数等于各电阻倒数之和;
11 1
–
R R1 R2
(4)并联电阻上电流的分配与电阻成反比。
I
两电阻并联时的分流公式:
+ U –
R
I1
R2 R1 R2
I
应用:
I2
R1 R1 R2
I
分流、调节电流等。(最广泛)
编辑版pppt
章目录 上一页 下一页 返回 退出
例1:图示为变阻器调节负载电阻RL两端电压的 分压电路。 RL = 50 ,U = 220 V 。中间环节是变 阻器,其规格是 100 、3 A。今把它平分为四段,
R2
R =R1+R2
(4)串联电阻上电压的分配与电阻成正比。
I
+ U –
两电阻串联时的分压公式:
R
应U1用:R1R1R2 U
U2
R2 R1 R2
U
降压、限流、调节电压等。 编辑版pppt
章目录 上一页 下一页 返回 退出
2.1.2 电阻的并联
I
特点:
+ I1 I2
(1)各电阻联接在两个公共的结点之间; (2)各电阻两端的电压相同;
(2) 若所选回路中包含恒流源支路, 则因恒流源两
端的电压未知,所以,有一个恒流源就出现一个未
知电压,因此,在此种情况下不可少列KVL方程。
编辑版pppt
章目录 上一页 下一页 返回 退出
例3:试求各支路电流。
a
c
+ 42V –
编辑版pppt
章目录 上一页 下一页 返回 退出
解: (4) 在 e 点:
U 220
IeaRea
《电工技术》教学课件 第二章 交流电路 知识点11:RLC并联交流电路的分析(一)-教学文稿

RLC并联电路的相量图如图2.11.3所示。
图2.11.3 RLC并联电路相量图
. U R L . I C B=B L C . I . I . U R L . I. I ' Ψ C B<B C L L .. . I I I + C . I . U . I R L . I ' Ψ C B>B C LL .. . I I I + C . I
式中,Y称为复导纳(简称导纳),实部是电导G,虚部是B=BC-BL,称
为电纳,单位均为西门子(S)。
Y=G+j(BC-BL)=G+jB
6
二、知识准备
将Y写成指数形式,则 Y G2 B2 arctan B Y ' G
式中,导纳模 Y G2 B2 ,单位为西门子(S), 导纳角 ' arctan B G 导纳模|Y|、G、B构成导纳三角形如图2.11.2。
图2.11.4电路图
12
. U R .I . I C . I
三、操作训练
•
解:以电压 U 为参考相量,画出相量图如图2.11.5所示,
图2.11.5 相量图
13
三、操作训练
由相量图可见,
•
IR
•
、I C
和
•
I
组成直角三角形,故可得:
I IR2 IC2 62 82 10A
故电流表A的读数为10A。
19
高等职业教育数字化学习中心
电气自动化技术专业教学资源库
谢 谢!
20
•
•
IR
U R
•
GU
•
•
•U U
•
IL
jL
jX L
图2.11.3 RLC并联电路相量图
. U R L . I C B=B L C . I . I . U R L . I. I ' Ψ C B<B C L L .. . I I I + C . I . U . I R L . I ' Ψ C B>B C LL .. . I I I + C . I
式中,Y称为复导纳(简称导纳),实部是电导G,虚部是B=BC-BL,称
为电纳,单位均为西门子(S)。
Y=G+j(BC-BL)=G+jB
6
二、知识准备
将Y写成指数形式,则 Y G2 B2 arctan B Y ' G
式中,导纳模 Y G2 B2 ,单位为西门子(S), 导纳角 ' arctan B G 导纳模|Y|、G、B构成导纳三角形如图2.11.2。
图2.11.4电路图
12
. U R .I . I C . I
三、操作训练
•
解:以电压 U 为参考相量,画出相量图如图2.11.5所示,
图2.11.5 相量图
13
三、操作训练
由相量图可见,
•
IR
•
、I C
和
•
I
组成直角三角形,故可得:
I IR2 IC2 62 82 10A
故电流表A的读数为10A。
19
高等职业教育数字化学习中心
电气自动化技术专业教学资源库
谢 谢!
20
•
•
IR
U R
•
GU
•
•
•U U
•
IL
jL
jX L
电工电子技术基础知识PPT通用课件

3 0011
8 1000
4 0100
9 1001
2.2.2 逻辑代数及应用
1 逻辑代数及基本运算 2 逻辑代数的运算法则
1 逻辑代数及基本运算
一、逻辑代数(布尔代数Boole Algebra)用来描述 数字电路和数字系统的结构和特性。
逻辑变量取值:0 1 分别代表两种对立的状态
一种状态
另一状态
高电平 真 是 有 低电平 假 非 无
平,则输出F 为低电平;只
R
有输入A、B 全为高电平时,
A
输出F 才为高电平。可见输
F 入与输出呈现与逻辑关系: B
与逻辑关系表达式
F = AB
与逻辑关系逻辑符号:
A
&
F
B
2、 二极管或门
与逻辑关系真值表:
AB F
00 0 01 0 10 0 11 1
A
只要输入A、B中一个为高
____、中间环节三部分组成。 • A.电阻 B.电容 C.电感 D.负载
1.2 正弦交流电的基本知识
1.2.1 正弦量 的三要素
1 频率与周期 2 振幅和有效值 3 相位、初相、相位差
引言
随时间按正弦规律变化的交流电压、电流称为 正弦电压、电流。
正弦量: 正弦电压、电流等物理量统称为正弦量。
对称正弦量特点为: U1 U 2 U 2 0
频率相同、幅值相等、 相位互差120°的三相电压称
u1 u2 u3 0 为对称正弦电压。
三相交流电压出现正幅值(或相应零值)的顺序称为 相序。 在此相序为1-2-3-1称为顺相序。 在电力系统中一般用黄、 绿、红区别1、2、3三相。
相序的实际意义:对三相电动机,如果相序反了,就会反转。
《电子电工技术》课件——第二章 单相交流电路

例2:已知相量,求瞬时值。
已知两个频率都为 1000 Hz 的正弦电流其相量形
式为: I1 100 60 A I2 10 e j30 A
求: i1、i2
解:
2
f
2 1000 6280
rad s
i1 100 2 sin(6280t 60 ) A
i2 10 2 sin(6280t 30 ) A
u i
90
U
IL
t
I I
C. 有效值 U IL
定义: X L L
则: U I X L
U IL
感抗(Ω) XL
感抗(XL =ωL )是频率的函数, 表示电感电路中电压、 电流有效值之间的关系,且只对正弦波有效。
ω
d. 相量关系
U
则:U I L e j90 I ( jX )
L
设: I I0
设: U1 a1 jb1 U 2 a2 jb2
则:
U U1 U2 (a1 a2 ) j(b1 b2 ) Ue j
2. 乘法运算
: 设
U1 U1e j1 U 2 U 2e j2
则: 3. 除法运算
U U1 U 2 U1 U 2 e j(12 )
则:
U1 U 2
U1 U2
U e j
U
指数式 极坐标形式
三、正弦量的相量运算
1、相量图运算
例:同频率正弦波相加 -- 平行四边形法则
u1 2U1 sin t 1
u2 2U2 sin t 2
U 2
U
同频率正弦波的 相量画在一起, 构成相量图。
2
1 U1
U U1 U 2
相量的复数运算
1. 加 、减运算
电工与电子技术基础第2版课件第2章

2.2 正弦量的相量图表示法
正弦量除可用三角函数、波形图表示外,但 可用随时间变化的旋转有向线段OA在y轴上的投影 来表示,如图2-4所示。称相量图法 。
y ω u1 t1 to O A ψ x Um u uo O ψ
ωt1
ωt
图2-4 用旋转的有向线段表示正弦量
用有向线段OA的长度表示正弦量的幅值Um(或Im), OA与x轴正向的夹角表示初相位ψ, OA随时间以逆时 针方向旋转的角速度表示ω,则OA在y轴上的投影为 OA=ASsin(ωt+ψ)。
(1) i 与 u 为 同频 率 ,且 u 超 前 i90° , 或 i 滞 后 u90°。 (2) Um (U)与Im(I)和ωL符合欧姆定律关系。ωL 的单位是欧姆,具有对i起阻碍的物理性质,称为 电抗,简称感抗,用XL表示,即 XL=ωL=2πfL
3.电感元件的功率关系 瞬时功率 p= ui=Imsinωt Umsin(ωt+90˚)=UIsin2ωt 图2-12b中p波形得 ,当p>0时,电感元件从外界(电 源)吸收电能,并转换为磁场能贮存于线圈中;当p<0 时,电感元件向外界释放能量,磁场能转换成电能, 并归还给电源。 有功功率P=0。即电感元件在交流电路中无能量 消耗,但电源与电感元件间存在能量的互换。用无功 功率Q来衡量能量互换的规模。规定Q等于瞬时功率p 的幅值,即 2 U Q=UI=I2XL= X L Q单位用乏 [尔] (Var)
在交流电路中,因各电流和电压多 +j A 为同一频率的正弦量,故可用有向线段 b r 来表示正弦量的最大值 ( 有效值 ) Im 、 ψ Um(I、U)和初相ψ ,称为正弦量的相量。 O a +1 在正弦量的大写字母上打“ •”表示,如 图2-5 有向线段的表示正弦量 幅值电流、电压相量用 I m、 U m表示,有 • U 效值电流、电压相量用 I 、 U 表示。将电 • 路中各电压、电流的相量画在同一坐标 φ I ψ 中,这样的图形称为相量图。 ψ 同频率的u和i可用图2-6相量图表示。 图2-6 u和i的相量图 即 U 超前 I φ°,I 或 U 滞后φ°。
电工技术的课件第二章1PPT .ppt

电工技术的课件第二章-1
(2-1)
第二章 电路的分析方法
§2.1 基本分析方法
2.1.1 电阻串.并联/电源的等效变换 2.1.2 支路电流法 2.1.3 结点电压法
§2.2 基本定理
2.2.1 叠加定理 2.2.2 等效电源定理
(2-2)
§2.1 基本分析方法
2.1.1 电阻的串.并联的等效变换
由6个方程求解。
(2-14)
支路电流法小结
解题步骤
结论与引申
1 对每一支路假设 1. 电流正方向可任意假设。
一未知电流
2. 原则上,有B个支路就设B个未知数。
(恒流源支路除外)
列电流方程: 2 对每个结点有
若电路有N个结点,
I1 I2 I3
I 0
则可以列出 (N-1) 结点方程。
列电压方程: 3 对每个回路有
设 : VB = 0 V
则由结点电流定律, 有:
I1+ I4= I2+ I3
I1
R1
I2
E1
A I3 R3
R2
B
R4 E3 I4
I1
E1 VA R1
、
I2
VA R2
I3
VA E3、 R3
I4
VA R4
(2-20)
由上各式可推出:
E1 E3
VA
1
R1 R3 11
1
求
R1 R2 R3 R4
欧姆定律列方程,就能得出结果。 缺点:电路中支路数多时,所需方程的个
数较多,求解不方便。
a
支路数 B=4
b
须列4个方程式
(2-17)
(2-1)
第二章 电路的分析方法
§2.1 基本分析方法
2.1.1 电阻串.并联/电源的等效变换 2.1.2 支路电流法 2.1.3 结点电压法
§2.2 基本定理
2.2.1 叠加定理 2.2.2 等效电源定理
(2-2)
§2.1 基本分析方法
2.1.1 电阻的串.并联的等效变换
由6个方程求解。
(2-14)
支路电流法小结
解题步骤
结论与引申
1 对每一支路假设 1. 电流正方向可任意假设。
一未知电流
2. 原则上,有B个支路就设B个未知数。
(恒流源支路除外)
列电流方程: 2 对每个结点有
若电路有N个结点,
I1 I2 I3
I 0
则可以列出 (N-1) 结点方程。
列电压方程: 3 对每个回路有
设 : VB = 0 V
则由结点电流定律, 有:
I1+ I4= I2+ I3
I1
R1
I2
E1
A I3 R3
R2
B
R4 E3 I4
I1
E1 VA R1
、
I2
VA R2
I3
VA E3、 R3
I4
VA R4
(2-20)
由上各式可推出:
E1 E3
VA
1
R1 R3 11
1
求
R1 R2 R3 R4
欧姆定律列方程,就能得出结果。 缺点:电路中支路数多时,所需方程的个
数较多,求解不方便。
a
支路数 B=4
b
须列4个方程式
(2-17)
电工技术第2章电路的分析方法课件
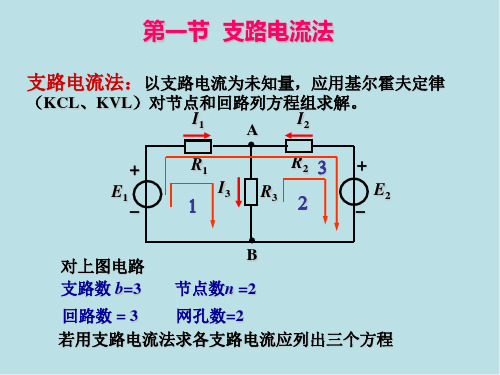
通常选用网孔列出的回路方程一定是独立的。
对网孔1:
R1 I1 +R3I3 =E1
对网孔2:
R2I2 +R3I3 =E2
联立三个方程,即可解出三个支路电流。
第一节 支路电流法
支路电流法的解题步骤: 1)确定支路数b,选定各支路电流的参考方
向; 2)确定节点数n,列出(n-1)个独立的节
点电流方程; 3)确定余下所需的方程数b-(n-1),选择网
第一节 支路电流法
支路电流法:以支路电流为未知量,应用基尔霍夫定律
(KCL、KVL)对节点和回路列方程组求解。
I1
A
I2
+
R1
R2 3 +
E1 -
I3
1
R3 2
E2 -
对上图电路 支路数 b=3
B 节点数n =2
回路数 = 3 网孔数=2 若用支路电流法求各支路电流应列出三个方程
第一节 支路电流法
第二节 网孔电流法
写成一般形式
R11Im1 + R12Im2 + R13Im3 E11
R21I m1
+
R22 Im2
+
R23 I m 3
E22
R31Im1 + R32Im2 + R33Im3 E33
E11 E1 - E3 - E4, E22 -E2 + E3, E33 E4 - E5 分别为网孔1、2、3中的电动势的代数和,凡电动势的正方 向与网孔电流方向一致时,该电动势前取正号,反之取负 号。
I2 I2 - I2
I3 I3 + I3
I1'
I2'
I1"
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对于含恒流源支路的电路,列节点电 压方程 时应按以下规则: 分母为:各支路电阻的倒数和,但不
考虑恒流源支路的电阻。
分子为:各支路电动势除以支路电阻, 并与恒流源一起求代数和。其符号为: 恒流源电流朝向未知节点时取正号,反 之取负号。电压源支路的写法同前。
a (2-13)
§2.2 基本定理
2.2.1 迭加定理 2.2.2 等效电源定理
应用迭加定理要注意的问题
1. 迭加定理只适用于线性电路。
2. 迭加时只将电源分别考虑,电路的结构和参数不变。 令各电源分别作用,暂不作用的恒压源应予以短路,
即令E=0;暂不作用的恒流源应予以开路,即令 Is=0。
E
Is =
+ Is E
3. 解题时要标明各支路电流、电压的正方向。原电
路中各电压、电流的最后结果是各分电压、分电
流的代数和。
a
(2-18)
4. 迭加原理只能用于电压或电流的计算,不能用来
求功率。如:
I3
R3
设: I3I3'I3"
则: P3 I32R3 (I3' I3")2R3
(I3')2R3 (I3")2R3
5. 运用迭加定理时也可以把电源分组求解,每个分 电路的电源个数可能不止一个。
=
+
a
(2-19)
齐性定理(线性电路的比例性)
电工技术的课件第二章-2
a (2-1)
第二章 电路的分析方法
§2.1 基本分析方法
2.1.1 电阻串.并联/电源的等效变换 2.1.2 支路电流法 2.1.3 结点电压法
§2.2 基本定理
2.2.1 叠加定理 2.2.2 等效电源定理
a (2-2)
支路电流法小结
解题步骤
结论与引申
1 对每一支路假设 1. 电流正方向可任意假设。
(一)戴维南定理 (二)诺顿定理
a (2-14)
2.2.1 迭加定理 概念: 在多个电源同时作用的线性电路(由线性元
件组成的电路)中,任何支路的电流或任意两点间
的电压,都是各个电源单独作用时所得结果的代
数和。
I1 A I2
R1
+ R3 _ E1
I3 R2 + E2 _
B 原电路
I1' A I2'
R1
在线性电路中,当某一电源的电压或电流
改变时,各支路的电压或电流也将按同一
比例变化。如:
I1
R1 R2
+
E1 -
I2
R3 E-激励 ; I-响应 I3 I=KE (K是比例系数)
显而易见:
若 E1 增加 n 倍,各电流也会增加 n 倍。
a
(2-20)
例
US
已知: US =1V、IS=1A 时, Uo=0V
结点电位法解题思路
假设一个参考点,令其电位为零, 求其它各结点电位, 求各支路的电流或电压。
结点电位法适用于支路数多,结点少的电路。如:
Va
a
共a、b两个结点,b设为
参考点后,仅剩一个未
b
知数(a点电位Va)。
a
(2-7)
结点电压法 应用举例
电路中只含两个 结点时,仅剩一个未 知数,此时可推出结点 电流公式如下。
3 对每个回路有 2. 独立回路的选择:
EU
#1 #2 #3 一般按网孔选择
4 解联立方程组
根据未知a 数的正负决定电流的实际方向(2。-3)
.P46 例:求IG
解:
解得:
a
(2-4)
支路电流法的优缺点
优点:支路电流法是电路分析中最基本的 方法之一。只要根据基尔霍夫定律、
欧姆定律列方程,就能得出结果。 缺点:电路中支路数多时,所需方程的个
式中分母为各支路电阻倒数和,分子 为各有源支路中电动势除以电阻后求其代 数和。电动势方向指向未知结点,则该项 为正,反之为负。
a
(2-9)
例2
I1
A
I3
I2
R3
R1 R2
++
B
R4 -
I5 R5
E1 -
- E2 I4 C
+ E5
结点电流方程:
I A点: 1 I 2 I 3
I B点: 3
I4
I5
B
I 1 I 1 ' I 1 "I 2 I 2 ' I 2 "I 3 I 3 ' I 3 "
a (2-16)
例
10 4A
10 10 -
I 20V +
用迭加原理求:
I= ?
解:
10
10
I´
4A
I'=2A
10 10
+
10 10 -
I " 20V +
I"= -1A
I = I'+ I"= 1A a
(2-17)
I3'
+ R3
R2
+
_ E1
B E1单a独作用
I A '' 1
I2''
R1 R3
I3''
R2 + E2 _
B
E2单独作用
(2-15)
I1 A I2
R1
I3
R3 R2
+ _ E1
+ E2 _ B
I1' A I2'
R1
I3'
R3
+
+
R2
_ E1
B
I '' A 1
I2''
R1
I3''
R3 R2
+ E2
_
数较多,求解不方便。
a
支路数 B=4
须列4个方程式
b a (2-5)
2.1.3 结点电压法
结点电位的概念: 在电路中任选一结点,设其电 位为零(用 标记),此点称为 参考点。其它各结点对参考点的电 压,便是该结点的电位。记为: “VX”(注意:电位为单下标)。
a (2-6)
结点电位法中的未知数:结点电位“VX”。
VBR 13R 14R 15VAR 13E R5 5
其中未知数仅有:VA、VB 两个。 a
(2-11)
结点电压法 应用举例
电路中含恒流源的情况 Is
设:VB 0
? 则: VA
1
E1 R1
IS
1
1
R1 R2 RS
a
A I2
RS R1
I1
R2
E1
B
V A
E1 R1
IS
11
ቤተ መጻሕፍቲ ባይዱ
R1 R2
(2-12)
设: VC 0V
则:各支路电流分别为 :
I1
E1 VA R1
、
I2
VA E2 R2
I3
VA VB 、 R3
I4 VB R4
a
I5
VB E5 R5
(2-10)
将各支路电流代入A、B 两结点电流方程, 然后整理得:
VA R 11R 12R 13 VB R 13 E R 1 1E R 2 2
一未知电流
2. 原则上,有B个支路就设B个未知数。
(恒流源支路除外)
列电流方程: 2 对每个结点有
若电路有N个结点,
I1 I2 I3
I w0ww.372则2.可cn以列中出国(最N大-1)的结资点料方库程下。 载
列电压方程:
1. 未知数=B,已有(N-1)个结点方程,
需补足 B -(N -1)个方程。
设 : VB = 0 V
则由结点电流定律, 有:
I1+ I4= I2+ I3
I1
R1
I2
E1
A I3 R3
R2
B
R4 E3 I4
I1
E1 VA R1
、
I2
VA R2
I3
a
VA E3、 R3
I4
VA R4
(2-8)
由上各式可推出:
E1 E3
VA
1
R1 R3 11
1
求
R1 R2 R3 R4
I1
I4
