求阴影部分的面积(一)
小学求阴影部分面积(例题加习题)

小学求阴影部分面积(例题和练习)【经典例题1】求如图阴影部分的面积。
(单位:厘米)考点:组合图形的面积;梯形的面积;圆、圆环的面积。
分析:阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答。
解答:解:(4+6)×4÷2÷2﹣3.14×÷2=10﹣3.14×4÷2=10﹣6.28=3.72(平方厘米)答:阴影部分的面积是3.72平方厘米.点评:组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用。
【巩固提高】1、如图,求阴影部分的面积.(单位:厘米)2、计算如图阴影部分的面积.(单位:厘米)3、求出如图阴影部分的面积:单位:厘米.4、求如图阴影部分的面积。
(单位:厘米)【经典例题2】求如图阴影部分面积。
(单位:厘米)考点:长方形正方形的面积;平行四边形的面积;三角形的周长和面积。
分析:图一中阴影部分的面积=大正方形面积的一半-与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积-平行四边形的面积。
再将题目中的数据代入公式中计算。
解答:图一中阴影部分的面积=6×6÷2-4×6÷2=6(平方厘米)图二中阴影部分的面积=(8+15)×(48÷8)÷2-48=21(平方厘米)点评:此题目是组合图形,需要把握好正方形、三角形、平行四边形、梯形的面积公式,再将题目中的数据代入相关公式进行计算。
【巩固提高】1、计算如图中阴影部分的面积.单位:厘米.2、求阴影部分的面积.单位:厘米.【经典例题3】如图是三个半圆,求阴影部分的周长和面积。
(单位:厘米)考点:组合图形的面积,圆和圆环的面积。
分析:观察图形可知,图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长等于直径为13厘米的圆的周长,再利用圆的周长公式即可计算;阴影部分的面积=大半圆的面积-两个小半圆的面积解答:解:周长:3.14×(10+3)=3.14×13=40.82(厘米)面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2=×3.14×(42.25﹣25﹣2.25)=×3.14×15=23.55(平方厘米)点评:此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键。
圆-阴影部分面积(含标准答案)

求阴影部分面积例1.求阴影部分的面积。
(单位:厘M)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘M)例2.正方形面积是7平方厘M,求阴影部分的面积。
(单位:厘M)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘M,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘M例3.求图中阴影部分的面积。
(单位:厘M)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘M。
例4.求阴影部分的面积。
(单位:厘M)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘M例5.求阴影部分的面积。
(单位:厘M)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘M另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘M,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘M?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘M(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘M) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘M(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘M)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘M例9.求阴影部分的面积。
圆-阴影部分面积(附答案)
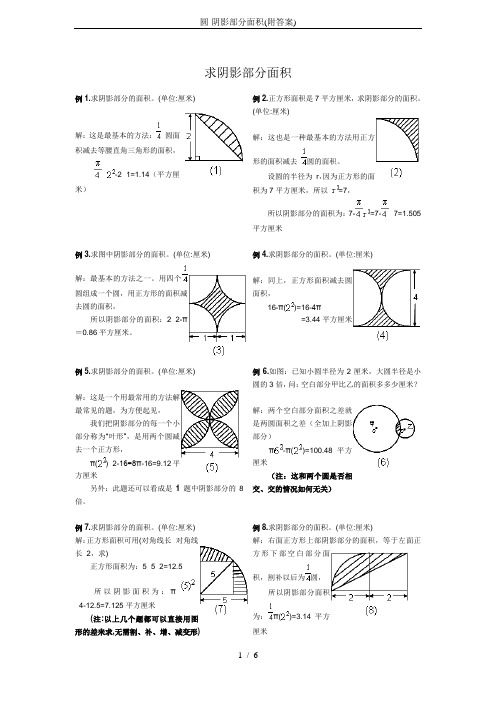
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
小升初数学复习专题:求阴影部分面积(含答案解析)

小升初数学复习专题:求阴影部分面积(含答案解析)1、几何图形计算公式:1) 正方形:周长=边长×4 C=4a面积=边长×边长S=a×a2) 正方体:表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3) 长方形:周长=(长+宽)×2 C=2(a+b)面积=长×宽S=ab4)长方体:表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)体积=长×宽×高V=abh5)三角形:面积=底×高÷2 s=ah÷26)平行四边形:面积=底×高s=ah7)梯形:面积=(上底+下底)×高÷2 s=(a+b)×h÷28)圆形:周长=直径×Π=2×Π×半径C=Πd=2Πr面积=半径×半径×Π9)圆柱体:侧面积=底面周长×高表面积=侧面积+底面积×2体积=底面积×高10)圆锥体:体积=底面积×高÷32、面积求解大致分为以下几类:Ø 从整体图形中减去局部;割补法:将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
练习题例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米)例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
五年级《圆》求阴影部分面积的十大方法
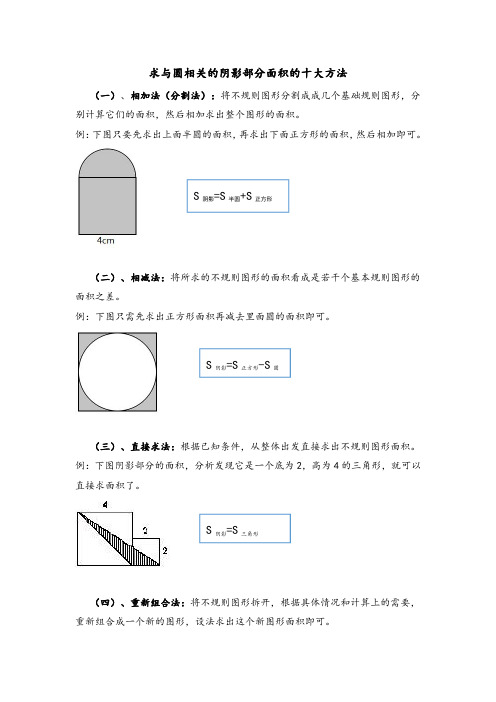
求与圆相关的阴影部分面积的十大方法(一)、相加法(分割法):将不规则图形分割成成几个基础规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例:下图只要先求出上面半圆的面积,再求出下面正方形的面积,然后相加即可。
(二)、相减法:将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
例:下图只需先求出正方形面积再减去里面圆的面积即可。
(三)、直接求法:根据已知条件,从整体出发直接求出不规则图形面积。
例:下图阴影部分的面积,分析发现它是一个底为2,高为4的三角形,就可以直接求面积了。
(四)、重新组合法:将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可。
S 阴影=S 半圆+S 正方形S 阴影=S 正方形-S 圆S 阴影=S 三角形例:下图可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
(五)、辅助线法:根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可。
例:下图虽然可以用相减法解决,但不如添加一条辅助线后用直接法计算2个三角形面积之和更简便。
(六)、割补法:把原图形的一部分切割下来,补在图形中的另一部分,使之成为规则图形,从而使问题得到解决。
例:下图只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半。
(七)、平移法:将图形中某一部分切割下来,平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积。
S 阴影=S 正方形-S 圆S 阴影=S 正方形÷2S 阴影=S 三角形①+S 三角形②例:下图可先沿中间切开,把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
(八)、旋转法:将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度,贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积。
求阴影部分的面积(一)ppt课件

A
D
精选
探讨二:太极图中,黑色部分的面积是多少呢?(π≈3)
精选
割补法:割、补的面积相等
探讨二:太极图中,黑色部分的面积怎么求呢?(π≈3)
S= S圆÷2 =3×10²÷2 =150(cm²)
精选
10cm 10cm
求阴影部分的面积是多少?
6cm
S阴影=4×6=24(cm²)
4cm
精选
等分法、 拼组法
精选
探讨五: 巧解法
已知大正方形的面积是80cm²,你会求圆的面积吗?
小正方形的边长=圆的半径
a
a=r
r
a²=r²
精选
小结
今天你有什么收获?
精选
2cm
精选
方法1:
2cm 2cm
5/29/2020
精选
方法1:
2cm 2cm
S空白=(S正方形-S圆)×2 S阴影=S正方形-S空白
5/29/2020
精选
方法2:
20
精选
方法2:
S阴影=2× S圆- S正方形
5/29/2020
精选
求阴影部分的面积是多少?
5/29/2020
精选
5/29/2020
求阴影部分的面积(一)
数学 人教版六年级上册
郑州市二七区大学路小学 赵精选延芳
S=S大-S小
S=a²
1 2
S圆
S=πr²
1 4
S圆
S=ah
S=1 ah
2 S=1 (a+b)h
2
S=ab
精选
和差法
探讨一:涂油漆部分的面积是多少呢?
3dm
精选
E
6dm
超全六年级阴影部分的面积(详细答案)
六年级阴影部分的面积1.求阴影部分的面积。
(单位:厘米)解:割补后如右图,易知,阴影部分面积为一个梯形。
梯形上底DE=7-4=3厘米,1S =S =DE AB)AD 2⨯+⨯阴梯形(=137)42⨯+⨯(=20(平方厘米)2、求阴影部分的面积。
解:S =S 阴梯形,梯形的上底是圆的直径,下底、高是圆的半径,S =S 阴梯形=124)22⨯+⨯(=6(2cm )3、如图,平行四边形的高是6厘米,面积是54平方厘米,求阴影三角形的面积。
解:S =AD AO ⨯ABCD =54平方厘米,且AO=6厘米,所以AD=9厘米。
由图形可知AED∆是等腰直角三角形,所以AE=AD ,OE=OF=AE-AO=9-6=3cm ,BO=BC-OC=9-3=6cm 。
1S =BO OF 2⨯⨯阴=1S =632⨯⨯阴=92cm 。
4、如图是一个平行四边形,面积是50平方厘米,求阴影积分的面积。
解:方法一:过C 点作CF AD ⊥交AD 于点F ,可知AECF 是长方形,面积=5×6=302cm ,ABE CFD S =S ∆∆=(50-30)÷2=102cm 。
方法二:BC=S ABCD ÷AE=50÷5=10cm ,BE=BC-EC=10-6=4cm ,ABE S ∆=BE ×AE ÷2 =4×5÷2=102cm5、下图是一个半圆形,已知AB=10厘米,阴影部分的面积为24.25平方厘米,求图形中三角形的高。
解:S =S -S ∆阴半圆=21AB 22π⎛⎫⨯⨯ ⎪⎝⎭-24.25=21103.1422⎛⎫⨯⨯ ⎪⎝⎭-24.25=152cm , 三角形的高=2S ∆÷AB=2×15÷10=3cm 。
6、如图,一个长方形长是10cm ,宽是4cm ,以A 点和C 点为圆心各画一个扇形,求画中阴影部分的面积是多少平方厘米?解:BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44⎛⎫- ⎪⎝⎭大圆小圆=ABCD 11S +S -S 44大圆小圆=()2213.1410-4-1044⨯⨯⨯ =25.942cm 。
重点小学小学六年级 阴影部分面积 专题复习 典型例题(含答案)
精心整理阴影部分面积专题 例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米) 解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r ,因为正方形的面积为7平方厘米,所以=7,7-×例3.解:用四个圆圆的面积, π=0.86解:同上,正方形面积减去圆π()=16- 例5.解:这是一个用最常用的方法解我们把阴影部分的每一个小部分称为“,是用两个圆减π(平方厘米倍。
解:两个空白部分面积之差就是两圆面积之差(全加上阴影平方例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求) 正方形面积为:5×5÷2=12.5 所以阴影面积为:π例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
(单位:厘米)解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米例11.求。
(π×解:三个部分拼成一个半圆平方例13.解:剪开移到凑成正方形的一半.所以:8×8÷2=32梯形面积减去圆面(4+10)×π厘例15.分析:此题比上面的题有一定难度,这是"叶形"的一个半.解:设三角形的直角边长为r,则=12,=6圆面积为:π÷2=3π。
(完整版)小学求阴影部分面积专题—含答案
(5)【史上最全小学求阴影部分面积专题一含答案】 小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区 分。
面积求解大致分为以下几类:1、 从整体图形中减去局部;2、 割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本 的平面图形的面积求阴影部分的面积。
(4)例1•求阴影部分的面积。
(单位:厘米) 例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)(2)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为 2厘米,大圆半径是小圆的 问:空白部分甲比乙的面积多多少即3倍, 厘22㈣厘米)3-10-(M)3(13)—了 —⑴)例8.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米) 例13.求阴影部分的面积。
(单位:厘米) 例10.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位 例14.求阴影部分的面积。
(单位:厘米)例7.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米) 3(12)2十“7I* --- 5 —积45(15)扇形,求阴影部分的周长。
BAE C(18)分的面积(佟)(20)(22?(21)例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形 ABCD 的面积是36平方厘米,求阴影部 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的 例21.图中四个圆的半径都是 1厘米,求阴影部分的面积。
例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例16.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是 12平方厘米,求阴影部分的面 例22.如图,正方形边长为 8厘米,求阴影部分的面积。
小学六年级圆_阴影部分面积(含答案)
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米) 解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘形的差来求,无需割、补、增、减变形) 米例9.求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等分法、 拼组法
探讨三:在长方形中,怎么求四个扇形的面积和呢?
6cm
4cm
思考:三角形中三个扇形的面积和怎么求?
4cm
4cm
4cm
思考:三角形中三个扇形的面积和怎么求?
4cm
4cm 4cm
9/2/2016
探讨四:阴影部分的面积怎么求? (π ≈3)
2cm
2cm
2cm
2cm
2cm
2cm
方法1:
E
6dm
B C 4dm
3dm A
中点
D
和差法
探讨一:涂油漆部分的面积是多少呢?
方法1: S阴影=S正方形-S△AEB-S△ADC =6²-6×6÷2-6×4÷2 =36-18-12 =6(dm²)
方法2:S=ah÷2 =(6-4)×6÷2 =12÷2 =6(dm²) 答:涂油漆部分的面积是6dm²
2cm
2cm
9/2/2016
方法1:
2cm
2cm
(S正方形-S圆) S空白= ×2 S阴影=S正方形-S空白
9/2/2016
方法2:
6
方法2:
S阴影=2× S圆- S正方形
9/2/2016
求阴影部分的面积是多少?
9/2/2016
9/2/2016
探讨五: 已知大正方形的面积是80cm² ,你会求圆的面积吗?
小正方形的边长=圆的半径
巧有什么收获?
E
6dm
B C 4dm
3dm A
D
探讨二:太极图中,黑色部分的面积是多少呢?(π ≈3)
割补法:割、补的面积相等
S= S圆÷2 =3×10²÷2 =150(cm²)
探讨二:太极图中,黑色部分的面积怎么求呢?(π ≈3)
10cm
10cm
求阴影部分的面积是多少?
6cm
4cm
S阴影=4×6=24(cm²)
求阴影部分的面积(一)
数学 人教版六年级上册
郑州市二七区大学路小学 赵延芳
1 S圆 2
S=S大-S小
1 S圆 4
1 S= ah 2 1 S= (a+b)h 2
S=πr²
S=a² S=ah
S=ab
和差法
探讨一:涂油漆部分的面积是多少呢?
E
6dm
B
C
4dm A D
3dm
和差法
探讨一:涂油漆部分的面积是多少呢?
