梁的挠度验算
工字钢、圆管及贝雷梁强度及挠度验算

工字钢强度及挠度验算 一、有关工字钢计算公式 1、一孔梁计算
2、两孔梁计算
注:1.在均布荷载作用下:M =表中系数×ql 2
;V =表中系数×ql ;EI
w 100ql 表中系数4⨯= 3、三孔梁计算
注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI
w 100ql 表中系数4
⨯=
二、工字钢强度及挠度验算 1、工字钢截面特性参数 W x —截面抵抗矩(cm3) I x —截面惯性矩(cm4) 2、强度验算
σ=M/W (N/mm2)
计算结果与f=215 N/mm2 (钢材强度设计值)比较
3、挠度验算
F max=挠度公式计算
与L/400比较
钢材的弹性模量E=206×103
圆管稳定性验算
1、查圆管截面特性表
查的圆管的回转半径ix及截面面积A
2、确定圆管长度L
3、计算圆管长细比λ=L/ix
4、查《钢结构设计规范》表C—2,确定圆管折减系数ψ
5、钢材容许应力[σ]=180MPa(轴向力)
6、圆管稳定条件
σ=F/A<ψ[σ]
贝雷梁受力计算1、321贝雷梁特性
321贝雷梁弹性模量E=2.1×105 MPa
单排单层(不加强)A=5.1×103
mm
2
,
单排单层(加强)A=10.2×103 mm
2
[σ]=210MPa
挠度计算式为
计算值要小于L/400。
简支梁最大挠度计算公式

简支梁最大挠度计算公式
由荷载标准值(不考虑荷载分项系数和动力系数)产生的最大挠度;梁的容许挠度值,对某些常用的受弯构件,规范根据实践经验规定的容许挠度值见附表2、1。
梁的挠度可按材料力学和结构力学的方法计算,也可由结构静力计算手册取用。
受多个集中荷载的梁(如吊车梁、楼盖主梁等),其挠度精确计算较为复杂,但与产生相同最大弯矩的均布荷载作用下的挠度接近。
于是,可采用下列近似公式验算梁的挠度:对等截面简支梁:
(5、12)对变截面简支梁:
(5、13)式中均布线荷载标准值;荷载标准值产生的最大弯矩;跨中毛截面惯性矩;支座附近毛截面惯性矩;l梁的长度;E 梁截面弹性模量。
计算梁的挠度值时,取用的荷载标准值应与附表2、1规定的容许挠度值相对应。
例如,对吊车梁,挠度应按自重和起重量最大的一台吊车计算;对楼盖或工作平台梁,应分别验算全部荷载产生挠度和仅有可变荷载产生挠度。
第 1 页共 1 页。
加固 梁 挠度 裂缝验算 pkpm

加固梁挠度裂缝验算 pkpm 下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!梁是建筑结构中承受荷载并传递荷载的重要构件,其受力情况对整个结构的安全性和稳定性起着至关重要的作用。
新规范混凝土梁挠度验算计算书
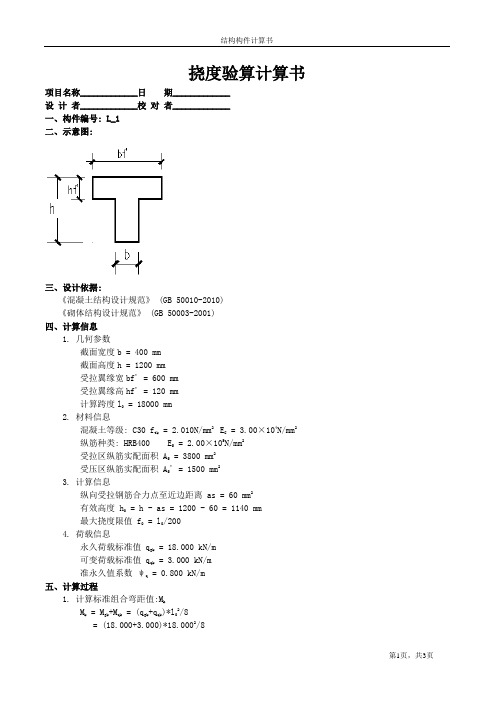
挠度验算计算书项目名称_____________日期_____________设计者_____________校对者_____________一、构件编号: L_1二、示意图:三、设计依据:《混凝土结构设计规范》 (GB 50010-2010)《砌体结构设计规范》 (GB 50003-2001)四、计算信息1. 几何参数截面宽度b = 400 mm截面高度h = 1200 mm受拉翼缘宽bf' = 600 mm受拉翼缘高hf' = 120 mm计算跨度l0 = 18000 mm2. 材料信息混凝土等级: C30 f tk = 2.010N/mm2E C= 3.00×104N/mm2纵筋种类: HRB400 E S= 2.00×105N/mm2受拉区纵筋实配面积 A S = 3800 mm2受压区纵筋实配面积 A S' = 1500 mm23. 计算信息纵向受拉钢筋合力点至近边距离 as = 60 mm2有效高度 h0 = h - as = 1200 - 60 = 1140 mm最大挠度限值 f0 = l0/2004. 荷载信息永久荷载标准值 q gk = 18.000 kN/m可变荷载标准值 q qk = 3.000 kN/m准永久值系数ψq = 0.800 kN/m五、计算过程1. 计算标准组合弯距值:M kM k = M gk+M qk = (q gk+q qk)*l02/8= (18.000+3.000)*18.0002/8= 850.500 kN*m2. 计算永久组合弯距值:M qM q = M gk+ψq*M qk = (q gk+ψq*q qk)*l02/8= (18.000+0.8*3.000)*18.0002/8= 826.200 kN*m3. 计算受弯构件的短期刚度:B S3.1 计算按荷载荷载效应的两种组合作用下,构件纵向受拉钢筋应力σSk = M k/(0.87*h0*A S)= (850.500×106/(0.87*1140*3800)= 225.666 N/mm2σSq = M q/(0.87*h0*A S)= (826.200×106/(0.87*1140*3800)= 219.219 N/mm23.2 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率T形截面积:A te= 0.5*b*h = 0.5*400*1200 = 240000mm2ρte = A S/A te = 3800/240000 = 1.583%3.3 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*f tk/(ρte*σSk)= 1.1-0.65*2.01/(1.583%*225.666)= 0.734ψq = 1.1-0.65*f tk/(ρte*σSq)= 1.1-0.65*2.01/(1.583%*219.219)= 0.7243.4 计算钢筋弹性模量与混凝土模量的比值αEαE = E S/E c= 2.00×105/3.00×104 = 6.6673.5 计算受压翼缘面积与腹板有效面积的比值γf'γf' = (bf'-b)*hf'/b/h0= (600-400)*120/400/1140= 0.0533.6 计算纵向受拉钢筋配筋率ρρ=A S/(b*h0)=3800/(400*1140)=0.833%3.7 计算受弯构件的短期刚度 B SB Sk = E S*A S*h02/(1.15*ψk+0.2+6*αE*ρ/(1+3.5*γf'))= 2.00*105*3800*11402/(1.15*0.734+0.2+6*6.667*0.833%/(1+3.5*0.053)) = 744.880×103 kN*m2B Sq = E S*A S*h02/(1.15*ψq+0.2+6*αE*ρ/(1+3.5*γf'))= 2.00*105*3800*11402/(1.15*0.724+0.2+6*6.667*0.833%/(1+3.5*0.053)) = 751.894×103 kN*m24. 计算受弯构件的长期刚度:B4.1 确定考虑荷载长期效应组合对挠度影响增大影响系数θρ'=A S'/(b*h0)=1500/(400*1140)=0.329%当0<ρ'<ρ时,θ在2-1.6间线性内插得θ=1.8424.2 计算受弯构件的长期刚度 BBk = M K/(M q*(θ-1)+M K)*B Sk= 850.500/(826.200*(1.842-1)+850.500)*744880.422= 409.715×103 kN*m2Bq = B Sq/θ= 751893.505/1.842= 408.171×103 kN*m2B = min(B Sk,B Sq= min(409715.038,408170.760)= 408.171×103 kN*m25. 计算受弯构件挠度f max = (q gk+Ψq*q qk)*l04/B*5/384= (18.000+0.8*3.000)*18.0004/408.171*5/384= 68.315mm ≤ f0=l0/200=18000/200=90.000mm,满足要求。
多跨梁挠度验算例题

多跨梁挠度验算例题挠度与刚度在材料力学对匀质材料梁的变形计算中,给出了简支梁在均布荷载q作用下的跨中挠度为:式中 f——梁的跨中最大挠度;M——跨中最大弯矩;β—挠度系数,与荷载形式及支承条件有关;EI——梁的截面抗弯刚度;l一梁的计算跨度。
从式(11—142)中可以看出,对于匀质弹性材料梁,当梁的截面尺寸、材料一定时EI为常数,其弯矩—挠度(M—f)呈线性关系,如图11-61中O-A虚线所示。
而钢筋混凝土构件则不同,其实测的M -f曲线表明,只有在荷载很小梁尚未开裂时(阶段1),M-f线才是一段直线,从开始出现裂缝到钢筋屈服时(阶段Ⅱ),M-f线开始偏离直线而逐渐向下弯曲,这说明构件刚度开始下降。
但这时梁仍处于正常使用阶段。
当继续加载时,受拉钢筋屈服(阶段Ⅲ),M-f线更偏向横轴(f轴),挠度值增长更快。
上述现象说明,钢筋混凝土梁的刚度不是一个常数,而是随着荷载的增加而降低。
从而,计算其变形问题就归结为计算它的抗弯问题了。
梁的抗弯刚度也就分成短期刚度和长期刚度两种:短期刚度B s表示在荷载短期效应作用下受弯构件截面的抗弯刚度;长期刚度B表示考虑了一部分荷载长期作用影响后截面的抗弯刚度。
短期刚度B s当截面开裂后,在荷载短期效应组合作用下,钢筋混凝土受弯构件的短期刚度可按下式计算:当计算出的ψ<0.2时,取ψ=0.2;若ψ>1.0时,取ψ=1.0;对直接承受重复荷载的构件,取ψ=1.0;α E——钢筋与混凝土的弹性模量比值;ρ——纵向受拉钢筋配筋率;r’ f——系数,按式(11—146)计算;f t k——混凝土轴心抗拉强度标准值;ρ t e——按截面的有效受拉混凝土面积Ate计算的纵向钢筋配筋率,即式中 Mk——按荷载效应的标准组合计算的弯矩,取计算区段内的最大弯矩值;M q——按荷载效应的准永久组合计算的弯矩,取计算区段内的最大弯矩值;θ——考虑荷载长期作用对挠度增大的影响系数,按下列规定取用:对钢筋混凝土受弯构件,当ρ’=0时,取θ=2.0;当ρ’=ρ时,取θ=1.6;当ρ’为中间取值时,θ按线性内插法取用。
矩形梁挠度计算

矩形梁挠度计算(1).基本资料挠度验算:L1弹性挠度fd =2.000mm 中梁弹性刚度增大系数Bk =1.000截面尺寸为b×h =200×500 mm受拉纵筋总面积As = 628 mm受压纵筋总面积As’= 490 mm钢筋弹性模量为Es = 200000 N/mm钢筋弹性模量为Ec = 30000 N/mm纵向受拉钢筋合力点至截面近边的距离as =35mm ho =465mm混凝土抗拉强度标准值ftk = 2.01N/mm按荷载效应的标准组合计算的弯矩值Mk =60.00kN·m按荷载效应的准永久值组合计算的弯矩值Mq =50.00kN·m设计时执行的规范:《混凝土结构设计规范》(GB 50010-2002),以下简称混凝土规范(2).挠度验算弹性刚度BcBc =Bk * Ec * I =1.00*30000.00*200*500^3/12 =62500.00kN·m按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte,按下式计算:ρte =As / Ate (混凝土规范8.1.2-4)Ate =0.5 * b * h =0.5*200*500 =50000mmρte =As / Ate =628/ 50000 =0.01256按荷载效应的标准组合计算的纵向受拉钢筋的等效应力σsk,按下列公式计算:受弯:σsk =Mk / (0.87 * ho * As)σsk =60000000/(0.87*465*628) =236N/mm裂缝间纵向受拉钢筋应变不均匀系数ψ,按混凝土规范式8.1.2-2 计算:ψ =1.1 - 0.65 * ftk / (ρte * σsk) =1.1-0.65*2.01/(0.013* 236) =0.660钢筋弹性模量与混凝土模量的比值αEαE =Es / Ec =200000/ 30000 =6.67受压翼缘面积与腹板有效面积的比值γf’γf’ = 0纵向受拉钢筋配筋率ρ =As / (b * ho) =628/(200*465) =0.00675钢筋混凝土受弯构件的Bs 按混凝土规范式8.2.3-1 计算:Bs =Es * As * ho ^ 2 / [1.15ψ + 0.2 + 6 * αE * ρ / (1 + 3.5γf’)]=200000*628*465^2/[1.15*0.660+0.2+6*6.667*0.00675/(1+3.5*0.000)] =22104.979 KNm 考虑荷载长期效应组合对挠度影响增大影响系数θρ’ =As’ / (b * ho) =490/(200*465) =0.00527按混凝土规范第8.2.5 条,θ =1.688受弯构件的长期刚度B,可按混凝土规范式8.2.2 计算:B =Mk / [Mq * (θ - 1) + Mk] * Bs =60/[ 50*(1.688-1)+ 60]*22104.98 = 14050.53 KNm挠度 f =fd * Bc / B =2.00*62500.00/14050.53=8.90mmf / Lo =1/ 899。
混凝土梁挠度计算公式

混凝土梁挠度计算公式
概述:
混凝土梁的挠度是指梁的弯曲变形程度,是衡量梁的刚度和受力性能的重要参数。
计算混凝土梁的挠度可以帮助工程师确定梁的设计是否满足要求,并进行必要的调整。
常用公式:
1. 单跨梁的挠度计算公式:
梁的挠度 = (5 * q * L^4) / (384 * E * I)
公式中的变量含义如下:
挠度:梁的弯曲变形程度,单位为米。
q:集中载荷,单位为牛顿。
L:梁的跨度,单位为米。
E:混凝土的弹性模量,单位为帕斯卡。
I:梁的截面惯性矩,单位为米的四次方。
2. 多跨梁的挠度计算公式:
梁的挠度 = (q * L^4) / (E * I) * ( (L^2) / 2 - L * x + x^2 / 3 )
公式中的变量含义如下:
挠度:梁的弯曲变形程度,单位为米。
q:集中载荷,单位为牛顿。
L:梁的跨度,单位为米。
E:混凝土的弹性模量,单位为帕斯卡。
I:梁的截面惯性矩,单位为米的四次方。
x:距离梁的起点的长度,单位为米。
注意事项:
1. 当梁的截面形状不规则或荷载不均匀分布时,需要根据具体
情况进行修正。
2. 在实际工程中,通常需要考虑梁的自重、弯矩和剪力等因素,并使用更复杂的公式进行计算。
参考资料:
[1] 林将进, 林曦然. 标准化建筑工程交底书[M]. 科学技术文献
出版社, 2014.
[2] 中国土木工程学会. 建筑结构设计规范[M]. 中国建筑工业出
版社, 2018.。
混凝土梁挠度检测方法

混凝土梁挠度检测方法一、引言混凝土梁是建筑工程中常用的结构元素,其强度和刚度对于整个工程结构的稳定性和安全性起着至关重要的作用。
但是,由于混凝土材料本身的物理特性和施工过程中的一些影响因素,混凝土梁会出现挠度问题。
因此,在工程结构验收和维护过程中,混凝土梁的挠度检测变得必不可少。
本文将介绍混凝土梁挠度检测的方法,包括静载试验法、动态反射法和激光测距法等。
二、静载试验法静载试验法是混凝土梁挠度检测中最为常用的方法之一,其基本原理是通过在混凝土梁上施加一定的荷载,测量荷载下梁的挠度,从而确定梁的刚度和弹性模量。
具体操作步骤如下:1. 准备工作首先,需要准备一组适当的荷载,以及测量梁的长度、宽度、高度等参数。
同时,还需要准备好测量仪器,例如位移计、应变计等。
2. 施加荷载将荷载均匀地分布在混凝土梁上,逐渐增加荷载大小,直至荷载达到预定值为止。
在施加荷载的过程中,需要及时记录下荷载与挠度之间的关系。
3. 测量挠度在荷载施加到预定值后,需要用位移计或应变计等测量仪器测量梁的挠度,记录下荷载下梁的挠度值。
4. 分析数据将施加荷载的过程中记录的荷载与挠度数据进行整理和分析,计算出梁的刚度和弹性模量。
根据计算结果,评估混凝土梁的质量和强度等参数。
三、动态反射法动态反射法是一种无损检测方法,也是混凝土梁挠度检测中的重要方法之一。
其基本原理是通过在混凝土梁上用锤敲击,产生动态载荷,测量梁的振动响应,从而确定梁的刚度和弹性模量。
具体操作步骤如下:1. 准备工作首先,需要准备好一组适当的锤子和传感器,例如加速度计、位移计等。
同时,还需要准备好数据采集软件和计算机等设备。
2. 敲击梁面用锤子在混凝土梁的表面敲击,产生动态载荷。
在敲击的过程中,需要保证敲击的位置均匀、力度适当,以及敲击频率稳定。
3. 测量振动响应在敲击梁面的同时,需要用加速度计、位移计等传感器测量梁的振动响应。
将测量到的数据记录下来。
4. 分析数据将测量到的振动响应数据进行整理和分析,计算出梁的刚度和弹性模量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梁的挠度验算是结构设计中的一个重要步骤,用于确保梁在承受载荷时不会发生过大的弯曲变形。
以下是一个简单的梁挠度验算过程:
确定梁的跨度:首先需要知道梁的跨度,即梁两端之间的距离。
计算均布载荷或集中载荷:确定梁上承受的载荷类型(均布载荷或集中载荷),并计算相应的数值。
计算支座反力:根据梁的支座约束条件,计算出支座反力。
使用挠度公式进行验算:挠度(ω)可由以下公式计算:
(ω = \frac{FL^3}{48EI})
其中,
F 是均布载荷或集中载荷的值,
L 是梁的跨度,
E 是梁材料的弹性模量,
I 是梁的惯性矩。
比较挠度与允许挠度:根据设计规范或标准,确定允许的最大挠度值。
如果计算出的挠度值超过允许的最大挠度值,则需要进行结构加固或重新设计。
考虑其他因素:在实际工程中,可能还需要考虑其他因素,如梁的自重、温度变化、施工误差等对挠度的影响。
请注意,以上是一个简化的梁挠度验算过程,实际工程中可能需要考虑更多的因素和复杂的边界条件。
在进行实际结构设计时,建议咨询专业的结构工程师或查阅相关的结构设计规范和标准。
