高三数学立体几何专题
高三数学立体几何专项练习题及答案

高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形?A. 正方体B. 圆柱体C. 正六面体D. 球体答案:C2. 一个有8个面的多面体,其中6个面是正方形,另外2个面是等边三角形,它的名字是?A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案:C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为?A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案:C4. 任意多面体的面数与顶点数、棱数的关系是?A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案:A5. 求下列多面体的棱数:(1)正六面体(2)正八面体(3)正十二面体答案:(1)正六面体的棱数为 12(2)正八面体的棱数为 24(3)正十二面体的棱数为 30二、填空题1. 下列说法正确的是:一棱锥没有底面时,它的底面是一个______。
答案:点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线,它与该棱垂足的连线相交于该多面体的______上。
答案:中点3. 对正八面体,下列说法不正确的是:_____条对角线与_____两两垂直。
答案:六,相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形,其高为8cm。
求棱锥体积。
解答:底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以,棱锥的体积为64 cm³。
2. 一个正四棱锥的底面是一个边长为10cm的正方形,其高为12cm。
求四棱锥的体积。
解答:底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以,四棱锥的体积为400 cm³。
高三数学二轮复习:立体几何

专题四 立体几何
第1讲 空间几何体
[考情考向分析]
1.以三视图为载体,考查空间几何体面积、体积的计算. 2.考查空间几何体的侧面展开图及简单的组合体问题.
内容索引
热点分类突破 真题押题精练
热规则 俯视图放在正(主)视图的下面,长度与正(主)视图的长度一样,侧(左)视 图放在正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图 的宽度一样.即“长对正、高平齐、宽相等”. 2.由三视图还原几何体的步骤 一般先依据俯视图确定底面再利用正(主)视图与侧(左)视图确定几何体.
跟踪演练3 (1)(2018·咸阳模拟)在三棱锥P-ABC中,PA⊥平面ABC,
AB⊥BC,若AB=2,BC=3,PA=4,则该三棱锥的外接球的表面积为
A.13π C.25π
B.20π
√D.29π
解析 答案
(2)(2018·四川成都名校联考)已知一个圆锥的侧面积是底面积的2倍,
√ 记该圆锥的内切球的表面积为S1,外接球的表面积为S2,则SS12 等于
例3 (1)(2018·百校联盟联考)在三棱锥P-ABC中,△ABC和△PBC均为
边长为3的等边三角形,且PA=326 ,则三棱锥P-ABC外接球的体积为
13 13 A. 6 π
10 10 B. 3 π
√C.5
15 2π
55 D. 6 π
解析 答案
(2)(2018·衡水金卷信息卷)如图是某三棱锥的三视
跟踪演练1 (1)(2018·衡水模拟)已知一几何体的正(主)视图、侧(左)视 图如图所示,则该几何体的俯视图不可能是
√
解析 答案
(2)(2018·合肥质检)在正方体ABCD-A1B1C1D1中,E是棱 A1B1的中点,用过点A,C,E的平面截正方体,则位于 截面以下部分的几何体的侧(左)视图为
立体几何 解答题专项训练-2022届高三数学三轮冲刺复习

(2)点M在线段EF上运动,当点M在什么位置时,平面MAB与平面FCB所成锐二面角最大?并求此时锐二面角的余弦值。
16、在四棱锥P﹣ABCD中,侧面PAB为等边三角形,底面ABCD为直角梯形,AB∥CD,∠DAB=90°,PB=PC=2,CD=AD=1,E为线段AB的中点,过直线CE的平面与线段PA,PD分别交于点M,N.
(1)求证:MN⊥PB;
(2)若直线PC与平面CEMN所成的角的余弦值为 ,求 的值.
17、如图所示,正方形 所在平面与梯形 所在平面垂直, , , , .
(1)求证:EF∥平面SAD.
(2)若G为线段AB上一动点,求平面EFG与平面ABCD间最小锐二面角的余弦值.
15、如图1所示,在矩形 中, , , 为 中点,将 沿 折起,使点 到点 处,且平面 平面 ,如图2所示.
(1)求证: ;
(2)在棱 上取点 ,使平面 平面 ,求直线 与平面 所成角的正弦值.
立体几何解答题专项训练
1、在如图所示的几何体中,四边形 是正方形,四边形 是梯形, , ,平面 平面 ,且 .
(1)求证: 平面 ;
(2)求平面 与平面 所成角的大小;
(3)已知点 在棱 上,且异面直线 与 所成角的余弦值为 ,求点 到平面 的距离.
2、如图,在梯形ABCD中,AB∥CD,∠BCD= ,四边形ACFE为矩形,且CF⊥平面ABCD,AB=CD=BC=CF=1。
(1)证明:平面 平面 .
(2)若 ,求二面角 的余弦值.
11、如图1,已知 为等边三角形,四边形 为平行四边形, ,把 沿 向上折起,使点E到达点P位置,如图2所示;且平面 平面 .
(1)证明: ;
(2)在(1)的条件下求二面角 的余弦值.
2022高考数学立体几何—空间中的动点问题全文

可编辑修改精选全文完整版立体几何—空间中的动点问题专题综述空间中的动点问题是指在一定的约束条件下,点的位置发生变化,在变化过程中找出规律,将动点问题转化为“定点”问题、将空间问题转化为平面问题、将立体几何的问题转化为解析几何的问题等,目的是把问题回归到最本质的定义、定理或现有的结论中去.立体几何中考查动点问题,往往题目难度较大,渗透化归与转化思想,对学生的逻辑推理能力要求较高.一般考查动点轨迹、动点的存在性、定值、范围、最值等问题,除了利用化动为定、空间问题平面化等方法,在几何体中由动点的变化过程推理出结果以外,也可以通过建系,坐标法构建函数,求得结果.专题探究探究1:坐标法解决动点问题建立空间直角坐标系,使几何元素的关系数量化,借助空间向量求解,省去中间繁琐的推理过程.解题步骤与空间向量解决立体几何问题一致,建立适当的空间直角坐标系由动点的位置关系,如在棱上或面内,转化为向量的关系,用参数表示动点的坐标通过空间向量的坐标运算表示出待求的量若求最值或取值范围,转化为函数问题,但要注意自变量的取值范围.一般坐标法用于解决动点的存在性问题、求最值、求范围问题.说明:对于求最值、范围问题,也可以直接通过几何体中的某个变量,构建函数,求最值或范围.(2022湖北省宜昌市模拟) (多选)在正方体1111ABCD A B C D -中,点为线段1AD 上一动点,则( ) A. 对任意的点,都有1B D CQ ⊥ B. 三棱锥1B B CQ -的体积为定值 C. 当为1AD 中点时,异面直线1B Q 与所成的角最小D. 当为1AD 中点时,直线1B Q 与平面11BCC B 所成的角最大【审题视点】以正方体为载体考查定点的定值、最值问题,正方体便于建立空间直角坐标系,可选择用坐标法解决.【思维引导】选项,可以用几何知识证明;选项,设出点坐标,用坐标表示出异面直线成角的余弦值或线面角的正弦值,求最值,得出点位置.【规范解析】解:对于:连接,1.CD因为在正方体1111ABCD A B C D -中, 1B D ⊥平面1ACD ,CQ ⊂平面1ACD , 1B D CQ ⊥,故正确; 对于:平面11//ADD A 平面11BCC B ,平面11ADD A 与平面11BCC B 的距离为正方体棱长,1123111326B B CQ Q BCB V V a a a --==⨯⋅=,为定值,故正确;对于:以为坐标原点,直线分别轴,建立空间直角坐标系如下图:设正方体1111ABCD A B C D -的棱长为2, ()[](),0,20,2Q x x x -∈,则1(2,2,2)B , ()2,2,0B , (0,2,0)C , 因此()12,2,B Q x x =---, ()2,0,0BC =-, 设异面直线1B Q 与所成的角为θ,则当时,,当时,当时,故当与1D 重合时,异面直线1B Q 与所成的角最小,故不正确;对于: ()12,2,B Q x x =---, 又是平面11BCC B 的一个法向量,设直线1B Q 与平面11BCC B 所成的角为α,则,所以当1x =时,sin α取得最大值63,而0,2πα⎡⎤∈⎢⎥⎣⎦, 因此α取得最大值,即当为1AD 中点时,直线1B Q 与平面11BCC B 所成的角最大, 故正确. 故选.ABD用一个参数表示动点的坐标,并求出参数范围,即为函数定义域转化为函数求最值,求出当函数取最值时的x 的值【探究总结】典例1是一道典型的研究动点问题的多选题,难度中等,但能够反映出坐标法研究最值范围问题的思路.建系设坐标,写出参数范围 根据向量运算构造函数求最值.(2021安徽省蚌埠市联考) 已知圆柱1OO 底面半径为1,高为π,是圆柱的一个轴截面,动点从点出发沿着圆柱的侧面到达点,其距离最短时在侧面留下的曲线Γ如图所示.将轴截面绕着轴1OO 逆时针旋转(0)θθπ<<后,边11B C 与曲线Γ相交于点.P(1)求曲线Γ长度; (2)当2πθ=时,求点1C 到平面的距离;(3)证明:不存在(0)θθπ<<,使得二面角D AB P --的大小为.4π探究2:化动为定点的位置在变化的过程中,有些量或位置关系是不变的,比如点到平面的距离不变,从而使几何体的体积不变;动点与另外一定点的连线与某条直线始终垂直,与某个平面始终平行.在证明体积为定值、证明位置关系时,要动中寻定,将动态的问题静态化:将动点转化为定点,寻找动直线所在的确定平面,从而解决问题.答题思路:1.动点到平面的距离为定值:证明平面,动点到平面的距离即为定点到平面的距离;2.为动点,为定点,证明:证明所在平面与垂直;3.为动点,为定点,证明平面:证明所在平面与平面平行.(2021湖南省四校联考) 在正三棱柱中,,,分别为的中点,P 是线段DF 上的一点.有下列三个结论:①平面;②;③三棱锥的体积时定值,其中所有正确结论的编号是 A. ①②B. ①③C. ②③D. ①②③【审题视点】求证关于动直线的线面平行或线线垂直,三棱锥的体积为定值问题,要化动为定.【思维引导】证明动直线所在平面与已知平面平行;证明定直线与动直线所在平面垂直;寻找过点与平面平行的直线,即得出点到平面的距离.【规范解析】解:如图,对于①,在正三棱柱中,,分别为的中点,平面平面,由平面,得平面,故①正确;对于②,在正三棱柱中,平面平面,平面平面平面,,平面平面,故②正确;对于③,平面平面,平面到平面的距离为定值,而有为定值,故是定值,线面平行,转化为面面平行异面直线垂直,转化为线面垂直体积的定值问题,转化点到平面的距离是定值,即通过线面平行或面面平行,得出动点到平面距离为定值故③正确.故选D .【探究总结】立体几何证明中经常出现,求证关于动直线的线面平行与线线垂直问题,其思路是转化为证明动直线所在的定平面与其他平面或直线的位置关系.关键是分析动点,动线或动面间的联系,在移动变化的同时寻求规律.(2021云南省曲靖市联考) 如图所示的几何体中,111ABC A B C -为直三棱柱,四边形为平行四边形,2CD AD =,60ADC ∠=︒,1.AA AC =(1)证明:,1C ,1B 四点共面,且11A C DC ⊥;(2)若1AD =,点是上一点,求四棱锥的体积,并判断点到平面11ADC B 的距离是否为定值?请说明理由.探究3: 巧用极端位置由于点位置连续变化,使研究的图形发生连续的变化,利用点的位置变化“极端”位置,避开抽象及复杂的运算,得到结论.常见题型:1.定值问题:几何体中存在动点,但所求结果是确定的,即随着动点位置的改变不会影响所求的量,故可以考虑动点在极端位置的情况,优化解题过程.2.范围问题:几何体中存在动点,结果会随着动点位置改变而改变,当动点从一侧极端位置移动到令一个极端位置的过程中,所求量在增大、或减小、或先增后减、或先减后增,通过求出极端位置处的值,及最值,从而得出范围;3.探究问题:探究满足条件的点是否存在,也可以转化为求出范围,从而得出结论.(2021湖南省株洲市模拟) 在正四面体中, 为棱的中点, 为直线上的动点,则平面与平面夹角的正弦值的取值范围是 .【审题视点】本例可用极端位置法分析,也可以建系,用坐标法解决.【思维引导】借助极端位置分析,不难看出经过和底边中线的平面与平面垂直,点在移动的过程中,存在一个位置使平面与经过和底边中线的平面平行,即平面平面,此时两平面所成角为,角最大;当点移动到无穷远时,平面平面,此时两平面所成角最小.【规范解析】解:由下左图 设为的中心,为的中点, 则在正四面体中平面, 为中点,为的中点,,故平面连接,并延长交于点, 连接,并延长交于点, 则过点的平面交直线于点. 则平面平面 即平面与平面的夹角的正弦值为1,点从取最值的位置处移动至直线的无穷远处的过程中, 平面与平面的夹角逐渐减小,即当点在无穷远处时,看作, 如下右图 故平面与平面的夹角即为平面与平面的夹角,求出其正弦值为. 综上可知:面与面的夹角的正弦值的取值范围为.【探究总结】借助极端位置解决典例3中的问题,首先利用几何知识,明确点在移动的过程中 ,所求量的变化情况,若在极端位置处取“最值”,问题就简化为求出极端位置处的值.(2021浙江省杭州市高三模拟)高为1的正三棱锥的底面边长为,二面角与二面角A PB C --之和记为,则在从小到大的变化过程中,的变化情况是( )A .一直增大B .一直减小C .先增大后减小D .先减小后增大专题升华结合几何知识,两平面成角的变化过程,即动点从一个极端位置变化到另一极端位置时,夹角大小的增减情况在极端位置处取“最值”,直接求出点该处时的夹角的正弦值,即为范围区间的一个端点几何体中研究动点问题往往难度较大,开放性强,技巧性高.总体思路是:用几何知识,经过逻辑推理,证明位置关系或求出表示出所求量;或者建立空间直角坐标系,将几何问题代数化,用空间向量研究动点问题,省去了繁杂的推理环节,但计算量较大.解决动点问题的策略不局限与上述方法,常用的的方法还有:运用条件直接推算,借助条件将几何体还原到长方体中去;构造函数,数形结合;还将空间问题转化为平面几何解决,如化折为直、利用解析几何的知识解决. 但只要我们熟练掌握这些基本方法,并灵活加以应用,不仅能化繁为简,化难为易,而且还可以得到简捷巧妙的解法.【答案详解】 变式训练1【解答】解:(1)在侧面展开图中为的长,其中AB AD π==,∴曲线Γ的长为2;π(2)当2πθ=时,建立如图所示的空间直角坐标系,则有()0,1,0A -、()0,1,0B 、1,0,2P π⎛⎫- ⎪⎝⎭、()11,0,C π-, 、(1,1,)2AP π=-、1(1,0,)OC π=-设平面的法向量为(,,)n x y z =,则2002n AB y n AP x y z π⎧⋅==⎪⎨⋅=-++=⎪⎩, 取2z =得(,0,2)n π=,所以点1C 到平面的距离为12||||4OC n d n ππ⋅==+; (3)假设存在满足要求的(0)θθπ<<, 在(2)的坐标系中,()sin ,cos ,P θθθ-,,设平面的法向量为111(,,)m x y z =,则111120sin (cos 1)0y x y z θθθ=⎧⎨-+++=⎩,取11x =得sin (1,0,)m θθ=,又平面的法向量为(1,0,0)k =,由二面角D AB P --的大小为4π, 则|cos ⟨,m k ⟩2212|sin .21sin θθθθ==⇒=+ sin (0)2πθθθ<<<,0θπ∴<<时,均有sin θθ<,与上式矛盾.所以不存在(0)θθπ<<使得二面角D AB P --的大小为.4π 变式训练2【解答】(1)证明:因为111ABC A B C -为直三棱柱, 所以,且,又四边形为平行四边形,//BC AD ,且BC AD =,,且,四边形为平行四边形,,1B 四点共面;,又1AA ⊥平面,AC ⊂平面,,四边形11A ACC 为正方形,连接1AC 交1A C 于,,在ADC ∆中,2CD AD =,,由余弦定理得,,所以,AD AC ⊥,又1AA ⊥平面ABCD ,AD ⊂平面ABCD ,1AA AD ⊥,,1AA ⊂平面11A ACC ,,AD ⊥平面11A ACC ,1AC ⊂平面11A ACC ,所以,又,平面,1A C ⊥平面, 1DC ⊂平面,(2)解:由(1)知:1A C ⊥平面,在Rt DAC 中,由已知得3AC =,,四棱锥的体积,//BC AD ,点到平面的距离为定值,即为点到平面的距离变式训练3【解析】解:设二面角为,二面角A PB C --为,当时,正三棱锥趋向于变为正三棱柱,;当时,正三棱锥趋向变为平面,.当正三棱锥为正四面体时,且,,故.当从小变大时,要经过从变为小于的角,然后变为的过程, 故只有选项符合.故选:.静夜思[ 唐] 李白原文译文对照床前明月光,疑是地上霜。
高三数学立体几何试题答案及解析

高三数学立体几何试题答案及解析1.已知三棱锥的三视图,则该三棱锥的体积是()A.B.C.D.【答案】B【解析】如图所示,,点P在侧面ABC的射影为O,.∴该三棱锥的体积.故选:B.【考点】由三视图求面积、体积.2.(本小题满分12分)直三棱柱中,,,分别是、的中点,,为棱上的点.(1)证明:;(2)是否存在一点,使得平面与平面所成锐二面角的余弦值为?若存在,说明点的位置,若不存在,说明理由.【答案】(1)证明见解析;(2)存在,点为中点.【解析】(1)先证明AB⊥AC,然后以A为原点建立空间直角坐标系A-xyz,则能写出各点坐标,由共线可得D(λ,0,1),所以,即DF⊥AE;(2)通过计算,面DEF的法向量为可写成,=(3,1+2λ,2(1-λ)),又面ABC的法向量=(0,0,1),令,解出λ的值即可.试题解析:(1)证明:,又,面又面以为原点建立如图所示的空间直角坐标系则,,,,设,且,即:(2)假设存在,设面的法向量为,则即:令由题可知面的法向量平面与平面所成锐二面角的余弦值为即:或(舍)当点为中点时,满足要求.【考点】1、二面角的平面角及求法;2、直线与平面垂直的性质.【方法点晴】本题考查空间中直线与直线的位置关系、空间向量及其应用,建立空间直角坐标系是解决问题的关键,属中档题.解题时一定要注意二面角的平面角是锐角还是钝角,否则很容易出现错误.3.已知正四棱锥中,,那么当该棱锥的体积最大时,它的高为()A.B.C.D.【答案】C【解析】设正四棱锥的高为,则,则,,所以四棱锥的体积,,由得,所以体积函数在区间上单调递增,在区间上单调递减,所以当时,体积有最大值,故选C.【考点】1.多面体体积;2.导数与函数最值.【方法点睛】本题主要考查本题主要考查立体几何中的最值问题,多面体体积公式、导数与函数等知识,属中档题.解决此类问题的两大核心思路:一是将立体问题转化为平面问题,结合平面几何的相关知识求解;二是建立目标函数的数学思想,选择合理的变量,利用导数、基本不等式或配方法求其最值.4.设三棱锥的三条侧棱两两互相垂直,且长度分别为,则其外接球的表面积为()A.B.C.D.【答案】B【解析】由题意可知其外接球的直径,所以外接球的表面积为.【考点】球的表面积公式.5.某几何体的三视图如图所示,则该几何体的体积为.【答案】【解析】该几何体为一个四棱锥,高为,底面为矩形,长宽分别为,因此体积为【考点】三视图6.已知是两条不同的直线,是三个不同的平面,则下列命题中正确的是()A.若B.若C.若D.若【答案】C【解析】垂直于同一平面的两个平面可能平行,也可能相交,所以A选项不正确;两个平面内存在两条平行的直线时,两平面可能相交,也可能平行,所以B选项不正确;,又,,所以C选项正确;若,则或,所以D不正确.故D正确.【考点】1线面位置关系;2面面位置关系.【易错点晴】本题主要考查的是空间点、线、面的位置关系,属于容易题.解题时一定要抓住题目中的重要字眼“真命题”,否则很容易出现错误.解决空间点、线、面的位置关系这类试题时一定要万分小心,除了作理论方面的推导论证外,利用特殊图形进行检验,也可作必要的合情推理.7.已知直线平面,直线平面,给出下列命题,其中正确的是()①;②;③;④A.②④B.②③④C.①③D.①②③【答案】C【解析】对①,因为直线平面,∥,则,又直线,所以,①对;对②,与的关系是:平行、相交或异面,②错;对③,因为直线平面,∥,所以,又由面面垂直的判定定理得,③对;对④,与可以平行或相交,④错,所以选C.本题可借助于长方体去判定.【考点】1.空间直线、平面的位置关系.【易错点晴】本题主要考查的是空间点、线、面的位置关系,属于中档题.解决空间点、线、面的位置关系这类试题时一定要万分小心,除了作理论方面的推导论证外,利用特殊图形或长方体作为载体进行检验,也可作必要的合情推理.8.利用一个球体毛坯切削后得到一个四棱锥P—ABCD,其中底面四边形ABCD是边长为1的正方形,,且,则球体毛坯体积的最小值应为()A.B.C.D.【答案】D【解析】若使得球体毛坯体积最小,则四棱锥各顶点应都在球上,由题意,将四棱锥补成一个长方体,则转化为求长方体外接球体积,长方体体对角线为外接球直径,体对角线长为,所以球的半径为,体积为.【考点】多面体的外接球.9.(2007•山东)下列几何体各自的三视图中,有且仅有两个视图相同的是()A.①②B.①③C.①④D.②④【答案】D【解析】利用三视图的作图法则,对选项判断,A的三视图相同,圆锥,四棱锥的两个三视图相同,棱台都不相同,推出选项即可.解:正方体的三视图都相同,而三棱台的三视图各不相同,圆锥和正四棱锥的,正视图和侧视图相同,所以,正确答案为D.故选D【考点】简单空间图形的三视图.10.如图是某几何体的三视图,其中正视图为正方形,俯视图是腰长为的等腰直角三角形,则该几何体的体积为_________________;表面积为________________.【答案】体积为;表面积为【解析】由题意可知三视图复原的几何体如图为四棱锥,是正方体的一部分,正方体的棱长为2;所以几何体的体积是正方体体积的一半减去,所求几何体的体积为;表面积为【考点】三视图,几何体的体积,表面积11.已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为()A.B.C.D.【答案】A【解析】根据该几何体的三视图可知几何体的形状是一个长为,宽为,高为的长方体挖去一个直径为高为的圆柱,该几何体的体积为,选A.【考点】1、三视图;2、组合体的体积.12.如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆千克,则共需油漆的总量为()A.千克B.千克C.千克D.千克【答案】B【解析】由三视图可知可间房由底部长宽高分别为的长方体与底面半径.母线长分别为圆锥体组合而成,所以其可刷漆的表面积为,则需要漆的总量为千克,故正确选项为B.【考点】空间几何体的表面积.13.若=(2,﹣1,0),=(3,﹣4,7),且(λ+)⊥,则λ的值是()A.0B.1C.﹣2D.2【答案】C【解析】利用(λ+)⊥⇔即可得出.解:∵=λ(2,﹣1,0)+(3,﹣4,7)=(3+2λ,﹣4﹣λ,7),(λ+)⊥,∴,∴2(3+2λ)﹣(﹣4﹣λ)+0=0,解得λ=﹣2.故选C.【考点】向量的数量积判断向量的共线与垂直.14.如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD,(Ⅰ)求证:平面PED⊥平面PAC;(Ⅱ)若直线PE与平面PAC所成的角的正弦值为,求二面角A﹣PC﹣D的平面角的余弦值.【答案】(Ⅰ)证明见解析(Ⅱ)【解析】(I)由面面垂直的性质定理证出PA⊥平面ABCD,从而得到AB、AD、AP两两垂直,因此以AB、AD、AP为x轴、y轴、z轴,建立坐标系o﹣xyz,得A、D、E、C、P的坐标,进而得到、、的坐标.由数量积的坐标运算公式算出且,从而证出DE⊥AC且DE⊥AP,结合线面垂直判定定理证出ED⊥平面PAC,从而得到平面PED⊥平面PAC;(II)由(Ⅰ)得平面PAC的一个法向量是,算出、夹角的余弦,即可得到直线PE与平面PAC所成的角θ的正弦值,由此建立关于θ的方程并解之即可得到λ=2.利用垂直向量数量积为零的方法,建立方程组算出=(1,﹣1,﹣1)是平面平面PCD的一个法向量,结合平面PAC的法向量,算出、的夹角余弦,再结合图形加以观察即可得到二面角A ﹣PC﹣D的平面角的余弦值.解:(Ⅰ)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AB⊥PA∴PA⊥平面ABCD结合AB⊥AD,可得分别以AB、AD、AP为x轴、y轴、z轴,建立空间直角坐标系o﹣xyz,如图所示可得A(0,0,0)D(0,2,0),E(2,1,0),C(2,4,0),P(0,0,λ)(λ>0)∴,,得,,∴DE⊥AC且DE⊥AP,∵AC、AP是平面PAC内的相交直线,∴ED⊥平面PAC.∵ED⊂平面PED∴平面PED⊥平面PAC(Ⅱ)由(Ⅰ)得平面PAC的一个法向量是,设直线PE与平面PAC所成的角为θ,则,解之得λ=±2∵λ>0,∴λ=2,可得P的坐标为(0,0,2)设平面PCD的一个法向量为=(x0,y,z),,由,,得到,令x0=1,可得y=z=﹣1,得=(1,﹣1,﹣1)∴cos<,由图形可得二面角A﹣PC﹣D的平面角是锐角,∴二面角A﹣PC﹣D的平面角的余弦值为.【考点】用空间向量求平面间的夹角;平面与平面垂直的判定;二面角的平面角及求法.15.已知正三棱锥的底面边长为,侧棱长为,则正三棱锥的体积为.【答案】【解析】∵正三棱锥的底面边长为,∴底面正三角形的高为,可得底面中心到三角形顶点的距离为,∵正三棱锥侧棱长为,∴正三棱锥的高,所以三棱锥的体积.所以答案应填:.【考点】棱柱、棱锥、棱台的体积.16.在等腰梯形中,,,,是的中点,将梯形绕旋转,得到(如图).(I)求证:;(II)求二面角的余弦值.【答案】(1)证明见解析;(2).【解析】(I)由题意容易证明四边形是平行四边形,.又为等腰梯形,,四边形是菱形,可证得,根据面面垂直的性质定理可证得平面,从而证得;(II)易证平面,以为坐标原点,建立空间直角坐标系,分别求出平面的法向量和平面的法向量,根据向量的夹角公式求得二面角的余弦值.试题解析:(I)证明:,是的中点,.又,四边形是平行四边形,.又为等腰梯形,,,四边形是菱形,,,即.平面平面,平面平面,平面.又平面,.(II)解:平面,同理平面.如图建立空间直角坐标系,设,则,,,,则,.设平面的法向量为,.设平面的法向量为,,设二面角的平面角为,,二面角的余弦值为.【考点】空间中垂直关系的证明及空间向量的应用.17.如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的正(主)视图与侧(左)视图的面积的比为.【答案】【解析】因为三棱锥的主视图与左视图都是三角形, 正视图和侧视图三角形的底边长都是正方体的棱长,高都是到底面的距离(都是正方体的棱长),所以,三棱锥的主视图与左视图的面积相等,即比值为,故答案为.【考点】1、几何体的三视图;2、三角形面积公式.18.如图,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则几何体的体积为()A.B.C.D.【答案】B【解析】如图所示,该几何体是一个底面为平行四边形,高为的棱柱,体积为,故选B.【考点】几何体的体积.19.如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为________.【答案】【解析】因为矩形是水平放置的一个平面图形的直观图,所以根据画直观图的基本原理知原图形是底边长为的平行四边形,其高是,因此面积是,故答案为.【考点】1、画直观图的基本原理;2、平行四边形的面积公式.20.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为()A.B.C.D.【答案】D【解析】由三视图知几何体是由正方体截取两个角得到,如图所示,故体积为.【考点】三视图.21.如图所示,四棱锥的底面是梯形,且,平面,是中点,.(Ⅰ)求证:平面;(Ⅱ)若,,求直线与平面所成角的大小.【答案】(I)证明见解析;(II).【解析】(I)取的中点,连结,证得,从而证得平面,根据平行四边形的性质,得,即可证明平面;(II)分别以的方向为轴的正方向,建立空间直角坐标系,求解出平面和向量,即可利用向量所成的角,得到直线与平面所成角的大小.试题解析:(Ⅰ)证明:取的中点,连结,如图所示.因为,所以.因为平面,平面,所以.又因为,所以平面.因为点是中点,所以,且.又因为,且,所以,且,所以四边形为平行四边形,所以,所以平面.(Ⅱ)解:设点O,G分别为AD,BC的中点,连结,则,因为平面,平面,所以,所以.因为,由(Ⅰ)知,又因为,所以,所以所以为正三角形,所以,因为平面,平面,所以.又因为,所以平面.故两两垂直,可以点O为原点,分别以的方向为轴的正方向,建立空间直角坐标系,如图所示.,,,所以,,,设平面的法向量,则所以取,则,设与平面所成的角为,则,因为,所以,所以与平面所成角的大小为.【考点】直线与平面垂直的判定与证明;直线与平面所成角的求解.22.如图,在三棱台中,平面平面,,BE=EF=FC=1,BC=2,AC=3.(Ⅰ)求证:BF⊥平面ACFD;(Ⅱ)求二面角B-AD-F的平面角的余弦值.【答案】(Ⅰ)证明见解析;(Ⅱ).【解析】(Ⅰ)先证,再证,进而可证平面;(Ⅱ)方法一:先找二面角的平面角,再在中计算,即可得二面角的平面角的余弦值;方法二:先建立空间直角坐标系,再计算平面和平面的法向量,进而可得二面角的平面角的余弦值.试题解析:(Ⅰ)延长,,相交于一点,如图所示.因为平面平面,且,所以平面,因此.又因为,,,所以为等边三角形,且为的中点,则.所以平面.(Ⅱ)方法一:过点作于Q,连结.因为平面,所以,则平面,所以.所以是二面角的平面角.在中,,,得.在中,,,得.所以二面角的平面角的余弦值为.方法二:如图,延长,,相交于一点,则为等边三角形.取的中点,则,又平面平面,所以,平面.以点为原点,分别以射线,的方向为,的正方向,建立空间直角坐标系.由题意得,,,,,.因此,,,.设平面的法向量为,平面的法向量为.由,得,取;由,得,取.于是,.所以,二面角的平面角的余弦值为.【考点】线面垂直,二面角.【方法点睛】解题时一定要注意二面角的平面角是锐角还是钝角,否则很容易出现错误.证明线面垂直的关键是证明线线垂直,证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线.23.直线a、b是异面直线,α、β是平面,若a⊂α,b⊂β,α∩β=c,则下列说法正确的是()A.c至少与a、b中的一条相交B.c至多与a、b中的一条相交C.c与a、b都相交D.c与a、b都不相交【答案】A【解析】利用空间中线线、线面、面面间的位置关系判断求解.解:由直线a、b是异面直线,α、β是平面,若a⊂α,b⊂β,α∩β=c,知:对于B,c可以与a、b都相交,交点为不同点即可,故B不正确;对于C,a∥c,b∩c=A,满足题意,故C不正确;对于D,c与a、b都不相交,则c与a、b都平行,所以a,b平行,与异面矛盾,故D不正确;对于A,由B,C、D的分析,可知A正确故选:A.24.已知某几何体的三视图如图所示,则该几何体的体积等于()A.B.160C.D.【答案】A【解析】由三视图知该几何体是由一个直三棱柱和一个四棱锥组合的组合体,其中直三棱柱的底面为左视图,高为,故体积.四棱锥的底面为边长为的正方形,高为,所以体积,所以该几何体的体积为.故选A.【考点】1、几何体的三视图;2、几何体的体积.【方法点睛】本题主要考查三视图及空间几何体的体积,属于中档题.空间几何体体积问题的常见类型及解题策略:(1)求简单几何体的体积时若所给的几何体为柱体椎体或台体,则可直接利用公式求解;(2)求组合体的体积时若所给定的几何体是组合体,不能直接利用公式求解,则常用转换法、分割法、补形法等进行求解. (3)求以三视图为背景的几何体的体积时应先根据三视图得到几何体的直观图,然后根据条件求解.25.中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为()A.1.2B.1.6C.1.8D.2.4【答案】B【解析】由题意得,即,解得,故选B.【考点】几何体的三视图及体积.26.某几何体的三视图如图所示(单位:cm),则该几何体的体积等于()cm3A.4+B.4+C.6+D.6+【答案】D【解析】由三视图还原原几何体如图,是一个半圆柱与一个直三棱柱的组合体,半圆柱的底面半径为,高为;直三棱柱底面是等腰直角三角形(直角边为),高为.∴.故本题选D.【考点】空间几何体的三视图.27.在正方体中,是的中点,则异面直线与所成角的余弦值等于_______,若正方体边长为1,则四面体的体积为_________.【答案】;【解析】异面直线与所成角为,,.【考点】立体几何中异面直线所成角的余弦值的求法以及三棱锥的体积的求法.28.如图,在四棱锥中,底面,,,,,点为棱的中点.(1)证明:;(2)若为棱上一点,满足,求二面角的余弦值.【答案】(1)证明见解析;(2).【解析】(1)以点为原点建立空间直角坐标系(如图),求得,,可得,即可证结论;(2)先根据确定的位置,在求出平面的一个法向量,可证平面一个的法向量为,利用空间向量夹角余弦公式即可得结论.试题解析:(1)证明:依题意,以点为原点建立空间直角坐标系(如图),可得,,,.由为棱的中点,得.向量,,故.所以.(2)向量,,,.由点在棱上,设,.故.由,得,因此,,解得.即.设为平面的法向量,则,即.不妨令,可得为平面的一个法向量.取平面的法向量,则.易知,二面角是锐角,所以其余弦值为.【考点】1、空间直线垂直的判定;2、空间向量夹角余弦公式.29.如图,在三棱锥中,底面,且,点是的中点, 交于点.(1)求证:平面;(2)当时, 求三棱锥的体积.【答案】(1)详见解析(2)【解析】(1)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的证明与寻找,往往从两个方面,一是利用线面垂直性质定理转化为线线垂直,另一是结合平几条件,如本题利用等腰三角形底边中线性质得(2)求三棱锥体积,关键在于确定高,即线面垂直.由(1)得平面,因此,这样只需在对应三角形中求出对应边即可.试题解析:(1)底面,面,又因为是的中点, 面由已知平面.(2)平面,平面,而,又又平面而.【考点】线面垂直判定与性质定理,三棱锥体积【思想点睛】垂直、平行关系证明中应用转化与化归思想的常见类型.(1)证明线面、面面平行,需转化为证明线线平行.(2)证明线面垂直,需转化为证明线线垂直.(3)证明线线垂直,需转化为证明线面垂直.30.过球表面上一点引三条长度相等的弦,且两两夹角都为60°,若球半径为,求弦的长度___________.【答案】【解析】依题意可知,这是一个正四面体的外接球. 若一个正四面体边长为,其外接球半径公式为:,即.【考点】球的内接几何体.【思路点晴】对棱相等的三棱锥,设三对棱长分别为,如下图所示三棱锥,请同学们推导其外接球半径公式,特别地,若一个正四面体边长为,其外接球半径公式为:.设几何体底面外接圆半径为,常见的图形有正三角形,直角三角形,矩形,它们的外心可用其几何性质求;而其它不规则图形的外心,可利用正弦定理来求.2.若长方体长宽高分别为则其体对角线长为;长方体的外接球球心是其体对角线中点.找几何体外接球球心的一般方法:过几何体各个面的外心分别做这个面的垂线,交点即为球心.31.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】D【解析】由题意得,根据给定的三视图可知,原几何体表示,左侧是一个底面半径为,高为半个圆锥,几何体的右侧是一个底面为底边为,高为的等腰三角形三棱锥,其中三棱锥的高为,所以几何体的体积为,故选D.【考点】几何体的三视图及体积的计算.32.已知直线与平面平行,是直线上的一定点,平面内的动点满足:与直线成.那么点轨迹是()A.两直线B.椭圆C.双曲线D.抛物线【答案】C【解析】题意画图如下,是直线上的定点,有一平面与直线平行,平面内的动点满足的连线与成角,因为空间中过与成角的直线组成两个相对顶点的圆锥,即为平行于圆锥轴的平面,点可理解为是截面与圆锥侧面的交点,所以点的轨迹为双曲线,故选C.【考点】1、空间点、线、面的位置关系;2、圆锥曲线的定义.33.三棱锥内接于球,,当三棱锥的三个侧面积和最大时,球的体积为.【答案】【解析】由于三角形的面积公式,当时取得最大值,所以当两两垂直时,侧面积和取得最大值.此时,由于三棱锥三条侧棱两两垂直,所以可以补形为正方体,三棱锥的外接球即正方体的外接球,其直径等于正方体的体对角线即,故求的体积为.【考点】几何体的外接球.【思路点晴】设几何体底面外接圆半径为,常见的图形有正三角形,直角三角形,矩形,它们的外心可用其几何性质求;而其它不规则图形的外心,可利用正弦定理来求.若长方体长宽高分别为则其体对角线长为;长方体的外接球球心是其体对角线中点.找几何体外接球球心的一般方法:过几何体各个面的外心分别做这个面的垂线,交点即为球心.三棱锥三条侧棱两两垂直,且棱长分别为,则其外接球半径公式为: .34.如图,在直三棱柱中,,过的中点作平面的垂线,交平面于,则与平面所成角的正切值为()A.B.C.D.【答案】C【解析】连接,则,由直三棱柱得,因此,因此为的中点,过作于,则为与平面所成角, ,选C.【考点】线面角35.如图,在四棱锥中,底面,底面是直角梯形,(1)在上确定一点,使得平面,并求的值;(2)在(1)条件下,求平面与平面所成锐二面角的余弦值.【答案】(1)(2)【解析】(1)由线面平行的性质定理,可得线线平行,再根据平行得相似,即得比例关系:取。
2022高三高考数学知识点第7章 高考专题突破4 高考中的立体几何问题

跟踪训练3 (2020·宜昌一中模拟)如图,在四棱锥 P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC, AD=DC=AP=2,AB=1,点E为棱PC的中点. (1)证明:BE⊥PD;
解 依题意,以点A为原点,以AB,AD,AP为x轴、y轴、z轴建立空间 直角坐标系如图, 可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2). 由E为棱PC的中点,得E(1,1,1). 证明 向量B→E=(0,1,1),P→D=(0,2,-2), 故B→E·P→D=0,所以B→E⊥P→D,所以 BE⊥PD.
设直线AM与平面PBC所成的角为θ,
则
sin
θ=|cos〈m,A→M〉|=
→ |m·AM|
→
=
|m|·|AM|
23×1+12×0+
2×
7 4
23×1=
42 7.
∴直线 AM 与平面 PBC 所成角的正弦值为
42 7.
命题点3 二面角
例3 (2020·全国Ⅰ)如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为
设平面QCD的一个法向量为n=(x,y,z),
[5分] [6分]
则DD→→CQ··nn==00,, 即ym=x+0,z=0,
令x=1,则z=-m, 所以平面QCD的一个法向量为n=(1,0,-m),
则 cos〈n,P→B〉=|nn|·|PP→→BB|=
1+0+m 3· m2+1.
[9分] [10分]
当且仅当m=1时取等号,
所以直线PB与平面QCD所成角的正弦值的最大值为
6 3
.
[12分]
答题模板
第一步:根据线面位置关系的相关定理,证明线面垂直. 第二步:建立空间直角坐标系,确定点的坐标. 第三步:求直线的方向向量和平面的法向量. 第四步:计算向量夹角(或函数值),借助基本不等式确定最值. 第五步:反思解题思路,检查易错点.
高三数学立体几何试题答案及解析
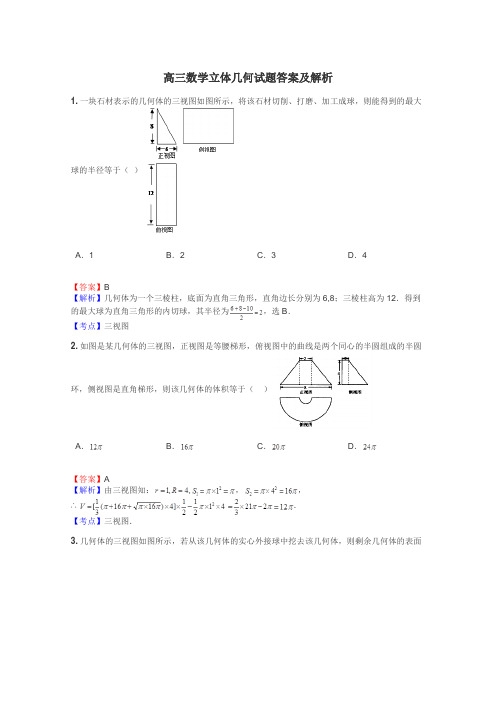
高三数学立体几何试题答案及解析1.一块石材表示的几何体的三视图如图所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4【答案】B【解析】几何体为一个三棱柱,底面为直角三角形,直角边长分别为6,8;三棱柱高为12.得到的最大球为直角三角形的内切球,其半径为,选B.【考点】三视图2.如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于()A.B.C.D.【答案】A【解析】由三视图知:,,∴.【考点】三视图.3.几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)()A.133B.100C.66D.166【答案】D【解析】由三视图知,该几何体为底面半径为3,搞为8的圆柱.其外接球时半径为5的球.则剩余几何体的表面积是球的表面积与该圆柱表面积的和,即.故选D.【考点】多面体及与其外接球的关系及几何体表面积计算问题.4.(本小题满分12分)如图,已知五面体,其中内接于圆,是圆的直径,四边形为平行四边形,且平面.(1)证明:;(2)若,,且二面角所成角的正切值是,试求该几何体的体积.【答案】(1)见解析;(2)8.【解析】(1)将问题转化为证明平面,再转化为证明(由直径可证)与(由平面可证);(2)考虑建立空间直角坐标系,通过求两个法向量的夹角来确定二面角所成角的正切值,并确定的长,进而可求得几何体的体积.试题解析:(1)证明:是圆的直径,,又平面,又平面,且,平面又平面,(2)设,以所在直线分别为轴,轴,轴,如图所示则,,,由(Ⅰ)可得,平面,平面的一个法向量是设为平面的一个法向量由条件得,,即不妨令,则,,.又二面角所成角的正切值是,,得该几何体的体积是【考点】1、空间直线与直线、直线与平面的垂直的判定与性质;2、二面角;3、空间几何体的体积.【方法点睛】用空间向量处理某些立体几何问题时,除要有应用空间向量的意识外,关键是根据空间图形的特点建立恰当的空间直角坐标系.若坐标系选取不当,计算量就会增大.总之树立用数解形的观念,即用数形结合的思想解决问题,而建立空间直角坐标系通常考虑以特殊点为坐标原点(如中点、正方体的顶点),特殊直线(如有两两垂直的直线)为坐标轴来建立.5.如图,在多面体中,为菱形,,平面,平面,为的中点,若平面.(1)求证:平面;(2)若,求二面角的余弦值.【答案】(1)见解析;(2).【解析】(1)证明线面垂直,只要证明这条直线与平面内两条相交直线垂直即可,取中点,连接,可证,先证,即可证明,即可证明结论成立;(2)建立空间直角坐标系,求出平面与平面的法向量,由空间向量公式直接计算即可.试题解析:(1)取AB的中点M,连结GM,MC,G为BF的中点,所以GM //FA,又EC面ABCD, FA面ABCD,∵CE//AF,∴CE//GM,∵面CEGM面ABCD=CM,EG// 面ABCD,∴EG//CM,∵在正三角形ABC中,CM AB,又AF CM∴EG AB, EG AF,∴EG面ABF.(2)建立如图所示的坐标系,设AB=2,则B()E(0,1,1) F(0,-1,2)=(0,-2,1),=(,-1,-1),=(,1, 1),设平面BEF的法向量=()则令,则,∴=()同理,可求平面DEF的法向量 =(-)设所求二面角的平面角为,则=.【考点】1.线面垂直的判定与性质;2.空间向量的应用.【方法点睛】本题主要考查线面垂直的判定与性质、空间向量的应用,属中档题.解答空间几何体中的平行、垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间的平行、垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;求二面角,则通过求两个半平面的法向量的夹角间接求解.此时建立恰当的空间直角坐标系以及正确求出各点的坐标是解题的关键所在.6.三棱锥及其三视图中的正视图和侧视图如下图所示,,则棱的长为.【答案】.【解析】由已知三视图可知,平面,且底面为等腰三角形.在中,,边上的高为,所以.在中,由可得,故应填.【考点】1、三视图.【易错点晴】本题主要考查了空间几何体的三视图及其空间几何体的面积、体积的计算,考查学生空间想象能力和计算能力,属中档题.其解题过程中容易出现以下错误:其一是不能准确利用已知条件的三视图得出原几何体的空间形状,即不能准确找出该几何体中线线关系、线面关系,导致出现错误;其二是计算不仔细,导致结果出现错误.解决这类问题的关键是正确地处理三视图与原几何体之间的关系.7.在三棱锥中,平面为侧棱上的一点,它的正视图和侧视图如图所示,则下列命题正确的是()A.平面且三棱锥的体积为B.平面且三棱锥的体积为C.平面且三棱锥的体积为D.平面且三棱锥的体积为【答案】C【解析】∵平面,∴,又,∴平面,∴,又由三视图可得在中,为的中点,∴平面.又平面.故.故选:C.【考点】1.直线与平面垂直的判定;2.命题的真假判断与应用;3.简单空间图形的三视图.8.已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于()A.B.C.D.【答案】C【解析】题设三视图是下图中几何体的三视图,由三视图中的尺寸,知其体积为,故选C.【考点】三视图与几何体的体积.9.如图,在三棱柱ABC A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证:(Ⅰ)DE∥平面ABC1;(Ⅱ)B1C⊥DE.【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析.【解析】(Ⅰ)取AA1的中点F,连DF,FE,根据中点易证线线平行,从而平面DEF∥平面ABC1,又因为DE平面DEF,所以B1C⊥DE;(Ⅱ)在菱形中B1C⊥BC1,又B1C⊥AB,易证B1C⊥平面ABC1,再根据面面平行的性质,得:B1C⊥平面DEF,从而证明B1C⊥DE.试题解析:(Ⅰ)如图,取AA1的中点F,连DF,FE.又因为D,E分别为A1C1,BB1的中点,所以DF∥AC1,EF∥AB.因为DF平面ABC1,AC1平面ABC1,故DF∥平面ABC1.同理,EF∥平面ABC1.因为DF,EF为平面DEF内的两条相交直线,所以平面DEF∥平面ABC1.因为DE平面DEF,所以DE∥平面ABC1.(Ⅱ)因为三棱柱ABC A1B1C1的侧面BCC1B1为菱形,故B1C⊥BC1.……9分又B1C⊥AB,且AB,BC1为平面ABC1内的两条相交直线,所以B1C⊥平面ABC1.而平面DEF∥平面ABC1,所以B1C⊥平面DEF,因为DE平面DEF,所以B1C⊥DE.【考点】1、线面平行;2、面面平行;3、线面垂直;4、三角形中位线.【方法点晴】本题主要考查的是线面平行、线线平行、线线垂直和线面垂直,属于中档题.解题时一定要注意得线线平行的常用证明方法,构造中位线和平行四边形是最常用方法.证明线面垂直的关键是证明线线垂直,证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线.10.已知,是两个不同的平面,,是两条不同的直线,则下列正确的是()A.若,,则B.若,,,则C.若,,,则D.若,,,则【答案】C.【解析】A:或者,异面,故A错误;B:根据面面垂直的判定可知B错误;C:正确;D:或,故D错误,故选C.【考点】空间中直线平面的位置关系.11.已知三条不重合的直线和两个不重合的平面,下列命题正确的是()A.若,,则B.若,,且,则C.若,,则D.若,,且,则【答案】D【解析】A.若,,则,错,有可能;B.若,,且,则,错,有可能;C.若,,则,错,有可能,或异面;D.若,,且,则,正确【考点】空间直线与平面,平面与平面的位置关系12.如图,三角形是边长为4的正三角形,底面,,点是的中点,点在上,且.(1)证明:平面平面;(2)求直线和平面所成角的正弦值.【答案】(1)证明见解析;(2).【解析】(1)由底面,可得,又,可证的平面,问题得证;(2)在第一问证明的基础上,应用面面垂直的性质定理容易作出平面的垂线,即得斜线的射影,找出角,解直角三角形可得线面角的正弦.试题解析:(1)证明∵底面,底面,∴,又,,∴平面.又平面,∴平面平面.(2)解:过点作,连结.平面平面,平面平面,平面,∴平面,∴为直线和平面所成角.∵是边长为的正三角形,∴,.又∵,∴,,∴.即直线和平面所成角的正弦值为.【考点】空间垂直关系的应用和证明,直线与平面所成的角.【方法点晴】证明面面垂直只能证明线面垂直,而要证明线面垂直就得证明线线垂直,结合题中已知的垂直条件,分析容易找到哪个平面的垂线,逐步完成证明,组织步骤时一定要思路条理;对于直线与平面所成的角遵循作—证(指)—求—答的解题步骤,应当结合条件和前面证明的结论找到平面的垂线是解题的关键,本题中在第一问证明的基础上有了平面的垂面,利用面面垂直的性质定理过直线上一点作交线的垂线即为平面的垂线,连接垂足和斜足即得射影,找到线面角后解直角三角形得解.13.一个几何体的三视图如图所示,则这个几何体的外接球表面积为()A.B.C.D.【答案】A【解析】几何体为一个三棱锥S-ABC,其中D为AC中点,且SD垂直平面ABC,BD垂直AC,则球心在SD上,设球半径为R,则外接球表面积为,选A.【考点】三视图【方法点睛】1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.2.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据.14.已知正三角形的三个顶点都在半径为的球面上,球心到平面的距离为,点是线段的中点,过点作球的截面,则截面面积的最小值是_________.【答案】【解析】因为过作球的截面,当截面与垂直时,截面圆的半径最小,所以当截面与垂直时,截面圆的面积有最小值.设正三角形的外接圆圆心为,在中,,所以.在中,,所以,所以截面面积为【考点】1、多面体的外接球;2、球的截面圆性质.【方法点睛】“切”“接”问题的处理规律:①“切”的处理:解决与球的内切问题主要是指球内切多面体与旋转体,解答时首先要找准切点,通过作截面来解决;②“接”的处理:把一个多面体的几个顶点放在球面上即为球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.15.(2015•金家庄区校级模拟)如图正方形BCDE的边长为a,已知AB=BC,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:①AB与DE所成角的正切值是;②AB∥CE;③VB﹣ACE的体积是a2;④平面ABC⊥平面ADC;⑤直线EA与平面ADB所成角为30°.其中正确的有.(填写你认为正确的序号)【答案】①③④⑤【解析】①由于BC∥DE,则∠ABC(或其补角)为AB与DE所成角;②AB和CE是异面直线;③根据三棱锥的体积公式即可求VB ﹣ACE的体积;④根据面面垂直的判定定理即可证明;⑤根据直线和平面所成角的定义进行求解即可.解:由题意,AB=BC,AE=a,AD⊥平面BCDE,AD=a,AC= a①由于BC∥DE,∴∠ABC(或其补角)为AB与DE所成角∵AB=a,BC=a,AC=a,∴BC⊥AC,∴tan∠ABC=,故①正确;②由图象可知AB与CE是异面直线,故②错误.③VB﹣ACE的体积是S△BCE×AD=×a3=,故③正确;(4)∵AD⊥平面BCDE,BC⊂平面BCDE,∴AD⊥BC,∵BC⊥CD,AD∩CD=D,∴BC⊥平面ADC,∵BC⊂平面ABC,∴平面ABC⊥平面ADC,故④正确;⑤连接CE交BD于F,则EF⊥BD,∵平面ABD⊥平面BDE,∴EF⊥平面ABD,连接F,则∠EAF为直线AE与平面ABD所成角,在△AFE中,EF=,AE=a,∴sin∠EAF==,则∠EAF=30°,故⑤正确,故正确的是①③④⑤故答案为:①③④⑤【考点】命题的真假判断与应用;空间中直线与直线之间的位置关系;平面与平面之间的位置关系.16.已知某几何体的三视图,则该几何体的体积是_______.【答案】.【解析】该几何体是一个四棱锥,底面是边长为2的正方形,高为,所以.【考点】1.空间几何体的表面积与体积;2.空间几何体的三视图与直观图.17.设三棱柱的侧棱垂直于底面,,且三棱柱的所有顶点都在同一球面上,则该球的表面积是.【答案】【解析】由题意可得:把三棱柱补成底面以2为边长的正方形,以为高的长方体,长方体的体对角线就是球的直径,所以,所以该球的表面积是;故填.【考点】空间几何体的表面积.18.某几何体的正视图与侧视图都是等腰梯形,则该几何体可以是下列几何体中的()①三棱台,②四棱台,③五棱台,④圆台.A.①②B.③④C.①③D.②④【答案】D【解析】由题意得,几何体的正视图和侧视图都是等腰梯形,则根据几何体的三视图的规则可知,该几何体可能为四棱台或圆台,故选D.【考点】空间几何体的三视图.【方法点晴】本题主要考查了空间几何体的三视图的应用,着重考查了推理和运算能力及空间想象能力,属于中档试题,解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则,还原出原几何体的形状,本题的解答中,只是给出了几何体的正视图和侧视图都是等腰梯形,从而可得这个几何体可能是四棱台或圆台.19.在直三棱柱中,,,且异面直线与所成的角等于,设.(1) 求的值;(2) 求三棱锥的体积.【答案】(1); (2)【解析】(1)由BC ∥B 1C 1可得∠A 1BC 就是异面直线A 1B 与B 1C 1所成的角,从而∠A 1BC =60°,再由AA 1⊥平面ABC ,AB=AC ,则A 1B=A 1C ,△A 1BC 为等边三角形, 由已知可得,即可求得 (2)连接B 1C ,则三棱锥B 1–A 1BC 的体积等于三棱锥C –A 1B 1B 的体积,△的面积, 又可得平面,利用三棱锥的体积公式可求得.试题解析:(1)∵BC ∥B 1C 1,∴∠A 1BC 就是异面直线A 1B 与B 1C 1所成的角,即∠A 1BC =60°,又AA 1⊥平面ABC ,AB=AC ,则A 1B=A 1C ,∴△A 1BC 为等边三角形, 由,, ∴; (2)连接B 1C ,则三棱锥B 1–A 1BC 的体积等于三棱锥C –A 1B 1B 的体积, 即:, △的面积,又平面,所以,所以.【考点】异面直线所成的角及三棱锥的体积的求法.20. 如图,在四棱锥中,已知棱,,两两垂直,长度分别为1,2,2.若(),且向量与夹角的余弦值为.(1)求的值;(2)求直线与平面所成角的正弦值.【答案】(1);(2).【解析】(1)以为坐标原点,、、分别为、、轴建立空间直角坐标系,写出,的坐标,根据空间向量夹角余弦公式列出关于的方程可求;(2)设岀平面的法向量为,根据,进而得到,从而求出,向量的坐标可以求出,从而可根据向量夹角余弦的公式求出,从而得和平面所成角的正弦值.试题解析:(1)依题意,以为坐标原点,、、分别为、、轴建立空间直角坐标系 ,因为,所以,从而,则由,解得(舍去)或. (2)易得,,设平面的法向量, 则,,即,且,所以,不妨取,则平面的一个法向量,又易得,故,所以直线与平面所成角的正弦值为.考点: 1、空间两向量夹角余弦公式;2、利用向量求直线和平面说成角的正弦.21.如图,在四棱锥中,平面,分别是棱的中点.(1)求证:平面;(2)求证:平面平面.【答案】(1)详见解析(2)详见解析【解析】(1)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与证明,往往需结合平面几何条件,如本题利用三角形中位线性质定理得(2)证明面面垂直,一般利用面面垂直判定定理,即从线面垂直出发给予证明,而线面垂直的证明,需多次利用线面垂直的判定与性质定理:先由平行四边形为菱形得,再由平面得,即,从而得平面试题解析:(1)设,连结,因为,为的中点,所以,所以四边形为平行四边形,所以为的中点,所以又因为平面,平面,所以平面.(2)(方法一)因为平面,平面所以,由(1)同理可得,四边形为平行四边形,所以,所以因为,所以平行四边形为菱形,所以,因为平面,平面,所以平面因为平面,所以平面平面.(方法二)连结,因为平面,平面,所以因为,所以,因为平面,平面,所以因为为的中点,所以,由(1),所以又因为为的中点,所以因为,平面,平面所以平面,因为平面,所以平面平面.【考点】线面平行判定定理,面面垂直判定定理22.如图,网格纸上小正方形的边长为1,粗线画出的是某个几何体的三视图,则该几何体的体积为()A.B.C.D.【答案】A【解析】因为网格纸上小正方形的边长为,有三视图可知,该几何体是下面为底面半径为高为的圆柱体的一半、上面是底面半径为高为的圆锥体的一半,所以体积为,故选A.【考点】1、几何体的三视图;2、圆柱及圆锥的体积公式.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.23.已知如图所示的三棱锥的四个顶点均在球的球面上,和所在的平面互相垂直,,,,则球的体积为()A.B.C.D.【答案】C【解析】因为,,,所以的中点为的外心,连接,则,又和所在的平面互相垂直,所以平面,上的每一点到距离相等,因此正三角形的中心即是外接球球心,其半径也是外接球半径,所以球半径,求体积为,故选C.【考点】1、外接球的性质及勾股定理;2、面面垂直及球的体积公式.【方法点睛】本题主要考查外接球的性质及勾股定理、面面垂直及三棱锥外接球体积的求法,属于难题.要求外接球的表面积和体积,关键是求出求的半径,求外接球半径的常见方法有:①若三条棱两垂直则用(为三棱的长);②若面(),则(为外接圆半径);③可以转化为长方体的外接球;④特殊几何体可以直接找出球心和半径.本题是根据方法④直接找出球心并求出半径进而得到求体积的.24.四棱锥的底面是正方形,,分别是的中点(1)求证:;(2)设与交于点,求点到平面的距离【答案】(1)证明见解析;(2).【解析】(1)要证明线面垂直,一般先证明线线垂直,本题中,由于是中点,因此有,而与垂直,从而与平面垂直,结论得证;(2)要求点到平面的距离,考虑三棱锥,的面积易求(为面积的一半),另外由(1)的结论,此三棱锥以为底时,是高,体积易求,从而所求距离易得.试题解析:(1)证明:连接,由于分别是的中点,所以,又,平面,故,又为正方形,故故,故(2)连接交于点,连接,则交线为,又,故,由于分别是的中点,故为的中点,又,故为三棱锥的高又故,又设点到平面的距离为,,所以【考点】线面垂直的判断,点到平面的距离.25.某几何体的三视图如图,则该几何体的体积为()A.B.C.D.【答案】C【解析】由题意得,由几何体的三视图,知该几何体是上下底面为梯形的直棱柱,所以该几何体的体积为,故选C.【考点】几何体的三视图及几何体的体积.【方法点晴】本题主要考查了空间几何体的三视图的应用,着重考查了推理和运算能力及空间想象能力,属于中档试题,解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则,还原出原几何体的形状,本题的解答中,该几何体是上下底面为梯形的直棱柱是解答本题的关键,属于基础题.26.一个几何体的三视图如图,则这个几何体的表面积是()A.B.C.D.【答案】C【解析】由题意得,根据给定的几何体的三视图,可知,原几何体为正方体的一部分,如图所示的红线部分,是一个棱长为的正四面体,所以此几何体的表面积为,故选C.【考点】几何体的三视图与表面积.27.某几何体的三视图如图所示(单位:cm),则该几何体的表面积是______cm2,体积是______cm3.【答案】80,40【解析】由三视图知该组合体是一个长方体上面放置了一个小正方体,,.【考点】三视图.【方法点睛】解决由三视图求空间几何体的表面积与体积问题,一般是先根据三视图确定该几何体的结构特征,再准确利用几何体的表面积与体积公式计算该几何体的表面积与体积.28.如图,在四棱锥中,平面平面,,,,,,.(Ⅰ)求证:平面;(Ⅱ)求直线PB与平面PCD所成角的正弦值;(Ⅲ)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值;若不存在,说明理由.【答案】(Ⅰ)见解析;(Ⅱ);(Ⅲ)存在,.【解析】(Ⅰ)由面面垂直的性质定理知AB⊥平面,根据线面垂直的性质定理可知,再由线面垂直的判定定理可知平面;(Ⅱ)取的中点,连结,以O为坐标原点建立空间直角坐标系O-xyz,利用向量法可求出直线PB与平面PCD所成角的正弦值;(Ⅲ)假设存在,根据A,P,M三点共线,设,根据BM∥平面PCD,即(为平面PCD的法向量),求出的值,从而求出的值.试题解析:(Ⅰ)因为平面平面,,所以平面.所以.又因为,所以平面.(Ⅱ)取的中点,连结.因为,所以.又因为平面,平面平面,所以平面.因为平面,所以.因为,所以.如图建立空间直角坐标系.由题意得,.设平面的法向量为,则即令,则.所以.又,所以.所以直线与平面所成角的正弦值为.(Ⅲ)设是棱上一点,则存在使得.因此点.因为平面,所以平面当且仅当,即,解得.所以在棱上存在点使得平面,此时.【考点】空间线面垂直的判定定理与性质定理;线面角的计算;空间想象能力,推理论证能力【名师】平面与平面垂直的性质定理的应用:当两个平面垂直时,常作的辅助线是在其中一个平面内作交线的垂线,把面面垂直转化为线面垂直,进而可以证明线线垂直(必要时可以通过平面几何的知识证明垂直关系),构造(寻找)二面角的平面角或得到点到面的距离等.29.如图,在四棱锥中,底面是菱形,,平面,,点分别为和中点.(1)求证:直线平面;(2)求三棱锥的表面积.【答案】(1)证明见解析;(2).【解析】(1)要证线面平行,一般先证线线平行,考虑到,是中点,因此取的中点,可证得且,从而得平行四边形,因此有,最终得线面平行;(2)要求三棱锥的表面积,必须求得它的各个面的面积,由平面,得,三角形和的面积可求,由题设又可证,这样就有,另两个面的面积又可求得.试题解析:(1)证明:作FM∥CD交PC于M.∵点F为PD中点,∴. ∴,∴AEMF为平行四边形,∴AF∥EM,∵,∴直线AF平面PEC.(2)连结可知,,由此;;;;因此三棱锥的表面积.【考点】线面平行的判断,多面体的表面积.30.在棱长为3的正方体中,在线段上,且,为线段上的动点,则三棱锥的体积为()A.1B.C.D.与点的位置有关【答案】B【解析】由于是定值,点到平面的距离是,因此点平面的距离是.所以三棱锥的体积,应选B.【考点】三棱锥体积的运算.31.如图,在多面体中,底面是边长为2的正方形,四边形是矩形,且平面平面,,和分别是和的中点.(1)求证:平面;(2)求.【答案】(1)证明见解析;(2).【解析】(1)运用线面平行的判定定理求证;(2)借助题设条件及转化化归的思想求解即可. 试题解析:(1)证明:设,连接,在中,因为,,所以,又因为平面,平面,所以平面.(2)因为四边形是正方形,所以,又因为平面平面,平面平面,且平面,所以平面,则到平面的距离为的一半,又因为,所以,所以.【考点】直线与平面的位置关系及棱锥公式的运用.32.如图,在三棱柱中,,,,在底面的射影为的中点,是的中点.(1)证明:平面;(2)求二面角的平面角的余弦值.【答案】(1)证明见解析;(2).【解析】(1)设为的中点,连接,依题意有,,故平面.根据分析有,故平面;(2)以的中点为原点,分别以射线为轴的正半轴,建立空间直角坐标系,利用向量法求得余弦值为.试题解析:(1)设为的中点,连接.由题意得:平面,所以.因为,所以,,故平面.由分别为的中点,得且,从而且,所以为平行四边形,故,又因为平面,所以平面.(2)方法一:作,且,连结.由,,得,由,,得与全等.由,得,因此为二面角的平面角.由,,,得,,由余弦定理得.方法二:以的中点为原点,分别以射线为轴的正半轴,建立空间直角坐标系,如图所示,由题意知各点坐标如下:,因此,,,设平面的法向量为,平面的法向量为,由,即,可取.由,即,可取,于是.由题意可知,所求二面角的平面角是钝角,故二面角的平面角的余弦值为.【考点】空间向量与立体几何.33.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,从左往右为半个圆锥,一个圆柱,一个半圆,故体积为.【考点】三视图.34.如图,在四棱柱中,底面,为线段上的任意一点(不包括两点),平面与平面交于.(1)证明:;(2)证明:平面.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)要证线线垂直,一般可证线面垂直,观察题中垂直条件,平面,则有,题中又有,从而有平面,因此结论得证;(2)要证线面平行,就是要证线线平行,直线是平面与平面的交线,因此要得平行,就要有线面平行,而这由可得平面,从而,结论得证.试题解析:(1)证明:因为平面,平面,所以.又,所以平面,而平面,所以.(2)在四棱柱中,,平面,平面,所以平面,又平面,平面与平面交于,所以,因为,所以,而平面,平面,所以平面.【考点】线面垂直的判定与性质,线面平行的判定与性质.【名师】证明线面(面面)平行(垂直)时要注意以下几点:(1)由已知想性质,由求证想判定,即分析法与综合法相结合寻找证题思路。
高三数学立体几何专题复习讲义资料
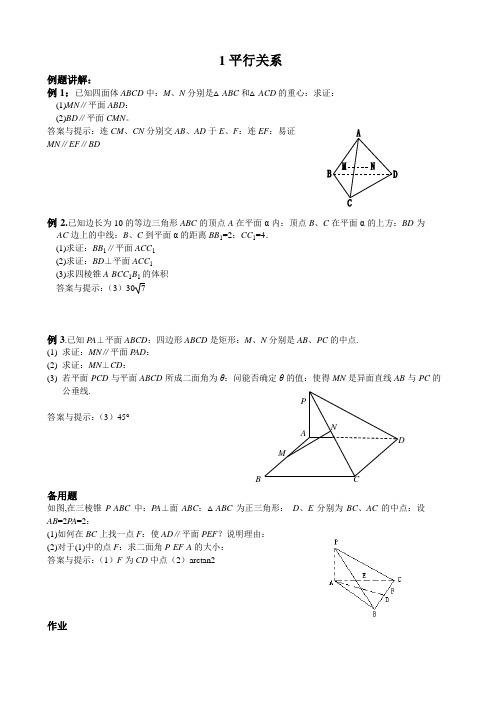
1平行关系例题讲解:例1:已知四面体ABCD 中:M 、N 分别是△ABC 和△ACD 的重心:求证:(1)MN ∥平面ABD : (2)BD ∥平面CMN 。
答案与提示:连CM 、CN 分别交AB 、AD 于E 、F :连EF :易证 MN ∥EF ∥BD例2.已知边长为10的等边三角形ABC 的顶点A 在平面α内:顶点B 、C 在平面α的上方:BD 为AC 边上的中线:B 、C 到平面α的距离BB 1=2:CC 1=4. (1)求证:BB 1∥平面ACC 1 (2)求证:BD ⊥平面ACC 1 (3)求四棱锥A -BCC 1B 1的体积 答案与提示:(3)307例3.已知P A ⊥平面ABCD :四边形ABCD 是矩形:M 、N 分别是AB 、PC 的中点.(1) 求证:MN ∥平面P AD : (2) 求证:MN ⊥CD :(3) 若平面PCD 与平面ABCD 所成二面角为θ:问能否确定θ的值:使得MN 是异面直线AB 与PC 的公垂线.答案与提示:(3)45°备用题如图,在三棱锥P -ABC 中:P A ⊥面ABC :△ABC 为正三角形: D 、E 分别为BC 、AC 的中点:设AB =2P A =2:(1)如何在BC 上找一点F :使AD ∥平面PEF ?说明理由: (2)对于(1)中的点F :求二面角P -EF -A 的大小: 答案与提示:(1)F 为CD 中点(2)arctan2作业D CB M AN P在正四棱柱ABCD -A 1B 1C 1D 1中:AA 1=12 AB :点E 、M 分别为A 1B 、C 1C 的中点:过A 1:B :M 三点的平面交C 1D 1于点N 。
(1)求证:EM ∥平面ABCD : (2)求二面角B -A 1N -B 1的正切值。
答案与提示:(2)arctan542垂直关系例题讲解:例1:如图,在三棱锥P -ABC 中:AB =BC =CA :P A ⊥底面ABC :D 为AB 的中点.(1)求证:CD ⊥PB :(2)设二面角A -PB -C 的平面角为α:且tan α=7:若底面边长为1:求三棱锥P -ABC 的体积. 答案与提示:(2)18例2:已知ABCD —A 1B 1C 1D 1是棱长为a 的正方体:E 、F 分别是棱AA 1和CC 1的中点:G 是A 1C 1的中点.(1)求证平面BFD 1E ⊥平面BGD 1: (2)求点G 到平面BFD 1E 的距离: (3)求四棱锥A 1-BFD 1E 的体积.答案与提示:(2)66a (3) 16a 3例3:四边形ABCD 中.AD ∥BC :AD =AB :∠BCD =45°:∠BAD =90°:将△ABD 沿对角线BD 折起:记折起点A 的位置为P :且使平面PBD ⊥平面BCD . (1)求证:CD ⊥平面PBD :(2)求证:平面PBC ⊥平面PDC : (3)求二面角P —BC —D 的大小.答案与提示:(2)先证PB ⊥面PCD (3)arctan 2备用题在三棱锥S -ABC 中:已知SA =4:AB =AC :BC =3 6 ,∠SAB =∠SAC =45°,SA 与底面ABC 所的角为30°.BA PD CE(1)求证:SA ⊥BC :(2)求二面角S —BC —A 的大小: (3)求三棱锥S —ABC 的体积. 答案与提示:(2)arctan 23 3 (3)9 2作业1.在四棱锥P -ABCD 中:已知PD ⊥底面ABCD :底面ABCD 为等腰梯形,且∠DAB =60°:AB =2CD :∠DCP =45°:设CD =a .(1)求四棱锥P -ABCD 的体积. (2)求证:AD ⊥PB . 答案与提示:(1)34a 32.如图:正三角形ABC 与直角三角形BCD 成直二面角:且∠BCD =90°:∠CBD =30°.(1)求证:AB ⊥CD :(2)求二面角D —AB —C 的大小: 答案与提示:(2)arctan 233 空间角例1、如图1:设ABC -A 1B 1C 1是直三棱柱:F 是A 1B 1的中点:且SC CBAAAB(1)求证:AF ⊥A 1C : (2)求二面角C -AF -B 的大小.解:(1)如图2:设E 是AB 的中点:连接CE :EA 1.由ABC -A 1B 1C 1是直三棱柱:知AA 1⊥平面ABC :而CE 平面ABC :所以CE ⊥AA 1:∵AB =2AA 1=2a :∴AA 1=a :AA 1⊥AE :知AA 1FE 是正方形:从而AF ⊥A 1E .而A 1E 是A 1C 在平面AA 1FE 上的射影:故AF ⊥A 1C :(2)设G 是AB 1与A 1E 的中点:连接CG .因为CE ⊥平面AA 1B 1B :AF ⊥A 1E :由三垂线定理:CG ⊥AF :所以∠CGE 就是二面角C -AF -B 的平面角.∵AA 1FE 是正方形:AA 1=a :∴11222EG EA a ==: ∴2216222CG a a =-=: ∴tan ∠CGE =6232CG EG a ===:∠CGE =60:从而二面角C -AF -B 的大小为60。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何专题【命题趋向】高考对空间想象能力的考查集中体现在立体几何试题上,着重考查空间点、线、面的位置关系的判断及空间角等几何量的计算.既有以选择题、填空题形式出现的试题,也有以解答题形式出现的试题.选择题、填空题大多考查概念辨析、位置关系探究、空间几何量的简单计算求解,考查画图、识图、用图的能力;解答题一般以简单几何体为载体,考查直线与直线、直线与平面、平面与平面的位置关系,以及空间几何量的求解问题,综合考查空间想象能力、推理论证能力和运算求解能力.试题在突出对空间想象能力考查的同时,关注对平行、垂直关系的探究,关注对条件或结论不完备情形下的开放性问题的探究.【考点透析】立体几何主要考点是柱、锥、台、球及其简单组合体的结构特征、三视图、直观图,表面积体积的计算,空间点、直线、平面的位置关系判断与证明,(理科)空间向量在平行、垂直关系证明中的应用,空间向量在计算空间角中的应用等.【例题解析】题型1 空间几何体的三视图以及面积和体积计算例1(2008高考海南宁夏卷)某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a b +的最大值为 A . 22B . 32C . 4D . 52分析:想像投影方式,将问题归结到一个具体的空间几何体中解决.解析:结合长方体的对角线在三个面的投影来理解计算,如图设长方体的高宽高分别为,,m n k ,=1n ⇒=,a =b =,所以22(1)(1)6a b -+-=228a b ⇒+=,22222()282816a b a ab b ab a b +=++=+≤++=∴4a b ⇒+≤当且仅当2a b ==时取等号.点评:本题是课标高考中考查三视图的试题中难度最大的一个,我们通过移动三个试图把问题归结为长方体的一条体对角线在三个面上的射影,使问题获得了圆满的解决.例2 (2008高考山东卷、2009年福建省理科数学高考样卷第3题)下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.9πB.10πC.11πD.12π分析:想像、还原这个空间几何体的构成,利用有关的计算公式解答.解析:这个空间几何体是由球和圆柱组成的,圆柱的底面半径是1,母线长是3,球的半径是1,故其表面积是22213214112ππππ⨯⨯+⨯⨯+⨯=,答案D.点评:由三视图还原空间几何体的真实形状时要注意“高平齐、宽相等、长对正”的规则.例3(江苏省苏州市2009届高三教学调研测试第12题)已知一个正三棱锥P ABC-的主视图如图所示,若32AC BC==,6PC=,则此正三棱锥的全面积为_________.分析:正三棱锥是顶点在底面上的射影是底面正三角形的中心的三棱锥,根据这个主试图知道,主试图的投影方向是面对着这个正三棱锥的一条侧棱,并且和底面三角形的一条边垂直,这样就知道了这个三棱锥的各个棱长.解析:这个正三棱锥的底面边长是3、高是6,故底面正三角形的中心到一个顶点的距离是233332⨯⨯=,故这个正三棱锥的侧棱长是22363+=,由此知道这个正三棱锥的侧面也是边长为3的正三角形,故其全面积是2343934⨯⨯=,答案93. 点评:由空间几何体的一个视图再加上其他条件下给出的问题,对给出的这“一个视图”要仔细辨别投影方向,这是三视图问题的核心. 题型2 空间点、线、面位置关系的判断例4(江苏苏州市2009届高三教学调研测试7)已知n m ,是两条不同的直线,βα,为两个不同的平面,有下列四个命题:①若βα⊥⊥n m ,,m n ⊥,则βα⊥; ②若n m n m ⊥,//,//βα,则βα//; ③若n m n m ⊥⊥,//,βα,则βα//; ④若βαβα//,//,n m ⊥,则n m ⊥.其中正确的命题是(填上所有正确命题的序号)_______________. 分析:根据空间线面位置关系的判定定理和性质定理逐个作出判断.解析:我们借助于长方体模型解决.①中过直线,m n 作平面γ,可以得到平面,αβ所成的二面角为直二面角,如图(1),故βα⊥①正确;②的反例如图(2);③的反例如图(3);④中由,m ααβ⊥可得m β⊥,过n 作平面γ可得n 与交线g 平行,由于m g ⊥,故m n ⊥.答案①④.点评:新课标的教材对立体几何处理的基本出发点之一就是使用长方体模型,本题就是通过这个模型中提供的空间线面位置关系解决的,在解答立体几何的选择题、填空题时合理地使用这个模型是很有帮助的. 例5(浙江省2009年高考省教研室第一次抽样测试理科第5题)设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题正确的是A .若,,//m n m n αβ⊥⊥,则//αβB .若//,//,//,m n αβαβ则//m nC .若,//,//m n αβαβ⊥,则m n ⊥D .若//,//,//,m n m n αβ则//αβ 分析:借助模型、根据线面位置关系的有关定理逐个进行分析判断. 解析:对于//αβ,结合,//,m n αβ⊥则可推得m n ⊥.答案C .点评:从上面几个例子可以看出,这类空间线面位置关系的判断类试题虽然形式上各异,但本质上都是以空间想象、空间线面位置关系的判定和性质定理为目标设计的,主要是考查考生的空间想象能力和对线面位置关系的判定和性质定理掌握的程度.题型3 空间平行与垂直关系的证明、空间几何体的有关计算(文科解答题的主要题型) 例6.(2009江苏泰州期末16)如图所示,在棱长为2的正方体1111ABCD A B C D -中,E 、F 分别为1DD 、DB 的中点.(1)求证:EF //平面11ABC D ; (2)求证:1EF B C ⊥; (3)求三棱锥EFC B V -1的体积.分析:第一问就是找平行线,最明显的就是1EF BD ;第二问转化为线面垂直进行证明;第三问采用三棱锥的等积变换解决.解析:(1)连结1BD ,如图,在B DD 1∆中,E 、F 分别为1D D ,DB 的中点,则111111////EF D BD B ABC D EF EF ABC D ⎫⎪⊂⇒⎬⎪⊄⎭平面平面平面11ABC D .(2)11111111111111111,//B C ABB C BC B C BD B C ABC D EF B CAB B C ABC D EF BD BD ABC D AB BC B ⊥⎫⎪⊥⊥⊥⎫⎫⎪⇒⇒⇒⊥⎬⎬⎬⊂⊂⎭⎭⎪⎪=⎭平面平面平面(3)CF ⊥平面11BDD B ,1CF EFB ∴⊥平面且2CF BF ==1132EF BD ==,222211(2)26B F BF BB =+=+=222211111(22)3B E B D D E =+=+=∴22211EF B F B E += 即190EFB ∠=,11113B EFC C B EF B EF V V S CF --∆∴==⋅⋅=11132EF B F CF ⨯⋅⋅⋅=11362132⨯⨯⨯⨯= .点评:这个题目也属于文科解答题的传统题型.空间线面位置关系证明的基本思想是转化,根据线面平行、垂直关系的判定和性质,进行相互之间的转化,如本题第二问是证明线线垂直,但问题不能只局限在线上,要把相关的线归结到某个平面上(或是把与这些线平行的直线归结到某个平面上,通过证明线面的垂直达到证明线线垂直的目的,但证明线面垂直又得借助于线线垂直,在不断的相互转化中达到最终目的.立体几何中的三棱柱类似于平面几何中的三角形,可以通过“换顶点”实行等体积变换,这也是求点面距离的基本方法之一. 例7.(江苏省苏州市2009届高三教学调研测试第17题)在四棱锥P ABCD -中,90ABC ACD ∠=∠=,60BAC CAD ∠=∠=,PA ⊥平面ABCD ,E 为PD 的中点,22PA AB ==.(1)求四棱锥P ABCD -的体积V ;(2)若F 为PC 的中点,求证PC ⊥平面AEF ; (3)求证CE ∥平面PAB .分析:第一问只要求出底面积和高即可;第二问的线面垂直通过线线垂直进行证明;第三问的线面平行即可以通过证明线线平行、利用线面平行的判定定理解决,也可以通过证明面面平行解决,即通过证明直线CE 所在的一个平面和平面PAB 的平行解决.解析:(1)在ABC ∆Rt 中,1,60AB BAC =∠=,∴3BC =2AC =. 在ACD Rt Δ中,2,60AC ACD =∠=,∴23,4CD AD ==. ∴1122ABCD S AB BC AC CD =⋅+⋅115132233222=⨯⨯⨯ 则155323323V =(2)∵PA CA =,F 为PC 的中点,∴AF PC ⊥. ∵PA ⊥平面ABCD ,∴PA CD ⊥,∵AC CD ⊥,PAAC A =,∴CD ⊥平面PAC ,∴CD PC ⊥.∵E 为PD 中点,F 为PC 中点,∴EF ∥CD ,则EF CD ⊥,∵AFEF F =,∴PC ⊥平面AEF . (3)证法一:取AD 中点M ,连,EM CM .则EM ∥PA ,∵EM ⊄平面PAB ,PA ⊂平面PAB ,∴EM ∥平面PAB .在ACD ∆Rt 中,60CAD ∠=,2AC AM ==,∴60ACM ∠=.而60BAC ∠=,∴MC ∥AB .∵MC ⊄平面PAB ,AB ⊂平面PAB , ∴MC ∥平面PAB .∵EM MC M =,∴平面EMC ∥平面PAB . ∵EC⊂平面EMC ,∴EC ∥平面PAB .证法二:延长,DC AB ,设它们交于点N , 连PN .∵60NAC DAC ∠=∠=,AC CD ⊥,∴C 为ND 的中点. ∵E 为PD 中点,∴EC ∥PN . ∵EC ⊄平面PAB , PN ⊂平面PAB , ∴EC ∥平面PAB .点评:新课标高考对文科的立体几何与大纲的高考有 了诸多的变化.一个方面增加了空间几何体的三视图、 表面积和体积计算,拓展了命题空间;另一方面删除了 三垂线定理、删除了凸多面体的概念、正多面体的概念 与性质、球的性质与球面距离,删除了空间向量,这就给立体几何的试题加了诸多的枷锁,由于这个原因课标高考文科的立体几何解答题一般就是空间几何体的体积和表面积的计算、空间线面位置关系的证明(主要是平行与垂直).题型4 空间向量在立体几何中的应用(理科立体几何解答题的主要题型)例8.(2009年福建省理科数学高考样卷第18题)如图,在棱长为2的正方体1111ABCD A B C D -中,E F 、分别为11A D 和1CC 的中点. (1)求证:EF ∥平面1ACD ;(2)求异面直线EF 与AB 所成的角的余弦值;(3)在棱1BB 上是否存在一点P ,使得二面角P AC P --的大小为30?若存在,求出BP 的长;若不存在,请说明理由.【解析】解法一:如图分别以1,,DA DC DD 所在的直线为x 轴、y 轴、z 轴建立空间直角坐标系D xyz -,由已知得()0,0,0D 、()2,0,0A 、()2,2,0B 、()0,2,0C 、()12,2,2B 、()10,0,2D ()1,0,2E 、、()0,2,1F .(1)取1AD 中点G ,则()1,0,1G ,()1,2,1CG =-,又()1,2,1EF =--,由EF CG =-,∴EF 与CG 共线.从而EF ∥CG ,∵CG ⊂平面1ACD , EF ⊄平面1ACD ,∴EF ∥平面1ACD . (2)∵()0,2,0AB =,6cos ,3||||26EF AB EF AB EF AB ⋅===⋅, ∴异面直线EF 与AB 所成角的余弦值为36. (3)假设满足条件的点P 存在,可设点()2,2,P t (02t <≤),平面ACP 的一个法向量为(),,n x y z =,则0,0.n ACn AP⎧⋅=⎪⎨⋅=⎪⎩∵()0,2,AP t=()2,2,0AC=-,∴220,20,x yy tz-+=⎧⎨+=⎩取2(1,1,) nt=-.易知平面ABC的一个法向量1(0,0,2)BB =,依题意知,1,30BB n =或150,∴14||cos,2BB N-==,即22434(2)4tt=+,解得3t=∵(0,2],∴在棱1BB上存在一点P,当BP的长为P AC B--的大小为30.解法二:(1)同解法一知()1,2,1EF=--,()12,0,2AD=-,()2,2,0AC=-,∴112EF AC AD=-,∴EF、AC、1AD共面.又∵EF⊄平面1ACD,∴EF∥平面1ACD.(2)、(3)同解法一.解法三:易知平面1ACD的一个法向量是()12,2,2DB=.又∵()1,2,1EF=--,由1EF DB⋅=·,∴1EF DB⊥,而EF⊄平面1ACD,∴EF∥平面1ACD.(2)、(3)同解法一.点评:本题主要考查直线与直线、直线与平面的位置关系、二面角的概念等基础知识;考查空间想像能力、推理论证能力和探索问题、解决问题的能力.利用空间向量证明线面平行的方法基本上就是本题给出的三种,一是证明直线的方向向量和平面内的一条直线的方向向量共线,二是证明直线的方向向量和平面内的两个不共线的向量共面、根据共面向量定理作出结论;三是证明直线的方向向量与平面的一个法向量垂直.例9(浙江宁波市2008学年度第一学期期末理科第20题)已知几何体A BCED-的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.(1)求异面直线DE 与AB 所成角的余弦值; (2)求二面角A ED B --的正弦值; (3)求此几何体的体积V 的大小.【解析】(1)取EC 的中点是F ,连结BF ,则BFDE ,∴FBA ∠或其补角即为异面直线DE与AB 所成的角.在BAF ∆中,42AB =25BF AF ==.∴10cos 5ABF ∠=. ∴异面直线DE 与AB 10 (2)AC ⊥平面BCE ,过C 作CG DE ⊥交DE 于G ,连结AG . 可得DE ⊥平面ACG ,从而AG DE ⊥, ∴AGC ∠为二面角A ED B --的平面角. 在ACG ∆Rt 中,90ACG ∠=,4AC =,85CG =,∴5tan AGC ∠=. ∴5sin AGC ∠=∴二面角A ED B --的的正弦值为53.(3)1163BCED V S AC =⋅⋅=,∴几何体的体积V 为16. 方法二:(坐标法)(1)以C 为原点,以,,CA CB CE 所在直线为,,x y z 轴建立空间直角坐标系. 则()4,0,0A ,(0,4,0)B ,(0,4,2)D ,()0,0,4E ,(0,4,2),(4,4,0)DE AB =-=-,∴10cos ,DE AB <>=∴异面直线DE 与AB 所成的角的余弦值为105. (2)平面BDE 的一个法向量为(4,0,0)CA =, 设平面ADE 的一个法向量为(,,)n x y z =, ,,n AD n DE ⊥⊥(4,4,2),(0,4,2)AD DE =-=- ∴0,0n AD n DE ==从而4420,420x y z y z -++=-+=, 令1y =,则(2,1,2)n =, 2cos ,3CA n <>=∴二面角A ED B --的的正弦值为53. (3)1163BCED V S AC =⋅⋅=,∴几何体的体积V 为16. 点评:本题考查异面直线所成角的求法、考查二面角的求法和多面体体积的求法.空间向量对解决三类角(异面直线角、线面角、面面角)的计算有一定的优势.对理科考生来说除了要在空间向量解决立体几何问题上达到非常熟练的程度外,不要忽视了传统的方法,有些试题开始部分的证明就没有办法使用空间向量.【专题训练与高考预测】说明:文科以选择题、填空题和解答题前三题为主.理科以选择题、填空题和解答题后三题为主. 一、选择题1.如图为一个几何体的三视图,尺寸如图所示,则该几何体的表面积为(不考虑接触点) ( )A . 63π++B . 1834π++C . 1823π++D . 32π+2.某几何体的三视图如图所示,根据图中数据,可得该几何体的体积是( ) A .323+ B .233+ C .2233- D . 3223-3.已知一个几何体的主视图及左视图均是边长为2的正三角形,俯视图是直径为2的圆,则此几何体的外接球的表面积为 ( )A .π34B .π38C .π316D .π332 4.一个水平放置的平面图形的斜二测直观图是一个底角为45,腰和上底长均为1的等腰梯形,则这个平面图形的面积是 ( )A .2221+B .221+C .21+D .22+5. 一个盛满水的三棱锥容器S ABC -,不久发现三条侧棱上各有一个小洞,,D E F ,且知:::2:1SD DA SE EB CF FS ===,若仍用这个容器盛水,则最多可盛原来水的( )A .2923B .2719C .3130D .2723 6. 点P 在直径为2的球面上,过P 作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和为最大值是( ) A .2705 B .3705 C .4155 D .61557.正方体''''ABCD A B C D -中,AB 的中点为M ,'DD 的中点为N ,异面直线'B M 与CN 所成的角是 ( )A .30B .90C .45D .608.已知异面直线a 和b 所成的角为50,P 为空间一定点,则过点P 且与,a b 所成角都是30 的直线有且仅有 ( )A . 1条B . 2条C . 3条D . 4条9.如图所示,四边形ABCD 中,//,,45,90AD BC AD AB BCD BAD =∠=∠=,将△ABD 沿BD折起,使平面ABD ⊥平面BCD ,构成三棱锥A BCD -,则在三棱锥A BCD -中,下列命题正确的是 ( )A .平面ABD ⊥平面ABCB .平面ADC ⊥平面BDCC .平面ABC ⊥平面BDCD .平面ADC ⊥平面ABC10.设x 、y 、z 是空间不同的直线或平面,对下列四种情形:① x 、y 、z 均为直线;② x 、y 是直线,z 是平面;③ z 是直线,x 、y 是平面;④ x 、y 、z 均为平面.其中使“x ⊥z 且y ⊥z ⇒x ∥y ”为真命题的是 ( )A . ③ ④B . ① ③C . ② ③D . ① ②11.已知三条不重合的直线m 、n 、l 两个不重合的平面α、β,有下列命题①若//,m n n α⊂,则//m α;②若l α⊥,m β⊥且l m ,则αβ;③若,m m αα⊂⊂,,m n ββ,则αβ;④若αβ⊥,m αβ=,n β⊂,n m ⊥,则n α⊥.中正确的命题个数是 ( ) A .1B . 2C .3D .4 12.直线AB 与直二面角l αβ--的两个面分别交于,A B 两点,且,A B 都不在棱上,设直线AB 与平面,αβ所成的角分别为,θϕ,则θϕ+的取值范围是 ( )A .(0,)2πB .0,2π⎛⎤ ⎥⎝⎦C .(,)2ππD .{}2π 二、填空题 13. 在三棱锥P ABC -中,2PA PB PC ===,30APB BPC CPA ∠=∠=∠=,一只蚂蚁从A 点出发沿三棱锥的侧面绕一周,再回到A 点,则蚂蚁经过的最短路程是 .14.四面体的一条棱长为x ,其它各棱长为1,若把四面体的体积V 表示成x 的函数()f x ,则()f x 的增区间为 ,减区间为 .15. 如图,是正方体平面展开图,在这个正方体中:① BM 与ED 平行; ② CN 与BE 是异面直线;③CN 与BM 成60角; ④DM 与BN 垂直. 以上四个说法中,正确说法的序号依次是 .16. 已知棱长为1的正方体1111ABCD A B C D -中,E 是11A B 的中点,则直线AE 与平面11ABC D 所成的角的正弦值是 . 三、解答题17.已知,如图是一个空间几何体的三视图.(1)该空间几何体是如何构成的;(2)画出该几何体的直观图;(3)求该几何体的表面积和体积.18.如图,已知等腰直角三角形RBC ,其中90RBC ∠=,2==BC RB .点,A D 分别是RB ,RC的中点,现将RAD ∆沿着边AD 折起到PAD ∆位置,使PA AB ⊥,连结PB 、PC .(1)求证:BC PB ⊥;(2)求二面角P CD A --的平面角的余弦值.19.如下图,在正四棱柱1111ABCD A B C D -中,112AA AB =,点,E M 分别为11,A B CC 的中点,过点1,,A B M 三点的平面1A BMN 交11C D 于点N .(1)求证:EM 平面1111A B C D ;(2)求二面角11B A N B --的正切值;(3)设截面1A BMN 把该正四棱柱截成的两个几何体的体积分别为12,V V (12V V <),求12:V V 的值.20. 如图,在四棱锥ABCD P -中,底面为直角梯形,//,90AD BC BAD ︒∠=,PA 垂直于底面ABCD ,N M BC AB AD PA ,,22====分别为PB PC ,的中点.(1)求证:DM PB ⊥;(2)求BD 与平面ADMN 所成的角;(3)求截面ADMN 的面积.21.如图,正方形ACDE 所在的平面与平面ABC 垂直,M 是CE 和AD 的交点,BC AC ⊥,且BC AC =.(1)求证:⊥AM 平面EBC ;(2)求直线AB 与平面EBC 所成的角的大小;(3)求二面角C EB A --的大小.22.已知斜三棱柱111ABC A B C -,90BCA ∠=,2AC BC ==,1A 在底面ABC 上的射影恰为AC的中点D ,又知11BA AC ⊥.(1)求证:1AC ⊥平面1A BC ; (2)求1CC 到平面1A AB 的距离;(3)求二面角1A A B C --的一个三角函数值.【参考答案】1.解析:C 该几何体是正三棱柱上叠放一个球.故其表面积为223132322418232ππ⎛⎫⨯⨯++⨯=+ ⎪⎝⎭. 2.解析:B 33的四棱柱,上半部分是一个底面边长为3的正方形、高为2的四棱锥,故其体积为133********⨯⨯+⨯⨯⨯=+. 3.解析:C 由三视图知该几何体是底面半径为1,高为3的圆锥,其外接球的直径为433. 4.解析:D 如图设直观图为''''O A B C ,建立如图所示的坐标系,按照斜二测画法的规则,在原来的平面图形中OC OA ⊥,且2OC =,1BC =,212122OA =+⨯=+,故其面积为()11222222⋅++⋅=+5.解析:D 当平面EFD 处于水平位置时,容器盛水最多2121sin 31sin 313131h ASB SB SA h DSE SE SD h S h S V V SAB SDE SAB C SDE F ⋅∠⋅⋅⋅⋅∠⋅⋅⋅=⋅⋅=∴∆∆--27431323221=⋅⋅=⋅⋅=h h SB SE SA SD 最多可盛原来水得42312727-=.6.解析:A 设三边长为,2,x x y ,则2254x y +=,令442cos ,2sin ,33cos 2sin 70555x y x y θθθθ==∴+=+≤. 7.解析:B 如图,取'AA 的中点P ,连结BP ,在正方形''ABB A 中易证'BP B M ⊥.8.解析:B 过点P 作a a ',b b ',若P a ∈,则取a 为a ',若P b ∈,则取b 为b '.这时a ',b '相交于P 点,它们的两组对顶角分别为50和130. 记a ',b '所确定的平面为α,那么在平面α内,不存在与a ',b '都成30的直线. 过点P 与a ',b '都成30角的直线必在平面α外,这直线在平面α的射影是a ',b '所成对顶角的平分线.其中射影是50对顶角平分线的直线有两条l 和l ',射影是130对顶角平分线的直线不存在.故答案选B .9.解析:D 如图,在平面图形中CD BD ⊥,折起后仍然这样,由于平面ABD ⊥平面BCD ,故CD ⊥平面ABD ,CD AB ⊥,又AB AD ⊥,故AB ⊥平面ADC ,所以平面ADC ⊥平面ABC .10.解析:C x 、y 、z 均为直线,显然不行;由于垂直于同一个平面的两条直线平行,故②,可以使“x ⊥z 且y ⊥z ⇒x ∥y ”为真命题;又由于垂直于同一条直线的两个平面平行,故③可以使“x ⊥z 且y ⊥z ⇒x ∥y ”为真命题;当x 、y 、z 均为平面时,也不能使“x ⊥z 且y ⊥z ⇒x ∥y ”为真命题.11.解析:B ①中有m α⊂的可能;l m 且l α⊥,可得m α⊥,又m β⊥,故αβ,②正确;③中当m n 时,结论不成立;④就是面面垂直的性质定理,④正确.故两个正确的.12.解析:B 如图,在Rt ADC ∆中,cos ,sin AD AB AC AB θϕ==,而AD AC >,即cos sin cos2πθϕϕ⎛⎫>=- ⎪⎝⎭,故2πθϕ<-,即2πθϕ+<,而当AB l ⊥时,2πθϕ+=.13.解析:22 将如图⑴三棱锥P ABC -,沿棱PA 展开得图⑵,蚂蚁经过的最短路程应是A A ',又∵30APB BPC CPA ∠=∠=∠=,'90APA ∠=,∴A A '=22.14.解析:60,⎛⎤ ⎥ ⎝⎦ ,⎪⎪⎭⎫⎢⎣⎡326, 2()34x f x x =-,利用不等式或导数即可判断. 15.解析:③④ 如图,逐个判断即可.16.解析:10 取CD 的中点F ,连接EF 交平面11ABC D 于O ,连AO .由已知正方体,易知EO ⊥平面11ABC D ,所以EAO ∠为所求.在EOA ∆Rt 中,111222EO EF A D ===2215()12AE =+=,10sin EO EAO AE ∠==.所以直线AE 与平面11ABC D 10.17.解析:(1)这个空间几何体的下半部分是一个底面边长为2的正方形高为1的长方体,上半部分是一个底面边长为2的正方形高为1的四棱锥.(2)按照斜二测的规则得到其直观图,如图.(3)由题意可知,该几何体是由长方体''''ABCD A B C D -与正四棱锥''''P A B C D -构成的简单几何体.由图易得:2,'1,'1AB AD AA PO ====,取''A B 中点Q ,连接PQ ,从而2222''112PQ PO O Q =+=+()()1'''''''''''''''''212.2S A B B C C D D A PQ A B B C C D D A AA AB AD =++++++++⋅= 体积11622122133V =⨯⨯+⨯⨯⨯=. 18.解析:(1)∵点A 、D 分别是RB 、RC 的中点,∴BC AD BC AD 21,//=. ∴90PAD RAD RBC ∠=∠=∠=,∴AD PA ⊥.∴ BC PA ⊥,∵A AB PA AB BC =⊥ ,,∴BC ⊥平面PAB . ∵⊂PB 平面PAB ,∴PB BC ⊥. (2)取RD 的中点F ,连结AF 、PF . ∵1==AD RA ,∴RC AF ⊥. ∵AD AP AR AP ⊥⊥,,∴⊥AP 平面RBC . ∵⊂RC 平面RBC ,∴AP RC ⊥. ∵,A AP AF = ∴⊥RC 平面PAF .∵⊂PF 平面PAF ,∴PF RC ⊥.∴AFP ∠是二面角P CD A --的平面角. 在RAD ∆Rt 中, 22212122=+==AD RA RD AF , 在PAF ∆Rt 中, 2622=+=AF PA PF , 332622cos ===∠PF AF AFP . ∴ 二面角P CD A --的平面角的余弦值是33. 19.解析:(1)设11A B 的中点为F ,连结1,EF FC .∵E 为1A B 的中点,∴EF112BB . 又1C M 112BB ,∴EF 1MC .∴四边形1EMC F 为平行四边形.∴1EMFC .∵EM ⊄平面1111A B C D ,1FC ⊂平面1111A B C D ,∴EM 平面1111A B C D .(2)作11B H A N ⊥于H ,连结BH ,∵1BB ⊥⊥平面1111A B C D ,∴1BH A N ⊥.∴1BHB ∠为二面角11B A N B --的平面角.∵EM ∥平面1111A B C D ,EM ⊂平面1A BMN ,平面1A BMN 平面11111A B C D A N = ,∴1EM A N .又∵1EM FC ,∴11A N FC .又∵11A FNC ,∴四边形11A FC N 是平行四边形.∴11NC A F =.设1AA a =,则112A B a =,1D N a =. 在11A D N ∆Rt中,1A N ==,∴sin ∠A 1ND 1=11111sin A D A ND A N ∠==. 在11A B H ∆Rt中,11111sin 2B H A B HA B a =∠== 在1BB H ∆Rt 中,111tan 44BB a BHB B H ∠===. (3)延长1A N 与11B C 交于P ,则P ∈平面1A BMN ,且P ∈平面11BB C C . 又∵平面1A BMN平面11BB C C BM = ,∴P BM ∈,即直线111,,A N B C BM 交于一点P .又∵平面1MNC ∥平面11BA B ,∴几何体111MNC BA B -为棱台. ∵112122A BB S a a a ∆=⋅⋅=,12111224MNC S a a a ∆=⋅⋅=, 棱台111MNC BA B -的高为112B C a =,故22311172346V a a a a ⎛⎫=⋅= ⎪ ⎪⎝⎭,3327172266V a a a a a =⋅⋅-=,.∴12717V V =. 20.解析:(1)因为N 是PB 的中点,AB PA =, 所以PB AN ⊥. 由PA ⊥底面ABCD ,得PA AD ⊥,又90BAD ︒∠=,即BA AD ⊥,∴ ⊥AD 平面PAB ,所以PB AD ⊥ ,∴ ⊥PB 平面ADMN ,∴DM PB ⊥.(2)连结DN , 因为⊥BP 平面ADMN ,即⊥BN 平面ADMN ,所以BDN ∠是BD 与平面ADMN 所成的角. 在ABD ∆Rt 中,2222BD BA AD =+=,在PAB ∆Rt 中,2222PB PA AB =+=,故122BN PB ==,在BDN ∆Rt 中, 21sin ==∠BD BN BDN ,又02BDN π≤∠≤,故BD 与平面ADMN 所成的角是6π.(3)由,M N 分别为PB PC ,的中点,得//MN BC ,且1122MN BC ==,又//AD BC ,故//MN AD ,由(1)得⊥AD 平面PAB ,又AN ⊂平面PAB ,故AD AN ⊥,∴四边形ADMN 是直角梯形,在Rt PAB ∆中,2222PB PA AB =+=,122AN PB ==,∴ 截面ADMN 的面积11152()(2)22224S MN AD AN =+⨯=+⨯=.法二: (1)以A 点为坐标原点建立空间直角坐标系A xyz -,如图所示(图略) 由22====BC AB AD PA ,得(0,0,0)A ,1(0,0,2),(2,0,0),(1,,1),(0,2,0)2P B M D 因为3(2,0,2)(1,,1)2PB DM ⋅=-- 0= ,所以DM PB ⊥.(2)因为 (2,0,2)(0,2,0)PB AD ⋅=-⋅0=,所以PB AD ⊥,又DM PB ⊥ , 故PB ⊥平面ADMN ,即(2,0,2)PB =-是平面ADMN 的法向量. 设BD 与平面ADMN 所成的角为θ,又(2,2,0)BD =-.则||1sin |cos ,|2||||4444BD PB BD PB BD PB θ⋅=<>===+⨯+,又[0,]2πθ∈,故6πθ=,即BD 与平面ADMN 所成的角是6π. 因此BD 与平面ADMN 所成的角为6π. (3)同法一. 21.解析:法一:(1)∵四边形ACDE 是正方形, EC AM AC EA ⊥⊥∴,.∵平面⊥ACDE 平面ABC ,又∵AC BC ⊥,⊥∴BC 平面EAC .⊂AM 平面EAC ,⊥∴BC AM . ⊥∴AM 平面EBC .(2)连结BM ,⊥AM 平面EBC ,ABM ∠∴是直线AB 与平面EBC 所成的角.设a BC AC EA 2===,则a AM 2=,a AB 22=, 21sin ==∠∴AB AM ABM , ︒=∠∴30ABM . 即直线AB 与平面EBC 所成的角为︒30(3)过A 作EB AH ⊥于H ,连结HM . ⊥AM 平面EBC ,EB AM ⊥∴.⊥∴EB 平面AHM .AHM ∠∴是二面角C EB A --的平面角.∵平面⊥ACDE 平面ABC ,⊥∴EA 平面ABC .⊥∴EA AB . 在EAB Rt ∆中, EB AH ⊥,有AH EB AB AE ⋅=⋅.由(2)所设a BC AC EA 2===可得a AB 22=,a EB 32=,322aEB AB AE AH =⋅=∴. 23sin ==∠∴AH AM AHM .︒=∠∴60AHM .∴二面角C EB A --等于︒60. 法二: ∵四边形ACDE 是正方形 ,EC AM AC EA ⊥⊥∴,,∵平面⊥ACDE 平面ABC ,⊥∴EA 平面ABC ,∴可以以点A 为原点,以过A 点平行于BC 的直线为x 轴,分别以直线AC 和AE 为y 轴和z 轴,建立如图所示的空间直角坐标系xyz A -.设2===BC AC EA ,则),0,2,2(),0,0,0(B A )2,0,0(),0,2,0(E C ,M 是正方形ACDE 的对角线的交点,)1,1,0(M ∴.(1)=)1,1,0(,)2,2,0()2,0,0()0,2,0(-=-=EC ,)0,0,2()0,2,0()0,2,2(=-=CB ,0,0=⋅=⋅∴CB AM EC AM , CB AM EC AM ⊥⊥∴,⊥∴AM 平面EBC .(2) ⊥AM 平面EBC ,AM ∴为平面EBC 的一个法向量,)0,2,2(),1,1,0(== ,21,cos =⋅=∴AM AB AM AB .︒=60,AM AB .∴直线AB 与平面EBC 所成的角为︒30.(3)设平面EAB 的法向量为),,(z y x =,则AE n ⊥且AB n ⊥,0=⋅∴AE n 且0=⋅AB n . ⎩⎨⎧=⋅=⋅∴.0),,()0,2,2(,0),,()2,0,0(z y x z y x 即⎩⎨⎧=+=.0,0y x z ,取1-=y ,则1=x , 则)0,1,1(-=n . 又∵为平面EBC 的一个法向量,且)1,1,0(=AM ,21cos -=⋅=∴AMn AM n ,设二面角C EB A --的平面角为θ,则21cos cos ==AM n θ,︒=∴60θ.∴二面角C EB A --等于︒60. 22.解析:法一:(1)因为1A D ⊥平面ABC ,所以平面11AA C C ⊥平面ABC ,又BC AC ⊥,所以BC ⊥平面11AAC C ,得1BC AC ⊥,又11BA AC ⊥,所以1AC ⊥平面1A BC ;(2)因为11AC A C ⊥,所以四边形11AAC C 为 菱形,故12AA AC ==,又D 为AC 中点,知160A AC ∠=.取1AA 中点F ,则1AA ⊥平面BCF ,从而面1A AB ⊥面BCF , 过C 作CH BF ⊥于H ,则CH ⊥面1A AB .在Rt BCF ∆中,2,3BC CF ==,故2217CH =, 即1CC 到平面1A AB 的距离为2217CH =.(3)过H 作1HG A B ⊥于G ,连CG ,则1CG A B ⊥, 从而CGH ∠为二面角1A A B C --的平面角, 在1Rt A BC ∆中,12A C BC ==,所以2CG =,在Rt CGH ∆中,42sin 7CH CGH CG ∠==, 故二面角1A A B C --的正弦值为427. 法二:(1)如图,取AB 的中点E ,则//DE BC ,因为BC AC ⊥,所以DE AC ⊥,又1A D ⊥平面ABC ,以1,,DE DC DA 为,,x y z 轴建立空间坐标系,则()0,1,0A -,()0,1,0C ,()2,1,0B ,()10,0,A t ,()10,2,C t ,()10,3,AC t =,()12,1,BA t =--,()2,0,0CB =,由10AC CB ⋅=,知1A C CB ⊥,又11BA AC ⊥,从而1AC ⊥平面1A BC ;(2)由1AC ⋅2130BA t =-+=,得3t =. 设平面1A AB 的法向量为(),,n x y z =,(13AA =,()2,2,0AB =,所以130220n AA y z n AB x y ⎧⋅==⎪⎨⋅=+=⎪⎩,设1z =,则()3,3,1n =-所以点1C 到平面1A AB 的距离1AC n d n⋅==217. (3)再设平面1A BC 的法向量为(),,m x y z =,(10,3CA =-,()2,0,0CB =,所以13020m CA y z m CB x ⎧⋅=-+=⎪⎨⋅==⎪⎩,设1z =, 则()0,3,1m =,故cos ,m n m n m n⋅<>==⋅7-,根据法向量的方向,可知二面角1A A B C --的余弦值为7.。
