上海市新知杯初中数学竞赛试题及答案
上海初一初中数学竞赛测试带答案解析

上海初一初中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.六位数由三位数重复构成,如256256,或678678等等,这类数能被何数整除(15届江苏初一2试)六位数六位数A.11;B.101;C.13;D.1001.2.两班学生参加一个测试,20名学生的一班,平均分是80分;30名学生的一班平均分是70分,两班所有学生的平均分是A.75分;B.74分;C.72分;D.77分.3.一个数被10除余9,被9除余8,被8除余7,…,被2除余1,则此数为A.59 ;B.1259;C.2519;D.非以上结论.4.0.000000375与下列数不等的是A.;B.;C.;D..5.若1+2+3+…+k之和为一完全平方,若n小于100,则k可能的值为A.8;B.1,8 ;C.8,49;D.1,8,49.6.若,则z等于(15届江苏初二1试)若A.;B.;C.;D..7.一同学在n天假期中观察:(1)下了7次雨,在上午或下午;(2)当下午下雨时,上午是晴天;(3)一共有5个下午是晴天;(4)一共有6个上午是晴天。
则n最小为A.7;B.9;C.10 ;D.11.8.如表所示,则x与y的关系式为()+x+1C.y=(x2+x+1)(x-1) D.非以上结论9.在下列图形中,各有一边长为4cm的正方形与一个8cm×2cm的长方形相重叠.问哪一个重叠的面积最大()10.运算※按下表定义,例如3※2=1,那么(2※4)※(1※3)=()A.1 ;B.2;C.3;D.4.二、填空题1.计算: .2.(17届江苏初一1试)计算等式,式中的应为 .3.三个连续的自然数的最小公倍数是168,那么这三个自然数的和等于 .4.将1,2,3,…,49,50任意分成10组,每组5个数,在每组中取数值居中的那个数为“中位数”,则这10个中位数的最大值是 .5.(15届江苏初一1试)时钟在2点时,分针与时针所夹的角为60°.从0时到3时,会有个时刻,分针与时针也能构成60°的角.6.图中阴影部分占(15届江苏初二1试)图中图形的(填几分之几).7.如图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长为1,则这个六边形的周长是 (17届江苏初一1试)如图如 .8.已知,点O在三角形内,且,则的度数是(17届江苏初一1试) 度.9.(17届江苏初三)在在在4点钟与5点钟之间,分钟与时钟成一条直线,那么此时时间是 .10.(15届江苏初一1试)一条一条直街上有5栋楼,按从左至右顺序编号为1、2、3、4、5,第k号楼恰好有k (k=1、2、3、4、5)个A厂的职工,相邻两楼之间的距离为50米.A厂打算在直街上建一车站,为使这5栋楼所有A厂职工去车站所走的路程之和最小,车站应建在距1号楼米处.上海初一初中数学竞赛测试答案及解析一、选择题1.六位数由三位数重复构成,如256256,或678678等等,这类数能被何数整除(15届江苏初一2试)六位数六位数A.11;B.101;C.13;D.1001.【答案】D【解析】析:六位数由三位数重复构成,说明这类数一定能被此三位数整除,不妨用构成的六位数除以三位数得到的数即所求的数.解答:解:256256÷256=1001,678678÷678=1001,设三位数abc,则重复构成的六位数为abcabc,abcabc÷abc=1001.故选D.点评:此题考查了学生对数的整除性问题的解答与掌握,此题解答的关键是用构成的六位数除以三位数得出要求的数.2.两班学生参加一个测试,20名学生的一班,平均分是80分;30名学生的一班平均分是70分,两班所有学生的平均分是A.75分;B.74分;C.72分;D.77分.【答案】B【解析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.解答:解:根据题意得:该组数据的平均数==74.故选B.点评:本题考查的是加权平均数的求法.本题易出现的错误是求80,70这四个数的平均数,对平均数的理解不正确.3.一个数被10除余9,被9除余8,被8除余7,…,被2除余1,则此数为A.59 ;B.1259;C.2519;D.非以上结论.【答案】C【解析】分析:这个最小正整数加上1是2、3、4、5、…10的最小公倍数,求得最小公倍数减1即可求得答案.解答:解:由题意可知所求最小正整数是2,3,4,5,…,10的最小公倍数减去1,2,3,4,5,…,10的最小公倍数是实际就是7,8,9,10的最小公倍数为2520,则所求最小数是2520-1=2519.故选C.点评:此题考查了带余数除法,主要利用求几个数的最小公倍数的方法解决问题.4.0.000000375与下列数不等的是A.;B.;C.;D..【答案】D【解析】分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.注意小数和分数相互间的转化.解答:解:0.000 000 375=3.75×10-7=3×10-7=≠.故选D.点评:本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.5.若1+2+3+…+k之和为一完全平方,若n小于100,则k可能的值为A.8;B.1,8 ;C.8,49;D.1,8,49.【答案】D【解析】分析:本题直接求解难度较大,故采用代入法,间接验证.解答:解:∵1+2+3+…+k=k(k+1)∴k(k+1)=n2,当k=1时,则k(k+1)=1,n=1,显然成立.当k=8时,则k(k+1)=36,此时n=6,成立;当k=49时,则k(k+1)=25×49,n=35,成立.故答案为D.点评:本题考查完全平方数.同学们对于做选择题目,采用将选项代入验证的方法,有时候起到事半功倍的效果,本题就是这样,如直接求解,难度非常大,这样求解简单多了.6.若,则z等于(15届江苏初二1试)若A.;B.;C.;D..【答案】D【解析】略7.一同学在n天假期中观察:(1)下了7次雨,在上午或下午;(2)当下午下雨时,上午是晴天;(3)一共有5个下午是晴天;(4)一共有6个上午是晴天。
最新上海市新知杯初中数学竞赛试题及答案(1)
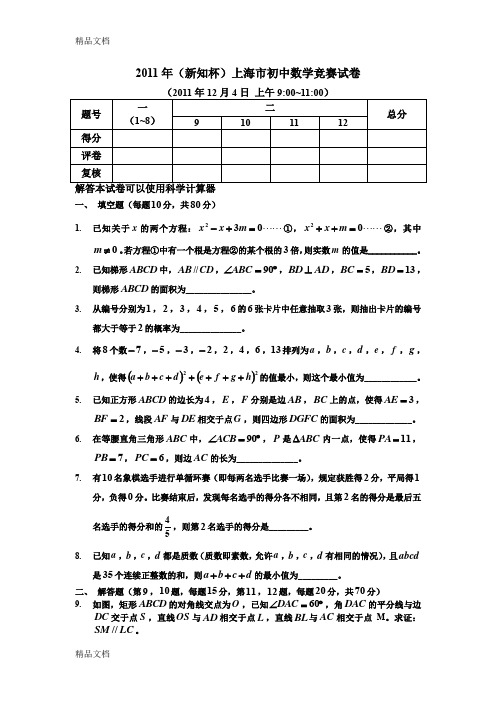
2011年(新知杯)上海市初中数学竞赛试卷一、 填空题(每题10分,共80分)1. 已知关于x 的两个方程: 032=+-m x x ①, 02=++m x x ②,其中0≠m 。
若方程①中有一个根是方程②的某个根的3倍,则实数m 的值是___________。
2. 已知梯形ABCD 中,AB //CD ,︒=∠90ABC ,AD BD ⊥,5=BC ,13=BD ,则梯形ABCD 的面积为_______________。
3. 从编号分别为1,2,3,4,5,6的6张卡片中任意抽取3张,则抽出卡片的编号都大于等于2的概率为______________。
4. 将8个数7-,5-,3-,2-,2,4,6,13排列为a ,b ,c ,d ,e ,f ,g ,h ,使得()()22h g f e d c b a +++++++的值最小,则这个最小值为____________。
5. 已知正方形ABCD 的边长为4,E ,F 分别是边AB ,BC 上的点,使得3=AE ,2=BF ,线段AF 与DE 相交于点G ,则四边形DGFC 的面积为_____________。
6. 在等腰直角三角形ABC 中,︒=∠90ACB ,P 是ABC ∆内一点,使得11=PA ,7=PB ,6=PC ,则边AC 的长为______________。
7. 有10名象棋选手进行单循环赛(即每两名选手比赛一场),规定获胜得2分,平局得1分,负得0分。
比赛结束后,发现每名选手的得分各不相同,且第2名的得分是最后五名选手的得分和的54,则第2名选手的得分是_________。
8. 已知a ,b ,c ,d 都是质数(质数即素数,允许a ,b ,c ,d 有相同的情况),且abcd是35个连续正整数的和,则d c b a +++的最小值为_________。
二、 解答题(第9,10题,每题15分,第11,12题,每题20分,共70分)9. 如图,矩形ABCD 的对角线交点为O ,已知︒=∠60DAC ,角DAC 的平分线与边DC 交于点S ,直线OS 与AD 相交于点L ,直线BL 与AC 相交于点M 。
初中数学竞赛试题_1

2021 年“新知杯〞初中数学竞赛一、填空题〔第1~5小题,每一小题8分,第6~10小题,每一小题10分,一共90分〕1. −1<2x −1<1,那么12 x的取值范围为 . 2. 在面积为1 的△ABC 中,P 为边BC 的中点,点Q 在边AC 上,且AQ=2QC 。
连接AP 、BQ 交于点R ,那么△ABR 的面积是 .3. 在△ABC 中,∠C=90°,∠A 、∠B 、∠C 的对边顺次为a 、b 、c 。
假设关于x 的方程 c(x 2 +1)-22bx-a(x 2-1) = 0的两根平方和为10,那么ab 的值是 . 4. 数x 1 ,x 2 ,…, x 100 满足如下条件:对于k = 1,2,…,100,x k 比其余99个数的和小k 。
那么x 25的值是 .5. 实数a 、b 、c ,且b ≠ 0。
假设实数x 1 ,x 2, y 1 ,y 2满足x 12+ax 22=b ,x 2y 1-x 1y 2=a , x 1y 1+ax 2y 2=c ,那么y 12+ay 22的值是 .6.如图,设P 是凸四边形ABCD 内一点,过P 分别作AB 、BC 、CD 、DA 的垂线,垂足分别为E 、F 、G 、H.AH=3,HD=4,DG=1,GC=5,CF=6,FB=4,且BE-AE=1。
那么四边形ABCD 的周长为 .第6题图 第7题图7. 如图,△ABC 的面积为1,点D 、G 、E 和F 分别在边AB 、AC 、BC 上,BD <DA ,DG ∥BC , DE ∥AC ,GF ∥AB.那么梯形DEFG 面积的最大可能值为 .8. 不超过1000 的正整数x ,使得x 和x+1 两者的数字和都是奇数。
那么满足条件的正整数x 有 个.9. k 为不超过50 的正整数,使得对任意正整数n ,2×36n+k×23n+1-1 都能被7 整除。
那么这样的正整数k 有 个.10. 使得22)1(++p p 是完全平方数的所有质数p 为 .二、〔20 分〕如图,在 Rt △ABC 中,∠C=90°,BC=2,AC=x ,点F 在边AB 上,点G 、H 在边BC 上,四边形EFGH 是一个边长为y 的正方形,且AE=AC.〔1〕求y 关于x 的函数解析式.〔2〕当x 为何值时,y 取到最大值?并求出y 的最大值.三、〔20 分〕求满足以下条件的正整数 n 的所有可能值:对这样的n ,能找到实数a 、b ,使得函数 b ax x nx f ++=21)(对任意整数x ,f 〔x 〕都是整数.四、〔20 分〕在一个盒子里有红、黄、黑三种颜色的小球一共88 个.从中任意取出24 个,就可以保证至少有10个小球是同色的.问在满足上述条件下,无论各种颜色的小球如何分配,至少要从盒子中任意取出多少个小球,才能保证至少有20 个小球是同色的?励志赠言经典语录精选句;挥动**,放飞梦想。
2013年上海市新知杯初中数学竞赛
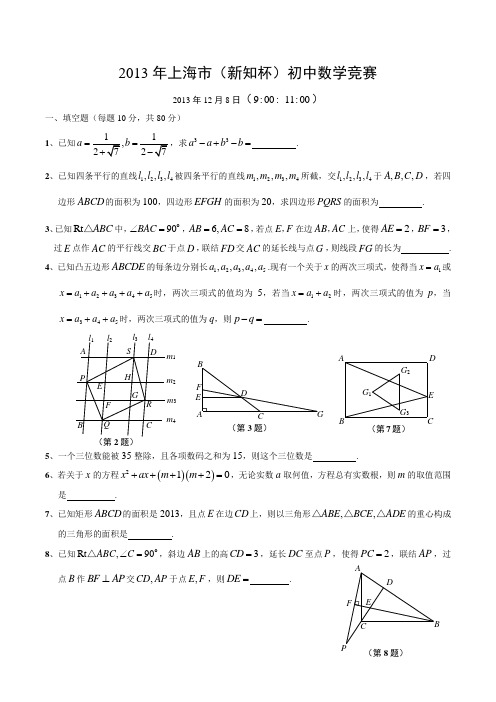
2013年上海市(新知杯)初中数学竞赛2013年12月8日(9:0011:00:)一、填空题(每题10分,共80分) 1、已知a b ==,求33a ab b -+-= . 2、已知四条平行的直线1234,,,l l l l 被四条平行的直线1234,,,m m m m 所截,交1234,,,l l l l 于,,,A B C D ,若四边形ABCD 的面积为100,四边形EFGH 的面积为20,求四边形PQRS 的面积为 . 3、已知Rt ABC △中,90BAC ∠=o,6,8AB AC ==,若点E ,F 在边AB ,AC 上,使得2AE =,3BF =,过E 点作AC 的平行线交BC 于点D ,联结FD 交AC 的延长线与点G ,则线段FG 的长为 . 4、已知凸五边形ABCDE 的每条边分别长12345,,,,a a a a a .现有一个关于x 的两次三项式,使得当1x a =或12345x a a a a a =++++时,两次三项式的值均为5,若当12x a a =+时,两次三项式的值为p ,当345x a a a =++时,两次三项式的值为q ,则p q -= .5、一个三位数能被35整除,且各项数码之和为15,则这个三位数是 .6、若关于x 的方程()()2120x ax m m ++++=,无论实数a 取何值,方程总有实数根,则m 的取值范围是 .7、已知矩形ABCD 的面积是2013,且点E 在边CD 上,则以三角形,,ABE BCE ADE △△△的重心构成的三角形的面积是 .8、已知Rt ,90ABC C ∠=o△,斜边AB 上的高3CD =,延长DC 至点P ,使得2PC =,联结AP ,过点B 作BF AP ⊥交,CD AP 于点,E F ,则DE = .G 3G 2G 1AC DE B (第7题)B(第2题)C A H GFER Q PS D l 1 l 2l 3 l 4 m1m 2m 3m 4(第3题)GD FE B AC E FDAC B(第8题)二、解答题(第9、10题,每题15分;第11、12题,每题20分,共70分)9、如图,已知正方形ABCD 的边长为1,线段PQ 过点C 且与射线,AD AB 相交与点,P Q .求:111AP AQ PQ++的最大值.10、给定非零实数a ,解下列方程组:,1.x xy a yy xy x a⎧-=⎪⎪⎨⎪-=⎪⎩11、已知一个正整数n ()1n >,若正整数n 满足能找到n 个整数12,n a a a L 使得:12122013n n a a a a a a +++==L L ,求n 的最小值.12、已知正整数,,,a b c d 满足()()2213;13a c d b c d =+=-,求所有满足条件的d 的值.ACDP 第9题参考答案:1、6427-2、6034、05、7356、21m -≤≤-7、6713 8、959、4410、x y ⎧=⎪⎨⎪=⎩11、512、85d =。
2018年新知杯上海市初中数学竞赛试题及答案

2018年新知杯上海市初中数学竞赛参考解答一、填空题(第1-5小题每题8分,第6-10小题每题10分,共90分) 1、对于任意实数a,b ,定义,a ∗b=a (a +b ) +b, 已知a ∗2.5=28.5,则实数a 的值是 。
【答案】4,132-2、在三角形ABC 中,22b 1,,2a AB BC a CA =-==,其中a,b 是大于1的整数,则b-a= 。
【答案】03、一个平行四边形可以被分成92个边长为1的正三角形,它的周长可能是 。
【答案】50,944、已知关于x 的方程4322(3)(2)20x x k x k x k ++++++=有实根,并且所有实根的乘积为−2,则所有实根的平方和为 。
【答案】55、如图,直角三角形ABC 中, AC=1,BC =2,P 为斜边AB 上一动点。
PE ⊥BC ,PF ⊥CA ,则线段EF 长的最小值为 。
6、设a ,b 是方程26810x x ++=的两个根,c ,d 是方程28610x x -+=的两个根,则(a+ c )( b + c )( a − d )( b − d )的值 。
【答案】2772第五题图BA7在平面直角坐标系中有两点P (-1,1) , Q (2,2),函数y =kx −1 的图像与线段PQ 延长线相交(交点不包括Q ),则实数k 的取值范围是 。
【答案】1332k <<8方程xyz =2018的所有整数解有 组。
【答案】729如图,四边形ABCD 中AB =BC =CD ,∠ABC =78°,∠BCD =162°。
设AD ,BC 延长线交于E ,则∠AEB = 。
【答案】21°10、如图,在直角梯形ABCD 中,∠ABC =∠BCD = 90°,AB =BC =10,点M 在BC 上,使得ΔADM 是正三角形,则ΔABM 与ΔDCM 的面积和是 。
【答案】300-二、(本题15分)如图,ΔABC 中∠ACB =90°,点D 在CA 上,使得CD =1, AD =3,并且∠BDC =3∠BAC ,求BC 的长。
2017年新知杯上海市数学竞赛

2017年新知杯上海市数学竞赛2017年(新知杯)上海市初中数学竞赛试卷2017年12月4日上午9:00~11:00)一、填空题(每题10分,共80分)1.已知关于x的两个方程:x-x+3m=……①,x+x+m=……②,其中m≠0.若方程①中有一个根是方程②的某个根的3倍,则实数m的值是___________。
2.已知梯形ABCD中,XXX,∠ABC=90°,BD⊥AD,BC=5,BD=13,则梯形ABCD的面积为_______________。
3.从编号分别为1,2,3,4,5,6的6张卡片中任意抽取3张,则抽出卡片的编号都大于等于2的概率为______________。
4.将8个数-7,-5,-3,-2,2,4,6,13排列为a,b,c,d,e,f,g,h,使得(a+b+c+d)+(e+f+g+h)的值最小,则这个最小值为____________。
5.已知正方形ABCD的边长为4,E,F分别是边AB,BC上的点,使得AE=3,BF=2,线段AF与DE相交于点G,则四边形DGFC的面积为_____________。
6.在等腰直角三角形ABC中,∠ACB=90°,P是△ABC内一点,使得PA=11,PB=7,PC=6,则边AC的长为______________。
7.有10名象棋选手进行单循环赛(即每两名选手比赛一场),规定获胜得2分,平局得1分,负得分。
比赛结束后,发现每名选手的得分各不相同,且第2名的得分是最后五名选手的得分和的4/5,则第2名选手的得分是_________。
8.已知a,b,c,d都是质数(质数即素数,允许a,b,c,d有相同的情况),且abcd是35个连续正整数的和,则a+b+c+d的最小值为_________。
二、解答题(第9,10题,每题15分,第11,12题,每题20分,共70分)9.如图,矩形ABCD的对角线交点为O,已知∠DAC=60°,角DAC的平分线与边DC交于点S,直线OS与AD相交于点L,直线BL与AC相交于点M。
2000-2022年(新知杯)历年上海市初中数学竞赛试卷及答案(试题全与答案分开)
2022上海市初中数学竞赛(新知杯)一、填空题(每题10分) 1.721,721-=+=b a ,那么.________33=-+-b b a a2.43214321//////,//////m m m m l l l l ,._______,20,100===EFGH ILKJ ABCD S S S 则3.F E AC AB A 、,,8,690==︒=∠在AB 上且3,2==BF AE 过点E 作AC 的平行线交BC 于D ,FD 的延长线交AC 的延长线于G ,那么.__________=GF4.凸五边形的边长为)(,,,,,54321x f a a a a a 为二次三项式;当1a x =或者5432a a a a x +++=时,5)(=x f ,当21a a x +=时,,)(p x f =当543a a a x ++=时,q x f =)(,那么.________=-q p 5.一个三位数是35的倍数且各个数位上数字之和为15,那么这个三位数为___________.6.关于x 的一元二次方程0)2)(1(2=++++m m ax x 对于任意的实数a 都有实数根,那么m 的取值范围是_________________.7.四边形ABCD 的面积为2022,E 为AD 上一点,CDE ABE BCE ∆∆∆,,的重心分别为321,,G G G ,那么321G G G ∆的面积为________________.8.直角三角形斜边AB 上的高3=CD ,延长DC 到P 使得2=CP ,过B 作AP BF ⊥交CD 于E ,交AP 于F ,那么._________=DE二、解答题〔第9题、第10题15分,第11题、第12题20分〕 9.︒=∠90BAC ,四边形ADEF 是正方形且边长为1,求CABC AB 111++的最大值. 10.a 是不为0的实数,求解方程组:⎪⎪⎩⎪⎪⎨⎧=-=-ax y xy a yxxy 111.:,1>n n a a a a ,,,,321 为整数且2013321321=⋅⋅⋅⋅=++++n n a a a a a a a a ,求n 的最小值.12.正整数d c a 、、、b 满足),13(),13(22-=+=d c b d c a 求所有满足条件的d 的值. 答案:1.27102- 2.60 3.265 4.0 5.735 6.12-≤≤-m 7.36718.599.CA BC AB 111++4221+≤ 10.经检验原方程组的解为:⎪⎩⎪⎨⎧+=+=1122a y a a x ,⎪⎩⎪⎨⎧+-=+-=1122a y a a x .11.【解析】2013,1,1,554321===-===a a a a a n 当满足题设等式,下证当4≤n 时,不存在满足等式要求的整数,不妨设n a a a a ≤≤≤≤ 321,(1)当4=n 时,611132013⨯⨯=,当4321,,,a a a a 中有负整数时,必为⎩⎨⎧==+⇒-==20132015,1434321a a a a a a ,假设2013,143==a a 不满足条件,当20152671,344343<≤+⇒≤⇒≥a a a a a 无解.不可能,当4321,,,a a a a 中无负整数时,显然20134≠a ,6714≤a ,容易验证等式不可能成立.(2)当3=n 时,当321,,a a a 中有负整数时,必为,121-==a a 显然等式不成立,当321,,a a a 中无负整数时,同上容易验证等式不可能成立.(3)当2=n 时,21,a a 均为正整数,同上易验证等式不可能成立. 综上所述,n 的最小值为5. 12.85=d2022上海新知杯初中数学竞赛答案2022年〔新知杯〕上海市初中数学竞赛试卷〔2022年12月9日 上午9:00~11:00〕一、填空题〔每题10分,共80分〕1. 的边上的高为,与边平行的两条直线将的面积三等分,那么直线与之间的距离为_____________。
2006年新知杯上海市初中数学竞赛
.
ABC 的面积为 S ,周长为 p , A′ B′ C′ 的三边在 ABC 外 ,且与对应边的 距离均为 h . 则 A′ B′ C′ 的周长为 ,面
8. 如图 4 ,
积为 . 9. 已知 n ( n > 1) 个整数 ( 可以相同) a1 , a2 , …, a n 满足 a1 + a2 + …+ a n = a1 a2 …an = 2 007. 则 n 的最小值是 . 10. 把能表示成两个正整数平方差的这 种正整数 , 从小到大排成一列 : a1 , a2 , …, 2 2 2 2 a n , …( 如 a1 = 2 - 1 = 3 , a2 = 3 - 2 = 5 , a3 2 2 2 2 ) . 那么 , a1 + = 4 - 3 = 7 , a4 = 3 - 1 = 8 , … a2 + …+ a100 的值是 . ( ) 二 、 20 分 如 图 5 , 已知半径分别为 1 、 2 的两 个同心圆 , 有一个 正 方 形 ABCD , 其中 , 点 A 、 D 在半 径为 2 的圆周上 , 点 B 、 C 图5 在半径为 1 的圆周上 . 求这 个正方形的面积 . ( 20 分) 关于 x 、 三、 y、 z 的方程组 3x +2y + z = a , xy + 2 yz + 3 zx = 6 有实数解 ( x , y , z ) . 求正实数 a 的最小值 . ( 20 分) 设 A 是给定的正有理数 . 四、 (1) 若 A 是一个三边长都是有理数的直 角三角形的面积 ,证明 : 一定存在 3 个正有理 2 2 2 2 数 x、 y、 z ,使得 x - y = y - z = A ; ( 2) 若存在 3 个正有理数 x 、 y、 z , 满足
2013年新知杯上海市初中数学竞赛
8
6
网3
= = >E D :— 1 6
.
3
在R t △D E F中 ,
而点 到边 A 的距离 为 D, 故点 的边
√ , 2 6 5
F D : √ h
j FG =3 FD =
4. 0 .
一
^
延长 D C到点 P, 使得 C P= 2 , 联结 A P , 过点 曰作 ,上 A P, 分别与 C D、 A P交于点 E、 则线段 D E
l 冬 I 1
3 . 在R t △A B C中 , 已知 B A C= 9 0 。 , A B=
的 长 为一
6 , A C= 8 , 点E 、 F在边 A B上 , 使得 A E= 2 , B F= 3 .
二、 9 . 原方程组为
x y 一口 =— —.
。
Y
①
。 ≥
:
:6 71
1
r 上
Y
,= ≤
x y一— —=— —
将 上 面 两式 相 乘 得
( 一 。 ) ( 一 ) = j ( ) 一 ( 。 + ) ( ) = 0 .
7. .
一
2≤ m ≤ 一 1
) ( + ・ 一 - ) = 一 笺 .
, ’
2 . 6 0 .
由 图易 得
S 四 边 脚 形 P 0 s一 :6 0 . 。
一
ห้องสมุดไป่ตู้
如图 4 , 设△ A B E、 △B C E、 △A D E 的重 心依 次为 、 y 、 z . 由 重 心 的 性 质 及 相
试题:2011年新知杯上海市初中数学竞赛试题(含答案解析)
2011年新知杯上海市初中数学竞赛试题一、填空题(每题10分,共80分)1.已知关于x的两个方程:错误!未找到引用源。
-x+3m=0……①,错误!未找到引用源。
+x+m=0……②,其中m≠0.若方程①有一个根是方程②的一个根的3倍,则实数m的值是_________。
2.已知梯形ABCD中AB‖CD,∠ABC=90°,BD⊥AD,BC=5,BD=13,则梯形ABCD的面积为______。
3.从编号为1、2、3、4、5、6的六张卡片中任意抽取三张,则抽出的卡片编号都大于2的概率为________.4.将8个数,-7,-5,-3,-2,2,4,6,13排列为a,b,c,d,e,f,g,h,使得+的值最小,则这个最小值为________.5.已知正方形ABCD边长为4,E、F分别在AB,BC上,AE=3,BF=2,AF,DE交于G,则四边形DGFC的面积为。
6.在等腰直角三角形ABC中,∠ACB=90°,P是△ABC内一点,使得PA=11,PB=7,PC=6,则AC边长为____________。
7.有10名象棋选手进行单循环赛,规定每场比赛胜方得2分,负方得0分,平局各得1分,比赛结束后发现每位选手得分各不同,且第二名的得分是最后五名选手得分之和的,则第二名选手得分是_______。
8.已知a,b,c,d都是素数(可以相同),并且abcd是35个连续正整数之和,则a+b+c+d 的最小值为_________.二、解答题(第9、10题每题15分,第11、12题每题20分,共70分)9.如图,矩形ABCD的对角线交于O,已知∠DAC=60°,∠DAC的平分线与DC交于S,直线OS,AD相交于L,直线BL与AC交于M。
求证:SM‖LC.10.求所有正整数组a ≥b ≥c ≥d ≥e ≥f ,使得a !=b !+c !+d !+e !+f !。
11.①求证:存在整数x ,y ,满足+4xy+=2022②是否存在整数x ,y ,满足+4xy+=2011?请证明你的结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
20XX 年(新知杯)上海市初中数学竞赛试卷
(20XX 年12月4日上午9:00~11:00)
题号一(1~8)
二
总分
9
10
11
12
得分评卷复核
解答本试卷可以使用科学计算器
一、填空题(每题10分,共80分)
1.
已知关于
x 的两个方程:
032
m x x
①,0
2
m x x
②,其中
0m。
若方程①中有一个根是方程②的某个根的3倍,
则实数m 的值是___________。
2.
已知梯形ABCD 中,AB //CD ,90ABC ,AD BD ,5BC ,13BD ,
则梯形
ABCD 的面积为_______________。
3.从编号分别为1,2,3,4,5,6的6张卡片中任意抽取
3张,则抽出卡片的编号
都大于等于
2的概率为______________。
4.
将8个数7,5,3,
2,2,4,6,13排列为a ,b ,c ,d ,e ,f ,g ,
h ,使得2
2
h g
f
e
d
c
b a
的值最小,则这个最小值为
____________。
5.
已知正方形
ABCD 的边长为4,E ,F 分别是边AB ,BC 上的点,使得3AE ,
2BF
,线段AF 与DE 相交于点G ,则四边形DGFC 的面积为_____________。
6.
在等腰直角三角形
ABC 中,
90ACB
,P 是
ABC 内一点,使得11PA
,
7PB
,6PC ,则边AC 的长为______________。
7.
有10名象棋选手进行单循环赛(即每两名选手比赛一场),规定获胜得
2分,平局得1
分,负得
0分。
比赛结束后,发现每名选手的得分各不相同,
且第
2名的得分是最后五
名选手的得分和的
5
4,则第
2名选手的得分是_________。
8.
已知a ,b ,c ,d 都是质数(质数即素数,允许a ,b ,c ,d 有相同的情况),且abcd
是
35个连续正整数的和,则d c b a 的最小值为_________。
二、解答题(第9,10题,每题15分,第11,12题,每题20分,共70分)
9.
如图,矩形ABCD 的对角线交点为O ,已知60DAC ,角DAC 的平分线与边DC 交于点S ,直线OS 与AD 相交于点L ,直线BL 与AC 相交于点M 。
求证:LC SM //。
O
M S
L
D
C
B
A
10.对于正整数n ,记n n 2
1!。
求所有的正整数组f e d c b a ,,,,,,使得
!!!!!!
f e d c b a ,且f e
d
c
b
a。
解
11.(1)证明:存在整数
x ,y ,满足202242
2
y
xy x
;
(2)问:是否存在整数
x ,y ,满足?201142
2
y
xy
x 证明你的结论。
12.对每一个大于
1的整数n ,设它的所有不同的质因数为
1p ,2p ,...,k p ,对于每个
k i
p i 1
,存在正整数i a ,使得1
i i a i
a i
p n
p
,
记
k
a k
a a p p p n
p 2
1
2
1
例如,8952100
2
6p 。
(1)试找出一个正整数
n ,使得n n p ;
(2)证明:存在无穷多个正整数n ,使得n .n
p 11。
解
学习必备欢迎下载。
