【K12教育学习资料】高三数学专题复习 中档题满分练(2)理
高考数学二轮复习练习:中档大题满分练(二)含答案

中档大题满分练2.三角函数与解三角形(B组)中档大题集训练,练就慧眼和规范,筑牢高考满分根基!1.已知△ABC中,角A,B,C所对的边分别是a,b,c,且asin A+csin C-bsin B =asin C.(1)求角B的大小.(2)设向量m=(cos A,cos 2A),n=(12,-5),边长a=4,当m·n取最大值时,求b的长.【解析】(1)由题意,asin A+csin C-bsin B=asin C,所以a2+c2-b2=ac,所以cos B===,B∈(0,π),所以B=.(2)因为m·n=12cos A-5cos 2A=-10+,所以当cos A=时,m·n取最大值, 此时,sin A=. 由正弦定理得,b=a·= .2.如图,在平面四边形ABCD中,∠ABC=π,AB⊥AD,AB=1.世纪金榜导学号(1)若AC=,求△ABC的面积.(2)若∠ADC=,CD=4,求sin∠CAD. 【解析】(1)在△ABC中,由余弦定理得, AC2=AB2+BC2-2AB·BC·cos∠ABC, 即5=1+BC2+BC,解得BC=或-2(舍去),所以△ABC的面积S△ABC=AB·BC·sin∠ABC=×1××=.(2)设∠CAD=θ,在△ACD中,由正弦定理得,=,即=,所以AC=.在△ABC中,∠BAC=-θ,∠BCA=θ-,则=,即=,即4=sin θ,整理得sin θ=2cos θ.又因为sin2θ+cos2θ=1,解得sin θ=,即sin∠CAD=.关闭Word文档返回原板块。
高三数学二轮复习中档题规范练二文
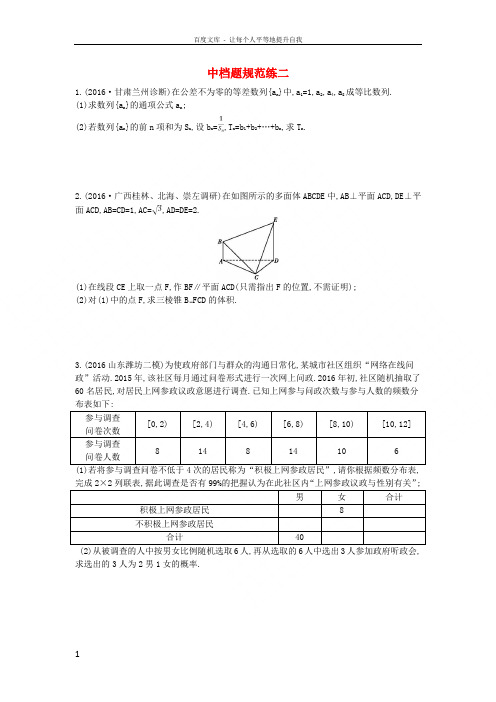
中档题规范练二1.(2016·甘肃兰州诊断)在公差不为零的等差数列{a n}中,a1=1,a2,a4,a8成等比数列.(1)求数列{a n}的通项公式a n;(2)若数列{a n}的前n项和为S n,设b n=,T n=b1+b2+…+b n,求T n.2.(2016·广西桂林、北海、崇左调研)在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AB=CD=1,AC=,AD=DE=2.(1)在线段CE上取一点F,作BF∥平面ACD(只需指出F的位置,不需证明);(2)对(1)中的点F,求三棱锥B FCD的体积.3.(2016山东潍坊二模)为使政府部门与群众的沟通日常化,某城市社区组织“网络在线问政”活动.2015年,该社区每月通过问卷形式进行一次网上问政.2016年初,社区随机抽取了60名居民,对居民上网参政议政意愿进行调查.已知上网参与问政次数与参与人数的频数分参与调查[0,2) [2,4) [4,6) [6,8) [8,10) [10,12] 问卷次数参与调查8 14 8 14 10 6问卷人数(1)若将参与调查问卷不低于4次的居民称为“积极上网参政居民”,请你根据频数分布表,完成2×2列联表,据此调查是否有99%的把握认为在此社区内“上网参政议政与性别有关”;男女合计积极上网参政居民8不积极上网参政居民合计40求选出的3人为2男1女的概率.4.(2016·安徽安庆二模)在平面直角坐标系中,以原点为极点,x轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的单位长度.已知曲线C的极坐标方程为ρ=2cos θ,直线l的参数方程为(t为参数,α为直线的倾斜角).(1)写出直线l的普通方程和曲线C的直角坐标方程;(2)若直线l与曲线C有唯一的公共点,求角α的大小.5.(2016·甘肃河西五市部分普通高中联考)已知不等式|x+2|+|x-2|<18的解集为A.(1)求集合A;(2)若∀a,b∈A,x∈(0,+∞),不等式a+b<x++m恒成立,求实数m的取值范围.中档题规范练二1.解:(1)设等差数列{a n}的公差为d,则依题意有解得d=1或d=0(舍去),所以a n=a1+(n-1)d=n.(2)由(1)得S n=,所以b n==2(-),所以T n=2[(1-)+(-)+(-)+…+(-)]=2(1-)=.2.解:(1)取CE的中点F,连接BF,BF∥平面ACD(如图).(2)因为AD2=AC2+CD2,所以∠ACD=90°.所以AC⊥CD.因为DE⊥平面ACD,所以AC⊥DE.因为DE∩CD=D,所以AC⊥平面CDE.因为DE⊥平面ACD,AB⊥平面ACD,所以AB∥DE.因为AB⊄平面CED,DE⊂平面CED,所以AB∥平面CED.所以B到平面FCD的距离为AC.又S△FCD=S△ECD=××1×2=,所以=AC·S△FCD=.3.解:(1)由题意知,积极上网参政的有8+14+10+6=38人,不积极上网参政的有8+14=22人,男女合计积极上网参政居民30 8 38不积极上网参政居民10 12 22合计40 20 60所以K2=≈,因为>,所以有99%的把握认为在此社区内“上网参政议政与性别有关”.(2)选取男居民人数为6×=4人,选取女居民人数为6×=2人,记4个男居民分别为A,B,C,D,2个女居民分别为甲、乙,则基本事件有(ABC),(ABD),(AB甲),(AB乙),(ACD),(AC甲),(AC乙),(AD甲),(AD乙),(A甲乙),(BCD),(BC甲),(BC乙),(BD甲),(BD乙),(B甲乙),(CD甲),(CD乙),(C甲乙),(D甲乙),共20种,满足条件的基本事件有12种,所以所求概率为P==.4.解:(1)当α=时,直线l的普通方程为x=-1;当α≠时,直线l的普通方程为y=tan α·(x+1).由ρ=2cos θ,得ρ2=2ρcos θ,所以曲线C的直角坐标方程为x2+y2=2x.(2)把x=-1+tcos α,y=tsin α代入x2+y2=2x,整理得t2-4tcos α+3=0.由Δ=16cos2α-12=0,得cos2α=,所以cos α=或cos α=-,故直线l的倾斜角α为或.5.解:(1)若|x+2|+|x-2|<18,则或或解得-9<x<9,所以A=(-9,9).(2)因为∀a,b∈A即∀a,b∈(-9,9), 所以a+b∈(-18,18),因为x++m≥2+m,所以(x++m)min=m+4,由题可知,m+4≥18,所以m≥14,所以m的取值范围为[14,+∞).。
高三数学复习 中档题训练2

高三数学复习 中档题训练21.设a 、b 是两个不共线的非零向量(t ∈R )①若a 与b 起点相同,t 为何值时,a ,t b ,31(a +b )三向量的终点在一直线上? ②若|a |=|b |且a 与b 夹角为60°,那末t 为何值时|a -t b |的值最小?解:①设a -t b =m[a -31(a +b )](m ∈R) 化简得 )132(-m a =)3(t m -b ∵a 与b 不共线 ∴⎪⎪⎪⎩⎪⎪⎪⎨⎧=-⎪⎪⎩⎪⎪⎨⎧==⇒=-0321230132t m t m m ∴t=21时,a 、t b 、31(a +b )终点在一直线上 ②|a -t b |2=(a -t b )2=|a |2+t 2|b |-2t ,|a | |b |cos 60°=(1+t 2-t )|a |2, ∴t=21时,|a -t b |有最小值||23a2.已知曲线轴与y d cx bx ax y L +++=23:相交于点A ,以其上一动点P (x 0,y 0)为切点的直线l 与y 轴相交于Q 点.(Ⅰ)求直线l 的方程,并用x 0表示Q 点的坐标;(Ⅱ)求.sin sin lim 0AQPAPQ x ∠∠+∞→ Ⅰ)解:c bx ax k c bx ax y d A ++=++='020223,23),,0(0002000200))(23(0),)(23(y x c bx ax y x x x c bx ax y y Q +-++==-++=-∴得令 )))(23(,0(00020y x c bx ax Q +-++∴(Ⅱ)由正弦定理得:2|||2|)(|2|lim sin sin lim )(|2|)(|23|sin sin 2020302020302020*********020*******==++++=∠∠∴+++--=-+-+---==∠∠+∞→+∞→a a cx bx ax x bx ax AQP APQ cx bx ax x bx ax d y x d y cx bx ax AP AQ AQP APQ x x 3.如图,直三棱柱111ABC A B C -中,底面是以ABC ∠为直角的等腰三角形,12,3,AC a BB a D ==是11A C 的中点,E 是1B C 的中点。
2020高三数学专题复习 中档题满分练(2)理

∴f(x)=2sin,
令2x+=kπ+,得x=+(k∈Z).
故f(x)的对称轴方程为x=+(k∈Z).
(2)由f(α)=知2sin=,即sin=,
∴sin=sin=-cos 2
=-1+2sin2=-1+2×=-.
2.解 (1) ∵bn=3n,则bn+1=3n+3=bn+3,
因此cn=1-2n(n∈N*),
则cn+1=1-2n+1=2(1-2n)-1=2cn-1,
{cn}是“M类数列”.
3.(1)证明 由题意知,△ABC,△ACD都是边长为2的等边三角形,如图所示
,取AC中点O,连接BO,DO,则BO⊥AC,DO⊥AC,BO平分∠ABC.
又∵平面ACD⊥平面ABC,∴DO⊥平面ABC,作EF⊥平面ABC,
∴f(-x)=-f(x),∴f(x)是奇函数.
(3)解 设x1,x2∈(-∞,+∞),x1<x2,
∵x2>x1,∴x2-x1>0,∴f(x2-x1)<0,
f(x2)<f(x1),∴f(x)是R上的减函数.
∵f(1)=-,∴f(-1)=,∴f(-2)=1.
∴不等式f(x2-2ax-1)≤1即是f(x2-2ax-1)≤f(-2),
2020高三数学专题复习 中档题满分练(2)理
编 辑:__________________
时 间:_________________
高三数学专题复习 中档题满分练(2)理
1.已知函数f(x)=2asin ωxcos ωx+2cos2ωx-(a>0,ω>0)的最大值为2,且最小正周期为π.
(1)求函数f(x)的解析式及其对称轴方程;
所以cos〈n1,n2〉==,
(高考题 模拟题)高考数学 基础巩固练(二)理(含解析)-人教版高三全册数学试题

基础巩固练(二)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2019·高考)已知复数z=2+i,则z·z=( )A. 3B. 5 C.3 D.5答案 D解析解法一:∵z=2+i,∴z=2-i,∴z·z=(2+i)(2-i)=5.故选D.解法二:∵z=2+i,∴z·z=|z|2=5.故选D.2.(2019·某某高考)已知全集U={-1,0,1,2,3},集合A={0,1,2},B={-1,0,1},则(∁U A)∩B=( )A.{-1} B.{0,1}C.{-1,2,3} D.{-1,0,1,3}答案 A解析∵U={-1,0,1,2,3},A={0,1,2},∴∁U A={-1,3}.又∵B={-1,0,1},∴(∁U A)∩B={-1}.故选A.3.(2019·某某二模)某几何体的三视图如图所示,则这个几何体的直观图可以是( )答案 B解析由正视图排除A,C;由侧视图排除D,故B正确.4.(2019·某某呼和浩特市高三3月第一次质量普查)在等比数列{a n}中,a2-a1=2,且2a2为3a1和a3的等差中项,则a4为 ( )A .9B .27C .54D .81 答案 B解析 根据题意,设等比数列{a n }的公比为q ,若2a 2为3a 1和a 3的等差中项,则有2×2a 2=3a 1+a 3,变形可得4a 1q =3a 1+a 1q 2,即q 2-4q +3=0,解得q =1或3;又a 2-a 1=2,即a 1(q -1)=2,则q =3,a 1=1,则a n =3n -1,则有a 4=33=27.故选B.5.(2019·某某市适应性试卷)函数f (x )=(x 3-x )ln |x |的图象是( )答案 C解析 因为函数f (x )的定义域关于原点对称,且f (-x )=-(x 3-x )ln |x |=-f (x ),∴函数是奇函数,图象关于原点对称,排除B ,函数的定义域为{x |x ≠0},由f (x )=0,得(x 3-x )ln |x |=0,即(x 2-1)ln |x |=0,即x =±1,即函数f (x )有两个零点,排除D ,f (2)=6ln 2>0,排除A.故选C.6.(2019·某某省内江二模)如果执行下面的程序框图,输出的S =110,则判断框处为( )A .k <10?B .k ≥11? C.k ≤10? D.k >11? 答案 C解析 由程序框图可知,该程序是计算S =2+4+…+2k =k (2+2k )2=k (k +1),由S =k (k +1)=110,得k =10,则当k =10时,k =k +1=10+1=11不满足条件,所以条件为“k ≤10?”.故选C.7.(2019·某某二模)勒洛三角形是由德国机械工程专家、机构运动学家勒洛(1829~1905)首先发现,所以以他的名字命名,其作法为:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形,现在勒洛三角形内部随机取一点,则此点取自等边三角形内部的概率为( )A.2π-332(π-3)B.32(π-3)C.32(π+3)D.2π-332(π+3)答案 B解析 如题图,设BC =2,以B 为圆心的扇形的面积为π×226=2π3,又∵△ABC 的面积为12×32×2×2=3,∴勒洛三角形的面积为3个扇形面积减去2个正三角形的面积,即为2π3×3-23=2π-23,故在勒洛三角形中随机取一点,此点取自等边三角形的概率为32π-23=32(π-3),故选B.8.(2019·某某一模)已知M (-4,0),N (0,4),点P (x ,y )的坐标x ,y 满足⎩⎪⎨⎪⎧x ≤0,y ≥0,3x -4y +12≥0,则MP →·NP →的最小值为( )A.25B.425 C .-19625 D .- 5 答案 C解析 由点P (x ,y )的坐标x ,y 满足⎩⎪⎨⎪⎧x ≤0,y ≥0,3x -4y +12≥0,作出可行域如图中阴影部分,则MP →·NP →=(x +2)2+(y -2)2-8的最小值为点A (-2,2)到直线3x -4y +12=0的距离的平方再减8,由d =|3×(-2)-4×2+12|5=25,可得(x +2)2+(y -2)2-8的最小值为-19625.故选C.9.(2019·某某一模)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,a =3,c =23,b sin A =a cos ⎝⎛⎭⎪⎫B +π6,则b =( )A .1 B. 2 C. 3 D. 5 答案 C解析 在△ABC 中,由正弦定理得asin A=bsin B,得b sin A =a sin B ,又b sin A =a cos ⎝⎛⎭⎪⎫B +π6,∴a sin B =a cos ⎝⎛⎭⎪⎫B +π6,即sin B =cos ⎝⎛⎭⎪⎫B +π6=cos B cos π6-sin B sin π6=32cos B -12sin B ,∴tan B =33,又B ∈(0,π),∴B =π6.∵在△ABC 中,a =3,c =23,由余弦定理得b =a 2+c 2-2ac cos B =9+12-2×3×23×32= 3.故选C. 10.(2019·某某某某高三3月模拟)若函数f (x )=sin ⎝⎛⎭⎪⎫ωx -π6(ω>0)在[0,π]上的值域为⎣⎢⎡⎦⎥⎤-12,1,则ω的最小值为( )A.23B.34C.43D.32 答案 A解析 ∵0≤x ≤π,∴-π6≤ωx -π6≤ωπ-π6,而f (x )的值域为⎣⎢⎡⎦⎥⎤-12,1,发现f (0)=sin ⎝ ⎛⎭⎪⎫-π6=-12,∴π2≤ωπ-π6≤7π6,整理得23≤ω≤43.则ω的最小值为23.故选A.11.(2019·某某模拟)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,点A 为双曲线右支上一点,线段AF 1交左支于点B ,若AF 2⊥BF 2,且|BF 1|=13|AF 2|,则该双曲线的离心率为( )A. 2B.655C.355D .3 答案 B解析 因|BF 1|=13|AF 2|,设|AF 2|=3t ,则|BF 1|=t ,t >0,由双曲线的定义可得|BF 2|=|BF 1|+2a =t +2a ,|AF 1|=|AF 2|+2a =3t +2a , 则|AB |=|AF 1|-|BF 1|=2t +2a ,由AF 2⊥BF 2,可得(2a +2t )2=(3t )2+(t +2a )2,解得t =23a ,则在直角三角形ABF 2中,cos A =3t 2t +2a =2a 103a =35,在△AF 1F 2中,可得cos A =(3t )2+(3t +2a )2-(2c )22·3t ·(3t +2a )=4a 2+16a 2-4c 216a 2=35,化为c 2=135a 2,则e =c a=135=655.故选B. 12.(2019·高考)数学中有许多形状优美、寓意美好的曲线,曲线C :x 2+y 2=1+|x |y 就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C 上任意一点到原点的距离都不超过2; ③曲线C 所围成的“心形”区域的面积小于3. 其中,所有正确结论的序号是( )A .①B .②C .①②D .①②③ 答案 C解析 由x 2+y 2=1+|x |y ,当x =0时,y =±1;当y =0时,x =±1;当y =1时,x =0,±1.故曲线C 恰好经过6个整点:A (0,1),B (0,-1),C (1,0),D (1,1),E (-1,0),F (-1,1),所以①正确.由基本不等式,当y >0时,x 2+y 2=1+|x |y =1+|xy |≤1+x 2+y 22,所以x 2+y 2≤2,所以x 2+y 2≤2,故②正确.如图,由①知长方形CDFE 面积为2,三角形BCE 面积为1,所以曲线C 所围成的“心形”区域的面积大于3,故③错误.故选C.第Ⅱ卷 (非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.(2019·某某一模)已知(a -x )(2+x )5的展开式中x 3的系数为40,则实数a 的值为________.答案 3解析 ∵(a -x )(2+x )5=(a -x )(32+80x +80x 2+40x 3+10x 4+x 5)的展开式中x 3的系数为40a -80=40,∴a =3.14.(2019·揭阳一模)在曲线f (x )=sin x -cos x ,x ∈⎝ ⎛⎭⎪⎫-π2,π2的所有切线中,斜率为1的切线方程为________.答案 x -y -1=0解析 由f (x )=sin x -cos x ,得f ′(x )=cos x +sin x =2sin ⎝⎛⎭⎪⎫x +π4,由2sin ⎝ ⎛⎭⎪⎫x +π4=1,得sin ⎝ ⎛⎭⎪⎫x +π4=22,∵x ∈⎝ ⎛⎭⎪⎫-π2,π2,∴x +π4∈⎝ ⎛⎭⎪⎫-π4,3π4,∴x +π4=π4,即x =0.∴切点为(0,-1),切线方程为y +1=x ,即x -y -1=0.15.(2019·某某一模)在四面体ABCD 中,AB =BC =1,AC =2,且AD ⊥CD ,该四面体外接球的表面积为________.答案 2π解析 如图,∵AB =BC =1,AC =2,∴AB ⊥BC ,又AD ⊥CD ,∴AC 的中点即为外接球的球心,外接球的半径为22,∴S 球=4π×12=2π.16.(2019·某某省十所名校高三尖子生第二次联考)若函数y =f (x )的图象存在经过原点的对称轴,则称y =f (x )为“旋转对称函数”,下列函数中是“旋转对称函数”的有________.(填写所有正确结论的序号)①y =⎩⎪⎨⎪⎧e x(x ≤0),ln x (0<x ≤1);②y =cos ⎝ ⎛⎭⎪⎫ln 1+x 1-x ;③y =ln (e3x+1).答案 ①②解析 对于①,y =e x(x ≤0)的反函数为y =ln x (0<x ≤1),所以函数y =⎩⎪⎨⎪⎧e x(x ≤0),ln x (0<x ≤1)关于直线y =x 对称,故①是“旋转对称函数”.对于②,令y =f (x )=cos ⎝ ⎛⎭⎪⎫ln 1+x 1-x ,则f (-x )=cos ⎝ ⎛⎭⎪⎫ln 1-x 1+x =cos ⎝ ⎛⎭⎪⎫-ln 1+x 1-x =cos ⎝ ⎛⎭⎪⎫ln 1+x 1-x =f (x ),所以函数y =cos ⎝ ⎛⎭⎪⎫ln 1+x 1-x 是偶函数,它的图象关于y 轴对称,故②是“旋转对称函数”.对于③,y =ln (e 3x+1)>ln e 3x=3x ,当x →+∞时,y →3x ,则函数y =ln(e3x+1)的图象只可能关于直线y =3x 对称,又y =ln (e3x+1)>ln 1=0,当x →-∞时,y →0,这与函数y =ln (e 3x+1)的图象关于直线y =3x 对称矛盾,故③不是“旋转对称函数”.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分.17.(本小题满分12分)(2019·某某某某高三第二次统考)已知数列{a n }中,a 1=1,a n-a n -1=2n -1(n ∈N *,n ≥2).(1)求数列{a n }的通项公式;(2)设b n =14a n -1,求数列{b n }的通项公式及其前n 项和T n .解 (1)当n ≥2时,由于a n -a n -1=2n -1,a 1=1,所以a n =(a n -a n -1)+(a n -1-a n -2)+…+(a 2-a 1)+a 1=1+3+…+(2n -1)=n 2, 又a 1=1满足上式,故a n =n 2(n ∈N *). (2)b n =14a n -1=14n 2-1=1(2n +1)(2n -1)=12⎝ ⎛⎭⎪⎫12n -1-12n +1.所以T n =b 1+b 2+…+b n=12⎝ ⎛⎭⎪⎫1-13+13-15+…+12n -1-12n +1=12⎝⎛⎭⎪⎫1-12n +1=n2n +1. 18.(本小题满分12分)(2019·某某质量检测)如图,已知三棱柱ABC -A 1B 1C 1,侧面ABB 1A 1为菱形,A 1C =BC .(1)求证:A 1B ⊥平面AB 1C ;(2)若∠ABB 1=60°,∠CBA =∠CBB 1,AC ⊥B 1C ,求二面角B -AC -A 1的余弦值. 解 (1)证明:因为侧面ABB 1A 1为菱形, 所以A 1B ⊥AB 1,记A 1B ∩AB 1=O ,连接CO , 因为A 1C =BC ,BO =A 1O , 所以A 1B ⊥CO ,又AB 1∩CO =O , 所以A 1B ⊥平面AB 1C .(2)解法一:因为∠CBA =∠CBB 1,AB =BB 1,BC =BC ,所以△CBA ≌△CBB 1,所以AC =B 1C . 又O 是AB 1的中点,所以CO ⊥AB 1, 又A 1B ⊥CO ,A 1B ∩AB 1=O , 所以CO ⊥平面ABB 1A 1.令BB 1=2,因为∠ABB 1=60°,侧面ABB 1A 1为菱形,AC ⊥B 1C ,O 为AB 1的中点, 所以CO =1.如图,以O 为坐标原点,OB 所在的直线为x 轴,OB 1所在的直线为y 轴,OC 所在的直线为z 轴建立空间直角坐标系.则O (0,0,0),A (0,-1,0),B (3,0,0),C (0,0,1),A 1(-3,0,0), 所以AB →=(3,1,0),AC →=(0,1,1),AA 1→=(-3,1,0),A 1C →=(3,0,1). 设平面ABC 的法向量为n 1=(x ,y ,z ), 则⎩⎪⎨⎪⎧n 1·AB →=0,n 1·AC →=0,即⎩⎨⎧3x +y =0,y +z =0,令x =1,则n 1=(1,-3,3),同理可得平面A 1AC 的一个法向量为n 2=(1,3,-3),cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=-57,由图知二面角B -AC -A 1为钝角, 所以二面角B -AC -A 1的余弦值为-57.解法二:因为∠CBA =∠CBB 1,AB =BB 1,BC =BC , 所以△CBA ≌△CBB 1, 所以AC =B 1C .设AB =2,因为∠ABB 1=60°,侧面ABB 1A 1为菱形,所以AA 1=AB 1=2,OA =OB 1=1,OB =OA 1= 3.又AC ⊥B 1C ,所以CO =1,AB =B 1C =2,又A 1C =BC ,O 为A 1B 的中点,所以BC =A 1C =2,所以△ABC 为等腰三角形,△A 1AC 为等腰三角形.如图,取AC 的中点M ,连接BM ,A 1M ,则∠BMA 1为二面角B -AC -A 1的平面角.在△BMA 1中,可得BM =A 1M =142,A 1B =23, 所以cos ∠BMA 1=BM 2+A 1M 2-A 1B 22BM ·A 1M =-57,所以二面角B -AC -A 1的余弦值为-57.19.(本小题满分12分)(2019·某某一模)已知F 为椭圆C :x 2a 2+y 2b2=1(a >b >0)的右焦点,点P (2,2)在C 上,且PF ⊥x 轴.(1)求C 的方程;(2)过F 的直线l 交C 于A ,B 两点,交直线x =4于点M .证明:直线PA ,PM ,PB 的斜率成等差数列.解 (1)因为点P (2,2)在C 上,且PF ⊥x 轴,所以c =2,设椭圆C 的左焦点为E ,连接EP ,则|EF |=2c =4,|PF |=2,在Rt △EFP 中,|PE |2=|PF |2+|EF |2=18,所以|PE |=3 2.所以2a =|PE |+|PF |=42,a =22, 又b 2=a 2-c 2=4,故椭圆C 的方程为x 28+y 24=1.(2)证明:由题意可设直线l 的方程为y =k (x -2), 令x =4,得M 的坐标为(4,2k ),由⎩⎪⎨⎪⎧x 28+y 24=1,y =k (x -2)得(2k 2+1)x 2-8k 2x +8(k 2-1)=0,设A (x 1,y 1),B (x 2,y 2),则有x 1+x 2=8k 22k 2+1,x 1x 2=8(k 2-1)2k 2+1. ①记直线PA ,PB ,PM 的斜率分别为k 1,k 2,k 3, 从而k 1=y 1-2x 1-2,k 2=y 2-2x 2-2,k 3=2k -24-2=k -22. 因为直线l 的方程为y =k (x -2),所以y 1=k (x 1-2),y 2=k (x 2-2), 所以k 1+k 2=y 1-2x 1-2+y 2-2x 2-2=y1x1-2+y2x2-2-2⎝⎛⎭⎪⎫1x1-2+1x2-2=2k-2·x1+x2-4x1x2-2(x1+x2)+4. ②①代入②,得k1+k2=2k-2·8k22k2+1-48(k2-1)2k2+1-16k22k2+1+4=2k-2,又k3=k-22,所以k1+k2=2k3,故直线PA,PM,PB的斜率成等差数列.20.(本小题满分12分)(2019·某某一模)十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏,新农村建设取得巨大进步,农民收入也逐年增加.为了更好地制定2019年关于加快提升农民年收入力争早日脱贫的工作计划,该地扶贫办统计了2018年50位农民的年收入并制成如下频率分布直方图:(1)根据频率分布直方图估计50位农民的年平均收入x(单位:千元)(同一组数据用该组数据区间的中点值表示);(2)由频率分布直方图可以认为该贫困地区农民年收入X服从正态分布N(μ,σ2),其中μ近似为年平均收入x,σ2近似为样本方差s2,经计算得s2=6.92,利用该正态分布,求:(ⅰ)在2019年脱贫攻坚工作中,若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?(ⅱ)为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1000位农民.若每个农民的年收入相互独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?附:参考数据与公式 6.92≈2.63,若X~N(μ,σ2),则①P(μ-σ<X≤μ+σ)=0.6827;②P(μ-2σ<X≤μ+2σ)=0.9545;③P(μ-3σ<X≤μ+3σ)=0.9973.解 (1)x =12×0.04+14×0.12+16×0.28+18×0.36+20×0.10+22×0.06+24×0.04=17.40.(2)由题意,X ~N (17.40,6.92).(ⅰ)∵P (x >μ-σ)=12+0.68272≈0.8414,∴μ-σ=17.40-2.63=14.77时,满足题意, 即最低年收入大约为14.77千元.(ⅱ)由P (X ≥12.14)=P (X ≥μ-2σ)=0.5+0.95452≈0.9773,得每个农民年收入不少于12.14千元的概率为0.9773,记1000个农民年收入不少于12.14千元的人数为ξ,则ξ~B (1000,p ),其中p =0.9773.于是恰好有k 个农民的年收入不少于12.14千元的概率是P (ξ=k )=C k1000p k(1-p )1000-k,从而由P (ξ=k )P (ξ=k -1)=(1001-k )×pk (1-p )>1,得k <1001p ,而1001p =978.233,∴当0≤k ≤978时,P (ξ=k -1)<P (ξ=k ), 当979≤k ≤1000时,P (ξ=k -1)>P (ξ=k ).由此可知,在走访的1000位农民中,年收入不少于12.14千元的人数最有可能是978. 21.(本小题满分12分)(2019·某某三模)已知a ∈R ,函数f (x )=2x+a ln x .(1)讨论函数f (x )的单调性;(2)若x =2是f (x )的极值点,且曲线y =f (x )在两点P (x 1,f (x 1)),Q (x 2,f (x 2))(x 1<x 2<6)处切线平行,在y 轴上的截距分别为b 1,b 2,求b 1-b 2的取值X 围.解 (1)f ′(x )=-2x 2+a x =ax -2x2,①当a ≤0时,f ′(x )<0在x ∈(0,+∞)上恒成立, ∴f (x )在(0,+∞)上单调递减;②当a >0时,x ∈⎝⎛⎭⎪⎫0,2a 时,f ′(x )<0,x ∈⎣⎢⎡⎭⎪⎫2a ,+∞时,f ′(x )>0,即f (x )在x ∈⎝ ⎛⎭⎪⎫0,2a 上单调递减,在x ∈⎣⎢⎡⎭⎪⎫2a,+∞上单调递增.(2)∵x =2是f (x )的极值点, ∴由(1)可知2a=2,∴a =1.设在P (x 1,f (x 1))处的切线方程为y -⎝ ⎛⎭⎪⎫2x 1+ln x 1=⎝ ⎛⎭⎪⎫-2x 21+1x 1(x -x 1),在Q (x 2,f (x 2))处的切线方程为y -⎝ ⎛⎭⎪⎫2x 2+ln x 2=⎝ ⎛⎭⎪⎫-2x 22+1x 2(x -x 2),∵这两条切线互相平行, ∴-2x 21+1x 1=-2x 22+1x 2,∴1x 1+1x 2=12. ∵1x 2=12-1x 1,且0<x 1<x 2<6, ∴16<12-1x 1<1x 1,∴14<1x 1<13,∴x 1∈(3,4). 令x =0,则b 1=4x 1+ln x 1-1,同理,b 2=4x 2+ln x 2-1.解法一:∵1x 2=12-1x 1,∴b 1-b 2=4⎝⎛⎭⎪⎫1x 1-1x 2+ln x 1-ln x 2=4⎝⎛⎭⎪⎫2x 1-12-ln 1x 1+ln ⎝⎛⎭⎪⎫12-1x1.设g (x )=8x -2-ln x +ln ⎝ ⎛⎭⎪⎫12-x ,x ∈⎝ ⎛⎭⎪⎫14,13,∴g ′(x )=8-1x -112-x =16x 2-8x +12x 2-x =(4x -1)22x 2-x<0, ∴g (x )在区间⎝ ⎛⎭⎪⎫14,13上单调递减, ∴g (x )∈⎝ ⎛⎭⎪⎫23-ln 2,0, 即b 1-b 2的取值X 围是⎝ ⎛⎭⎪⎫23-ln 2,0.解法二:∵x 2=2x 1x 1-2, ∴b 1-b 2=4⎝ ⎛⎭⎪⎫1x 1-1x 2+ln x 1-ln x 2=8x 1-2+ln ⎝ ⎛⎭⎪⎫x 12-1. 令g (x )=8x +ln ⎝ ⎛⎭⎪⎫x 2-1-2,其中x ∈(3,4),∴g ′(x )=-8x 2+1x -2=x 2-8x +16x 2(x -2)=(x -4)2x 2(x -2)>0,∴函数g (x )在区间(3,4)上单调递增,∴g (x )∈⎝ ⎛⎭⎪⎫23-ln 2,0, ∴b 1-b 2的取值X 围是⎝ ⎛⎭⎪⎫23-ln 2,0.解法三:∵x 1x 2=2(x 1+x 2),∴b 1-b 2=4x 1-4x 2+ln x 1-ln x 2=4(x 2-x 1)x 1x 2+ln x 1x 2=2(x 2-x 1)x 1+x 2+ln x 1x 2=2⎝ ⎛⎭⎪⎫1-x 1x 21+x 1x 2+ln x 1x 2.设g (x )=2(1-x )1+x +ln x ,则g ′(x )=-4(1+x )2+1x =(1-x )2x (1+x )2.∵x 1x 2=x 12-1∈⎝ ⎛⎭⎪⎫12,1,∴g ′(x )>0, ∴函数g (x )在区间⎝ ⎛⎭⎪⎫12,1上单调递增,∴g (x )∈⎝ ⎛⎭⎪⎫23-ln 2,0, ∴b 1-b 2的取值X 围是⎝ ⎛⎭⎪⎫23-ln 2,0.(二)选考题:10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)[选修4-4:坐标系与参数方程] (2019·某某模拟)已知曲线C 的极坐标方程为ρ=4cos θsin 2θ,直线l 的参数方程为⎩⎪⎨⎪⎧x =t cos α,y =1+t sin α(t 为参数,0≤α<π).(1)把曲线C 的极坐标方程化为直角坐标方程,并说明曲线C 的形状; (2)若直线l 经过点(1,0),求直线l 被曲线C 截得的线段AB 的长.解 (1)将曲线C 的极坐标方程ρ=4cos θsin 2θ化为ρ2sin 2θ=4ρcos θ,得到曲线C 的直角坐标方程为y 2=4x ,故曲线C 是顶点为O (0,0),焦点为F (1,0)的抛物线.(2)直线l 的参数方程为⎩⎪⎨⎪⎧x =t cos α,y =1+t sin α(t 为参数,0≤α<π).若直线l 经过点(1,0),则α=3π4,∴直线l 的参数方程为⎩⎪⎨⎪⎧x =t cos 3π4=-22t ,y =1+t sin 3π4=1+22t (t 为参数).将其代入y 2=4x ,得t 2+62t +2=0.设A ,B 对应的参数分别为t 1,t 2,则t 1+t 2=-62,t 1t 2=2.|AB |=|t 1-t 2|=(t 1+t 2)2-4t 1t 2=(-62)2-4×2=8.23.(本小题满分10分)[选修4-5:不等式选讲] (2019·某某模拟)已知函数f (x )= |x +1|+|x -3|-m 的定义域为R . (1)某某数m 的取值X 围;(2)若m 的最大值为n ,当正数a ,b 满足23a +b +1a +2b =n 时,求7a +4b 的最小值.解 (1)∵函数的定义域为R , ∴|x +1|+|x -3|-m ≥0恒成立,设函数g (x )=|x +1|+|x -3|,则m 不大于函数g (x )的最小值, 又|x +1|+|x -3|≥|(x +1)-(x -3)|=4, 即函数g (x )的最小值为4,∴m ≤4. (2)由(1)知n =4,∴7a +4b =14(6a +2b +a +2b )⎝ ⎛⎭⎪⎫23a +b +1a +2b =14⎝ ⎛⎭⎪⎫5+2(3a +b )a +2b +2(a +2b )3a +b ≥ 14⎝⎛⎭⎪⎫5+2×23a +b a +2b ·a +2b 3a +b =94, 当且仅当a +2b =3a +b ,即b =2a =310时取等号.∴7a +4b 的最小值为94.。
高考理科数学中档大题保分专练15套(经典珍藏解析版)

(Ⅱ)若选取的是 12 月 1 日与 12 月 5 日的两组数据,请根据 12 月 2 日至 12 月 4 日的数据,
求 y 关于 x 的线性回归方程 y bx a ;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过 2 颗,则认为
得到的线性回归方程是可靠的,试问(Ⅱ)中所得的线性回归方程是否可靠?
i 1
xi2
112
132
122
434
2
, 3x
432 ,由公式求
得
第 2 页 共 57 页
中档大题保分专练 15 套
3
b
xi yi
i 1
977 972 5 ,a y bx 3
3
xi 2
2
3x
434 432
2
i 1
.
x 2 cos
4.
(广西名校第一次摸底)已知曲线
M
的参数方程为
12 月 2 日
12 月 3 日
12 月 4 日
12 月 5 日
温差 x (℃) 10
11
13
12
8
发芽数 y(颗) 23
25
30
26
16
该农科所确定的研究方案是:先从这 5 组数据中选取 2 组,用剩下的 3 组数据求线性回归方
程,再对被选取的 2 组数据进行检验.
(Ⅰ)求选取的 2 组数据恰好是不相邻的 2 天数据的概率;
,
∴曲线 N 的普通方程为 3x y 16 0 .……………………………………5 分
(Ⅱ)圆 M 的圆心 M 0 ,2 ,半径 r 2.
2 16
d
7
点 M 到直线 N 的距离为
金版教程2022高考数学理二轮复习训练:中档题专练
中档题专练建议用时:30分钟1.[2021·皖北协作区联考(二)]设△ABC 的三内角A ,B ,C 所对的边分别为a ,b ,c 且b (cos A -3cos C )=(3c -a )cos B .(1)求sin Asin C 的值;(2)若cos B =16,且△ABC 的周长为14,求b 的值. 解 (1)由正弦定理得,(cos A -3cos C )sin B =(3sin C -sin A )cos B ,化简可得sin(A +B )=3sin(B +C ).又A +B +C =π, 所以sin C =3sin A ,因此sin A sin C =13.(2)由sin A sin C =13得c =3a ,由余弦定理及cos B =16得 b 2=a 2+c 2-2ac cos B =a 2+9a 2-6a 2×16=9a 2.所以b =3a .又a +b +c =14,从而a =2,因此b =6.2.[2021·济宁模拟]如图,在四棱锥P -ABCD 中,底面ABCD 是菱形,∠ADC =60°,侧面PDC 是正三角形,平面PDC ⊥平面ABCD ,CD =2,M 为PB 的中点.(1)求证:P A ⊥平面CDM ; (2)求二面角D -MC -B 的余弦值.解 (1)证法一:取P A 中点N ,连接MN ,DN ,又M 为PB 的中点,所以MN ∥AB ,又菱形ABCD 中AB ∥CD ,所以MN ∥CD , 所以C 、D 、M 、N 四点共面. 取DC 的中点为O ,连接PO .由于侧面PDC 是正三角形,平面PDC ⊥平面ABCD ,所以PO ⊥底面ABCD , 由于底面ABCD 为菱形且∠ADC =60°,DC =2,DO =1,有OA ⊥DC , 由于PO ∩AO =O ,所以DC ⊥平面POA ,所以DC ⊥P A , 在△P AD 中,PD =AD =2,N 为P A 的中点,所以DN ⊥P A , 又DN ∩DC =D ,DN ⊂平面CDNM ,DC ⊂平面CDNM , 所以P A ⊥平面CDNM ,即P A ⊥平面CDM . 证法二:取DC 的中点为O ,连接PO .由于侧面PDC 是正三角形,平面PDC ⊥平面ABCD ,所以PO ⊥底面ABCD , 由于底面ABCD 为菱形且∠ADC =60°,DC =2,DO =1,有OA ⊥DC ,以O 为原点,分别以OA 、OC 、OP 所在直线为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系,则A (3,0,0)、P (0,0,3)、B (3,2,0)、C (0,1,0)、D (0,-1,0).∴M ⎝ ⎛⎭⎪⎫32,1,32,∴DM →=⎝ ⎛⎭⎪⎫32,2,32,P A →=(3,0,-3),DC→=(0,2,0), ∴P A →·DM →=3×32+0×2+(-3)×32=0, ∴P A →·DC →=3×0+0×2+(-3)×0=0, ∴P A →⊥DM →,P A →⊥DC→,∴P A ⊥平面DMC . (2)CM →=⎝ ⎛⎭⎪⎫32,0,32,CB →=(3,1,0). 设平面BMC 的一个法向量n =(x ,y ,z ), n ·CM →=0,得x +z =0,n ·CB →=0,得3x -y =0, 取x =-1,则y =-3,z =1, ∴法向量n =(-1,-3,1),由(1)知平面CDM 的法向量可取P A →=(3,0,-3), ∴cos 〈n ,P A →〉=n ·P A →|n |·|P A →|=-235·6=-105,观看可知二面角D -MC -B 为钝角, 所以所求二面角的余弦值是-105.3.[2021·贵州七校联考(一)]交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T ,其范围为[0,10],分别有5个级别:T ∈[0,2)畅通;T ∈[2,4)基本畅通;T ∈[4,6)轻度拥堵;T ∈[6,8)中度拥堵;T ∈[8,10]严峻拥堵.早高峰时段(T ≥3),从贵阳市交通指挥中心随机选取了二环以内50个交通路段,依据交通指数数据绘制的直方图如图所示:(1)据此直方图估算交通指数T ∈[4,8)时的中位数和平均数;(2)据此直方图求出早高峰二环以内的3个路段至少有2个严峻拥堵的概率是多少?(3)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为35分钟,中度拥堵为45分钟,严峻拥堵为60分钟,求此人所用时间的数学期望.解 (1)由直方图知:T ∈[4,8)时交通指数的中位数为5+1×0.20.24=356. T ∈[4,8)时交通指数的平均数为4.5×0.2+5.5×0.24+6.5×0.2+7.5×0.16=4.72.(2)设大事A 为“1条路段严峻拥堵”,则P (A )=0.1, 则3条路段中至少有2条路段严峻拥堵的概率为: P =C 23×⎝⎛⎭⎪⎫1102×⎝⎛⎭⎪⎫1-110+C 33×⎝⎛⎭⎪⎫1103=7250,所以3条路段中至少有2条路段严峻拥堵的概率为7250. (3)由题意,所用时间X 的分布列如下表:X30354560P 0.1 0.44 0.36 0.1则E (X )=30×0.1+35×0.44+45×0.36+60×0.1=40.6, 所以此人上班路上所用时间的数学期望是40.6分钟.中档题专练(二)建议用时:30分钟1.若数列{x n }满足:1x n +1-1x n=d (d 为常数,n ∈N *),则称{x n }为调和数列.已知数列{a n }为调和数列,且a 1=1,1a 1+1a 2+1a 3+1a 4+1a 5=15.(1)求数列{a n }的通项a n ;(2)数列⎩⎨⎧⎭⎬⎫2n a n 的前n 项和为S n ,是否存在正整数n ,使得S n ≥2021?若存在,求出n 的取值集合;若不存在,请说明理由.解 (1)依题意⎩⎨⎧⎭⎬⎫1a n 为等差数列,由1a 1+1a 2+1a 3+1a 4+1a 5=15得5a 3=15,即1a 3=3,∴公差d =1a 3-1a 12=1,故1a n=n 即a n =1n .(2)S n =1×21+2×22+…+n ×2n ① 2S n =1×22+…+(n -1)2n +n ×2n +1② ②-①得S n =n ×2n +1-(2+22+…+2n )=(n -1)2n +1+2.由于S n 是递增的,当n =7时S 7=6×28+2<2021; 当n =8时S 8=7×29+2>211>2021.所以存在正整数n ,使得S n ≥2021,n 的取值集合为{n |n ≥8,n ∈N *} 2.[2021·广州综合测试(一)]袋子中装有大小相同的白球和红球共7个,从袋子中任取2个球都是白球的概率为17,每个球被取到的机会均等.现从袋子中每次取1个球,假如取出的是白球则不再放回,设在取得红球之前已取出的白球个数为X .(1)求袋子中白球的个数; (2)求X 的分布列和数学期望.解 (1)设袋子中有n (n ∈N *)个白球,依题意得,C 2nC 27=17,即n (n -1)27×62=17,化简得,n 2-n -6=0,解得,n =3或n =-2(舍去). ∴袋子中有3个白球.(2)由(1)得,袋子中有4个红球,3个白球. X 的可能取值为0,1,2,3, P (X =0)=47,P (X =1)=37×46=27,P (X =2)=37×26×45=435,P (X =3)=37×26×15×44=135. ∴X 的分布列为: ∴E (X )=0×47+1×27+2×435+3×135=35.3.在△ABC 中,∠ABC =90°,AB =6,BC =8,EF ∥AB ,CE ∶EB =5∶3,将三角形△EFC 折起,使C 在面ABC 的射影落在B 点上.(1)若M 是BC 的中点,在线段AC 上找一点H ,使MH ∥面ABEF ,试确定H 点的位置.(2)求点B 到面AEC 的距离.(3)若BM→=λBC →(0<λ<1),是否存在λ,使得平面MAE 与平面CEF 所成的锐二面角的余弦值为1415?若存在,求出λ的值;若不存在,请说明理由.解 (1)取AC 中点H ,连接MH ,则MH ∥AB ,由于AB ⊂ABEF ,MH ⊄面ABEF ,所以MH ∥面ABEF ,即H 为AC 中点.(2)△EFC ∽△BAC ,∴EF BA =EC BC =58=EF 6,∴EF =154,CB =52-32=4.以B 为原点,直线BE 为x 轴,BA 直线为y 轴,BC 直线为z 轴建立空间直角坐标系,E (3,0,0),F ⎝ ⎛⎭⎪⎫3,154,0,C (0,0,4),B (0,0,0),A (0,6,0),CE→=(3,0,-4),AC→=(0,-6,4),BC →=(0,0,4),设平面AEC 的法向量为n =(x ,y ,z ),则有n ⊥CE →,n ⊥AC →,⎩⎨⎧3x -4z =0,-6y +4z =0.令y =2,则n =(4,2,3),则d =BC →·n |n |=1229=122929.(3)设M (0,0,m ),∵BM→=λBC →,∴m =4λ,AM →=(0,-6,m ),AE →=(3,-6,0),设平面AEM 的法向量为n 1=(x 1,y 1,z 1),则n 1⊥AM →,n 1⊥AE →,则⎩⎨⎧-6y 1+mz 1=0,3x 1-6y 1=0,令y 1=1,则n 1=⎝ ⎛⎭⎪⎫2,1,6m ,CE →=(3,0,-4),EF →=⎝ ⎛⎭⎪⎫0,154,0,设平面CEF 的法向量为n 2=(x 2,y 2,z 2),则n 2⊥CE →,n 2⊥EF →,则⎩⎪⎨⎪⎧3x 2-4z 2=0,154y 2=0,令z 2=3,则n 2=(4,0,3),cos θ=2×4+18m22+12+⎝ ⎛⎭⎪⎫6m 2·42+32=1415,解得m =3,∴λ=34,∴存在λ使得平面MAE 与平面CEF 所成的锐二面角的余弦值为1415.中档题专练(三)建议用时:30分钟1.已知在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且tan A =3cbc 2+b 2-a 2.(1)求角A 的大小;(2)当a =3时,求c 2+b 2的最大值,并推断此时△ABC 的外形. 解 (1)由已知及余弦定理,得sin A cos A =3cb 2cb cos A ,sin A =32, 由于A 为锐角,所以A =60°.(2)解法一:由正弦定理,得a sin A =b sin B =c sin C =332=2,所以b =2sin B ,c =2sin C =2sin(120°-B ). c 2+b 2=4[sin 2B +sin 2(120°-B )]=4⎣⎢⎡⎦⎥⎤1-cos2B 2+1-cos (240°-2B )2 =4⎣⎢⎡⎦⎥⎤1-12cos2B -12⎝ ⎛⎭⎪⎫-12cos2B -32sin2B=4-cos2B +3sin2B =4+2sin(2B -30°).由⎩⎪⎨⎪⎧0°<B <90°,0°<120°-B <90°,得30°<B <90°,所以30°<2B -30°<150°, 当sin(2B -30°)=1,即B =60°时,(c 2+b 2)max =6, 此时C =60°,△ABC 为等边三角形.解法二:由余弦定理得(3)2=b 2+c 2-2bc cos60°=b 2+c 2-bc =3. 而bc ≤b 2+c 22(当且仅当b =c 时取等号),则3≥b 2+c 22,即b 2+c 2≤6(当且仅当b =c 时取等号). 故c 2+b 2的最大值为6,此时△ABC 为等边三角形.2.[2021·漳州八校联考(三)]我国政府对PM2.5接受如下标准:PM2.5日均值m (微克/立方米) 空气质量等级 m <35 一级 35≤m ≤75 二级 m >75超标某市环保局从180天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).(1)求这10天数据的中位数;(2)从这10天的数据中任取3天的数据,记ξ表示空气质量达到一级的天数,求ξ的分布列;(3)以这10天的PM2.5日均值来估量这180天的空气质量状况,其中大约有多少天的空气质量达到一级.解 (1)10天的中位数为(38+44)/2=41(微克/立方米) (2)由N =10,M =4,n =3,ξ的可能值为0,1,2,3利用P (ξ=k )=C k 4·C 3-k 6C 310(k =0,1,2,3)即得分布列:ξ 01 2 3 P16 12 310 130(3)一年中每天空气质量达到一级的概率为25,由η~B ⎝ ⎛⎭⎪⎫180,25,得到E (η)=180×25=72(天),一年中空气质量达到一级的天数为72天.3.[2021·广州综合测试(一)]如图1,在边长为4的菱形ABCD 中,∠DAB =60°,点E ,F 分别是边CD ,CB 的中点,AC ∩EF =O ,沿EF 将△CEF 翻折到△PEF ,连接P A ,PB ,PD ,得到如下图2的五棱锥P -ABFED ,且PB =10.(1)求证:BD ⊥平面POA ; (2)求二面角B -AP -O 的正切值.解 (1)证明:∵点E ,F 分别是边CD ,CB 的中点,∴BD ∥EF .∵菱形ABCD 的对角线相互垂直,∴BD ⊥AC .。
高三数学中档题训练1-5(带详细答案)
..Word 资料.高三数学中档题训练1班级 姓名1.集合A={1,3,a },B={1,a 2},问是否存在这样的实数a ,使得B ⊆A , 且A ∩B={1,a }?若存在,求出实数a 的值;若不存在,说明理由.2、在ABC ∆中,a 、b 、c 分别是三内角A 、B 、C 的对应的三边,已知222b c a bc +=+。
(Ⅰ)求角A 的大小: (Ⅱ)若222sin 2sin 122B C+=,判断ABC ∆的形状。
3. 设椭圆的中心在原点,焦点在x 轴上,离心率23=e .已知点)23,0(P 到这个椭圆上的点的最远距离为7,求这个椭圆方程.4.数列{}n a 为等差数列,n a 为正整数,其前n 项和为n S ,数列{}n b 为等比数列,且113,1a b ==,数列{}n a b 是公比为64的等比数列,2264b S =.(1)求,n n a b ;(2)求证1211134n S S S +++<L .高三数学中档题训练2班级 姓名1.已知函数()116-+=x x f 的定义域为集合A ,函数()()m x x x g ++-=2lg 2的定义域为集合 B. ⑴当m=3时,求()B C A R I ;⑵若{}41<<-=x x B A I ,求实数m 的值.2、设向量(cos ,sin )m θθ=u r ,(22sin ,22cos )n θθ=+-r ,),23(ππθ--∈,若1m n •=u r r ,求:(1))4sin(πθ+的值; (2))127cos(πθ+的值.3.在几何体ABCDE 中,∠BAC=2π,DC ⊥平面ABC ,EB ⊥平面ABC ,F 是BC 的中点,AB=AC=BE=2,CD=1(Ⅰ)求证:DC ∥平面ABE ;(Ⅱ)求证:AF ⊥平面BCDE ;(Ⅲ)求证:平面AFD ⊥平面AFE .4. 已知ΔOFQ 的面积为2 6 ,且OF FQ m ⋅=u u u r u u u r.(1)设 6 <m <4 6 ,求向量OF FQ u u u r u u u r与的夹角θ正切值的取值范围;(2)设以O 为中心,F 为焦点的双曲线经过点Q (如图),OF c =u u u r ,m=( 6 4-1)c 2,当OQ u u u r 取得最小值时,求此双曲线的方程.ABCDEF..Word 资料.高三数学中档题训练3班级 姓名1. 已知向量a =(3sin α,cos α),b =(2sin α, 5sin α-4cos α),α∈(3π2π2,), 且a ⊥b . (1)求tan α的值; (2)求cos(π23α+)的值.2、某隧道长2150m ,通过隧道的车速不能超过20m/s 。
配套K12高三数学专题复习 中档题满分练(3)理
中档题满分练(三)1.已知向量a =(2sin x ,-cos x ),b =(3cos x ,2cos x ),f (x )=a·b +1.(1)求函数f (x )的最小正周期,并求当x ∈⎣⎢⎡⎦⎥⎤-π12,2π3 时f (x )的取值范围;(2)将函数f (x )的图象向左平移π3个单位,得到函数g (x )的图象,在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若g ⎝ ⎛⎭⎪⎫A 2=1,a =2,b +c =4,求△ABC 的面积.2.如图,在底面是菱形的四棱锥P -ABCD 中,∠ABC =60°,PA =AC =1,PB =PD =2,点E 在PD 上,且PE =2ED .(1)求二面角P -AC -E 的大小;(2)试在棱PC 上确定一点F ,使得BF ∥平面AEC .3.(2015·杭州模拟)已知函数f (x )=x 2-(a +1)x -4(a +5),g (x )=ax 2-x +5,其中a ∈R .(1)若函数f (x ),g (x )存在相同的零点,求a 的值.(2)若存在两个正整数m ,n ,当x 0∈(m ,n )时,有f (x 0)<0与g (x 0)<0同时成立,求n 的最大值及n 取最大值时a 的取值范围.4.(2015·无锡质检)各项均为正数的数列{a n }的前n 项和为S n ,已知点(a n -1,a n )(n ∈N *,n ≥2)在函数y =3x 的图象上,且S 4=80.(1)求数列{a n }的通项公式;(2)在a n 与a n +1之间插入n 个数,使这n +2个数组成公差为d n 的等差数列,设数列⎩⎨⎧⎭⎬⎫1d n 的前n 项和为P n .①求P n ;②若16P n +6n 3n ≤40027成立,求n 的最大正整数值.中档题满分练(三)1.解 (1)f (x )=a·b +1=23sin x cos x -2cos 2x +1 =3sin 2x -cos 2x =2sin ⎝⎛⎭⎪⎫2x -π6 ∴f (x )的最小正周期T =2π2=π. 当x ∈⎣⎢⎡⎦⎥⎤-π12,2π3时,-π3≤2x -π6≤76π,sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-32,1, 因此f (x )的取值范围是[-3,2].(2)依题意,g (x )=f ⎝ ⎛⎭⎪⎫x +π3=2sin ⎝⎛⎭⎪⎫2x +π2=2cos 2x . 由g ⎝ ⎛⎭⎪⎫A 2=1,得2cos A =1,∴cos A =12, ∵0<A <π,∴A =π3, 在△ABC 中,a 2=b 2+c 2-2bc cos A =(b +c )2-3bc ,∴4=42-3bc ,则bc =4,故S △ABC =12bc sin A =12×4×sin π3= 3. 2.解 (1)∵底面ABCD 是菱形,∠ABC =60°,∴AB =AD =AC =1,在△PAB 中,由PA 2+AB 2=2=PB 2,知PA ⊥AB .同理,PA ⊥AD ,且AB ∩AD =A ,∴PA ⊥平面ABCD .建立如图所示的空间直角坐标系A -xyz ,则A (0,0,0),B ⎝⎛⎭⎪⎫32,-12,0,C ⎝ ⎛⎭⎪⎫32,12,0,P (0,0,1),D (0,1,0),E ⎝ ⎛⎭⎪⎫0,23,13. ∴AC →=⎝ ⎛⎭⎪⎫32,12,0,AE →=⎝ ⎛⎭⎪⎫0,23,13. 设平面ACE 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·AC →=0,n ·AE →=0,即⎩⎪⎨⎪⎧32x +12y =0,23y +13z =0. 取y =-3,则n =(1,-3,23).同理,平面ACP 的一个法向量为m =⎝ ⎛⎭⎪⎫32,-32,0, ∴cos 〈n ,m 〉=n ·m |n ||m |=1×32+3×324×3=12, ∴〈n ,m 〉=60°.故二面角P -AC -E 的大小为60°.(2)设PF →=λPC →(0<λ<1),∵PC →=⎝ ⎛⎭⎪⎫32,12,-1,BP →=⎝ ⎛⎭⎪⎫-32,12,1, ∴BF →=BP →+PF →=BP →+λPC →=⎝ ⎛⎭⎪⎫-32,12,1+⎝ ⎛⎭⎪⎫32λ,12λ,-λ =⎝ ⎛⎭⎪⎫32(λ-1),12(λ+1),1-λ, 由BF ∥平面AEC ,知BF →⊥n ,∴32(λ-1)×1+12(λ+1)×(-3)+(1-λ)×23=0, 解得λ=12. ∴当点F 是棱PC 的中点时,BF ∥平面AEC .3.解 (1)解方程x 2-(a +1)x -4(a +5)=0得:x =-4,或x =a +5,由函数f (x ),g (x )存在相同的零点,则-4,或a +5为方程ax 2-x +5=0的根,将-4代入ax 2-x +5=0:得16a +9=0,解得:a =-916, 将a +5代入ax 2-x +5=0得:a 3+10a 2+24a =0,解得:a =-6,或a =-4,或a =0,综上a 的值为-916,或-6,或-4,或0. (2)令f (x )<0,则-4<x <a +5,∵正整数m ,n ,∴a +5>0,即a >-5,即N =(0,a +5),令g (x )<0,即ax 2-x +5<0的解集为M ,则由题意得区间(m ,n )⊂M ∩N .①当a <0时,因为g (0)=5>0,故只能g (a +5)=a [(a +5)2-1]<0,即a >-4,或a <-6,又因为a >-5,所以-4<a <0,此时n ≤a +5<5.∵正整数m ,n ,∴m <n ≤4,当且仅当⎩⎪⎨⎪⎧-4<a <0,4≤a +5<5,g (3)=9a +2≤0,即-1≤a ≤-29时,n 的最大值为4. ②当a =0时,M ∩N =∅,不合题意,③当a >0时,因为g (0)=5>0,所以g (a +5)=a [(a +5)2-1]>0,故⎩⎪⎨⎪⎧0<12a <a +5,Δ=1-20a >0无解,综上,n 的最大值为4,a 的取值范围是-1≤a ≤-29. 4.解 (1)依题意,a n =3a n -1(n ∈N *,n ≥2), ∴数列{a n }为等比数列,且公比q =3.又S 4=a 1(1-34)1-3=80,∴a 1=2.因此数列{a n }的通项公式a n =2·3n -1. (2)①由(1)知,a n +1=2·3n ,依题意,d n =2·3n -2·3n -1n +1=4·3n -1n +1,1d n =n +14·3n -1. ∴P n =24×1+34×3+44×32+…+n +14×3n -1,(*) 则13P n =24×3+34×32+…+n 4×3n -1+n +14·3n ,(**) (*)-(**),23P n =12+14⎝ ⎛⎭⎪⎫13+132+…+13n -1-n +14·3n =12+14·13⎝ ⎛⎭⎪⎫1-13n -11-13-n +14·3n =58-2n +58·3n . ∴P n =1516-2n +516·3n -1. ②16P n +6n 3n =15-2n +53n -1+6n 3n =15-153n , 解不等式15-153n ≤40027,3n ≤81,则n ≤4. 所以n 的最大正整数为4.。
高中数学中档题1,4
高三数学中档题训练(一)1、已知向量OA=3i-4j,OB=6i-3j,OC=(5-m)I-(3+m)j,其中i、j分别是直角坐标系内x轴与y轴正方向上的单位向量.①若A、B、C能构成三角形,求实数m应满足的条件;②若△ABC为直角三角形,且∠A为直角,求实数m的值.2、已知数列{a n}的前n项之和为S n,且S n=a(a n-1)(a≠0,a≠1,n∈N n)(1)求数列{a n}的通项公式;(2)数列{b n}=2n+b(b是常数),且a1=b1,a2>b2,求a的取值范围.3、如图,在三棱锥P-ABC 中,PA ⊥底面ABC ,△ABC 为正三角形,D 、E 分别是BC 、CA 的中点.(1)证明:平面PBE ⊥平面PAC ; (2)如何在BC 上找一点F ,使AD//平面PEF ?并说明理由; (3)若PA=AB=2,对于(2)中的点F ,求三棱锥B-PEF 的体积.4、某种细菌两小时分裂一次,(每一个细菌分裂成两个,分裂所需的时间忽略不计),研究开始时有两个细菌,在研究过程中不断进行分裂,细菌总数y 是研究时间t 的函数,记作y=f(t)(1)写出函数y=f(t)的定义域和值域;(2)在所给坐标系中画出y=f(t);(0≤t<6)的图象;(3)写出研究进行到n 小时(n ≤0,n ∈Z)时细菌的总数有多少个(用关于n 的式子表示).答案在第9页A B D CFP高三数学中档题训练(二)1、求函数x x x f 4131)(3-=的单调区间,并求f(sinx)的最大值.2、数列{a n }共有k 项(k 为定值),它的前n 项和S n =2n 2+n(1≤n ≤k ,n ∈N),现从k 项中抽取一项(不抽首项、末项),余下的k-1项的平均值是79.(1)求数列{a n }的通项.(2)求出k 的值并指出抽取的第几项.3、若一个三棱锥的三个侧面中有两个是等腰直角三角形,另一个是边长为1的正三角形,试求所有的满足上述条件的三棱锥的体积.4、某服装公司生产的衬衫,若每件定价80元,则在某市年销售量为8万件. 若该服装公司在该市设立代理商来销售该衬衫,代理商要收取代销费,代销费是销售额的p%(即每销售100元时收取p 元). 为此,该衬衫每件的价格要提高到%180p 元,而每年销售量将减少0.62p 万件.(1)设该衬衫每年销售额为y 元,试写y 与p 的函数关系式,并指出这个函数的定义域; (2)若代理商对衬衫每年收取的代理费不小于16万元,求p 的取值范围.高三数学中档题训练(三)1、已知:A 、B 是△ABC 的两个内角,j BA i b A m 2sin 252cos ++-=,其中i 、j 为互相垂地的单位向量. 若|m |=423,试求tanA ·tanB 的值.2、如图,直三棱柱ABC-A 1B 1C 1中,AB=AC=4,∠BAC=90°,侧面ABB 1A 1为正方形,D 为正方形ABB 1A 1的中心,E 为BC 的中点.(1)求证:平面DB 1E ⊥平面BCC 1B 1; (2)求异面直线A 1B 与B 1E 所成的角.1A 1C BA C D1B E3、某银行准备新设一种定期存款业务,经预测,存款量与利率的平方成正比,比例系数为K(K>0),货款的利率为4.8%,又银行吸收的存款能全部放货出去.(1)若存款的利率为x ,x ∈(0,0.048),试写出存款量g(x)及银行应支付给储户的利息(x);(2)存款利率定为多少时,银行可获得最大收益?4、已知函数f(x)=nxx a x a a n 2210a …++++(n ∈N n),且y=f(x)的图象经过点(1,n 2),数列{a n }(n ∈N +)为等差数列.(1)求数列{a n }的通项公式;(2)当n 为奇函数时,设g(x)=)]()([21x f x f --,是否存在自然数m 和M ,使不等式m<g(21)<M 恒成立,若存在,求出M-m 的最小值;若不存在,说明理由.高三数学中档题训练(四)1、已知函数)R (2sin 3cos 2)(2∈++=a a x x x f .(1)若x ∈R ,求f (x )的单调递增区间;(2)若x ∈[0,2π]时,f (x )的最大值为4,求a 的值,并指出这时x 的值.2、设两个向量1e 、2e ,满足|1e |=2,|2e |=1,1e 、2e 的夹角为60°,若向量2172e te +与向量21te e +的夹角为钝角,求实数t 的取值范围.3、如图,平面VAD ⊥平面ABCD ,△VAD 是等边三角形,ABCD 是矩形,AB ∶AD =2∶1,F 是AB 的中点.(1)求VC 与平面ABCD 所成的角;(2)求二面角V -FC -B 的度数;(3)当V 到平面ABCD 的距离是3时,求B 到平面VFC 的距离.4、已知数列{n a }中531=a ,112--=n n a a (n ≥2,+∈N n ),数列}{n b ,满足11-=n n a b(1)求证数列{n b }是等差数列;(2)求数列{n a }中的最大项与最小项,并说明理由; (3)记++=21b b S n …n b +,求1)1(+-n nS b n高三数学中档题训练(一)答案1、①当m ≠21时,A 、B 、C 三点能构成三角形; ②当m=47时,三角形ABC 为直角三角形,且∠A=90°.2、(1)n n a a a )1(-= (2))2,1()1,21(⋃3、(1) ∵PA ⊥底面ABC ,∴PA ⊥BE又∵△ABC 是正三角形,且E 为AC 的中点,∴BE ⊥CA又PA A CA =⋂,∴BE ⊥平面PAC ∵BE ⊂平面PBE ,∴平面PBE ⊥平面PAC. (2)取CD 的中点F ,则点F 即为所求. ∵E 、F 分别为CA 、CD 的中点,∴EF//AD 又EF ⊂平面PEF ,AD ⊄平面PEF ,∴AD//平面PEF. (3)43 4、 (1)函数y=f(t)的定义域为[0,+∞);值域为{y|y=2n,n ∈N *} (2)(3)y=⎪⎩⎪⎨⎧⋅⋅-为奇数时当为偶数当n n n,22n ,22212 高三数学中档题训练(二)答案1、f(sinx)有最大值121. 2、(1)a n =4n-1(1≤n ≤k) (2)抽取的是第20项. 3、1 2 3 4 5 6x12 3 4 5 6 78y4、解:(1))31400p (0 )62.08(%180<<--=p p y(2)16100)6.08(%180≥⨯--pp p 10311000100411.32≤≤∴≤+-∴p p p高三数学中档题训练(二)答案1、91 2、(1)证明:延长B 1D 至A ,连结AE∵三棱柱为直三棱柱,∴平面BCC 1B 1⊥平面ABC 又△ABC 中AB=AC ,E 为AB 中点 ∴AE ⊥BC ∴AE ⊥平面BCC 1B 1又∵AC ⊂平面B 1DE ∴平面B 1DE ⊥平面BCC 1B 1 (2)63 3、(1)由题意,存款量g(x)=Kx 2,银行应支付的利息h(x)=x ·g(x)=Kx 36(2)存款利率为3.2%时,银行可获得最大利益4、(1)据题意:f(1)=n 2 即a 0+a 1+a 2+……+a n =n 2令n=1 则a 0+a 1=1,a 1=1-a 0 令n=2 则a 0+a 1+a 2=22,a 2=4-(a 0+a 1)=4-1=3令n=3 则a 0+a 1+a 2+a 3=32,a 3=9-(a 0+a 1+a 2)=9-4=5 ∵{a n }为等差数列 ∴d=a 3-a 2=5-3=2 a 1=3-2=1 a 0=0 a n =1+(n-1)·2=2n-1(2)由(1)f(x)=a 1x 1+a 2x 2+a 3x 3+…+a n x nn 为奇数时,f(-x)=-a 1x 1+a 2x 2-a 3x 3+…+a n-1x n-1-a n x ng(x)=n n n n x a x a x a x a x a x f x f +++++=----22553311)]()([21n n n n g )21)(12()21)(52()21(9)21(5211)21(253-+-++⋅+⋅+⋅=-2753)21)(12()21)(52()21(9)21(5)21(1)21(41+-+-++⋅+⋅+⋅=n n n n g相减得 253)21)(12(])21()21()21[(4211)21(43+--++++⋅=n n n g∴n n n g )21(32)21(913914)21(+-= 令n n n C )21(32= ∵*1N n ,021)21(32∈≤-⋅⋅=-+n C C n n n ∴C n+1≤C n ,C n 随n 增大而减小 又n )21(913⋅随n 增大而减小 ∴g(21)为n 的增函数,当n=1时,g(21)=21 而914)21(32)21(913914<-⋅-n n n 914)21(21<≤∴g ∴使m<g(21)<M 恒成立的自然m 的最大值为0,M 最小值为2. M-m 的最小值为2.高三数学中档题训练(三)答案解析:1、(1)a x a x x x f +++=+++=1)6π2sin(212cos 2sin 3)(. 解不等式2ππ26π22ππ2+≤+≤-k x k . 得)Z (6ππ3ππ∈+≤≤-k k x k∴ f (x )的单调增区间为3ππ[-k ,)Z ](6ππ∈+k k .(2)∵ 0[∈x ,2π], ∴ 6π76π26π≤+≤x .∴ 当2π6π2=+x 即6π=x 时,a x f +=3)(max . ∵ 3+a =4,∴ a =1,此时6π=x . 2、解析:由已知得421=e ,122=e ,160cos 1221=⨯⨯=⋅ e e .∴ 71527)72(2)()72(222212212121++=+++=++⋅t t te e e t te te e e te . 欲使夹角为钝角,需071522<++t t . 得 217-<<-t . 设)0)((722121<+=+λte e i e te . ∴ ⎩⎨⎧==λλt t 72,∴ 722=t .∴ 214-=t ,此时14-=λ. 即214-=t 时,向量2172e te +与21te e +的夹角为π . ∴ 夹角为钝角时,t 的取值范围是(-7,214-) (214-,21-). 3、解析:(甲)取AD 的中点G ,连结VG ,CG .(1)∵ △ADV 为正三角形,∴ VG ⊥AD .又平面VAD ⊥平面ABCD .AD 为交线,∴ VG ⊥平面ABCD ,则∠VCG 为CV 与平面ABCD所成的角.设AD =a ,则a VG 23=,a DC 2=. 在Rt △GDC 中, a a a GD DC GC 23422222=+=+=. 在Rt △VGC 中,33tan ==∠GC VG VCG . ∴ 30=∠VCG . 即VC 与平面ABCD 成30°.(2)连结GF ,则a AF AG GF 2322=+=. 而 a BC FB FC 2622=+=. 在△GFC 中,222FC GF GC +=. ∴ GF ⊥FC .连结VF ,由VG ⊥平面ABCD 知VF ⊥FC ,则∠VFG 即为二面角V -FC -D 的平面角. 在Rt △VFG 中,a GF VG 23==. ∴ ∠VFG =45°. 二面角V -FC -B 的度数为135°.(3)设B 到平面VFC 的距离为h ,当V 到平面ABCD 的距离是3时,即VG =3. 此时32==BC AD ,6=FB ,23=FC ,23=VF . ∴ 921==⋅∆FC VF S VFC , 2321==⋅∆BC FB S BFC . ∵ VCF B FCB V V V --=, ∴ VFC FBC S h S VG ∆∆⋅⋅⋅⋅=3131. ∴ 93123331⋅⋅=⨯⨯h . ∴ 2=h 即B 到面VCF 的距离为2解析:(1)4、4、 4、1112111111-=--=-=---n n n n n a a a a b , 而 1111-=--n n a b , ∴ 11111111=-=-=-----n n n n n a a a b b .)(+∈N n ∴ {n b }是首项为251111-=-=a b ,公差为1的等差数列. (2)依题意有n n b a 11=-,而5.31)1(25-=-+-=⋅n n b n , ∴ 5.311-=-n a n . 对于函数5.31-=x y ,在x >3.5时,y >0,0<y',在(3.5,∞+)上为减函数. 故当n =4时,5.311-+=n a n 取最大值3 而函数5.31-=x y 在x <3.5时,y <0,0)5.3(12<--=x y',在(∞-,3.5)上也为减函数.故当n =3时,取最小值,3a =-1. (3)2)5)(1(2)25225)(1(1-+=-+-+=+n n n n S n ,5.3-=n b n ,∴ ∞→+∞→=-+--=-n n n n n n n n S b n 2)5)(1()5.3)(1(2lim )1(lim 1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中档题满分练(二)
1.已知函数f (x )=2a sin ωx cos ωx +23cos 2
ωx -3(a >0,ω>0)的最大值为2,且最小正周期为π.
(1)求函数f (x )的解析式及其对称轴方程; (2)若f (α)=43,求sin ⎝ ⎛⎭⎪⎫4α+π6的值.
2.(2015·温州模拟)对于给定数列{a n },如果存在实常数p ,q ,使得a n +1=pa n +q 对于任意n ∈N *
都成立,我们称数列{a n }是“M 类数列”.
(1)已知数列{b n }是“M 类数列”且b n =3n ,求它对应的实常数p ,q 的值;
(2)若数列{c n }满足c 1=-1,c n -c n +1=2n
(n ∈N *
),求数列{c n }的通项公式,判断{c n }是否为“M 类数列”并说明理由.
3.(2015·金华模拟)在如图所示的空间几何体中,平面ACD ⊥平面ABC ,△ACD 与△ACB 是边长为2的等边三角形,BE =2,BE 和平面ABC 所成的角为60°,且点E 在平面ABC 上的射影落在∠ABC 的平分线上.
(1)求证:DE ∥平面ABC ; (2)求二面角E -BC -A 的余弦值.
4.(2015·金华十校联考)已知f (x )的定义域为R ,且当x ,y ∈R 时,恒有f (x +y )=f (x )+f (y ). (1)求f (0)的值; (2)证明:f (x )是奇函数;
(3)如果x >0时,f (x )<0,且f (1)=-12,试求使f (x 2
-2ax -1)≤1对x ∈[2,4]恒成立
的实数a 的取值范围.
中档题满分练(二)
1.解 (1)f (x )=a sin 2ωx +3cos 2ωx =a 2
+3sin(2ωx +φ)⎝
⎛
⎭
⎪⎫
其中tan φ=3a ,
由题意知:f (x )的最小正周期为π,由2π
2ω
=π,知ω=1,
由f (x )最大值为2,故a 2
+3=2,又a >0,∴a =1,tan φ=3,φ=π3.
∴f (x )=2sin ⎝
⎛⎭⎪⎫2x +π3, 令2x +π3=k π+π2,得x =π12+k π
2(k ∈Z ).
故f (x )的对称轴方程为x =π12+k π
2
(k ∈Z ).
(2)由f (α)=43知2sin ⎝ ⎛⎭⎪⎫2α+π3=43,即sin ⎝ ⎛⎭⎪⎫2α+π3=23, ∴sin ⎝ ⎛⎭⎪⎫4α+π6=sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫2α+π3-π2=-cos 2⎝ ⎛⎭⎪⎫2α+π3 =-1+2sin 2
⎝ ⎛⎭⎪⎫2α+π3=-1+2×⎝ ⎛⎭
⎪⎫232
=-19.
2.解 (1) ∵b n =3n ,则b n +1=3n +3=b n +3, 由“M 类数列”定义,得p =1,q =3. (2)∵c n -c n +1=2n (n ∈N *
), ∴c n +1-c n =-2n
(n ∈N *
),
则c 2-c 1=-2,c 3-c 2=-4,c 4-c 3=-8,… ∴c n -c n -1=-2
n -1
(n ≥2),
以上式子累加得
c n =-(1+2+4+…+2n -1)=1-2n (n ≥2),
其中c 1=-1也满足上式. 因此c n =1-2n
(n ∈N *
), 则c n +1=1-2
n +1=2(1-2n
)-1=2c n -1,
{c n }是“M 类数列”.
3.(1)证明 由题意知,△ABC ,△ACD 都是边长为2的等边三角形,如图所示
,取AC 中点O ,连接BO ,DO ,则BO ⊥AC ,DO ⊥AC ,BO 平分∠ABC . 又∵平面ACD ⊥平面ABC ,∴DO ⊥平面ABC ,作EF ⊥平面ABC , 那么EF ∥DO ,根据题意,点F 落在BO 上, ∴∠EBF =60°,易求得EF =DO =3, ∴四边形DEFO 是平行四边形,
∴DE ∥OF ,又DE ⊄平面ABC ,OF ⊂平面ABC ,∴DE ∥平面ABC . (2)解 建立如图所示的空间直角坐标系O -xyz ,
可知平面ABC 的一个法向量为n 1=(0,0,1),B (0,3,0),C (-1,0,0),E (0,3-1,
3),∴BC →
=(-1,-3,0),BE →
=(0,-1,3),设平面BCE 的一个法向量为n 2=(x ,y ,
z ),则⎩⎪⎨⎪⎧n 2·BC →
=0,n 2·BE →
=0,
可求得n 2=(-3,3,1).
所以cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=13
13
,
又由图知,所求二面角的平面角是锐角, 所以二面角E -BC -A 的余弦值为
1313
. 4.(1)解 ∵对任意实数x ,y 有f (x +y )=f (x )+f (y ), ∴令x =y =0得f (0)=2f (0), ∴f (0)=0.
(2)证明 ∵f (x )的定义域为R , ∴f (x )的定义域关于原点对称.
又令y =-x ,则有f (0)=f (x )+f (-x ), ∴f (-x )=-f (x ),∴f (x )是奇函数. (3)解 设x 1,x 2∈(-∞,+∞),x 1<x 2, ∵x 2>x 1,∴x 2-x 1>0,∴f (x 2-x 1)<0,
f (x 2)<f (x 1),∴f (x )是R 上的减函数.
∵f (1)=-12,∴f (-1)=1
2
,∴f (-2)=1.
∴不等式f (x 2
-2ax -1)≤1即是f (x 2
-2ax -1)≤f (-2), ∴x 2
-2ax -1≥-2,
即x 2-2ax +1≥0对x ∈[2,4]恒成立.
法一 即a ≤x 2+1
2x
对x ∈[2,4]恒成立.
令g (x )=x 2+1
2x
,则由g (x )在x ∈[2,4]上单调递增,
∴g (x )min =g (2)=1+14=54,∴a ≤5
4.
法二 令φ(x )=x 2
-2ax +1(x ∈[2,4]), 当a <2时,φ(x )在[2,4]上单调递增, φ(x )min =φ(2)=5-4a ≥0,解得a ≤5
4,
故a ≤5
4
满足题意;
当2≤a ≤4时,φ(x )min =φ(a )=1-a 2
≥0, 解得-1≤a ≤1,此时与2≤a ≤4矛盾; 当a >4时,φ(x )在[2,4]上单调递减,
φ(x )min =φ(4)=17-8a ≥0,解得a ≤17
8,
此时与a >4矛盾. 由上述可知,a ≤5
4.。
