人教版高中数学必修一《基本初等函数》之《幂函数》表格式教学设计
新人教A版必修1《幂函数》教案

-强调幂函数的单调性、奇偶性、过定点等性质。
-结合具体幂函数,如f(x) = x^2、f(x) = x^3等,讲解其性质并举例说明。
-核心内容三:常见幂函数的图像与性质
-详细分析正比例函数、反比例函数、二次函数、三次函数的图像及其性质。
-引导学生观察图像,总结性质,并能运用性质解决相关问题。
2.教学难点
4.数学抽象:帮助学生从具体实例中抽象出幂函数的一般规律,培养学生的数学抽象思维。
三、教学难点与重点
1.教学重点
-核心内容一:幂函数的定义及其一般形式
-重点讲解幂函数的一般形式f(x) = x^a,强调a为常数的特点。
-通过实例展示,让学生理解不同a值对应的幂函数图形差异。
-核心内容二:幂函数的性质
-难点三:幂函数在实际问题中的应用
-学生可能不知道如何将幂函数应用于实际问题,如计算面积、体积等。
-教师应设计相关实际问题,引导学生运用幂函数知识解决问题,提高应用能力。
-难点四:幂函数性质的应用与拓展
-学生可能难以将幂函数性质应用于更广泛的数学问题。
-教师可通过举例,如数学竞赛题等,展示幂函数性质在更复杂问题中的应用,拓展学生思维。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解幂函数的基本概念。幂函数是形如f(x) = x^a的函数,其中a为常数。幂函数在数学中具有重要地位,广泛应用于实际问题中。
2023年高中数学幂函数教学教案(7篇)

2023高中数学幂函数教学教案(7篇)高中数学必修1《幂函数》教案篇一1、教学目标学问目标:(1)把握幂函数的形式特征,把握详细幂函数的图象和性质。
(2)能应用幂函数的图象和性质解决有关简洁问题。
力量目标:培育学生发觉问题,分析问题,解决问题的力量。
情感目标:(1)加深学生对讨论函数性质的根本方法和流程的阅历。
(2)渗透辨证唯物主义观点和方法论,培育学生运用详细问题详细分析的方法分析问题、解决问题的力量。
2、教学重点:从详细函数归纳熟悉幂函数的一些性质并简洁应用。
教学难点:引导学生概括出幂函数的性质。
3、教学方法和教学手段:探究发觉法和多媒体教学4、教学过程:问题情境问题1写出以下y关于x的函数解析式:①正方形边长x、面积y②正方体棱长x、体积y③正方形面积x、边长y④某人骑车x秒内匀速前进了1m,骑车速度为y⑤一物体位移y与位移时间x,速度1m/s问题2是否为指数函数?上述函数解析式有什么共同特征?(教师将解析式写成指数幂形式,以启发学生归纳,)板书课题并归纳幂函数的定义。
(二)新课讲解幂函数的定义:一般地,我们把形如的函数称为幂函数(powerfunction),其中是自变量,是常数。
为了加深对定义的理解,请同学们判别以下函数中有几个幂函数?①y=②y=2x2我们了解了幂函数的概念以后我们一起来讨论幂函数的性质。
问题3幂函数具有哪些性质?用什么方法讨论这些性质的呢?我们请同学们回忆一下在前面学习指数函数、对数函数我们一起讨论了哪些性质呢?(学生争论,教师引导)(引发学生作图讨论函数性质的兴趣。
函数单调性的推断,既可以使用定义,也可以通过图象解决,直观,易理解。
)在初中我们已经学习了幂函数的图象和性质,请同学们在同一坐标系中画出它们的图象。
依据你的学习经受,你能在同一坐标系内画出函数的图象吗?(学生作图,教师巡察。
将学生作图用实物投影仪演示,指出优点和错误之处。
教师利用几何画板演示,通过超级链接几何画板演示。
人教版高中必修一《幂函数》教案

人教版高中必修一《幂函数》教案一、教学目标1.了解幂函数的定义和特点;2.学习叠加思想,并掌握简单的幂函数叠加方法;3.能够解决一些实际问题。
二、教学重难点1.幂函数的定义及其特点;2.幂函数的叠加思想;3.幂函数的绘图方法;三、教学过程1.引入幂函数的定义:$y=x^p(p\\in \\mathbb{R})$让学生发现x的取值范围对函数图象的影响,并对函数图象进行描述。
2. 概念讲解1.首先讲解幂函数的定义,指出它是一种基本函数;2.介绍幂函数的性质,让学生知道幂函数的图像不可能横切x轴;3.引入幂函数的叠加思想,让学生知道可以将不同的函数图像叠加在一起。
3. 具体例子讲解1.书写公式,说明函数图象的性质;2.给出幂函数的图象,描出函数的图象;3.确定函数图象的性质,让学生明白函数图象的变化。
4. 例题解析1.给出实际问题,提供数据;2.根据实际问题列出函数式,确定函数图象;3.通过实际问题,解释函数图象的意义。
5. 分组讨论1.将学生分成若干小组,每组做一道练习题;2.每组向其他组展示自己的想法、方法及结果;3.学生之间相互交流,共同探讨出最佳答案。
四、教学方法1.板书法:结合具体例子进行讲解;2.案例法:让学生通过实际问题练习解题思路;3.分组讨论法:提高学生探究问题、思考问题和解决问题的能力。
五、教学帮助1.帮助学生理解定义和性质;2.尤其帮助学生掌握幂函数的叠加思想,找出函数图象的变化规律。
六、课堂反馈1.倾听学生提出的疑问和问题;2.鼓励并指导学生提出自己的解决方案;3.搜集学生反馈,及时调整教学进度和方法。
七、课堂作业1.完成教师布置的作业;2.阅读教材给出的例题;3.自己找出一些幂函数的例子进行探究。
人教版高中必修1(B版)3.3幂函数课程设计

人教版高中必修1(B版)3.3幂函数课程设计一、背景与目的幂函数作为数学分析中的一种基本函数,是大学教育中非常重要的课程内容,但是在高中数学中,尤其是在必修课中,幂函数的教学并不够充分。
因此,本课程设计旨在通过引导学生深入探究幂函数的性质与应用,提升学生对幂函数的认识与理解,为大学数学课程打下更加牢固的基础。
二、教学内容与方法1. 教学内容本课程设计主要围绕以下内容展开:1.幂函数的定义与性质;2.幂函数的图像与变化趋势;3.幂函数与指数函数的关系;4.幂函数的应用:指数函数模型。
2. 教学方法1.探究式教学法。
此方法通过引导学生自主学习、自主探究的方式,让学生体验到数学发现的乐趣,增强他们对知识的掌握及运用能力。
在本课程设计中,可以让学生通过编写程序或利用数学软件,探究幂函数的各种性质与变化趋势。
2.讨论式教学法。
此方法通过给学生一定的问题或案例,引导学生进行思考和探讨,培养学生的合作意识、批判思维和创造力。
在本课程设计中,可以通过案例分析的方式,让学生探讨幂函数在生活中的应用,并结合实际问题进行计算与解答。
三、教学过程1. 课前准备1.设备:计算机、投影仪、数学软件等;2.材料:教材相关内容、探究性课题、案例等;3.学生:提前学习幂函数基本知识,具备使用数学软件的能力。
2. 教学步骤第一步:幂函数的定义与性质1.进行知识普及,回顾幂函数的定义;2.引导学生自主探究幂函数性质:奇偶性、单调性、零点、渐进线、极值点等;3.通过数学软件绘制幂函数图像,让学生了解幂函数在不同情况下的变化趋势和特点。
第二步:幂函数与指数函数的关系1.回顾指数函数的定义与性质;2.引导学生探究幂函数与指数函数的关系,并解释幂函数的性质对其图像的影响。
第三步:幂函数的应用1.结合生活实际问题,引导学生运用幂函数进行模型构建与解答;2.通过案例分析,让学生掌握幂函数在实际问题中的应用。
四、课程评估1. 教学成果评估1.以小组形式完成探究性课题的撰写与汇报,评选出优秀课题;2.编写课程设计反思材料,评价本课程设计的教学效果。
人教版高中数学必修一《基本初等函数》之《幂函数》教学案
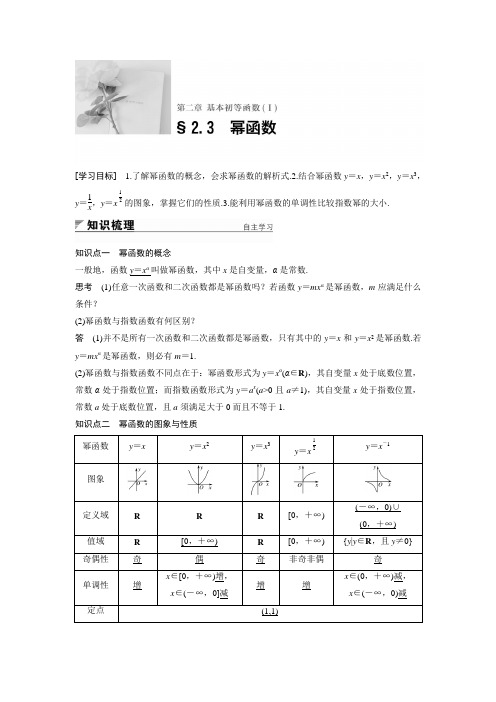
[学习目标] 1.了解幂函数的概念,会求幂函数的解析式.2.结合幂函数y =x ,y =x 2,y =x 3,y =1x,y =x 21的图象,掌握它们的性质.3.能利用幂函数的单调性比较指数幂的大小.知识点一 幂函数的概念一般地,函数y =x α叫做幂函数,其中x 是自变量,α是常数.思考 (1)任意一次函数和二次函数都是幂函数吗?若函数y =mx α是幂函数,m 应满足什么条件?(2)幂函数与指数函数有何区别?答 (1)并不是所有一次函数和二次函数都是幂函数,只有其中的y =x 和y =x 2是幂函数.若y =mx α是幂函数,则必有m =1.(2)幂函数与指数函数不同点在于:幂函数形式为y =x α(α∈R ),其自变量x 处于底数位置,常数α处于指数位置;而指数函数形式为y =a x (a >0且a ≠1),其自变量x 处于指数位置,常数a 处于底数位置,且a 须满足大于0而且不等于1. 知识点二 幂函数的图象与性质 幂函数y =xy =x 2y =x 3y =x 21y =x -1图象定义域 R R R [0,+∞) (-∞,0)∪ (0,+∞) 值域 R [0,+∞)R [0,+∞) {y |y ∈R ,且y ≠0}奇偶性 奇 偶奇 非奇非偶 奇单调性 增x ∈[0,+∞)增, x ∈(-∞,0]减增 增x ∈(0,+∞)减, x ∈(-∞,0)减定点(1,1)题型一 幂函数的概念例1 (1)已知(2,2)在幂函数f (x )的图象上,求f (2)的值; (2)已知函数f (x )=(a 2-3a +3)255-+a a x (a 为常数)为幂函数,且在(0,+∞)上单调递减,求实数a 的值.解 (1)设f (x )=x α, ∵(2,2)在f (x )的图象上, ∴f (2)=(2)α=2,∴α=2. 故f (x )=x 2,f (2)=22=4.(2)∵f (x )为幂函数,∴a 2-3a +3=1, 得a =1或a =2.当a =1时,f (x )=x ,在(0,+∞)上单调递增,不合题意. 当a =2时,f (x )=x -1,在(0,+∞)上单调递减,符合题意. 综上,得a 的值为2.反思与感悟 1.幂函数的特点:系数为1,底数为自变量,指数为常数.2.当α>0时,幂函数在第一象限内单调递增;当α<0时,幂函数在第一象限内单调递减. 跟踪训练1 函数f (x )=(m 2-m -1)23+-mm x 是幂函数,且当x ∈(0,+∞)时,f (x )是增函数,求f (x )的解析式.解 根据幂函数定义得,m 2-m -1=1,解得m =2或m =-1, 当m =2时,f (x )=x 3在(0,+∞)上是增函数, 当m =-1时,f (x )=x-3在(0,+∞)上是减函数,不合题意.∴f (x )的解析式为f (x )=x 3. 题型二 幂函数的图象例2 如图所示,图中的曲线是幂函数y =x n 在第一象限的图象,已知n 取±2,±12四个值,则相应于c 1,c 2,c 3,c 4的n 依次为( )A.-2,-12,12,2B.2,12,-12,-2C.-12,-2,2,12D.2,12,-2,-12答案 B解析 考虑幂函数在第一象限内的增减性.注意当n >0时,对于y =x n ,n 越大,y =x n 递增速度越快,n <0时看|n |的大小.根据幂函数y =x n 的性质,在第一象限内的图象当n >0时,n 越大,y =x n 递增速度越快,故c 1的n =2,c 2的n =12,当n <0时,|n |越大,曲线越陡峭,所以曲线c 3的n =-12,曲线c 4的n =-2,故选B.反思与感悟 幂函数图象的特征:(1)在第一象限内,直线x =1的右侧,各幂函数图象对应的指数逆时针增大;在第一象限内,直线x =1的左侧,指数也呈逆时针增大.(2)幂函数y =x α,若α>0,在第一象限内函数单调递增;若α<0,在第一象限内函数单调递减.(3)图象的凹凸性:在第一象限内,当0<α<1,曲线上凸;当α>1,曲线下凹;当α<0,曲线下凹.跟踪训练2 如图是幂函数y =x m 与y =x n 在第一象限内的图象,则( )A.-1<n <0<m <1B.n <-1,0<m <1C.-1<n <0,m >1D.n <-1,m >1答案 B解析 方法一 在(0,1)内取同一值x 0,作直线x =x 0,与各图象有交点,如图所示.根据“点低指数大”,有0<m <1,n <-1.方法二 根据幂函数图象增减性知m >0,n <0,由x =1右侧指数逆时针增大,知n <-1,由图象上凸知0<m <1,故选B. 题型三 比较幂的大小 例3 比较下列各组数的大小. (1)325-和3.125-;(2)898-和(19)98;(3)(34)-2和3-4;(4)(-13)-3和251. 解 (1)函数y =x25-在(0,+∞)上为减函数,又3<3.1,所以325->3.125-.(2)函数y =x 98在(0,+∞)上为增函数,又18>19,所以(18)98>(19)98,即898->(19)98.(3)3-4=(32)-2=9-2,函数y =x-2在(0,+∞)上为减函数,又34<9,所以(34)-2>9-2,即(34)-2>3-4.(4)因为(-13)-3<0,251>0,所以(-13)-3<251.反思与感悟 1.比较幂值的大小,关键在于构造适当的函数:(1)若指数相同而底数不同,则构造幂函数;(2)若指数不同而底数相同,则构造指数函数.2.若指数与底数都不同,需考虑是否能把指数或底数化为相同,是否可以引入中间量. 跟踪训练3 比较下列各组数的大小: (1)⎝⎛⎭⎫230.5与⎝⎛⎭⎫350.5;(2)-3.143与-π3; (3)⎝⎛⎭⎫1243与⎝⎛⎭⎫3421.解 (1)∵y =x 0.5在[0,+∞)上是增函数且23>35,∴⎝⎛⎭⎫230.5>⎝⎛⎭⎫350.5.(2)∵y =x 3是R 上的增函数,且3.14<π, ∴3.143<π3,∴-3.143>-π3.(3)∵y =⎝⎛⎭⎫12x是减函数,∴⎝⎛⎭⎫1243<⎝⎛⎭⎫1221. y =x 21是[0,+∞)上的增函数, ∴⎝⎛⎭⎫3421>⎝⎛⎭⎫1221.∴⎝⎛⎭⎫3421>⎝⎛⎭⎫1243. 题型四 幂函数的奇偶性 例4 判断下列函数的奇偶性: (1)y =x 31;(2)y =x -2;(3)y =x32-.解 (1)f (-x )=(-x )31=-x 31=-f (x ), 又∵y =x 31定义域为R ,∴y =x 31为奇函数.(2)f (x )=x -2=1x 2,定义域为(-∞,0)∪(0,+∞),又f (-x )=1(-x )2=1x 2=f (x ),∴f (x )为偶函数. (3)f (x )=x32-=321x=1x 3. ∴f (x )的定义域为(0,+∞),不关于原点对称. ∴f (x )为非奇非偶函数.反思与感悟 幂函数的奇偶性.y =x n ,当n =pq (p ,q ∈Z )是最简分数时,若p ,q 均为奇数,则y =x n 是奇函数;若p 为偶数,q 为奇数,则y =x n 是偶函数;若q 为偶数,则y =x n 为非奇非偶函数.跟踪训练4 函数y =x 59在[-1,1]上是( ) A.增函数且是奇函数 B.增函数且是偶函数 C.减函数且是奇函数 D.减函数且是偶函数答案 A解析 由幂函数的性质知当α>0时,y =x α在第一象限内是增函数, ∴y =x 59在x ∈[0,1]上是增函数.设f (x )=x 59,x ∈[-1,1],则f (-x )=(-x )59=-x 59=-f (x ),∴f (x )=x 59是奇函数. ∵奇函数的图象关于原点对称, ∴x ∈[-1,0]时,y =x 59也是增函数.当x =0时,y =0,故y =x 59在[-1,1]上是增函数且是奇函数.故选A.忽略幂函数定义致误例5 函数y =(a 2+1)211-a x是幂函数,求a 的取值范围.错解 根据幂函数的定义y =x α,α为常数, 知指数11-a2有意义,有1-a 2≠0,即a ≠±1,所以a 的取值范围是{a |a ≠±1}.正解 根据幂函数的定义y =x α,α为常数, 知a 2+1=1,即a =0, 此时指数11-a 2有意义,所以a 的取值范围为{0}. 易错警示错误原因纠错心得错解中只注意了指数要有意义,忽略了前面的系数应为1. 若给出的函数为幂函数,则此时该函数是形如y =x α的函数,且具有如下特征:①系数为1;②底数为自变量;③指数为常数.这是我们解题的有效切入点,应准确把握.跟踪训练5 幂函数y =(m 2-m -1)223--m m x ,当x ∈(0,+∞)时为减函数,求实数m 的值,并求函数的定义域. 解 因为y =(m 2-m -1)223--m m x为幂函数,所以m 2-m -1=1,即(m -2)(m +1)=0, 所以m =2或m =-1.当m =2时,m 2-2m -3=-3,y =x-3是幂函数,且在(0,+∞)上是减函数.当m =-1时,m 2-2m -3=0,y =x 0=1(x ≠0)不是减函数, 所以m =2,此时y =x -3.所以函数的定义域是{x |x ∈R 且x ≠0}.1.下列给出的函数中,是幂函数的是( ) A.y =3x B.y =2x 3 C.y =x -3 D.y =x 3-1答案 C2.若函数y =(k 2-k -5)x 2是幂函数,则实数k 的值为( ) A.3 B.2 C.3或-2 D.k ≠3且k ≠-2 答案 C解析 由幂函数的概念可知k 2-k -5=1,即k 2-k -6=0,得k =-2,或k =3. 3.幂函数f (x )=x 23的大致图象为( )答案 B解析 由于f (0)=0,所以排除C ,D 选项,而f (-x )=(-x )23=3(-x )2=3x 2=x 23=f (x ),且f (x )的定义域为R ,所以f (x )是偶函数,图象关于y 轴对称.故选B. 4.设f (x )=(m -1)22-m x,若f (x )为正比例函数,则m =________;若f (x )是反比例函数,则m=________;若f (x )是幂函数,则m =________. 答案 ±3 -1 2解析 f (x )=(m -1)22-mx.若f (x )是正比例函数,则⎩⎪⎨⎪⎧m -1≠0,m 2-2=1,∴m =±3.若f (x )是反比例函数,则⎩⎪⎨⎪⎧ m -1≠0,m 2-2=-1,即⎩⎪⎨⎪⎧m ≠1,m 2=1,∴m =-1.若f (x )是幂函数,则m -1=1,∴m =2.5.若a =(12)53,b =(15)53,c =(-2)3,则a ,b ,c 的大小关系为________.答案 a >b >c解析 ∵y =x 53在(0,+∞)上为增函数. ∴(12)53>(15)53,即a >b >0. 而c =(-2)3=-23<0,∴a >b >c .1.幂函数y =x α的底数是自变量,指数是常数,而指数函数正好相反,底数是常数,指数是自变量.2.幂函数在第一象限内指数变化规律在第一象限内直线x =1的右侧,图象从上到下,相应的指数由大变小;在直线x =1的左侧,图象从下到上,相应的指数由大变小.3.简单幂函数的性质(1)所有幂函数在(0,+∞)上都有定义,并且当自变量为1时,函数值为1,即f (1)=1. (2)如果α>0,幂函数在[0,+∞)上有意义,且是增函数. (3)如果α<0,幂函数在x =0处无意义,在(0,+∞)上是减函数.一、选择题1.下列函数是幂函数的是( ) A.y =5x B.y =x 5 C.y =5x D.y =(x +1)3答案 B解析 函数y =5x 是指数函数,不是幂函数;函数y =5x 是正比例函数,不是幂函数;函数y =(x +1)3的底数不是自变量x ,不是幂函数;函数y =x 5是幂函数. 2.已知幂函数f (x )的图象经过点⎝⎛⎭⎫2,22,则f (4)的值为( ) A.16 B.116 C.12 D.2答案 C解析 设f (x )=x a ,则有2a=22,解得a =-12,即f (x )=x 21-,所以f (4)=421-=12.3.设α∈⎩⎨⎧⎭⎬⎫-1,1,12,3,则使函数y =x α的定义域为R 且为奇函数的所有α值为( )A.1,3B.-1,1C.-1,3D.-1,1,3答案 A解析 可知当α=-1,1,3时,y =x α为奇函数,又∵y =x α的定义域为R ,则α=1,3. 4.设a =⎝⎛⎭⎫2553,b =⎝⎛⎭⎫2552,c =⎝⎛⎭⎫3552,则a ,b ,c 的大小关系是( ) A.a >b >c B.c >a >b C.a <b <c D.b >c >a答案 C解析 ∵函数y =⎝⎛⎭⎫25x 在R 上是减函数,又35>25, ∴⎝⎛⎭⎫2553<⎝⎛⎭⎫2552,即a <b .又∵函数y =x 52在R 上是增函数,且35>25,∴⎝⎛⎭⎫3552>⎝⎛⎭⎫2552,即c >b ,∴a <b <c . 5.函数y =x 31的图象是( )答案 B解析 函数y =x 31是幂函数,幂函数在第一象限内的图象恒过定点(1,1),排除A 、D.当x >1时,x >x 31,故幂函数y =x 31图象在直线y =x 的下方,排除C.6.若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”.那么函数解析式为f (x )=x 2,值域为{1,4}的“同族函数”共有( ) A.7个 B.8个 C.9个 D.无数个 答案 C解析 值域为{1,4},∴其定义域由1,-1,2,-2组成,∴有{1,2},{1,-2},{-1,2}{-1,-2},{1,-1,-2},{1,-1,2},{1,2,-2},{-1,2,-2},{1,-1,2,-2},共有9种情况. 二、填空题7.已知幂函数f (x )=x m 的图象经过点(3,13),则f (6)=________.答案136解析 依题意13=(3)m =32m,所以m2=-1,m =-2,所以f (x )=x -2,所以f (6)=6-2=136.8.若y =249--a a x是偶函数,且在(0,+∞)内是减函数,则整数a 的值是________.答案 1,3,5,-1解析 由题意得,a 2-4a -9应为负偶数, 即a 2-4a -9=(a -2)2-13=-2k (k ∈N *), (a -2)2=13-2k ,当k =2时,a =5或-1;当k =6时,a =3或1.9.已知幂函数f (x )=x 21,若f (10-2a )<f (a +1),则a 的取值范围是________. 答案 (3,5]解析 因为f (x )=x 21=x (x ≥0), 易知f (x )在(0,+∞)上为增函数, 又f (10-2a )<f (a +1), 所以⎩⎪⎨⎪⎧a +1≥0,10-2a ≥0,a +1>10-2a ,解得⎩⎪⎨⎪⎧a ≥-1,a ≤5,a >3.所以3<a ≤5.10.幂函数f (x )=(m 2-m -1)x 2m -3在(0,+∞)上是减函数,则实数m =________.答案 -1解析 ∵f (x )=(m 2-m -1)x 2m -3为幂函数,∴m 2-m -1=1, ∴m =2或m =-1.当m =2时,f (x )=x ,在(0,+∞)上为增函数,不合题意,舍去;当m =-1时,f (x )=x -5,符合题意.综上可知,m =-1. 三、解答题11.已知幂函数f (x )的图象过点(25,5). (1)求f (x )的解析式;(2)若函数g (x )=f (2-lg x ),求g (x )的定义域、值域. 解 (1)设f (x )=x α,则由题意可知25α=5, ∴α=12,∴f (x )=x 21.(2)∵g (x )=f (2-lg x )=2-lg x , ∴要使g (x )有意义,只需2-lg x ≥0, 即lg x ≤2,解得0<x ≤100.∴g (x )的定义域为(0,100],又2-lg x ≥0,∴g (x )的值域为[0,+∞).12.已知函数f (x )=(a 2-a +1)x a+1为幂函数,且为奇函数. (1)求a 的值;(2)求函数g (x )=f (x )+[f (x )]2在[0,12]上的值域. 解 (1)因为函数f (x )=(a 2-a +1)x a +1为幂函数,所以a 2-a +1=1,解得a =0或a =1.当a =0时,f (x )=x ,函数是奇函数;当a =1时,f (x )=x 2,函数是偶函数.故a =0.(2)由(1)知g (x )=x +x 2=(x +12)2-14. 当x =0时,函数取得最小值g (0)=0;当x =12时,函数取得最大值g (12)=12+14=34. 故g (x )在区间[0,12]上的值域为[0,34]. 13.已知幂函数f (x )=(m -1)2242-+m m x在(0,+∞)上单调递增,函数g (x )=2x -k . (1)求m 的值;(2)当x ∈[1,2]时,记f (x ),g (x )的值域分别为集合A ,B ,若A ∪B =A ,求实数k 的取值范围. 解 (1)依题意,得(m -1)2=1,解得m =0或m =2.当m =2时,f (x )=x -2在(0,+∞)上单调递减,与题设矛盾,舍去.∴m =0.(2)由(1)可知f (x )=x 2.当x ∈[1,2]时,f (x ),g (x )单调递增,∴A =[1,4],B =[2-k,4-k ].∵A ∪B =A ,∴B ⊆A ,∴⎩⎪⎨⎪⎧2-k ≥1,4-k ≤4,⇒0≤k ≤1. ∴实数k 的取值范围是[0,1].。
《幂函数》教学设计

普通高中教科书数学必修第一册(人教A版2019)3.3幂函数一、教学目标:(一)了解幂函数的概念,会求幂函数的解析式.(二)通过具体实例,会画y=x,y=x2,y=x3,y=x-1,y=x12的图象,描述它们的变化规律,总结掌握幂函数的性质.(三)能利用幂函数的单调性比较指数幂的大小.二、教学重难点重点:幂函数的概念、图象和性质.难点:利用幂函数的性质解决有关问题.三、教学用具:ppt、geogebra软件四、教学过程:(一)情境导入前面学习了函数的概念,利用函数概念和对函数的观察,研究了函数的一些性质.本节我们利用这些知识研究一类新的函数.先看几个实例. 1.如果张红以1元/kg的价格购买了某种蔬菜wkg,那么她需要支付 p=w元,这里p是w的函数;2.如果正方形的边长为x,那么正方形的面积y=x2,这里y是x的函数; 3.如果立方体的棱长为b,那么立方体的体积V=b3,这里V是b的函数; 4.如果一个正方形场地的面积为S,那么正方形场地的边长c=√S,这里c是S的函数;5.如果某人t s内骑车行进了1km,那么他骑车的平均速度v=1km/s,t 即v=t−1,这里v是t的函数.(二)探究活动1:请观察1—5中的函数解析式,讨论它们有何共同特征.1.p=w;2.y=x2;3.V=b3;,即v=t−1.4.c=√S,即c=s12;5.v=1t实际上,这些函数的解析式都有幂的形式,而且都是以幂的底数为自,-1;它们都是形如y=xα的变量;幂的指数都是常数,分别是1,2,3,12函数.【设计意图】将实际问题转化为数学问题,引导学生经历从实例中用函数思维方式抽象出幂函数的形式,进而引出新知识的定义和形式. (三)概念新知幂函数的定义:一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.1.练习:(1)下列函数哪些是幂函数()①y=x3②y=(1)x③y=4x2④y=x5+12⑤y=(x-1)2 ⑥y=x ⑦y=2x(2)若f(x)=(m2-4m-4)x m是幂函数,则m=_____.结论:底数只能是自变量x,指数只能是常数,幂的系数只能是1, 解析式只能是一项;判断一个函数是不是幂函数的依据是该函数是否为y=xα(α为常数)的形式;反过来,若一个函数为幂函数,那么它也一定具有这个形式.在我们解决某些问题的时候这个结论有奇效.【设计意图】通过引导学生从函数的思维方式归纳出幂函数的定义,然后再通过练习和思考,学生进一步理解幂函数的定义.(四)探究活动2(数到形),−1时的图象与性质.现对于幂函数,我们只研究α=1,2,3,12请同学们尝试在同一坐标系中画出这五个函数的大致图象.(取点要具有代表性)老师用geogebra软件进行展示【设计意图】通过课前预习的网络作业让学生先独立画出三个幂函数的图像,然后课堂上在同一直角坐标系中通过描点法画出另外两个幂函数,在画的过程中体会图像的变化趋势,掌握幂函数的特征.(五)探究活动3(形到数)结合幂函数图像和解析式,将你发现的结论填写在下表.【设计意图】由形到数,发现并归纳5个常见幂函数的图像性质. (六)性质探究探究活动4:观察α=1,2,3,1/2 ,-1时幂函数的图形,填写以下研究报告1.特殊幂函数的性质(1) y=x,y=x2,y=x3,y=x12,y=x-1主要分布在第象限,第象限无图像.(2)函数y=x,y=x2,y=x3,y=x12和y=x-1的图像都通过点;(3)函数y=x,y=x3,y=x-1是,函数y=x2是;(4)在区间(0,+∞)上,函数y=x,y=x2,y=x3,y=x12,函数y=x-1;(5)在第一象限内,函数y=x-1的图像向上与y轴,向右与x轴.2.一般幂函数的性质:(1)第一象限均有图像,第四象限均无图像(2)幂函数图像都过点(1,1);α>0,函数过(0,0)(3)α为偶数时,幂函数是偶函数;α为奇数时,幂函数是奇函数.(4)当α>0时,幂函数在区间(0,+∞)上单调递增;当α<0时,幂函数在区间(0,+∞)上单调递减(5)一般地,幂函数的图像在直线x=1的右侧,指数大的在上,指数小的在下(指大图高),在y轴与直线x=1之间正好相反(指大图低).【设计意图】引导学生通过观察函数的图像,分析归纳出五个函数图像各自性质的基础上,再归纳幂函数的共性和差异性,进而得出幂函数的基本性质.(七)应用提升例1.在下列四个图形中,y =x-12的大致图像是( )例2 比较下列各组数的大小.(1) (2) (3)(八)当堂检测1.下列函数是幂函数的是( )A .y =5x 2B .y =x 5−1 C .y =x 8D.y =(x +1)22.若 f (x )=(m 2-2m -2)x m是幂函数,且在第一象限为增函数,则m =( )A .−1 B. 3 C. -1或3 D.13.已知幂函数y =f(x)的图像经过点(4, 12 ),则 f (2)=( )A .14B.4C.√22D.√24.下列正确的是( )A.(1.5)3<(1.4)3B. (0.1)0.3>(0.2)0.3C. (11.5)−3<(11.6)−3D. (0.6)3<(0.6)0.5111.5 1.4--,1.23,1.330.53 ,0.50.55.若(3-2m)12>(m+1)12,求实数m的取值范围.五.归纳总结1.幂函数概念:一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.2.幂函数性质:(1)幂函数图象都过点(1,1).(2)α为偶数时,幂函数是偶函数。
人教版高中数学必修一《基本初等函数》之《幂函数》表格式教案

§2.3幂函数(教案)教材分析:幂函数是函数的重要内容之一,新课程标准将其列为基本初等函数之一,并与 指数函数、对数函数安排在一起。
新课程标准对幂函数提出了明确的要求:(1)通过实例,了解幂函数的概念;结合函数x y =;21x y =;2x y =;1-=x y ;3x y =的图像,了解它们的变化情况。
(2)利用计算工具,比较指数函数、对数函数以及幂函数增长差异。
(3)收集一些社会生活中普遍使用的函数模型(指数函数、对数函数、幂函数、分段函数等)的实例,了解函数模型的广泛应用。
上面的表述中,可以看出:指数函数、对数函数、幂函数三类不同函数的增长变化是认识的核心。
所以幂函数教学必须分两个层次来进行,一是幂函数概念及其简单性质,二是函数模型的应用。
本节课为前一层次。
所以幂函数的教学要求不能过高,也不能太低,必须体现以下三点: (1) 通过实例,了解幂函数的概念;(2) 结合函数x y =;21x y =;2x y =;1-=x y ;3x y =的图像,了解它们的变化情况。
(3) 与指数函数、对数函数的性质比较,概括y x α=在第一象限的简单性质。
其中(1)和(2)在新课标中已经明确指出,(3)作为培养学生概括能力目标,课本的复习与小结中也有涉及。
前面已经学习了指数函数、对数函数,得到了教系统的函数知识和研究函数的方法, 通过本节的幂函数学习,使函数内容的学习再一次得到广泛的回顾和整理,可以进一步深化学生对函数概念的理解与认识。
在各种数学思想方法的领悟、应用上也得到一次提高。
学情分析:本班的学生为普通校的平行班的学生,学生的数学基础,理解能力,运算能力、思维能力一般,但是通过前面的指数函数,对数函数的学习来看,学生通过数形结合来学习,学生还是有强烈的求知欲望,所以除了课标的要求外,还是酌情补充了概括y x α=在第一象限的简单性质。
学法指导1、针对以上情况,在教学中,我注意面向全体,发挥学生的主体性,引导学生积极地观察问题,分析问题,激发学生的求知欲和学习积极性,指导学生积极思维,主动获取知识,养成良好的学习方法,并逐步学会独立提出问题,解决问题。
人教版高中必修1幂函数教案

人教版高中必修1幂函数教案《人教版高中必修1幂函数教案》这是优秀的教学设计文章,希望可以对您的学习工作中带来帮助!§2.3幂函数一.教学目标:1.知识技能(1)理解幂函数的概念;(2)通过具体实例了解幂函数的图象和性质,并能进行初步的应用.2.过程与方法类比研究一般函数,指数函数、对数函数的过程与方法,研究幂函数的图象和性质.3.情感、态度、价值观(1)进一步渗透数形结合与类比的思想方法;(2)体会幂函数的变化规律及蕴含其中的对称性.二.重点、难点重点:从五个具体的幂函数中认识的概念和性质难点:从幂函数的图象中概括其性质三.学法与教具(1)学法:通过类比、思考、交流、讨论,理解幂函数的定义和性质 ;(2)教学用具:多媒体四.教学过程:1导入新课1.如果张红购买了每千克1元的水果w千克,那么她需要付的钱数p(元)和购买的水果量w(千克)之间有何关系?根据函数的定义可知,这里p是w的函数.2.如果正方形的边长为a,那么正方形的面积S=a2,这里S是a的函数.3.如果正方体的边长为a,那么正方体的体积V=a3,这里V是a的函数.4.如果正方形场地面积为S,那么正方形的边长a=S,这里a是S的函数.5.如果某人t s内骑车行进了1 km,那么他骑车的速度v=t-1km/s,这里v是t的函数.以上是我们生活中经常遇到的几个数学模型,你能发现以上几个函数解析式有什么共同点吗?(右边指数式,且底数都是变量).(适当引导:从自变量所处的位置这个角度)(引入新课,书写课题:幂函数).2新知探究提出问题:问题①:给出下列函数:y=x,y=x,y=x2,y=x-1,y=x3,考察这些解析式的特点,总结出来,是否为指数函数?问题②:根据①,如果让我们起一个名字的话,你将会给他们起个什么名字呢?请给出一个一般性的结论.讨论结果:①通过观察发现这些函数的变量在底数位置,解析式右边都是幂,因为它们的变量都在底数位置上,不符合指数函数的定义,所以都不是指数函数.②由于函数的指数是一个常数,底数是变量,类似于我们学过的幂的形式,因此我们称这种类型的函数为幂函数,如果我们用字母α来表示函数的指数,就能得到一般的式子,即幂函数的定义:一般地,形如y=xα(x∈R)的函数称为幂函数,其中x是自变量,α是常数.如y=x2,y=x,y=x3等都是幂函数,幂函数与指数函数、对数函数一样,都是基本初等函数.练1判断下列函数哪些是幂函数.(1)y=0.2x;(2)y=x-3;(3)y=x-2;(4)y=x;(5)y=2x2 ;(6)y=-x-1活动:学生独立思考,讨论回答,教师巡视引导,及时评价学生的回答.根据幂函数的定义判别,形如y=xα(x∈R)的函数称为幂函数,变量x的系数为1,指数α是一个常数,严格按这个标准来判断.解:(1)y=0.2x的底数是0.2,因此不是幂函数;(2)y=x-3的底数是变量,指数是常数,因此是幂函数;(3)y=x-2的底数是变量,指数是常数,因此是幂函数;(4)y=x的底数是变量,指数是常数,因此是幂函数.(5)的变量x2的系数为2,因此不是幂函数;(6)的变量x3的系数为-1,因此不是幂函数点评:判断函数是否是幂函数要严格按定义来判断.提出问题:问题③:我们前面学习指对数函数的性质时,用了什么样的思路?研究幂函数的性质呢?问题④:画出y=x,y=x,y=x2,y=x-1,y=x3五个函数图象,完成下列表格.讨论结果:③我们研究指对数函数时,根据图象研究函数的性质,由具体到一般;一般要考虑函数的定义域、值域、单调性、奇偶性;有时也通过画函数图象,从图象的变化情况来看函数的定义域、值域、单调性、奇偶性等性质,研究幂函数的性质也应如此.④学生用描点法,也可应用函数的性质,如奇偶性、定义域等,画出函数图象.利用描点法,在同一坐标系中画出函数y=x,y=x,y=x2,y=x3,y=x-1的图象.列表:图1让学生通过观察图象,分组讨论,探究幂函数的性质和图象的变化规律,教师注意引导学生用类比研究指数函数、对数函数的方法研究幂函数的性质.通过观察图象,完成表格.提出问题:问题⑤:通过对以上五个函数图象的观察,哪个象限一定有幂函数的图象?哪个象限一定没有幂函数的图象?哪个象限可能有幂函数的图象,这时可以通过什么途径来判断?问题⑥:通过对以上五个函数图象的观察和填表,你能类比出一般的幂函数的性质吗?讨论结果:⑤第一象限一定有幂函数的图象;第四象限一定没有幂函数的图象;而第二、三象限可能有,也可能没有图象,这时可以通过幂函数和定义域和奇偶性来判断.⑥幂函数y=xα的性质:(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1)(原因:1x=1);(2)当α>0时,幂函数的图象都通过原点,并且在[0,+∞)上是增函数(从左往右看,函数图象逐渐上升).特别地,当α>1时,x∈(0,1),y=x2的图象都在y=x图象的下方,形状向下凸,α越大,下凸的程度越大.当0<α<1时,x∈(0,1),y=x2的图象都在y=x的图象上方,形状向上凸,α越小,上凸的程度越大.(3)当α<0时,幂函数的图象在区间(0,+∞)上是减函数.在第一象限内,当x向原点靠近时,图象在y轴的右方无限逼近y轴正半轴,当x慢慢地变大时,图象在x轴上方并无限逼近x轴的正半轴.活动:考虑到学生已经学习了指数函数与对数函数,对函数的学习、研究有了一定的经验和基本方法,所以教学流程又分两条线,一条以内容为明线,另一条以研究函数的基本内容和方法为暗线,教学过程中同时展开,学生相互讨论,必要时,教师将解析式写成指数幂形式,以启发学生归纳,学生作图,教师巡视,学生小组讨论,得到结论,必要时,教师利用几何画板演示.3典例精析例1比较下列各组数的大小:(1)1.10.1,1.20.1;(2)0.24-0.2,0.25-0.2;(3)0.20.3,0.30.3,0.30.2.活动:学生先思考或回忆,然后讨论交流,教师适时提示点拨.比较数的大小,常借助于函数的单调性.对(1)(2)可直接利用幂函数的单调性.对(3)只利用幂函数的单调性是不够的,还要利用指数函数的单调性,事实上,这里0.30.3可作为中间量.解:(1)由于要比较的数的指数相同,所以利用幂函数的单调性,考察函数y=x0.1的单调性,在第一象限内函数单调递增,又因为1.1<1.2,所以1.10.1<1.20.1.(2)由于要比较的数的指数相同,所以利用幂函数的单调性,考察函数y=x-0.2的单调性,在第一象限内函数单调递减,又因为0.24<0.25,所以0.24-0.2>0.25-0.2.(3)首先比较指数相同的两个数的大小,考察函数y=x0.3的单调性,在第一象限内函数单调递增,又因为0.2<0.3,所以0.20.3<0.30.3.再比较同底数的两个数的大小,考察函数y=0.3x的单调性,它在定义域内函数单调递减,又因为0.2<0.3,所以0.30.3<0.30.2.所以0.20.3<0.30.3<0.30.2.另外,本题还有图象法,计算结果等方法,留作同学们自己完成.点评:指数相同的幂的大小比较可以利用幂函数的单调性;底数相同的幂的大小比较可以利用指数函数的单调性例2.证明幂函数f(x)=在[0,+∞)上是增函数.活动:学生先思考或讨论,再回答,教师根据实际,可以提示引导.证明函数的单调性一般用定义法,有时利用复合函数的单调性.证明:任取x1,x2∈[0,+∞),且x1f(x1)-f(x2)===,因为x1-x2<0,x1+x2>0,所以<0.所以f(x1)点评:证明函数的单调性要严格按步骤和格式书写,利用作商的方法比较大小,f(x1)与f(x2)的符号要一致.4知能训练1.下列函数中,既是幂函数又是奇函数的是( )A.y=2xB.y=2x3C.y=D.y=2x2.下列结论正确的是( )A.幂函数的图象一定过原点B.当α<0时,幂函数y=xα是减函数C.当α>0时,幂函数y=xα是增函数D.函数y=x2既是偶函数,也是幂函数3.下列函数中,在(-∞,0)是增函数的是( )A.y=x3B.y=x2C.y=D.y=x4.已知某幂函数的图象经过点(2,),则这个函数的解析式为. 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2.3 幂函数
教学目标:
知识与技能通过具体实例了解幂函数的图象和性质,并能进行简单的应用.
过程与方法能够类比研究一般函数、指数函数、对数函数的过程与方法,来研究幂函数的图象和性质.
情感、态度、价值观体会幂函数的变化规律及蕴含其中的对称性.
教学重点:
重点从五个具体幂函数中认识幂函数的一些性质.
难点画五个具体幂函数的图象并由图象概括其性质,体会图象的变化规律.
教学程序与环节设计:
创设情境问题引入.
组织探究幂函数的图象和性质.
尝试练习幂函数性质的初步应用.
巩固反思复述幂函数的图象规律及性质.
作业回馈幂函数性质的初步应用.
课外活动利用图形计算器或计算机探索一
般幂函数的图象规律.
教学过程与操作设计:
环节教学内容设计
阅读教材P90的具体实例(1)~( 5),思考下列问题:
1.它们的对应法则分别是什么?
创
2.以上问题中的函数有什么共同特征?
设
(答案)
师生双边互动生:独立思考完成引例.
师:引导学生分析归纳概括得出结论.
师生:共同辨析这种新
情
1.( 1)乘以 1;( 2)求平方;( 3)求立方;( 4)函数与指数函数的异
境开方;( 5)取倒数(或求- 1 次方).同.
2.上述问题中涉及到的函数,都是形如y x
的函数,其中x 是自变量,是常数.
材料一:幂函数定义及其图象.师:说明:
一般地,形如幂函数的定义来
y x (a R)自于实践,它同指数函的函数称为幂函数,其中为常数.数、对数函数一样,也
是基本初等函数,同样下面我们举例学习这类函数的一些性质.
也是一种“形式定义”
作出下列函数的图象:
的函数,引导学生注意
1
组
( 1)y x;( 2)y x2;( 3)y x2;辨析.
( 4)y x 1;(5) y x3.生:利用所学知识和方
织[解 ] ○1列表(略)法尝试作出五个具体
幂函数的图象,观察所
○图象
2图象,体会幂函数的变探化规律.
究师:引导学生应用画函
数的性质画图象,如:
定义域、奇偶性.
师生共同分析,强调画
图象易犯的错误.
环节教学内容设计师生双边互动
材料二:幂函数性质归纳.
( 1)所有的幂函数在(
0 , +∞)都有定义,
并且图象都过点( 1, 1);
( 2 ) 0 时,幂函数的图象通过原点,并 1
且在区间 [0,
) 上是增函数. 特别地, 当
时,
幂函数的图象下凸; 当 0
1
时,幂函数的图象
上凸;
( 3)
0时,幂函数的图象在区间 (0, ) 上
是减函数. 在第一象限内, 当 x 从右边趋向原点时,
图象在 y 轴右方无限地逼近 y 轴正半轴,当 x 趋于
时,图象在 x 轴上方无限地逼近 x 轴正半轴.
材料三:观察与思考
组
观察图象,总结填写下表:
师:引导学生观察图
象,归纳概括幂函数的的性质及图象变化规律.
生:观察图象, 分组讨论,探究幂函数的性质和图象的变化规律, 并展示各自的结论进行交流评析,并填表.
2
1
y x
y x
3
y x 1
y x
y x 2
织
定义域
值域
探
奇偶性
单调性
定点
究
材料五:例题
[例 1]
(教材 P 92 例题) [例 2]
比较下列两个代数值的大小: ( 1) (a
1)1. 5 , a 1.5
2
2
(2) (2
a 2 ) 3 , 2
3
2
[例 3] 讨论函数 y
x 3 的定义域、 奇偶性, 作 出它的图象,并根据图象说明函数的单调性.
环节 呈现教学材料
师:引导学生回顾讨论函数性质的方法, 规范解题格式与步骤.
并指出函数单调性是判别大小的重要工具,幂函数的图象可以在单调性、 奇偶性基础上较快描出.
生:独立思考, 给出解答,共同讨论、评析.
师生互动设计
1.利用幂函数的性质,比较下列各题中两个幂的值的大小:
3
3
( 1) 2.3 4 , 2.44 ;
6
6
( 2) 0.315 , 0.355 ;
3
3
尝 (3)( 2) 2,( 3) 2;
试 1
1
练 (4)1.1 2, 0.9 2.
习
3
2.作出函数 y
x 2
的图象,根据图象讨论这 个函数有哪些性质,并给出证明.
3.作出函数 y
x 2 和函数 y (x
3) 2的图
象,求这两个函数的定义域和单调区间.
4.用图象法解方程:
( 1) x x
1;
( 2) x 3 x 2
3.
1.如图所示,曲线是幂
函数 y
x 在第一象限内的
图象,已知
分别取
1,1, 1
,2 四个值,则相应图
2
探
象依次为: .
究
与
发
2.在同一坐标系内,作出下列函数的图象,
现
你能发现什么规律?
1
( 1) y
x 3 和 y
x 3 ;
5
4
( 2) y
x 4 和 y x 5
.
1.在函数 y
1 , y 2x
2 , y x 2 x, y 1 作业 中,幂函数的个数为: x 2
回馈
A . 0
B . 1
C . 2
D . 3
规律 1:在第一象限,
作直线 x
a(a 1) ,
它同各幂函数图象相交,按交点从下到上的
顺序,幂指数按从小到大的顺序排列.
规律 2:幂指数互为倒数的幂函数在第一象限内的图象关于直线
y x 对称.
环节 呈现教学材料 师生互动设计
2y f (x)
的图象过点 (2, 2 ) ,.已知幂函数
试求出这个函数的解析式.
3.在固定压力差(压力差为常数)下,当气
体通过圆形管道时,其流量速率R 与管道半径r 的四次方成正比.
(1)写出函数解析式;
(2)若气体在半径为 3cm 的管道中,流量速
率为 400cm 3
r 的管道时,/s,求该气体通过半径为
其流量速率R 的表达式;
( 3 )已知( 2 )中的气体通过的管道半径为5cm,计算该气体的流量速率.
4. 1992 年底世界人口达到54. 8 亿,若人口的平均增长率为x% , 2008 年底世界人口数为y
(亿),写出:
(1)1993 年底、 1994 年底、 2000 年底的世界人口数;
( 2) 2008 年底的世界人口数y 与 x 的函数解析式.
课
外利用图形计算器探索一般幂函数y x 的图活
象随的变化规律.
动
收
1.谈谈五个基本幂函数的定义域与对应幂函
获数的奇偶性、单调性之间的关系?
与
体2.幂函数与指数函数的不同点主要表现在哪
会些方面?。
