转动角度角速度角加速度与基点的位置无关
刚体角速度及角加速度与基点选取无关的证明

刚体角速度及角加速度与基点选取无关的证明赵利新冯继昌安阳师范学院摘要:刚体的角速度及角加速度与所选基点无关,这是一个熟知的事实。
但是大部分教材却没有给出其证明过程,或者只是提了提,这里给出较为严格的证明。
而这个证明结论,有利于刚体的运动分析和进一步学习,那么证明这个结论,首先通过分析平面运动的分解。
引出其角速度及角加速度与基点无关,然后,再通过画图验证和严密的数学推理推导其正确性。
关键词:基点角速度角加速度平面运动位置矢量引言:刚体在做平面运动时,其角速度,角加速度是解决刚体一些问题的关键性知识点,而它们与基点选取无关的证明,讲的详细的也很少。
而我们通过学习有关刚体的知识,以及翻阅资料,逐步对这个问题有更深刻的体会。
想更严格的证明一下,证明过程首先以刚体平面运动的特点进行分析讨论,从而引出角速度与角加速度与基点无关的证明。
一分析刚体平面运动的特点,引出其结论我们用复合运动的方法,对平面运动的刚体进行研究,即把比较复杂的平面运动看成两个简单运动-平面中运动,如图(a),t瞬时的合成。
讨论刚体平面运动的一般情况,选取一特殊平面图形S在o xy+ 时刻,位于2位置。
其中S上A,B两点的绝对轨迹如图(a)所示时S处于1位置,而在t tx Ay,此平动系并不一定固结于某一实体(例如车架),是为我们以A为原点,建立一平动坐标系''造成一个可以利用的约束条件,人为设置的抽象平动系,该平动系的原点A称为基点。
分析从位置1到位置2的运动过程。
可以得到以下结论:(1)刚体平面运动可以分解为跟随任意选择的基点建立的平动系的平动(牵连运动),和相对此平动系的转动(相对运动)。
从图中可以看到。
AB 从1到达2的A B ''可以选跟随 x Ay ''平动至A B ''' ()AB A B ''' ,然后在相对于A '转过090ϕ= 而得到(2)将平面运动分解为平动和转动时,若基点选择不同,则平动规律随基点的选取而不同,转动规律却与基点的选取无关。
理论力学判断题

1。
作曲线运动的动点在某瞬时的法向加速度为零,则运动其轨迹在该点的曲率必为零.(× )2。
刚体作定点运动时,其瞬时转动轴上所有点相对固定系的速度都为零,所以在运动过程中瞬时转动轴相对固定系始终静止不动。
( × )3. 刚体作平面运动时,平面图形内两点的速度在任意轴上的投影相等.(× )平面运动不是平动!!!!4。
在复合运动问题中,点的相对加速度是其相对速度对时间的相对导数。
( √ )5。
在刚体复合运动中,角速度合成公式为:( × )记住这个肯定是错的6. 刚体的角速度是刚体相对参考系的转角对时间的导数。
( × )7。
在复合运动问题中,定参考系可以是相对地面运动的,而动参考系可以是相对地面静止不动的。
( √ )8。
速度投影定理只适用于作平面运动的刚体,不适用于作一般运动的刚体。
(× )可以9. 刚体作平动时,刚体上各点的轨迹均为直线。
( × )刚体视作整体10。
圆轮沿直线轨道作纯滚动,只要轮心作匀速运动,则轮缘上任意一点的加速度的方向均指向轮心。
(√ )圆心是加速度瞬心11。
理想约束的约束反力不做功。
(× )不做虚功12。
真实位移是虚位移之一.(× )可能不位移13 如果所作的受力图是一个显然不平衡的力系,那么受力图一定有错。
(× )14 跨过滑轮的柔绳两端的拉力一定相等。
(× )拉力不是张力15.如果作一般运动的刚体的角速度不为零,在刚体或其延拓部分上一定存在速度等于零的点。
(× )角速度和速度同直线即角速度的线速度与平动速度方向垂直第五题思路:将杆分成小微元,写出每个微元的加速度和重力,代入达朗贝尔-拉各朗日原理(将求和号改为积分号1 刚体作平面运动时,如果刚体的瞬时角速度和角加速度都不等于零,则刚体的瞬时加速度中心一定存在。
( √ )2 刚体作定点运动时,若其角速度向量相对刚体不动,则相对固定参考系也不动;反之亦然.( √ )3.速度投影定理给出的刚体上两点速度间的关系只适用于作平面运动的刚体。
理论力学复习题
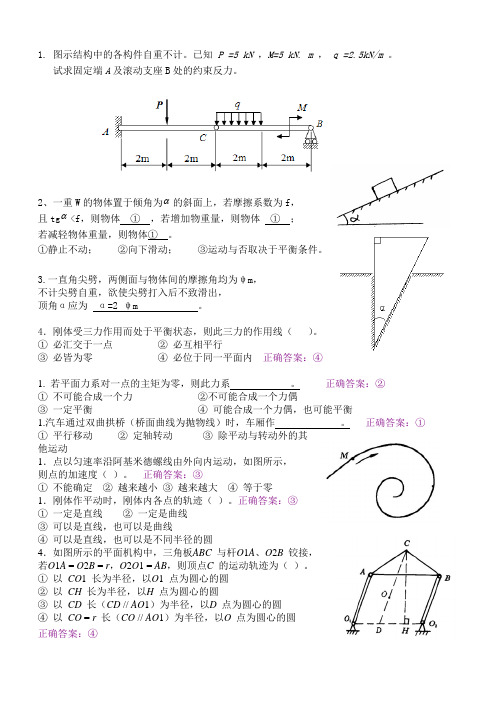
1.图示结构中的各构件自重不计。
已知P =5 kN ,M=5 kN. m,q =2.5kN/m 。
试求固定端A及滚动支座B处的约束反力。
2、一重W的物体置于倾角为α的斜面上,若摩擦系数为f,且tgα<f,则物体①,若增加物重量,则物体①;若减轻物体重量,则物体①。
①静止不动;②向下滑动;③运动与否取决于平衡条件。
3.一直角尖劈,两侧面与物体间的摩擦角均为ψm,不计尖劈自重,欲使尖劈打入后不致滑出,顶角α应为α=2 ψm 。
4.刚体受三力作用而处于平衡状态,则此三力的作用线()。
①必汇交于一点②必互相平行③必皆为零④必位于同一平面内正确答案:④1. 若平面力系对一点的主矩为零,则此力系。
正确答案:②①不可能合成一个力②不可能合成一个力偶③一定平衡④可能合成一个力偶,也可能平衡1.汽车通过双曲拱桥(桥面曲线为抛物线)时,车厢作。
正确答案:①①平行移动②定轴转动③除平动与转动外的其他运动1.点以匀速率沿阿基米德螺线由外向内运动,如图所示,则点的加速度()。
正确答案:③①不能确定②越来越小③越来越大④等于零1.刚体作平动时,刚体内各点的轨迹()。
正确答案:③①一定是直线②一定是曲线③可以是直线,也可以是曲线④可以是直线,也可以是不同半径的圆4.如图所示的平面机构中,三角板ABC 与杆O1A、O2B 铰接,若O1A = O2B = r,O2O1 = AB,则顶点C 的运动轨迹为()。
①以CO1 长为半径,以O1 点为圆心的圆②以CH 长为半径,以H 点为圆心的圆③以CD 长(CD // AO1)为半径,以D 点为圆心的圆④以CO = r 长(CO // AO1)为半径,以O 点为圆心的圆正确答案:④1.直角曲杆OBC 可绕O 轴转动,如图所示。
已知:OB=10cm 。
图示位置ϕ=60°,曲杆的角速度ω=0.2rad/s,角加速度α= 0.2rad/s2,则曲杆上M 点的法向加速度的大小为(),方向为();切向加速度的大小为(),方向为()。
刚体平面运动习题

第8章 刚体平面运动习题1.是非题(对画√,错画×)8-1.刚体平面运动为其上任意一点与某一固定平面的距离始终平行的运动。
( ) 8-2.平面图形的运动可以看成是随着基点的平移和绕基点的转动的合成.( ) 8-3.平面图形上任意两点的速度在某固定轴上投影相等。
( ) 8-4.平面图形随着基点平移的速度和加速度与基点的选择有关。
( ) 8-5.平面图形绕基点转动的角速度和角加速度与基点的选择有关。
( ) 8-6.速度瞬心点处的速度为零,加速度也为零。
( ) 8-7.刚体的平移也是平面运动。
( ) 2.填空题(把正确的答案写在横线上)8-8.在平直轨道作纯滚动的圆轮,与地面接触点的速度为 。
8-9.平面图形上任意两点的速度在 上投影相等。
8-10.某瞬时刚体作平移,其角速度为 ;刚体上各点速度 ;各点加速度 。
3.简答题8-11.确定图示平面运动物体的速度瞬心位置。
题8-11图(a) (b)(c)8-12.若刚体作平面运动,下面平面图形上A 、B 的速度方向正确吗? 题8-12图(a) (b) (c)8-13.下面图形中O 1A 和AC 的速度分布对吗?8-14.圆轮做曲线滚动,某瞬时轮心的速度o v 和加速度o a ,轮的半径为R ,则轮心的角加速度等于多少?速度瞬心点处的加速度大小和方向如何确定?题8-13图B8-15.用基点法求平面图形个点的加速度时,为什么没有科氏加速度? 4.计算题8-16.椭圆规尺AB 由曲柄OC 带动,曲柄以匀角速度o ω绕O 轴转动,如图所示,若取C 为基点,OC=BC=AC=r ,试求椭圆规尺AB 的平面运动方程。
8-17.半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动,如图所示。
曲柄以匀角加速度α绕O轴转动,设初始时角速度0=ω、角加速度0=α、转角0=ϕ,若选动齿轮的轮心C 点为基点,试求动齿轮的平面运动方程。
题8-16图题8-17图8-18.曲柄连杆机构,已知OA =40cm ,连杆AB =1m ,曲柄OA 绕O 轴以转速180=n r/min 匀速转动,如图所示。
理论力学试题
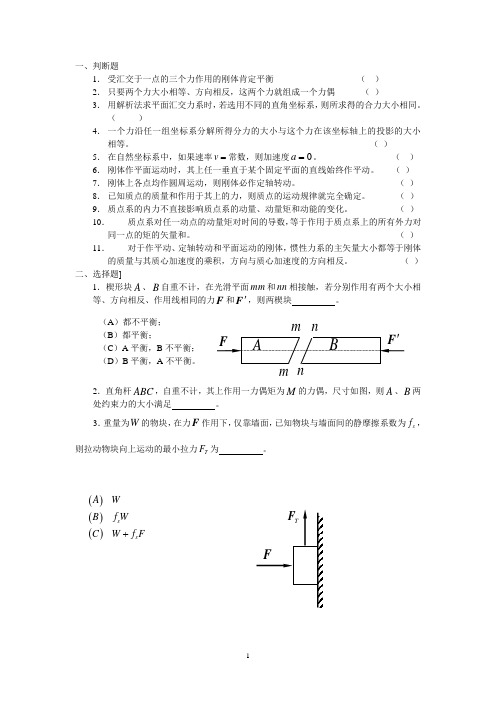
在图6所示平行四边形机构中,O1A=O2B=O1O2/2=AB/2=l,已知O1A以匀角速度转动,并通过AB上套筒C带动CD杆在铅直槽内平动,如以O1A杆为参考系,在图示位置时O1A,O2B为铅直,AB为水平,CAB之中点,试分析此瞬时套筒上销钉C的运动。(每4分)
17.C点的牵连速度的大小为()
计算题在图示机构中,杆 以速度 向作匀速运动。求当 时, 杆的角速度。
计算题(20分)已知:平面机构如图,轮 沿水平面纯滚动,滑块 上铰接两直杆 、 , 穿过作定轴转动的套筒 , ,图示瞬时, 。求:图示瞬时时, 、 杆的角速度 ;点 的加速度 ; 杆的角加速度
四.计算题(15分)。平面机构如图所示,已知 , , 。在图示位置时, 水平, 铅直, 。杆 的角速度为 ,角加速度为 ,求此时滑块 的加速度 和摇杆 的角速度和角加速度。
计算题(16分)。均质圆轮 、 重量均为 ,半径为 。轮 在一矩为 的常力偶的作用下逆时针旋转,使系统由静止开始运动。设绳子不可伸长,绳子与轮之间无相对滑动,且不计质量和轴承摩擦。试求: 轮心 位移为 时的速度和加速度; 两轮间绳子的张力
解(1)运动关系
轮 作定轴转动,轮 作平面运动且其速度瞬心在 ,所以
6.圆轮绕固定轴 转动,某瞬时轮缘上一点的速度 和 如图所示,则。
7.平面四杆机构如图。已知 ,在图示位置时, 杆水平, 杆铅直。且 ,则该位置 杆与 杆的角速度 与 的关系式。
8.曲柄连杆机构中的曲柄 ,连杆 和滑块 的质量均为 ,且曲柄与连杆的长度均为 ,由已知 等于常数,当机构运动到图示位置时,系统的动能为。
解杆平面运动,运动分析如图12-25(a),在断开瞬时
根据平面运动的加速度基点法,有
转动角度角速度角加速度与基点的位置无关46页PPT

END
•
29、在一切能够接受法律支配的人类 的状态 中,哪 里没有 法律, 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律,也可以废除 法律。 ——塞·约翰逊
置无关
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
转动角度角速度角加速度与基点的位
•
26、我们像鹰一样,生来就是自由的 ,但是 为了生 存,我 们不得 不为自 己编织 一个笼 子,然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理,即 克
•
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
刚体转动的角速度ω与基点的选取无关

(O ,Oz) : 与欧拉角定义相同,但在此为固定值
(O ,Os) : 与欧拉角定义不同—— Os与ON不同,Os并非 O、Oxy的交线,而是与O 相交的圆锥母线。
: 与欧拉角定义不同;表示圆锥绕z轴转过的角度(在此意义
上与欧拉角相同)
, : 仍用来确定z轴的方位;, ,确定 刚体位置唯一确定
自由度:3 —— 刚体的自由度6-约束条件数3
4. 定点转动
刚体上三点到固定平面的距离不变
刚体上有一点固定不动; 自由度:3 —— 6-定点坐标数3
5. 一般运动
刚体运动不受任何约束,自由度为6 可看作平动和转动的合成: 基点平动+绕基点的转动
基点可任选 上述1~4均为一般运动的特例
(二)欧,除非基点A是定点,此时为定点转动。
(2) 对平面平行运动的情形,vA ω,满足这一条件,因此,
设有某点s速度为零,则:vs
ω : vA ω ωrs - rA ω 0
abc abc bca cab
ωrs - rA ω ωωrs - rA 0
vA ω 0
说明 :
vA ω 0
(1) 对作一般三维转动的刚体,通常 vA与 ω并不垂直,不满足
以后会看到,即使在固定参考系中 处理刚体动力学问题,许多力学量采 用活动坐标系表达更为方便。
为此,将角速度转变为在活动坐标系中的表示:
(五)刚体内任意点的速度和加速度
P点:刚体内的任意点 A点:刚体内的任意点,作为基点
大小不变
(5.7)
说明:
基点A的 绕基点A的 平动速度 转动速度
(1) 基点A可任选(在刚体上或与刚体固着),基点A不同,
理论力学试卷及答案-B
专业年级理论力学试题考试类型:闭卷试卷类型:B卷考试时量:120分钟一、判断题:(10分,每题1分,共10题)1、只要保持平面力偶的力偶矩大小和转向不变,可将力偶的力和力臂作相应的改变,而不影响其对刚体作用效应的大小。
()2、加减平衡力系原理既适用于刚体,也适用于弹性体。
()3、力偶可以与一个力等效,也可以用一个力来平衡。
()4、二力构件的约束反力必沿两约束点的连线方向。
()5、力系平衡的充要条件是:力系的主矢和对任意一点的主矩同时等于零。
()6、静不定问题中,作用在刚体上的未知力可以通过独立平衡方程全部求出。
()7、固定铰链支座约束既能限制构件的移动,也能限制构件的转动。
()8、同一平面图形上任意两点的速度在这两点连线上的投影相等。
()9、平面运动中,平移的速度和加速度与基点的选择无关,而平面图形绕基点转动的角速度和角加速度与基点的选择有关。
()10、轮系传动中两轮的角速度与其半径成正比。
()二、填空题:(15分,每空1分,共7题)1、作用在刚体上两个力平衡的充要条件是:两个力的大小,方向,作用在上。
2、在两个力作用下保持平衡的构件称为。
3、刚体作平移时,其上各点的轨迹形状,在每一瞬时,各点的速度和加速度。
4、刚体的简单运动包括和。
5、力对物体的作用效应取决于三个要素,力的、和。
6、动点在某瞬时的绝对速度等于它在该瞬时的与的矢量和。
7、平面力系向作用面内任一点简化,一般情形下,可以得到一个和。
三、选择题:(20分,每题2分,共10题)1、下列不是研究点的运动学的方法是()(A)基点法(B)矢量法(C)直角坐标法(D)自然法2、下列不属于理论力学研究内容的是()(A)静力学(B)运动学(C)动力学(D)材料力学3、刚体受处于同一平面内不平行的三力作用而保持平衡状态,则此三力的作用线( ) (A)汇交于一点(B)互相平行(C)都为零(D)其中两个力的作用线垂直4、如果两个力系满足下列哪个条件,则该两个力系为等效力系()(A)两个力系的主矢相等(B)两个力系的主矩相等(C)两个力系的主矢和主矩分别对应相等(D)两个力系作用在同一刚体上5、如图所示,点M沿螺线自内向外运动,它走过的弧长与时间的一次方成正比,则点的加速度越来越,点M越跑越。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24
2.如图已知v ,,R ,求v ,?
轮瞬心在Cv
Cv
A
o
v = Rcos
v
vO OCv v tan
25
3. 已知尺寸,、 r. 求vc?
C
A
r
A
vc
C
r
解:
AC
r ACv
vc AC CCv
Cv
26
4. 已知、 r,求v A?
可见 :
0时, Cv 存在且唯一。
0时, Cv 在远处。
20
b.速度瞬心法:
选速度瞬心Cv为基点,任一点M的速度大小为:
vM Cv M
且vM Cv M
结论:某瞬时,S上任一点速度等于该点随图形绕瞬心 转动时的速度。
注:
1. Cv可在S外,必在运动平面上。
2. C v位置连续变化,形成 定瞬心轨迹 动瞬心轨迹
aP a
n PC
2
a P aC a
2 2
n PC
v v aC r1 r1 r2
2
r1
ቤተ መጻሕፍቲ ባይዱ
C
v aC
n a PC
r2 v r1 r1 r2
P
r2
vp 0 ap 0
当轮加速滚动时,a p变化吗? 问:
答:否。
o
18
4.2.2 瞬心法
基点法的特殊形式之一。
vBA AB, vBA AB
vA
x
x
结论:S上任一点速度等于基点速度与该点绕基点圆周运 动速度的矢量和。
12
例:已知OA=l, OB=2l, AB角速度为,曲柄连杆机构在 图示位置时,求AB杆角速度及滑块B的速度。
13
解: 1. 首先分析A,B两点的速度方向 2. 选择A点为基点,列基点法 方程 vB vA vBA
解:
vo 2 rω ωo 2ω r r
r
A
vA
o
r
v A 2 rωo 4 rω
27
5. 已知ao、、 R,求 ?
o
R
vo
ao
解:
vo Rω
对t 求导 ao R
Cv
ao cos R
28
4.2.3 投影法
问:基点法公式 在任何方向的投影式成立, 在何方向获得最简形式? 速度投影法公式
AB 0 vB vA Rω
aA
R
30 o
B
vB
aB
aB a A aBA
aB cos30o a A cos60o
1 aB R ctg60 R 2 3
2 o
17
例:已知轮C纯滚(匀速), r1 , r2 , v 已知,求
aP ?
v 解: a C r1 r2
vC v A vCA
vCA r r
l
ve
C
vCA
r
vA
vr
r
2 2 vC vA vCA
15
2. 加速度基点法
由 aa ae a a
r
n r
有:a B a A a a BA
n BA
τ a BA AB
n 当 0时 a BA 0
10
4. 2 平面图形上各点的速度与 加速度
4.2.1 基点法
1. 速度基点法
y v BA
y
A
vA
B
已知S上v ,ω(A为基点),求S上任一点 A B的v ? O B
在基点A固连一平移的动系,选B为动点
vA
x
x
11
由va ve vr
y v BA
y
A
O
vA
B
v B v A v BA
vA
vBA
vB
3. 利用平行四边形法则求未知量
vBA
60
vA l
vB
3 vBA vA ctan 60 l 3 2 3 AB vBA / AB vB vA / sin 60 l 3 3
vA
14
思考 1. 已知 l, r, ,r ,求vc。
解:
vA l
问:基点可任选,选什么基点,公式最简? 答:选S上速度为零的点。 速度瞬心法: a.速度瞬心Cv—某瞬时S上速度为零的点。
19
如图已知S上v A , ,求 Cv ?
Cv
解: vCv vA vCv A 0 vCv A vA
vA
Cv 必在 vA 的垂线上。
ACv vA
A
vA
a BA
y
y
A
O
B
a
n BA
aA
n a BA =AB 2
aA
x
aB AB a A AB
x
n 当 0时 a BA 0 a BA BA .
有
aB AB aA AB
16
思考: 已知 R、、 30 求
o
A
vB 、 aB ?
R
30 o
B
A
vA
解:
A
x
若不变,则为平移运动; 若A不动,则为定轴转动
注:
1.基点可任选,常选运动已知点。
8
2. v A ,a A与基点选择有关, ,,与基点选择无关。
B A
B A
A
B
B
A
A B 求导 A B A B
9
转动角度、角速度、角加速度与基点的位置无关
第4章 刚体的平面运动
本章要点:研究刚体的运动方程以及刚体 上不同点的运动量(速度、加速度)之间 的关系;基点法、瞬心法,投影法
一、实例:
2
3
4
二、定义—刚体内任意点在运动过程中始终与某 固定平面保持等距。(轨迹为平面曲线)
三、任务: 1、运动方程;
2、两点间的运动关系。
四、方法:运动合成法——在平面运动刚体上 任选一基点,在基点固连一平动系,其他点 相对基点做圆周运动。
将 v B v A v BA
在 AB连线上投影
v BA AB
有
v B AB v A AB
vB cos v A cos
基点法投影式.
或
29
结 论: S 上任意两点的速度在这两点 连线上投影相等.
21
例如:
Cv
定
动
c.速度瞬心求法: • Cv在过某点且垂直于该点速度矢量的直线上 • 速度沿该垂直线线性分布,与到速度瞬心的距离成 正比
22
思考:
A
Cv有哪些具体求法?
vA
Cv
B
B
A
vA
vB
A
Cv
C v1
AB瞬时平移
B
23
下图速度分布对吗? 不对
1. 求AB的瞬心
A
o
A B
C
Cv
Cv
5
4. 1 刚体平面运动方程
确定运动的独立参数
一、运动的简化
刚体 图S 线段AB 平移+转动
6
平面运动分解为平移和转动
故刚体平面运动可以看成是平移和转动的合成。
7
二、运动方程
xA x t yA y t t
o
y
y
B
x
