整式培优拓展题含答案
整式的加减培优题

整式的加减培优题1、已知-3x+4x^2=5,求x的值。
2、若-4x^3+3y^2n=wx^5yn+3是同类项,则m=5,n=2.3、当1≤m<2时,化简(m^2-m-2)/(m-1)。
4、使(ax^2-2xy+y^2)-(-ax^2+bxy+2y^2)=6x^2-9xy+cy^2成立,那么a=-3,b=-2,c=3.5、已知623mn^2xy+xy的和是单项式,则代数式9m^2-5mn-17的值为-623xy。
6、若A是三次多项式,B是四次多项式,则A+B一定是不高于四次的多项式或单项式。
7、若a-3b=5,则2a-3b+3b-a-15的值是-2a-10.8、其中单项式有x^2y,多项式有x+3y,a,0.1x,2x-y,1-1/(2π3x)。
9、若代数式4x-2x^2+5的值是7,那么代数式2x-x+1的值等于-1.10、若多项式32(k^2-2x+k)-2x-6是关于x的二次多项式,则k=4.11、一个关于字母x,y的多项式,除常数项外,其余各项的次数都是4,这个多项式最多有5项。
12、如果22n-3(m+1)a+a是关于a的二次三项式,那么应满足的条件是n=2,m=1.13、当x=3时,多项式ax+bx+cx-5的值是7,那么当x=-3时,它的值是-23a+11b-5c-5.14、每千克m元的甲种糖a千克与每千克n元的乙种糖b千克混合制成什锦糖,那么每千克什锦糖应定价为(ma+nb)/(a+b)元。
15.合并同类项:1) 4x^2+3x+532) 9x^2-3+2x-2x^23) 2b4) -2x^2+7x-316、求整式3x-5x^2+2与2x+x-3的差为-5x^2+x+5.17、已知A=x-2xy,B=y+3xy,求2A-3B的值为-6xy-x-y。
18、化简求值:5abc-2a^2b+3abc-2(4ab-ab)=6abc-6ab,其中a,b,c满足a-1+b-2+c^2=22.1、如果关于x的代数式-2x+mx+nx-5x-1的值与x的取值无关,则m=7,n=-5.2、代数式(2x+ax-2y+6)的值与字母x的取值无关,求2a-5b的值。
《整式及其加减》单元测试培优题及答案

《整式及其加减》单元测试培优题及答案整式及其加减培优检测卷时间:100分钟满分:120分、选择题(每小题3分,共18分,每小题只有一个正确选项)1.下列各式:①s2X —②0 :③S=n;④x今:⑤t ;®X2.其中代数式有()A.3个B.4个C.5个D.6个2.单项式—2xy 3的系数与次数分别是()A. — 2,4B.2,3C. — 2,3D.2,43.下面计算正确的是()A.3x 2— x2 = 3B.3a2 + 2a3 = 5a53C.3 + x = 3xD. — 0.75ab +_ ba = 044.小明父亲拟用不锈钢制造一个上部是一个长方形、下部是一个正方形的窗户,相关数据(单位:米)如图所示,那么制造这个窗户所需不锈钢的总长是()A.(4a + 2b)米B.(5a + 2b)米C.(6a +2b)米D.(a 2+ab)米5.若 m — n = 1,则(m — n)2— 2m + 2n 的值是()A.3B.2C.1D.—16.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律, m 的值应是()A.110B.158C.168D.178二、填空题(本大题共6小题,每小题3分,共18分)7.钢笔每支a元,铅笔每支b元,买2支钢笔和3支铅笔共需___________ 元.18.当a = 1,b = — 2时,代数式2a +-b1 2 3的值是2 ---------------9.若— 7x m +2y 与— 3x 4y n是同类项,贝U m = ________ ,n = ________ .10.若关于a , b的多项式3(a2— 2ab — b2) — (a2+ mab + 2b2)中不含有ab 项,贝U m = _______ .11.一个三角形一条边长为a + b,另一条边比这条边长2a + b,第三条边比这条边短3a — b,则这个三角形的周长为 ____________ .a b — 5 3x2+ 512.规定)=ad — bc,若)=6,则—11x 2 + 6cd 2 x2— 3三、(本大题共5小题,每小题6分,共30分)13.用含字母的式子表示.2(1)甲数为x,乙数比甲数的3大2,则乙数为多少?4(2)2018年3月2日,大型记录电影《厉害了,我的国》登陆全国各大院线.某影院针对这一影片推出了特惠活动:票价每人30元,团体购票超过10人,票价可享受八折优惠,学校计划组织全体教师观看此影片•若观影人数为a(a > 10),则应付票价总额为多少元?14.计算:(1)2(m 2— n2 + 1) — 2(m 2 + n2) + mn ;(2)3a — 2b — [ — 4a + (c + 3b)].315.化简求值: + 3xy 2,其中 x = 3, y =3x 2y — 2xy 2— 2 xy —;x 2y+ xy16.我校甲、乙、丙三位同学给希望工程捐款,已知甲同学捐款x元,乙同学的捐款金额比甲同学捐款金额的 3倍少8元,丙同学的捐款金额是甲、乙两3同学捐款总金额的一,求甲、乙、丙三位同学的捐款总金额•417.老师在黑板上书写了一个正确的验算过程,随后用手掌捂住了一个二次三项式,形式如下:(1)求所捂的二次三项式;⑵若—x2 + 2x = 1,求所捂二次三项式的值.四、(本大题共3小题,每小题8分,共24分)18.有理数a , b , c在数轴上的位置如图所示.(1)c + b _______ 0 , a + c _______ 0 , b — a ______ 0(填“>”“v” 或”);(2)试化简:|b — a| + |a + c| — |c + b|.19.若代数式(4x 2-mx -3y +4)-(8nx 2-x+2y-3)的值与字母 x 的取值无关,求代数式(-m 2+2mn - n 2)-2(mn -3m 2)+3(2n 2-mn)的值.20.如图是小明家的住房结构平面图(单位:米),他打算把卧室以外的部分都铺上地砖 .(1)若铺地砖的价格为 80 元/ 平方米,那么购买地砖需要花多少钱(用代数式表示)?(2)已知房屋的高为 3 米,现需要在客厅和卧室的墙壁上贴壁纸,那么需要多少平方米的壁纸(计算时不扣除门、窗所占的面积)(用代数式表示)?五、(本大题共 2 小题,每小题 9 分,共 18 分)21.小明去文具用品商店给同学买 A 品牌的水笔,已知甲、乙两商店都有 A 品牌的水笔,且标价都是 1.5 元/ 支,但甲、乙两商店的优惠条件不同 .甲商店:若购买不超过 10 支,则按标价付款;若一次购买 10 支以上,则超过 10 支的部分按标价的 60% 付款 .乙商店:全部按标价的 80% 付款 .(1)设小明要购买的 A 品牌的水笔是 x(x 〉10)支,请用含 x 的式子分别表示在甲、乙两个商店购买 A 品牌的水笔所需的费用;(2)若小明要购买 A 品牌的水笔 30 支,你认为甲、乙两商店中,到哪个商店购买比较省钱?请说明理由22.阅读材料:“如果代数式 5a+3b 的值为- 4,那么代数式 2(a +b)+4(2a + b)的值是多少?”我们可以这样来解:原式= 2a + 2b + 8a + 4b = 10a + 6b.把式子5a + 3b = — 4两边同乘以2,得10a + 6b = — 8.仿照上面的解题方法,完成下面的问题:⑴已知a2 + a = 0,求a2 + a+ 2017的值;(2)已知 a— b = — 3,求 3(a — b) — a + b + 5 的值;(3)已知 a2 + 2ab = — 2 , ab — b2 = — 4,求 2a2 + 5ab — b2的值.六、 (本大题共 12 分)23.用三角形和六边形按如图所示的规律拼图案⑴ 第4个图案中,三角形有________ 个,六边形有_________ 个;(2)第n(n为正整数)个图案中,三角形与六边形各有多少个?(3)第2017个图案中,三角形与六边形各有多少个?(4)是否存在某个符合上述规律的图案,其中有100个三角形与30个六边形?如果有,指出是第几个图案;如果没有,说明理由.参考答案与解析1.B2.A3.D4.B5.D6.B 解析:根据排列规律可知10下面的数是12,10右面的数是14. v 8 =2 X 4 -0,22 = 4 X 6 2,44 = 6 X 8 4,二 m= 12 X 1410 = 158.故选 B.7.(2a + 3b)8.4 9.1 1 10. — 6 11.2a + 5b 12.7113.解:(1)乙数为—x + 2.(3分)3⑵应付票价总额为30a X 0.8 24a元.(6分)14.解:(1)原式=—4n2 + mn + 2.(3 分)(2)原式二 7a — 5b — c.(6 分)15.解:原式=3x2y — 2xy 2 + 2xy — 3x 2y — xy + 3xy 2 = xy 2 + xy.(3 分)当 x1 1 1 2二 3 , y =——时,原式二3—3 2 + 3 X——=—才.(6 分)316.解:由题意可知乙同学捐(3x — 8)元,丙同学捐—(x + 3x — 8)元,(3分)43则甲、乙、丙三位同学的捐款总金额为x + (3x — 8) +一(x + 3x — 8) = (7x — 14)(元).(6 分)17.解:⑴因为x2— 5x + 1 + 3x = x2 - 2x + 1,故所捂的二次三项式为 x2—2x + 1.(3 分)(2)若一x2 + 2x = 1,贝U x2— 2x + 1 =—(— x2 + 2x) + 1 =— 1 + 1 = 0.(6 分)18.解:⑴ v V > (3 分)(2)原式=b — a —(a +c) + (c + b) = b — a —a — c+ c + b = 2b — 2a.(8 分)19.解:(4x 2— mx — 3y + 4)—(8nx 2— x + 2y — 3) = 4x2— mx —3y + 4 —8nx 2+ x — 2y + 3 = (4 — 8n)x 2 + (1 — m)x — 5y + 7.(3 分)工上式的值与字母x 的1取值无关,•••8n— 0,1 — m = 0 ,••• n亍,m = 1.(5 分)二原式=—n2+ 2mn1—n2—2mn + 6m 2+ 6n2—3mn = 5m 2+ 5n 2—3mn = 5 XI2+ 5 x _ 2—21193 x 1 x=—.(8 分)2 420.解:(1)铺地砖的面积为2x • 4y + x •11xy(平方米).则购买地砖需要花 80 X 11xy =880xy(元).(4 分)⑵\[2(2x + 4y) + 2(2x + ] X 3 =(24x + 36y)(平方米).即需要(24x + 36y)平方米的壁纸.(8分)21.解:(1)在甲商店购买 A品牌的水笔所需的费用为 1.5 X 10佩—10)X 1.5 X 60%(0^x + 6)(元);(3分)在乙商店购买A品牌的水笔所需的费用为 1.5x X 80%4.2x(元).(6 分)⑵ 当x二30时,在甲商店购买需花费0.9 X 306二33(元),在乙商店购买需花费1.2 X 30 36(元).因为33〈 36,所以在甲商店购买比较省钱.(9分)22.解:(1)因为 a2 + a = 0,所以 a2+ a+ 2017 = 0 + 2017 =2017.(3 分)(2)因为 a — b = — 3,所以 3(a — b)— a + b + 5 = 3 X (——(— 3) + 5 =—1.(6 分)(3)因为 a2 + 2ab = — 2, ab — b2= — 4,所以 2a2 + 5ab — b2 = 2a2 +4ab + ab — b2 = 2 x ( 2) + (— 4) = — 8.(9 分)23.解: (1)10 4(2 分)(2)观察发现,第 1 个图案中有 4 个三角形与 1 个六边形,以后每个图案都比它前一个图案增加 2 个三角形与 1 个六边形,则第 n 个图案中三角形的个数为4 + 2(n — 1) = (2n + 2)个,六边形的个数为n个.(5分)(3)第2017个图案中,三角形的个数为 2 X 2017 42 = 4036(个),六边形的个数为 2017 个.(8 分)(4)不存在.(9 分)理由如下:假设存在这样的一个图案,其中有 30 个六边形,则这个图案是第30个图案,而第30个图案中三角形的个数为 2 X 30 42 = 62工100,所以这样的图案不存在.(12分)。
整式培优拓展题[含答案解析]
![整式培优拓展题[含答案解析]](https://img.taocdn.com/s3/m/41e9ec49c281e53a5902ff08.png)
第二章《整式》培优专题一、找规律题 (一)、代数式找规律1、观察下列单项式:54325,4,3,2,a a a a a --,…(1)观察规律,写出第2010和第2011个单项式; (2)请你写出第m 个单项式和第n+1个单项式。
(m 为自然数)答案:(1)-2010a 2010;2011a 2011(2)ma^m(m 为奇数),-ma^m(m 为偶数)2、有一个多项式为332456b a b a b a a -+-…,按这种规律写下去,第六项是= ab 5,最后一项是= b 6。
3、(1)观察一列数2,4,8,16,32,…发现从第二项开始,每一项与前一项之比是一个常数,这个常数是= 2 ,根据此规律,如果n a (n 为正整数)表示这个数列的第n 项,那么18a = 218,n a = 2n。
(2)如果欲求203233331+++++ 的值,可令203233331+++++= S ①,将①式两边同乘以3,得 3s=3+32+33+34+…+321,②由②减去①式,得S= (321-1)/2 ;(3)由上可知,若数列1a ,2a ,3a ,…n a ,n a ,从第二项开始每一项与前一项之比的常数为q ,则n a = a 1q n-1,(用含1a ,q ,n 的代数式表示),如果这个常数q ≠1,那么1a +2a +3a +…+n a = a 1(1-q n)/(1-q) (用含1a ,q ,n 的代数式表示)。
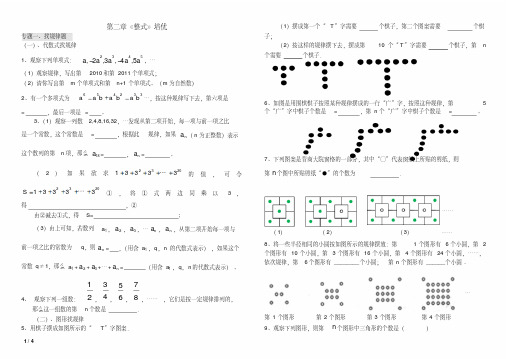
4、 观察下列一组数:21,43,65,87,…… ,它们是按一定规律排列的,那么这一组数的第n 个数是 (2n-1)/2n . (二)、图形找规律5、用棋子摆成如图所示的“T ”字图案.(1)摆成第一个“T ”字需要 5 个棋子,第二个图案需要 8 个棋子;(2)按这样的规律摆下去,摆成第10个“T ”字需要 32 个棋子,第n 个需要 (3n+2)个棋子.6、如图是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中棋子个数是= 15 ,第n 个“广”字中棋子个数是= 2n+5 。
整式培优拓展题[含答案解析]
![整式培优拓展题[含答案解析]](https://img.taocdn.com/s3/m/0a3c5ccf27284b73f24250c2.png)
第二章《整式》培优专题一、找规律题(一)、代数式找规律1、观察下列单项式:54325,4,3,2,aaaaa--,…(1)观察规律,写出第2010和第2011个单项式;(2)请你写出第m个单项式和第n+1个单项式。
(m为自然数)答案:(1)-2010a2010;2011a2011(2)ma^m(m为奇数),-ma^m(m为偶数)2、有一个多项式为332456bababaa-+-…,按这种规律写下去,第六项是= ab5,最后一项是= b6 。
3、(1)观察一列数2,4,8,16,32,…发现从第二项开始,每一项与前一项之比是一个常数,这个常数是= 2 ,根据此规律,如果na(n为正整数)表示这个数列的第n项,那么18a= 218,na= 2n。
(2)如果欲求203233331+++++ 的值,可令203233331+++++=S①,将①式两边同乘以3,得 3s=3+32+33+34+…+321,②由②减去①式,得S= (321-1)/2 ;(3)由上可知,若数列1a,2a,3a,…na,na,从第二项开始每一项与前一项之比的常数为q,则na= a1q n-1,(用含1a,q,n的代数式表示),如果这个常数q≠1,那么1a+2a+3a+…+na= a1(1-q n)/(1-q) (用含1a,q,n的代数式表示)。
4、观察下列一组数:21,43,65,87,……,它们是按一定规律排列的,那么这一组数的第n个数是(2n-1)/2n .(二)、图形找规律5、用棋子摆成如图所示的“T”字图案.(1)摆成第一个“T”字需要 5 个棋子,第二个图案需要 8 个棋子;(2)按这样的规律摆下去,摆成第10个“T”字需要 32 个棋子,第n个需要(3n+2)个棋子.6、如图是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中棋子个数是= 15 ,第n个“广”字中棋子个数是= 2n+5 。
7、下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n个图中所贴剪纸“●”的个数为 3n+2 .8、将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有___46______个小圆;第n个图形有_(_n2+n+4_)______个小圆.9、观察下列图形,则第n个图形中三角形的个数是( D )A. 22n+ B.44n+C.44n- D.4n10、观察如下图的点阵图和相应的等式,探究其中的规律:(1)在④和⑤后面的横线上分别写出相应的等式;(2)通过猜想写出与第n个点阵相对应的等式1+3+5+……+(2n-1)=n211、下图是某同学在沙滩上用石于摆成的小房子:观察图形的变化规律,写出第n个小房子用了[(n+1)2+(2n-1)] 块石子。
整式的加减(培优篇)

初一(上)数学整式的加减(培优篇)关卡一:单项式、多项式1.(1)单项式是关于的五次单项式,则 ;z yx n 123-z y x ,,,=n (2)关于的多项式是二次三项式,则 , ;x b x x x a b-+--3)4(=a =b (3)如果是关于的五次四项式,那么 。
52)2(4232+---+-x x q x xp x =+q p 2.如果关于的多项式与是次数相同的多项式,求的值x 21424-+x ax x x b53+4322123-+-b b b 3.已知是关于的三次三项式,求的值.5)1(3||2+--y m yx m y x ,1322+-m m 4.若多项式是关于的五次二项式,求的值()22532mx y n y +--x y ,222m mn n -+5.如果为四次三项式,则________。
()1233m xy m xy x ---+m =关卡二:同类项1.my x 22与是同类项,则=_____,=_____.y x n3-m n 2.单项式与是同类项,则的值为( ) 1-+-a b a b x y x 23b a -A .2 B . C .0 D .12-3.如果与的和是单项式,那么与取值为( )2522+-n m b a23-n ab m n A . B . C . D .3,2==n m 2,3==n m 2,3=-=n m 2,3-==n m 4.已知与是同类项,则的值是( )y xn 72001+y x m 322002+-2)2(n m -A .16 B .4×2001 C .-4×2002 D .5关卡三:去括号、添括号法则去括号法则: (1)括号前面是”+”号,去掉”+”号和括号,括号里的各项不变号;(2)括号前面是”-”号,去掉”-”号和括号,括号里的各项都变号.添括号法则: (1)添括号时,括号前添“+”号,括到括号里的各项都不变符号; (2)添括号时,括号前添“-”号,括到括号里的各项都改变符号。
第二章-整式的加减能力培优专题训练(含答案)

第二章 整式的加减能力培优专题一 用代数式表示实际问题1.10名学生的平均成绩是x ,如果另外5名学生每人得84分,那么整个组的平均成绩是( )2.某种商品进价为a 元/件,在销售旺季,商品售价较进价高30%;销售旺季过后,商品又以7折(即原售价的70%)的价格开展促销活动,这时一件该商品的售价为( ).A.a 元B.0.7 a 元C.1.03 a 元D.0.91a 元专题二 单项式的系数与次数3.代数式-23xy 3的系数与次数分别是( )A .-2,4B .-6,3C .-2,3D .-8,44.如果-33a m b 2是7次单项式,则m 的值是( )A .6B .5C .4D .2 5.写出含有字母x ,y 的四次单项式 .(答案不唯一,只要写出一个)6.判断下列各式是否是单项式,是单项式的写出系数和次数.3a , 12 xy 2,-5xy4 ,a π ,-x , 13 (a +1), 1x .专题三 考查多项式的项、项数与次数7.如果一个多项式的次数是6,则这个多项式的任何一项的次数都( )A.小于6B.等于6C.不大于6D.不小于68.若2210a a +-=,则2242013a a ++= .9.m 为何值时,2123(2)3m m x y xy -+-是五次二项式专题一 同类项及合并同类项1.如果单项式13a x y +与32b x y 的和是单项式,那么b a = .2. 把(x -3)2-2(x -3)-5(x -3)2+(x -3)中的(x -3)看成一个整体合并同类项,结果应是() A .-4(x -3)2-(x -3) B .4(x -3)2-x (x -3)C .4(x -3)2-(x -3)D .-4(x -3)2+(x -3)3.多项式2x 4-(a +1)x 3+(b -2)x 2-3x -1,不含x 3项和x 2项,求ab 的值.4.化简,求值:22211332424a b a b a -+--,其中13a =,3b =-.专题二 去括号法则的应用5.下列去括号中,正确的是 ( )A.a 2-(2a -1)=a 2-2a -1B.a 2+(-2a -3)=a 2-2a +3C.3a -[5b -(2c -1)]=3a -5b +2c -1D.-(a +b )+(c -d )=-a -b -c +d6.不改变代数式a -(b -3c )的值,把代数式括号前的“-”号变成“+”号,结果应是( )A.a +(b -3c )B.a +(-b -3c )C.a +(b +3c )D.a +(-b +3c )7. 先去括号,再合并同类项(1)(3x +1)-2(4-x ); (2)3(2a -3b )+5(a +b )-4(3a -2b );(3)6a 2-2ab -2(3a 2+12ab ); (4)2a -[3b -5a -(2a -7b )].专题三 多项式加减及其在生活中的应用9.已知A =2x 2-9x -11,B =3x 2-6x +4.求(1)A -B ;(2)21A +2B .10.若a 2+2b 2=5,求多项式(3a 2-2ab +b 2)-(a 2-2ab -3b 2)的值.8.下图为某学校校园的总体规划图(单位:m ),试计算这个学校的占地面积.小丽说:学校的占地面积可以用代数式表示为100a +200a +240b +60b.小明说:也可以表示为(100+200)a +(240+60)b.小虎说:还可以表示为(100+200)(a +b ).你认为他们说的对吗?如何用数学知识加以解释?专题三 多项式加减及其在生活中的应用9.已知A =2x 2-9x -11,B =3x 2-6x +4.求(1)A -B ;(2)21A +2B .10.若a 2+2b 2=5,求多项式(3a 2-2ab +b 2)-(a 2-2ab -3b 2)的值.11.小明同学在计算5x 2+3xy +2y 2加上某多项式A 时,由于粗心,误算成减去这个多项式,而得到2x 2-3xy +4y 2,求正确的运算结果.12.有这样一道题目:“当a =0.35,b =-0.28时,求多项式7a 3-3(2a 3b -a 2b -a 3)+(6a 3b -3a 2b )-(10a 3-3)的值”.小敏指出,题中给出的条件a =0.35,b =-0.28是多余的,她的说法有道理吗?为什么?1. B 解析:先求出这15个人的总成绩10x +5×84=10x +420,再除以15可求得平均值为1042015x . 2. D 解析 :因为商品每件a 元,按进价提高30%出售,则售价为(1+30%)a =1.3a 元,商品以7折销售时售价为1.3a ×70% =0.91a 元.3. D 解析:该单项式的因数是-23,即-8,所以该单项式的系数是-8.字母x 、y 的指数分别是1和3,指数和是4,所以该单项式的次数是4.4. B 解析:由题意得,所有字母的指数和为7,即m +2=7,则m =5.5.解析:根据四次单项式的定义,x 2y 2,x 3y ,xy 3等都符合题意(答案不唯一).6.解析:3a 表示3与a 相乘,是单项式,系数为3,次数为1;12 xy 2表示12 与xy 2相乘,是单项式,系数为12,次数为3; -5xy 4 表示-54 与xy 相乘,是单项式,系数为-54,次数为2; a π 表示1π 与a 相乘,是单项式,系数为1π,次数为1; -x 表示-1与x 相乘,是单项式,系数为-1,次数为1;13 (a +1)表示a 与1的和的31倍,含有加法运算,不是单项式. 1x表示1与x 的商,不是单项式. 7.C 解析:由于多项式的次数是“多项式中次数最高的项的次数”,因此六次多项式中,次数最高的项是六次的,其余项的次数可以是六次的,也可以是小于六次的,却不能是大于六次的.因此六次多项式中的任何一项都是不大于六次的.8.2015 解析:222420132(2)2013220132015a a a a ++=++=+=.9.解析:根据条件,有m 2-1+2=5,且m +2≠0.所以m =2.10. 4n -2 解析:第1个图案中阴影小三角形的个数是2;第2个图案中阴影小三角形的个数是6=2+4×1;第三个图案中阴影小三角形的个数是10=2+4×2;第4个图案中阴影小三角形的个数是14=2+4×3;…,所以第n 个图案中阴影小三角形的个数是2+4(n -1)=4n -2.11. n (n +1)+2或 n 2+n +2 解析:根据图形可知:第一个图形中阴影部分小正方形个数为4=2+2=1×2+2,第二个图形中阴影部分小正方形个数为8=6+2=2×3+2,第三个图形中阴影部分小正方形个数为14=12+2=3×4+2,…所以第n 个图形中阴影部分小正方形个数为n (n +1)+2或 n 2+n +2.12.(1)64 8 15 (2)2(1)1n -+ 2n 21n - 解析:(1)观察所给数阵可知,每行最右侧的数是该行序号的平方.每一行数字的个数是每行的序号乘以2减去1.所以第8行的最后一个数是自然数8的平方,即82=64,共有2×8-1=15个数;(2)第n -1行的最后一个数为2(1)n -,所以第n 行的第一个数是2(1)1n -+,最后一个数为2n ,第n 行共有2n -1个数.2.2整式的加减专题一 同类项及合并同类项1.如果单项式13a x y +与32b x y 的和是单项式,那么b a = .2. 把(x -3)2-2(x -3)-5(x -3)2+(x -3)中的(x -3)看成一个整体合并同类项,结果应是( )A .-4(x -3)2-(x -3)B .4(x -3)2-x (x -3)C .4(x -3)2-(x -3)D .-4(x -3)2+(x -3)3.多项式2x 4-(a +1)x 3+(b -2)x 2-3x -1,不含x 3项和x 2项,求ab 的值.4.化简,求值:22211332424a b a b a -+--,其中13a =,3b =-.专题二 去括号法则的应用5.下列去括号中,正确的是 ( )A.a 2-(2a -1)=a 2-2a -1B.a 2+(-2a -3)=a 2-2a +3C.3a -[5b -(2c -1)]=3a -5b +2c -1D.-(a +b )+(c -d )=-a -b -c +d6.不改变代数式a -(b -3c )的值,把代数式括号前的“-”号变成“+”号,结果应是( )A.a +(b -3c )B.a +(-b -3c )C.a +(b +3c )D.a +(-b +3c )7. 先去括号,再合并同类项(1)(3x +1)-2(4-x ); (2)3(2a -3b )+5(a +b )-4(3a -2b );(3)6a 2-2ab -2(3a 2+12ab ); (4)2a -[3b -5a -(2a -7b )].8.下图为某学校校园的总体规划图(单位:m ),试计算这个学校的占地面积.小丽说:学校的占地面积可以用代数式表示为100a +200a +240b +60b.小明说:也可以表示为(100+200)a +(240+60)b.小虎说:还可以表示为(100+200)(a +b ).你认为他们说的对吗?如何用数学知识加以解释?专题三 多项式加减及其在生活中的应用9.已知A =2x 2-9x -11,B =3x 2-6x +4.求(1)A -B ;(2)21A +2B .10.若a 2+2b 2=5,求多项式(3a 2-2ab +b 2)-(a 2-2ab -3b 2)的值.11.小明同学在计算5x 2+3xy +2y 2加上某多项式A 时,由于粗心,误算成减去这个多项式,而得到2x 2-3xy +4y 2,求正确的运算结果.12.有这样一道题目:“当a =0.35,b =-0.28时,求多项式7a 3-3(2a 3b -a 2b -a 3)+(6a 3b -3a 2b )-(10a 3-3)的值”.小敏指出,题中给出的条件a =0.35,b =-0.28是多余的,她的说法有道理吗?为什么?知识要点:1.同类项:所含的字母相同,并且相同字母的指数也相同的项叫做同类项.几个常数项也是同类项.2.合并同类项:把多项式中的同类项合并成一项,即把它们的系数相加作为新的系数,而字母部分不变,叫做合并同类项.3.合并同类项法法则:合并同类项后,所得项的系数是合并同类项前各同类项的系数的和,且字母连同它的指数不变.4.去括号法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.5.整式加减的运算法则:一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.温馨提示:1.同类项的注意事项:(1)“两相同”:一是所含字母相同;二是相同字母的指数也相同,二者缺一不可.(2)“两无关”:一是与系数大小无关;二是与所含字母的顺序无关.2.去括号法则注意事项:(1)括号外有系数时,将系数乘以括号内每一项,不能只给括号内第一项乘.(2)如果括号外的因数是负数,去括号后原括号内每一项的符号都与原来的符号相反,不要忘记给后面的各项改变符号.(3)注意多层括号的去法:对于含有多层括号的题目,应先观察式子的特点,再考虑去括号的顺序,以使运算简便.一般由内向外,先去小括号,再去中括号,最后去大括号;但有时也可以由外向内,先去大括号,再去中括号,最后去小括号.3.多项式加减:(1)两个多项式相减,需要将每个多项式先用括号括起来.(2)求多项式的值时,遇到分数、负数的平方或者立方时,需要用括号将这些数括起来.方法技巧:1.去大括号时,要将中括号看作一个整体,去中括号时,要将小括号看作一个整体.2.合并同类项的基本步骤:(1)标出同类项;(2)将同类项写在一起;(3)合并同类项.3.多项式的求值问题,一般需要先合并同类项,再代入字母的值计算.当出现分数的乘方、负数的乘方时要加小括号.若已知代数式中每个字母的值则采用直接代入法;若代数式中字母的值没有一个个给出时,常采用整体代入法求解.【008-2】答案:1. 8 解析:由题意知a +1=3, b =3,解得a =2, b =3,所以823==b a .2. A 解析:(x -3)2-2(x -3)-5(x -3)2+(x -3)=(1-5)(x -3)2+(-2+1)(x -3)=-4(x -3)2-(x -3).3.解析:因为多项式不含x 3项和x 2项,所以a +1=0,b -2=0解得a =-1,b =2.所以ab =-1×2=-1.4.解析:22211332424a b a b a -+--=21313(1)()2244a b +-+--=2a b -.当13a =,3b =-时,原式=21()(3)3--=139+=139. 5. C 6. D7.解析:(1)原式=3x +1-8+2x =5x -7; (2)原式=6a -9b +5a +5b -12a +8b =-a +4b ;(3)原式=6a 2-2ab -6a 2-ab = -3ab ; (4)原式=2a -(3b -5a -2a +7b )=2a -3b +5a +2a -7b =9a -10b.8.解析:他们说的都是对的,小丽说的是把整个学校的面积分成了教学区、操场、学生活动区、图书馆,把每个部分的面积表示出来后就可以得到100a +200a +240b +60b ;小明是把教学区和操场看成是一个长为(100+200),宽为a 的长方形,面积为(100+200)a ,学生活动区和图书馆看成是一个长为(240+60),宽为b 的长方形,面积为(240+60)b ,从而总面积为(100+200)a +(240+60)b ;小虎是把整个学校的面积看成是长为(100+200),宽为(a +b )的长方形,面积为(100+200)(a +b ).9.解析:(1)A -B =(2x 2-9x -11)-(3x 2-6x +4)=2x 2-9x -11-3x 2+6x -4=-x 2-3x -15;(2)21A +2B =21(2x 2-9x -11)+2(3x 2-6x +4)=x 2-92x -112+6x 2-12x +8=7x 2-233x +25. 10.原式=3a 2-2ab +b 2-a 2+2ab +3b 2=2a 2+4b 2=2(a 2+2b 2)=2×5=10.11.解析:(5x 2+3xy +2y 2)-A =2x 2-3xy +4y 2.A =(5x 2+3xy +2y 2)-(2x 2-3xy +4y 2)=5x 2+3xy +2y 2-2x 2+3xy -4y 2=3x 2+6xy -2y 2.所以(5x 2+3xy +2y 2)+(3x 2+6xy -2y 2)=8x 2+9xy .即正确的运算结果为8x 2+9xy .12.解析:她的说法有道理,因为原式=7a 3-6a 3b +3a 2b +3a 3+6a 3b -3a 2b -10a 3+3=3,所以原式的值与a ,b 无关.因此所给条件是多余的.。
整式培优拓展题(含部分答案)
=
,最后一项是 = 。
3、(1)观察一列数 2,4,8,16,32,…发现从第二项开始,每一项与前一项之比
是一个常数,这个常数是 =
,根据此 规律,如果 an ( n 为正整数)表示
这个数列的第 n 项,那么 a18 =
, an =
。
( 2 ) 如 果 欲 求 1 3 32 33
320 的 值 , 可 令
个需要
个棋子.
个棋子,第二个图案需要
个棋
10 个“ T ”字需要
个棋子,第 n
6、如图是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第
5
个“广”字中棋子个数是 =
,第 n 个“广”字中棋子个数是 =
。
7、下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则
第 n 个图中所贴剪纸“●”的个数为
专题一、找规律题 (一)、代数式找规律
第二章《整式》培优
1、观察下列单项式: a, 2a2,3a3, 4a4,5a5 ,…
( 1)观察规律,写出第 2010 和第 2011 个单项式; ( 2)请你写出第 m 个单项式和第 n+1 个单项式。(m 为自然数)
2、有一个多项式为 a 6 a 5b a 4b2 a 3b 3 …,按这种规律写下去,第六项是
。
15、已知代数式 x2 xy =2, y2 xy =5,则 2x2 5xy 3y 2 的值是多少 ?
16、当 x=2010 时, ax3 bx 1 2010 ,那么 x= - 2010 时, ax3 bx 1 的值
是多少? ……
…… 专题三:绝对值问题
17、 a,b,c 在数轴上的位置如图所示 ,
化
九年级数学下册2023年中考专题培优训练:整式与因式分解【含答案】

九年级数学下册2023年中考专题培优训练:整式与因式分解一、单选题1.下列说法正确的是( )A .的项是,2B .是二次三项式3x−23x 2x 2y +xy 2−x C .与是同类项D .单项式的系数是3x 2y −4yx 2−3πx 2y −32.若5x =125y ,3y =9z ,则x :y :z 等于( )A .1:2:3B .3:2:1C .1:3:6D .6:2:13.下列叙述中,正确的是( )A .单项式 的系数是0,次数是3x 2y B .a 、 、0、 都是单项式π22C .多项式 是六次三项式3a 3b +2a 2+1D . 是二次二项式m +n24.如图,7张全等的小长方形纸片(既不重叠也无空隙)放置于矩形ABCD 中,设小长方形的长为a ,宽为b(a>b),若要求出两块黑色阴影部分的周长和,则只要测出下面哪个数据( )A .aB .bC .a+bD .a-b5.下列运算正确的是( )A .a 2+a 3=a 5B .a 2•a 3=a 6C .(a 2)3=a 8D .a 3÷a 2=a6.下列运算正确的是( )A .(x 3)3=x 9B .(﹣2x )3=﹣6x 3C .2x 2﹣x=xD .x 6÷x 3=x 27.下列单项式中,与 是同类项的是( )0.3ab 2A .B .C .D .2a 2ba 2b 2−14b 2a 3ab8.下列计算错误的是( )A .3 =2B .﹣2+|﹣2|=0C .x 2•x 3=x 6D .(﹣3)2=93−339.下列各式变形中,是因式分解的是( )A .B .a 2−2ab +b 2−1=(a−b)2−1x 4−1=(x 2+1)(x +1)(x−1)C .D .(x +2)(x−2)=x 2−42x 2+2x =2x 2(1+1x )10.长方形的一边为2a﹣3b ,另一边比它小a﹣b ,则此长方形的另一边为( )A .3a﹣4bB .3a﹣2bC .a﹣2bD .a﹣4b11.下列说法中,正确的是( ) A .单项式 的系数 12πxy 212B .单项式 的次数为2−5x 2y C .多项式x 2+2xy+18是二次三项式D .多项式 x 3 - x 2y 2-1次数最高项的系数是 12231212.如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S 1+S 2=9,且AC+BC =10,则AB 的长为( )A .6B .7C .8D .62二、填空题13.已知a=2255,b=3344,c=5533,d=6622,则a ,b ,c ,d 的大小关系是 .14.分解因式:x 3-4x 2+4x= .15.若 ,则 的值为 .2x =2,4y =4216.七年级一班有2a﹣b 个男生和3a+b 个女生,则男生比女生少 人.三、计算题17.计算: (26−5)2019×(26+5)202018.计算:(1)(﹣2)+(﹣3)﹣(+1)﹣(﹣6);(2)﹣22﹣(﹣2)2×0.25÷;12(3)(3x﹣2)﹣(x﹣3);(4)5﹣2(a 2b﹣ab 2)+(3a 2b+ab 2).19.利用乘法公式计算:5002-499×501.20.已知,求代数式的值.x 2+2x−4=0x (x−2)2−x 2(x−6)−3四、综合题21.如图①是一个长为2m ,宽为2n 的长方形(m >n ),用剪刀沿图中虚线剪开,把得到的四块相同的长方形按图2那样拼成一个正方形.(1)图②中,中间的小正方形(阴影部分)的边长为 (用含m 、n 的式子表示);(2)观察图②,可得到(m+n )2、(m﹣n )2和4mn 之间的等量关系,请直接写出这个等量关系式;(3)若m+n =5,mn =,利用(2)的关系式求(m﹣n )2的值.9422.把四张形状大小完全相同的小长方形卡片(如图1),分两种不同形式不重叠的放在一个底面长为m ,宽为n 的长方形盒子底面(如图2、图3),盒子底面未被卡片覆盖的部分用阴影表示.(1)求图2中阴影部分图形的周长;(用含m 、n 的式子直接写出答案)(2)求图3中两个阴影部分图形的周长和.(用含有m 、n 的式子表示)23.已知x 1,x 2 是关于x 的方程(x -2)(x -m )=(p -2)(p -m )的两个实数根.(1)求x 1,x 2 的值;(2)若x 1,x 2 是某直角三角形的两直角边的长,问当实数m ,p 满足什么条件时,此直角三角形的面积最大?并求出其最大值.24.黑板上有一个正确的整式加法式,小明不小心擦去了前面的多项式,如下:+ (x 2-124xy+2y 2)=3x 2-xy.(1)求出擦去的多项式;(2)当x=-1,y=2时,求擦去的多项式的值.答案解析部分1.【答案】C 2.【答案】D 3.【答案】B 4.【答案】A 5.【答案】D 6.【答案】A 7.【答案】C 8.【答案】D 9.【答案】B 10.【答案】C 11.【答案】C 12.【答案】C13.【答案】a >b >c >d 14.【答案】x (x-2)215.【答案】1216.【答案】a+2b17.【答案】解:原式 =[(26−5)(26+5)]2019×(26+5)=(−1)2019(26+5)=−26−518.【答案】(1)解:原式=﹣2﹣3﹣1+6=0;(2)解:原式=﹣4﹣4××214=﹣4﹣2=﹣6;(3)解:(3x﹣2)﹣(x﹣3)=3x﹣2﹣x+3=2x+1;(4)解:5﹣2(a 2b﹣ab 2)+(3a 2b+ab 2)=5﹣2a 2b+2ab 2+3a 2b+ab 2=a 2b+3ab 2+5.19.【答案】解:原式=5002-(500+1)(500-1)=5002-5002+1=1.20.【答案】解:原式=x(x 2−4x +4)−x 3+6x 2−3=x 3−4x 2+4x−x 3+6x 2−3=2x 2+4x−3∵,∴x 2+2x−4=0x 2+2x =4原式=2(x 2+2x)−3=2×4−3=521.【答案】(1)解:由图②可知,中间的小正方形(阴影部分)的边长为;m−n (2)解:由图②可得,大正方形的边长为,m +n ∴大正方形的面积可以表示为,(m +n)2又∵大正方形由4个小长方形和一个小正方形组成,∴大正方形的面积还可以表示为,(m−n)2+4mn ∴.(m +n)2=(m−n)2+4mn (3)解:∵,(m +n)2=(m−n)2+4mn ∴把m+n =5,mn =代入得:,94(m +n)2=(m−n)2+4mn 52=(m−n)2+4×94解得:.(m−n)2=1622.【答案】(1)解:图2中阴影部分图形的周长是:2m +2n(2)解:设小长方形的宽为x ,长为y ,根据题意得:2x +y =m , PF =y ,EQ =2x ,PQ =EQ +PF﹣EF =y +2x﹣n =m﹣n ,EP +FQ =n﹣(m﹣n )=2n﹣m ,则两个阴影部分图形的周长和是:2m +2(2n﹣m )=4n23.【答案】(1)解:原方程变为:x 2-(m + 2)x + 2m = p 2-(m + 2)p + 2m ,∴x 2-p 2-(m + 2)x +(m + 2)p = 0,(x -p )(x + p )-(m + 2)(x -p )= 0,即 (x -p )(x + p -m -2)= 0,∴x 1 = p , x 2 = m + 2-p .(2)解:∵ 直角三角形的面积为 x 1x 2= p(m+2-p)1212= −12p 2+12(m +2)p= −12[p 2−(m +2)p +(m +22)2−((m +2)24)]= ,−12(p−m +22)2+(m +2)28∴ 当且m >-2时,以x 1,x 2为两直角边长的直角三角形的面积最大,最大面积为 p =m +22 (或 ).(m +2)2812p224.【答案】(1)解:(3x 2−xy)−12(x 2−4xy +2y 2)=3x 2−xy−12x 2+2xy−y 2= 52x 2+xy−y 2(2)解:当x=-1,y=2时,原式= = = 52×(−1)2+(−1)×2−2252−2−4−72。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章《整式》培优
专题一、找规律题
(一)、代数式找规律
1、观察下列单项式:5
4325,4,3,2,a a a a a --,…
(1)观察规律,写出第2010和第2011个单项式;
(2)请你写出第m 个单项式和第n+1个单项式。
(m 为自然数)
2、有一个多项式为332456b a b a b a a -+-…,按这种规律写下去,第六项是= ,最后一项是= 。
3、(1)观察一列数2,4,8,16,32,…发现从第二项开始,每一项与前一项之比是一个常数,这个常数是= ,根据此 规律,如果n a (n 为正整数)表示这个数列的第n 项,那么18a = ,n a = 。
(2)如果欲求203233331+++++Λ的值,可令203233331+++++=ΛS ①,将①式两边同乘以3,得 ,②
由②减去①式,得S= ;
(3)由上可知,若数列1a ,2a ,3a ,…n a ,n a ,从第二项开始每一项与前一项之比的常数为q ,则n a = ,(用含1a ,q ,n 的代数式表示),如果这个常数q ≠1,那么
1a +2a +3a +…+n a = (用含1a ,q ,n 的代数式表示)。
4、 观察下列一组数:21,43,65,87
,…… ,它们是按一定规律排列的,那么这一组数的第n 个数是 .
(二)、图形找规律
5、用棋子摆成如图所示的“T ”字图案.
(1)摆成第一个“T ”字需要 个棋子,第二个图案需要 个棋子;
(2)按这样的规律摆下去,摆成第10个“T ”字需要 个棋子,第n 个需要 个棋子.
6、如图是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中棋子个数是= ,第n 个“广”字中棋子个数是= 。
7、下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n 个图中所贴剪纸“●”的个数为
.
8、将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有________个小圆; 第n 个图形有______个小圆.
9、观察下列图形,则第n 个图形中三角形的个数是( )
A. 22n + B .44n + C .44n - D .4n 10、观察如下图的点阵图和相应的等式,探究其中的规律:
(1)在④和⑤后面的横线上分别写出相应的等式;
(2)通过猜想写出与第n 个点阵相对应的等式_____________
11、下图是某同学在沙滩上用石于摆成的小房子:
观察图形的变化规律,写出第n 个小房子用了[(n+1)2+(2n-1)] 块石子。
解析:第一个小房子:5=1+4=1+22
第二个小房子:12=3+9=3+32
第三个小房子:21=5+16=5+42
第四个小房子:32=7+25=7+52
……………………
第n 个小房子:(n+1)2+(2n-1)
(1)
(2) (3) ……
…… 第1个图形 第2个图形 第3个图形
第4个图形 …
……
第1个
第2个 第3个 ……
①②③④ ⑤
c a b 0 专题二:整体代换问题 12、若a a -2=2010,则()201022--a a = 。
13、若式子6432+-x x 的值是9,则163
42+-x x 的值是= 。
14、 (2010•常州)若实数a 满足122+-a a =0,则542+-a a = 。
15、已知代数式xy x +2=2,xy y +2=5,则2
2352y xy x ++的值是多少?
16、当x=2010时,201013=++bx ax ,那么x=-2010时,13++bx ax 的值是多少?
专题三:绝对值问题
17、,,a b c 在数轴上的位置如图所示,
化简:|||1||||1||23|a b b a c c b ++-------
18、有理数a 、b 在数轴上位置如图所示,试化简b b b 322231-++--.
19、有理数a 、b 、c 在数轴上的对应点如图,化简代数式:c b a c b a b a -+--++-2
:
专题四:综合计算问题
20、若212y x m -与n y x 2-的和是一个单项式,则m= ,n= 。
21、如果关于x 的代数式1522
2--++-x nx mx x 的值与x 的取值无关,则m= ,n= 。
22、已知m 、n 是系数,且y xy mx +-22与y nxy x 3232++的差中不含二次项,求222n mn m ++的值。
23、已知1abc =,求
111
a b c ab a bc b ac c ++++++++的值。
24、已知2215,6m mn mn n -=-=-,求2232m mn n --的值。
25、已知,a b 均为正整数,且1ab =,求
11
a b a b +++的值。
26、已知210m m +-=,求3222005m m ++的值。
27、若(x 2+mx+8)(x 2-3x+n )的展开式中不含x 3和x 2项,求m 和n 的值。
28、3(22+1)(24+1)(28+1)……(232+1)+1的个位数是多少。
解:3(22+1)(24+1)(28+1)……(232+1)+1
=(22-1)(22+1)(24+1)(28+1)……(232+1)+1
=(24-1) (24+1)(28+1)……(232+1)+1
=(28-1) (28+1)……(232+1)+1
=264-1+1
=264= (24)16=(16)16
∵16的任何次方的个位数都是6
∴3(22+1)(24+1)(28+1)……(232+1)+1的个位数是6.
专题五:应用问题
29、一位同学做一道题:“已知两个多项式A ,B ,计算2A+B ”。
他误将“2A+B ”看成“A+2B ”,求得的结果为7292+-x x 。
已知B=232
-+x x ,求原题的正确答案。
30、某地电话拨号入网有两种收费方式,用户可以任选其一。
A :计时制:0.05元/分;B :包月制:50元/月(限一部个人住宅电话上网)。
此外,每一种上网方式都加收通信费0.02元/分。
(1)某用户每月上网时间为x 小时,请你分别写出两种收费方式下改用户应该支付的费用;
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
31、小星和小月玩猜数游戏,小星说:“你随便选定三个一位数,按这样的步骤去算:①把第一个数乘以2;②加上5;③乘以5;④加上第二个数;⑤乘以10;⑥加上第三个数。
只要你告诉我最后的得数,我就能知道你所想的三个一位数。
”小月不相信。
但试了几次,小星都猜对了,你知道小星是怎样猜的吗?如果小月告诉小星的数是484,你知道小月所想的三个一位数是什么吗?
分析:设这三个数分别是abc ,再根据①把第一个数乘以2;②加上5;③乘以5;④加上第二个数;⑤乘以10;⑥加上第三个数,把所得的式子化简,再减去250把第一个数除以100,第二个数除以10即可.
解答:解:设这三个数分别是a 、b 、c ,
∵①把第一个数乘以2;②加上5;③乘以5;④加上第二个数;⑤乘以10;⑥加上第三个数,
∴[(2a+5)×5+b]×10+c
=[10a+b+25]×10+c
=100a+10b+c+250,再减去250,把第一个数除以100,第二个数除以10即可得出这三个数.
∴484-250=234=2×100+3×10+4 ∴a=2,b=3,c=4
32、七年级一班的小明和小王是好朋友。
有一次,小王拿出一副扑克牌,让小明从中任意抽出一张牌,且让他将牌上的点数默记心中。
小王说:“请你将点数乘2加3后再乘5,再减去25,算出答案后告诉我,我就知道你所抽的牌是几点。
”小明算完后说“100”。
小王马上宣布:“你抽的牌是J 。
”小明很佩服。
你能帮小明分析其中的奥秘吗?若小明算出的答案是120,他抽到的是哪张牌?
分析:设这个数为x,在根据“将点数乘2加3后再乘5,再减去25”,设计算后所得到数是y,那么y=(2x+3)×5-25。
解答:设这个数为x,计算后所得到数是y,
∵将这个数乘2加3后再乘5,再减去25
∴(2x+3)×5-25=y
10(x-1)=y
X=y/10+1
∴当y=120时,x=120/10+1=13
即,答案是120时,他所抽到的牌是K。
