打靶法(含Matlab程序)
重要:MATLAB常微分方程(组)数值解法

Matlab常微分方程求解问题分类
边值问题:
初值问题:
• 定解附加条件在自变量 的一端
• 一般形式为: y' f (x, y)
y(a)
y0
• 初值问题的数值解法一 般采用步进法,如 Runge-Kutta法
➢ 在自变量两端均给定附加 条件
y' f (x, y)
➢ 一般形式:y(a)y1, y(b)y2
1.根据常微分方程要求的求解精度与速度要求
求解初值问题:
y
'
y
2x y
y ( 0 ) 1
(0x1)
比较ode45和ode23的求解精度和速度
ode45和ode23的比较-1
function xODE clear all clc
format long
y0 = 1; [x1,y1] = ode45(@f,[0,1],y0); [x2,y2] = ode23(@f,[0,1],y0); plot(x1,y1,'k-',x2,y2,'b--') xlabel('x') ylabel('y')
rD = k(3)*C(2)-k(5)*C(4);
rE = k(4)*C(3)+k(5)*C(4);
% Mass balances dCdt = [rA; rB; rC; rD; rE];
三个串联的CSTR等温反应器(例4-3)
function IsothermCSTRs clear all clc CA0 = 1.8; % kmol/m^3 CA10 = 0.4; % kmol/m^3 CA20 = 0.2; % kmol/m^3 CA30 = 0.1; % kmol/m^3 k = 0.5; % 1/min tau = 2; stoptime = 2.9; % min [t,y] = ode45(@Equations,[0 stoptime],[CA10 CA20 CA30],[],k,CA0,tau); disp(' Results:') disp(' t CA1 CA2 CA3') disp([t,y]) plot(t,y(:,1),'k--',t,y(:,2),'b:',t,y(:,3),'r-') legend('CA_1','CA_2','CA_3') xlabel('Time (min)') ylabel('Concentration') % -----------------------------------------------------------------function dydt = Equations(t,y,k,CA0,tau) CA1 = y(1); CA2 = y(2); CA3 = y(3); dCA1dt = (CA0-CA1)/tau - k*CA1; dCA2dt = (CA1-CA2)/tau - k*CA2; dCA3dt = (CA2-CA3)/tau - k*CA3; dydt = [dCA1dt; dCA2dt; dCA3dt];
光学专业毕业设计:激光光斑尺寸的测量和研究.

激光光斑尺寸的测量和研究摘要激光光斑尺寸是标志激光器性能的重要参数,也是激光器在应用中的重要参量。
本文主要介绍了两种测量激光光斑尺寸的方法:刀口扫描法,CCD 法。
分析了利用刀口法测量高斯光束腰斑大小的测量实验装置,并阐述了具体的测量过程。
此方法对激光光斑大小测量是可行的。
实验装置简单实用。
CCD法是利用CCD作为探测传感器,可以更精确地测出激光器的光斑尺寸和束腰光斑尺寸,克服了传统测量的繁杂过程,并用计算机控制及数据处理,测量精度得到提高,为激光器性能研究和光信息处理提供了一种新的方法。
本文给出了这两种方法测得的数据及处理结果。
结果表明,刀口扫描法对高能量光束半径的测量特别实用,装置简单,可在普通实验室进行测量。
CCD法检测的直观性好,不需要辅助的逐行扫描机械移动,成像精度和检测精度高。
关键词激光光斑尺寸;Matlab;CCD传感器;刀口法The Measurement and Research of Laser SpotSizeAbstractThe size of Laser spot is not only one important parameter of laser performance, but also in laser application.This paper introduces two methods of measuring laser spot diameter: scanning method, CCD: knife method. We analyze of measurement is cut the size of the gaussian beam waist measurement device spot, and elaborates on process of the measurement. Using this method of laser spot size measurement is feasible. The experiment device is simple and practical. CCD method uses the CCD sensor as a detection can be more accurate to measure the size of the laser spot and waist size spot, overcoming traditional measurement process and using computer control to deal with data processing, and the measurement accuracy is improved, providing a new method for laser performance study and light information processing. At the same time, it gives two methods of measured data and processing results.The results show that the method of blade scanning is practical for high-energy beams radius’s measurement. Simple device can be operated in ordinary laboratory. CCD detection method is visually good, and do not need to manufacture progress ive-scan auxiliary of the machine movement, the imaging accuracy and precision is the higherKeywords Laser spot size; Matlab; CCD sensor; knife-edge method.哈尔滨理工大学学士学位论文目录摘要 (I)Abstract (II)第1章绪论 (4)1.1 课题背景 (4)1.2 国内外研究现状 (5)1.3 论文研究的内容 (7)第2章激光光斑测量方法探究 (8)2.1 刀口扫描法测激光光斑直径研究 (8)2.2 CCD测激光光斑直径方法 (12)2.3 本章小结 (20)第3章激光光斑尺寸的测量与数据分析 (21)3.1 刀口法测光斑直径 (21)3.1.1 90/10刀口法理论及方法 (21)3.1.2 计算理论 (23)3.1.3 实验数据处理 (23)3.1.4 实验分析 (25)3.2 CCD法测激光光斑方法 (25)3.2.1 用CCD拍摄光斑图像 (25)3.2.2 Matlab的图片处理 (26)3.2.3 图像处理结果 (26)3.2.4 实验分析 (29)3.3 本章小结 (30)结论 (31)致谢 (32)参考文献 (33)附录A 英文原文 (34)附录B 中文译文 (38)附录C Matlab程序 (42)第1章绪论1.1课题背景激光技术对国民经济及社会发展有着重要作用,激光技术是二十世纪与原子能、半导体及计算机齐名的四项重大发明之一。
非线性微分方程边值问题打靶算法Matlab程序

非线性微分方程边值问题打靶算法Matlab程序【非线性微分方程边值问题打靶算法】参见:// matlabsky /thread-828-1-1.html【线性微分方程边值问题打靶算法】参见 :// matlabsky /thread-827-1-1.html 【线性微分方程边值问题有限差分算法】参见:// matlabsky /thread-829-1-1.html下面我们讲解下【非线性微分方程边值问题打靶算法】对于边值问题线性边值问题时,p、q和r只是x的函数,但是非线性时它们是x,y和y'的函数我们将问题转换为如下初值问题现在我们需要做的就是找到那个m,使得y(b)=beta,换句话说y现在由两个变量最终控制,即m和x。
对于这个求m的问题,我们可以使用牛顿迭代法得到(1)先给出一个初值m=1(2)计算出对应的y(b)为yb,这个直接使用ode45计算,得到y(end,1)就是yb(3)根据beta和yb的差异更新m(4)将新的m带入(2)重新计算yb并更新m(5)如此迭代直到m稳定或者在允许误差范围内下面详细描述了Matlab代码的运行过程以下内容需要回复才能看到复制内容到剪贴板代码:function [t,x]=nlineshoot(funcn,funcv,tspan,bound,tol,varargin)%对微分方程y''=p*y'+q*y+r,a<t<b,u(a)=alpha,u(b)=beta,其中p,q和r为x,y和y'的函数%只要对应修改p,q,r并将y'用x(2)替换,y用x(1)替换,就可以了%funcn=@(t,x)[x(2);p*x(2)+q*x(1)+r];%funcv=@(t,x)[x(2);p*x(2)+q*x(1)+r;x(4);x(3)*dF/dy+x(4)*dF/y'];%%% Example%F=y''=2y*y',y(0)=-1,y(pi/2)=1%%由方程有p=2y=2*x(1),q=r=0%dF/dy=2*y'=2*x(2) %y'用x(2)替换,y用x(1)替换%dF/dy'=2*y=2*x(1)%%funcn=@(t,x)[x(2);2*x(1)*x(2)];%funcv=@(t,x)[x(2);2*x(1)*x(2);x(4);2*x(2)*x(3)+2*x(1)*x(4)]; %tspan=[0 pi/2];%bound=[-1 1];%tol=1e-8;%[t,y]=nlineshoot(funcn,funcv,tspan,bound,tol);%plot(t,y)%legend('x1','x2')%%by dynamic%see also :// matlabsky%2009.3.12%%lb=bound(1);ub=bound(2);m0=0;m=1;while norm(m-m0)>tolm0=m;[t,x]=ode45(funcv,tspan,[lb;m;0;1],varargin);m=m0-(x(end,1)-ub)/x(end,3);end[t,x]=ode45(funcn,tspan,[lb;m]);下面的图形是代码中附带实例的运行结果线性微分方程边值问题打靶算法Matlab程序【非线性微分方程边值问题打靶算法】参见:// matlabsky /thread-828-1-1.html 【线性微分方程边值问题打靶算法】参见:// matlabsky /thread-827-1-1.html【线性微分方程边值问题有限差分算法】参见:// matlabsky /thread-829-1-1.html注意该算法只能完成二阶常微分方程双边值问题求解,至于其他形式的边值问题必须先转换到二阶形式对于下面的二阶常微分方程利用上面方程的线性结果和两个特殊的初值问题,我们可以构造两个等效的常微分初值方程初值问题,对于初值问题我们就可以直接使用ode**计算器或者龙哥库塔算法求解了。
打靶法求边值问题教材

本科毕业论文(设计)论文(设计)题目:打靶法求边值问题学院:理学院专业:数学应用数学班级:091学号:0907010228学生姓名:钟玲声指导教师:汪萌萌2013 年21日打靶法求边值问题目录摘要: (1)引言: (2)第一章常微分方程初值问题的解法 (3)1.1常微分方程的离散化______________________________________________ 31.2 欧拉(Euler)方法________________________________________________ 41.3 改进的Euler方法_______________________________________________ 61.4 龙格一库塔(Runge—Kutta)方法_________________________________1.5 4阶龙格一库塔公式______________________________________________ 91.6 线性多步法_____________________________________________________ 9第二章边值问题的数值解法 (11)2.1 打靶法________________________________________________________ 112.2 差分法________________________________________________________ 15第三章Matlab数值解 (166)3.1 常微分方程的解法_____________________________________________ 1563.2 打靶法的matlab实现_________________________________________ 23致谢: (27)主要参考文献 (27)摘要常微分方程在很多领域都有非常重要的应用,然而很多常微分方程的解是无法用解析解写出的,因而要借助于数值方法。
Blasius方程的数值解matlab程序
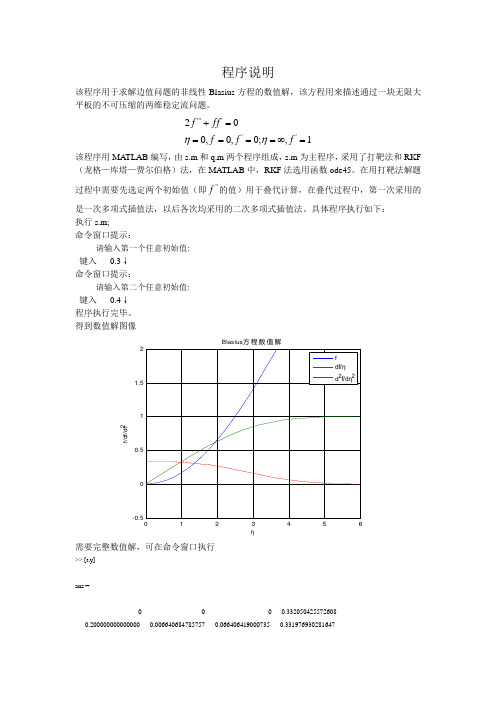
程序说明该程序用于求解边值问题的非线性Blasius 方程的数值解,该方程用来描述通过一块无限大平板的不可压缩的两维稳定流问题。
1,;0,0,002''''''=∞=====+f f f ff f ηη该程序用MATLAB 编写,由s.m 和q.m 两个程序组成,s.m 为主程序,采用了打靶法和RKF (龙格—库塔—费尔伯格)法,在MATLAB 中,RKF 法选用函数ode45。
在用打靶法解题过程中需要先选定两个初始值(即''f 的值)用于叠代计算,在叠代过程中,第一次采用的是一次多项式插值法,以后各次均采用的二次多项式插值法。
具体程序执行如下: 执行s.m;命令窗口提示:请输入第一个任意初始值:键入 0.3↓ 命令窗口提示:请输入第二个任意初始值:键入 0.4↓ 程序执行完毕。
得到数值解图像-0.500.511.52ηf /d f /d f 2Blasius 方程数值解需要完整数值解,可在命令窗口执行>> [t,y] ans =0 0 0 0.332050425572608 0.200000000000000 0.006640684785757 0.066406419000735 0.3319769302816470.400000000000000 0.026559272491103 0.132761397348084 0.331462940642616 0.600000000000000 0.059730061368740 0.198934248154027 0.3300728033338630.800000000000000 0.106097295537842 0.264705999557182 0.3273817832153041.000000000000000 0.165563030884709 0.329773792361296 0.322998326329412 1.200000000000000 0.237944237268780 0.393767481958191 0.316583378968660 1.400000000000000 0.322968836895193 0.456258456070615 0.307858224411080 1.600000000000000 0.420294********* 0.516758058641145 0.2966520460002811.800000000000000 0.529490839159120 0.574751902433704 0.2829211708769292.000000000000000 0.650009069470154 0.629751523134094 0.266750311286562 2.200000000000000 0.781182207029520 0.681296249300408 0.248352130535080 2.400000000000000 0.922272805631476 0.728973480703094 0.228082678389961 2.600000000000000 1.072479822282861 0.772447069758408 0.2064502635288602.800000000000000 1.230950137421495 0.811497584068625 0.1840142968552943.000000000000000 1.396787909544558 0.846029638656905 0.161369816626103 3.200000000000000 1.569069925345089 0.876070752645320 0.139126737097636 3.400000000000000 1.746915448703586 0.901760052525514 0.117863021963319 3.600000000000000 1.929487686151937 0.923331516492812 0.0980812457014453.800000000000000 2.116000403451031 0.941109242755617 0.0801396036425374.000000000000000 2.305719389785077 0.955505958092905 0.064250507286456 4.200000000000000 2.498005168266955 0.966955902144841 0.050519855519064 4.400000000000000 2.692328249616070 0.975867585098678 0.038977900754526 4.600000000000000 2.888218573285013 0.982674751981711 0.0294990019228064.800000000000000 3.085282916536712 0.987795856832908 0.0218594718910815.000000000000000 3.283237819572969 0.991545649832639 0.015900519799442 5.199999999999999 3.481838760901607 0.994236090376837 0.011361976112965 5.400000000000000 3.680886843280485 0.996153067540022 0.007933845886624 5.600000000000000 3.880258990903193 0.997474930939695 0.0054398826722105.800000000000000 4.079850604119796 0.998372294598017 0.0036575684193946.000000000000000 4.279588937153525 0.998971602331846 0.002407067561230 6.199999999999999 4.479425460802378 0.999361358663418 0.001555212097374 6.400000000000000 4.679324566790177 0.999611493625153 0.000983390226568 6.600000000000000 4.879263841128227 0.999767925072873 0.0006102416322996.800000000000000 5.079227857910512 0.999864205602870 0.0003709387997757.000000000000000 5.279206991685719 0.999922223141772 0.000220942955724 7.200000000000000 5.479195185941113 0.999956397738357 0.000129191951169 7.400000000000000 5.679188612800127 0.999976292967110 0.000073770638928 7.600000000000000 5.879185121366138 0.999987457696780 0.0000415764274927.800000000000000 6.079183286194299 0.999993777418038 0.0000227021832828.000000000000000 6.279182432445944 0.999997116397916 0.000012416083429 8.199999999999999 6.479182046435597 0.999998998619281 0.000006410840147 8.400000000000000 6.679181959675744 0.999999908695243 0.000003431483786 8.600000000000000 6.879181996919892 1.000000408873378 0.0000017369825648.800000000000001 7.079182104284974 1.000000668341604 0.0000008322352839.000000000000000 7.279182257219148 1.000000765370094 0.000000489499078查看叠代过程,可在命令窗口执行>> Y Y =0.300000000000000 0.400000000000000 0.333115369726614 0.332050425572608 >> x x =0.934567382019033 1.132157258022684 1.002137820445041 1.000000765370094 %Y 表示0=η时''f 的值,x 表示∞=η(实际为9)时对应''f 下'f 的值。
打靶法的一个c程序

zjia[0]=zding[0]+dlts;//zjia[0]=s(i)+dlts(i)
dydx[0]=zjia[0];//y'=z[0]
dzdx[0]=1.5*yding[0]*yding[0];//z'=f(x,y,z)=1.5*y*y
for(j=0;j<5;j++)
{
h=0.2+0.2*j;
//
cout<<zout<<endl;//yout从这里输出,切记!!!//
z=zout;
cout<<h6;
} for(i=0;i<n;i++)
{
dzm=0.0;
dzt=0.0;
yt=0.0;
zt=0.0;
dzf=0.0;
}
}
void main()
{
double F[1],Fs[1],zjia[1],dlts=0.00001;
dydx[0]=z[0];//y'=z[0] dzdx[0]=1.5*y[0]*y[0];//z'=f(x,y,z)=1.5*y*y } // 子过程RK4
void rk4(int n,double h,double x,double y[],double z[],double dydx[],double dzdx[],double yout[],double zout[]) {
rk4(n,h,x,yding,zjia,dydx,dzdx,yout,zout);
//
cout<<"yout["<<h<<"]="<<yout[0]<<endl;
基于最小值原理的壁面攀爬机器人时间最优控制
·智能控制技术·徐林孙树栋陈立彬等基于最小值原理的壁面攀爬机器人37 基于最小值原理的壁面攀爬机器人时间最优控制徐林,孙树栋,陈立彬,杨建元(西北工业大学机电学院,陕西西安710072)摘要:首先简要介绍了一种新型双索牵引壁面攀爬机器人结构,并建立了该系统的数学模型。
其次,依据庞特里雅金最小值原理推出了机器人本体两点间运动时间最优的控制律,并将该非线性方程组的求解看作是一个两点边值问题,通过引入简单打靶法以及一种初值猜测技术来求解该方程组。
最后,数值仿真表明所建模型及控制规律是可行的。
关键词:壁面攀爬机器人;最小值原理;时间最优控制;两点边值问题;打靶法中图分类号:TP242. 3 文献标识码:A 文章编号:1672 - 1616( 2006) 21 - 0037 - 05随着城市规模的不断扩大,越来越多的高层建筑如雨后春笋般涌现出来,人们在惊叹现代建筑艺术、享受现代生活的同时,又面临着一个关系生命安危的问题———那就是高层消防和救援问题。
研究人员已经提出了利用消防特种机器人和高空作业机器人的方法。
但是,现有的消防特种机器人大多只能在地面作业;而高空作业机器人,由于一部分采用的是吸附的运动方式, 使得其移动速度较慢,可携带的负载也较轻,无法快速进入着火点实施有效的消防和救援作业;另一部分采用楼顶预置水平轨道的吊篮型装置,虽然其运动迅速,且有一定的负载能力,但是预置楼顶轨道的要求致使这种装置不适用于消防、救灾等作业。
针对高空消防、救援等作业的特殊要求,我们提出一种特殊的机器人组合系统,使机器人本体能携带较大负载且能快速到达着火点实施侦察、消防及救援工作。
1 时间最优控制模型建立1 . 1 原理简述和分析攀爬机器人组合系统工作原理可简述为:通过一种无限程攀爬装置将地面动力电机的绕转扭矩经牵引钢丝绳远距离传递给机器人本体,本体利用摩擦力作用将该扭矩转化为其攀升的动力,从而实现了通过地面电机对机器人本体壁面运动的驱动。
数学实验“微分方程组边值问题数值算法(打靶法,有限差分法)”实验报告(内含matlab程序)
西京学数学软件实验任务书课程名称数学软件实验班级数0901学号0912020107姓名李亚强微分方程组边值问题数值算法(打靶法,有限差分法)实验课题熟悉微分方程组边值问题数值算法(打靶法,有限差实验目的分法)运用Matlab/C/C++/Java/Maple/Mathematica等其中实验要求一种语言完成微分方程组边值问题数值算法(打靶法,有限差分法)实验内容成绩教师实验二十七实验报告1、实验名称:微分方程组边值问题数值算法(打靶法,有限差分法)。
2、实验目的:进一步熟悉微分方程组边值问题数值算法(打靶法,有限差分法)。
3、实验要求:运用Matlab/C/C++/Java/Maple/Mathematica 等其中一种语言完成程序设计。
4、实验原理:1.打靶法:对于线性边值问题(1)⎩⎨⎧==∈=+'+''βα)(,)(],[)()()(b y a y b a x x f y x q y x p y 假设是一个微分算子使:L ()()Ly y p x y q x y '''=++则可得到两个微分方程:,,)(1x f Ly =α=)(1a y 0)(1='a y ,, (2)⇔)()()(111x f y x q y x p y =+'+''α=)(1a y 0)(1='a y ,,02=Ly 0)(2=a y 1)(2='a y ,, (3)⇔0)()(222=+'+''y x q y x p y 0)(2=a y 1)(2='a y 方程(2),(3)是两个二阶初值问题.假设是问题1y(2)的解,是问题(3)的解,且,则线性边值问2y 2()0y b ≠题(1)的解为: 。
1122()()()()()y b y x y x y x y b β-=+2.有限差分法:基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似, 积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组 , 解此方程组就可以得到原问题在离散点上的近似解。
打靶法
用某种离散化数值步骤求出常微分方程边值问题在离散点上的近似解的方法。
各种实际问题导出不同类型的边值问题。
较简单的有二阶常微分方程两点边值问题:求函数y=y(x),x∈【α,b】,使它满足微分方程和边值条件式中ƒ、g1、g2为已知函数;α与b为两个给定的端点。
较一般地有一阶常微分方程组两点边值问题:求N个函数使其满足微分方程组和边值条件式中诸ƒn、g i是已知函数;r为给定的自然数。
有些问题因求解区间是无穷区间而被称作奇异边值问题,相应的边界条件变为对解在无穷远处渐近行为的限制,例如,要求y(x)在区间【0,)上平方可积或要求当x趋于无穷时,y(x)趋于某极限值。
还有些实际问题因要求解满足多个点上的条件而被称作多点边值问题。
近年来,对反映边界层现象的奇异摄动边值问题提出了一些新的数值解法。
此外,关于存在多个解的分歧现象数值解问题也引起人们的注意。
打靶法主要思路是:适当选择和调整初值条件,(选什么)求解一系列初值问题,使之逼近给定的边界条件。
如果将描述的曲线视作弹道,那么求解过程即不断调整试射条件使之达到预定的靶子,所以称作打靶法或试射法,此类方法的关键是设计选取初值的步骤。
对非线性边值问题可通过下列步骤求数值解:①计算初值问题的数值解y1。
若g(y1(b),y姈(b))=B,近似地满足,则y1即为所求;否则进行②。
②计算初值问题的数值解y2,若g(y2(b),y娦(b))=B近似地满足,则y2即为所求;否则令m=3进行③。
③将g(y(b),y┡(b))视为y(α)的函数,用线性逆插值法调整初值,即计算然后进行④。
④计算初值问题的数值解y m并进行判定:若b点边值条件近似地满足,则y m即为所求;否则令m+1崊m转向③继续计算直到满意为止。
特别地,若微分方程是线性的,则打靶法变成线性组合法,即根据常微分方程理论适当选取初值可得到一组线性独立解,利用它们的线性组合导出边值问题的解。
例如线性方程边值问题的数值解可通过两个初值问题数值解来实现。
打靶法(含Matlab程序)
西京学数学软件实验任务书动方向控制减速的推力,主要的控制量只有一个减速推力,减速还会消耗燃料让登月器的质量减小。
所以在极坐标下系统的状态就是x‘=[质量m,角度theta,高度r,角速度omega,径速度v]这五个量,输入就是减速力F。
先列微分方程,dx/dt=f(x)+B*F,其中x是5*1的列向量,质量dm/dt=-F/2940,剩下几个翻下极坐标的手册。
把这个动力学模型放到matlab里就能求解了,微分方程数值解用ode45。
第一问F=0,让你求椭圆轨道非常容易。
注意附件1里说15公里的时候速度是s。
算完以后验证一下对不对,对的话就是他了,不对的话说明这个椭圆轨道有进动,到时再说。
(2) 算出轨道就能计算减速力了。
这时候你随便给个常数减速力到方程里飞船八成都能降落,但不是最优解。
想想整个过程,开始降落之前飞船总机械能就那么多,你需要对飞船做负功让机械能减到0。
题目里写发动机喷出翔的相对速度是一定的,直觉告诉我飞船速度快的时候多喷一些速度慢的时候少喷一些,可以提高做负功的效率。
但是多喷也不能超过上限7500N,所以这就是一个带约束优化问题,matlab里边有专用的优化函数,用fmincon就好。
找出最优解以后把过程画出来,看看F可不可以是那5个状态量的线性组合,如果是的话就非常happy,不是的话再说。
三四阶段你可以扯点图像识别,什么二维复利叶分解找平坦区域,怎么一边下降一边根据自身状态调整路径之类的。
五六阶段还真不知道说什么。
一二阶段肯定是重点啦(3) 误差分析其实还挺难的。
可能的误差来源是地球的引力,月亮绕地球向心加速度,太阳的引力(可能会很小),对自身速度、角度的测量误差(比如你测出自身当前速度100m/s但实际上是105m/s),控制的时候F大小以及角度的误差(比如你想朝正前方向喷2000N但实际上偏了2度而且F=2010N之类)。
上一问已经求出了最优控制策略和飞船路线,把这些扰动加进去以后算出新的路线减掉理想路线求偏差,然后随便用个卡尔曼滤波器把误差给校正All for Joy2014/9/13 11:14:38老师的思路,求大神解答给我一份呀实验二十七实验报告实验名称:微分方程组边值问题数值算法(打靶法,有限差分法)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西京学数学软件实验任务书动方向控制减速的推力,主要的控制量只有一个减速推力,减速还会消耗燃料让登月器的质量减小。
所以在极坐标下系统的状态就是x‘=[质量m,角度theta,高度r,角速度omega,径速度v]这五个量,输入就是减速力F。
先列微分方程,dx/dt=f(x)+B*F,其中x是5*1的列向量,质量dm/dt=-F/2940,剩下几个翻下极坐标的手册。
把这个动力学模型放到matlab里就能求解了,微分方程数值解用ode45。
第一问F=0,让你求椭圆轨道非常容易。
注意附件1里说15公里的时候速度是1.7km/s。
算完以后验证一下对不对,对的话就是他了,不对的话说明这个椭圆轨道有进动,到时再说。
(2) 算出轨道就能计算减速力了。
这时候你随便给个常数减速力到方程里飞船八成都能降落,但不是最优解。
想想整个过程,开始降落之前飞船总机械能就那么多,你需要对飞船做负功让机械能减到0。
题目里写发动机喷出翔的相对速度是一定的,直觉告诉我飞船速度快的时候多喷一些速度慢的时候少喷一些,可以提高做负功的效率。
但是多喷也不能超过上限7500N,所以这就是一个带约束优化问题,matlab里边有专用的优化函数,用fmincon就好。
找出最优解以后把过程画出来,看看F可不可以是那5个状态量的线性组合,如果是的话就非常happy,不是的话再说。
三四阶段你可以扯点图像识别,什么二维复利叶分解找平坦区域,怎么一边下降一边根据自身状态调整路径之类的。
五六阶段还真不知道说什么。
一二阶段肯定是重点啦(3) 误差分析其实还挺难的。
可能的误差来源是地球的引力,月亮绕地球向心加速度,太阳的引力(可能会很小),对自身速度、角度的测量误差(比如你测出自身当前速度100m/s但实际上是105m/s),控制的时候F大小以及角度的误差(比如你想朝正前方向喷2000N但实际上偏了2度而且F=2010N之类)。
上一问已经求出了最优控制策略和飞船路线,把这些扰动加进去以后算出新的路线减掉理想路线求偏差,然后随便用个卡尔曼滤波器把误差给校正All for Joy2014/9/13 11:14:38老师的思路,求大神解答给我一份呀实验二十七实验报告一、实验名称:微分方程组边值问题数值算法(打靶法,有限差分法)。
二、实验目的:进一步熟悉微分方程组边值问题数值算法(打靶法,有限差分法)。
三、实验要求:运用Matlab/C/C++/Java/Maple/Mathematica 等其中一种语言完成程序设计。
四、实验原理:1.打靶法:对于线性边值问题⎩⎨⎧==∈=+'+''βα)(,)(],[)()()(b y a y b a x x f y x q y x p y (1)假设L 是一个微分算子使:()()Ly y p x y q x y '''=++则可得到两个微分方程:)(1x f Ly =,α=)(1a y ,0)(1='a y⇔)()()(111x f y x q y x p y =+'+'',α=)(1a y ,0)(1='a y (2) 02=Ly ,0)(2=a y ,1)(2='a y ⇔0)()(222=+'+''y x q y x p y ,0)(2=a y ,1)(2='a y (3) 方程(2),(3)是两个二阶初值问题.假设1y 是问题(2)的解,2y 是问题(3)的解,且2()0y b ≠,则线性边值问题(1)的解为:1122()()()()()y b y x y x y x y b β-=+ 。
2.有限差分法:基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似, 积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组 , 解此方程组就可以得到原问题在离散点上的近似解。
然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。
五、实验内容:%线性打靶法function[k,X,Y,wucha,P]=xxdb(dydx1,dydx2,a,b,alpha,beta,h) n=fix((b-a)/h); X=zeros(n+1,1); CT1=[alpha,0];Y=zeros(n+1,length(CT1)); Y1=zeros(n+1,length(CT1)); Y2=zeros(n+1,length(CT1));X=a:h:b;Y1(1,:)= CT1;CT2=[0,1];Y2(1,:)= CT2;for k=1:nk1=feval(dydx1,X(k),Y1(k,:))x2=X(k)+h/2;y2=Y1(k,:)'+k1*h/2;k2=feval(dydx1,x2,y2);k3=feval(dydx1,x2,Y1(k,:)'+k2*h/2);k4=feval(dydx1, X(k)+h,Y1(k,:)'+k3*h);Y1(k+1,:)=Y1(k,:)+h*(k1'+2*k2'+2*k3'+k4')/6,k=k+1;endu=Y1(:,1)for k=1:nk1=feval(dydx2,X(k),Y2(k,:))x2=X(k)+h/2;y2=Y2(k,:)'+k1*h/2;k2=feval(dydx2,x2,y2);k3=feval(dydx2,x2,Y2(k,:)'+k2*h/2);k4=feval(dydx2, X(k)+h,Y2(k,:)'+k3*h);Y2(k+1,:)=Y2(k,:)+h*(k1'+2*k2'+2*k3'+k4')/6,k=k+1;endv=Y2(:,1)Y=u+(beta-u(n+1))*v/v(n+1)for k=2:n+1wucha(k)=norm(Y(k)-Y(k-1)); k=k+1;endX=X(1:n+1);Y=Y(1:n+1,:);k=1:n+1;wucha=wucha(1:k,:);P=[k',X',Y,wucha'];plot(X,Y(:,1),'ro',X,Y1(:,1),'g*',X,Y2(:,1),'mp')xlabel('轴\it x'); ylabel('轴\it y')legend('是边值问题的数值解y(x)的曲线','是初值问题1的数值解u(x)的曲线', '是初值问题2的数值解v(x)的曲线')title('用线性打靶法求线性边值问题的数值解的图形')%有限差分法function[k,A,B1,X,Y,y,wucha,p]=yxcf(q1,q2,q3,a,b,alpha,beta,h) n=fix((b-a)/h); X=zeros(n+1,1);Y=zeros(n+1,1); A1=zeros(n,n);A2=zeros(n,n); A3=zeros(n,n); A=zeros(n,n);B= zeros(n,1);for k=1:nX=a:h:b;k1(k)=feval(q1,X(k)); A1(k+1,k)=1+h*k1(k)/2;k2(k)=feval(q2,X(k));A2(k,k)=-2-(h.^2)*k2(k);A3(k,k+1)= 1-h*k1(k)/2; k3(k)=feval(q3,X(k));endfor k=2:nB(k,1)=(h.^2)*k3(k);endB(1,1)=(h.^2)*k3(1)-(1+h*k1(1)/2)*alpha;B(n-1,1)=(h.^2)*k3(n-1)-(1+h*k1(n-1)/2)*beta;A=A1(1:n-1,1:n-1)+A2(1:n-1,1:n-1)+A3(1:n-1,1:n-1);B1=B(1:n-1,1);Y=A\B1;Y1=Y'; y=[alpha;Y;beta];for k=2:n+1wucha(k)=norm(y(k)-y(k-1)); k=k+1;endX=X(1:n+1); y=y(1:n+1,1); k=1:n+1;wucha=wucha(1:k,:); plot(X,y(:,1),'mp')xlabel('轴\it x'); ylabel('轴\it y'),legend('是边值问题的数值解y(x)的曲线')title('用有限差分法求线性边值问题的数值解的图形'),p=[k',X',y,wucha'];打靶法3.Matlab源代码:创建M 文件:functionys=dbf(f,a,b,alfa,beta,h,eps)ff=@(x,y)[y(2),f(y(1),y(2),x)];xvalue=a:h:b;%x取值范围n=length(xvalue)s0=a-0.01;%选取适当的s的初值x0=[alfa,s0];%迭代初值flag=0;%用于判断精度y0=rk4(ff,a,x0,h,a,b);if abs(y0(1,n)-beta)<=eps flag=1;y1=y0;elses1=s0+1;x0=[alfa,s1];y1=rk4(ff,a,x0,h,a,b);if abs(y1(1,n)-beta)<=epsflag=1;endendif flag~=1while abs(y1(1,n)-beta)>epss2=s1-(y1(1,n)-beta)*(s1-s0)/(y1(1,n)-y0(1,n)); x0=[alfa,s2];y2=rk4(ff,a,x0,h,a,b);s0=s1;s1=s2;y0=y1;y1=y2;endendxvalue=a:h:b;yvalue=y1(1,:);ys=[xvalue',yvalue'];functionx=rk4(f,t0,x0,h,a,b)%rung-kuta法求每个点的近似值(参考大作业一)t=a:h:b;%迭代区间m=length(t);%区间长度t(1)=t0;x(:,1)=x0;%迭代初值for i=1:m-1L1=f(t(i),x(:,i));L2=f(t(i)+h/2,x(:,i)'+(h/2)*L1);L3=f(t(i)+h/2,x(:,i)'+(h/2)*L2);L4=f(t(i)+h,x(:,i)'+h*L3);x(:,i+1)=x(:,i)'+(h/6)*(L1+2*L2+2*L3+L4); end4.举例求二阶非线性方程的边值问题:在matlab 控制台中输入:f=@(x,y,z)(x^2+z*x^2);x0l=0;x0u=2*exp(-1);alfa=0;beta=2;h=0.01dbf(f,x0l,x0u,y0l,y0u,h,1e-6); >> y=ans(:,2);x=ans(:,1);>> plot(x,y,'-r')>>结果:再输入:>> m=0:0.01:2;>> n=m.*exp(-1/2*m);>> plot(n,m)>> plot(x,y,'-r',n,m,'-b')。
