6 第一章 集合与常用逻辑用语 章末复习提升课
章末梳理1-【新教材】人教A版(2019)高中数学必修第一册课件(共44张PPT)

(2)因为 A∩B=∅,所以 0∉B,且 1∉B,所以 a≥1.
返回导航
第一章 集合与常用逻辑用语
数学(必修 · 第一册 · RJA)
[归纳提升] 利用集合的运算求参数的范围的注意点 (1)要弄清楚集合运算的结果或可能的结果,再根据其中的结果判定 参数的值或范围. (2)当集合的运算较为复杂时,要借助于数轴或韦恩图解决问题. (3)注意参数的值或范围应该满足集合中元素的互异性.
返回导航
第一章 集合与常用逻辑用语
数学(必修 · 第一册 · RJA)
常用逻辑用语是数学语言的重要组成部分,是逻辑思维的基本语 言,也是数学表达和交流的工具.结合初中学过的平面几何和代数知 识,我们学习了常用逻辑用语,发现初中学过的数学定义、定理、命题 都可以用常用逻辑用语表达,利用常用逻辑用语表述数学内容、进行推 理论证,可以大大提升表述的逻辑性和准确性,从而提升我们的逻辑推 理素养.
定义法是判断充分、必 要条件最根本、最适用 的方法
集合 法
记条件p,q对应的集合分别是A,
B.若A B,则p是q的充分不必要条
件;若A B,则p是q的必要不充分条 件;若A=B,则p是q的充要条件
适用于“当所要判断的 命题与方程的根、不等 式的解集以及集合有 关,或所描述的对象可 以用集合表示”的情况
所以∁RA={x|x<0或x>2}.
因为(∁RA)∪B=R.(如图)
返回导航
第一章 集合与常用逻辑用语
数学(必修 · 第一册 · RJA)
所以 aa+≤03,≥2, 所以-1≤a≤0.即 a 的取值范围是[-1,0]. (2)由(1)知当(∁RA)∪B=R 时,-1≤a≤0,则 a+3∈[2,3], 所以 A⊆B,这与 A∩B=∅矛盾. 即这样的 a 不存在.
高一数学第1章 (原卷版)

第1章 集合与常用逻辑用语章末测试(提升)一.单选题(每题5分,每题只有一个选项为正确答案,共8题40分)1.(2021·山东)已知集合{{},1,,A B m B A ==⊆,则m =( )A .0B .0或3C .1D .1或32.(2021·青海西宁市)如果甲是乙的充要条件,丙是乙的充分不必要条件,那么丙是甲的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件3.(2021·安徽池州市)集合{}{}201A x x ax a =++=⊆,则a 为( )A .12-B .()0,4a ∈C .()[),04,a ∈-∞⋃+∞D .()10,42a ⎧⎫∈-⋃⎨⎬⎩⎭4.(2021·陕西西安市第三中学高一期末)已知集合{}13A x x =-≤≤,集合{}11B x m x m =-≤≤+.若B A ⊆,则m 的取值范围是( ) A .(],2-∞ B .[]1,3-C .[]3,1-D .[]0,25.(2021·全国高三专题练习)已知集合(){}223A x y xy x Z y Z =+≤∈∈,,,,则A 中元素的个数为( )A .9B .8C .5D .46.(2021·浙江高三专题练习)若命题:“x R ∃∈,220ax ax -->”为假命题,则实数a 的取值范围是( ) A .(][),80,-∞-+∞ B .()8,0- C .(],0-∞D .[]8,0-7.(2021·黑龙江)命题2:,240p x R ax ax ∃∈+-≥为假命题的一个充分不必要条件是( )A .40aB .40a -≤<C .30a -≤≤D .42a -≤≤8.(2021·浙江)已知集合{}*N 0A x x y =∈=≥∣,若B A ⊆且集合B 中恰有2个元素,则满足条件的集合B 的个数为( ). A .1 B .3C .6D .10二、多选题(每题至少有2个选项为正确答案,每题5分,4题共20分)9.(2021·江西)已知集合{|1}A x ax ==,{0B =,1,2},若A B ⊆,则实数a 可以为( ) A .12B .1C .0D .以上选项都不对10.(2021·广东湛江市)已知集合{}23180A x x x =∈--<R ,{}22270B x x ax a =∈++-<R ,则下列命题中正确的是( ) A .若A B =,则3a=- B .若A B ⊆,则3a =-C .若B =∅,则6a ≤-或6a ≥D .若BA 时,则63a -<≤-或6a ≥11.(2021·台州市书生中学高一开学考试)已知命题0:p x R ∃∈,使得200220x ax a +++”,若命题p是假命题,则实数a 的取值是( ) A .0 B .1C .2D .312.(2021·浙江宁波市·镇海中学高一期末)若“()00,2x ∃∈,使得200210x x λ-+<成立”是假命题,则实数λ可能的值是( )A .1B .C .3D .三.填空题(每题5分,共20分)13.(2021·全国高一单元测试)已知:2p x >,:1q x >,则p 是q 的_______________(充分条件”、“必要条件”、“充要条件”、“既不充分也不必要条件”中选择一个填空).14.(2021·辽宁)已知命题“2,230x x ax a ∃∈-+R ”是假命题,则实数a 的取值范围是________. 15.(2021·贵溪市实验中学)已知:12p x -≤<,2:21q a x a ≤≤+,若p 是q 的必要条件,则实数a的取值范围是16.(2021·浙江高一期末)命题“2,430x R ax ax ∀∈++>”为真,则实数a 的范围是__________ 四.解答题(17题10分,其余每题12分,共70分)17.(2021·全国高一单元测试)若集合{}2560A x x x =+-=,(){}222130B x x m x m =+++-=.(1)若0m =,写出A B 的子集;(2)若A B B =,求实数m 的取值范围.18.(2021·广东广州市·广雅中学高一期末)设集合11|4322x A x ⎧⎫=≤≤⎨⎬⎩⎭,{}|121B x m x m =-≤≤+. (1)若3m =,求()RA B ⋃;(2)若A B B =,求m 的取值范围;19.(2021·湖南省东安县第一中学高一期末)在①{14}=-<<∣B xx ,②R{6}B x x =>∣,③{7}B x x =≥∣这三个条件中任选一个,补充在下面的问题中.问题:已知集合{10}=<<-∣A x a x a , ,若AB =∅,求a 的取值范围.注:如果选择多个条件分别解答,按第一个解答计分.20.(2021·江苏南通市·高一期末)已知集合{}2540P xx x =-+≤∣,{}11S x m x m =-≤≤+∣. (1)用区间表示集合P ;(2)是否存在实数m ,使得x P ∈是x S ∈的______条件.若存在实数m ,求出m 的取值范围:若不存在,请说明理由.请从如下三个条件选择一个条件补充到上面的横线上: ①充分不必要;②必要不充分;③充要.21.(2021·全国高二课时练习)已知命题“关于x 的方程2250x mx m +++=有两个不相等的实数根”是假命题.(1)求实数m 的取值集合A ;(2)设集合{|121}B x a x a =-≤≤-,若x A ∈是x B ∈的充分不必要条件,求实数a 的取值范围.21.(2021·全国高一单元测试)已知集合{}22|,,A x x m n m n Z ==-∈(1)判断8,9,10是否属于集合A ;(2)已知集合{}|21,B x x k k Z ==+∈,证明:“x A ∈”的充分条件是“x B ∈”;但“x B ∈”不是“x A ∈”的必要条件;(3)写出所有满足集合A 的偶数.。
《第一章 集合与常用逻辑用语》章节复习及练习

[解析] 由 x2-8x-20≤0,得-2≤x≤10,由 x2-2x+1-m2≤0(m>0),
得 1-m≤x≤1+m(m>0).
因为 p 是 q 的充分不必要条件,所以 p⇒q 且 q⇒/ p.
集合的并、交、补运算
【例1】 已知全集U={0,1,2,3,4,5,6},集合A={x∈N|1<x≤4},B ={x∈R|x2-3x+2=0}.
(1)用列举法表示集合A与B; (2)求A∩B及∁U(A∪B). [解] (1)由题知,A={2,3,4},B={x∈R|(x-1)(x-2)=0}={1,2}. (2)由题知,A∩B={2},A∪B={1,2,3,4},所以∁U(A∪B)={0,5,6}.
1≤
2
< 1 , ∪B={x|-2<x≤3}.
(2)由已知可求得∁RA
∵(∁RA)∩B=B,∴B⊆∁RA.
< 1 ,或 > 3
2
当B=⌀时,2a≥a+2,解得a≥2;
当 B≠ 时,
2 < +2, +2 ≤ 1 或
2 2
2
< +2, ≥ 3,
解得 a≤
3 2
或
32≤a<2.
综上可得,a 的取值范围是 a≤
3 2
或
a≥32
解题技巧:
1.若所给集合是有限集,则首先把集合中的元素一一列举 出来,然后结合交集、并集、补集的定义来求解.另外,针对 此类问题,在解答过程中也常常借助Venn图来求解.这样处 理起来比较直观、形象,且解答时不易出错.
2023高考数学基础知识综合复习第1讲集合与常用逻辑用语 课件(共21张PPT)

所以(∁RA)∩B=(1,3).
(2)由(1)知A=[-3,1].
∁RA=(-∞,-3)∪(1,+∞),B=(-2a,3a).
又(∁RA)∪B=R,
得
-2 < -3,
3
解得 a> .
2
3 > 1,
3
2
即 a 的取值范围为( ,+∞).
考点一
考点二
考点三
则其否定“∃x∈R,x2-2x≤0”是真命题,C满足;对于选项D,因为
x2+2x+2=(x+1)2+1>0恒成立,所以“∃x∈R,x2+2x+2≤0”是假命题,
所以其否定“∀x∈R,x2+2x+2>0”,是真命题,所以D满足.故选CD.
考点一
考点二
考点三
全称量词命题的否定是存在量词命题,存在量词命题的否定是全称
素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A
是集合B的子集,记作A⊆B(或B⊇A),读作A包含于B(或B包含A).
(2)真子集的概念:如果集合A⊆B,但存在元素x∈B且x∉A,我们称集
合A是集合B的真子集,记作A⫋B(或B⫌A),读作A真包含于B(或B真
包含A).
(3)空集的概念:不含任何元素的集合叫作空集,记作⌀.空集是任何
集合的子集,是任何非空集合的真子集.
3.集合的运算
(1)并集的定义:A∪B={x|x∈A,或x∈B};
(2)交集的定义:A∩B={x|x∈A,且x∈B};
(3)补集的定义:∁UA={x|x∈U,且x∉A}.
4.充分条件、必要条件
高中数学必修第一册第1章章末复习

√A.{a|a≥2}
B.{a|a≤1}
ห้องสมุดไป่ตู้
C.{a|a≥1}
D.{a|a≤2}
解析 如图
12345
4.已知集合A={1,3,2-m},集合B={3,m2},则“B⊆A”的充要条件是实数m= ___-__2___.
解析 若B⊆A, 则m2=1或m2=2-m, 得m=1或m=-1,或m=-2, 当m=1时,A={1,3,1}不成立, 当m=-1时,A={1,3,3}不成立, 当m=-2时,A={1,3,4},B={3,4},满足条件. 即m=-2, 则“B⊆A”的充要条件是实数m=-2.
12345
本课结束
√C.∀m,n∈Z,使得m2≠n2+2 019
D.以上都不对
(2)设命题p:∀x∈R,x2+ax+2<0,若綈p为真,则实数a的取值范围是__R__.
解析 綈p:∃x∈R,x2+ax+2≥0为真命题, 显然a∈R.
3 随堂演练
PART THREE
1.设全集U=R,集合A={x|-3<x<1},B={x|x+1≥0},则∁U(A∪B)等于
A.{x|x≤-3或x≥1} C.{x|x≤3}
B.{x|x<-1或x≥3}
√D.{x|x≤-3}
解析 A={x|-3<x<1},B={x|x≥-1}, 所以A∪B={x|x>-3},∁U(A∪B)={x|x≤-3},故选D.
12345
2.下列命题中是全称量词命题并且是真命题的是 A.∀x∈R,x2+2x+1>0 B.∃x∈N,2x为偶数
第一章 集合与常用逻辑用语
内容索引
NEIRONGSUOYIN
知识网络 考点突破 随堂演练
人教版(新教材)高中数学第一册(必修1)精品课件:第一章集合与常用逻辑用语章末复习课

【例1】 (1)设集合A={1,2,4},集合B={x|x=a+b,a∈A,b∈A},则集合B中元
素的个数是( )
A.4
B.5
C.6
D.7
(2)已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是( )
A.1
B.3
ቤተ መጻሕፍቲ ባይዱ
C.5
D.9
解析 (1)∵a∈A,b∈A,x=a+b,所以x=2,3,4,5,6,8,∴B中有6个元素, 故选C. (2)当x=0,y=0时,x-y=0;当x=0,y=1时,x-y=-1;当x=0,y=2时,x-y =-2;当x=1,y=0时,x-y=1;当x=1,y=1时,x-y=0;当x=1,y=2时,x -y=-1;当x=2,y=0时,x-y=2;当x=2,y=1时,x-y=1;当x=2,y=2时, x-y=0.根据集合中元素的互异性知,B中元素有0,-1,-2,1,2,共5个. 答案 (1)C (2)C
【训练4】 (1)若p:x2+x-6=0是q:ax+1=0的必要不充分条件,则实数a的值为 ________. (2) 若 - a<x< - 1 成 立 的 一 个 充 分 不 必 要 条 件 是 - 2<x< - 1 , 则 a 的 取 值 范 围 是 ________.
解析 (1)p:x2+x-6=0,即x=2或x=-3. q:ax+1=0,当 a=0 时,方程无解;当 a≠0 时,x=-1a. 由题意知p q,q p,故a=0舍去;
当 a≠0 时,应有-1a=2 或-1a=-3,解得 a=-12或 a=13. 综上可知,a=-12或 a=13. (2)根据充分条件、必要条件与集合间的包含关系,应有{x|-2<x<-1} {x|-a<x< -1},故有a>2. 答案 (1)-12或13 (2)a>2
高中数学《第一章集合与常用逻辑用语复习课》教学设计
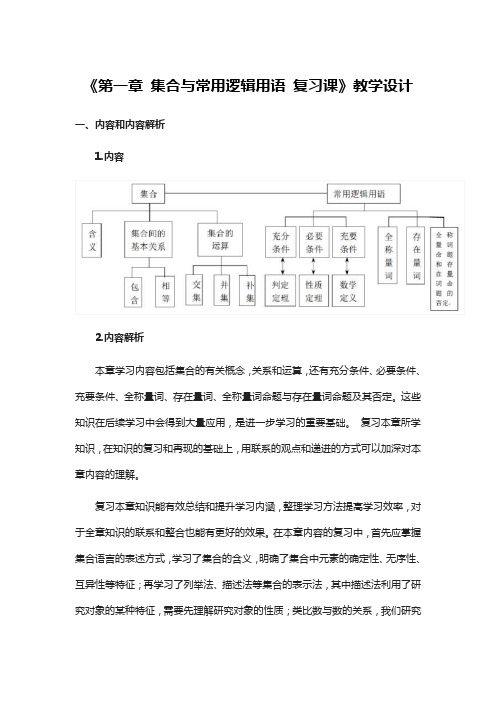
《第一章集合与常用逻辑用语复习课》教学设计一、内容和内容解析1.内容2.内容解析本章学习内容包括集合的有关概念,关系和运算,还有充分条件、必要条件、充要条件、全称量词、存在量词、全称量词命题与存在量词命题及其否定。
这些知识在后续学习中会得到大量应用,是进一步学习的重要基础。
复习本章所学知识,在知识的复习和再现的基础上,用联系的观点和递进的方式可以加深对本章内容的理解。
复习本章知识能有效总结和提升学习内涵,整理学习方法提高学习效率,对于全章知识的联系和整合也能有更好的效果。
在本章内容的复习中,首先应掌握集合语言的表述方式,学习了集合的含义,明确了集合中元素的确定性、无序性、互异性等特征;再学习了列举法、描述法等集合的表示法,其中描述法利用了研究对象的某种特征,需要先理解研究对象的性质;类比数与数的关系,我们研究了集合之间的包含关系与相等关系,这些关系是由元素与集合的关系决定的,其中集合的相等关系很重要;类比数的运算,我们学习了集合的交、并、补运算,通过这些运算可以得到与原有集合紧密关联的集合,由此可以表示研究对象的某些关系。
常用逻辑用语是数学语言的重要组成部分,是逻辑思维的基本语言,也是数学表达和交流的工具。
充分条件、必要条件和充要条件,全称量词命题,存在量词命题及它们的否定都能与许多已学过的内容进行融合,如初中学习过的数学定义、定理、命题及许多代数结论等都可以用常用逻辑用语表示。
利用常用逻辑用语表述数学内容,进行推理论证,可以大大提升表述的逻辑性和准确性,提升逻辑推理素养。
结合以上分析,确定本节课的教学重点是:引领复习全章重点内容。
二、目标和目标解析1.目标(1)理解集合的含义,表示法,明确元素与集合,集合与集合的关系;(2)理解并掌握集合的运算法,能解决集合的交、并、补运算问题;(3)能通过“若p,则q”形式命题的真假性,判断充分条件、必要条件、充要条件;(4)能辨别全称量词命题和存在量词命题的真假,并能写出否定形式。
高三数学(文 新课标)一轮复习课件:第一章 集合与常用逻辑用语 ppt

2019年6月1日
缘分让我们相遇,缘分让我们在一起
1
2.常用逻辑用语 (1)理解命题的概念.
(2)了解“若 p,则 q”形式的命题及其逆命题、否命题
与逆否命题,会分析四种命题的相互关系. (3)理解必要条件、充分条件与充要条件的含义. (4)了.解逻辑联结词“或”“且”“非”的含义. (5)理解全称量词和存在量词的意义.
第一章 集合与常用逻辑用语
考纲链接
1.集合 (1)集合的含义与表示 ①了解集合的含义,体会元素与集合的属于关系. ②能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题. (2)集合间的基本关系 ①理解集合之间包含与相等的含义,能识别给定集合的子集. ②在具体情境中,了解全集与空集的含义. (3)集合的基本运算 ①理解两.个集合的并集与交集的含义,会求两个简单集合的并集与交集. ②理解在给定集合中一个子集的补集的含义,会求给定子集的补集. ③能使用韦恩(Venn)图表达集合间的基本关系及集合的基本运算.
=∅,则实数 a 的取值范围为________.
2019年6月1日
缘分让我们相遇,缘分让我们在一起
19
解:(1)因为{1,a+b,a}=0,ba,b,a≠0, 所以 a+b=0,ba=-1,从而 b=1, 所以 a=-1,b=1,所以 b-a=2.故填 2. (2)由 A=∅知方程 ax2+3x-2=0 无实根, 当 a=0 时,x=23不合题意,舍去;
(6)能正确地对含一个量词的命题进行否定 .
2019年6月1日
缘分让我们相遇,缘分让我们在一起
2
• 1.1 集合及其运算
2019年6月1日
缘分让我们相遇,缘分让我们在一起
3
1.集合的基本概念
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章末复习提升课主题1集合的基本概念(1)已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是()A.1B.3C.5 D.9(2)若-3∈{x-2,2x2+5x,12},则x=________.【解析】(1)①当x=0时,y=0,1,2,此时x-y的值分别为0,-1,-2;②当x=1时,y=0,1,2,此时x-y的值分别为1,0,-1;③当x=2时,y=0,1,2,此时x-y的值分别为2,1,0.综上可知,x-y的可能取值为-2,-1,0,1,2,共5个,故选C.(2)由题意知,x-2=-3或2x2+5x=-3.①当x-2=-3时,x=-1.把x=-1代入,得集合的三个元素为-3,-3,12,不满足集合中元素的互异性;②当2x2+5x=-3时,x=-32或x=-1(舍去),当x=-32时,集合的三个元素为-72,-3,12,满足集合中元素的互异性,由①②知x=-32.【答案】(1)C(2)-3 2解决集合的概念问题应关注的两点(1)研究一个集合,首先要看集合中的代表元素,然后再看元素的限制条件,当集合用描述法表示时,注意弄清其元素表示的意义是什么.(2)对于含有字母的集合,在求出字母的值后,要注意检验集合是否满足互异性.已知集合A={0,m,m2-3m+2},且2∈A,则实数m为() A.2 B.3C.0或3 D.0,2,3均可解析:选B.由2∈A可知:若m=2,则m2-3m+2=0,这与m2-3m+2≠0相矛盾;若m2-3m+2=2,则m=0或m=3,当m=0时,与m≠0相矛盾,当m=3时,此时集合A={0,3,2},符合题意.主题2集合的基本关系已知集合A={x|x<-1或x≥1},B={x|2a<x≤a+1,a<1},若B⊆A,则实数a的取值范围为________.【解析】因为a<1,所以2a<a+1,所以B≠∅.画数轴如图所示.由B⊆A知,a+1<-1或2a≥1.即a<-2或a≥12.由已知a<1,所以a<-2或12≤a<1,即所求a的取值范围是a<-2或12≤a<1.【答案】a<-2或12≤a<1(1)判断两集合关系的两种常用方法一是化简集合,从表达式中寻找两集合间的关系;二是用列举法表示各集合,从元素中寻找关系.(2)处理集合间关系问题的关键点已知两集合间的关系求参数时,关键是将两集合间的关系转化为元素间的关系,进而转化为参数满足的关系.解决这类问题常常需要合理利用数轴、Venn 图帮助分析.同时还要注意“空集”这一“陷阱”,尤其是集合中含有字母参数时,要分类讨论,讨论时要不重不漏.1.已知集合M={x|x2-3x+2=0},N={0,1,2},则下列关系正确的是() A.M=N B.M NC.N⊆M D.N M解析:选B.由集合M={x|x2-3x+2=0}={1,2},N={0,1,2},可知M N.2.已知M={a||a|≥2},A={a|(a-2)(a2-3)=0,a∈M},则集合A的子集共有()A.1个B.2个C.4个D.8个解析:选B.|a|≥2⇒a≥2或a≤-2.又a∈M,(a-2)(a2-3)=0⇒a=2或a=±3(舍),即A中只有一个元素2,故A的子集只有2个,选B.3.已知集合A={x|0<x≤4},B={x|x<a},当A⊆B时,实数a的取值范围为a>c,则c=________.解析:A={x|0<x≤4},B={x|x<a},由A⊆B,得a>4.所以c=4.答案:4主题3集合的运算(1)设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B =()A.{1,-3} B.{1,0}C.{1,3} D.{1,5}(2)若集合A={x|-2<x<1},B={x|x<-1或x>3},则A∩B=()A.{x|-2<x<-1} B.{x|-2<x<3}C.{x|-1<x<1} D.{x|1<x<3}(3)设全集为R,集合A={x|3≤x<6},B={x|2<x<9}.①分别求A∩B,(∁R B)∪A;②已知C={x|a<x<a+1},若C⊆B,求实数a的取值构成的集合.【解】(1)选C.由A∩B={1}得1∈B,所以m=3,B={1,3}.(2)选A.A∩B={x|-2<x<-1}.(3)①A∩B={x|3≤x<6}.因为∁R B ={x |x ≤2或x ≥9},所以(∁R B )∪A ={x |x ≤2或3≤x <6或x ≥9}. ②因为C ⊆B ,如图所示.所以⎩⎪⎨⎪⎧a ≥2,a +1≤9,解得2≤a ≤8,所以所求集合为{a |2≤a ≤8}.(1)集合基本运算的方法①定义法或Venn 图法:集合是用列举法给出的,运算时可直接借助定义求解,或把元素在Venn 图中表示出来,借助Venn 图观察求解;②数轴法:集合是用不等式(组)给出的,运算时可先将不等式在数轴中表示出来,然后借助数轴求解.(2)集合与不等式结合的运算包含的类型及解决办法①不含字母参数:直接将集合中的不等式解出,在数轴上求解;②含有字母参数:若字母的取值影响到不等式的解,要先对字母分类讨论,再求解不等式,然后在数轴上求解.(一题两空)已知集合A ={x |-3<x ≤6},B ={x |b -3<x <b +7},M ={x |-4≤x <5},全集U =R .(1)A ∩M =________;(2)若B ∪(∁U M )=R ,则实数b 的取值范围为________. 解析:(1)因为A ={x |-3<x ≤6}, M ={x |-4≤x <5},所以A ∩M ={x |-3<x <5}. (2)因为M ={x |-4≤x <5}, 所以∁U M ={x |x <-4或x ≥5},又B ={x |b -3<x <b +7},B ∪(∁U M )=R , 所以⎩⎪⎨⎪⎧b -3<-4,b +7≥5,解得-2≤b <-1.所以实数b 的取值范围是-2≤b <-1. 答案:(1){x |-3<x <5} (2)-2≤b <-1 主题4 充分条件、必要条件的判定及应用(1)“x =1”是“x 2-4x +3=0”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件(2)设x ∈R ,则“2-x ≥0”是“-1≤x -1≤1”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件【解析】 (1)若x =1,则x 2-4x +3=0,是充分条件. 若x 2-4x +3=0,则x =1或x =3,不是必要条件. 故选A.(2)由-1≤x -1≤1,得0≤x ≤2,因为0≤x ≤2⇒x ≤2,x ≤2⇒\0≤x ≤2,故“2-x ≥0”是“-1≤x -1≤1”的必要不充分条件,故选B.【答案】 (1)A (2)B判断充分、必要条件的方法(1)定义法:直接判断若p 则q ,若q 则p 的真假.(2)等价法:利用A ⇒B 与﹁B ⇒﹁A ,B ⇒A 与﹁A ⇒﹁B ,A ⇔B 与﹁B ⇔﹁A 的等价关系,对于条件或结论是否定式的命题,一般运用等价法.(3)利用集合间的包含关系判断:若A ⊆B ,则A 是B 的充分条件或B 是A 的必要条件;若A =B ,则A 是B 的充要条件.1.(2020·济南高一检测)“a ≠1或b ≠2”是“a +b ≠3”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件解析:选B.因为“a ≠1或b ≠2”包括三种情况,即a ≠1,b =2,或a =1,b ≠2,或a ≠1且b ≠2,所以a ≠1或b ≠2⇒\a +b ≠3,a +b ≠3⇒a ≠1或b ≠2,所以“a ≠1或b ≠2”是“a +b ≠3”的必要不充分条件.故选B.2.若a ,b 都是实数,试从①ab =0;②a +b =0;③a (a 2+b 2)=0;④ab >0中选出满足下列条件的式子,用序号填空:(1)使a ,b 都为0的必要条件是________; (2)使a ,b 都不为0的充分条件是________; (3)使a ,b 至少有一个为0的充要条件是________. 解析:①ab =0⇔a =0或b =0,即a ,b 至少有一个为0;②a +b =0⇔a ,b 互为相反数,则a ,b 可能均为0,也可能为一正数一负数; ③a (a 2+b 2)=0⇔a =0,b 为任意实数; ④ab >0⇔⎩⎪⎨⎪⎧a >0,b >0或⎩⎪⎨⎪⎧a <0,b <0,即a ,b 同为正数或同为负数.综上可知:(1)使a,b都为0的必要条件是①②③;(2)使a,b都不为0的充分条件是④;(3)使a,b至少有一个为0的充要条件是①.答案:(1)①②③(2)④(3)①主题5全称量词命题与存在量词命题写出下列命题的否定,并判断其真假.(1)p:每一个素数都是奇数;(2)p:能被3整除的数,也能被4整除;(3)p:有些实数的绝对值是正数;(4)p:某些平行四边形是矩形.【解】(1)由于全称量词“每一个”的否定为“存在一个”,因此,﹁p:存在一个素数不是奇数,是真命题.(2)省略了全称量词“所有”,命题的否定为存在一个能被3整除的数,不能被4整除,是真命题.(3)由于存在量词“有些”的否定为“所有”,因此,﹁p:所有实数的绝对值都不是正数,是假命题.(4)由于存在量词“某些”的否定为“每一个”,因此,﹁p:每一个平行四边形都不是矩形,是假命题.全称量词命题、存在量词命题的真假判定(1)全称量词命题的真假判定:要判定一个全称量词命题为真,必须对限定集合M中每一个x验证p(x)成立,一般用代数推理的方法加以证明;要判定一个全称量词命题为假,只需举出一个反例即可.(2)存在量词命题的真假判定:要判定一个存在量词命题为真,只要在限定集合M中,能找到一个x0,使p(x0)成立即可;否则,这一存在量词命题为假.1.命题“∀x∈R,∃n∈N*,使得n≥x2”的否定形式是()A.∀x∈R,∃n∈N*,使得n<x2B.∀x∈R,∀n∈N*,使得n<x2C.∃x∈R,∃n∈N*,使得n<x2D.∃x∈R,∀n∈N*,使得n<x2解析:选 D.将“∀”改写为“∃”,“∃”改写为“∀”,再否定结论可得,命题的否定为“∃x∈R,∀n∈N*,使得n<x2”.2.判断下列命题的真假.(1)平面内存在两条相交直线垂直于同一条直线;(2)任何实数都有算术平方根;(3)每个平面四边形的内角和都是360°;(4)至少有一个整数n,使得n2+n为奇数.解:(1)由于平面内垂直于同一条直线的两条直线互相平行,因此平面内不可能存在两条相交直线垂直于同一条直线,故该命题为假命题.(2)当a<0时,实数a不存在算术平方根,故该命题为假命题.(3)任意平面四边形的内角和都是360°,是真命题.(4)因为n2+n=n(n+1),当n为奇数时,n+1为偶数;当n为偶数时,n+1为奇数,故n(n+1)一定是偶数,所以不存在一个整数n,使得n2+n为奇数.故该命题为假命题.。
