第四章 理想流体动力学和平面势流
流体力学第4章9

2014-10-1
28
通过流管中有效截面面积为A的流体体积流量和质量流量分 别积分求得,即
qV vdA
qm vdA
在工程计算中为了方便起见,引入平均流速的概念。平均 流速是一个假想的流速,即假定在有效截面上各点都以相 同的平均流速流过,这时通过该有效截面上的体积流量仍
A
A
与各点以真实流速流动时所得到的体积流量相同。
述三点原因,欧拉法在流体力学研究中广泛被采用。当然
拉格朗日法在研究爆炸现象以及计算流体力学的某些问题 中还是方便的。
2014-10-1 11
第二节 流体运动的一些基本概念
一、流动的分类 (1)按照流体性质分为理想流体的流动和粘性流体的流动, 不可压缩流体的流动和可压缩流体的流动。 (2)按照运动状态分为定常流动和非定常流动,有旋流动 和无旋流动,层流流动和紊流流动,亚声速流动和超声速 流动
在流场中的一些点,流体质点不断流过空间点,空间点上 的速度指流体质点正好流过此空间点时的速度。
用欧拉法求流体质点其他物理量的时间变化率也可以采用
下式的形式,即
D( ) ( ) (V )( ) Dt t
式中,括弧内可以代表描述流体运动的任一物理量,如密
D( ) 度、温度、压强,可以是标量,也可以是矢量。 称为 Dt ( ) 全导数, 称为当地导数, (V )( )称为迁移导数。 t
1、系统:包含确定不变的物质的任何集合。 系统以外的一切称为外界。 边界的性质: ① 边界随流体一起运动; ② 边界面的形状和大小可随时间变化; ③ 系统是封闭的,没有质量交换,可以有能 量交换; ④ 边界上受到外界作用在系统上的表面力;
2014-10-1 31
2、控制体:被流体所流过的,相对于某 个坐标系来讲,固定不变的任何体积。 控制面的性质: ① 总是封闭表面; ② 相对于坐标系是固定的; ③ 在控制面上可以有质量、能量交换; ④ 在控制面上受到控制体以外物体加在 控制体内物体上的力;
工程流体水力学第四章习题答案
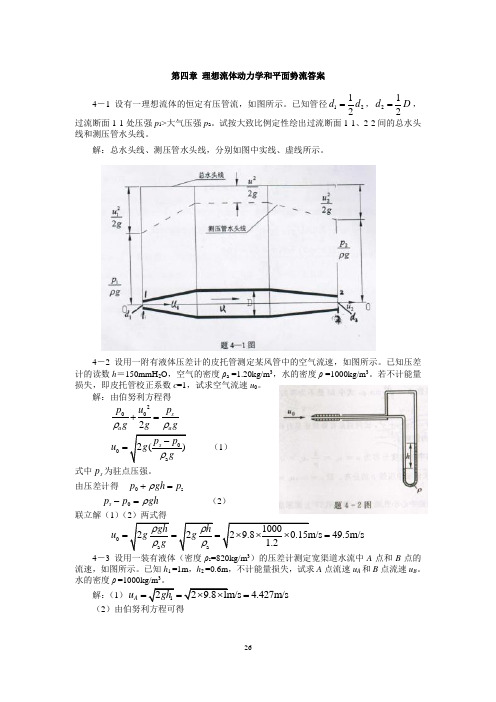
第四章 理想流体动力学和平面势流答案4-1 设有一理想流体的恒定有压管流,如图所示。
已知管径1212d d =,212d D =,过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解:总水头线、测压管水头线,分别如图中实线、虚线所示。
4-2 设用一附有液体压差计的皮托管测定某风管中的空气流速,如图所示。
已知压差计的读数h =150mmH 2O ,空气的密度ρa =1.20kg/m 3,水的密度ρ =1000kg/m 3。
若不计能量损失,即皮托管校正系数c =1,试求空气流速u 0。
解:由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=(1) 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= (2)联立解(1)(2)两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4-3 设用一装有液体(密度ρs =820kg/m 3)的压差计测定宽渠道水流中A 点和B 点的流速,如图所示。
已知h 1 =1m ,h 2 =0.6m ,不计能量损失,试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解:(1)1229.81m/s 4.427m/s A u gh ==⨯⨯= (2)由伯努利方程可得22A AA u p h g gρ+= (1)22B BB u p h g gρ+= (2)式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由(1)、(2)式可得2222A B A BA B p p u u h h g g gρ-=+-- (3) 由压差计得,22ρρρρ--++=A A s B B p gh gh gh gh p ,所以220.82A BA B p p h h h h gρ-=+-- (4) 由(3)式、(4)式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
流体力学第四章

• 在每一个微元流束的有效截面上,各点的速度可认为是相同的 总流:无数微元流束的总和。
38
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
均匀流与非均匀流·渐变流和急变流
均匀流——同一条流线上各空间点上的流速相 同的流动,流线是平行直线,各有效截面上的 流速分布沿程不变 非均匀流——同一条流线上各空间点上的流速不 同的流动,流线不是平行直线,即沿流程方向速 度分布不均
迹线· 流线 1、迹线 1)定义:某一质点在某一时段内的运动轨迹 线。 2)迹线的微分方程
dx dy dz dt ux u y uz
烟火的轨迹为迹线
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
25
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
一维、二维和三维流动
三维流动:流动参数是x、y、z三个坐标的函数
的流动。
二维流动:流动参数是x、y两个坐标的函数的
流动。
一维流动:是一个坐标的函数的流动。
26
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
x= x (t)
dux ux ux dx ux dy ux dz ax dt t x dt y dt z dt
(1)当地加速度(时变加速度):流动过程中流体 由于速度随时间变化而引起的加速度; (2)迁移加速度(位变加速度):流动过程中流体 由于速度随位置变化而引起的加速度。
北航水力学 第四章理想流体动力学和恒定平面势流解读

z1
p1
u12 2g
z2
p2
u22 2g
4.2.2 由动能定理推导理想流体的伯努利方程
推导过程同学们自学
z1
p1
u12 2g
z2
p2
u22 2g
本公式是由动能定理推导而得,它使伯努利方程有更加明确的 物理意义,说明伯努利方程是一能量方程。
第三节 元流伯努利方程的意义和应用
4.3.1 沿流线的伯努利方程的水力学意义
可见,在同一流线上各点的流函数为一常数,故等流函数线就是流线。
2、平面内任意两点流函数值的差等于通过这两点连线的流量。
y ABdrBnA x
d r dxi dy j
n cos i sin j dy i dx j
dr dr V ui v j
dq V
ndr
u
dy dr
v
dx dr
等 线和等Ψ线,这两族曲线互相垂直,构
成流网。
两族曲线所构成的正交网络,称为流网
流网的特征:
流网
等 线和速度矢量垂直,或者说, 等 线与等Ψ线(流线)垂直,
【例题】
已知90度角域内无粘流动,速度分布
ux kx uy ky
(k 0, x 0, y 0)
求:(1)判断该流场是否存在速度势函数, 若存在请给出并画出等势线;
流动。但粘滞性对流动 的影响很微小时,影响可以忽略。 --机械能守恒
引入势流的意义:使问题简化。
波浪运动,无分离的边界层外部的流动,多孔介质的流动(渗流) 等等可以看为势流。
4.4.1 流速势函数
以二维流动为例,根据流体运动学,它与无旋流动等价
由 ux 0 无旋流的条件→涡量 z 0
流体力学教学大纲

中央广播电视大学“开放教育试点”土木工程专业(专升本)流体力学课程教学大纲中央广播电视大学2001年12月《流体力学》教学大纲第一部分大纲说明一、课程的性质与任务流体力学是中央广播电视大学“开放教育试点”工学科土建类土木工程专业的一门公共必修课程。
该课程的主要任务是使学生掌握流体(水流)运动的一般规律和有关的基本概念、基本原理、基本方法和一定的试验技能,注意培养学生发现和解决问题的能力,为学习专业课程、从事专业技术工作或进行科学研究打下基础。
二、课程的教学基本要求学生学完本课程后应达到下列基本要求:1.具有一定的理论基础。
正确理解流体力学的基本概念。
掌握连续性方程、能量方程、动量方程的应用。
掌握水流运动的分析方法。
认识量纲分析与实验的关系。
2.对工程中的一般流体问题具有分析和计算的能力。
3.掌握一定的实验技能与方法,具有测量运动参数、分析实验数据和编写实验报告的能力。
三、课程教学要求的层次有关定义、定理、性质、特征等概念的内容按“知道、了解、理解”三个层次要求;有关计算、解法、公式、法则等方法的内容按“会、掌握、熟练掌握”三个层次要求;实验按“观察、学会、能、测定、掌握、应用”六个层次要求。
第二部分学时、教学安排、教材与教学环节一、学时分配与学分1.学时分配本课程共72学时2.学分本课程共4学分。
二、教学安排流体力学课程安排在第三学期,一个学期完成全部教学任务。
三、文字教材根据远距离教育要求,本课程的文字教材以文字主教材和文字辅助教材两部分组成,并采用合一式编排。
文字教材是学生学习课程的主要用书,主教材部分的内容是课程的基本内容,是教学的主要依据。
辅教材部分的内容是对主教材相应内容进行归纳、总结,通过例题与习题,帮助学生理解和掌握课程的内容。
文字教材是学生获得知识和提高能力的重要媒体之一,教材的内容要具有科学性,概念叙述要准确无误,方法的阐述要详细,论证要清楚,要体现远程开放教育的特点,要适合成人、以业余学习为主的特点,要便于自学。
第4章理想流体动力学

Q=0.036m3/s,水柱的来流速度V=30m/s,若被截取的流量
Q=0.012m3/s,试确定水柱作用在板上的合力R和水流的偏
转角
(略去水的重量及粘性)。 解:设水柱的周围均为大气压。由于不计重力,因此由伯努利方程可知
由连续方程
取封闭的控制面如图,并建立 坐标,设平板对射流柱的作用力为 (由于不考虑粘性,仅为压力)。由动量定理
<<
,
<<
以及与水箱A中流出的流量相比,从B中吸出的流量为小量。) 解:(1)在
及
的假定下,本题可看作小孔出流 由Torricelli定理
处为基准,对水箱 自由液面及最小截面
建立总流伯努利方程 其中
, 故 要使最小截面处压强
低于大气压即为负值必须使 由连续方程
得 故
得此时的条件应为 (2)若从水槽中吸出水时,需具备的条件为 或者 将 代入
时,
例如,当 则
【4.18】 如图,锅炉省煤气的进口处测得烟气负压 h1=10.5mmH2O,出口负压h2=20mmH2O。如炉外空气 ρ=1.2kg/m3,烟气的密度ρ'= 0.6 kg/m3,两测压断面高度 差H=5m,试求烟气通过省煤气的压强损失。 解:本题要应用非空气流以相对压强表示的伯努利方程形式。 由进口断面1至出口断面2列伯努利方程
即 或者 ,
由于 将上述不等式代入
得 【4.14】 如图,一消防水枪,向上倾角
水管直径D=150mm,压力表读数p=3m水柱高,喷嘴直径 d=75mm,求喷出流速,喷至最高点的高程及在最高点的 射流直径。 解:不计重力,对压力表截面1处至喷咀出口2处列伯努利方程
其中
得
式得
另外,由连续方程 得 上式代入
工程流体力学习题及答案
第1章绪论选择题【】按连续介质的概念,流体质点是指:()流体的分子;(b)流体内的固体颗粒;(c)几何的点;(d)几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
解:流体质点是指体积小到可以看作一个几何点,但它又含有大量的分子,且具有诸如速度、密度及压强等物理量的流体微团。
()【】与牛顿内摩擦定律直接相关的因素是:()切应力和压强;(b)切应力和剪切变形速度;(c)切应力和剪切变形;(d)切应力和流速。
解:牛顿内摩擦定律是,而且速度梯度是流体微团的剪切变形速度,故。
()【】流体运动黏度υ的国际单位是:()m2/s;(b)N/m2;(c)kg/m;(d)N·s/m2。
解:流体的运动黏度υ的国际单位是。
()【】理想流体的特征是:()黏度是常数;(b)不可压缩;(c)无黏性;(d)符合。
解:不考虑黏性的流体称为理想流体。
()【】当水的压强增加一个大气压时,水的密度增大约为:()1/20 000;(b)1/1 000;(c)1/4 000;(d)1/2 000。
解:当水的压强增加一个大气压时,其密度增大约。
()【】从力学的角度分析,一般流体和固体的区别在于流体:()能承受拉力,平衡时不能承受切应力;(b)不能承受拉力,平衡时能承受切应力;(c)不能承受拉力,平衡时不能承受切应力;(d)能承受拉力,平衡时也能承受切应力。
解:流体的特性是既不能承受拉力,同时具有很大的流动性,即平衡时不能承受切应力。
()【】下列流体哪个属牛顿流体:()汽油;(b)纸浆;(c)血液;(d)沥青。
解:满足牛顿内摩擦定律的流体称为牛顿流体。
()【】时空气和水的运动黏度,,这说明:在运动中()空气比水的黏性力大;(b)空气比水的黏性力小;(c)空气与水的黏性力接近;(d)不能直接比较。
解:空气的运动黏度比水大近10倍,但由于水的密度是空气的近800倍,因此水的黏度反而比空气大近50倍,而黏性力除了同流体的黏度有关,还和速度梯度有关,因此它们不能直接比较。
第4章流体动力学基础1
2、连续性微分方程有哪几种形式?不可压缩流体的连续性 、连续性微分方程有哪几种形式? 微分方程说明了什么问题? 微分方程说明了什么问题? 质量守恒
第二节 元流的伯努利方程
欧拉运动微分方程组各式分别乘以 , , ( 欧拉运动微分方程组各式分别乘以dx,dy,dz(流场任意相邻两点间距 各式分别乘以 ds的坐标分量): 的坐标分量): 的坐标分量
1 ( Xdx +Ydy + Zdz) − ρ ( ∂p dx + ∂p dy + ∂p dz) = dux dx + ∂x ∂y ∂z dt duy dt
dy + duz dz dt
<I> 考虑条件 、 考虑条件 1、恒定流
<II>
<III>
一、在势流条件下的积分
∂p ∂p =0 ∂t
∂ux ∂uy ∂uz = = =0 ∂t ∂t ∂t
∂ux ∂y ∂uy ∂z ∂ux ∂z
= = =
∂uy ∂x ∂uz ∂y ∂uz ∂x
积分得:
z+γ +
p
u2 2g
=c
•
理想势流(无黏性) 理想势流(无黏性)伯努利方程
z+γ +
p
或
u2 2g
=c
p2 u22 2g
z1 + γ +
p1
u12 2g
= z2 + γ +
在同一恒定不可压缩流体重力势流 恒定不可压缩流体重力势流中 物理意义:在同一恒定不可压缩流体重力势流中 ,各点的总比能值相等 即在整个势流场中,伯努利常数 均相等。(应用条件 均相等。(应用条件: 即在整个势流场中,伯努利常数C均相等。(应用条件:“——”所示) ”所示)
流体力学ppt课件-流体动力学
g
g
2g
水头
,
z
p
g
v2
2g
总水头, hw 水头损失
第二节 热力学第一定律——能量方程
水头线的绘制
总水头线
hw
对于理想流体,总水
1
v12 2g
2
v22 2g
头线是沿程不变的,
测压管水头线
p2
为一水平直线,对于
g
实际流体,总水头沿 程降低,但测压管水
p1 g
头线沿程有可能降低、
z2
不变或者升高。
z1
v2 A2 e2
u22 2
gz2
p2
v1A1 e1
u12 2
gz1
p1
微元流管即为流线,如果不 可压缩理想流体与外界无热 交换,热力学能为常数,则
u2 gz p 常数
2
这个方程是伯努利于1738年首先提出来的,命名为伯努利 方程。伯努利方程的物理意义是沿流线机械能守恒。
第二节 热力学第一定律——能量方程
皮托在1773年用一根弯成直角的玻璃管,测量了法国塞纳河 的流速。原理如图所示,在液体管道某截面装一个测压管和 一个两端开口弯成直角的玻璃管(皮托管),皮托管一端正 对来流,一端垂直向上,此时皮托管内液柱比测压管内液柱 高h,这是因为流体流到皮托管入口A点受到阻滞,速度降为 零,流体的动能变化为压强势能,形成驻点A,A处的压强称 为总压,与A位于同一流线且在A上游的B点未受测压管的影 响,其压强与A点测压管测得的压强相等,称为静压。
第四章 流体动力学
基本内容
• 雷诺输运公式 • 能量方程 • 动量方程 • 流体力学方程应用
第一节 雷诺输运方程
• 前面解决了流体运动的表示方法,但要在流 体上应用物理定律还有困难.
流体力学《流体力学》学习大纲学习目的:本课程是专业基础课程之一
《流体力学》学习大纲学习目的:本课程是专业基础课程之一,它的任务和目的是使学生掌握流体力学的基本概念、基本原理、基本方法和基本技能,并具有一定的分析、解决本专业中涉及流体力学问题的能力,为学习后续专业课程、从事专业技术工作或进行科学研究打下坚实的基础。
学习要求:要求学生通过本课程学习,应该能够掌握流体的主要物理物质;能够掌握流体静压强的分布规律和总压力的计算;能够掌握不可压缩、恒定流动条件下理想流体与粘性流体的基本概念、流动规律、基本方程;能够运用基本理论和基本方程分析一些基本流动,掌握流体在运动状态下基本力学参量计算的基本方法;能够掌握孔口、管嘴、短管、长管的计算;能够掌握明渠均匀流的水力计算,掌握恒定明渠非均匀渐变流的微分方程,学会分析水面曲线;能够掌握堰流分类及其计算;能够掌握渗流基本定律,了解完全井的浸润线方程和出流量计算;能够正确理解因次分析和相似原理对实验的指导意义。
1. 绪论1. 了解流体的主要物理性质:惯性,重力特性,粘性和压缩性和膨胀性,理解掌握流体的粘性和牛顿内摩擦定律。
2. 理解质量力和表面力,掌握其表示方法。
3. 流体的力学模型:连续介质模型,理想流体模型,不可压缩流体模型。
了解流体力学的主要研究方法。
2. 流体静力学1. 理解和掌握静压强及其特性。
2. 了解欧拉平衡微分方程的推导,理解欧拉平衡微分方程的物理意义。
3. 掌握流体静力学基本方程,掌握点压强的计算方法,掌握压强的计算基准和表示方法,掌握静压强分布图,了解压强的量测方法。
4. 掌握计算作用于平面和曲面上的液体总压力。
3. 流体运动学1. 了解描述流体运动的两种方法:拉格朗日法,欧拉法;了解质点加速度表达式。
2. 掌握迹线、流线的概念;掌握描述流体运动的一些基本概念:流管和流束,过流断面,元流和总流,流量,断面平均流速等。
3. 掌握流体运动的连续性微分方程和总流的连续性方程。
4. 了解流体运动微分方程。
5. 掌握实际流体元流w h g u p z g u p z +++=++2222222111γγ和总流伯努利方程+=++2211112z g v p z αγ w h g v p ++22222αγ的物理意义、几何意义以及应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二节 伯努利方程
1 2 1 2 1 2 2 2 2 2 2 2 u u u dx u u u dy u u u x y z x y z x y z dz x 2 y 2 z 2
x, y C d uy dx ux dy 0
dx dy 得平面流线方程:u u x y
第三节 恒定平面势流
(2)不可压缩流体的平面流动中,任意两条流线 的流函数之差dψ 等于这两条流线间所通过的单位 宽度流量dq。
dq un dn u ndn
u x cos n, x u y cos n, y dn
或 2 0
称为流函数的拉普拉斯方程形式 适用条件:不可压缩流体的平面有势流动。
第三节 恒定平面势流
(2)极坐标
d ur rd u dr
1 r u r ur
2.流函数的物理意义 (1)流函数等值线 x, y C 就是流线。
q 亦即网格内流量q=常数,又 u n u n
,所以各网格内
1
意义: 已知一点流速 其他各点流速
u2
2
n1
第三节 恒定平面势流
2 2 p p u u p 压强场: 1 2 z2 z1 2 1 g g 2g
已知一点压强 其他各点压强
2.质量力:ρ dxdydz 由牛顿第二运动定律 F ma ,x方向有:
dx p PM pM A p dydz 2 x dx p PN pN A p dydz 2 x
第一节 理想流体的运动微分方程—欧拉运 动微分方程
du y duz 1 p p p dux f dx f dy f dz dx dy dz dx dy dz x x y z dt y z dt dt
<Ⅰ> <Ⅱ> <Ⅲ>
一、在势流条件下的积分 1.恒定流 2.均匀不可压缩流体,即 =const f x f y 0, f z g 3.质量力只有重力,
du y du x du z dx dy dz <Ⅲ> dt dt dt
u y u y u y ux ux ux ux uy uz uy uz dy dx u x y z y z x x u z u z u z ux uy uz dz y z x
dj ur dr u rd
r 1 j u r ur
第三节 恒定平面势流
三、流函数 1.流函数的形式 (1)直角坐标 ux u y 连续性微分方程: x y
u y ux 0 x y
y uy x ux
dux p dx p dx p dydz p dydz f x dxdydz dxdydz x 2 x 2 dt
u y ux uz 1 p dux ux fx ux uy uz x dt t x y z
ux u y u y uz ux uz 4.有势流动,满足式: , , y x z y z x
第二节 伯努利方程 <Ⅰ> f x dx f y dy f z dz gdz
p 1 p p p dx dy dz d <Ⅱ> x y z
p u2 z C g 2g
注意:积分常数C,在非粘性、不可压恒定流中, 沿同一流线保持不变。一般不同流线各不相 同。
第二节 伯努利方程
三、皮托管
pc u 2 H g 2 g
pc Hp g
u2 h 2g
u 2gh
第三节 恒定平面势流
一、基本方程组 对于不可压缩恒定二元势流,有以下条件: 1.平面无旋,即 z 0
第三节 恒定平面势流
d uy dx ux dy 0 ,为流线斜率 等流线簇:(x,y)=C,
uy dy dx const ux
dy dy 1 dx j const dx const
为流线斜率。
,得证。
(2)流网中每一网格的边长之比(s/n)等于j 和的增值之比(j/),若取j=,则流网 网格为正方形网格。
必要条件 uy dx ux dy 存在全微分dψ,
d u y dx ux dy dx dy x y
第三节 恒定平面势流
式中:ψ—不可压缩流体平面流动的流函数。 u x u y 对平面势流,有 y x ,则
2 2 2 0 2 x y
u y u y u y 1 p du y u y fy ux uy uz y dt t x y z uz uz uz 1 p duz uz fz ux uy uz z dt t x y z
第二节 伯努利方程
2 p1 u12 p2 u2 z1 z2 g 2g g 2g
第二节 伯努利方程
物理意义:在同一恒定不可压缩流体重力势流中, 理想流体各点的总比能相等,即在整个 势流场中,伯努利常数C均相等。
物理意义 z
p g
几何意义 位置水头 压强水头
单位重流体的位能 (比位能) 单位重流体的压能 (比压能)
u2 u2 u2 u2 dx dy dz d x 2 y 2 z 2 2
u2 p 由以上得: gdz d d 2 p u2 理想势流伯努利方程: z g 2 g C
u x u y 0 2.恒定流,即 t t
3.不可压缩流体,即 =const。
第三节 恒定平面势流
欧拉运动微分方程可简化为:
u x u x 1 p fx ux uy x x y u u 1 p fy ux y u y y y x y
第二节 伯努利方程
u2 2g
单位重流体的动能 (比动能) 单位重流体总势能 (比势能) 单位重流体总能量
流速水头 测压管水头
p z g p u2 z g 2g
(总比能)
总水头
第二节 伯努利方程
(二)沿流线的积分 1.只有重力作用的不可压缩恒定流,有 <Ⅰ> -gdz 1 <Ⅱ> dp
dx dy dz ux , u y , uz 2.恒定流中流线与迹线重合: dt dt dt 2 1 u 2 2 <Ⅲ> ux dux u y du y uz duz d ux2 u y uz d 2 2
第二节 伯努利方程
沿流线(或元流)的能量方程:
不可压缩流体的连续性微分方程为:
ux u y 0 x y
第三节 恒定平面势流
二、流速势函数(势函数) u x 存在条件:不可压缩无旋流,即 z 0 或 y 必要条件 ux dx uy dy 存在全微分dj 1、直角坐标 j ux x j j ux dx u y dy dj dx dy j
x y
uy y
u y x
Байду номын сангаас
式中:j—无旋运动的流速势函数,简称势函数。
第三节 恒定平面势流
代入连续性微分方程
2j 2j 2 0 2 x y
ux u y 0 x y
2 j 0 或
,有:
即势函数的拉普拉斯方程形式。 适用条件:不可压缩流体的有势流动。 2、极坐标 j
第三节 恒定平面势流
证明:取相邻两线间的差值 为Δ C,流线间隔为Δ n,等 势线间隔为Δ s,
us
us
q C A n n
j j C s s s
s n
第三节 恒定平面势流
*2.流网的绘制 3.流网的应用 流速场:因流网中,任两相邻流线之间ψ相同,
ux dy uy dx d
第三节 恒定平面势流
四、流网 流网:恒定平面势流中,流线簇与等势线簇构成的 正交网格。 1.流网的性质 (1)等势线与等流函数线处处正交 等势线簇:j(x,y)=C,dj uy dx ux dy 0
ux dy 为等势线斜率。 dx j const uy
第四章 理想流体动力学和 平面势流
第一节 理想流体的运动微分方程—欧拉运 动微分方程 理想流体的动水压强特性与静水压强特 性相同: 动压强的方向总是沿着作用面的内法线 方向; 理想流体中任一点的动压强大小与其作 用面的方位无关,即
px py pz p
第一节 理想流体的运动微分方程—欧拉运 动微分方程 1.表面力 τ =0
