2021年人教版高中数学必修第一册:第4章《章末复习课》(含答案详解)
部编版高中数学必修一第四章指数函数与对数函数带答案知识点总结(超全)

(名师选题)部编版高中数学必修一第四章指数函数与对数函数带答案知识点总结(超全)单选题1、已知函数f (x )=log a (x −b )(a >0且a ≠1,a ,b 为常数)的图象如图,则下列结论正确的是( )A .a >0,b <−1B .a >0,−1<b <0C .0<a <1,b <−1D .0<a <1,−1<b <02、下列计算中结果正确的是( )A .log 102+log 105=1B .log 46log 43=log 42=12 C .(log 515)3=3log 515=−3D .13log 28=√log 283=√33 3、若32是函数f (x )=2x 2−ax +3的一个零点,则f (x )的另一个零点为( ) A .1B .2C .(1,0)D .(2,0)4、Logistic 模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位:天)的Logistic 模型:I(t)=K1+e −0.23(t−53),其中K 为最大确诊病例数.当I (t ∗)=0.95K 时,标志着已初步遏制疫情,则t ∗约为( )(ln19≈3)A .60B .63C .66D .695、果农采摘水果,采摘下来的水果会慢慢失去新鲜度.已知某种水果失去新鲜度h 与其采摘后时间t (天)满足的函数关系式为ℎ=m ⋅a t .若采摘后10天,这种水果失去的新鲜度为10%,采摘后20天,这种水果失去的新鲜度为20%.那么采摘下来的这种水果多长时间后失去40%新鲜度( )A .25天B .30天C .35天D .40天6、下列各组函数中,表示同一个函数的是( )A .y =1与y =x 0B .y =x 与y =(√x)2C .y =2log 2x 与y =log 2x 2D .y =ln 1+x 1−x 与y =ln (1+x )−ln (1−x )7、设f(x)=log 2(1x+a +1)是奇函数,若函数g(x)图象与函数f(x)图象关于直线y =x 对称,则g(x)的值域为( )A .(−∞,−12)∪(12,+∞)B .(−12,12)C .(−∞,−2)∪(2,+∞)D .(−2,2)8、已知0<a <1,b <−1,则函数y =a x +b 的图像必定不经过( )A .第一象限B .第二象限C .第三象限D .第四象限多选题9、若函数y =a x −(b +1)(a >0且a ≠1)的图像过第一、三、四象限,则必有( ).A .0<a <1B .a >1C .b >0D .b <010、(多选题)下列计算正确的是( )A .√(−3)412=√−33B .(a 23b 12)(−3a 12b 13)÷(13a 16b 56)=−9a a >0,b >0 C .√√93=√33D .已知x 2+x −2=2,则x +x −1=211、已知a ,b 均为正实数,若log a b +log b a =52,a b =b a ,则ab =( )A .12B .√22C .√2D .2填空题12、对数型函数f (x )的值域为[0,+∞),且在(0,+∞)上单调递增,则满足题意的一个函数解析式为______.部编版高中数学必修一第四章指数函数与对数函数带答案(十三)参考答案1、答案:D分析:根据函数图象及对数函数的性质可求解.因为函数f (x )=log a (x −b )为减函数,所以0<a <1又因为函数图象与x 轴的交点在正半轴,所以x =1+b >0,即b >−1又因为函数图象与y 轴有交点,所以b <0,所以−1<b <0,故选:D2、答案:A分析:直接根据对数的运算性质及换底公式计算可得;解:对于A :log 102+log 105=log 10(2×5)=log 1010=1,故A 正确;对于B :log 46log 43=log 36,故B 错误; 对于C :(log 515)3=(log 55−1)3=(−log 55)3=−1,故C 错误; 对于D :13log 28=13log 223=13×3log 22=1,故D 错误; 故选:A3、答案:A分析:由32是函数f (x )=2x 2−ax +3的一个零点,可得a 值,再利用韦达定理列方程解出f (x )的另一个零点. 因为32是函数f (x )=2x 2−ax +3的一个零点,所以f (32)=2×(32)2−a ×32+3=0,解得a =5.设另一个零点为x 0,则x 0+32=52,解得x 0=1,所以f (x )的另一个零点为1.故选:A .4、答案:C分析:将t =t ∗代入函数I (t )=K 1+e −0.23(t−53)结合I (t ∗)=0.95K 求得t ∗即可得解.∵I (t )=K 1+e −0.23(t−53),所以I (t ∗)=K 1+e −0.23(t ∗−53)=0.95K ,则e 0.23(t∗−53)=19,所以,0.23(t ∗−53)=ln19≈3,解得t ∗≈30.23+53≈66.故选:C.小提示:本题考查对数的运算,考查指数与对数的互化,考查计算能力,属于中等题.5、答案:B分析:根据给定条件求出m 及a 10的值,再利用给定公式计算失去40%新鲜度对应的时间作答.依题意,{10%=m ⋅a 1020%=m ⋅a 20,解得m =120,a 10=2,当ℎ=40%时,40%=120⋅a t , 即40%=120⋅a 10⋅a t−10,解得a t−10=4=(a 10)2=a 20,于是得t −10=20,解得t =30,所以采摘下来的这种水果30天后失去40%新鲜度.故选:B6、答案:D分析:分别计算每个选项中两个函数的定义域和对应关系,定义域和对应关系都相同的是同一个函数,即可得正确选项.对于A :y =1定义域为R ,y =x 0定义域为{x|x ≠0},定义域不同不是同一个函数,故选项A 不正确; 对于B :y =x 定义域为R ,y =(√x)2的定义域为{x|x ≥0},定义域不同不是同一个函数,故选项B 不正确; 对于C :y =2log 2x 的定义域为{x|x >0},y =log 2x 2定义域为{x|x ≠0},定义域不同不是同一个函数,故选项C 不正确;对于D :由1+x 1−x >0可得(x +1)(x −1)<0,解得:−1<x <1,所以y =ln 1+x 1−x 的定义域为{x|−1<x <1},由{1+x >01−x >0可得−1<x <1,所以函数y =ln (1+x )−ln (1−x )的定义域为{x|−1<x <1}且y =ln (1+x )−ln (1−x )=ln 1+x 1−x ,所以两个函数定义域相同对应关系也相同是同一个函数,故选项D 正确, 故选:D.7、答案:A分析:先求出f(x)的定义域,然后利用奇函数的性质求出a 的值,从而得到f(x)的定义域,然后利用反函数的定义,即可求出g(x)的值域.因为f(x)=log 2(1x+a +1),所以1x+a +1=1+x+a x+a >0可得x <−a −1或x >−a ,所以f(x)的定义域为{x|x <−a −1或x >−a},因为f(x)是奇函数,定义域关于原点对称,所以−a −1=a ,解得a =−12, 所以f(x)的定义域为(−∞,−12)∪(12,+∞), 因为函数g(x)图象与函数f(x)图象关于直线y =x 对称,所以g(x)与f(x)互为反函数,故g(x)的值域即为f(x)的定义域(−∞,−12)∪(12,+∞).故选:A .8、答案:A解析:根据指数函数的图象结合图象的平移可得正确的选项.因为0<a <1,故y =a x 的图象经过第一象限和第二象限,且当x 越来越大时,图象与x 轴无限接近.因为b <−1,故y =a x 的图象向下平移超过一个单位,故y =a x +b 的图象不过第一象限.故选:A .9、答案:BC分析:对底数a 分情况讨论即可得答案.解:若0<a <1,则y =a x −(b +1)的图像必过第二象限,而函数y =a x −(b +1)(a >0且a ≠1)的图像过第一、三、四象限,所以a >1.当a >1时,要使y =a x −(b +1)的图像过第一、三、四象限,则b +1>1,即b >0.故选:BC小提示:此题考查了指数函数的图像和性质,属于基础题.10、答案:BC解析:根据根式运算和指数幂的运算法则求解判断.A. √(−3)412=√3412=√33,故错误;B. (a 23b 12)(−3a 12b 13)÷(13a 16b 56)=−9a23+12−16b 12+13−56=−9a ,故正确; C. √√93=916=(32)16=313=√33,故正确;D. 因为x 2+x −2=(x +x −1)2−2=2,所以(x +x −1)2=4,则x +x −1=±2,故错误; 故选:BC11、答案:AD分析:令t =log a b ,代入可求出t ,可得a 与b 的关系式,再代入a b =b a 即可求出a ,b 的值. 令t =log a b ,则t +1t =52, 所以2t 2−5t +2=0,即(2t −1)(t −2)=0,解得t =12或t =2,即log a b =12或log a b =2,所以a =b 2或a 2=b ,因为a b =b a ,代入得2b =a =b 2或b =2a =a 2,所以a =4,b =2或a =2,b =4,所以a b =2或a b =12.故选:AD.小提示:本题主要考查了对数的运算及性质,属于中档题.12、答案:f (x )=|log 2(x +1)|(答案不唯一,满足f (x )=|log a (x +b )|,a >1,b ≥1即可) 分析:根据题意可利用对数函数的性质和图像的翻折进行构造函数.∵函数f (x )的值域为[0,+∞),且在(0,+∞)上单调递增,∴满足题意的一个函数是f (x )=|log 2(x +1)|.所以答案是:f (x )=|log 2(x +1)|(答案不唯一)。
人教A版高中数学必修第一册第四章章末重构拓展课件

题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
17.(本小题满分15分)设函数f (x)=log2(ax-bx),且f (1)=1,f (2)= log212. (1)求a,b的值; (2)求函数f (x)的零点; (3)设g(x)=ax-bx,求g(x)在[0,4]上的值域.
类型3 指数函数、对数函数的性质及应用 1.以函数的性质为依托,结合运算考查函数的图象性质,以及利用 性质进行大小比较、方程和不等式求解等.在解含对数式的方程或 不等式时,不能忘记对数中真数大于0,以免出现增根或扩大范围. 2.掌握指数函数、对数函数的图象及性质,提升数学运算和逻辑推 理素养.
√ √
时间/min 0
1
2
3
4
水温/℃ 100.00 92.00 84.80 78.37 72.53
5 67.27
设茶水温度从100 ℃开始,经过x min后的温度为y ℃,现给出以下 三种函数模型: ①y=kx+b(k<0,x≥0); ②y=kax+b(k>0,0<a<1,x≥0); ③y=loga(x+k)+b(a>1,k>0,x≥0).
√ √ √
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
√ √
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
高中数学(必修1)全套教材含答案(超好)

特别说明:《高中数学教材》是根据最新课程标准,参考独家内部资料,结合自己颇具特色的教学实践和卓有成效的综合辅导经验精心编辑而成;本套资料分必修系列和选修系列及部分选修4系列。
欢迎使用本资料!本套资料所诉求的数学理念是:(1)解题活动是高中数学教与学的核心环节,(2)精选的优秀试题兼有巩固所学知识和检测知识点缺漏的两项重大功能。
本套资料按照必修系列和选修系列及部分选修4系列的章节编写,每章或节分三个等级:[基础训练A组],[综合训练B组],[提高训练C组]目录:数学1(必修)数学1(必修)第一章:(上)集合[训练A、B、C]数学1(必修)第一章:(中)函数及其表[训练A、B、C]数学1(必修)第一章:(下)函数的基本性质[训练A、B、C] 数学1(必修)第二章:基本初等函数(I)[基础训练A组]数学1(必修)第二章:基本初等函数(I)[综合训练B组]数学1(必修)第二章:基本初等函数(I)[提高训练C组]数学1(必修)第三章:函数的应用[基础训练A组]数学1(必修)第三章:函数的应用[综合训练B组]数学1(必修)第三章:函数的应用[提高训练C组](数学1必修)第一章(上) 集合[基础训练A 组]一、选择题1.下列各项中,不可以组成集合的是( ) A .所有的正数 B .等于2的数 C .接近于0的数 D .不等于0的偶数 2.下列四个集合中,是空集的是( )A .}33|{=+x xB .},,|),{(22R y x x y y x ∈-=C .}0|{2≤x x D .},01|{2R x x x x ∈=+- 3.下列表示图形中的阴影部分的是( )A .()()A CB CB .()()AB A CC .()()A B B CD .()A B C4.下面有四个命题:(1)集合N 中最小的数是1;(2)若a -不属于N ,则a 属于N ; (3)若,,N b N a ∈∈则b a +的最小值为2;(4)x x 212=+的解可表示为{}1,1; 其中正确命题的个数为( )A .0个B .1个C .2个D .3个 5.若集合{},,M a b c =中的元素是△ABC 的三边长, 则△ABC 一定不是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形6.若全集{}{}0,1,2,32U U C A ==且,则集合A 的真子集共有( ) A .3个 B .5个 C .7个 D .8个二、填空题1.用符号"∈”或"∉”填空(1)0______N ,5______N ,16______N (2)1______,_______,______2R Q Q e C Q π-(e 是个无理数) (3{}|,,x x a a Q b Q =∈∈ 2. 若集合{}|6,A x x x N =≤∈,{|}B x x =是非质数,C AB =,则C 的A B C非空子集的个数为。
部编版高中数学必修一第四章指数函数与对数函数带答案知识点归纳总结(精华版)

(名师选题)部编版高中数学必修一第四章指数函数与对数函数带答案知识点归纳总结(精华版)单选题1、已知a =log 20.6,b =log 20.8,c =log 21.2,则( ) A .c >b >a B .c >a >b C .b >c >a D .a >b >c2、函数y =|lg(x +1)|的图像是( )A .B .C .D .3、若f(x)={(6−a)x −a,x <1log a x +3,x ≥1是定义在R 上的增函数,实数a 的取值范围是( )A .[1,5]B .[32,5)C .(32,5)D .(1,5)4、化简(1og 62)2+log 62⋅log 63+2log 63−6log 62的值为( ) A .−log 62B .−log 63C .log 63D .-15、青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L 和小数记录表的数据V 的满足L =5+lgV .已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为( )(√1010≈1.259) A .1.5B .1.2C .0.8D .0.66、已知函数f (x )={−2x,x <0−x 2+2x,x ≥0若关于x 的方程f (x )=12x +m 恰有三个不相等的实数解,则m 的取值范围是( ) A .[0,34]B .(0,34)C .[0,916]D .(0,916) 7、中国的5G 技术领先世界,5G 技术的数学原理之一便是著名的香农公式:C =Wlog 2(1+SN ).它表示:在受噪声干扰的信道中,最大信息传递速度C 取决于信道带宽W ,信道内信号的平均功率S ,信道内部的高斯噪声功率N 的大小,其中SN 叫做信噪比.当信噪比比较大时,公式中真数中的1可以忽略不计.按照香农公式,若不改变带宽W ,而将信噪比SN从1000提升至4000,则C 大约增加了( )附:lg2≈0.3010A .10%B .20%C .50%D .100%8、已知函数f (x )=x 2+e x −12(x <0)与g (x )=x 2+ln (x +a )图象上存在关于y 轴对称的点,则a 的取值范围是( )A .√e )B .(−∞,√e )C .√e )D .(0,√e )多选题9、若直线y =2a 与函数y =|a x −1|(a >0,且a ≠1)的图象有两个公共点,则a 的取值可以是( ) A .14B .13C .12D .2 10、已知函数f(x)=2x 2x +1+m(m ∈R)则下列说法正确的是( )A .f (x )的定义域为R .B .若f(x)为奇函数,则m =−12 C .f(x)在R 上单调递减D .若m =0,则f(x)的值域为(0,1) 11、已知函数f(x)=1−2x1+2x ,则下面几个结论正确的有( ) A .f(x)的图象关于原点对称 B .f(x)的图象关于y 轴对称 C .f(x)的值域为(−1,1) D .∀x 1,x 2∈R ,且x 1≠x 2,f (x 1)−f (x 2)x 1−x 2<0恒成立填空题12、函数f(x)=lg(kx)−2lg(x+1)仅有一个零点,则k的取值范围为________.部编版高中数学必修一第四章指数函数与对数函数带答案(四十七)参考答案1、答案:A分析:由对数函数得单调性即可得出结果. ∵y =log 2x 在定义域上单调递增,∴log 20.6<log 20.8<log 21.2,即c >b >a . 故选:A. 2、答案:A分析:由函数y =lgx 的图象与x 轴的交点是(1,0)结合函数的平移变换得函数y =|lg(x +1)|的图象与x 轴的公共点是(0,0),即可求解.由于函数y =lg(x +1)的图象可由函数y =lgx 的图象左移一个单位而得到,函数y =lgx 的图象与x 轴的交点是(1,0),故函数y =lg(x +1)的图象与x 轴的交点是(0,0),即函数y =|lg(x +1)|的图象与x 轴的公共点是(0,0),显然四个选项只有A 选项满足. 故选:A. 3、答案:B分析:由题意得{6−a >1a >1log a 1+3≥(6−a)−a ,解不等式组可求得答案 因为f(x)={(6−a)x −a,x <1log a x +3,x ≥1是定义在R 上的增函数,所以{6−a >1a >1log a 1+3≥(6−a)−a ,解得32≤a <5, 故选:B 4、答案:A分析:运用对数的运算性质即可求解. 解析:(log 62)2+log 62⋅log 63+2log 63−6log 62=log 62(log 62+log 63)+2log 63−2=log 62+2log 63−2=2(log 62+log 63)−log 62−2=2−log 62−2=−log 62故选:A. 5、答案:C分析:根据L,V 关系,当L =4.9时,求出lgV ,再用指数表示V ,即可求解. 由L =5+lgV ,当L =4.9时,lgV =−0.1, 则V =10−0.1=10−110=√1010≈11.259≈0.8.故选:C. 6、答案:D分析:根据题意,作出函数f (x )={−2x, x <0,−x 2+2x,x ≥0 与y =12x +m 的图像,然后通过数形结合求出答案.函数f (x )={−2x, x <0,−x 2+2x,x ≥0的图像如下图所示:若关于x 的方程f (x )=12x +m 恰有三个不相等的实数解,则函数f (x )的图像与直线y =12x +m 有三个交点, 若直线y =12x +m 经过原点时,m =0,若直线y =12x +m 与函数f (x )=12x +m 的图像相切,令−x 2+2x =12x +m ⇒x 2−32x +m =0,令Δ=94−4m=0⇒m=916.故m∈(0,916).故选:D.7、答案:B分析:根据题意,计算出log24000log21000的值即可;当SN =1000时,C=Wlog21000,当SN=4000时,C=Wlog24000,因为log24000log21000=lg4000lg1000=3+2lg23≈3.60203≈1.2所以将信噪比SN从1000提升至4000,则C大约增加了20%,故选:B.小提示:本题考查对数的运算,考查运算求解能力,求解时注意对数运算法则的运用.8、答案:B分析:f(x)=x2+e x−12(x<0)关于y轴对称的函数为:f(−x)=x2+e−x−12(x>0),函数f(x)=x2+e x−12(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,即f(−x)=g(x)有解,通过数形结合即可得解.f(x)=x2+e x−12(x<0)关于y轴对称的函数为:f(−x)=x2+e−x−12(x>0),函数f(x)=x2+e x−12(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,即f(−x)=g(x)有解,即x2+e−x−12=x2+ln(x+a),整理的:e−x−12=ln(x+a),y=e−x−12和y=ln(x+a)的图像存在交点,如图:临界值在x=0处取到(虚取),此时a=√e,和y=ln(x+a)的图像存在交点,故当a<√e时y=e−x−12故选:B.9、答案:AB分析:对a分类讨论,利用数形结合分析得解.,(1)当a>1时,由题得0<2a<1,∴0<a<12因为a>1,所以此种情况不存在;,(2)当0<a<1时,由题得0<2a<1,∴0<a<12因为0<a<1,所以0<a<1.2故选:AB小提示:方法点睛:取值范围问题的求解,常用的方法:(1)函数法;(2)导数法;(3)数形结合法;(4)基本不等式法. 要根据已知条件灵活选择方法求解.10、答案:ABD分析:根据函数的定义域的求法,可判定A正确;根据函数的奇偶性列出方程,求得m的值,可判定B正确,化简f(x)=−12x+1+m+1,结合指数函数的单调性,可判定C错误;化简函数f(x)=1−12x+1,结合指数函数的值域,可判定D正确.由题意,函数f(x)=2x2x+1+m(m∈R),对于A中,由2x+1≠0,所以函数f(x)的定义域为R,所以A正确;对于B中,由函数f(x)为奇函数,则满足f(−x)=−f(x),即2−x2−x+1+m=−2x2x+1−m,所以2m=−2x2x+1−2−x2−x+1=−2x2x+1−12x12x+1=−2x2x+1−12x+1=−1,即m=−12,所以B不正确;对于C中,由f(x)=2x2x+1+m=2x+1−12x+1+m=−12x+1+m+1,因为函数y=2x+1为单调递增函数,则y=−12x+1递增函数,所以f(x)函数在R上单调递减,所以C不正确;对于D中,当m=0时,可得f(x)=2x2x+1=1−12x+1,因为2x+1>1,可得−1<−12x+1<0,所以1−12x+1∈(0,1),即函数f (x )的值域为(0,1),所以D 正确. 故选:ABD. 11、答案:ACD分析:利用奇函数的定义和性质可判断AB 的正误,利用参数分离和指数函数的性质可判断CD 的正误. 对于A ,f(x)=1−2x 1+2x ,则f(−x)=1−2−x 1+2−x =2x −11+2x=−f(x),则f(x)为奇函数,故图象关于原点对称,故A 正确.对于B ,计算f(1)=−13,f(−1)=13≠f(1),故f(x)的图象不关于y 轴对称,故B 错误. 对于C ,f(x)=1−2x 1+2x=−1+21+2x,1+2x =t,t ∈(1,+∞),故y =f(x)=−1+2t,易知:−1+2t∈(−1,1),故f(x)的值域为(−1,1),故C 正确. 对于D ,f(x)=1−2x1+2x =−1+21+2x , 因为y =1+2x 在R 上为增函数,y =−1+21+t为(1,+∞)上的减函数,由复合函数的单调性的判断法则可得f (x )在R 上单调递减, 故∀x 1,x 2∈R ,且x 1≠x 2,f(x 1)−f(x 2)x 1−x 2<0恒成立,故D 正确.故选:ACD.小提示:方法点睛:复合函数的单调性的研究,往往需要将其转化为简单函数的复合,通过内外函数的单调性结合“同增异减”的原则来判断. 12、答案:(−∞,0)∪{4}分析:由题意f(x)仅有一个零点,令y 1=kx 、y 2=(x +1)2,即y 1、y 2在f(x)定义域内只有一个交点,讨论k >0、k <0并结合函数图象,求k 的范围.由题意,f(x)=lg(kx)−2lg(x +1)=0,即lg(kx)=lg(x +1)2, ∴在f(x)定义域内,y 1=kx 、y 2=(x +1)2只有一个交点, 当k >0时,即(0,+∞)上y 1、y 2只有一个交点;∴仅当y 1、y 2相切,即x 2+(2−k)x +1=0中Δ=(2−k)2−4=0,得k =4或k =0(舍),∴当k=4时,(0,+∞)上y1、y2只有一个交点;当k<0时,即(−1,0)上y1、y2只有一个交点,显然恒成立.∴k∈(−∞,0)∪{4}.所以答案是:(−∞,0)∪{4}。
高中数学选择性必修第一册章末复习课
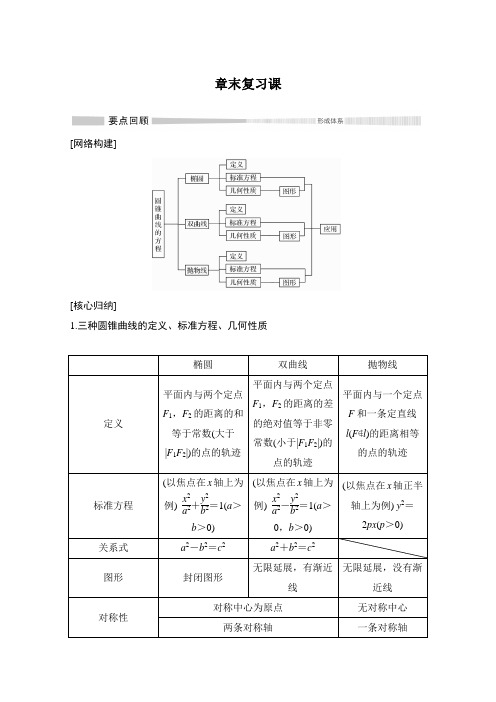
章末复习课[网络构建][核心归纳]1.三种圆锥曲线的定义、标准方程、几何性质椭圆双曲线抛物线定义平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹平面内与一个定点F和一条定直线l(F∉l)的距离相等的点的轨迹标准方程(以焦点在x轴上为例)x2a2+y2b2=1(a>b>0)(以焦点在x轴上为例)x2a2-y2b2=1(a>0,b>0)(以焦点在x轴正半轴上为例) y2=2px(p>0)关系式a2-b2=c2a2+b2=c2图形封闭图形无限延展,有渐近线无限延展,没有渐近线对称性对称中心为原点无对称中心两条对称轴一条对称轴2.求圆锥曲线的标准方程 (1)椭圆、双曲线的标准方程求椭圆、双曲线的标准方程包括“定位”和“定量”两方面,一般先确定焦点的位置,再确定参数.当焦点位置不确定时,要分情况讨论.也可将椭圆方程设为Ax 2+By 2=1(A >0,B >0,A ≠B ),其中当1A >1B 时,焦点在x 轴上,当1A <1B 时,焦点在y 轴上;双曲线方程可设为Ax 2+By 2=1(AB <0),当1A <0时,焦点在y 轴上,当1B <0时,焦点在x 轴上.另外,与已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)共渐近线的双曲线方程可设为x 2a 2-y 2b 2=λ(λ≠0);已知所求双曲线为等轴双曲线,其方程可设为x 2-y 2=λ(λ≠0). (2)抛物线的标准方程求抛物线的标准方程时,先确定抛物线的方程类型,再由条件求出参数p 的大小.当焦点位置不确定时,要分情况讨论,也可将方程设为y 2=2mx (m ≠0)或x 2=2my (m ≠0),然后建立方程求出参数m 的值. 3.直线与圆锥曲线有关的问题(1)直线与圆锥曲线的位置关系,可以通过讨论直线方程与曲线方程组成的方程组的实数解的个数来确定,通常消去方程组中的变量y (或x )得到关于变量x (或y )的一元二次方程,考虑该一元二次方程的判别式Δ,则有Δ>0⇔直线与圆锥曲线相交于两点;Δ=0⇔直线与圆锥曲线相切于一点;Δ<0⇔直线与圆锥曲线无交点. (2)直线l 截圆锥 曲线所得的弦长|AB |=(1+k 2)(x 1-x 2)2=⎝ ⎛⎭⎪⎫1+1k 2(y 1-y 2)2(k ≠0),其中k 是直线l 的斜率,(x 1,y 1),(x 2,y 2)是直线与圆锥曲线的两个交点A ,B 的坐标,且(x 1-x 2)2=(x 1+x 2)2-4x 1x 2,(y 1-y 2)2=(y 1+y 2)2-4y 1y 2,x 1+x 2,x 1x 2,y 1+y 2,y 1y 2可由一元二次方程的根与系数的关系整体给出.要点一 数形结合思想“数形结合”指的是在处理数学问题时,能够将抽象的数学语言与直观的几何图形有机结合起来思索,促使抽象思维和形象思维的和谐结合,通过对规范图形或示意图形的观察分析,化抽象为直观,化直观为精确,从而使问题得到解决. 【例1】 双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,若P 为双曲线上一点,且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为( ) A.(1,3) B.(1,3] C.(3,+∞) D.[3,+∞)解析 如图所示,由|PF 1|=2|PF 2|知P 在双曲线的右支上, 则|PF 1|-|PF 2|=2a , 又|PF 1|=2|PF 2|, ∴|PF 1|=4a ,|PF 2|=2a . 在△F 1PF 2中,由余弦定理得 cos ∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1||PF 2|=16a 2+4a 2-4c 22×4a ·2a =54-c 24a 2=54-e 24,∵0<∠F 1PF 2≤π,且当点P 是双曲线的右顶点时,∠F 1PF 2=π, ∴-1≤cos ∠F 1PF 2<1,∴-1≤54-e 24<1,且e >1,解得1<e ≤3.故选B. 答案 B【训练1】 抛物线y 2=2px (p >0)上有A (x 1,y 1),B (x 2,y 2),C (x 3,y 3)三点,F 是它的焦点,若2|BF |=|AF |+|CF |,则( ) A.2x 2=x 1+x 3 B.2y 2=y 1+y 3 C.2x 3=x 1+x 2D.2y 3=y 1+y 2解析 如图,过A ,B ,C 分别作准线的垂线,垂足分别为A ′,B ′,C ′,由抛物线定义知:|AF |=|AA ′|,|BF |=|BB ′|,|CF |=|CC ′|. ∵2|BF |=|AF |+|CF |, ∴2|BB ′|=|AA ′|+|CC ′|. 又∵|AA ′|=x 1+p2, |BB ′|=x 2+p2, |CC ′|=x 3+p2,∴2⎝ ⎛⎭⎪⎫x 2+p 2=x 1+p 2+x 3+p 2,∴2x 2=x 1+x 3, 故选A. 答案 A要点二 分类讨论思想分类讨论思想是指当所给的对象不能进行统一研究时,我们就需要对研究的对象进行分类,然后对每一类进行研究,得出每一类的结论,最后综合各类的结果得到整个问题的结果.如曲线方程中含有的参数的取值范围不同,对应的曲线也不同,这时要讨论字母的取值范围,有时焦点位置也要讨论,直线的斜率是否存在也需要讨论.【例2】 如果双曲线的两条渐近线的方程为y =±34x ,求此双曲线的离心率. 解 当双曲线的焦点在x 轴上时, 由已知可得b a =34,∵c 2=a 2+b 2,∴e 2=⎝ ⎛⎭⎪⎫c a 2=a 2+b 2a 2=1+b 2a 2=2516,∴双曲线的离心率e =54;同理,当焦点在y 轴上时,可求得离心率e =53. 故双曲线的离心率为54或53.【训练2】 求适合下列条件的椭圆的标准方程. (1)椭圆的长轴长是短轴长的2倍,且过点P (2,-6); (2)椭圆过点P (2,0),且e =22. 解 (1)设椭圆的标准方程为x 2a 2+y 2b 2=1或y 2a 2+x 2b 2=1(a >b >0). 由已知得a =2b .①∵椭圆过点P (2,-6),∴4a 2+36b 2=1或36a 2+4b 2=1.② 由①②得a 2=148,b 2=37或a 2=52,b 2=13. 故所求椭圆的标准方程为x 2148+y 237=1或y 252+x 213=1. (2)当焦点在x 轴上时,∵椭圆过点P (2,0),∴a =2. 又c a =22,∴c = 2. ∴b 2=a 2-c 2=2.此时椭圆的标准方程为x 24+y 22=1.当焦点在y 轴上时,∵椭圆过点P (2,0),∴b =2.又c a =22,∴a 2-b 2a =22,∴a 2=8. 此时椭圆的标准方程为y 28+x 24=1.故所求椭圆的标准方程为x 24+y 22=1或y 28+x 24=1. 要点三 函数与方程思想圆锥曲线中的许多问题,若能运用函数与方程的思想去分析,则往往能较快地找到解题的突破口.最值问题是高中数学中常见的问题,在圆锥曲线问题中也不例外,而函数思想是解决最值问题最有利的武器.我们通常可用建立目标函数的方法解有关圆锥曲线的最值问题.方程思想是从分析问题的数量关系入手,通过联想与类比,将问题中的条件转化为方程或方程组,然后通过解方程或方程组使问题获解,方程思想是高中数学中最基本、最重要的思想方法之一,在高考中占有非常重要的地位.【例3】 已知椭圆mx 2+ny 2=1(m >0,n >0且m ≠n )与直线x +y -1=0相交于A ,B 两点,C 是AB 的中点,若|AB |=22,OC 的斜率为22,求椭圆的方程. 解 法一 设A (x 1,y 1),B (x 2,y 2),代入椭圆方程并作差,得m (x 1+x 2)(x 1-x 2)+n (y 1+y 2)(y 1-y 2)=0.①∵A ,B 为直线x +y -1=0上的点, ∴y 1-y 2x 1-x 2=-1. 由已知得y 1+y 2x 1+x 2=k OC =22,代入①式可得n =2m .直线x +y -1=0的斜率k =-1. 又|AB |=1+k 2|x 2-x 1|=2|x 2-x 1|=22,∴|x 2-x 1|=2.联立mx 2+ny 2=1与x +y -1=0可得(m +n )x 2-2nx +n -1=0,且由已知得x 1,x 2是方程(m +n )x 2-2nx +n -1=0的两根,∴x 1+x 2=2n m +n,x 1x 2=n -1m +n,∴4=(x 2-x 1)2=(x 1+x 2)2-4x 1x 2 =⎝ ⎛⎭⎪⎫2n m +n 2-4·n -1m +n.② 将n =2m 代入②式,解得m =13,∴n =23.∴所求椭圆的方程是x 23+23y 2=1.法二 由⎩⎪⎨⎪⎧mx 2+ny 2=1,x +y -1=0得(m +n )x 2-2nx +n -1=0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=2nm +n ,x 1x 2=n -1m +n ,且直线AB 的斜率k =-1, ∴|AB |=(k 2+1)(x 1-x 2)2=(k 2+1)[(x 1+x 2)2-4x 1x 2]=2·4n 2-4(m +n )(n -1)m +n.∵|AB |=22,∴2·4n 2-4(m +n )(n -1)m +n =22,∴m +n -mn m +n=1.①设C (x ,y ),则x =x 1+x 22=n m +n ,y =1-x =mm +n .∵OC 的斜率为22,∴m n =22,将其代入①式得,m =13,n =23.∴所求椭圆的方程为x 23+23y 2=1.【训练3】 若双曲线x 2a 2-y 216=1(a >0)的离心率为53,则a =________. 解析 由离心率公式,有a 2+16a 2=⎝ ⎛⎭⎪⎫532(a >0),得a =3.故填3.答案 3要点四 化归与转化思想将所研究的对象在一定条件下转化并归结为另一种研究对象的思想方法称之为化归与转化思想.一般将有待解决的问题进行转化,使之成为大家熟悉的或容易解决的问题模式.转化与化归思想在圆锥曲线中经常应用,如把求参数的取值范围问题转化为解不等式(组)问题,把陌生的问题转化为熟悉的问题,需要注意转化的等价性.【例4】 已知点A (4,-2),F 为抛物线y 2=8x 的焦点,点M 在抛物线上移动,当|MA |+|MF |取最小值时,点M 的坐标为( ) A.(0,0) B.(1,-22) C.(2,-4)D.⎝ ⎛⎭⎪⎫12,-2 解析 过点M 作准线l 的垂线,垂足为E ,则由抛物线定义知|MF |=|ME |.当点M 在抛物线上移动时,|MF |+|MA |的值在变化,显然M 移到M ′,使AM ′∥Ox 即A ,M ,E 共线时,|ME |+|MA |最小,把y =-2代入y 2=8x ,得x =12, ∴M ⎝ ⎛⎭⎪⎫12,-2.答案 D【训练4】 如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线C :y 2=4x 上存在不同的两点A ,B 满足P A ,PB 的中点均在C 上.(1)设AB 中点为M ,证明:PM 垂直于y 轴;(2)若P 是半椭圆x 2+y 24=1(x <0)上的动点,求△P AB 面积的取值范围.(1)证明 设P (x 0,y 0),A ⎝ ⎛⎭⎪⎫14y 21,y 1,B ⎝ ⎛⎭⎪⎫14y 22,y 2. 因为P A ,PB 的中点在抛物线上, 所以y 1,y 2为方程⎝ ⎛⎭⎪⎫y +y 022=4×14y 2+x 02,即y 2-2y 0y +8x 0-y 20=0的两个不同的实根.所以y 1+y 2=2y 0,所以AB 的中点M 的纵坐标为y 0, 因此PM 垂直于y 轴.(2)解 由(1)可知⎩⎪⎨⎪⎧y 1+y 2=2y 0,y 1y 2=8x 0-y 20,所以|PM |=18(y 21+y 22)-x 0=18[(y 1+y 2)2-2y 1y 2]- x 0=34y 20-3x 0, |y 1-y 2|=(y 1+y 2)2-4y 1y 2=22(y 20-4x 0).因此,△P AB 的面积S △P AB =12|PM |·|y 1-y 2| =324(y 20-4x 0)32.因为x 20+y 204=1, 又-1≤x 0<0,所以y 20-4x 0=-4x 20-4x 0+4∈[4,5],因此,△P AB 面积的取值范围是⎣⎢⎡⎦⎥⎤62,15104.。
高中数学(必修1)全套教材含答案(超好)之欧阳育创编

特别说明:《高中数学教材》是根据最新课程标准,参考独家内部资料,结合自己颇具特色的教学实践和卓有成效的综合辅导经验精心编辑而成;本套资料分必修系列和选修系列及部分选修4系列。
欢迎使用本资料!本套资料所诉求的数学理念是:(1)解题活动是高中数学教与学的核心环节,(2)精选的优秀试题兼有巩固所学知识和检测知识点缺漏的两项重大功能。
本套资料按照必修系列和选修系列及部分选修4系列的章节编写,每章或节分三个等级:[基础训练A组],[综合训练B组],[提高训练C组]目录:数学1(必修)数学1(必修)第一章:(上)集合 [训练A、B、C]数学1(必修)第一章:(中)函数及其表 [训练A、B、C]数学1(必修)第一章:(下)函数的基本性质[训练A、B、C]数学1(必修)第二章:基本初等函数(I)[基础训练A组]数学1(必修)第二章:基本初等函数(I)[综合训练B组]数学1(必修)第二章:基本初等函数(I ) [提高训练C 组]数学1(必修)第三章:函数的应用[基础训练A 组] 数学1(必修)第三章:函数的应用[综合训练B 组] 数学1(必修)第三章:函数的应用[提高训练C 组] (数学1必修)第一章(上) 集合[基础训练A 组]一、选择题1.下列各项中,不可以组成集合的是( )A .所有的正数B .等于2的数C .接近于0的数D .不等于0的偶数2.下列四个集合中,是空集的是( )A .}33|{=+x xB .},,|),{(22R y x x y y x ∈-=C .}0|{2≤x xD .},01|{2R x x x x ∈=+-3.下列表示图形中的阴影部分的是( ) A .()()A C B CB .()()A B A CC .()()A B B CD .()A B C4.下面有四个命题:(1)集合N 中最小的数是1;(2)若a -不属于N ,则a 属于N ;(3)若,,N b N a ∈∈则b a +的最小值为2;(4)x x 212=+的解可表示为{}1,1;其中正确命题的个数为( )A .0个B .1个C .2个D .3个A B C5.若集合{},,M a b c =中的元素是△ABC 的三边长,则△ABC 一定不是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形6.若全集{}{}0,1,2,32U U C A ==且,则集合A 的真子集共有( )A .3个B .5个C .7个D .8个二、填空题1.用符号“∈”或“∉”填空(1)0______N ,5______N ,16______N (2)1______,_______,______2R Q Q e C Q π-(e 是个无理数)(3{}|,,x x a a Q b Q =+∈∈ 2. 若集合{}|6,A x x x N =≤∈,{|}B x x =是非质数,C A B =,则C 的非空子集的个数为。
人教版版高中数学必修1全册课后习题及答案整理汇总

人教版高中数学必修1课后习题答案第一章 集合与函数概念1.1集合1.1.1集合的含义与表示练习(第5页)1.(1)中国∈A ,美国∉A ,印度∈A ,英国∉A ;中国和印度是属于亚洲的国家,美国在北美洲,英国在欧洲.(2)1-∉A2{|}{0,1}A x x x ===. (3)3∉B 2{|60}{3,2}B x x x =+-==-.(4)8∈C ,9.1∉C 9.1N ∉.2.解:(1)因为方程290x -=的实数根为123,3x x =-=,所以由方程290x -=的所有实数根组成的集合为{3,3}-;(2)因为小于8的素数为2,3,5,7,所以由小于8的所有素数组成的集合为{2,3,5,7}; (3)由326y x y x =+⎧⎨=-+⎩,得14x y =⎧⎨=⎩,即一次函数3y x =+与26y x =-+的图象的交点为(1,4),所以一次函数3y x =+与26y x =-+的图象的交点组成的集合为{(1,4)};(4)由453x -<,得2x <, 所以不等式453x -<的解集为{|2}x x <.1.1.2集合间的基本关系练习(第7页)1.解:按子集元素个数来分类,不取任何元素,得∅;取一个元素,得{},{},{}a b c ;取两个元素,得{,},{,},{,}a b a c b c ;取三个元素,得{,,}a b c ,即集合{,,}a b c 的所有子集为,{},{},{},{,},{,},{,},{,,}a b c a b a c b c a b c ∅.2.(1){,,}a a b c ∈ a 是集合{,,}a b c 中的一个元素;(2)20{|0}x x ∈= 2{|0}{0}x x ==;(3)2{|10}x R x ∅=∈+= 方程210x +=无实数根,2{|10}x R x ∈+==∅;(4){0,1}N (或{0,1}N ⊆) {0,1}是自然数集合N 的子集,也是真子集;(5){0}2{|}x x x = (或2{0}{|}x x x ⊆=) 2{|}{0,1}x x x ==;(6)2{2,1}{|320}x x x =-+= 方程2320x x -+=两根为121,2x x ==.3.解:(1)因为{|8}{1,2,4,8}B x x ==是的约数,所以AB ;(2)当2k z =时,36k z =;当21k z =+时,363k z =+,即B 是A 的真子集,B A ; (3)因为4与10的最小公倍数是20,所以A B =.1.1.3集合的基本运算练习(第11页)1.解:{3,5,6,8}{4,5,7,8}{5,8}A B == ,{3,5,6,8}{4,5,7,8}{3,4,5,6,7,8}A B == .2.解:方程2450x x --=的两根为121,5x x =-=,方程210x -=的两根为121,1x x =-=,得{1,5},{1,1}A B =-=-, 即{1},{1,1,5}A B A B =-=- .3.解:{|}A B x x = 是等腰直角三角形,{|}A B x x = 是等腰三角形或直角三角形.4.解:显然{2,4,6}U B =ð,{1,3,6,7}U A =ð,则(){2,4}U A B = ð,()(){6}U U A B = ðð.1.1集合习题1.1 (第11页) A 组1.(1)237Q ∈ 237是有理数; (2)23N ∈ 239=是个自然数;(3)Q π∉π是个无理数,不是有理数; (4R 是实数;(5Z3=是个整数; (6)2N ∈ 25=是个自然数.2.(1)5A ∈;(2)7A ∉; (3)10A -∈. 当2k =时,315k -=;当3k =-时,3110k -=-;3.解:(1)大于1且小于6的整数为2,3,4,5,即{2,3,4,5}为所求;(2)方程(1)(2)0x x -+=的两个实根为122,1x x =-=,即{2,1}-为所求;(3)由不等式3213x -<-≤,得12x -<≤,且x Z ∈,即{0,1,2}为所求.4.解:(1)显然有20x ≥,得244x -≥-,即4y ≥-,得二次函数24y x =-的函数值组成的集合为{|4}y y ≥-;(2)显然有0x ≠,得反比例函数2y x=的自变量的值组成的集合为{|0}x x ≠;(3)由不等式342x x ≥-,得45x ≥,即不等式342x x ≥-的解集为4{|}5x x ≥.5.(1)4B -∉; 3A -∉; {2}B ; B A ; 2333x x x -<⇒>-,即{|3},{|2}A x x B x x =>-=≥;(2)1A ∈; {1}-A ; ∅A ; {1,1}-=A ; 2{|10}{1,1}A x x =-==-;(3){|}x x 是菱形{|}x x 是平行四边形; 菱形一定是平行四边形,是特殊的平行四边形,但是平行四边形不一定是菱形;{|}x x 是等边三角形{|}x x 是等腰三角形.等边三角形一定是等腰三角形,但是等腰三角形不一定是等边三角形.6.解:3782x x -≥-,即3x ≥,得{|24},{|3}A x x B x x =≤<=≥,则{|2}A B x x =≥ ,{|34}A B x x =≤< .7.解:{|9}{1,2,3,4,5,6,7,8}A x x ==是小于的正整数,则{1,2,3}A B = ,{3,4,5,6}A C = ,而{1,2,3,4,5,6}B C = ,{3}B C = ,则(){1,2,3,4,5,6}A B C = ,(){1,2,3,4,5,6,7,8}A B C = .8.解:用集合的语言说明这项规定:每个参加上述的同学最多只能参加两项,即为()A B C =∅ .(1){|}A B x x = 是参加一百米跑或参加二百米跑的同学; (2){|}A C x x = 是既参加一百米跑又参加四百米跑的同学.9.解:同时满足菱形和矩形特征的是正方形,即{|}B C x x = 是正方形,平行四边形按照邻边是否相等可以分为两类,而邻边相等的平行四边形就是菱形,即{|}A B x x =是邻边不相等的平行四边形ð, {|}S A x x =是梯形ð.10.解:{|210}A B x x =<< ,{|37}A B x x =≤< ,{|3,7}R A x x x =<≥或ð,{|2,10}R B x x x =≤≥或ð,得(){|2,10}R A B x x x =≤≥ 或ð,(){|3,7}R A B x x x =<≥ 或ð,(){|23,710}R A B x x x =<<≤< 或ð, (){|2,3710}R A B x x x x =≤≤<≥ 或或ð.B 组1.4 集合B 满足A B A = ,则B A ⊆,即集合B 是集合A 的子集,得4个子集.2.解:集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示两条直线21,45x y x y -=+=的交点的集合, 即21(,)|{(1,1)}45x y D x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭,点(1,1)D 显然在直线y x =上,得D C .3.解:显然有集合{|(4)(1)0}{1,4}B x x x =--==,当3a =时,集合{3}A =,则{1,3,4},A B A B ==∅ ;当1a =时,集合{1,3}A =,则{1,3,4},{1}A B A B == ;当4a =时,集合{3,4}A =,则{1,3,4},{4}A B A B == ; 当1a ≠,且3a ≠,且4a ≠时,集合{3,}A a =,则{1,3,4,},A B a A B ==∅ .4.解:显然{0,1,2,3,4,5,6,7,8,9,10}U =,由U A B = ,得U B A ⊆ð,即()U U A B B = ðð,而(){1,3,5,7}U A B = ð,得{1,3,5,7}U B =ð,而()U U B B =ðð,即{0,2,4,6,8.9,10}B =.第一章 集合与函数概念1.2函数及其表示1.2.1函数的概念练习(第19页)1.解:(1)要使原式有意义,则470x +≠,即74x ≠-, 得该函数的定义域为7{|}4x x ≠-;(2)要使原式有意义,则1030x x -≥⎧⎨+≥⎩,即31x -≤≤, 得该函数的定义域为{|31}x x -≤≤.2.解:(1)由2()32f x x x =+,得2(2)322218f =⨯+⨯=,同理得2(2)3(2)2(2)8f -=⨯-+⨯-=,则(2)(2)18826f f +-=+=,即(2)18,(2)8,(2)(2)26f f f f =-=+-=;(2)由2()32f x x x =+,得22()3232f a a a a a =⨯+⨯=+, 同理得22()3()2()32f a a a a a -=⨯-+⨯-=-,则222()()(32)(32)6f a f a a a a a a +-=++-=,即222()32,()32,()()6f a a a f a a a f a f a a =+-=-+-=.3.解:(1)不相等,因为定义域不同,时间0t >;(2)不相等,因为定义域不同,0()(0)g x x x =≠.1.2.2函数的表示法练习(第23页)1,y ==,且050x <<,即(050)y x =<<.2.解:图象(A )对应事件(2),在途中遇到一次交通堵塞表示离开家的距离不发生变化;图象(B )对应事件(3),刚刚开始缓缓行进,后来为了赶时间开始加速;图象(D )对应事件(1),返回家里的时刻,离开家的距离又为零; 图象(C )我出发后,以为要迟到,赶时间开始加速,后来心情轻松,缓缓行进.3.解:2,2|2|2,2x x y x x x -≥⎧=-=⎨-+<⎩,图象如下所示.4.解:因为sin 60= ,所以与A 中元素60 相对应的B;因为sin 45=B 相对应的A 中元素是45 .1.2函数及其表示习题1.2(第23页)1.解:(1)要使原式有意义,则40x -≠,即4x ≠,得该函数的定义域为{|4}x x ≠;(2)x R ∈,()f x =都有意义, 即该函数的定义域为R ;(3)要使原式有意义,则2320x x -+≠,即1x ≠且2x ≠,得该函数的定义域为{|12}x x x ≠≠且;(4)要使原式有意义,则4010x x -≥⎧⎨-≠⎩,即4x ≤且1x ≠, 得该函数的定义域为{|41}x x x ≤≠且.2.解:(1)()1f x x =-的定义域为R ,而2()1x g x x=-的定义域为{|0}x x ≠,即两函数的定义域不同,得函数()f x 与()g x 不相等;(2)2()f x x =的定义域为R ,而4()g x =的定义域为{|0}x x ≥,即两函数的定义域不同,得函数()f x 与()g x 不相等;(32x =,即这两函数的定义域相同,切对应法则相同,得函数()f x 与()g x 相等.3.解:(1)定义域是(,)-∞+∞;-∞+∞,值域是(,)(2)定义域是(,0)(0,);-∞+∞,值域是(,0)(0,)-∞+∞(3)定义域是(,)-∞+∞;-∞+∞,值域是(,)(4)定义域是(,)-∞+∞,值域是[2,)-+∞.4.解:因为2()352f x x x =-+,所以2(3(5(28f =⨯-⨯+=+即(8f =+同理,22()3()5()2352f a a a a a -=⨯--⨯-+=++,即2()352f a a a -=++;22(3)3(3)5(3)231314f a a a a a +=⨯+-⨯++=++,即2(3)31314f a a a +=++;22()(3)352(3)3516f a f a a f a a +=-++=-+, 即2()(3)3516f a f a a +=-+.5.解:(1)当3x =时,325(3)14363f +==-≠-,即点(3,14)不在()f x 的图象上;(2)当4x =时,42(4)346f +==--,即当4x =时,求()f x 的值为3-;(3)2()26x f x x +==-,得22(6)x x +=-, 即14x =.6.解:由(1)0,(3)0f f ==,得1,3是方程20x bx c ++=的两个实数根,即13,13b c +=-⨯=,得4,3b c =-=,即2()43f x x x =-+,得2(1)(1)4(1)38f -=--⨯-+=,即(1)f -的值为8.7.图象如下:8.解:由矩形的面积为10,即10xy =,得10(0)y x x =>,10(0)x y y=>,由对角线为d ,即d =,得(0)d x =>,由周长为l ,即22l x y =+,得202(0)l x x x =+>, 另外2()l x y =+,而22210,xy d x y ==+,得(0)l d ===>,即(0)l d =>.9.解:依题意,有2(2d x vt π=,即24v x t d π=, 显然0x h ≤≤,即240v t h d π≤≤,得204h d t vπ≤≤, 得函数的定义域为2[0,]4h d v π和值域为[0,]h .10.解:从A 到B 的映射共有8个.分别是()0()0()0f a f b f c =⎧⎪=⎨⎪=⎩,()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()0()1()0f a f b f c =⎧⎪=⎨⎪=⎩,()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()0f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()1()1()0f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩.B组1.解:(1)函数()r f p =的定义域是[5,0][2,6)- ;(2)函数()r f p =的值域是[0,)+∞; (3)当5r >,或02r ≤<时,只有唯一的p 值与之对应.2.解:图象如下,(1)点(,0)x 和点(5,)y 不能在图象上;(2)省略.3.解:3, 2.522,211,10()[]0,011,122,233,3x x x f x x x x x x --<<-⎧⎪--≤<-⎪⎪--≤<⎪==≤<⎨⎪≤<⎪≤<⎪⎪=⎩图象如下4.解:(1,步行的路程为12x -,得125x t -=+,(012)x ≤≤,即125x t -=,(012)x ≤≤.(2)当4x =时,12483()55t h -=+=≈.第一章 集合与函数概念1.3函数的基本性质1.3.1单调性与最大(小)值练习(第32页)1.答:在一定的范围内,生产效率随着工人数量的增加而提高,当工人数量达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率随着工人数量的增加而降低.由此可见,并非是工人越多,生产效率就越高.2.解:图象如下[8,12]是递增区间,[12,13]是递减区间,[13,18]是递增区间,[18,20]是递减区间.3.解:该函数在[1,0]-上是减函数,在[0,2]上是增函数,在[2,4]上是减函数,在[4,5]上是增函数.4.证明:设12,x x R ∈,且12x x <,因为121221()()2()2()0f x f x x x x x -=--=->,即12()()f x f x >, 所以函数()21f x x =-+在R 上是减函数.5.最小值.1.3.2单调性与最大(小)值练习(第36页)1.解:(1)对于函数42()23f x x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有4242()2()3()23()f x x x x x f x -=-+-=+=,所以函数42()23f x x x =+为偶函数;(2)对于函数3()2f x x x =-,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有33()()2()(2)()f x x x x x f x -=---=--=-,所以函数3()2f x x x =-为奇函数;(3)对于函数21()x f x x+=,其定义域为(,0)(0,)-∞+∞ ,因为对定义域内每一个x 都有22()11()()x x f x f x x x-++-==-=--,所以函数21()x f x x+=为奇函数;(4)对于函数2()1f x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有22()()11()f x x x f x -=-+=+=,所以函数2()1f x x =+为偶函数.2.解:()f x 是偶函数,其图象是关于y 轴对称的;()g x 是奇函数,其图象是关于原点对称的.习题1.3A 组1.解:(1)函数在5(,2-∞上递减;函数在5[,)2+∞上递增; (2)函数在(,0)-∞上递增;函数在[0,)+∞上递减.2.证明:(1)设120x x <<,而2212121212()()()()f x f x x x x x x x -=-=+-,由12120,0x x x x +<-<,得12()()0f x f x ->, 即12()()f x f x >,所以函数2()1f x x =+在(,0)-∞上是减函数;(2)设120x x <<,而1212211211()()x x f x f x x x x x --=-=,由12120,0x x x x >-<,得12()()0f x f x -<, 即12()()f x f x <,所以函数1()1f x x=-在(,0)-∞上是增函数.3.解:当0m >时,一次函数y mx b =+在(,)-∞+∞上是增函数; 当0m <时,一次函数y mx b =+在(,)-∞+∞上是减函数,令()f x mx b =+,设12x x <,而1212()()()f x f x m x x -=-,当0m >时,12()0m x x -<,即12()()f x f x <, 得一次函数y mx b =+在(,)-∞+∞上是增函数;当0m <时,12()0m x x ->,即12()()f x f x >,得一次函数y mx b =+在(,)-∞+∞上是减函数.4.解:自服药那一刻起,心率关于时间的一个可能的图象为5.解:对于函数21622100050x y x =-+-, 当162405012()50x =-=⨯-时,max 307050y =(元),即每辆车的月租金为4050元时,租赁公司最大月收益为307050元.6.解:当0x <时,0x ->,而当0x ≥时,()(1)f x x x =+,即()(1)f x x x -=--,而由已知函数是奇函数,得()()f x f x -=-,得()(1)f x x x -=--,即()(1)f x x x =-, 所以函数的解析式为(1),0()(1),0x x x f x x x x +≥⎧=⎨-<⎩.B 组1.解:(1)二次函数2()2f x x x =-的对称轴为1x =,则函数()f x 的单调区间为(,1),[1,)-∞+∞,且函数()f x 在(,1)-∞上为减函数,在[1,)+∞上为增函数, 函数()g x 的单调区间为[2,4],且函数()g x 在[2,4]上为增函数;(2)当1x =时,min ()1f x =-,因为函数()g x 在[2,4]上为增函数, 所以2min ()(2)2220g x g ==-⨯=.2.解:由矩形的宽为x m ,得矩形的长为3032x m -,设矩形的面积为S , 则23033(10)22x x x S x --==-,当5x =时,2max 37.5S m =, 即宽5x =m 才能使建造的每间熊猫居室面积最大,且每间熊猫居室的最大面积是237.5m .3.判断()f x 在(,0)-∞上是增函数,证明如下:设120x x <<,则120x x ->->,因为函数()f x 在(0,)+∞上是减函数,得12()()f x f x -<-, 又因为函数()f x 是偶函数,得12()()f x f x <,所以()f x 在(,0)-∞上是增函数.复习参考题A 组1.解:(1)方程29x =的解为123,3x x =-=,即集合{3,3}A =-;(2)12x ≤≤,且x N ∈,则1,2x =,即集合{1,2}B =;(3)方程2320x x -+=的解为121,2x x ==,即集合{1,2}C =.2.解:(1)由PA PB =,得点P 到线段AB 的两个端点的距离相等,即{|}P PA PB =表示的点组成线段AB 的垂直平分线; (2){|3}P PO cm =表示的点组成以定点O 为圆心,半径为3cm 的圆.3.解:集合{|}P PA PB =表示的点组成线段AB 的垂直平分线,集合{|}P PA PC =表示的点组成线段AC 的垂直平分线, 得{|}{|}P PA PB P PA PC == 的点是线段AB 的垂直平分线与线段AC 的垂直平分线的交点,即ABC ∆的外心.4.解:显然集合{1,1}A =-,对于集合{|1}B x ax ==,当0a =时,集合B =∅,满足B A ⊆,即0a =; 当0a ≠时,集合1{}B a =,而B A ⊆,则11a =-,或11a=,得1a =-,或1a =, 综上得:实数a 的值为1,0-,或1.5.解:集合20(,)|{(0,0)}30x y A B x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭ ,即{(0,0)}A B = ; 集合20(,)|23x y A C x y x y ⎧-=⎫⎧==∅⎨⎨⎬-=⎩⎩⎭,即A C =∅ ; 集合3039(,)|{(,2355x y B C x y x y ⎧+=⎫⎧==-⎨⎨⎬-=⎩⎩⎭ ; 则39()(){(0,0),(,)}55A B B C =- .6.解:(1)要使原式有意义,则2050x x -≥⎧⎨+≥⎩,即2x ≥,得函数的定义域为[2,)+∞;(2)要使原式有意义,则40||50x x -≥⎧⎨-≠⎩,即4x ≥,且5x ≠, 得函数的定义域为[4,5)(5,)+∞ .7.解:(1)因为1()1x f x x-=+, 所以1()1a f a a -=+,得12()1111a f a a a-+=+=++, 即2()11f a a+=+; (2)因为1()1x f x x-=+, 所以1(1)(1)112a a f a a a -++==-+++,即(1)2a f a a +=-+.8.证明:(1)因为221()1x f x x +=-, 所以22221()1()()1()1x x f x f x x x +-+-===---,即()()f x f x -=; (2)因为221()1x f x x +=-, 所以222211()11()()111()x x f f x x x x++===---, 即1()()f f x x=-.9.解:该二次函数的对称轴为8k x =, 函数2()48f x x kx =--在[5,20]上具有单调性,则208k ≥,或58k ≤,得160k ≥,或40k ≤,即实数k 的取值范围为160k ≥,或40k ≤.10.解:(1)令2()f x x -=,而22()()()f x x x f x ---=-==,即函数2y x -=是偶函数;(2)函数2y x -=的图象关于y 轴对称;(3)函数2y x -=在(0,)+∞上是减函数; (4)函数2y x -=在(,0)-∞上是增函数.B 组1.解:设同时参加田径和球类比赛的有x 人,则158143328x ++---=,得3x =,只参加游泳一项比赛的有15339--=(人), 即同时参加田径和球类比赛的有3人,只参加游泳一项比赛的有9人.2.解:因为集合A ≠∅,且20x ≥,所以0a ≥.3.解:由(){1,3}U A B = ð,得{2,4,5,6,7,8,9}A B = ,集合A B 里除去()U A B ð,得集合B , 所以集合{5,6,7,8,9}B =.4.解:当0x ≥时,()(4)f x x x =+,得(1)1(14)5f =⨯+=;当0x <时,()(4)f x x x =-,得(3)3(34)21f -=-⨯--=; (1)(5),1(1)(1)(3),1a a a f a a a a ++≥-⎧+=⎨+-<-⎩.5.证明:(1)因为()f x ax b =+,得121212(()222x x x x a f a b x x b ++=+=++,121212()()()222f x f x ax b ax b a x x b ++++==++, 所以1212()()(22x x f x f x f ++=; (2)因为2()g x x ax b =++,得22121212121()(2)(242x x x x g x x x x a b ++=++++,22121122()()1[()()]22g x g x x ax b x ax b +=+++++ 2212121()(22x x x x a b +=+++,因为2222212121212111(2)()()0424x x x x x x x x ++-+=--≤,即222212121211(2)()42x x x x x x ++≤+,所以1212()()(22x x g x g x g ++≤.6.解:(1)函数()f x 在[,]b a --上也是减函数,证明如下:设12b x x a -<<<-,则21a x x b <-<-<,因为函数()f x 在[,]a b 上是减函数,则21()()f x f x ->-,又因为函数()f x 是奇函数,则21()()f x f x ->-,即12()()f x f x >,所以函数()f x 在[,]b a --上也是减函数; (2)函数()g x 在[,]b a --上是减函数,证明如下:设12b x x a -<<<-,则21a x x b <-<-<,因为函数()g x 在[,]a b 上是增函数,则21()()g x g x -<-, 又因为函数()g x 是偶函数,则21()()g x g x <,即12()()g x g x >,所以函数()g x 在[,]b a --上是减函数.7.解:设某人的全月工资、薪金所得为x 元,应纳此项税款为y 元,则0,02000(2000)5%,2000250025(2500)10%,25004000175(4000)15%,40005000x x x y x x x x ≤≤⎧⎪-⨯<≤⎪=⎨+-⨯<≤⎪⎪+-⨯<≤⎩ 由该人一月份应交纳此项税款为26.78元,得25004000x <≤,25(2500)10%26.78x +-⨯=,得2517.8x =,所以该人当月的工资、薪金所得是2517.8元.新课程标准数学必修1第二章课后习题解答第二章 基本初等函数(I )2.1指数函数练习(P54)1. a 21=a ,a 43=43a ,a53-=531a,a32-=321a.2. (1)32x =x 32,(2)43)(b a +=(a +b )43,(3)32n)-(m =(m -n )32,(4)4n)-(m =(m -n )2,(5)56q p =p 3q 25,(6)mm 3=m213-=m 25.3. (1)(4936)23=[(76)2]23=(76)3=343216;(2)23×35.1×612=2×321×(23)31×(3×22)61=231311--×3613121+=2×3=6;(3)a 21a 41a 81-=a 814121-+=a 85;(4)2x 31-(21x 31-2x 32-)=x 3131+--4x 3221--=1-4x -1=1x4-.练习(P58)1.如图图2-1-2-142.(1)要使函数有意义,需x -2≥0,即x ≥2,所以函数y =32-x 的定义域为{x |x ≥2};(2)要使函数有意义,需x ≠0,即函数y =(21)x 1的定义域是{x ∣x ≠0}.3.y =2x (x ∈N *)习题2.1 A 组(P59)1.(1)100;(2)-0.1;(3)4-π;(4)x -y .2解:(1)623ba ab=212162122123)(⨯⨯⨯b a a b =23232121--⨯b a =a 0b 0=1.(2)a aa2121=212121a a a⨯=2121a a ⨯=a 21.(3)415643)(mm m m m ∙∙∙=4165413121mm m m m ∙∙=4165413121+++mm=m 0=1.点评:遇到多重根号的式子,可以由里向外依次去掉根号,也可根据幂的运算性质来进行.3.解:对于(1),可先按底数5,再按键,再按12,最后按,即可求得它的值.答案:1.710 0;对于(2),先按底数8.31,再按键,再按12,最后按即可. 答案:2.881 0;对于(3)这种无理指数幂,先按底数3,再按键,再按键,再按2,最后按即可.答案:4.728 8;对于(4)这种无理指数幂,可先按底数2,其次按键,再按π键,最后按即可.答案:8.825 0.4.解:(1)a 31a 43a 127=a1274331++=a 35;(2)a 32a 43÷a 65=a654332-+=a 127;(3)(x 31y43-)12=12431231⨯-⨯yx =x 4y -9;(4)4a 32b 31-÷(32-a 31-b 31-)=(32-×4)31313132+-+b a =-6ab 0=-6a ;(5))2516(462r ts -23-=)23(4)23(2)23(6)23(2)23(452-⨯-⨯-⨯--⨯-⨯rts =6393652----rt s =36964125s r r ;(6)(-2x 41y 31-)(3x 21-y 32)(-4x 41y 32)=[-2×3×(-4)]x 323231412141++-+-yx=24y ;(7)(2x 21+3y41-)(2x 21-3y41-)=(2x 21)2-(3y 41-)2=4x -9y21-;(8)4x 41 (-3x 41y 31-)÷(-6x21-y32-)=3231214141643-++-⨯-y x =2xy 31.点评:进行有理数指数幂的运算时,要严格按法则和运算顺序,同时注意运算结果的形式,但结果不能既有分数指数又有根式,也不能既有分母又有负指数.5.(1)要使函数有意义,需3-x ∈R ,即x ∈R ,所以函数y =23-x 的定义域为R .(2)要使函数有意义,需2x +1∈R ,即x ∈R ,所以函数y =32x +1的定义域为R .(3)要使函数有意义,需5x ∈R,即x ∈R,所以函数y =(21)5x的定义域为R .(4)要使函数有意义,需x ≠0,所以函数y =0.7x1的定义域为{x |x ≠0}.点评:求函数的定义域一是分式的分母不为零,二是偶次根号的被开方数大于零,0的0次幂没有意义.6.解:设经过x 年的产量为y ,一年内的产量是a (1+100p ),两年内产量是a (1+100p )2,…,x 年内的产量是a (1+100p )x ,则y =a (1+100p )x(x ∈N *,x ≤m ).点评:根据实际问题,归纳是关键,注意x 的取值范围.7.(1)30.8与30.7的底数都是3,它们可以看成函数y =3x ,当x =0.8和0.7时的函数值;因为3>1,所以函数y =3x 在R 上是增函数.而0.7<0.8,所以30.7<30.8.(2)0.75-0.1与0.750.1的底数都是0.75,它们可以看成函数y =0.75x ,当x =-0.1和0.1时的函数值;因为1>0.75,所以函数y =0.75x 在R 上是减函数.而-0.1<0.1,所以0.750.1<0.75-0.1.(3)1.012.7与1.013.5的底数都是1.01,它们可以看成函数y =1.01x ,当x =2.7和3.5时的函数值;因为1.01>1,所以函数y =1.01x 在R 上是增函数.而2.7<3.5,所以1.012.7<1.013.5.(4)0.993.3与0.994.5的底数都是0.99,它们可以看成函数y =0.99x ,当x =3.3和4.5时的函数值;因为0.99<1,所以函数y =0.99x 在R 上是减函数.而3.3<4.5,所以0.994.5<0.993.3.8.(1)2m ,2n 可以看成函数y =2x ,当x =m 和n 时的函数值;因为2>1,所以函数y =2x 在R 上是增函数.因为2m <2n ,所以m <n .(2)0.2m ,0.2n 可以看成函数y =0.2x ,当x =m 和n 时的函数值;因为0.2<1,所以函数y =0.2x 在R 上是减函数.因为0.2m <0.2n ,所以m >n .(3)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为0<a <1,所以函数y =a x 在R 上是减函数.因为a m <a n ,所以m >n .(4)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为a >1,所以函数y =a x 在R 上是增函数.因为a m >a n ,所以m >n .点评:利用指数函数的单调性是解题的关键.9.(1)死亡生物组织内碳14的剩余量P 与时间t 的函数解析式为P=(21)57301.当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量为P=(21)573057309⨯=(21)9≈0.002.答:当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量约为死亡前含量的2‰,因此,还能用一般的放射性探测器测到碳14的存在.(2)设大约经过t 万年后,用一般的放射性探测器测不到碳14,那么(21)537010000t <0.001,解得t >5.7.答:大约经过6万年后,用一般的放射性探测器是测不到碳14的.B 组1. 当0<a <1时,a 2x -7>a 4x -12⇒x -7<4x -1⇒x >-3;当a >1时,a 2x -7>a 4x -1⇒2x -7>4x -1⇒x <-3.综上,当0<a <1时,不等式的解集是{x |x >-3};当a >1时,不等式的解集是{x |x <-3}.2.分析:像这种条件求值,一般考虑整体的思想,同时观察指数的特点,要注重完全平方公式的运用.解:(1)设y =x 21+x21-,那么y 2=(x 21+x21-)2=x +x -1+2.由于x +x -1=3,所以y =5.(2)设y =x 2+x -2,那么y =(x +x -1)2-2.由于x +x -1=3,所以y =7.(3)设y =x 2-x -2,那么y =(x +x -1)(x -x -1),而(x -x -1)2=x 2-2+x -2=5,所以y =±35.点评:整体代入和平方差,完全平方公式的灵活运用是解题的突破口.3.解:已知本金为a 元.1期后的本利和为y 1=a +a ×r =a (1+r ),2期后的本利和为y 2=a (1+r )+a (1+r )×r =a (1+r )2,3期后的本利和为y 3=a (1+r )3,…x 期后的本利和为y =a (1+r )x .将a =1 000,r =0.022 5,x =5代入上式得y =a (1+r )x =1 000×(1+0.022 5)5=1000×1.02255≈1118.答:本利和y 随存期x 变化的函数关系式为y =a (1+r )x ,5期后的本利和约为1 118元.4.解:(1)因为y 1=y 2,所以a 3x +1=a -2x .所以3x +1=-2x .所以x =51-.(2)因为y 1>y 2,所以a 3x +1>a -2x .所以当a >1时,3x +1>-2x .所以x >51-.当0<a <1时,3x +1<-2x .所以x <51-.2.2对数函数练习(P64)1.(1)2log 83=; (2)2log 325=; (3)21log 12=-; (4)2711log 33=-2.(1)239=;(2)35125=;(3)2124-=; (4)41381-=3.(1)设5log 25x =,则25255x ==,所以2x =;(2)设21log 16x =,则412216x -==,所以4x =-;(3)设lg1000x =,则310100010x ==,所以3x =;(4)设lg 0.001x =,则3100.00110x -==,所以3x =-;4.(1)1; (2)0; (3)2; (4)2; (5)3; (6)5.练习(P68)1.(1)lg()lg lg lg xyz x y z =++;(2)222lg lg()lg lg lg lg lg 2lg lg xy xy z x y z x y z z =-=++=++;(3)3311lg()lg lg lg lg 3lg lg 22xy x y z x y z =-=+-=+-;(4)2211lg()lg (lg lg )lg 2lg lg 22y z x y z x y z =-=-+=--.2.(1)223433333log (279)log 27log 9log 3log 3347⨯=+=+=+=;(2)22lg1002lg1002lg104lg104====;(3)5lg 0.00001lg105lg105-==-=-; (4)11ln 22e ==3. (1)22226log 6log 3log log 213-===; (2)lg 5lg 2lg101+==;(3)555511log 3log log (3log 1033+=⨯==;(4)13333351log 5log 15log log log 31153--====-.4.(1)1; (2)1; (3)54练习(P73)1.函数3log y x =及13log y x =的图象如右图所示.相同点:图象都在y 轴的右侧,都过点(1,0)不同点:3log y x =的图象是上升的,13log y x =的图象是下降的关系:3log y x =和13log y x =的图象是关于x 轴对称的.2. (1)(,1)-∞; (2)(0,1)(1,)+∞ ;(3)1(,3-∞; (4)[1,)+∞3. (1)1010log 6log 8< (2)0.50.5log 6log 4< (3)2233log 0.5log 0.6> (4) 1.5 1.5log 1.6log 1.4>习题2.2 A 组(P74)1. (1)3log 1x =; (2)41log 6x =; (3)4log 2x =; (4)2log 0.5x= (5) lg 25x = (6)5log 6x =2. (1)527x = (2) 87x = (3) 43x =(4)173x =(5) 100.3x = (6) x e =3. (1)0;(2) 2;(3) 2-;(4)2;(5) 14-; (6) 2.4. (1)lg 6lg 2lg 3a b =+=+;(2) 3lg 42lg 22log 4lg 3lg 3ab===;(3) 2lg122lg 2lg 3lg 3log 1222lg 2lg 2lg 2ba+===+=+; (4)3lg lg 3lg 22b a=-=-5. (1)x ab =; (2) mx n=;(3) 3n x m=;(4)x =.6. 设x 年后我国的GDP 在1999年的GDP 的基础上翻两番,则(10.073)4x += 解得 1.073log 420x =≈. 答:设20年后我国的GDP 在1999年的GDP 的基础上翻两番.7. (1)(0,)+∞; (2) 3(,1]4.8. (1)m n <;(2) m n <;(3) m n >;(4)m n >.9. 若火箭的最大速度12000v =,那么62000ln 112000ln(161402MM M M e m m m m ⎛⎫+=⇒+=⇒+=⇒≈ ⎪⎝⎭答:当燃料质量约为火箭质量的402倍时,火箭的最大速度可达12km/s.10. (1)当底数全大于1时,在1x =的右侧,底数越大的图象越在下方.所以,①对应函数lg y x =,②对应函数5log y x =,③对应函数2log y x =.(2)略. (3)与原函数关于x 轴对称.11. (1)235lg 25lg 4lg 92lg 52lg 22lg 3log 25log 4log 98lg 2lg 3lg 5lg 2lg 3lg 5⋅⋅=⨯⨯=⨯⨯= (2)lg lg lg log log log 1lg lg lg a b c b c a b c a a b c⋅⋅=⨯⨯=12. (1)令2700O =,则312700log 2100v =,解得 1.5v =. 答:鲑鱼的游速为1.5米/秒.(2)令0v =,则31log 02100O=,解得100O =. 答:一条鱼静止时的耗氧量为100个单位.B 组1. 由3log 41x =得:143,43x x -==,于是11044333x x -+=+=2. ①当1a >时,3log 14a <恒成立;②当01a <<时,由3log 1log 4a a a <=,得34a <,所以304a <<.综上所述:实数a 的取值范围是3{04a a <<或1}a >3. (1)当1I = W/m 2时,112110lg 12010L -==;(2)当1210I -= W/m 2时,121121010lg 010L --==答:常人听觉的声强级范围为0120dB .4. (1)由10x +>,10x ->得11x -<<,∴函数()()f x g x +的定义域为(1,1)- (2)根据(1)知:函数()()f x g x +的定义域为(1,1)-∴ 函数()()f x g x +的定义域关于原点对称又∵ ()()log (1)log (1)()()a a f x g x x x f x g x -+-=-++=+∴()()f x g x +是(1,1)-上的偶函数.5. (1)2log y x =,0.3log y x =; (2)3x y =,0.1x y =.习题2.3 A 组(P79)1.函数y =21x是幂函数.2.解析:设幂函数的解析式为f (x )=x α,因为点(2,2)在图象上,所以2=2α.所以α=21,即幂函数的解析式为f (x )=x 21,x ≥0.3.(1)因为流量速率v 与管道半径r 的四次方成正比,所以v =k ·r 4;(2)把r =3,v =400代入v =k ·r 4中,得k =43400=81400,即v =81400r 4;(3)把r =5代入v =81400r 4,得v =81400×54≈3 086(cm 3/s ),即r =5 cm 时,该气体的流量速率为3 086 cm 3/s .第二章 复习参考题A 组(P82)1.(1)11; (2)87; (3)10001; (4)259.2.(1)原式=))(()()(212121212212122121b a b a b a b a -+++-=ba b b a a b b a a -++++-2121212122=b a b a -+)(2;(2)原式=))(()(1121----+-a a a a a a =aa a a 11+-=1122+-a a .3.(1)因为lg 2=a ,lg 3=b ,log 125=12lg 5lg =32lg 210lg2∙=3lg 2lg 22lg 1+-,所以log 125=b a a +-21.(2)因为2log 3a =,3log 7b=37147log 27log 56log 27⨯=⨯=2log 112log 377++=7log 2log 11)7log 2(log 33333÷++÷=b ab a ÷++÷111)1(3=13++ab ab .4.(1)(-∞,21)∪(21,+∞);(2)[0,+∞).5.(32,1)∪(1,+∞);(2)(-∞,2);(3)(-∞,1)∪(1,+∞).6.(1)因为log 67>log 66=1,所以log 67>1.又因为log 76<log 77=1,所以log 76<1.所以log 67>log 76.(2)因为log 3π>log 33=1,所以log 3π>1.又因为log 20.8<0,所以log 3π>log 20.8.7.证明:(1)因为f (x )=3x ,所以f (x )·f (y )=3x ×3y =3x +y .又因为f (x +y )=3x +y ,所以f (x )·f (y )=f (x +y ).(2)因为f (x )=3x ,所以f (x )÷f (y )=3x ÷3y =3x -y .又因为f (x -y )=3x -y ,所以f (x )÷f (y )=f (x -y ).8.证明:因为f (x )=lgxx+-11,a 、b ∈(-1,1),所以f (a )+f (b )=lgb b a a +-++-11lg 11=lg )1)(1()1)(1(b a b a ++--,f (ab b a ++1)=lg (ab b a ab ba +++++-1111)=lg b a ab b a ab +++--+11=lg )1)(1()1)(1(b a b a ++--.所以f (a )+f (b )=f (abba ++1).9.(1)设保鲜时间y 关于储藏温度x 的函数解析式为y =k ·a x (a >0,且a ≠1).因为点(0,192)、(22,42)在函数图象上,所以022192,42,k a k a ⎧=⋅⎪⎨=⋅⎪⎩解得⎪⎩⎪⎨⎧≈==.93.0327,19222a k 所以y =192×0.93x ,即所求函数解析式为y =192×0.93x .(2)当x =30 ℃时,y ≈22(小时);当x =16 ℃时,y ≈60(小时),即温度在30 ℃和16 ℃的保鲜时间约为22小时和60小时.(3)图象如图:图2-210.解析:设所求幂函数的解析式为f (x )=x α,因为f (x )的图象过点(2,22),所以22=2α,即221-=2α.所以α=21-.所以f (x )=x 21-(x >0).图略,f (x )为非奇非偶函数;同时它在(0,+∞)上是减函数.B 组1.A2.因为2a =5b =10,所以a =log 210,b =log 510,所以a 1+b 1=10log 12+10log 15=lg 2+lg 5=lg 10=1.3.(1)f (x )=a 122+-x 在x ∈(-∞,+∞)上是增函数.证明:任取x 1,x 2∈(-∞,+∞),且x 1<x 2.f (x 1)-f (x 2)=a 122+-x -a +1222+x =1222+x -1221+x =)12)(12()22(21221++-x x x x .因为x 1,x 2∈(-∞,+∞),所以.012.01212>+>+x x 又因为x 1<x 2,所以2122x x <即2122x x <<0.所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).所以函数f (x )=a 122+-x 在(-∞,+∞)上是增函数.(2)假设存在实数a 使f (x )为奇函数,则f (-x )+f (x )=0,即a 121+--x +a 122+-x =0⇒a =121+-x +121+x =122+x +121+x =1,即存在实数a =1使f (x )=121+--x 为奇函数.4.证明:(1)因为f (x )=2x x e e --,g (x )=2xx e e -+,所以[g (x )]2-[f (x )]2=[g (x )+f (x )][g (x )-f (x )]=22)(22(xx x x x x x x e e e e e e e e -----++++=e x ·e -x =e x -x =e 0=1,即原式得证.(2)因为f (x )=2x x e e --,g (x )=2xx e e -+,所以f (2x )=222x x e e -+,2f (x )·g (x )=2·2x x e e --·2x x e e -+=222xx e e --.所以f (2x )=2f (x )·g (x ).(3)因为f (x )=2x x e e --,g (x )=2x x e e -+,所以g (2x )=222xx e e -+,[g (x )]2+[f (x )]2=(2xx e e -+)2+(2xx e e --)2=4222222x x x x e e e e --+-+++=222xx e e -+.所以g (2x )=[f (x )]2+[g (x )]2.5.由题意可知,θ1=62,θ0=15,当t =1时,θ=52,于是52=15+(62-15)e -k ,解得k ≈0.24,那么θ=15+47e -0.24t . 所以,当θ=42时,t ≈2.3;当θ=32时,t ≈4.2.答:开始冷却2.3和4.2小时后,物体的温度分别为42 ℃和32 ℃.物体不会冷却到12 ℃.6.(1)由P=P 0e -k t 可知,当t =0时,P=P 0;当t =5时,P=(1-10%)P 0.于是有(1-10%)P 0=P 0e -5k ,解得k =51-ln 0.9,那么P=P 0e t )9.0ln 51(.所以,当t =10时,P=P 0e 9.01051n I ⨯⨯=P 0e ln 0.81=81%P 0.答:10小时后还剩81%的污染物.(2)当P=50%P 0时,有50%P 0=P 0e t )9.0ln 51(,解得t =9.0ln 515.0ln ≈33.答:污染减少50%需要花大约33h .(3)其图象大致如下:图2-3新课程标准数学必修1第三章课后习题解答第三章 函数的应用3.1函数与方程练习(P88)1.(1)令f (x )=-x 2+3x +5,作出函数f (x )的图象(图3-1-2-7(1)),它与x 轴有两个交点,所以方程-x 2+3x +5=0有两个不相等的实数根.(2)2x (x -2)=-3可化为2x 2-4x +3=0,令f (x )=2x 2-4x +3,作出函数f (x )的图象(图3-1-2-7(2)),它与x 轴没有交点,所以方程2x (x -2)=-3无实数根.(3)x2=4x-4可化为x2-4x+4=0,令f(x)=x2-4x+4,作出函数f(x)的图象(图3-1-2-7(3)),它与x轴只有一个交点(相切),所以方程x2=4x-4有两个相等的实数根.(4)5x2+2x=3x2+5可化为2x2+2x-5=0,令f(x)=2x2+2x-5,作出函数f(x)的图象(图3-1-2-7(4)),它与x轴有两个交点,所以方程5x2+2x=3x2+5有两个不相等的实数根.图3-1-2-72.(1)作出函数图象(图3-1-2-8(1)),因为f(1)=1>0,f(1.5)=-2.875<0,所以f(x)=-x3-3x+5在区间(1,1.5)上有一个零点.又因为f(x)是(-∞,+∞)上的减函数,所以f(x)=-x3-3x+5在区间(1,1.5)上有且只有一个零点.(2)作出函数图象(图3-1-2-8(2)),因为f(3)<0,f(4)>0,所以f(x)=2x·ln(x-2)-3在区间(3,4)上有一个零点.又因为f(x)=2x·ln(x-2)-3在(2,+∞)上是增函数,所以f(x)在(3,4)上有且仅有一个零点.(3)作出函数图象(图3-1-2-8(3)),因为f(0)<0,f(1)>0,所以f(x)=e x-1+4x-4在区间(0,1)上有一个零点.又因为f(x)=e x-1+4x-4在(-∞,+∞)上是增函数,所以f(x)在(0,1)上有且仅有一个零点.(4)作出函数图象(图3-1-2-8(4)),因为f(-4)<0,f(-3)>0,f(-2)<0,f(2)<0,f(3)>0,所以f(x)=3(x+2)(x-3)(x+4)+x在(-4,-3),(-3,-2),(2,3)上各有一个零点.图3-1-2-8练习(P91)1.由题设可知f(0)=-1.4<0,f(1)=1.6>0,于是f(0)·f(1)<0,所以函数f(x)在区间(0,1)内有一个零点x0.下面用二分法求函数f(x)=x3+1.1x2+0.9x-1.4在区间(0,1)内的零点.取区间(0,1)的中点x1=0.5,用计算器可算得f(0.5)=-0.55.因为f(0.5)·f(1)<0,所以x0∈(0.5,1).再取区间(0.5,1)的中点x2=0.75,用计算器可算得f(0.75)≈0.32.因为f(0.5)·f(0.75)<0,所以x0∈(0.5,0.75).同理,可得x0∈(0.625,0.75),x0∈(0.625,0.687 5),x0∈(0.656 25,0.687 5).由于|0.687 5-0.656 25|=0.031 25<0.1,所以原方程的近似解可取为0.656 25.2.原方程可化为x+lgx-3=0,令f(x)=x+lgx-3,用计算器可算得f(2)≈-0.70,f(3)≈0.48.于是f(2)·f(3)<0,所以这个方程在区间(2,3)内有一个解x0.下面用二分法求方程x=3-lgx在区间(2,3)的近似解.取区间(2,3)的中点x1=2.5,用计算器可算得f(2.5)≈-0.10.因为f(2.5)·f(3)<0,所以x0∈(2.5,3).再取区间(2.5,3)的中点x2=2.75,用计算器可算得f(2.75)≈0.19.因为f(2.5)·f(2.75)<0,所以x0∈(2.5,2.75).同理,可得x0∈(2.5,2.625),x0∈(2.562 5,2.625),x0∈(2.562 5,2.593 75),x0∈(2.578 125,2.593 75),x0∈(2.585 937 5,2.59 375).由于|2.585 937 5-2.593 75|=0.007 812 5<0.01,所以原方程的近似解可取为2.593 75.习题3.1 A组(P92)1.A,C 点评:需了解二分法求函数的近似零点的条件.2.由x,f(x)的对应值表可得f(2)·f(3)<0,f(3)·f(4)<0,f(4)·f(5)<0,又根据“如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点.”可知函数f(x)分别在区间(2,3),(3,4),(4,5)内有零点.3.原方程即(x+1)(x-2)(x-3)-1=0,令f(x)=(x+1)(x-2)(x-3)-1,可算得f(-1)=-1,f(0)=5.于是f(-1)·f(0)<0,所以这个方程在区间(-1,0)内有一个解.下面用二分法求方程(x+1)(x-2)(x-3)=1在区间(-1,0)内的近似解.取区间(-1,0)的中点x1=-0.5,用计算器可算得f(-0.5)=3.375.因为f(-1)·f(-0.5)<0,所以x0∈(-1,-0.5).再取(-1,-0.5)的中点x2=-0.75,用计算器可算得f(-0.75)≈1.58.因为f(-1)·f(-0.75)<0,所以x0∈(-1,-0.75).同理,可得x0∈(-1,-0.875),x0∈(-0.937 5,-0.875).由于|(-0.875)-(-0.937 5)|=0.062 5<0.1,所以原方程的近似解可取为-0.937 5.4.原方程即0.8x-1-lnx=0,令f(x)=0.8x-1-lnx,f(0)没有意义,用计算器算得f(0.5)≈0.59,f(1)=-0.2.于是f(0.5)·f(1)<0,所以这个方程在区间(0.5,1)内有一个解.下面用二分法求方程0.8x-1=lnx在区间(0,1)内的近似解.取区间(0.5,1)的中点x1=0.75,用计算器可算得f(0.75)≈0.13.因为f(0.75)·f(1)<0,所以x0∈(0.75,1).再取(0.75,1)的中点x2=0.875,用计算器可算得f(0.875)≈-0.04.因为f(0.875)·f(0.75)<0,所以x0∈(0.75,0.875).同理,可得x0∈(0.812 5,0.875),x0∈(0.812 5,0.843 75).由于|0.812 5-0.843 75|=0.031 25<0.1,所以原方程的近似解可取为0.843 75.5.由题设有f(2)≈-0.31<0,f(3)≈0.43>0,于是f(2)·f(3)<0,所以函数f(x)在区间(2,3)内有一个零点.。
新版高一数学必修第一册第四章全部配套练习题(含答案和解析)

新版高一数学必修第一册第四章全部配套练习题(含答案和解析)4.1 指 数基 础 练巩固新知 夯实基础1.下列各式中正确的个数是( )①n a n =(na )n =a (n 是奇数且n >1,a 为实数); ②n a n =(na )n =a (n 是正偶数,a 是实数); ③3a 3+b 2=a +b (a ,b 是实数). A .0 B .1 C .2 D .3 2.化简3a a 的结果是( )A .aB .a 21 C .a2 D .a 31 3.4(-2)4运算的结果是( ) A .2B .-2C .±2D .不确定4.614- 3338+30.125的值为________. 5.化简(π-4)2+3(π-4)3的结果为________. 6.若x <0,则|x |-x 2+x 2|x |=________. 7.写出使下列各式成立的x 的取值范围: (1) 3⎝⎛⎭⎫1x -33=1x -3; (2)(x -5)(x 2-25)=(5-x )x +5.8.(1)化简:3xy 2·xy -1·xy ·(xy )-1(xy ≠0); (2)计算:221-+(-4)02+12-1-(1-5)0·832.能 力 练综合应用 核心素养9.下列各式成立的是( ) A.3m 2+n 2=(m +n )32B .(ba )2=a 21b 21C.6(-3)2=(-3)31D.34=23110.x -2+x 2=22且x >1,则x 2-x-2的值为( )A .2或-2B .-2 C. 6 D .2 11.设a 21-a21-=m ,则a 2+1a等于( )A .m 2-2B .2-m 2C .m 2+2D .m 212.如果x =1+2b ,y =1+2-b ,那么用x 表示y 等于( ) A.x +1x -1 B.x +1x C.x -1x +1 D.x x -113.若a >0,且a x =3,a y =5,则a22yx +=________.14.已知a ∈R ,n ∈N *,给出四个式子:①6(-2)2n ;②5a 2;③6(-3)2n +1;④9-a 4,其中没有意义的是________.(只填式子的序号即可)15.若代数式2x -1+2-x 有意义,化简4x 2-4x +1+24(x -2)4.16.根据已知条件求下列值:(1)已知x =12,y =23,求x +y x -y -x -y x +y 的值;(2)已知a ,b 是方程x 2-6x +4=0的两根,且a >b >0,求a -ba +b的值.【参考答案】1. B 解析 对①,由于n 是大于1的奇数,故①正确;对①,由于n 是偶数,故na n 中a 可取任意实数,而(na )n 中a 只能取非负数,故①错误;对①,b 2=|b |,故结果错误. 2. B 解析 原式=321aa =323a =a 21. 3. A 解析 根据根式的性质得4-24=|-2|=2,选A.4. 32解析 原式=f(522)- 错误!+ 错误! =错误!-错误!+错误!=错误!.5. 0 解析 原式=|π-4|+π-4=4-π+π-4=0.6. 1 解析 ①x <0,①原式=-x -(-x )+-x-x =-x +x +1=1.7. 解 (1)由于根指数是3,故1x -3有意义即可,此时x -3≠0,即x ≠3.(2)①x -5x 2-25=x -52x +5=(5-x )x +5,①⎩⎪⎨⎪⎧x +5≥0x -5≤0,①-5≤x ≤5.8.解 (1)原式=[xy 2·(xy -1) 21]31·(xy )21·(xy )-1=x 31·y 32|x |61|y |61-·|x |21-·|y |21-=x 31·|x |31-=⎩⎪⎨⎪⎧1, x >0-1, x <0. (2)原式=12+12+2+1-22=22-3. 9. D 解析 被开方数是和的形式,运算错误,A 选项错;(b a )2=b 2a 2,B 选项错;6-32>0,(-3)31<0,C 选项错.故选D.10.D 解析因为x -2+x 2=22且x >1,所以x 2>x -2,x 2-x -2>0,故x 2-x -2=x 2+x-22-4=8-4=2.11. C 解析 将a 21-a 21-=m 平方得(a 21-a21-)2=m 2,即a -2+a -1=m 2,所以a +a -1=m 2+2,即a +1a=m 2+2①a 2+1a=m 2+2. 12. D 解析 由x =1+2b ,得2b =x -1,y =1+2-b =1+12b =1+1x -1=x x -1.13. 9 5 解析 a22yx +=(a x )2·(a y )21=32·521=9 5.14. ① 解析 ①中,(-2)2n >0,①6-22n 有意义;①中,根指数为5,①5a 2有意义;①中,(-3)2n +1<0,①6-32n +1没有意义;①中,根指数为9,①9-a 4有意义.15.解 由2x -1+2-x 有意义,则⎩⎪⎨⎪⎧2x -1≥0,2-x ≥0,即12≤x ≤2.故4x 2-4x +1+24x -24=2x -12+24x -24=|2x -1|+2|x -2|=2x -1+2(2-x )=3.16.解 (1)x +y x -y -x -yx +y=错误!-错误!=错误!. 将x =12,y =23代入上式得:原式=4 12×2312-23=413-16=-2413=-83; (2)①a ,b 是方程x 2-6x +4=0的两根,①⎩⎪⎨⎪⎧a +b =6ab =4,①a >b >0,①a >b . ⎝ ⎛⎭⎪⎫a -b a +b 2=a +b -2ab a +b +2ab =6-246+24=210=15, ①a -ba +b=15=55.4.2 第1课时 指数函数及其性质基 础 练巩固新知 夯实基础1.下列函数中,指数函数的个数为( )①y =⎝⎛⎭⎫12x -1;①y =a x (a >0,且a ≠1);①y =1x;①y =⎝⎛⎭⎫122x -1. A .0个 B .1个 C .3个D .4个2.当x ①[-2,2)时,y =3-x -1的值域是( )A .(-89,8]B .[-89,8]C .(19,9)D .[19,9]3.函数y =2x -1的定义域是( )A .(-∞,0)B .(-∞,0]C .[0,+∞)D .(0,+∞)4.函数f (x )=a x 与g (x )=-x +a 的图象大致是( )5.函数y =a x -5+1(a ≠0)的图象必经过点________.6.若函数f (x )=⎩⎪⎨⎪⎧2x ,x <0,-2-x ,x >0,则函数f (x )的值域是________.7.函数f (x )=a x -1(a >0,且a ≠1)的定义域是(-∞,0],求实数a 的取值范围.8.已知函数f (x )=a x -1(x ≥0)的图象经过点(2,12),其中a >0且a ≠1.(1)求a 的值;(2)求函数y =f (x )(x ≥0)的值域.能 力 练综合应用 核心素养9.函数y =5-|x |的图象是( )10.已知函数f (x )=⎩⎪⎨⎪⎧2x ,x >0,x +1,x ≤0.若f (a )+f (1)=0,则实数a 的值等于( )A .-3B .-1C .1D .311.函数f (x )=a x-b的图象如图所示,其中a ,b 均为常数,则下列结论正确的是( )A.a >1,b <0B.a >1,b >0C.0<a <1,b >0D.0<a <1,b <012.若函数f (x )=(a 2-2a +2)(a +1)x 是指数函数,则a =________.13.已知函数f (x )=a x +b (a >0,且a ≠1),经过点(-1,5),(0,4),则f (-2)的值为________. 14.方程|2x -1|=a 有唯一实数解,则a 的取值范围是________. 15.求函数y =(12)x 2-2x +2(0≤x ≤3)的值域.16.已知-1≤x ≤2,求函数f (x )=3+2×3x +1-9x 的最大值和最小值.【参考答案】1. B 解析 由指数函数的定义可判定,只有①正确.2. A 解析 y =3-x -1,x ①[-2,2)上是减函数,①3-2-1<y ≤32-1,即-89<y ≤8.3. C 解析 由2x -1≥0,得2x ≥20,①x ≥0.4. A 解析 当a >1时,函数f (x )=a x 单调递增,当x =0时,g (0)=a >1,此时两函数的图象大致为选项A.5. (5,2) 解析 指数函数的图象必过点(0,1),即a 0=1,由此变形得a 5-5+1=2,所以所求函数图象必过点(5,2).6. (-1,0)①(0,1) 解析 由x <0,得0<2x <1;由x >0,①-x <0,0<2-x <1,①-1<-2-x <0,①函数f (x )的值域为(-1,0)①(0,1).7.解 由题意,当x ≤0时,a x ≥1,所以0<a <1,故实数a 的取值范围是0<a <1. 8.解 (1)①f (x )的图象过点(2,12),①a 2-1=12,则a =12.(2)由(1)知,f (x )=(12)x -1,x ≥0.由x ≥0,得x -1≥-1,于是0<(12)x -1≤(12)-1=2,所以函数y =f (x )(x ≥0)的值域为(0,2]. 9. D 解析 当x >0时,y =5-|x |=5-x =(15)x ,又原函数为偶函数,故选D.10. A 解析 依题意,f (a )=-f (1)=-21=-2,①2x >0,①a ≤0,①f (a )=a +1=-2,故a =-3,所以选A.11. D 解析 从曲线的变化趋势,可以得到函数f (x )为减函数,从而有0<a <1;从曲线位置看,是由函数y =a x(0<a <1)的图象向左平移|-b |个单位长度得到,所以-b >0,即b <0. 12. 1 解析 由指数函数的定义得⎩⎪⎨⎪⎧a 2-2a +2=1,a +1>0,a +1≠1,解得a =1.13. 7 解析 由已知得⎩⎪⎨⎪⎧a -1+b =5,a 0+b =4,解得⎩⎪⎨⎪⎧a =12,b =3,所以f (x )=⎝⎛⎭⎫12x+3,所以f (-2)=⎝⎛⎭⎫12-2+3=4+3=7 14. a ≥1或a =0 解析 作出y =|2x -1|的图象,如图, 要使直线y =a 与图象的交点只有一个,①a ≥1或a =0.15. 解 令t =x 2-2x +2,则y =(12)t ,又t =x 2-2x +2=(x -1)2+1,①0≤x ≤3,①当x =1时,t min =1,当x =3时,t max =5.故1≤t ≤5,①(12)5≤y ≤(12)1,故所求函数的值域[132,12].16. 解 设t =3x ,①-1≤x ≤2,①13≤t ≤9,则f (x )=g (t )=-(t -3)2+12,故当t =3,即x =1时,f (x )取得最大值12;当t =9,即x =2时,f (x )取得最小值-24.4.2 第2课时 指数函数及其性质的应用基 础 练巩固新知 夯实基础1.若(12)2a +1<(12)3-2a ,则实数a 的取值范围是( )A .(1,+∞)B .(12,+∞) C .(-∞,1)D .(-∞,12)2.若函数f (x )=(1-2a )x 在实数集R 上是减函数,则实数a 的取值范围是( )A.⎝⎛⎭⎫12,+∞B.⎝⎛⎭⎫0,12C.⎝⎛⎭⎫-∞,12 D.⎝⎛⎭⎫-12,12 3.设f (x )为奇函数,且当x ≥0时,f (x )=e x -1,则当x <0时,f (x )=( )A .e -x -1 B .e -x +1 C .-e -x -1D .-e -x +14.函数y =a x 在[0,1]上的最大值与最小值的和为3,则函数y =2ax -1在[0,1]上的最大值是( )A .6B .1C .3 D.325.函数y =12221-+⎪⎭⎫ ⎝⎛x x 的值域是( )A .(-∞,4)B .(0,+∞)C .(0,4]D .[4,+∞)6.满足方程4x +2x -2=0的x 值为________. 7.比较下列各组数的大小:(1)0.7-0.3与0.7-0.4;(2)2.51.4与1.21.4; (3)1.90.4与0.92.4.8.已知函数f (x )=⎝⎛⎭⎫13ax 2-4x +3.(1)若a =-1时,求函数f (x )的单调增区间; (2)如果函数f (x )有最大值3,求实数a 的值.能 力 练综合应用 核心素养9.函数f (x )=⎩⎪⎨⎪⎧-x +3a ,x <0,a x ,x ≥0(a >0,且a ≠1)是R 上的减函数,则a 的取值范围是( )A .(0,1) B.⎣⎡⎭⎫13,1 C.⎝⎛⎦⎤0,13 D.⎝⎛⎦⎤0,23 10.若函数f (x )=a |2x -4|(a >0,a ≠1),满足f (1)=19,则f (x )的单调递减区间是( )A .(-∞,2]B .[2,+∞)C .[-2,+∞)D .(-∞,-2]11.已知函数f (x )=a 2-x (a >0且a ≠1),当x >2时,f (x )>1,则f (x )在R 上( )A .是增函数B .是减函数C .当x >2时是增函数,当x <2时是减函数D .当x >2时是减函数,当x <2时是增函数12.已知定义在R 上的奇函数f (x )和偶函数g (x )满足f (x )+g (x )=a x -a -x +2(a >0,且a ≠1).若g (2)=a ,则f (2)等于( )A .2 B.154 C .174 D .a 213.已知a =5-12,函数f (x )=a x ,若实数m 、n 满足f (m )>f (n ),则m 、n 的关系为( ) A .m +n <0B .m +n >0C .m >nD .m <n14.已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=1-2-x ,则不等式f (x )<-12的解集是________________.15.函数y =32x +2·3x -1,x ①[1,+∞)的值域为______________.16.用清水漂洗衣服,若每次能洗去污垢的34,要使存留污垢不超过原来的1%,则至少要漂洗________次.17. 已知f (x )=x (12x -1+12).(1)求f (x )的定义域;(2)判断f (x )的奇偶性,并说明理由; (3)求证:f (x )>0.18. 已知定义域为R 的函数f (x )=b -2x2x +a 是奇函数.(1)求a ,b 的值;(2)用定义证明f (x )在(-∞,+∞)上为减函数.(3)若对于任意t ①R ,不等式f (t 2-2t )+f (2t 2-k )<0恒成立,求k 的范围.【参考答案】1. B 解析 ①函数y =(12)x 在R 上为减函数,①2a +1>3-2a ,①a >12.2. B 解析 由已知,得0<1-2a <1,解得0<a <12,即实数a 的取值范围是⎝⎛⎭⎫0,12.故选B. 3. D 解析 由题意知f (x )是奇函数,且当x ≥0时,f (x )=e x -1,则当x <0时,-x >0,则f (-x )=e -x -1=-f (x ),得f (x )=-e -x +1.故选D.4. C 解析 函数y =a x 在[0,1]上是单调的,最大值与最小值都在端点处取到,故有a 0+a 1=3,解得a =2,因此函数y =2ax -1=4x -1在[0,1]上是单调递增函数,当x =1时,y max =3.5. C 解析 设t =x 2+2x -1,则y =(12)t .因为t =(x +1)2-2≥-2,y =(12)t 为关于t 的减函数,所以0<y =(12)t ≤(12)-2=4,故所求函数的值域为(0,4].6. 0 解析 设t =2x (t >0),则原方程化为t 2+t -2=0,①t =1或t =-2.①t >0,①t =-2舍去.①t =1,即2x =1,①x =0. 7.解 (1)①y =0.7x 在R 上为减函数,又①-0.3>-0.4,①0.7-0.3<0.7-0.4.(2)在同一坐标系中作出函数y =2.5x 与y =1.2x 的图象,如图所示.由图象可知2.51.4>1.21.4.(3)①1.90.4>1.90=1,0.92.4<0.90=1,①1.90.4>0.92.4. 8. 解 (1)当a =-1时,f (x )=⎝⎛⎭⎫13-x 2-4x +3, 令g (x )=-x 2-4x +3=-(x +2)2+7,由于g (x )在(-2,+∞)上递减,y =⎝⎛⎭⎫13x在R 上是减函数, ①f (x )在(-2,+∞)上是增函数,即f (x )的单调增区间是(-2,+∞).(2)令h (x )=ax 2-4x +3,f (x )=⎝⎛⎭⎫13h (x ),由于f (x )有最大值3,所以h (x )应有最小值-1;因此必有⎩⎪⎨⎪⎧a >0,12a -164a=-1,解得a =1,故当f (x )有最大值3时,a 的值为1. 9. B 解析 由单调性定义,f (x )为减函数应满足:⎩⎪⎨⎪⎧0<a <1,3a ≥a 0,即13≤a <1,故选B.10. B 解析 由f (1)=19得a 2=19,所以a =13(a =-13舍去),即f (x )=(13)|2x -4|.由于y =|2x -4|在(-∞,2]上递减,在[2,+∞)上递增,所以f (x )在(-∞,2]上递增,在[2,+∞)上递减. 11. A 解析 令2-x =t ,则t =2-x 是减函数,因为当x >2时,f (x )>1,所以当t <0时,a t >1.所以0<a <1,所以f (x )在R 上是增函数,故选A.12. B 解析 ①f (x )是奇函数,g (x )是偶函数,①由f (x )+g (x )=a x -a -x +2,①得f (-x )+g (-x )=-f (x )+g (x )=a -x -a x +2,① ①+①,得g (x )=2,①-①,得f (x )=a x -a -x .又g (2)=a ,①a =2,①f (x )=2x -2-x ,①f (2)=22-2-2=154.13. D 解析 ①0<5-12<1,①f (x )=a x =(5-12)x,且f (x )在R 上单调递减,又①f (m )>f (n ),①m <n . 14.(-∞,-1) 解析 ①f (x )是定义在R 上的奇函数,①f (0)=0.当x <0时,f (x )=-f (-x )=-(1-2x )=2x -1.当x >0时,由1-2-x <-12,(12)x >32,得x ①①;当x =0时,f (0)=0<-12不成立;当x <0时,由2x -1<-12,2x <2-1,得x <-1.综上可知x ①(-∞,-1).15.[14,+∞) 解析]令3x =t ,由x ①[1,+∞),得t ①[3,+∞).①y =t 2+2t -1=(t +1)2-2≥(3+1)2-2=14.故所求函数的值域为[14,+∞).16. 4 解析 经过第一次漂洗,存留量为总量的14;经过第二次漂洗,存留量为第一次漂洗后的14,也就是原来的⎝⎛⎭⎫142,经过第三次漂洗,存留量为原来的⎝⎛⎭⎫143,…,经过第x 次漂洗,存留量为原来的⎝⎛⎭⎫14x ,故解析式为y =⎝⎛⎭⎫14x .由题意,⎝⎛⎭⎫14x ≤1100,4x ≥100,2x ≥10,①x ≥4,即至少漂洗4次. 17. (1)解 由于2x -1≠0和2x ≠20,故x ≠0,所以函数f (x )的定义域为{x ①R |x ≠0}. (2)解 函数f (x )是偶函数.理由如下:由(1)知函数f (x )的定义域关于原点对称,因为f (x )=x (12x -1+12)=x 2·2x +12x -1,所以f (-x )=-x 2·2-x +12-x -1=-x 2·2-x +1·2x 2-x-1·2x=-x 2·1+2x 1-2x =x 2·2x +12x -1=f (x ),所以f (x )为偶函数.(3)证明 由(2)知f (x )=x 2·2x +12x -1.对于任意x ①R ,都有2x +1>0,若x >0,则2x>20,所以2x-1>0,于是x 2·2x +12x -1>0,即f (x )>0,若x <0,则2x<20,所以2x-1<0,于是x 2·2x +12x -1>0,即f (x )>0,综上知:f (x )>0.18.解 (1)①f (x )为R 上的奇函数,①f (0)=0,b =1.又f (-1)=-f (1),得a =1.(2)任取x 1,x 2①R ,且x 1<x 2,则f (x 1)-f (x 2)=122112212211+--+-x x x x =)12)(12()12)(21()12)(21(211221+++--+-x x x x x x =)12)(12()22(22112++-x x x x ①x 1<x 2,①1222xx->0,又(12x+1)(22x+1)>0,f (x 1)-f (x 2)>0①f (x )为R 上的减函数.(3)①t ①R ,不等式f (t 2-2t )+f (2t 2-k )<0恒成立,①f (t 2-2t )<-f (2t 2-k ) ①f (x )是奇函数,①f (t 2-2t )<f (k -2t 2),①f (x )为减函数,①t 2-2t >k -2t 2. 即k <3t 2-2t 恒成立,而3t 2-2t =3(t -13)2-13≥-13.①k <-13.4.3.1 对数的概念基 础 练巩固新知 夯实基础1.有以下四个结论:①lg(lg 10)=0;①ln(ln e)=0;①若10=lg x ,则x =10;①若e =ln x ,则x =e2.其中正确的是( ) A.①① B.①① C.①① D.①①2.ln e 等于( )A.0B.12 C.1 D.2 3.已知log x 16=2,则x 等于( )A.±4B.4C.256D.2 4.若log 3(a +1)=1,则log a 2+log 2(a -1)=________. 5.=________.6.将下列指数式化成对数式,对数式化成指数式. (1)35=243;(2)2-5=132; (3)log 1381=-4;(4)log 2128=7.7.已知6a =8,试用a 表示下列各式. ①log 68;①log 62;①log 26.8.求下列各式中的x 的值.(1)log x 27=32; (2)log 2x =-23; (3)log x (3+22)=-2; (4)log 5(log 2x )=0;能 力 练综合应用 核心素养9.设a =log 310,b =log 37,则3a -b 的值为( )A.107B.710C.1049D.491010.1)log (3t -= 等于( )A.-2B.-4C.2D.411.已知log 3(log 5a )=log 4(log 5b )=0,则ab 的值为( ) A.1 B.-1 C.5D.1512.方程3log 2x =127的解是________. 13.若log (1-x )(1+x )2=1,则x =________.14.求32log 92log 3223-++的值.15.若x =log 43,求(2x -2-x )2的值.16.已知x =log 23,求23x -2-3x2x -2-x.【参考答案】1.C 解析 lg(lg 10)=lg 1=0,ln(ln e)=ln 1=0,故①①正确;若10=lg x ,则x =1010,故①错误;若e =ln x ,则x =e e ,故①错误.2. B 解析 设ln e =x ,则e x=e =12e ,①x =12.3. B 解析 ①log x 16=2,①x 2=16,①x =±4,注意到x >0,①x =4.4. 1 解析 由log 3(a +1)=1得a +1=3,即a =2,所以log a 2+log 2(a -1)=log 22+log 21=1+0=1.5. 8 解析 设t =,则(3)t =81,4233t =,t2=4,t =8.6.解 (1)log 3243=5;(2)log 2132=-5;(3)⎝⎛⎭⎫13-4=81;(4)27=128. 7.解 ①log 68=a .①由6a=8得6a=23,即362a = ,所以log 62=a3.①由362a =得326a= ,所以log 26=3a .8.解 (1)由log x 27=32,得x 32=27,①x =2723=32=9.(2)由log 2x =-23,得2-23=x ,①x =1322=322.(3)由log x (3+22)=-2,得3+22=x -2,①x =(3+22)-12=2-1. (4)由log 5(log 2x )=0,得log 2x =1.①x =21=2. 9. A 解析 3a -b =3a ÷3b =3log 310÷3log 37=10÷7=107.10. A 解析 3-22=2-22+1=(2)2-22+12=(2-1)2=⎝ ⎛⎭⎪⎫12+12=(2+1)-2.设1)log (3t -=,则(2+1)t=3-22=(2+1)-2,①t =-2. 11. A 解析 由log 3(log 5a )=0得log 5a =1,即a =5,同理b =5,故ab =1. 12. 18 解析 3log 2x =3-3,①log 2x =-3,x =2-3=18.13. -3 解析 由题意知1-x =(1+x )2,解得x =0或x =-3.验证知,当x =0时,log (1-x )(1+x )2无意义, 故x =0时不合题意,应舍去.所以x =-3.14.解 32232log 92log 3log 322log 9323223-++=⨯+=4×3+99=12+1=13.15. 解析 (2x -2-x )2=(2x )2-2+(2-x )2=4x +14x -244log 3log 31424=+- =3+13-2=43.16.解 由x =log 23,得2x =3,①2-x =12x =13,①23x =(2x )3=33=27,2-3x =123x =127, ∴23x-2-3x2x -2-x=27-1273-13=272-13×27-9=72872=919.4.3.2 对数的运算基 础 练巩固新知 夯实基础1.若a>0,且a≠1,则下列说法正确的是( )A .若M =N ,则log a M =log a NB .若log a M =log a N ,则M =NC .若log a M 2=log a N 2,则M =ND .若M =N ,则log a M 2=log a N 2 2.log 29log 23=( ) A.12B .2 C.32 D.923.(多选题)下列等式不成立的是( )A .ln e =1B .13a 2=a -23C .lg(MN )=lg M +lg ND .log 2(-5)2=2log 2(-5)4.设a =log 32,则log 38-2log 36用a 表示的形式是( )A .a -2B .3a -(1+a)2C .5a -2D .-a 2+3a -15.计算:2713 +lg4+2lg5-e ln3=__ __.6.lg 5+lg 20的值是________.7.若log a b·log 3a =4,则b 的值为________.8.溶液的酸碱度是通过pH 刻画的,已知某溶液的pH 等于-lg[H +],其中[H +]表示该溶液中氢离子的浓度(单位:mol/L),若某溶液的氢离子的浓度为10-5 mol/L ,则该溶液的pH 为__ __.9.已知log a 2=m ,log a 3=n .(1)求a 2m-n的值;(2)求log a 18.能 力 练综合应用 核心素养10.若ab>0,给出下列四个等式:①lg(ab)=lga +lgb; ①lg ab =lga -lgb ;①12lg ⎝⎛⎭⎫a b 2=lg a b ;①lg(ab)=1log ab 10. 其中一定成立的等式的序号是( )A .①①①①B .①①C .①①D .①11.已知2a =5b =M ,且2a +1b=2,则M 的值是( )A .2B .2 5C .±25D .40012.已知2x =3,log 483=y ,则x +2y 的值为( )A .3B .8C .4D .log 4813.若x log 34=1,则4x +4-x 的值为( )A .83B .103 C .2D .114.若lg2=a ,lg3=b ,则lg12lg15等于( ) A .2a +b 1+a +b B .2a +2b 1+a +b C .2a +b 2-a +b D .2a +b1-a +b15.(多选题)设a ,b ,c 都是正数,且4a =6b =9c ,那么( )A .ab +bc =2acB .ab +bc =acC .2c =2a +1bD .1c =2b -1a16.lg 52+2lg2-(12)-1=__ __.17.若log a x =2,log b x =3,log c x =6,则log abc x =_ _. 18.求下列各式的值:(1)2log 525+3log 264; (2)lg(3+5+3-5); (3)(lg5)2+2lg2-(lg2)2.19.设a ,b 是方程2(lgx)2-lgx 4+1=0的两个实根,求lg(ab)·(log a b +log b a)的值.【参考答案】1. B [解析] 在A 中,当M =N≤0时,log a M 与log a N 均无意义,因此log a M =log a N 不成立,故A 错误;在B 中,当log a M =log a N 时,必有M>0,N>0,且M =N ,因此M =N 成立,故B 正确;在C 中,当log a M 2=log a N 2时,有M≠0,N≠0,且M 2=N 2,即|M|=|N|,但未必有M =N ,例如M =2,N =-2时,也有log a M 2=log a N 2,但M≠N ,故C 错误;在D 中,若M =N =0,则log a M 2与log a N 2均无意义,因此log a M 2=log a N 2不成立,故D 错误.2. B [解析] 原式=log 29log 23=log 232log 23=2.3.CD [解析] 根据对数式的运算,可得ln e =1,故A 成立;由根式与指数式的互化可得13a 2=a -23 ,故B 成立;取M =-2,N =-1,发现C 不成立;log 2(-5)2=log 252=2log 25, 故D 不成立,故选CD .4. A [解析] ①a =log 32,①log 38-2log 36=3log 32-2(log 32+1)=3a -2(a +1)=a -2.5. 2 [解析] 2713 +lg4+2lg5-e ln3=(33)13 +(lg4+lg25)-e ln3=3+2-3=2. 6. 1 [解析] lg 5+lg 20=lg 100=lg10=1.7. 81 [解析] log a b·log 3a =lgb lga ·lga lg3=lgblg3=4,所以lgb =4lg3=lg34,所以b =34=81.8. 5 [解析] 由题意可知溶液的pH 为-lg[H +]=-lg10-5=5.9. [解析] (1)因为log a 2=m ,log a 3=n ,所以a m =2,a n =3.所以a 2m -n =a 2m ÷a n =22÷3=43.(2)log a 18=log a (2×32)=log a 2+log a 32=log a 2+2log a 3=m +2n .10. D [解析] ①ab>0,①a>0,b>0或a<0,b<0,①①①中的等式不一定成立;①ab>0,①a b >0,12lg ⎝⎛⎭⎫a b 2=12×2lgab =lg ab ,①①中等式成立;当ab =1时,lg(ab)=0,但log ab 10无意义,①①中等式不成立.故选D.11. B [解析] ①2a =5b =M ,①a =log 2M =lg M lg2,b =log 5M =lg Mlg5,①1a =lg2lg M ,1b =lg5lg M ,①2a +1b =2lg2lg M +lg5lg M =lg4+lg5lg M =lg20lg M =2, ①2lg M =lg20,①lg M 2=lg20,①M 2=20,①M >0,①M =2 5.12. A [解析] x +2y =log 23+2log 483=log 49+log 4(83)2=log 4(9×649)=log 464=3,故选A .13.B [解析] 由x log 34=1得x =log 43,所以4x +4-x =3+13=103,故选B .14. D [解析]lg12lg15=lg3+2lg2lg3+1-lg2=2a +b 1-a +b. 15. AD [解析] 由a ,b ,c 都是正数,可设4a =6b =9c =M ,①a =log 4M ,b =log 6M ,c =log 9M ,则1a =log M 4,1b =log M 6,1c =log M 9,①log M 4+log M 9=2log M 6,①1c +1a =2b,即1c =2b -1a,去分母整理得ab +bc =2ac ,故选AD . 16. -1 [解析] lg 52+2lg2-(12)-1=lg 52+lg4-2=-1. 17. 1 [解析] ①log a x =1log x a =2,①log x a =12.同理log x c =16,log x b =13. ①log (abc )x =1log x abc =1log x a +log x b +log x c=1. 18.[解] (1)①2log 525=2log 552=4log 55=4,3log 264=3log 226=18log 22=18,①2log 525+3log 264=4+18=22.(2)原式=12lg(3+5+3-5)2=12lg(3+5+3-5+29-5)=12lg10=12. (3)(lg5)2+2lg2-(lg2)2=(lg5)2-(lg2)2+2lg2=(lg5+lg2)(lg5-lg2)+2lg2=lg10(lg5-lg2)+2lg2=lg5+lg2=lg10=1.19.[解] 原方程可化为2(lgx)2-4lgx +1=0.设t =lgx ,则方程化为2t 2-4t +1=0,①t 1+t 2=2,t 1·t 2=12. 又①a ,b 是方程2(lgx)2-lgx 4+1=0的两个实根,①t 1=lga ,t 2=lgb ,即lga +lgb =2,lga·lgb =12. ①lg(ab)·(log a b +log b a)=(lga +lgb)·⎝⎛⎭⎫lgb lga +lga lgb =(lga +lgb)·(lgb )2+(lga )2lga·lgb=(lga +lgb)·(lga +lgb )2-2lga·lgblga·lgb =2×22-2×1212=12, 即lg(ab)·(log a b +log b a)=12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021年人教版高中数学必修第一册:第4章《章末复习课》
(含答案详解)
1、指数与对数的运算【例1】计算:(1)2log32-log3+log38-5log53;(2)1.5-×0+80.25×+(×)6-.[解] (1)原式=log3-3=2-3=-1.(2)原式=+2×2+22×33-=21+4×27=110.指数、对数的运算应遵循的原则指数式的运算首先留意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算,其次若出现分式则要留意分子、分母因式分解以到达约分的目的.对数运算首先留意公式应用过程中范围的改变,前后要等价,娴熟地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.7n1.设3x=4y=36,则+的值为( )A.6B.3C.2D.1D [由3x=4y=36得x=log336,y=lo
2、g436,∴+=2log363+log364=log369+log364=log3636=1.]指数函数、对数函数的图象及应用【例2】(1)若函数y=logax(a0,且a≠1)的图象如下图,则以下函数正确的选项是( )A B C D(2)已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x.①如图,画出函数f(x)的图象;②依据图象写出f(x)的单调区间,并写出函数的值域.(1)B [由已知函数图象可得,loga3=1,所以a=3.A项,函数解析式为y=3-x,在R上单调递减,与图象不符;C项中函数的解析式为y=(-x)3=-x3,当x0时,y0,这与图象不符;D项中函数解析式为y=log3(-x),在(-∞,0)上为单调
3、递减函数,与图象不符;B项中对应函数解析式为y=x3,7n 与图象相符.应选B.](2)[解] ①先作出当x≥0时,f(x)=x的图象,利用偶函数的图象关于y轴对称,再作出f(x)在x∈(-∞,0)时的图象.②函数f(x)的单调递增区间为(-∞,0),单调递减区间为[0,+∞),值域为(0,1].1.识别函数的图象从以下几个方面入手:(1)单调性:函数图象的改变趋势;(2)奇偶性:函数图象的对称性;(3)特别点对应的函数值.2.指数函数与对数函数图象经过定点的实质是a0=1,loga1=0.2.函数y=1+log(x-1)的图象肯定经过点( )A.(1,1)B.(1,0)C.(2,1)D.(2,0)C [把y=logx的图象向右平移1个单位,再向上平移1个单位即可
4、得到y=1+log(x-1)的图象,故其经过点(2,1).]比较大小【例3】若0xy1,则( )A.3y3xB.logx3logy3C.log4xlog4y7nD.xyC [因为0xy1,则对于A,函数y=3x在R上单调递增,故3x3y,A错误.对于B,依据底数a对对数函数y=logax的影响:当0a1时,在x∈(1,+∞)上“底小图高”.因为0xy1,所以logx3logy3,B错误.对于C,函数y=log4x在(0,+∞)上单调递增,故log4xlog4y,C正确.对于D,函数y=x在R上单调递减,故xy,
5、D错误.]1.比较两数大小常用的方法有单调性法、图象法、中间值法等.2.当两个数都是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.3.比较多个数的大小时,先利用“0”“1”作为分界点,然后
在各部分内再利用函数性质比较大小.4.含参数的问题,要依据参数的取值进行分类商量.3.设a=log2π,b=logπ,c=π-2,则( )A.abcB.bacC.acbD.cbaC [∵a=log2πlog22=1,b =logπlog1=0,c=π-2=,即0c1,∴acb,应选C.]指数函数、对数函数的性质【例4】(
6、1)设函数f(x)=ln(1+x)-ln(1-x),则f(x)是( )A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数7nD.偶函数,且在(0,1)上是减函数(2)已知a0,a≠1且loga3loga2,若函数f(x)=logax在区间[a,3a]上的最大值与最小值之差为1.①求a的值;②若1≤x≤3,求函数y=(logax)2-loga+2的值域.(1)A [由题意可得,函数f(x)的定义域为(-1,1),且f(-x)=ln(1-x)-ln(1+x)=-f(x),故f(x)为奇函数.又f(x)=ln=ln,易知y=-1在(0,1)上为增函数,故f(x)在(0,1)上为增函数.](2)[
7、解] ①因为loga3loga2,所以f(x)=logax在[a,3a]上为增函数.又f(x)在[a,3a]上的最大值与最小值之差为1,所以loga(3a)-logaa=1,即loga3=1,所以a=3.②函数y=(log3x)2-log3+2=(log3x)2-log3x+2=2+.令t=log3x,因为1≤x≤3,所以0≤log3x≤1,即0≤t≤1.所以y=2+∈,所以所求函数的值域为.1.把本例(1)的函数f(x)改为“f(x)=ln(x+)”,推断其奇偶性.[解] ∵f(x)=ln(x+),∴其定义域为R,又f(-x)=ln(-x +),∴f(x)+f(-x)=ln(x+)+ln(-x+)=ln1=0,∴f(-x)=
-f(x),∴f(x)为奇函数.2
8、.把本例(2)②中的函数改为“y=a2x+ax-1”,求其最小值.[解] 由题意可知y=32x+3x-1,令3x=t,则t∈[3,27],∴f(t)=t2+t-1=2-,t∈[3,27],∴当t=3时,f(t)min=f(3)=9+3-1=11.7n1.讨论函数的性质要树立定义域优先的原则.2.换元法的作用是利用整体代换,将问题转化为常见问题.该类问题中,常设u=logax或u=ax,转化为一元二次方程、二次函数等问题.要留意换元后u的取值范围.函数的应用【例5】一种放射性元素,最初的质量为500g,按每年10%衰减.(1)求t年后,这种放射性元素的质量w的表达式;(2)由求出的函数表达式,求这种放射性元素的半衰期(结果精确到0.1).[解] (1)最初的质量为
9、500g.经过1年,w=500(1-10%)=500×0.9;经过2年,w =500×0.92;由此推知,t年后,w=500×0.9t.(2)由题意得500×0.9t=250,即0.9t=0.5,两边同时取以10为底的对数,得lg0.9t=lg0.5,即tlg0.9=lg0.5,所以t=≈6.6.即这种放射性元素的半衰期约为6.6年.指数函数模型的应用在实际问题中,有关人口增长、银行利率、细胞分裂等增长率问题常可以用指数函数模型表示.通常可以表示为y=N(1+p)x(其中N为基础数,p为增长率,x 为时间)的形式.4.某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次可使杂质含量削减,问至少应过滤几次才能使产品到达市场要求?(已知:
10、lg2≈0.3010,lg3≈0.4771)7n[解] 设过滤n次能使产品
到达市场要求,依题意,得×n≤,即n≤.则n(lg2-lg3)≤-(1+lg2),故n≥≈7.4,考虑到n∈N,故n≥8,即至少要过滤8次才能到达市场要求.7。
