大学物理角动量和力矩汇编
物理概念角动量与力矩

物理概念角动量与力矩物理概念:角动量与力矩角动量和力矩是物理学中重要的概念,在描述物体运动和力学性质时起着关键作用。
本文将详细介绍角动量和力矩的定义、计算方法以及在实际问题中的应用。
一、角动量的概念与计算方法角动量是描述物体绕某一轴旋转的性质,它与物体的质量、几何形状和旋转速度等因素有关。
角动量的定义如下:角动量L = Iω其中,L表示角动量,I代表物体的转动惯量,ω表示物体的角速度。
转动惯量是物体旋转惯性的度量,它与物体的质量分布和绕轴旋转的位置有关。
计算角动量的方法有两种常见的形式:数量积和矢量积。
1. 数量积方式计算角动量当物体的旋转轴与角速度方向相同时,可以用数量积方式计算角动量。
此时,角动量的计算公式为:L = Iω2. 矢量积方式计算角动量当物体的旋转轴与角速度方向不重合时,需要使用矢量积方式计算角动量。
此时,角动量的计算公式为:L = Iωn其中,n为物体旋转轴与角速度的法向量。
二、力矩的概念与计算方法力矩是描述物体受力产生转动效果的物理量。
当物体受力作用于某一点时,力就产生了力矩。
力矩的定义如下:力矩 M = r × F其中,M表示力矩,r表示力作用点到旋转轴的距离,F表示力的大小。
力矩的方向由右手定则给出,即拇指指向旋转轴,其余四指指向力的方向,手掌垂直于旋转平面内。
计算力矩的方法有两种常见的形式:数量积和矢量积。
1. 数数量积方式计算力矩当力和力臂的方向相同或者反向时,可以用数量积方式计算力矩。
此时,力矩的计算公式为:M = rF2. 矢量积方式计算力矩当力和力臂的方向不重合时,需要使用矢量积方式计算力矩。
此时,力矩的计算公式为:M = r × F三、角动量与力矩的关系与应用角动量和力矩是密切相关的物理量,它们之间存在如下关系:L = r × p其中,L表示角动量,r表示物体到旋转轴的距离,p表示物体的动量。
这一关系表明,角动量和力矩可以通过动量和物体到旋转轴的距离相互转化。
大学物理第1-4章经典力学部分归纳总结

应用
机械能守恒定律可以用于解决一些简单的运动学问题, 如自由落体、抛体运动等。
05 万有引力定律
万有引力定律的发现与意义
发现
牛顿通过观察苹果落地等现象,发现 了万有引力定律。
意义
万有引力定律揭示了自然界中物体之 间的相互作用规律,为经典力学的发 展奠定了基础。
万有引力定律的内容与公式
内容
任意两个质点之间都存在相互吸引的力,大小与两质点质量的乘积成正比,与它们之间距离的二次方成反比。
经典力学与许多其他学科领域密切相关, 如材料科学、工程学和天文学等,鼓励学 生在跨学科应用中拓展知识。
关注前沿研究
实践与实验
了解经典力学在前沿科学研究中的应用, 关注最新研究成果和技术进展。
通过实验和实践巩固理论知识,提高动手 能力和实验技能。
THANKS FOR WATCHING
感谢您的观看
工作原理等。
04 能量与动量定理
能量定义与计算
要点一
定义
能量是物体做功的能力,可以表示为系统动能和势能之和 。
要点二
计算
能量可以用数学公式进行计算,如动能公式 (E_k = frac{1}{2}mv^2),势能公式 (E_p = mgh) 等。
动量定理与冲量
定理
动量 (p = mv) 是物体质量和速度的乘积,冲量 (I = Delta p) 是动量的变化量。
03
经典力学在日常生活和工程应用中有着广泛的应用,如车辆 运动、机械运转、天体运动等。
章节概览
第1章
牛顿运动定律
第3章
能量和力做功
第2章
动量和角动量
第4章
万有引力和相对论基础
02 牛顿运动定律
角动量公式大全

角动量公式大全
1. 质点的角动量。
- 对于质点,角动量→L=→r×→p,其中→r是质点相对于参考点的位置矢量,→p = m→v是质点的动量(m为质点质量,→v为质点的速度)。
- 在直角坐标系下,如果→r=(x,y,z),→p=(p_x,p_y,p_z),则L_x = yp_z -
zp_y,L_y=zp_x - xp_z,L_z = xp_y - yp_x。
2. 刚体定轴转动的角动量。
- 对于刚体绕定轴转动,角动量L = Iω,其中I是刚体对该轴的转动惯量,ω是刚体绕轴转动的角速度。
- 对于由多个质点组成的刚体,I=∑_im_ir_i^2(离散质点情况),对于质量连续分布的刚体,I=∫ r^2dm,这里r是质点到转动轴的垂直距离。
3. 角动量定理相关公式。
- 角动量定理→M=(d→L)/(dt),其中→M是合外力矩。
- 在刚体定轴转动中,M = Iα(α为角加速度),这是由M=(dL)/(dt)(L =
Iω)推导而来,因为(dL)/(dt)=I(dω)/(dt)=Iα。
4. 角动量守恒定律。
- 当→M=0时,→L=常量。
- 在刚体定轴转动中,如果合外力矩为零,则Iω=常量,例如在花样滑冰运动员旋转时,收缩手臂(I减小),则ω增大以保持角动量守恒。
大学物理角动量和力矩
dL
M ex
dt
惯性系中成立
ch4
质点系对惯性系中某给定参考点的角动量的时间
变化率,等于作用在该质点系上所有外力对该给
定参考点的总力 矩
dL
M
ex
dt
i
ri
Fi
ex
4.角动量守恒定律(普遍的)
If no external torques act upon a system of particles, the angular momentum remains costant.
dL
M ex
M in
dt
2.质点系对固定点的总内力矩为零 3.质点系的角动量定理
The rate change of the totle angular momentum
about any axis is equal to the external torque
about that axis.
2)观察质点的匀速直线运动:质 点相对于参考点的掠面速度不变
动量、动能都不能对上述现象作 出统一描述,需要引入新的物理 量。
r 参考点O
v 质点m
ch4
2.质点对参考点的角动量
(Angular Momentum)
L = r mv r p
What counts for angular momentum is not how fast it is going away from the origin, but how much it is going around the origin.
在计算氢原子的 角动量时的应用
ch4
牛顿力学:角动量和力矩

力矩的定义:力与力臂的乘积
力矩的分类:静态力矩和动态力矩
静态力矩:力与力臂的乘积,用于描述物体在静止状态下的转动情况
动态力矩:力与力臂的乘积,用于描述物体在运动状态下的转动情况
实例
开门:门把手的转动产生力矩,使门打开
自行车:脚踏板的转动产生力矩,使自行车前进
扳手:扳手的转动产生力矩,使螺栓拧紧或松开
角动量的计算公式:L=r×p,其中r是质点到旋转轴的距离,p是质点的动量
角动量的单位:国际单位制中的单位是kg·m²/s
角动量的方向:角动量的方向与力矩的方向相同,与旋转轴的方向垂直
实例
地球自转:角动量守恒原理在地球自转中的应用
冰上运动员:角动量守恒原理在冰上运动员旋转中的应用
自行车:角动量守恒原理在自行车行驶中的应用
陀螺仪:角动量守恒原理在陀螺仪中的应用
力矩
3
定义
Байду номын сангаас
力矩:力与力臂的乘积
力矩的方向:垂直于力臂,与力同向或反向
力臂:力作用点到转动轴的距离
计算方法
力矩的定义:力与力臂的乘积
力矩的计算公式:M=F*L
力矩的方向:与力臂垂直,与力同向
力矩的性质:力矩的大小与力的大小、力臂的长度以及两者之间的夹角有关
分类
拧开瓶盖:瓶盖的转动产生力矩,使瓶盖拧开
感谢观看
汇报人:XX
性质:角动量是守恒的,即一个封闭系统中的角动量总和保持不变
守恒定律
角动量守恒的应用:解释天体运动、陀螺仪等物理现象
角动量守恒定律:在封闭系统中,角动量总是守恒的
角动量守恒的条件:系统不受外力矩作用,或者外力矩的矢量和为零
角动量守恒与能量守恒的关系:角动量守恒是能量守恒的一种表现形式
物理学中的角动量与力矩

物理学中的角动量与力矩角动量与力矩是物理学中重要的概念,它们在描述物体运动和作用力时起着重要的作用。
本文将深入探讨角动量和力矩的定义、性质以及它们在自然界和工程领域中的应用。
一、角动量的定义与性质1. 角动量的定义角动量是物体绕某一轴线旋转时所具有的物理量,用L表示,单位是kg·m²/s。
角动量与物体的质量、角速度和转动轴线的位置有关。
2. 角动量的计算公式对于一个质量为m,距离转动轴线距离为r的物体,其角动量的计算公式为L = mvr,其中v是物体的线速度。
3. 角动量守恒定律在没有外力或外力矩作用下,系统的总角动量将保持不变。
即L初= L末。
这一定律在自然界的很多现象中得到了验证,如行星绕太阳的运动和旋转体的守恒。
二、力矩的定义与性质1. 力矩的定义力矩是力对物体产生转动效果的物理量,用M表示,单位是N·m。
力矩与力的大小、力的作用点与转动轴的距离有关。
2. 力矩的计算公式对于一个施加在物体上的力F,作用点到转动轴的距离为d,力矩的计算公式为M = Fd。
3. 力矩的性质a. 力矩的方向始终垂直于力的方向和转动轴,并遵循右手定则。
b. 大小上,力矩等于力和转动轴上的距离的乘积,即M = Fd。
c. 在平衡条件下,物体所受到的合力矩为零。
三、角动量与力矩的关系1. 角动量与力矩的联系在刚体绕固定轴线转动时,其角动量的变化率等于力矩的大小。
即dL/dt = M。
2. 角动量定理根据角动量的变化率等于力矩的公式,可以得到角动量定理:角动量的变化率等于物体所受到的合外力矩,即dL/dt = ΣMext。
3. 角动量守恒与力矩平衡如果物体所受到的合外力矩为零,即ΣMext = 0,那么根据角动量定理可知,系统的总角动量将保持不变,即角动量守恒。
四、角动量与力矩的应用1. 自然界中的应用a. 行星绕太阳运动:根据角动量守恒定律,行星绕太阳的运动过程中,行星运动速度和离太阳距离的乘积保持不变。
大学物理力学部分归纳总结

运动学部分解题指导
1、已知运动方程,求速度,加速度,用微分法。
两 大 类
? v
?
? dr
,
? a
?
? dv
dt
dt
型 2、已知加速度和初始条件,求速度、位移、路
程和运动方程(或已知速度和初始条件,求位移、
路程和运动方程),用积分法。
? ? t?
? v ? v0 ?
a ?dt
t0
? ? t?
? r ? r0 ?
3、功率
P
?
dW
?
? F
?dr?
?
? F
?v?
?
Fv cos?
dt dt
6
4、保守力作功与势能概念: dW ? ? dEp
? WA?
B
?
B
? f
?dr?
?
Ep ( A) ?
EP (B)
?
?[Ep (B) ?
Ep ( A)]
A
万有引力势能
重力势能
? E p
?
? r
?
G
mM r2
dr
?
?G
mM r
0
? Ep ? (? mg)dz ? mgz
? (3)判断过程中对某点(或某轴)合外力矩是否为零,或者 角动量守恒条件是否成立。
? (4)若守恒条件成立,确定正方向,列方程,求解
? 分解综合法:对于较为复杂问题,不是只用一个定理、定律
就能解决,要将整个过程分解成几个子过程,对每一子过程
应用上述方法。
18
典型习题分析
? 例题(1) 如图所示,木块 A的质量为 1.0kg ,木块B的
9、功率
大学物理力矩与角动量

z
z
M
Fz
F
Fx
ˆF ˆ ˆ F Fx i j F k y z ˆM ˆ ˆ M M xi j M k y z
o
r
P
Fy
x
y
y
x
ˆ yj ˆ zk ˆ ) (F i ˆF ˆ ˆ) ( xi j F k x y z ˆ xF ˆ ˆ ˆ ˆ ˆ xFy k z j yFx k yFz i zFx j zF y i ˆ ( zF xF ) ˆ ˆ ( yFz zFy )i x z j ( xF y yFx )k
5
一、力矩(moment of force)
6
力对参考点的力矩 定义:作用于质点 P 的力 F 对参考点 O 的力矩等于力的作用 点位矢与力的叉积,即:
M r F
大小
M | M | rF sin Fd F r
M
F
F
O
方向
r、F、M 成右手螺旋关系。
d
r
P
M内 ri f ij 0
i 1, i j n
f ij
mi
ri
ri j
mj
o
rj
f ji
即:质点组内力矩的矢量和恒为零,只需考虑外力矩。
23
对质点系的所有质点应用角动量定理并取和
M 外 ri Fi 外 dLi d dL ( Li ) dt dt dt
质点对参考点的角动量的增量等于作 用于质点的力对同一参考点的角冲量 (angular impulse)。
L2 L1 Mdt
16
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角动量守恒
dL
0
或
L 常量
dt
ch4
5.几种特殊情况 ▪ 有心力场中的质点(系)对“心”的角动量总 是守恒的
▪ 质点系的重力的合力矩可集中到质心处理 Mg r Cmg
ch4
6. 守恒条件
角动量守恒:合外力对固定点的力矩为零 与参考系、研究系统和参考点都有关系
动量守恒:合外力为零 与参考系和研究系统有关系
ch4
z
v// v
v
Or//
O’
r r
ch4
§4-2 力矩和角动量定理
一、力矩和质点的角动量定理
1.力矩 (torque)
M rF
力对某点的力矩 单位:N·m
2.质点的角动量定理:质点对任一固定点的角
动量的时间变d化L率,M等于外力对该点的力矩 dt
ch4
[例题4.1]圆锥摆由一根长为l的绳子悬挂着一个质量为m的
质点系的总动能等于相对于质心系的动能加上 随质心整体平移的动能,即
Ek Ek'
1 2
m vc2
❖ 两质点体系的动能
Ek
Ekc
Ekr
1 2
mv
2 c
1 2
mr u2
❖ 碰撞 — 动量守恒
ch4
第四章 角动量守恒
§4-1 质点的角动量
1.引入
1)开普勒:若以太阳 为中心,行星的位置矢量 在相等时间内扫过(sweep through)相等的面积。
The rate change of the totle angular momentum
about any axis is equal to the external torque
about that axis.
dL
M ex
dt
惯性系中成立
ch4
质点系对惯性系中某给定参考点的角动量的时间
变化率,等于作用在该质点系上所有外力对该给
保守系机械能守恒:合外力作功为零 与参考系和研究系统有关系
三、质心系的角动量定理
M
MCex
rC
Fiex
L LC mrC vC
dL
M ex
ch4
dt
固有角动量 轨道角动量
对质心角动量+随质心角动量
质心系的角动量定理
M
ex C
dLC dt
角动量定理对惯性系成立,但站在质心系上时,无 论其是否是惯性系,则角动量定理形式上仍成立
ch4
ω
只受重力作用的质点系对 质心的角动量守恒
ch4
[例题4.2]质量为m1和m2的两个质点的位矢和速度分别为r1,
v1和r2 , v2,试求:两质点相对于它们的质心的动量和角动
量LC。
质 心 位 矢rC
mi ri
i
m
质 心 速 度vC
mivi
i
m
r
r
rC
p1 mr u
v
定参考点的总力 矩
dL
M
ex
dt
i
ri
Fi ex
4.角动量守恒定律(普遍的)
If no external torques act upon a system of particles, the angular momentum remains costant.
如果质系所受到的总外力矩为零 ,则质点系的
v
vC
p2 mr u
Lc r1' p1' r2' p2'
mr r12 u r12 (mr u)
在计算氢原子的
角动量时的应用
ch4
本章习题:4 –1,3,4,5,9(1),10(2,3,4)
描述质点的运动方向相对于参考点的变化或物体 的转动特征的物理量
Angular momentum depends upon the position of the axis abour which it is to be calculated.
3.质点对z轴的角动量
Lz = Lcos
θ是L到z轴的角 可以在z轴上任意找一点, 求出质点对该点的角动量, 再求z轴分量
2)观察质点的匀速直线运动:质 点相对于参考点的掠面速度不变
动量、动能都不能对上述现象作 出统一描述,需要引入新的物理 量。
r 参考点O
v 质点m
ch4
2.质点对参考点的角动量
(Angular Momentum)
L = r mv r p
What counts for angular momentum is not how fast it is going away from the origin, but how much it is going around the origin.
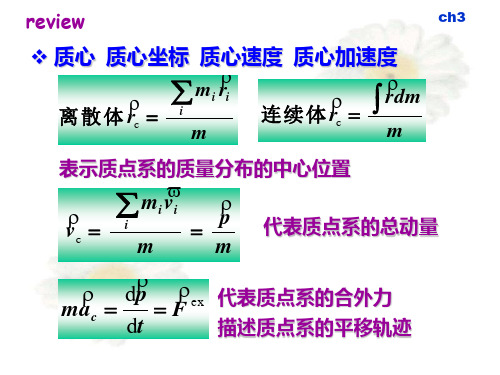
review
ch3
❖ 质心 质心坐标 质心速度 质心加速度
离 散 体
rc
mi ri
i
m
连续体
rc
rdm
m
表示质点系的质量分布的中心位置
vc
mi vi
i
p
m
m
代表质点系的总动量
mac
dp dt
F
ex
代表质点系的合外力 描述质点系的平移轨迹
ch3
❖ 质点系的动能 — 克尼希定理
作匀速圆周运动的小球构成。若摆线与铅垂线成 角,试
求摆球的速率。
研究对象:圆锥摆
参考系:实验室
选择参考点:支点O 受力与运动分析
dL
M
dt
v sin gl
cos
g l cos
ch4
速度调节器
cos
g
2l
ch4
二、质点系的角动量定理
1.质点系角dL动量M随ex时间M的in 变化率 dt
2.质点系对固定点的总内力矩为零 3.质点系的角动量定理
