第八章组合变形
合集下载
第八章 组合变形

例题
[ 已知: 例8.1 已知: = 15kN , e = 300mm, 许用拉应力σ 1 ] = 32 MPa, P
试设计立柱直径d 试设计立柱直径d。
解: 将力P向立柱轴线简化,立柱 向立柱轴线简化, 将力 向立柱轴线简化 承受拉伸和弯曲两种基本变 形 任意横截面上的轴力和弯矩 为:
FN = P = 15kN
cos ϕ sin ϕ + I I z y
2 2
ω= ω
2
y
+ω
2
z
Fl 3 = 3E
ωz I z tanψ = = tan ϕ ωy I y
I 一般情况下, z ≠ I y , 故 ϕ ≠ ψ ,这表明挠度所在 一般情况下, 的平面与外力作用平面并不重合。 的平面与外力作用平面并不重合。
以矩形截面的悬臂梁为例,在端部C点受力F 以矩形截面的悬臂梁为例,在端部C点受力F,F通过截面 ϕ 形心,与y轴夹角为 形心, 建立坐标系, 建立坐标系,将F分解 分解 成沿y和 的分量 成沿 和z的分量
Fy = F cosϕ
Fz = F sin ϕ
图6.4
梁的斜弯曲可看成由Fy、Fz分别产生的两个平面弯 Fy、 曲叠加而成。且危险截面均为固定端处截面。 曲叠加而成。且危险截面均为固定端处截面。其上弯矩 值为: 值为:
σ1
σw
4×15×103 32×15×103 ×300 + ≤ 32 2 3 πd πd
d = 114mm
所示起重机的最大吊重F=12kN,许用应 例8.2 图a所示起重机的最大吊重 所示起重机的最大吊重 , 试为横梁AB选择合适的工字钢 选择合适的工字钢。 力 [σ ] = 100MPa ,试为横梁 选择合适的工字钢。 的受力图, 解:根据横梁AB的受力图,由 根据横梁 的受力图 平衡方程可得: 平衡方程可得:
第8章 组合变形(土木)

F F
350
F
350
M
FN
y1
A 15000 mm 2 z0 75mm z1 125 mm
I y 5.31 10 7 mm 4
y
z0
z1
150 50 150
(2)立柱横截面的内力 50 FN F M F 350 75 10 3
425 F 10 3 N.m
危险点在1,2点。
max
b 9cm
h 2b 18cm
屋 顶 桁 架 结 构 的 简 化
例: 图示悬臂梁由25b工字钢制成,弹性模量 E=200GPa。荷载和几何尺寸如图所示,试求: (1) 求梁上C点的应力;
(2) 求梁内最大拉应力和最大压应力。 q q=5kN/m
C C P=2kN y
t .max 667 F t
t 30 106 F
667 667
45000 N
c.max 934F c
t .max
c.max
c 120 106 F
934 934
128500 N
许可压力为 45000N 45kN F
FN
c. max
Mz1 FN Iy A
t .max
c.max
425 10 3 F 0.125 F 5 5.31 10 15 10 3 934 F Pa
F
350
t .max 667 F c.max 934 F
M
FN
(4)求压力F
说明:
1. 必须是线弹性材料,加载在弹性范围内,服从虎克定律;
2. 必须是小变形,保证能按构件初始形状或尺寸进行分解与叠 加计算,且能保证与加载次序无关. 图示纵横弯曲问题,横截面上内 力为
350
F
350
M
FN
y1
A 15000 mm 2 z0 75mm z1 125 mm
I y 5.31 10 7 mm 4
y
z0
z1
150 50 150
(2)立柱横截面的内力 50 FN F M F 350 75 10 3
425 F 10 3 N.m
危险点在1,2点。
max
b 9cm
h 2b 18cm
屋 顶 桁 架 结 构 的 简 化
例: 图示悬臂梁由25b工字钢制成,弹性模量 E=200GPa。荷载和几何尺寸如图所示,试求: (1) 求梁上C点的应力;
(2) 求梁内最大拉应力和最大压应力。 q q=5kN/m
C C P=2kN y
t .max 667 F t
t 30 106 F
667 667
45000 N
c.max 934F c
t .max
c.max
c 120 106 F
934 934
128500 N
许可压力为 45000N 45kN F
FN
c. max
Mz1 FN Iy A
t .max
c.max
425 10 3 F 0.125 F 5 5.31 10 15 10 3 934 F Pa
F
350
t .max 667 F c.max 934 F
M
FN
(4)求压力F
说明:
1. 必须是线弹性材料,加载在弹性范围内,服从虎克定律;
2. 必须是小变形,保证能按构件初始形状或尺寸进行分解与叠 加计算,且能保证与加载次序无关. 图示纵横弯曲问题,横截面上内 力为
《材料力学》课程讲解课件第八章组合变形

强度条件(简单应力状态)——
max
对有棱角的截面,最大的正应力发生在棱角点处,且处于单向应力状态。
max
N A
M zmax Wz
M ymax Wy
x
对于无棱角的截面如何进行强度计算——
1、确定中性轴的位置;
y
F z
M z F ey M y F ez
ez F ey z
y
zk yk z
y
x
1、荷载的分解
F
Fy F cos
Fz F sin
z
2、任意横截面任意点的“σ”
x
F
y
(1)内力: M z (x) Fy x F cos x
M y (x) Fz x F sin x
(2)应力:
Mz k
M z yk Iz
My k
M y zk Iy
(应力的 “+”、“-” 由变形判断)
F
1, 首先将斜弯曲分解
为两个平面弯曲的叠加 Fy F cos
z
L2
L2
Fz F sin
z
2, 确定两个平面弯曲的最大弯矩
y
Mz
Fy L 4
M
y
Fz L 4
3, 计算最大正应力并校核强度
max
My Wy
Mz Wz
217.8MPa
查表: Wy 692.2cm3
4, 讨论 0
y
Wz 70.758cm3
的直径为d3,用第四强度理论设计的直径为d4,则d3 ___=__ d4。
(填“>”、“<”或“=”)
因受拉弯组合变形的杆件,危险点上只有正应力,而无切应力,
r3 1 3 2 4 2
r4
材料力学 第八章 组合变形

度理论校核此杆的强度。 解:①外力分析
y ZC
Mx z P2z
P2y 400N YA 457N Z A 20.1N
P2Z 70.5N YC 257N Z C 90.6N
YA A 150
T M x 120Nm
B 200
C YC D 100
P2y
x
y
M Z (Nm) M (Nm)
建立图示杆件的强度条件
解:①外力向形心
x A 150 P1 T A 150 B 200 C T B 200 C 100 D 简化并分解
z
z P2z D P2y x 弯扭组合变形 y
100
M Z (Nm) M (Nm)
y
②每个外力分量对应 x 的内力方程和内力图 X
(Nm) My (Nm) Mz
x X
125 37.8 162.8MPa
孔移至板中间时
N 100 103 2 A 631.9mm 10(100 x) x 36.8mm 6 σ max 162.8 10
偏心拉伸或压缩:
CL11TU11
任意横截面上的内力: N P,M y Pa,M z Pb
第八章 组合变形
§8–1 组合变形和叠加原理
§8–2 拉(压)弯组合 §8–4 偏心压缩 截面核心 §8-4 弯曲与扭转
§8–1组合变形和叠加原理
一、组合变形 :在复杂外载作用下,构件的变形会包含几种简
单变形,当几种变形所对应的应力属同一量级时,不能忽略
之,这类构件的变形称为组合变形。 P P
弯曲与扭转
P1
80ºP2 z
x A 150 B 200 C 100 D
y
第八章 组合变形

(cm)
max 22 100MPa [ c ]
木柱不安全。
讨论:木柱是否可用 ?怎样用 ? 作业 :8-7,-9,-11
第8章 复杂内力时杆件应力计算
8-3 弯扭组合变形
l
y
F
危险点处的主应力
x
z
M
'
D
32
3
mห้องสมุดไป่ตู้
M Z Fl W W Z Z T m Wt Wt
y
My
z
(a y 0)
iz2 z0 0, y0 a y yF
y0 0, z0 az
2 iy
( yF z F ) y
中性轴
(0 az)
zF
第8章 复杂内力时杆件应力计算
8-2 偏心压缩
F
x
z
(三)中性轴 zF yF 1 2 z0 2 y0 0 中性轴方程 iy iz
( yF z F ) y
z
中性轴4
3 4 5
中性轴3
1 2
y
iz2 ay yF
az i
2 y
中性轴1 中性轴2
zF
第8章 复杂内力时杆件应力计算
8-2 偏心压缩
F
x
z
iz2 ( yF z F ) a y yF
(三)中性轴 (四)截面核心
对于钢筋混凝土偏心受压柱,为避免出 现拉应力须控制荷载作用点位置,使中 性轴离开截面或仅与截面相切。这些点 位于截面的一区域内,这个区域称为截 面核心。
第8章 复杂内力时杆件应力计算
一、组合变形
在复杂外载作用下,构件的变形可以看成几种
第八章组合变形时的强度计算
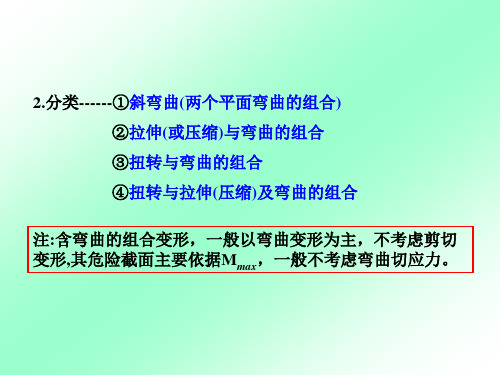
Iy
IY
由 mz 产生的正应力
s"' MZ .y Fyp y
IZ
IZ
假设C 点在第一象限内,根据杆件的变形可知, s ',s '',s ''' 均为拉应
力,由叠加原理,即得 C点处的正应力为:
σ σ' σ'' σ'''
任意横截面 n-n上的 C点的正应力为
c
σ F F zP z F yP y
与y轴的夹角θ为:
tgθ z0 Mz Iy Iy tgφ y0 My Iz Iz
公式中角度 是横截面上合成弯矩 M 的矢量与 y 轴的夹角 . 横截面上合成弯矩 M 为:
M
M
2 y
M
2 z
tgθ Iy tgφ Iz
讨论:
(1) 一般情况下,截面的 IzIy ,故中性轴与合成弯矩 M 所在平面不垂直,此为斜弯曲的受力特征。导致挠曲线与外 力(合成弯矩)所在面不共面,此为斜弯曲的变பைடு நூலகம்特征。
s s ' s '' My z - Mz y
Iy
Iz
式中,Iy和Iz分别为横截面对于两对称轴y和z的惯性矩; M y和Mz分别是截面上位于水平和铅垂对称平面内的弯矩,且 其力矩矢量分别与y轴和z轴的正向相一致。在具体计算中,
也可以先不考虑弯矩M y、Mz和坐标y、z的正负号,以它们的 绝对值代入,然后根据梁在P1和P2分别作用下的变形情况, 来判断上式右边两项的正负号。
FN A
Mz Wz
158 MPa
s
所以强度是安全
【例8-4】矩形截面柱如图所示。P1的作用线与杆轴线重合, P2作用在 y 轴上。已知, P1= P2=80kN,b=24cm , h=30cm。 如要使柱的m—m截面只出现压应力,求P2的偏心距e。
《材料力学》第八章组合变形
解 (1)外力分析,确定变形类型—拉弯组合;
(2)内力分析,确定危险截面—整个轴;
M=600(kN·cm) FN=15(kN)
(3)应力计算,确定危险点—a、b点;
P产生拉伸正应力: t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲:的正应力:wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知: P=2kN,L求=:1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2.画弯矩图,确定危险截面--固定端截面。 3.画应力分布图,确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中,在计算中,往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉(压)的组合怎么处理?
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm,材料为45钢, [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的,转速为n=966r/min。带轮的直径为D=132 mm,
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为:M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y),
与弯矩Mz、My对应的正应力分别为σ’和σ”,故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸(或压缩)的组合、扭转与弯曲的组合 的强度计算。
重点: 弯曲与拉伸(或压缩)的组合,扭转与弯曲的组合。
(2)内力分析,确定危险截面—整个轴;
M=600(kN·cm) FN=15(kN)
(3)应力计算,确定危险点—a、b点;
P产生拉伸正应力: t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲:的正应力:wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知: P=2kN,L求=:1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2.画弯矩图,确定危险截面--固定端截面。 3.画应力分布图,确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中,在计算中,往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉(压)的组合怎么处理?
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm,材料为45钢, [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的,转速为n=966r/min。带轮的直径为D=132 mm,
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为:M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y),
与弯矩Mz、My对应的正应力分别为σ’和σ”,故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸(或压缩)的组合、扭转与弯曲的组合 的强度计算。
重点: 弯曲与拉伸(或压缩)的组合,扭转与弯曲的组合。
材料力学第8章组合变形
MB
M
2 yB
M
2 zB
(364 N m)2 (1000N m)2 1064N m
•由Mz图和My图可知, B截面上的总弯矩最大, 并且由扭矩图可见B截 面上的扭矩与CD段其 它横截面上相同,TB =-1000 N·m,于是判 定横截面B为危险截面。
3. 根据MB和TB按第四强度理论建立的强度条件为
Wp
r4
M 2 0.75T 2
W
300N.m 1400N
300N.m
1500N 200
150
300N.m
128.6N.m
120N.m
(2)作内力图
危险截面E 左处
T 300N.m
M
M
2 y
M
2 z
176N.m
(3)由强度条件设计d
r3
M2 T2 W
W d 3
32
32 M 2 T 2
第8章 组合变形
8.1 组合变形和叠加原理 8.2 拉伸或压缩与弯曲的组合 8.3 偏心压缩和截面核心 8.4 扭转与弯曲的组合 8.5 组合变形的普遍情况
8.1 组合变形和叠加原理
组合变形——实际构件由外力所引起的变形包含两种或两 种以上的基本变形。如压力框架、烟囱、传动轴、有吊车 的立柱。 叠加原理——如果内力、应力、变形等与外力成线性关系, 则在小变形条件下,复杂受力情况下组合变形构件的内力, 应力,变形等力学响应可以分成几个基本变形单独受力情 况下相应力学响应的叠加,且与各单独受力的加载次序无 关。 前提条件:
即 亦即 于是得
r4
M 2 0.75T 2 [ ]
W
•请同学们按
照第三强度理 (1064 N m)2 0.75(1000 N m)2 100106 Pa W
第八章组合变形构件的强度-
1.外力分析
Fx F cos; Fy F sin 2.内力分析
FN Fx F cos FS Fy F sin M z Fy (l x) 上侧受拉
F sin(l x)
m
xm l
z
Fx
x
Fy
F
y
z
FS
FN x
y Mz
§8-2 弯曲与拉伸(或压缩)得组合
一、拉(压)与弯曲组合变形
第八章组合变形构件的强度
第八章 组合变形构件得强度
轴向拉(压)
F
内
FN
力
FN F
扭转
m
x
T
T m
F
应
T
力
FN (x)
A
max
(ρ) T ρ Ip
对称弯曲
FS
M
σ
τ FS
M
My
;
FS
S
z
Iz
bI z
§8-1 概述 一、组合变形
F2
F1
Me
F1 — 轴向拉伸 F2 — 弯曲变形 Me — 扭转变形
F2
2
F1
1
z
FN F1
A bh
x 3
My Wy
F1 b h b2
2 6
3F1 bh
4
l
l
y
Mz Wz
F1 h b h2
2 6
3F1 bh
1
F1 bh
3F1 bh
3F1 bh
F1 bh
3
2
F1 bh
3F1 bh
3F1 bh
7 F1 bh
4
F1 bh
3F1 bh
3F1 bh
Fx F cos; Fy F sin 2.内力分析
FN Fx F cos FS Fy F sin M z Fy (l x) 上侧受拉
F sin(l x)
m
xm l
z
Fx
x
Fy
F
y
z
FS
FN x
y Mz
§8-2 弯曲与拉伸(或压缩)得组合
一、拉(压)与弯曲组合变形
第八章组合变形构件的强度
第八章 组合变形构件得强度
轴向拉(压)
F
内
FN
力
FN F
扭转
m
x
T
T m
F
应
T
力
FN (x)
A
max
(ρ) T ρ Ip
对称弯曲
FS
M
σ
τ FS
M
My
;
FS
S
z
Iz
bI z
§8-1 概述 一、组合变形
F2
F1
Me
F1 — 轴向拉伸 F2 — 弯曲变形 Me — 扭转变形
F2
2
F1
1
z
FN F1
A bh
x 3
My Wy
F1 b h b2
2 6
3F1 bh
4
l
l
y
Mz Wz
F1 h b h2
2 6
3F1 bh
1
F1 bh
3F1 bh
3F1 bh
F1 bh
3
2
F1 bh
3F1 bh
3F1 bh
7 F1 bh
4
F1 bh
3F1 bh
3F1 bh
第八章组合变形及连接部分的计算
P2 a
m
z
x
P1
m
x
y
m
z x
My
m
y
P1 在 m—m 面内产生的弯矩为 My = P1 x (使梁在 XZ 平面内弯曲,y 为中性轴)
P2 a
m
z
x
P1
m
x
y
m
MZ z x
My
m
y
P2 在 m—m 面内产生的弯矩为 MZ = P2 (x-a) (使梁在 XY 平面内弯曲,z 为中性轴)
二 、 梁横截面上的应力分析 (任意点 C(y, z) 的正应力)
z
tg Iy tg
Iz
M
y
梁的挠曲线一般仍是一条空间曲线,故梁的扰曲线方程仍应分别 按两垂直面内的弯曲来计算,不能直接用合成弯矩进行计算。
四、 强度分析
中性轴
Байду номын сангаас
作平行于中性轴的两直线分别与
D1 z
o
横截面周边相切于 D1 、D2两点
,D1 、D2 两点分别为横截面上
最大拉应力点和最大压应力点。
D2
A 截面: D 截面:
(max
)A
M zA Wz
M W
yA y
(21.5103)q
(max
)D
M zD Wz
M yD Wy
(16.02103)q
梁的危险点在 A 截面棱角处
max
(max )A
M zA Wz
M yA Wy
(21.5103)q
[]
160106
[q] 160103 7.44kN/m 21.5
§8-1 概述
一、 组合变形概念 : 构件在荷载作用下发生两种或两种 以上的基本变形,则构件的变形称为组合变形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M
z
M
y
Wz
Wy
25
t max
M y max M z W Wz y
或 t max
My M z max W Wz y
材料力学
中南大学土木建筑学院
②圆形截面
c m ax
中性轴
Iy 中性轴与 Mz C tan a tan j tan j y轴的夹角 z j Iz t m ax j 中性轴与弯矩作用面垂直,且弯矩作用 M My 面与截面的两个交点即为最大正应力点。 M作用面 y 圆截面 Iy=Iz=I 且 Mz=Msinj, My=Mcosj
中南大学土木建筑学院
16
§8.2
相互垂直平面内的弯曲-斜弯曲
F1
F3 F4 F5
F2 一、概念 外力:作用线不与形心主惯性轴重合; 内力: 弯矩矢不与形心主惯性轴重合 (可分解成两个形心主惯性轴方向的分量); 变形:挠曲线不与载荷共面。
材料力学 中南大学土木建筑学院
17
斜弯曲
q
平面弯曲
F1
F
材料力学
材料力学
中南大学土木建筑学院
31
解:查附录可得 Wz=309cm3,Wy=40.9 cm3 对A截面,由强度条件有
m ax
M W
z z
M
y
Fl Wz
0 .4 F l Wy
[ ]
Wy
F 10.8kN
B截面,由强度条件有
m ax
M W
z z
M
y
0 .5 F l Wz
2 0.456qa 2 0.383qa
材料力学
中南大学土木建筑学院
28
危险截面:由弯矩图,可确定A、D两截面为危险截面 A、D截面在xoz、 xoy平面的弯曲截面系数,可查表得
W z 237 10
6
m,
3
W y 3 1 .5 1 0
6
m
3
按叠加法,在xoz主轴平面内、 xoy主轴平面内的 弯曲正应力,在x方向叠加 截面A
ql
2
3
材料力学
中南大学土木建筑学院
34
由型钢表试选25a工字钢,查得25a工字钢的Wz=401.88cm3, Wy=48.283 cm3,自重q1=0.37 KN/m。考虑原载荷和自重共同 1 引起的最大弯矩为 M ( q q ) l ,于是,强度条件为
2 max
8
1
max M
max
x
2、内力计算
Mz My
x y
材料力学
弯矩用矢量 表示如图 z
Mz
j
C
z
My
M y
2 z
M为合成弯矩
M M
2 y
M
且 tan j
M M
z y
中南大学土木建筑学院
20
3、应力计算
横截面上的正应力由两部分叠加 其中 Mz
M zy Iz
M yz Iy
Mz
j
C
z My
My
M
y
注意:式中的弯矩均取正值,y、z是代数 值。若y、z为正时引起的应力为压应力, 则式子前面加负号。 M yz M zy 叠加得 Iz Iy
t max
M y max M z W Wz y
或 t max
My M z max W Wz y
材料力学
中南大学土木建筑学院
24
m ax
M z y m ax Iz
M y z m ax Iy
解:图中所有外载荷虽在同一平面但并不位于梁的形心主惯性 平面内,所以是斜弯曲。将均布载荷q向形心主惯性轴分解 为 qy=qcosj,qz=qsinj
M
z max
1 8
q yl
2
1 8
ql cos j
2
在檩条跨中处弯矩最大,其值为
M
材料力学
y max
1 8
q zl
2
1 8
ql sin j
最大拉应力作用点坐标:
t m ax
M z yt Iz M y zt Iy
yt
D 2
s in j , t z
D 2
cos j
1 I
( M sin j
D 2
sin j M co s j
D 2
co s j )
M W
M
2 y
M
2 z
W
D 32
3
W
材料力学
中南大学土木建筑学院
材料力学
tan a
z0 y0
Iy Iz
M M
z y
Iy Iz
tan j
中南大学土木建筑学院
22
5、截面上的最大正应力
中性轴
M作用面 离中性轴最远的点正应力最大。 c m a x 作与中性轴平行并与截面边界相 切的两条直线,切点分别为最大 Mz
j
C
z My
t m ax
拉应力点和最大压应力点。
ql 2 8W z
Wz cos j sin j [ ] Wy
由于工字钢的型号未知,所以Wz和Wy均是未知的,但对于 工字钢,Wz /Wy 之值通常在8~10之间。故解此题时,可暂设 Wz /Wy =8。所以,将强度条件改写为
3 2 2 W z 4 10 N/m 5 m cos j sin j 0 . 866 0 . 5 8 380 . 2 cm Wz 6 8[ ] Wy 8 160 10 Pa
1 .5 1 0 6
3
hb 6
3
0 .0 5 0 .0 7 5
2 y m ax
2
1 2 10 6 0 .0 7 5 0 .0 5
2
96M Pa
圆截面梁
m ax
M
2 z m ax
M
1 .5 32
2
2
3
2
10
9
3
9 2 .8 M P a
W
65 10
max max
max max
D1
t max c max
M y max M z 或 W Wz y
t m ax c m ax
D2
My M z m ax W Wz y
危险点处于单向应力状态,因此
常见截面形式
①矩形及矩形组合截面(有棱角) 最大正应力在离形心最远的棱角上。
M
a y
c m ax
C
z
t m ax
23
m ax
M z y m ax Iz
M y z m ax Iy
M
z
M
y
Wz
Wy
M
y
材料力学
中南大学土木建筑学院
max
My Wy
max
Mz Wz
正应力是坐标的线性函数。
材料力学 中南大学土木建筑学院
21
4、中性轴的位置
中性轴
M作用面 Mz
j
C
正应力等于零的点的连线为中性轴。
设中性轴上一点的坐标为(y0、z0) 中性轴方程
M
z
z My
y0
M
y
z0
0
Iz
Iy
M
a y
由以上方程可知y0、z0正负相反或为零。
即中性轴过形心,且位于2、4象限内。 中性轴与 y轴的夹角
26
1.5kN
z
1kN
x
h b
1m
矩形截面梁如图。已知b =50mm , h=75mm ,求梁内的最大正应力。 如改为d=65mm的圆截面,最大 正应力为多少?
m ax
M
z m ax
1m
y
M
y m ax
矩形 截面梁
Wz M
z m ax 2
Wy M
y m ax 2
bh 6
0 .8 F l Wy
[ ]
Wy
F 6.6 kN
取梁的许用载荷[F]=6KN
材料力学 中南大学土木建筑学院
32
图所示由工字钢制造的檩条倾斜地安装在屋架上,檩条受有 从屋面传来的铅直载荷作用。已知j=300,檩条跨度l =5m, 均布载荷q=4kN/m,檩条的许用应力[ ]=160MPa。试选择工 字钢的型号。
材料力学 中南大学土木建筑学院
11
三、连接件
铆钉、键、螺栓、销钉等起到连接作用的构件。
F F F F m FFmF NhomakorabeaF
F
F
材料力学
中南大学土木建筑学院
12
材料力学
中南大学土木建筑学院
13
键 连 接
M
材料力学
中南大学土木建筑学院
14
F
m
a
m
F
n
l
n
l
15
材料力学
中南大学土木建筑学院
榫齿 连接
材料力学
中南大学土木建筑学院
18
二、斜弯曲的正应力强度条件
例:分析图示斜弯曲的应力计算方法
