概率论课件-随机变量及其分布
合集下载
概率论课件第二章
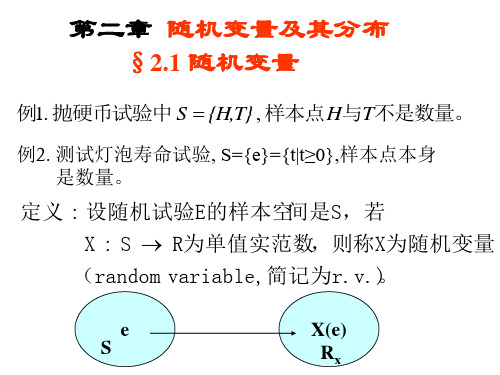
第二章 随机变量及其分布 §2.1 随机变量
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S，若 X : S R为单值实范数，则称X为随机变量 （random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. （=1） 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S，若 X : S R为单值实范数，则称X为随机变量 （random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. （=1） 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
《概率论与数理统计》课件-第2章随机变量及其分布 (1)
则称X服从参数为λ的泊松分布, 记为 X ~ P() .
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
泊松分布的应用
“稠密性”问题(一段时间内,电话交换中心接到的呼叫次 数,公共汽车车站候车的乘客数,售票窗口买票的人数， 原子放射的粒子数，保险公司在一定时期内被索赔的次 数等)都服从泊松分布.
随机变量的分布函数
1.定义: 设X为一随机变量, x为任意实数, 称函数 F(x)=P{X≤x}为X的分布函数.
注: ① F(x)是一普通函数, 其定义域为 ,; ② F x的值为事件X x的概率; ③ F x可以完全地描述随机变量取值的规律性.
例如: Pa X b PX b PX a
连续型随机变量及概率密度函数
1.定义: 设X ~ F(x), 若存在一个非负可积的函数 f (x),
使 x R, 有
F ( x)
PX
x
x
f
(t)dt
,
则称X为连续型随机变量, f (x) 称为X的概率密度函数或
分布密度函数.
2.几何意义:
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
二、随机变量的概念
定义： 设试验E的样本空间为 , 若对于每个样本
点 , 均有一个实数 X ()与之对应, 这样就得
到一个定义在 上的单值函数 X X () , 称X为随
机变量.
X
样本空间
实数
注: ① 随机变量是一个定义在样本空间上的实函数, 它取值的随机性是由样本点的随机性引起的;
x 1
x0
0 x x
不是 (不满足规范性)
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
泊松分布的应用
“稠密性”问题(一段时间内,电话交换中心接到的呼叫次 数,公共汽车车站候车的乘客数,售票窗口买票的人数， 原子放射的粒子数，保险公司在一定时期内被索赔的次 数等)都服从泊松分布.
随机变量的分布函数
1.定义: 设X为一随机变量, x为任意实数, 称函数 F(x)=P{X≤x}为X的分布函数.
注: ① F(x)是一普通函数, 其定义域为 ,; ② F x的值为事件X x的概率; ③ F x可以完全地描述随机变量取值的规律性.
例如: Pa X b PX b PX a
连续型随机变量及概率密度函数
1.定义: 设X ~ F(x), 若存在一个非负可积的函数 f (x),
使 x R, 有
F ( x)
PX
x
x
f
(t)dt
,
则称X为连续型随机变量, f (x) 称为X的概率密度函数或
分布密度函数.
2.几何意义:
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
二、随机变量的概念
定义： 设试验E的样本空间为 , 若对于每个样本
点 , 均有一个实数 X ()与之对应, 这样就得
到一个定义在 上的单值函数 X X () , 称X为随
机变量.
X
样本空间
实数
注: ① 随机变量是一个定义在样本空间上的实函数, 它取值的随机性是由样本点的随机性引起的;
x 1
x0
0 x x
不是 (不满足规范性)
概率论与数理统计课件第2章
X0
1
pk 03.5
0.25
4
625
0.0625
X的分布函数为
2 0.125
0
x0
0.5
0 x1
F
(
x)
0.75 0.875
1 x 2 2 x3
0.9375 3 x 4
Байду номын сангаас
1
x4
0.0
分布函数 是累计概率
例3 有人对随机变量X的分布列表述如下:
X -1
0 12 3
P
a 0.16
a2 2a 0.3
第2章 随机变量及其分布
2.1 随机变量及其分布函数 2.2 离散型随机变量及其分布律 2.3 几种常见的离散型分布 2.4 连续型随机变量及其密度函数 2.5 正态分布 2.6 随机变量函数及其分布
2.1 随机变量及其分布函数
一、随机变量 二、随机变量的分布函数
信息管理学院 徐晔
一、随机变量
例
包含出现1点
包含出现1,2点
包含出现1,2,3点
包含出现1,2,3,4 点 包含出现1,2,3,4,5 点包含出现1,2,3,4,5,6 点
分布函数的性质
F(x) P(X x), （ x ）
(1) F x 在 , 上是一个不减函数 ,
即对 x1 , x2 , 且 x1 x2 ,都有 F x1 F x2 ;
样本点
1， 4， 5 2， 3， 4 2， 3， 5 2， 4， 5 3， 4， 5
黑球数 X
1 2 2 1 1
由上表可以看出，该随机试验的每一个结果都对应
着变量 X 的一个确定的取值，因此变量 X 是样本空
间Ω上的函数：
概率论与数理统计课件：随机变量及其分布
随机变量及其分布
首页 返回 退出
§2.2 离散型随机变量及其分布律
定义 设离散型随机变量 X 所有可能取的值为xk , k = 1, 2,
X 取各个可能值的概率,即事件{ X xk } 的概率，为
P{ X xk } pk , k 1, 2, .
称此为离散型随机变量 X 的分布律.
随机变量及其分布
首页 返回 退出
定义2.1 设随机试验E, 其样本空间S, 若对样本
空间每一个样本点e, 都有唯一一个实数X(e)与之对
应，那么就把这个定义域为S的单值实值函数X=X(e),
称为随机变量。
随机变量通常用大写字母X,Y,Z 或希腊字母 ξ,η等表示.
而表示随机变量所取的值时,一般采用小写字母x,y,z等.
量方面，如，投掷一枚均匀骰子，我们观察出现的点
数。
记X=“出现的点数”
则X的可能取1, 2, …, 6中任一个数，可见X是变量；
又X取那个值不能事先确定，故此X的取值又带有随机
性.
有了随机变量，有关事件的表示也方便了，如
{X=2}, {X≤2}, ……
随机变量及其分布
首页 返回 退出
这样的例子还有很多. 又如，研究手机的使用寿命
或写成
随机变量及其分布
5
P( X k )
6
k 1
1
, k 1, 2,
6
首页 返回 退出
常见离散型随机变量
（一）“0-1”分布
设随机变量 X 只可能取 0 和1 两个值，它的分布律
为
k
P X k p（
1 p)1k k 0,1
(0 p 1)
海南大学《概率论与数理统计》课件 第四章 随机变量及其分布
例如：X 0 取出的n个产品中没有次品；
X 3 取出的n个产品中至多有3个次品；
X 3 取出的n个产品中有超过3个的次品.
8
关于随机变量的补充说明
• 引入随机变量之后, 可以更方便地表示事件。 • 随机变量的确定不仅与样本空间有关, 也与试验
的研究目的有关。 • 随机变量满足函数的单值对应关系。 • 随机变量不仅有取值的不同, 取到这些值的概率
②正则性： p( xi ) 1 . i 1
这两条性质也是随机变量分布列的充要条件。
由概率的意义和随机变量的完备性容易证明。
25
二、离散型随机变量的分布函数
由分布列可以写出其分布函数 F ( x) P( xi ) xi x
它的图形是有限（或无穷）级数的阶梯函数〔右连续 〕
F(x)
1
0
x
26
27
X的分布列为
X1 2 3 P 0.6 0.3 0.1
X的分布函数为
0, x 1; 0.6, 1 x 2; F ( x) 0.9, 2 x 3; 1 , x 3.
注意：由分布列求分布函数是概率累加的过程.
并且，总有： 当x xmin时，F ( x) 0; 当x xmax时，F ( x) 1.
解 (1) 根据分布函数的性质可知
F() 1, F() 0
依题意可得
18
F() A π B 1 2
F() A π B 0 2
联立上面两个方程可以解得 A 1,B 1 2π
(2) 随机变量 X 落在(-1,1)内的概率可以表示为
P{1 X 1} F (1 0) F (1)
P{a X b} F(b 0) F(a 0);
P{a X b} F(b 0) F(a).
X 3 取出的n个产品中至多有3个次品；
X 3 取出的n个产品中有超过3个的次品.
8
关于随机变量的补充说明
• 引入随机变量之后, 可以更方便地表示事件。 • 随机变量的确定不仅与样本空间有关, 也与试验
的研究目的有关。 • 随机变量满足函数的单值对应关系。 • 随机变量不仅有取值的不同, 取到这些值的概率
②正则性： p( xi ) 1 . i 1
这两条性质也是随机变量分布列的充要条件。
由概率的意义和随机变量的完备性容易证明。
25
二、离散型随机变量的分布函数
由分布列可以写出其分布函数 F ( x) P( xi ) xi x
它的图形是有限（或无穷）级数的阶梯函数〔右连续 〕
F(x)
1
0
x
26
27
X的分布列为
X1 2 3 P 0.6 0.3 0.1
X的分布函数为
0, x 1; 0.6, 1 x 2; F ( x) 0.9, 2 x 3; 1 , x 3.
注意：由分布列求分布函数是概率累加的过程.
并且，总有： 当x xmin时，F ( x) 0; 当x xmax时，F ( x) 1.
解 (1) 根据分布函数的性质可知
F() 1, F() 0
依题意可得
18
F() A π B 1 2
F() A π B 0 2
联立上面两个方程可以解得 A 1,B 1 2π
(2) 随机变量 X 落在(-1,1)内的概率可以表示为
P{1 X 1} F (1 0) F (1)
P{a X b} F(b 0) F(a 0);
P{a X b} F(b 0) F(a).
概率论课件：第二章随机变量及其概率分布
π 3π ⎞ ⎛ π 0 ⎟ 22.设随机变量 X 的分布律为 ⎜ 2 2 ⎟ ，求 Y 的分布律： ⎜ ⎝ 0.3 0.2 0.4 0.1 ⎠
（1） Y = ( 2 X − π ) ;
2
（2） Y = cos( 2 X − π ). ⎧2 x , 0 < x < 1 f ( x) = ⎨ ⎩0 , 其它
它意味着第 i 次（ i ≥ k ）成功，且 i − 1 次试验中成功 k − 1 次，设这两个事件分别为A1 ，A2，
则A = A 1 A 2 , 且P(A) = P(A 1 A 2 ) = P(A 1 )P(A 2 )(A 1与A 2 独立 ), 而 P(A 1 ) = p,
1 k −1 1 k −1 i − k P( A2 ) = Cik−− ⋅ q i −1−( k −1) = Cik−− q . 1 p 1 ⋅ p
, ( 2,6),
, (6,1),
例如(6,1) , (6,6)} .这里，
8
5 36
9
4 36
10
3 36
11
2 36
12
1 36
PK
1 36
2 36
3 36
4 36
5 36
6 36
概率 P{X = k }, k = 0,1,2,3.
2、分析： 显然 X 服从离散型概率分布，而且 X 的可能取值为 0，1，2，3.问题归结为求
∴ X 的分布律为：
P{X = 0} = P ( A1 ) = 1 / 2; P{X = 1} = P ( A1 A2 ) = 1 / 2 2 ; P{X = 2} = P ( A1 A2 A3 ) = 1 / 2 3 ;
X Pi
《概率论》课件
物理学
描述粒子在气体或液体中的运动状态。
金融学
用于股票价格和收益率的分析。
隐马尔科夫模型
定义
隐马尔科夫模型是一种特殊的马尔科夫模型 ，其中观测状态与隐藏状态有关，而隐藏状 态之间相互独立。
应用
语音识别、手写识别、生物信息学等领域。
05
大数定律与中心极限定理
大数定律及其应用
大数定律
在独立重复试验中，当试验次数趋于无穷时，事件发 生的频率趋于该事件发生的概率。
《概率论》ppt课 件
目录
• 概率论简介 • 概率的基本性质 • 随机变量及其分布 • 随机过程与马尔科夫链 • 大数定律与中心极限定理 • 贝叶斯统计推断
01
概率论简介
概率论的定义
概率论
研究随机现象的数学学科，通过数学模型和公式 来描述随机事件、随机变量和随机过程。
随机变量
表示随机现象的数值变量，其取值具有随机性。
THANKS
感谢观看
计算机科学
概率论在计算机科学中用于算法设计和数据 挖掘等领域。
02
概率的基本性质
概率的公理化定义
概率的公理化定义是概率论的基础，它规定了概率的几个基本性质，包括非负性 、规范性、可加性和有限可加性。
非负性指的是任何事件的概率都不小于0；规范性指的是必然事件的概率为1；可 加性指的是两个独立事件的概率等于它们各自概率的和；有限可加性指的是任意 有限个两两独立的事件的概率等于这些事件概率的和。
应用
在统计学中，大数定律用于估计样本的统计量和参数 ，如平均值、方差等。
中心极限定理及其应用
中心极限定理
无论随机变量的分布是什么，当样本量足够大时，样 本均值的分布近似正态分布。
概率论与数理统计-第二章-随机变量及其分布函数ppt课件
表格: X
x1 x2
pk
p1 p2
概率分布图：
1P
xn
pn
0.5
x4 x3
x1
x2
X
.
由概率的性质易知离散型随机变量的分布列
pk
满足下列特征性质:
k 1
① pk 0(k 1,2,) [非负性]
②
pk 1 [规范性]用于确定待定参数
k 1
③ F( x) P( X x) P(X xi ). xi x
1. 2
.
【例2】设随机变量X的分布函数为
aex b, x 0
F(x)
0,
x0
解： 因为 F(x) 在 x=0 点右连续
求: 常数 a 和 b。
所以 lim F ( x) lim (ae x b) a b 0
x0
x0
又因为 F () lim (ae x b) b 1 x
1、两点分布 或（0 - 1）分布
two-point distribution
定义1 设离散型随机变量X的分布列为
X0 1 pk 1 p p
其中 0<p<1
则称 X 服从（0 - 1）分布，记作 X ～（0 - 1）分布
F(x)
（0 - 1）分布的分布函数
0 , x0 F ( x) 1 p, 0 x 1
X = “三次试验中 A 发生的次数”，
{ X 2} A1A2 A3 A1A2 A3 A1A2 A3 P{X 2} P(A1A2 A3 A1A2 A3 A1A2 A3 )
P(A1A2 A3 ) P(A1A2 A3 ) P(A1A2A3 ) P(A1)P(A2)P(A3) P(A1)P(A2)P(A3) P(A1)P(A2 )P(A3 ) C32 p2(1 p)32
概率论与数理统计ppt课件
称这种试验为等可能概型(或古典概型)。
*
例1：一袋中有8个球，其中3个为红球，5个为黄球，设摸到每一球的可能性相等，从袋中不放回摸两球， 记A={恰是一红一黄}，求P(A)． 解：
（注：当L>m或L<0时，记 ）
例2：有N件产品，其中D件是次品，从中不放 回的取n件， 记Ak＝{恰有k件次品}，求P(Ak)． 解：
*
第四章 随机变量的数字特征 4.1 数学期望 4.2 方差 4.3 协方差及相关系数 4.4 矩、协方差矩阵 第五章 大数定律和中心极限定理 5.1 大数定律 5.2 中心极限定理 第六章 数理统计的基本概念 6.1 总体和样本 6.2 常用的分布
*
第七章 参数估计 7.1 参数的点估计 7.2 估计量的评选标准 7.3 区间估计 第八章 假设检验 8.1 假设检验 8.2 正态总体均值的假设检验 8.3 正态总体方差的假设检验 8.4 置信区间与假设检验之间的关系 8.5 样本容量的选取 8.6 分布拟合检验 8.7 秩和检验 第九章 方差分析及回归分析 9.1 单因素试验的方差分析 9.2 双因素试验的方差分析 9.3 一元线性回归 9.4 多元线性回归
解： 设 Ai={ 这人第i次通过考核 }，i=1,2,3 A={ 这人通过考核 }，
亦可：
*
例：从52张牌中任取2张，采用(1)放回抽样，（2）不放 回抽样，求恰是“一红一黑”的概率。
利用乘法公式
与 不相容
（1）若为放回抽样：
（2）若为不放回抽样：
解： 设 Ai={第i次取到红牌}，i=1,2 B={取2张恰是一红一黑}
①
②
①
1 2 N
①
②
1 2 N
……
随机变量及其分布PPT课件
35
例8. 某类灯泡使用时数在1000小时以上 的概率是0.2，求三个灯泡在使用1000 小时以后最多只有一个坏了的概率.
解: 设X为三个灯泡在使用1000小时已坏的灯
泡数 . X ~ B (3, 0.8)，
P(X k)C3k (0.8)k (0.把2)观3察k ,一个k 灯泡0,的1,2使,3用
随后单调减少.
..
0
n=13,p=0.5
..n
当(n+1)p为整数时，二项概率P(X=k) 在k=(n +1)p和k =(n+1)p-1处达到最大 值.
课下请自行证明上述结论.
31
例6. 将一枚均匀骰子抛掷3次， 令X 表示3次中出现“4”点的次数
不难求得，
X的概率分布列是：
P{
X
k}C3k
(
依题意x可取值0第i个路口遇红灯i123路口3路口2路口118x表示该汽车首次遇到红灯前已通过的路口的个数路口3路口2路口1路口3路口2路口1第i个路口遇红灯i123路口3路口2路口1第i个路口遇红灯i123某加油站替公共汽车站代营出租汽车业务每出租一辆汽车可从出租公司得到3因代营业务每天加油站要多付给职工服务费60元
一般地，我们给出如下定义:
定义1 ：Байду номын сангаасxk(k=1,2, …)是离散型随 机变量X所取的一切可能值，称
P(X xk ) pk, k=1,2,… …
为离散型随机变量X的概率分布列
简称分布列, 又称分布律.
其中 pk (k=1,2, …) 满足：
（1） pk 0,
用这两条性质判断
k=1,2, … 一个函数是否是
P( X k) a k , k =0,1,2, …, 0
例8. 某类灯泡使用时数在1000小时以上 的概率是0.2，求三个灯泡在使用1000 小时以后最多只有一个坏了的概率.
解: 设X为三个灯泡在使用1000小时已坏的灯
泡数 . X ~ B (3, 0.8)，
P(X k)C3k (0.8)k (0.把2)观3察k ,一个k 灯泡0,的1,2使,3用
随后单调减少.
..
0
n=13,p=0.5
..n
当(n+1)p为整数时，二项概率P(X=k) 在k=(n +1)p和k =(n+1)p-1处达到最大 值.
课下请自行证明上述结论.
31
例6. 将一枚均匀骰子抛掷3次， 令X 表示3次中出现“4”点的次数
不难求得，
X的概率分布列是：
P{
X
k}C3k
(
依题意x可取值0第i个路口遇红灯i123路口3路口2路口118x表示该汽车首次遇到红灯前已通过的路口的个数路口3路口2路口1路口3路口2路口1第i个路口遇红灯i123路口3路口2路口1第i个路口遇红灯i123某加油站替公共汽车站代营出租汽车业务每出租一辆汽车可从出租公司得到3因代营业务每天加油站要多付给职工服务费60元
一般地，我们给出如下定义:
定义1 ：Байду номын сангаасxk(k=1,2, …)是离散型随 机变量X所取的一切可能值，称
P(X xk ) pk, k=1,2,… …
为离散型随机变量X的概率分布列
简称分布列, 又称分布律.
其中 pk (k=1,2, …) 满足：
（1） pk 0,
用这两条性质判断
k=1,2, … 一个函数是否是
P( X k) a k , k =0,1,2, …, 0
概率论第2章ppt课件
(5) P{恰好2.5分钟}
.
11
第2章 随机变量及其分布
解：
习题19
(1) P{至多3分钟} P { X 3 } F X (3 ) 1 e 0 .4 3 0 .69 (2) P{至少4分钟}
P { X 4 } 1 P { X 4 } 1 F X ( 4 ) e 0 .4 4 0 .20
同理 P{X2}5219 P{X3}4217
36 36
36 36
P{X4}3215 P{X5}2213
36 36
36 36
P{X 6} 1 36
.
3
第2章 随机变量及其分布
习题8
8. 甲乙两人投篮，投中的概率分别为0.6和0.7。今各投三次。求(1)两人投中次数 相等的概率；(2)甲比乙投中次数多的概率.
.
9
第2章 随机变量及其分布
习题16
16. 有一繁忙的汽车站，每天有大量汽车通过，设一辆汽车在一天的某段时间内 出事故的概率为0.0001. 在某天的该时间段内有1000量汽车通过。问出事故的车辆 数不小于2的概率是多少？(利用泊松定理计算)
解：令在该段时间内发生事故的车辆数目为X, 根据题意知：
0
20
22 4
令 y x2
AI1A1 4
I b3/2
.
15
第2章 随机变量及其分布
习题22(2)
22(2) 研究了英格兰在1875年~1951年期间，在矿山
发生导致不少于10人死亡的事故的频繁程度，得知
相继两次事故之间的时间T(日)服从指数分布，其
概率密度为
fT
(t)
1
et
241
, /241
(1) 解：从8杯酒中随机地挑选4杯，共有
概率论与数理统计课件：多维随机变量及其分布
多维随机变量及其分布
首页 返回 退出2
在实际问题中, 试验结果有时需要同时用两个或两
个以上的随机变量来描述.
如， 炮弹的弹着点的位置, (X, Y)是一个二维随
机变量.
又如，研究天气变化状况，令X, Y, Z分别表示
温度、湿度、风速，则(X, Y, Z)是一个三维随机变量.
研究多维随机变量有必要将多个变量作为一个整
二元函数
F ( x , y ) P{( X x ) (Y y )} P ( X x , Y y )
称为随机变量(X,Y)的联合分布函数。
一维随机变量X的联合分布
函数F ( x ) P ( X x ).
多维随机变量及其分布
首页 返回 退出
F(x,y)=P(X≤x,Y≤y)
y
F ( , y ) 0,
o
F ( x , ) 0,
F ( , ) 0, F ( , ) 1;
4 F ( x , y )关于x和y分别右连续；
x1
F ( x1 , y ) F ( x2 , y )
5 对于任意x1 x2 , y1 y2 , 有矩形公式
…
…
…
…
X
性质： 1 pij 0, i , j 1, 2, ;
2
p
i 1 j 1
多维随机变量及其分布
ij
1.
首页 返回 退出
例1 从1,2,3,4中任取一个数记为X、再从1,2, ⋯ ,
中任取一个数记为Y,求 ( X, Y ) 的联合分布律及P
( X=2Y ).
解：
可以证明，f(x,y)满足联合密度的性质。
随机变量及其分布复习课件.ppt
有
F(x) x f(t)dt，
则称X为连续型随机变量，其中f(x)称为X的概率 密度函数，简称概率密度。
（II）概率密度的性质
( 1 ) 非 负 性 ： f( x ) 0 ， x R .
(2)规 范 性 ：f(x)dx1. 4
( 3 )对 于 任 意 实 数 a b, 有
P{aXb}abf(x)dx . F(b)F(a)
求这个区间的端点,分二种情形讨论之：
17
（1）区间的一个端点是无穷大，即已知P(X < x) = p1 或P(X > x) = p2，求x .
利用 或
然后反查标准正态分布表，即可求出x （2）区间关于μ对称，不妨设为(μ−a,μ+a)，而 P(μ−a<X<μ+a) = p，求a
18
四.随机变量的函数的分布 1.离散型随机变量函数的分布
几种重要的 离散型分布
均指 正 匀数 态 分分 分 布布 布
二项分布的 正态近似
二项分布的 泊松近似
二项 分布
泊几
松何
分分 布 布 21
例题选讲
例1 甲、乙、丙3人进行独立射击 每人的命中率依 次为03 04 06 设每人射击一次 试求3人命中总 数之概率分布律 分析 求离散型随机变量的概率分布的步骤为:(1) 写
23
例2 投掷一个均匀骰子n 次，求(1)恰好得到一个6点的概 率；(2)至少得到一个6点的概率；(3)为了以0.5的概率保 证至少得到一个6点，则至少要投掷几次？
所以至少要投掷4次.
24
例3 设 X 的分布律为 X 1012 1111 p 4444
求 Y X 2 的分布律 .
解 Y 的可能值为 (1)2, 02,12, 22; 即 0, 1, 4.
F(x) x f(t)dt，
则称X为连续型随机变量，其中f(x)称为X的概率 密度函数，简称概率密度。
（II）概率密度的性质
( 1 ) 非 负 性 ： f( x ) 0 ， x R .
(2)规 范 性 ：f(x)dx1. 4
( 3 )对 于 任 意 实 数 a b, 有
P{aXb}abf(x)dx . F(b)F(a)
求这个区间的端点,分二种情形讨论之：
17
（1）区间的一个端点是无穷大，即已知P(X < x) = p1 或P(X > x) = p2，求x .
利用 或
然后反查标准正态分布表，即可求出x （2）区间关于μ对称，不妨设为(μ−a,μ+a)，而 P(μ−a<X<μ+a) = p，求a
18
四.随机变量的函数的分布 1.离散型随机变量函数的分布
几种重要的 离散型分布
均指 正 匀数 态 分分 分 布布 布
二项分布的 正态近似
二项分布的 泊松近似
二项 分布
泊几
松何
分分 布 布 21
例题选讲
例1 甲、乙、丙3人进行独立射击 每人的命中率依 次为03 04 06 设每人射击一次 试求3人命中总 数之概率分布律 分析 求离散型随机变量的概率分布的步骤为:(1) 写
23
例2 投掷一个均匀骰子n 次，求(1)恰好得到一个6点的概 率；(2)至少得到一个6点的概率；(3)为了以0.5的概率保 证至少得到一个6点，则至少要投掷几次？
所以至少要投掷4次.
24
例3 设 X 的分布律为 X 1012 1111 p 4444
求 Y X 2 的分布律 .
解 Y 的可能值为 (1)2, 02,12, 22; 即 0, 1, 4.
概率论-随机变量函数的分布
个连续型r.v，它的概率密度为
fY
(
y
)
f
[h(
y)]
dh( y dy
)
,
y
0,
其它
其中， min g(x), max g(x),
a xb
a xb
x=h (y) 是 y=g (x) 的反函数 .
此定理的 证明与前 面的解题 思路类似
注意 利用以上公式直接写出Y g( x) 的概率 密度时，要注意两点：
即
z y
FX (z y) fX ( x)dx
于是
FZ (z)
z y
fY ( y)[ f X ( x)dx]dy
fY
(
y)FX
(z
y)dy
将上式两边关于z求导，得
FZ (z) ຫໍສະໝຸດ fZ (z)fY ( y) fX (z y)dy
由X和Y的对称性, fZ (z) 又可写成
fZ (z) fX ( x) fY (z x)dx
y)
fY
(
y)dy
z
1
e
ydy,
0
0 z 1
fZ
(z)
z z 1
fX
(z
y)
fY
(
y)dy
0,
z 1 e ydy, z 1
z 1
其他
1 ez , 0 z 1
(e
1)e
z
,
z 1
0,
其他
f
X
(
x
)
1,
0,
0
x 其它
1 ,
e y , y 0
fY ( y)
0,
其它
方法二
若由卷积公式
fY
(
y
)
f
[h(
y)]
dh( y dy
)
,
y
0,
其它
其中， min g(x), max g(x),
a xb
a xb
x=h (y) 是 y=g (x) 的反函数 .
此定理的 证明与前 面的解题 思路类似
注意 利用以上公式直接写出Y g( x) 的概率 密度时，要注意两点：
即
z y
FX (z y) fX ( x)dx
于是
FZ (z)
z y
fY ( y)[ f X ( x)dx]dy
fY
(
y)FX
(z
y)dy
将上式两边关于z求导，得
FZ (z) ຫໍສະໝຸດ fZ (z)fY ( y) fX (z y)dy
由X和Y的对称性, fZ (z) 又可写成
fZ (z) fX ( x) fY (z x)dx
y)
fY
(
y)dy
z
1
e
ydy,
0
0 z 1
fZ
(z)
z z 1
fX
(z
y)
fY
(
y)dy
0,
z 1 e ydy, z 1
z 1
其他
1 ez , 0 z 1
(e
1)e
z
,
z 1
0,
其他
f
X
(
x
)
1,
0,
0
x 其它
1 ,
e y , y 0
fY ( y)
0,
其它
方法二
若由卷积公式
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
即每次试验结果 互不影响
19
独立重复地抛n次硬币，每次只有两个可能的 结果:正面，反面，
P出现正面 1 2
将一颗骰子抛n次，设A={得到1点}，则每次
试验只有两个结果：A, A,
P A 1 6
从52张牌中有放回地取n次，设A={取到红
牌}，则每次只有两个结果： A, A,
P A 1 2
如果是不放回抽样呢？
P( X 2) P( A1A2 A3) (1 p)2 p ；
P( X 3) P( A1A2 A 3) (1 p)3 ；
10
X0
1
2
3
p p p(1-p) (1-p)2p (1-p)3
11
例：若随机变量X的概率分布律为
P( X k ) c k ，k 0,1, 2, , 0
检查产品的质量是否合格，对新生婴儿 的性别进行登记，检验种子是否发芽以 及前面多次讨论过的“抛硬币”试验都 可以用（0－1）分布的随机变量来描述 。
17
一个随机试验,设A是一随机事件,且
P(A)=p,(0<p<1).若仅考虑事件A发生与否,
定义一个服从参数为p的0-1分布的随机变
量:
X
1,
0,
21
设A在n重贝努利试验中发生X次，则
P( X k) Cnk pk (1 p)nk，k 0，1，，n
并称X服从参数为p的二项分布，记
X ~ B(n，p)
n
注：1 ( p q)n Cnk pk qnk 其中q 1 p k 0
22
推导：以n=3为例,设Ai={ 第i次A发生 }
P( X 0) P( A1A 2 A3) (1 p)3
它的分布律还可以写为
P( X k) pk (1 p)1k , k 0, 1.
15
对于一个随机试验，如果它的样本空间只
包含两个元素，即 S {e1 , e2} ，我们总能
在S上定义一个服从（0－1）分布的随机
变量。
0, X X (e) 1,
当e e1, 当e e2.
来描述这个随机试验的结果。
3
定 义 ： 设 随 机 试 验 的 样 本 空 间 为 S e , 若
X X (e) 为定义在样本空间 S 上的实值单值函数， 则称 X X (e) 为随机变量。
一般采用大写英文字母 X ,Y , Z 来表示随机变量
引入随机变量的目的是用来描述随机现象
4
一 般 的 , 若 I是 一 个 实 数 集 合 ,{ X I }记
二项分布随机变量概率分布律
24
例：有一大批产品，其验收方案如下： 先作第一次检验,从中任取10件，经检 验无次品接受这批产品，次品数大于2 拒收；否则作第二次检验，从中任取5 件，仅当5件中无次品便接受这批产品， 设产品的次品率为p．求这批产品能被 接受的概率.
解：设A={接受该批产品}。 设X为第一次抽得 的次品数，Y为第2次抽得的次品数.
k!
求常数c.
12
解：
1 P{X k}
k 0
k
c
ce
k0 k !
c e
几个重要的离散型随机变量
一、0－1分布
若X的分布律为：
X 01 p qp
随机变量只可能 取0、1 两个值
(p+q=1,p>0,q>0)
则称X服从参数为p的0-1分布，或两点分布.
记为
X ~ 0 1( p) 或 B(1, p)
则X～B(10,p)，Y～B(5,p)，且{X=i}与{Y=j}独立。
P( A) P(X 0) P(1 X 2且Y＝0)
P(X 0) P(1 X 2) P(Y 0)
P(X 0) (P(X 1) P(X 2)) P(Y 0)
(1 p)10 [10 p(1 p)9 45 p2 (1 p)8] (1 p)5
P{X 1} P{X 0} P{X 1} 1/ 2
X 01
2
3
p
1/8 3/8 3/8 1/8
6
§2 离散型随机变量及其分布
定义：取值至多可数的随机变量为离散
型的随机变量。概率分布(分布律)为
X x1
pk p1
x2 …
xi
…
p2 …
pi
…
pi 0, pi 1 i 1
7
概率分布
写出所有可能取值 写出取每个可能取值相应的概率
若A发生, 若 A 不 发 生 (即A发 生 ).
来描述这个随机试验的结果。只有两个
可能结果的试验，称为Bernoulli试验。
二、二项分布
n重贝努利试验：设试验E只有两个可能的 结果：A与A ,p(A)=p,0<p<1,将E独立地重 复进行n次，则称这一串重复的独立试验为 n重贝努利试验。
在相同条件下 重复进行
第二章 随机变量及其分布
随机变量 离散型随机变量 概率分布函数 连续型随机变量 随机变量的函数
1
§1 随机变量
常见的两类试验结果：
示数的——降雨量； 候车人数； 发生交通事故的次数…
示性的——明天天气（晴，云…）； 化验结果（阳性，阴性）…
中心问题：将试验结果数量化
s e
x
X=X(e)－－为S上的 单值函数，X为实数
则{X I}为事件{e : X (e) I}
常见的两类随机变量
离散型的 连续型的
例：掷硬币3次，出现正面的次数记为X.
样本点e TTT TTH THT HTT HHT HTH THH HHH X(e)的值 0 1 1 1 2 2 2 3
P{X 0} P{TTT} 1/ 8
P{X 1} P{TTH,THT, HTT} 3 / 8
P( X 1) P( A1A 2 A3 A1A 2 A3 A1A 2 A3 ) C31 p1(1 p)31
P( X 2) P( A1A 2 A3 A1A 2 A3 A1A 2 A3 ) C32 p 2 (1 p)32
P( X 3) P( A1A 2 A3 ) p3
一般 P( X0,1, 2, , n
例：某人骑自行车从学校到火车站， 一路上要经过3个独立的交通灯，设各 灯工作独立，且设各灯为红灯的概率 为p，0<p<1，以X表示首次停车时所通 过的交通灯数，求X的概率分布律。
解：设Ai={第i个灯为红灯}，则P(Ai)=p， i=1,2,3 且A1,A2,A3相互独立。
P( X 0) P( A1) p ； P( X 1) P( A1A2 ) (1 p) p ；