华南农业大学 数学2 试卷
华南农业大学 数学2 试卷

2 SX n1 1 SY2 n2 1 1 1 n1 n2 2 n1 n2
服从(
D
)
2
A 自由度为 n1 n2 1的 t 分布 C 自由度为 n1 n2 1的 t 分布
A
n 1
B 自由度为 n1 n2 2 的 t 分布 D 自由度为 n1 n2 2 的 t 分布
y bx a ,在计算公式 a bX Lxy 6、求随机变量 Y 与 X 的线性回归方程 Y b L xx
中, Lxx xi x
i 1 n
2
, Lxy
1
。
二、单项选择题(每小题 2 分,共 2¥6=12 分)
1、设 A,B 是两个随机事件,则必有( )
7、 某厂生产某种产品使用了 3 种不同的催化剂 (因素 A) 和 4 种不同的原料 (因 素 B) ,各种搭配都做一次试验测得成品压强数据。由样本观察值算出各平方 和分别为:SSA=25.17,SSB=69.34,SSE=4.16,SST=98.67,试列出方差分析 表, 据此检验不同催化剂和不同原料在检验水平 =0.05 下对产品压强的影响 有没有统计意义? ( F0.05 (2,6) 5.14, F0.05 (3,6) 4.76, F0.05 (4,6) 4.53 )
五、综合实验(本题 8 分,开卷,解答另附于《数学实验报告》中)
6
华南农业大学期末考试试卷(A 卷)
2006 学年第二学期
考试类型: (闭卷) 学号 题号 得分 评阅人 一 姓名 二 三 四
考试科目:
应用数学(解答)
考试时间:120分钟 年级专业 五 总分
11学年第二学期大学数学2试卷(A卷)-参考答案
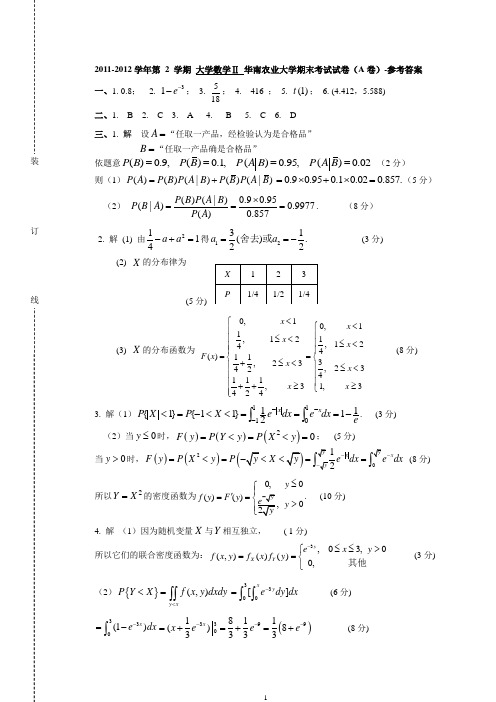
2011-2012学年第 2 学期 大学数学Ⅱ 华南农业大学期末考试试卷(A 卷)-参考答案 一、1. 0.8; 2. 31e --; 3. 518; 4. 416 ; 5. )1(t ; 6. (4.412,5.588) 二、1. B 2. C 3. A 4. B 5. C 6. D 三、1. 解 设A =“任取一产品,经检验认为是合格品” B =“任取一产品确是合格品” 依题意()0.9,()0.1,()0.95,()0.02P B P B P A B P A B ==== (2分) 则(1)()()(|)()(|)P A P B P A B P B P A B =+0.90.950.10.020.857.=⨯+⨯=(5分)(2) ()(|)0.90.95(|)0.9977()0.857P B P A B P B A P A ⨯===. (8分) 2. 解 (1) 由2114a a -+=得1231().22舍去或a a ==- (3分) (2) X 的分布律为 (5分) (3) X 的分布函数为 0,10,111,12,1244()113,23,234241111,3,3424x x x x F x x x x x <⎧<⎧⎪⎪⎪≤<⎪≤<⎪⎪⎪==⎨⎨+≤<⎪⎪≤<⎪⎪⎪⎪≥++≥⎩⎪⎩ (8分)3. 解(1)111011{1}{11}12x x P X P X e dx e dx e ---<=-<<===-⎰⎰. (3分)(2)当0y ≤时,()()()20F y P Y y P X y =<=<=; (5分) 当0y >时,()()(20x x F y P X y P X dx dx --=<=<== (8分)所以2Y X =的密度函数为0,0()()0y f y F y y ≤⎧⎪'==>. (10分)4. 解 (1)因为随机变量X 与Y 相互独立, ( 1分)所以它们的联合密度函数为:3,03,0(,)()()0,y X Y e x y f x y f x f y -⎧≤≤>==⎨⎩其他(3分)(2){}(,)y x P Y X f x y dxdy <<=⎰⎰3300[]x y edy dx -=⎰⎰ (6分) 330(1)x e dx -=-⎰3390181()333xx e e --=+=+()9183e -=+ (8分)(3)解:由密度函数可知~(0,3),~(3)X U Y E (10分) 所以,22(30)311(),(),12439D X D Y -==== (12分) 由X 与Y 相互独立,得3131()()()4936D X Y D X D Y -=+=+= (14分) 四、1. 解 检验假设 20:0.0004H σ=,21:0.0004H σ≠. (1分) 依题意,取统计量:222(1)~(1)n S n χχσ-=-,15n =. (3分) 查表得临界值:220.0252(1)(14)26.1n αχχ-==,220.97512(1)(14) 5.63n αχχ--==, (5分) 计算统计量的观测值得: 22140.02521.8750.0004χ⨯==. (6分) 因2220.9750.025(14)(14)χχχ<<,故接受原假设0H ,即认为总体方差与规定的方差无显著差异. (8分) 2. 解 (1)(2) 解 因为F =5.6681>0.01(3,16) 5.29F =,所以拒绝0H ,即认为不同的贮藏方法对粮食含水率的影响在检验水平0.01α=下有统计意义. (8分)3. 解 2.10=x ,239=y (2分)6.252.10101066221012=⨯-=-=∑=x n x l i i xx (3分)6622392.101025040101=⨯⨯-=-=∑=y x n y x l i i i xy (4分)故1662ˆ25.8625.6xy xx l l β==≈;01ˆˆ23925.8610.224.77y x ββ=-=-⨯=- (6分) 因此所求回归直线方程为 ˆ24.7725.86y x =-+ (8分)。
(2)高等数学B2试卷参考答案

华南农业大学期末考试试卷(A 卷)2009学年第2学期 考试科目: 高等数学B Ⅱ 考试类型:(闭卷)考试 考试时间:120分钟学号 姓名 年级专业一、 填空题(本大题共5小题,每小题3分,共15分)1. 试定义函数在点的值的 ,使得函数在该点连续。
2.函数在点处可微分的必要条件是函数在该点处连续或可偏导;充分条件是函数的偏导数在该点处连续。
3.设函数在闭区域上连续,且,则。
4. 判断敛散性:已知且,则是收敛的。
5. 已知某二阶常系数非齐次线性微分方程的通解为,则该微分方程为。
二、选择题(本大题共5小题,每小题3分,共15分) 1. 直线与平面的交点是(B )。
(A )(9,2,-3)。
(B )(2,9,11)。
(C )(2,11,13)。
(D )(11,9,2)。
2. 若级数在处收敛,则此级数在处(A )。
(A )绝对收敛。
(B )条件收敛。
(C )发散。
(D )收敛性不能确定。
3.二元函数 在点处 (C )(A )连续,偏导数存在。
(B )连续,偏导数不存在。
(C )不连续,偏导数存在。
(D )不连续,偏导数不存在。
4. 设是连续的奇函数,是连续的偶函数, ,则以下结论正确的是( A )。
(A ) 。
(B ) 。
(C ) 。
(A ) 。
5. 微分方程的一个特解应具有形式(A,B,C 是待定常数)( B )。
(A )。
(B )。
(C )。
(D )。
三、计算题(本大题共5小题,每小题6分,共30分) (1)设,其中和具有连续导数,求。
【解】(2)求由方程所确定的函数的全微分。
【解】方程两边求微分得 整理得(3)交换积分次序。
【解】(4)求差分方程在给定初始条件下的特解。
【解】特征方程为,所以对应的齐次方程的通解为。
又不是特征根,故可令特解为,代入原方程,得比较系数可得,,故非齐次方程的一个特解为,于是非齐次方程的通解为,由所给初始条件,可得,所以方程满足给定初始条件下的特解为。
2013大学数学2A_华南农业大学期末考试试卷讲解

华南农业大学期末考试试卷(卷)装订学年第学期考试科目:大学数学Ⅱ考试类型:(闭卷)考试考试时间:分钟学号姓名年级专业题号一二三四总分得分评阅人得分线一、填空题(本大题共 6 小题,每小题 3 分,共 18 分)1. 随机事件A与B互不相容,且 A B,则 P(A) ______________.2. 设随机变量的分布律为P( X k) 1 , k 1,2, ,则 P( X 4) =___________2k3.已知离散型随机变量 X 的概率分布为:P(X 1) 0.2, P( X 2) 0.3, P( X 3) 0.5求 X 的方差为 D ( X ) =___________4. X1, X 2 , X 3是来自于标准正态总体X12服从X 的一个样本,则统计量1(X22 X 32)2的分布是 ______________5. X1, X2 X n是来自于正态总体 X ~ N( ,2),当已知时,则方差 2 的置信度为 1 的置信区间是 ___________________6. 一元线性回归模型为y 01 x, ~ N (0, 2 ) ,若( x i, y i), i 1,2 n为一组观察值,则参数1的估计量为? 1=(用 x i , y i , x, y 的表达式)第1页共7页得分二、单项选择题(本大题共 6 小题,每小题 3 分,共 18 分)1.假设任意的随机事件 A 与 B ,则下列一定有()A. P(A B) 1B.P(A B) 1 P( AB)C. P(A B) 0D.0 P(A B)1装2.连续型随机变量X 的密度函数 f (x) 和分布函数 F ( x) ,则下列正确的是()A. xf (t )dt B. F ( x) f (x)dx订F (x)C. F (x) 1 f (t )dtD. F ( x) 1+f(t )dt .x x3.设随机变量 X 和 Y 相互独立,且 X ~ N (1, 2),Y ~ N ( 1,2),则下列正确的是线()A. P( X Y 0) 0.5B. P(X Y 1) 0.5C. P( X Y 0) 0.5D. P(X Y 1) 0.5 .4. 设 X1, X2 X n是来自于标准正态分布总体X 的一个样本, X 和S分别是该样本均值和样本标准差,则下列正确的是()A. X ~ N(0,1)B. nX ~ N(0,1)C. X~ t(n 1)nD. X i2 ~ 2 (n) S i 15. 设 X1, X2 , X3是来自于均值为的指数分布总体的一个样本,其中未知,则下列估计量中不是的无偏估计量() .2 X1 X 2 2X 3B. 2XA. T1 5 T22 X1 3X2 2X 3D. 2XC. T3 7 T4 115X73X822X323X36.设总体X ~ N ( ,2 ),其中 2 已知, x1, x2,x n是来自于该总体的样本观测值,记 x 为样本均值,对假设检验H 0 :0vs H1 :0第2页共7页取检验统计量为 Un x,则在显著性水平下拒绝域为()A. { U u /2 }B.{U u }C. { U u }D.{U u /2 }装订 线得分三、计算题 (本大题共 4 小题,共 40 分)(本题 10 分) 发报台分别以概率 0.6 和 0.4 发出信号“.”和“ - ”,?由于通信系统受到干扰, 当发出信号“.”时,收报台分别以概率 0.8 及 0.2 收到信号 “ .”和“ - ”,同样,当发报台发出信号“ - ”时,收报台分别以概率 0 .9 和 0.1 收到信号“- ”和“ .”.求 (1) 收报台收到信号“ .”的概率.(2) 当收报台收到信号“ .”时,发报台确系发出信号“ .”的概率.(本题 10 分) 设随机变量 X 的密度函数为 f ( x) Ce |x| ,x求:( 1)常数 C ;(2) X 落在区间( 0, 1)内的概率;(3) P( X 5)第3页共7页(本题 10 分)设随机变量X 的概率密度函数为f ( x)exx0,求0 x0(1)随机变量X的分布函数F X (x)装(2)求YX 2的概率密度函数f Y ( y)订线(本题 10 分)设X和Y的联合分布函数为 f (x, y) 2e x 2 y x 0, y 0 ,求0 其他(1) X 和 Y 的边缘密度函数(2) X 和 Y 相互独立吗?请说明理由(3) 求Y 的期望 E(Y ) 和方差 D (Y)第4页共7页得分四、解答题(本大题共 3 小题,每题 8 分,共 24 分)(本题 8 分)假定某地一旅游者的消费额X 服从正态分布N ( ,2),且标准装差 =12 元,现在要对该地旅游者的平均消费额E( X ) 加以估计,为了能以95% 的置信度相信这种估计误差小于2 元,问至少要调查多少人?( u0.9751.96,u0.951.64)订线(本题 8 分)假定考试成绩服从正态分布,在一次英语测验中随机抽取36 位考生的成绩,算得平均成绩为66.5 分,标准差为15 分,问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70 分?( t0.975 (35) 2.0301, t0.95 (35) 1.6896)第5页共7页装订线(本题 8 分)用 4 种不同的安眠药在兔子上试验,特选24 只健康的兔子,随机的把它们均分为 4 组,各组服 1 组安眠药,安眠药的数据经过统计分析后,形成下面的方差分析表:来源平方和自由度均方和 F 值安眠药 2.54 ( ) ( ) ( )误差( ) ( ) ( )总和3.87()(1)给出本实验的原假设,检验统计量(2)在方差分析表中,填入括号内的数字以完成方差分析表。
学应用概率统计大学数学2试卷(A卷)附答案

2011-2012学年第 2 学期 考试科目: 大学数学Ⅱ一、填空题(本大题共6小题,每小题3分,共18分)1. 设A 、B 为两个随机事件,已知()0.3,()0.4,()0.5P A P B P A B ===U ,则()P A B =U ______________.2. 设随机变量X 服从参数为3的泊松分布,则(1)P X ≥= ______________.3. 设二维离散型随机变量),(Y X 的联合分布律为:),(Y X 的联合分布函数为),(y x F ,则(1,3)F =______________.4. 设随机变量X 表示100次独立重复射击命中目标的次数,每次命中目标的概率为0.2, 则2X 的数学期望是______________.5. 设X 、Y相互独立,且都服从标准正态分布,则~Z =______________. (要求写出分布及其参数).6. 设由来自总体~(,0.81)X N μ,容量为9的样本得到样本均值5=X ,则未知参数μ的置信度为95%的置信区间为___________________.( 0.025 1.96u =) 二、单项选择题(本大题共6小题,每小题3分,共18分)1. 某人花钱买了C B A 、、三种不同的奖券各一张.已知各种奖券中奖是相互独立的, 中奖的概率分别为,02.0)(,01.0)(,03.0)(===C p B P A p 如果只要有一种奖券中奖此人就一定赚钱, 则此人赚钱的概率约为( ). A. 0.05B. 0.06C. 0.07D. 0.082. 设A 、B 为两个随机事件,且B A ⊂,()0>B P ,则下列选项必然正确的是( ). A. ()()B A P A P < B. ()()B A P A P >C. ()()B A P A P ≤D. ()()B A P A P ≥3. 下列各函数中可以作为某个随机变量X 的分布函数的是( ).A. 21,0()11,0x F x x x ⎧≤⎪=+⎨⎪>⎩ B. 0,0() 1.1,011,1x F x x x <⎧⎪=≤≤⎨⎪>⎩14. 设随机变量()2~2,3X N ,随机变量25Y X =-+, 则~Y ( ). A. (1,41)N B. (1,36)N C. (1,18)N - D. (1,13)N -5. 设某地区成年男子的身高()100,173~N X ,现从该地区随机选出20名男子,则这20名男子身高平均值的方差为( ).A. 100B. 10C. 5D. 0.56. 设12,,,n X X X ⋅⋅⋅是取自总体X 的一个样本, X 为样本均值,则不是总体期望μ的无偏估计量的是( ).A. XB. 123X X X +-C. 1230.20.30.5X X X ++D. 1nii X=∑三、计算题(本大题共4小题,共40分)1.(本题8分)已知一批产品中90%是合格品,检查时,一个合格品被误认为是次品的概率为0.05,一个次品被误认为是合格品的概率为0.02,求: (1)一个产品经检查后被认为是合格品的概率;(2)一个经检查后被认为是合格品的产品确是合格品的概率.2.(本题8分)设离散型随机变量X 只取1,2,3三个可能值,取各相应值的概率分别是21,,4a a -,求:(1) 常数a ; (2) 随机变量X 的分布律; (3) 随机变量X 的分布函数()F x .3.(本题10分)设随机变量X 的密度函数为:()1()2x f x e x -=-∞<<+∞.(1) 求{1}P X <; (2) 求2Y X =的密度函数.4.(本题14分)设随机变量X 与Y 相互独立,它们的密度函数分别为1,03()30,X x f x ⎧≤≤⎪=⎨⎪⎩其他, 33,0()0,0y Y e y f y y -⎧>=⎨≤⎩ 试求:(1) (,)X Y 的联合密度函数; (2) ()P Y X <; (3)()D X Y -.四、解答题(本大题共3小题,每小题8分,共24分)1. 从一台车床加工的一批轴料中抽取15件测量其椭圆度,计算得样本方差220.025s =,已知椭圆度服从正态分布,问该批轴料椭圆度的总体方差与规定的方差200.0004σ=有无显著差异(取检验水平0.05α=)?(20.025(14)26.1χ=, 20.975(14) 5.63χ=, 20.025(15)27.5χ=,20.975(15) 6.26χ=)2. 某粮食加工厂用4种不同的方法贮藏粮食,一段时间后,分别抽样化验其含水率,每种方法重复试验次数均为5次,所得粮食含水率的方差分析表的部分数据如下. (0.05(4,19) 5.01F=,0.01(4,16) 4.77F=,0.01(3,16) 5.29F=) (1) 完成下面的方差分析表.(2) 给出分析结果.3. 有人认为企业的利润水平和它的研究费用间存在着近似的线性关系. 下面是某10个企业的利润水平(x )与研究费用(y )的调查资料:102101=∑=i ix,2390101=∑=i i y ,10661012=∑=i ix ,6243001012=∑=i iy ,25040101=∑=i i i y x建立研究费用y 与企业利润水平x 的回归直线方程.2011-2012学年第 2 学期 大学数学Ⅱ 华南农业大学期末考试试卷(A 卷)-参考答案 一、1. 0.8; 2. 31e --; 3.518; 4. 416 ; 5. )1(t ; 6. (4.412,5.588) 二、1. B 2. C 3. A 4. B 5. C 6. D 三、1. 解 设A =“任取一产品,经检验认为是合格品” B =“任取一产品确是合格品” 依题意()0.9,()0.1,()0.95,()0.02P B P B P A B P A B ==== (2分)则(1)()()(|)()(|)P A P B P A B P B P A B =+0.90.950.10.020.857.=⨯+⨯=(5分) (2) ()(|)0.90.95(|)0.9977()0.857P B P A B P B A P A ⨯===. (8分)2. 解 (1) 由2114a a -+=得1231().22舍去或a a ==- (3分) (2) X 的分布律为(5分)(3) X 的分布函数为 0,10,111,12,1244()113,23,234241111,3,3424x x x x F x x x x x <⎧<⎧⎪⎪⎪≤<⎪≤<⎪⎪⎪==⎨⎨+≤<⎪⎪≤<⎪⎪⎪⎪≥++≥⎩⎪⎩ (8分) 3. 解(1)111011{1}{11}12x x P X P X e dx e dx e---<=-<<===-⎰⎰. (3分)(2)当0y ≤时,()()()20F y P Y y P X y =<=<=; (5分) 当0y >时,()()(20xx F y P X y P X dx dx --=<=<<== (8分) 所以2Y X =的密度函数为0,0()()0y f y F y y ≤⎧⎪'==>. (10分) 4. 解 (1)因为随机变量X 与Y 相互独立, ( 1分)所以它们的联合密度函数为:3,03,0(,)()()0,y X Y e x y f x y f x f y -⎧≤≤>==⎨⎩其他 (3分)(2){}(,)y xP Y X f x y dxdy <<=⎰⎰330[]xy e dy dx -=⎰⎰ (6分)330(1)x e dx -=-⎰3390181()333x x e e --=+=+()9183e -=+ (8分) (3)解:由密度函数可知~(0,3),~(3)X U Y E (10分)所以,22(30)311(),(),12439D X D Y -==== (12分) 由X 与Y 相互独立,得3131()()()4936D X Y D X D Y -=+=+=(14分) 四、1. 解 检验假设 20:0.0004H σ=,21:0.0004H σ≠. (1分)依题意,取统计量:2222(1)~(1)n S n χχσ-=-,15n =. (3分)查表得临界值:220.0252(1)(14)26.1n αχχ-==,220.97512(1)(14) 5.63n αχχ--==, (5分)计算统计量的观测值得: 22140.02521.8750.0004χ⨯==. (6分)因2220.9750.025(14)(14)χχχ<<,故接受原假设0H ,即认为总体方差与规定的方差无显著差异.(8分) 2. 解 (1)(2) 解 因为F =5.6681>0.01(3,16) 5.29F =,所以拒绝0H ,即认为不同的贮藏方法对粮食含水率的影响在检验水平0.01α=下有统计意义. (8分)3. 解 2.10=x ,239=y (2分)6.252.10101066221012=⨯-=-=∑=x n x l i i xx (3分)6622392.101025040101=⨯⨯-=-=∑=y x n y x l i i i xy (4分)故1662ˆ25.8625.6xy xx l l β==≈;01ˆˆ23925.8610.224.77y x ββ=-=-⨯=- (6分) 因此所求回归直线方程为 ˆ24.7725.86yx =-+ (8分)。
最新-17-1华南农业大学大学数学2试卷(1)资料
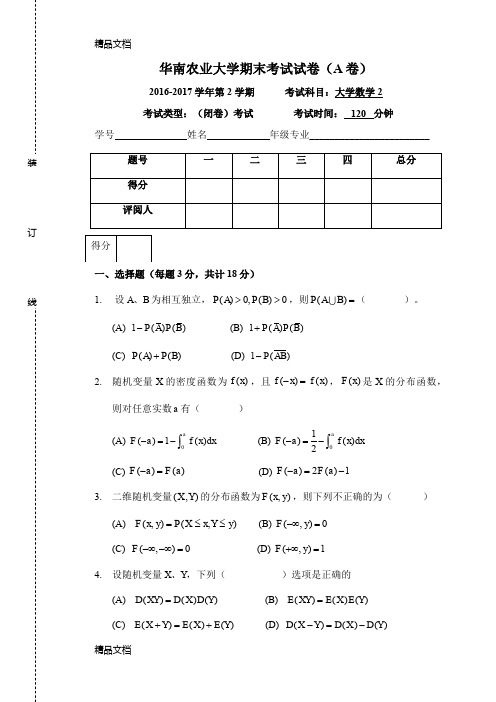
华南农业大学期末考试试卷(A 卷)2016-2017学年第 2 学期 考试科目:大学数学2 考试类型:(闭卷)考试 考试时间: 120 分钟学号 姓名 年级专业________________________一、选择题(每题3分,共计18分)1. 设A 、B 为相互独立,()0,()0P A P B >>,则()P A B =( )。
(A) 1()()P A P B - (B) 1()()P A P B + (C) ()()P A P B + (D) 1()P AB -2. 随机变量X 的密度函数为()f x ,且()()f x f x -=,()F x 是X 的分布函数,则对任意实数a 有( )(A) 0()1()aF a f x dx -=-⎰ (B) 01()()2aF a f x dx -=-⎰ (C) ()()F a F a -= (D) ()2()1F a F a -=-3. 二维随机变量(,)X Y 的分布函数为(,)F x y ,则下列不正确的为( )(A) (,)(,)F x y P X x Y y =≤≤ (B) (,)0F y -∞= (C) (,)0F -∞-∞=(D) (,)1F y +∞= 4. 设随机变量X 、Y ,下列( )选项是正确的(A) ()()()D XY D X D Y = (B) ()()()E XY E X E Y = (C) ()()()E X Y E X E Y +=+ (D) ()()()D X Y D X D Y -=-5. 若样本12,n X X X 来自于正态分布总体2(,)N μσ,其中标准差σ已知,则对于均值μ的置信度为1α-的区间估计为( )(A) 22[((X t n X t n αα--+-(B) 22[X X ααμμ-+(C) 22[X u X u αα-+(D) [X u X u αα-+6. 若样本12,n X X X 来自于正态分布总体2(,)N μσ,其中期望μ已知,在假设检验20:16H σ=与21:16H σ≠中,使用的检验统计量为( )(A)22116nii Xμ=-∑ (B)21()16nii Xμ=-∑(C)21()16nii XX =-∑ (D)22116nii XX =-∑二、填空题(每空3分,共计18分)1. 已知()P A =0.5,()P B =0.6,(|)P B A =0.8,则()P A B =______________2. 设随机变量X 服从泊松分布(2)P ,则(2)P X ≤=_____________3. 连续型随机变量的分布函数220()00x a be x F x x -⎧⎪+≥=⎨⎪<⎩,则a =___ _______ b=____________4. 假设~(1,4)X N -(正态分布),~(2)Y E (指数分布),且,X Y 相互独立,则(2)D X Y -= _________ 5. 样本12,n X X X 来自于正态分布总体2(,)N μσ,则样本均值X 服从___________________ (具体参数及分布)三、计算题(每题8分,共计48分)1. 中国有两支球队上海上港队和广州恒大队参与亚冠联赛,根据数据分析知,上海上港队夺冠的概率为0.92,广州恒大队夺冠的概率为0.93。
高等数学下试题及参考答案
华南农业大学期末考试试卷(A卷)2016~2017学年第2 学期 考试科目:高等数学A Ⅱ 考试类型:(闭卷)考试 考试时间: 120 分钟 学号 姓名 年级专业一、填空题(本大题共5小题,每小题3分,共15分)1.二元函数2ln(21)z y x =-+的定义域为 。
2. 设向量(2,1,2)a =,(4,1,10)b =-,c b a λ=-,且a c ⊥,则λ= 。
3.经过(4,0,2)-和(5,1,7)且平行于x 轴的平面方程为 。
4.设yz u x =,则du = 。
5.级数11(1)np n n∞=-∑,当p 满足 条件时级数条件收敛。
二、单项选择题(本大题共5小题,每小题3分,共15分) 1.微分方程2()'xy x y y+=的通解是( )A .2x y Ce =B .22x y Ce =C .22y y e Cx =D .2y e Cxy = 2.求极限(,)(0,0)limx y →= ( )A .14 B .12- C .14- D .123.直线:327x y zL ==-和平面:32780x y z π-+-=的位置关系是( ) A .直线L 平行于平面π B .直线L 在平面π上 C .直线L 垂直于平面π D .直线L 与平面π斜交4.D 是闭区域2222{(,)|}x y a x y b ≤+≤,则Dσ= () A .33()2b a π- B .332()3b a π- C .334()3b a π- D .333()2b a π-5.下列级数收敛的是 ( )A .11(1)(4)n n n ∞=++∑ B .2111n n n ∞=++∑ C .1121n n ∞=-∑ D.1n ∞=三、计算题(本大题共7小题,每小题7分,共49分) 微分方程'x y y e +=满足初始条件0x =,2y =的特解。
1. 求2. 计算二重积分22Dx y dxdy x y++⎰⎰,其中22{(,):1,1}D x y x y x y =+≤+≥。
华南农业大学07数分2期中试卷
1 华南农业大学期中考试试卷2007学年第2学期 考试科目: 数学分析II 考试类型:(闭卷) 考试时间: 110 分钟学号学号 姓名姓名 年级专业年级专业 题号一 二 三 四 总分总分 得分一. 填空填空 (每小题4分,共20分) 1.已知()ln x f x x¢=,则()f x =_____________. 2.反常积分()21 0a dx a x +¥>=ò_____________. 3. 曲线段[]ln ,1,y x x e =Î绕x 轴旋转一周所得旋转体的体积为______. 4. 对于积分23201x x dx -ò,若作变换sin x t =是否可以?说明理由。
是否可以?说明理由。
___________________________________________________________. 5. 极限1111lim 122n n n n n ®¥æö++++=ç÷++èø ________________. 二. 计算下列积分(每小题8分,共40分)分)1.10111dx x ++ò 2.10ln xdx ò 3.()3221x dx x +ò4.21dx x x -ò5.02cos2dx x p+ò2 三. 讨论下列反常积分的敛散性。
(每小题10分,共20分)分)1. 1sin x dx x+¥ò 2.101x dx x a -+¥+ò四. 应用题应用题 (每小题10分,共20分) 1.利用定积分求由曲线22y x =-与2y x =-所围图形的面积。
(要求画图)2. 设曲线方程为0sin , 0xy tdt x p =££ò,求曲线的长度。
华南农业大学2014-2015大学数学2期末试卷(A)及答案
华南农业大学期末考试试卷(A 卷)后附答案2014-2015学年第 2 学期 考试科目:大学数学Ⅱ 考试类型:(闭卷)考试 考试时间: 120 分钟学号姓名年级专业一、填空题(本大题共6小题,每小题3分,共18分)1.事件A 、B 为两个事件,若()0.6P A =,(|)0.4P B A =,则()P A B =2.设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤=其它,,02cos )(πx x A x f ,则系数A =3.已知随机变量X N Y N ~()~()-1131,,,且X 与Y 相互独立,若Z X Y =-+27,则Z 服从分布(写出具体分布及其参数)。
4. 以X 表示接连10次独立重复射击命中目标的次数,已知每次射击命中目标的概率为0.4,则2()E X =______.5.设来自总体X N ~(.)μ,092的容量为9的样本得样本均值X =5,则未知参数μ的置信度为95%的置信区间是6.设总体2~(,)X N μσ,其中μ未知,12,,n X X X 为其一个样本,样本均值为X ,样本方差为2S ,检验原假设2200:H σσ=与备择假设2210:H σσ≠,该检验统计量为__________________(用22,,n S σ来表示)二、单项选择题(本大题共6小题,每小题3分,共18分) 1. 下述函数中,可作为某个随机变量的分布函数的是()A. 21(),1F x x =+当x R ∈ B. 11()arctan 2F x x π=+,当x R ∈C. ⎪⎩⎪⎨⎧≤>-=-.0,0;0 ),1(21)(x x e x F xD. ()2F x x =,当01x <<2. 设X 和Y 相互独立,且分别服从)1,0(N 和)1,1(N ,则()。
A.2/1}0{=≤+Y X PB. 2/1}1{=≤-Y X PC. 2/1}0{=≤-Y X PD. 2/1}1{=≤+Y X P3. 设)(Y X ,的概率密度⎩⎨⎧≤≤≤≤=其它,,,,02010)(y x C y x f ,则=C ()A. 3B. 1/3C.1/2D. 24. 设随机变量,X Y 的期望与方差都存在, 则下列各式中成立的是( ).A.()E X Y EX EY +=+B.()E XY EX EY =⋅C.()D X Y DX DY +=+D. ()D XY DX DY =⋅5. 总体2~(,)X N μσ,从总体中抽取容量为n 的样本,样本均值为X ,则统计量2X Y n S μ⎛⎫-= ⎪⎝⎭服从()分布。
【免费下载】年高数BⅡ评分标准
1 x
y x
xy ez
ez
f
f
2
2
3y2 xz xy ez
ቤተ መጻሕፍቲ ባይዱ
x y2
x
y
)
...........5分
0 .........7分
,
z 2 z
, x
.....3分
........ 4分
.......6分
.
y 2
1
4
(x0 , y0 )
(B) I dx
(D) I dx
0
2
1
1
3
4
2 x x2
2x x2
1 1 x2
1 1 x2
f (x, y)dy
f (x, y)dy
3
所以有
4.交错级数
n1
(A) 绝对收敛 (B)条件收敛
(1)n1
1 3n1
5.差分方程 yt1 2 yt t 2 2t 的特解形式为( C ).
2. 设是z 由f所(x确, y定) 的隐x函2 数y求3 ez xyz 0
f
2
y x
x z y z x y
1 y
解:对方程两边求微分,得 dz 2x yz dx 3y2 xz dy
2z
y 2
(6 y
(6 y
x
(A) yt kt 2 2t ;
(C) yt at 3 bt 2 Ct 2t ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、已知随机变量 X 服从参数为 的指数分布,且 P X 1 (1)参数 ; (2) P X 2 X 1
1 ,求 2
4
0, 1 4、设一维随机变量 X 的分布函数为: FX x 2 sin x 1 , 1,
(1) X 的概率密度; (2) 随机变量 Y=2(X+1)的数学期望。
( A) P( AB) 1 2
B P( AB) 1 3
2 C P( AB) 3
D P( AB) 12 25
)
3、设 X,Y 为相互独立的两个随机变量,则下列不正确的结论是(
( A) E ( XY ) E ( X ) E (Y ) (C ) D( X Y ) D( X ) D(Y )
)
( 5、在对一元线性回归方程的统计检验中,回归平方和 SSR 的自由度是:
B n 2
C 1
D 1, n 2
,
6、设总体 X
~ N , 2 ,从 X 中抽取一容量为 n 的样本,样本均值为 X
2
X 则统计量 Y n 服从什么分布?( S
7、 某厂生产某种产品使用了 3 种不同的催化剂 (因素 A) 和 4 种不同的原料 (因 素 B) ,各种搭配都做一次试验测得成品压强数据。由样本观察值算出各平方 和分别为:SSA=25.17,SSB=69.34,SSE=4.16,SST=98.67,试列出方差分析 表, 据此检验不同催化剂和不同原料在检验水平 =0.05 下对产品压强的影响 有没有统计意义? ( F0.05 (2,6) 5.14, F0.05 (3,6) 4.76, F0.05 (4,6) 4.53 )
4、设两总体 X ~ N 1 ,
B D XY D X D Y D XY
2 2
0
2
, Y ~ N , , 未知,从 X 中抽取一容量为
n1 的样本,从 Y 中抽取一容量为 n2 的样本,作假设检验:
H 0 : 1 2 , H1 : 1 2 ,
则有 P
T1 T2 1 。
)假设总体 X 服从区间 [0, a] 上的均匀分布,从期望考虑, a 的矩估
ˆ 2X a
( X 是样本均值) 。
)用 MINITAB 软件求回归方程,在菜单中选择如下命令即可得:
Stat ANOVA Balanced ANOVA......
2 4、设总体 X 服从正态分布 N ,
X
Y
1
1 1 5
2
1 6
3
1 b 9
,
1 2
10
a
X 1 , X 2 ,..., X n 是它的一个样本,则样本均值 X 的方差是________。
5、假设正态总体的方差未知,对总体均值 作区间估计。现抽取了一个容量 为 n 的样本,以 X 表示样本均值,S 表示样本均方差,则 的置信度为 1- 的置信区间为:_______________________________。
则二维随机变量(X、Y)的联合概率密度为 2、 (
)设 x 是服从标准正态分布 N 0,1 的随机变量的分布函数,
X 是服从正态分布 N 3、 (
a 1 , 的随机变量,则有 P X a 2
2
)设二维随机变量(X、Y)的联合概率密度为
C P A B P A P B
D P A B P A P A P B
2 4 5 , P B , P B A 5 5 6
2、设 A,B 是两个随机事件, P A 则(
A
)
A P AB
f x, y ,随机变量
Z g X , Y 的数学期望存在,则 E Z
4、 (
x
y
g x, y f x, y dxdy
)设总体 X 的分布中的未知参数 的置信度为 1 的置信区间为
T1 , T2 ,
5、 ( 计是 6、 (
X P 0 1 p 1 p
,
1 ,则 p=________。 4
2、 设一维连续型随机变量 X 服从正态分布 N 2, 0.2 , 则随机变量 Y 2 X 1 的概率密度函数为__________________________。 3、设二维离散型随机变量 X、Y 的联合分布律为: 则 a, b 满足条件:___________________。
华南农业大学期末考试试卷(A 卷)
2006 学年第二学期 考试类型: (闭卷)
学号 题号 得分 评阅人 一 姓名 二 三 四
考试科目:
应用数学
考试时间:120分钟
年级专业 五 总分
一、 填空题(每小题 2 分,共 2¥6=12 分)
1、设服从 0—1 分布的一维离散型随机变量 X 的分布律是: 若 X 的方差是
五、综合实验(本题 8 分,开卷,解答另附于《数学实验报告》中)
6
华南农业大学期末考试试卷(A 卷)
2006 学年第二学期
考试类型: (闭卷) 学号 题号 得分 评阅人 一 姓名 二 三 四
考试科目:
应用数学(解答)
考试时间:120分钟 年级专业 五 总分
一、 填空题(每小题 2 分,共 2¥6=12 分)
)
A N 0,1 B t n 1 C 2 n 1 D F 1, n 1
2
三、判别题(每小题 2 分,共 2¥6=12 分)
(请在你认为对的小题对应的括号内打“√”,否则打“X”) 1、 ( ) 设随机变量 X 的概率密度为
f X ( x) , 随机变量 Y 的概率密度为 fY ( y ) , f X ( x ) fY ( y ) 。
四、计算题(每小题 8 分,共 8¥7=56 分)
1、某连锁总店属下有 10 家分店,每天每家分店订货的概率为 p,且每家分 店的订货行为是相互独立的,求 (1) 每天订货分店的家数 X 的分布律; (2) 某天至少有一家分店订货的概率。
3
2、现有十个球队要进行乒乓球赛,第一轮是小组循环赛,要把十支球队平分成 两组, 上届冠亚军作为种子队分别分在不同的两组, 其余八队抽签决定分组, 甲队抽第一支签,乙队抽第二支签。 (1)求:甲队抽到与上届冠军队在同一组的概率; (2)求:乙队抽到与上届冠军队在同一组的概率; (3)已知乙队抽到与上届冠军队在同一组,求:甲队也是抽到与上届冠军队 在同一组的概率。
2
n
。
5、假设正态总体的方差未知,对总体均值 作区间估计。现抽取了一个容量 为 n 的样本,以 X 表示样本均值, S 表示样本均方差,则 的置信度为
1
1 的置信区间为: X t 2 n 1 , X t 2 n 1 n n
y bx a 6、 求随机变量 Y 与 X 的线性回归方程 Y a bX , 在计算公式 b Lxy Lxx
( A) P( A B) P( A) P( B) (C ) P( A B) P( A) P( B )
( B) P( A B) P( A) P( AB) ( D) P( A B) P( A) P( A) P( B)
2、设 A,B 是两个随机事件, P A 2 , P B 4 , P B A 5 5 5 6 则( )
1 2
B P AB
1 3
C P AB
2 3
D P AB
B
12 25
3、设 X,Y 为相互独立的两个随机变量,则下列不正确的结论是(
)
A E XY E X E Y C D X Y D X D Y
1、设服从 0—1 分布的一维离散型随机变量 X 的分布律是:
X P
0 1 p
1 p
若 X 的方差是
1 ,则 p 4
1 2
2、 设一维连续型随机变量 X 服从正态分布 N 2, 0.2 , 则随机变量 Y 2 X 1
1 e 1.6
y 5 2
1.6
的概率密度函数为
Y ~ N 5,
x 2 x ,求: 2 2 x 2
5、 设二维随机变量(X,Y)的联合概率密度为
4 xy , f x, y 0,
0 x 1, 0 y 1 其余地方
,求
(1)该二维随机变量的联合分布函数值 F
,1 1 2
;
(2)二维随机变量(X,Y)的函数 Z=X+Y 的分布函数值 FZ(1)。
C
)
( 5、在对一元线性回归方程的统计检验中,回归平方和 SSR 的自由度是:
B n 2
C 1 D 1, n 2
4、设两总体 X ~ N 1 ,
( B) D( XY ) D( X ) D(Y ) ( D) XY 0
2 2
2
, Y ~ N , , 未知,从 X 中抽取一容量为
n1 的样本,从 Y 中抽取一容量为 n2 的样本,作假设检验:
H 0 : 1 2 , H1 : 1 2 ,
T 所用统计量 X Y
2 SX n1 1 SY2 n2 1 1 1 n1 n2 2 n1 n2
服从(
D
)
2
A 自由度为 n1 n2 1的 t 分布 C 自由度为 n1 n2 1的 t 分布
