自感和互感磁场能量
合集下载
14电磁感应2(自感互感、磁场能量)
§14-3 自感和互感
I
一、自感 1．当一线圈中的电流变化时，它所激发的磁 场通过线圈自身的磁通量也在变化，使线 圈自身产生感应电动势。 这种因线圈中电流变化而在线圈自身所引 起的感应现象叫做自感现象，所产生的电 动势叫做自感电动势。
R
L
S2 S1
S
L
闭合开关， 2比S1先亮 S
断开开关，S闪一下熄灭
电流增大时，dI 0 ， L 0 ，即 L与电流反
向，阻碍电流增大；
dI 电流减小时， 0 ， L 0 ，即 L与电流同 dt dt
向，阻碍电流减小
I
例1 、 试计算长直螺线管的自感。 已知：匝数N,横截面积S,长度l ,磁导率
μ
l
自感的计算步骤：
S
LH dl I B H B H
单位长度导线内磁能为：
R
P
Wm wm dV
V
R
0
I 2 r 2 I 2 2rdr 2 4 8 R 16
§14-5 位移电流 麦克斯韦方程组
一、电磁场的基本规律 静电场：
D dS q
S
E dl 0
l
（对真空或电介质都成立）
稳恒磁场：
例、如图，求同轴传输线之磁能及自感系数 R2 I I 解: H B dV 2rldr R 1 2r 2r 1 W V wdV V H 2 dV 2 R2 1 I 2 ( ) 2rldr R1 2 2r I 2 l R2 ln( ) 4 R1 I 2 l R2 1 2 LI W ln( ) 4 R1 2 l R2 可得同轴电缆 L ln( ) 的自感系数为 2 R1
I
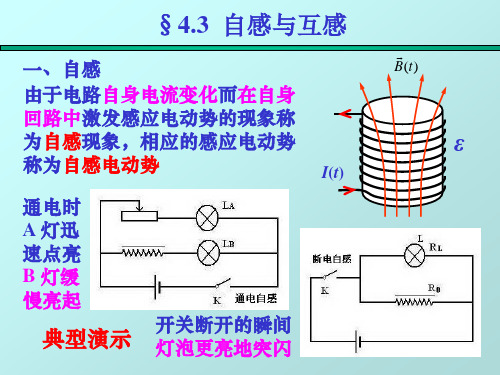
一、自感 1．当一线圈中的电流变化时，它所激发的磁 场通过线圈自身的磁通量也在变化，使线 圈自身产生感应电动势。 这种因线圈中电流变化而在线圈自身所引 起的感应现象叫做自感现象，所产生的电 动势叫做自感电动势。
R
L
S2 S1
S
L
闭合开关， 2比S1先亮 S
断开开关，S闪一下熄灭
电流增大时，dI 0 ， L 0 ，即 L与电流反
向，阻碍电流增大；
dI 电流减小时， 0 ， L 0 ，即 L与电流同 dt dt
向，阻碍电流减小
I
例1 、 试计算长直螺线管的自感。 已知：匝数N,横截面积S,长度l ,磁导率
μ
l
自感的计算步骤：
S
LH dl I B H B H
单位长度导线内磁能为：
R
P
Wm wm dV
V
R
0
I 2 r 2 I 2 2rdr 2 4 8 R 16
§14-5 位移电流 麦克斯韦方程组
一、电磁场的基本规律 静电场：
D dS q
S
E dl 0
l
（对真空或电介质都成立）
稳恒磁场：
例、如图，求同轴传输线之磁能及自感系数 R2 I I 解: H B dV 2rldr R 1 2r 2r 1 W V wdV V H 2 dV 2 R2 1 I 2 ( ) 2rldr R1 2 2r I 2 l R2 ln( ) 4 R1 I 2 l R2 1 2 LI W ln( ) 4 R1 2 l R2 可得同轴电缆 L ln( ) 的自感系数为 2 R1
磁场中的磁能与自感现象
实验验证方法
静态实验法
通过测量静态情况下两个线圈之间的互感系数来验证互感现象的存在。这种方法需要使用 精密的测量仪器和稳定的电源来提供恒定的电流。
动态实验法
通过改变线圈中的电流或线圈之间的相对位置来观察感应电动势的变化情况。这种方法需 要使用示波器、电流计等实验
汇报人：XX 2024-01-16
contents
目录
• 磁场与磁能基本概念 • 磁能计算与储存方式 • 自感现象及其产生原因 • 互感现象与自感现象关系 • 磁场中能量转换与传递过程 • 总结回顾与拓展延伸
01
磁场与磁能基本概念
磁场定义及性质
磁场定义
磁场是一种存在于磁体周围的特 殊物质，它对放入其中的磁体产 生磁力作用。
影响因素探讨：距离、角度等
距离
线圈之间的距离越近，互感作用越强。当两 个线圈紧密靠近时，它们之间的磁通量变化 会更加显著，从而导致更大的感应电动势。
角度
线圈之间的相对角度也会影响互感作用。当 两个线圈的法线方向相互平行时，它们之间 的磁通量变化最大，互感作用最强。随着相 对角度的增大，磁通量变化减小，互感作用 减弱。
互感和自感之间联系和区别
联系
自感和互感都是电磁感应现象，都遵循 法拉第电磁感应定律。在电路分析中， 自感和互感往往同时存在，相互影响。
VS
区别
自感是单个线圈中电流变化时产生的感应 电动势，而互感是两个或多个线圈之间相 互作用产生的感应电动势。此外，自感系 数仅与线圈本身的结构和电流变化率有关 ，而互感系数则与线圈之间的相对位置、 形状、大小以及周围介质有关。
超导线圈应用案例
超导线圈在磁共振成像（MRI）、粒子加速器等领域有重要 应用。例如，在MRI中，超导线圈产生的强磁场和梯度磁场 用于对人体进行成像。
大学物理,电磁感应12.4自感和互感
要求自感电动势，应先求出自感系数。
9
12.3 自感和互感
自感应用：
第12章 电磁感应
日光灯镇流器；高频扼流圈；自感线圈与电 容器组合构成振荡电路或滤波电路。 通电后，启辉器辉光放电，金属片受热形变 互相接触，形成闭合回路，电流流过，日光灯灯 丝加热释放电子。 同时，启辉器接通辉光熄灭， 金属片冷却断开，电路切断，镇流器线圈中产生 比电源电压高得多的自感电动势，使灯管内气体 电离发光。 自感危害：电路断开时，产生自感电弧。
dI 1 dI 1 dΨ21 M 21 M ε 21 dt dt dt
当线圈 2 中的电流变化时，在线圈 1 中产生的 互感电动势为：
dΨ12 dI 2 dI 2 ε12 M 12 M dt dt dt
20
12.3 自感和互感
第12章 电磁感应
ε12
dI 2 = -M dt
4
12.3 自感和互感
2、自感系数 L
根据毕奥—萨尔定律： μ0 Idl r dB 4π r 3
第12章 电磁感应
I
B
线圈中的电流在空间任意一点激发的磁感应 强度的大小与线圈中的电流强度成正比，即： 穿过线圈自身总的磁通量与电流 I 成正比，
写成：
Φ LI
L 为自感系数。
解：设长直导线中电流 I ，
矩形线圈平面上的磁链数为： dr I
N B dS
M I
0 I N ldr a 2r 0 NIl a b ln 2 a 0 Nl a b ln 2 a
s ab
r
l
a
b
24
12.3 自感和互感
思考？ 若已知矩形线圈中有电流：
9
12.3 自感和互感
自感应用：
第12章 电磁感应
日光灯镇流器；高频扼流圈；自感线圈与电 容器组合构成振荡电路或滤波电路。 通电后，启辉器辉光放电，金属片受热形变 互相接触，形成闭合回路，电流流过，日光灯灯 丝加热释放电子。 同时，启辉器接通辉光熄灭， 金属片冷却断开，电路切断，镇流器线圈中产生 比电源电压高得多的自感电动势，使灯管内气体 电离发光。 自感危害：电路断开时，产生自感电弧。
dI 1 dI 1 dΨ21 M 21 M ε 21 dt dt dt
当线圈 2 中的电流变化时，在线圈 1 中产生的 互感电动势为：
dΨ12 dI 2 dI 2 ε12 M 12 M dt dt dt
20
12.3 自感和互感
第12章 电磁感应
ε12
dI 2 = -M dt
4
12.3 自感和互感
2、自感系数 L
根据毕奥—萨尔定律： μ0 Idl r dB 4π r 3
第12章 电磁感应
I
B
线圈中的电流在空间任意一点激发的磁感应 强度的大小与线圈中的电流强度成正比，即： 穿过线圈自身总的磁通量与电流 I 成正比，
写成：
Φ LI
L 为自感系数。
解：设长直导线中电流 I ，
矩形线圈平面上的磁链数为： dr I
N B dS
M I
0 I N ldr a 2r 0 NIl a b ln 2 a 0 Nl a b ln 2 a
s ab
r
l
a
b
24
12.3 自感和互感
思考？ 若已知矩形线圈中有电流：
大学物理-12第十二讲 感生电动势、自感、互感、磁场能量
3.按定义 L I
18
二、互感应
●由于一个载流回路中电流发生变化而引起邻近另 一回路中产生感生电流的现象称为“互感现象”， 所产生的电动势称为 “互感电动势”。
21N 2 21M 21I1 12N 1 12M 12I2
从能量观点可证明：
M12M21M
M称为互感系数简称互感 单位：亨利（H）
同理：
bo
ov r b E感dr0
ab oabo
o
E 感
L R2 L2 dB
2
4 dt
h
a
b
L
方向ab (Ub Ua )
9
vv
Байду номын сангаас法2： 用 LE感dl 求
vv
dE感dl
r 2
dB dt
cos
dl
h 2
dB dt
dl
vv
LE感dl
b h dB dl
a 2 dt 1 hL dB
缆单位长度的自感系数。
解： 两导体圆筒间磁场
B
I
2r
R2 R1
AB
通过单位长度一段的磁通量
I l 1
B vdS vR R 12Bldr2 IlnR R 1 2
DC
单位长度的自感系数 L lnR2 I 2 R1
17
总结L的计算方法 1.设回路电流为I，写出B的表达式（一般由安培
环路定理）
vv
2.计算磁通 B d S, N
LE库dvl
0
v
Ñ 感生电场是非保守力场 LE感dl 0
3
例：在半径为R 的长直螺线管中通有变化的电流，使
管内磁场均匀增强，求螺线管内、外感生电场的场强
18
二、互感应
●由于一个载流回路中电流发生变化而引起邻近另 一回路中产生感生电流的现象称为“互感现象”， 所产生的电动势称为 “互感电动势”。
21N 2 21M 21I1 12N 1 12M 12I2
从能量观点可证明：
M12M21M
M称为互感系数简称互感 单位：亨利（H）
同理：
bo
ov r b E感dr0
ab oabo
o
E 感
L R2 L2 dB
2
4 dt
h
a
b
L
方向ab (Ub Ua )
9
vv
Байду номын сангаас法2： 用 LE感dl 求
vv
dE感dl
r 2
dB dt
cos
dl
h 2
dB dt
dl
vv
LE感dl
b h dB dl
a 2 dt 1 hL dB
缆单位长度的自感系数。
解： 两导体圆筒间磁场
B
I
2r
R2 R1
AB
通过单位长度一段的磁通量
I l 1
B vdS vR R 12Bldr2 IlnR R 1 2
DC
单位长度的自感系数 L lnR2 I 2 R1
17
总结L的计算方法 1.设回路电流为I，写出B的表达式（一般由安培
环路定理）
vv
2.计算磁通 B d S, N
LE库dvl
0
v
Ñ 感生电场是非保守力场 LE感dl 0
3
例：在半径为R 的长直螺线管中通有变化的电流，使
管内磁场均匀增强，求螺线管内、外感生电场的场强
第28讲 自感与互感 磁场能量
9.3 自感与互感
dB dI 感 dt dt
?
自感和互感现象
dI L L dt dI1 21 M dt
一 自感 1. 自感现象
当一个线圈中的电流发生变化时，它所激发的 磁场穿过线圈自身的磁通量发生变化，从而在 线圈本身产生感应电动势，这种现象称为自感 现象，相应的电动势称为自感电动势。
4. 自感系数的物理意义
dI const 时， 当线圈中的电流变化率为定值，即 dt L越大，产生的εL越大，因此线圈阻碍电流变化的能 力越强。所以线圈的自感系数L的物理意义为：
自感 L有维持原电路状态的能力, 自感系数L就是 这种能力大小的量度,它表征回路电磁惯性的大小。
dI L L dt
L0=L1+L2+2M =2L+2M
所以 L=L0/2-M < L0/2。
证毕。
9.4 磁场的能量
1 自感磁能 当电路中电流从 0 增加到稳定值 I0 时，电路附近 的空间逐渐建立起一定强度的磁场，磁场也具有 能量。 电源反抗自感电动势所做的功，就在建立磁场的 过程中转化为磁场的能量。 ─自感磁能
0 I 0 B 2 r 0 r R1 R1 r R2 r R2
I
R2 R1
l
取体积元为薄柱壳
d 2 rldr
1 B2 dV Wm wm dV V 2 V 0
r
dr
Wm wm dV
V
V
再根据
R2
R1
1 0 I 2 0 I 2 l R2 ( ) 2 rldr ln( ) 2 0 2 r 4 R1
5.自感的计算方法 • 假设线圈中电流为I; • 计算线圈中的全磁通Ψm ; m N B dS • 由L= Ψm / I, 求出L.
dB dI 感 dt dt
?
自感和互感现象
dI L L dt dI1 21 M dt
一 自感 1. 自感现象
当一个线圈中的电流发生变化时，它所激发的 磁场穿过线圈自身的磁通量发生变化，从而在 线圈本身产生感应电动势，这种现象称为自感 现象，相应的电动势称为自感电动势。
4. 自感系数的物理意义
dI const 时， 当线圈中的电流变化率为定值，即 dt L越大，产生的εL越大，因此线圈阻碍电流变化的能 力越强。所以线圈的自感系数L的物理意义为：
自感 L有维持原电路状态的能力, 自感系数L就是 这种能力大小的量度,它表征回路电磁惯性的大小。
dI L L dt
L0=L1+L2+2M =2L+2M
所以 L=L0/2-M < L0/2。
证毕。
9.4 磁场的能量
1 自感磁能 当电路中电流从 0 增加到稳定值 I0 时，电路附近 的空间逐渐建立起一定强度的磁场，磁场也具有 能量。 电源反抗自感电动势所做的功，就在建立磁场的 过程中转化为磁场的能量。 ─自感磁能
0 I 0 B 2 r 0 r R1 R1 r R2 r R2
I
R2 R1
l
取体积元为薄柱壳
d 2 rldr
1 B2 dV Wm wm dV V 2 V 0
r
dr
Wm wm dV
V
V
再根据
R2
R1
1 0 I 2 0 I 2 l R2 ( ) 2 rldr ln( ) 2 0 2 r 4 R1
5.自感的计算方法 • 假设线圈中电流为I; • 计算线圈中的全磁通Ψm ; m N B dS • 由L= Ψm / I, 求出L.
电磁感应 4-3 自感互感、磁场能量
任何磁场的能量
(不一定均匀磁场)
Wm
V wmdV
V
1 BHdV 2
电场 能量
磁场 能量
电场能量与磁场能量的对比
存储在器件中
存储在场中
We
1 2
CU
2
we
1 2
D
E
We V wedV
Wm
1 2
LI
2
wm
1 2
B
H
Wm V wmdV
若同时存在 电场和磁场
w
1
B
H
1
D
E
2
一、电感线圈存储的能量
前面演示自感的典型实验，当开关 突然断开后，灯泡会更亮地突闪。 这说明电感线圈中存储了某种形式 的能量，在开关断开后释放出来了
K
A
I
i
L
自感为 L 通有电流 I 的线圈所具有的磁能等于电流消 失过程中 (I → 0) 自感电动势所做的功，Wm = AL
dt 时间内通过灯泡的电量 q = i dt
的磁场中的，因此我们考虑磁场能量与磁感应强度之
间的关系。以长直螺线管为例，其自感 L = μn2V 忽略边缘效应，其内部的磁感应强度 B = μnI
Wm
1 2
LI 2
1 2
n2I 2V
1 2
B2
V
单位体积 磁场能量
wm
1 2
B2
1 2
BH
1 2
H 2
磁能 密度
wm
1 2
B
H
虽从长直螺线管特例推出，但对任何磁场均普遍适用
l
dr
穿过线框的磁通量为
2r
r
Φ
B dS
7-4自感与互感 7-5磁场能量
π
Φ = Φ = d
2π
μN Ih
2π
R
R2
1
dr r
μ N I h ln ( R 2 ) =
R1 R μ N h 2) I ( = Φ Ψ N = ln 2π R1 2 Ψ R μ 2) N h ( ln L= = 2π I R1
2
二、互感（mutual induction）
若两回路几何形状、尺寸及相对位置不变，周围无铁 磁性物质。实验指出：
磁场的 能量
磁场的能量：
螺线管（特例）：
1 Wm = 2 L I
2
H=n I B =μ n I L = μ n 2V 2 2 1μ 2 1 H 1 2 Wm = 2 L I = μ n V ( n ) = 2 H V 2
1 2 1 wm = 2 μ H = B H 2 Wm = V wmdV
互感电动势：
ε
ε
I2 d d Ψ 12 = M 12= dt dt I1 d d Ψ 21 = M 21= dt dt
讨论： 1. 互感系数和两回路的几何形状、尺寸，它们的相 对位置，以及周围介质的磁导率有关。 2. 互感系数的大小反映了两个线圈磁场的相互影响程 度。
[例1] 有两个直长螺线管，它们绕在同一个 圆柱面上 。 已知： N 1、 μ 0、 N 2、 S、 l 求：互感系数
Φ 12∝ I 2 Φ 21∝ I 1
Φ 12 = M 12 I 2 Φ 21 = M 21 I 1
M 12 = M 21 =M
I1 I2
Φ 21
实验和理论都可以证明：
Φ 12
若两线圈的匝数分别为 N 1 ， N 2 则有：
Ψ 12 NΦ 1 12 = M I 2 = NΦ M I 1 =Ψ 21 2 21 =
电感的自感与互感现象
电感的自感与互感现象电感是电路中常见的元件，它具有自感和互感两种重要的物理现象。
本文将详细介绍电感的自感和互感现象。
一、自感现象自感是指电流在电感中产生的磁通量对电流自身的感应作用。
当电流通过一个线圈时，会形成一个磁场，这个磁场会将一部分能量储存起来，形成磁能。
当电流发生变化时，线圈的磁场也随之变化，产生电动势。
这种电动势的方向与电流变化的方向相反，试图阻止电流变化。
这种现象称为自感现象。
自感现象的数学表达式为：ε = -L * dI/dt其中，ε表示自感电动势，L表示电感的自感系数，dI/dt表示电流变化的速率。
根据这个公式，我们可以看出，自感电动势与电流变化的速率呈线性关系。
二、互感现象互感是指两个或者多个线圈之间通过磁场相互感应产生的电动势现象。
当一个线圈中的电流发生变化时，将会生成一个磁场，这个磁场会穿过另一个线圈，从而在另一个线圈中产生电动势。
这种现象称为互感现象。
互感现象的数学表达式为：ε = -M * dI1/dt其中，ε表示互感电动势，M表示互感系数，dI1/dt表示第一个线圈电流的变化速率。
互感系数M与线圈的结构有关，正比于线圈的匝数和相对位置。
互感现象不仅存在于两个线圈之间，还可以存在于一个线圈的不同部分。
当线圈自身的一部分对另一部分产生感应时，也会发生互感现象。
三、电感对电路的影响电感具有阻碍电流变化的特性，这对电路有着重要的影响。
1. 自感对电路的影响：在直流电路中，自感会形成一个扼流圈，阻碍电流的变化。
这可以用来稳定直流电压，避免电流的突变。
在交流电路中，自感会引起电路的阻抗变化。
阻抗由电阻和电感共同决定，而电感对不同频率的电流具有不同的阻抗。
这使得电感在交流电路中可以用作滤波器、隔直流器等。
2. 互感对电路的影响：互感在变压器、电感耦合放大器等电路中起着重要作用。
变压器利用互感现象将电压变换到合适的水平，实现电能传输和变压变流。
电感耦合放大器则通过互感将信号传递到输出电路，增加信号的幅度。
自感互感磁场能量
• 互感电动势
21
d(M 21I1) dt
M 21
dI1 dt
I1
dM 21 dt
若回路周围不存在铁磁质
且两线圈结构、相对位置 及其周围介质分布不变时
21
M 21
dI1 dt
同理
12
M12
dI2 dt
讨论
(1) 可以证明： M 21 M12 M
L1
L2
(2) 互感反映了线圈本身的电磁性质。 M
Ψ LI
L ——自感系数
自感 L 是反映线圈本身的电磁性质的物理量，如果回路周围 不存在铁磁质，自感 L 与电流 I 无关，仅由回路的匝数、几 何形状和大小以及周围介质的磁导率决定。
3. 自感电动势
自感电动势
＝
L
d
dt
d(LI ) dt
L dI dt
I dL dt
对一般不含铁磁质的回路，L为常数
通交流电的电磁铁 真空环
§10.3 自感 互感
一. 自感现象 自感系数 自感电动势
1. 自感现象
线圈电流变化 I I (t)
穿过自身磁通变化 Φm (t)
I
B
在线圈中产生感应电动势
dΦm
dt
—自感电动势遵从法拉第定律
2. 自感系数
根据毕 — 萨定律可知空间任意点的B与I 成正比，因此穿过 线圈自身总的磁通量与电流 I 成正比
• 电磁阻尼
• 电子感应加速器
电子感应加速器是利用感生电场对电子进行加速的设备。
原理：在 圆柱形电磁铁的两极N、S 间隙中安放一个环形真空 室，由电子枪射入真空室中的电子 : (1) 受磁场的洛仑兹力控制在真空室圆轨道上运行; (2) 利用变化磁场产生的感生电场使电子加速，一般小 型电子感应器可将电子加速到几十万电子伏特，大型的 可达数百万电子伏特。
物理人教版高中选择性必修二(2019年新编)2-4互感和自感 讲义
第二章电磁感应第4节互感和自感【素养目标】1. 了解什么是互感现象,了解互感现象在生活和生产中的应用和防止。
2. 了解什么是自感现象,了解自感现象在生活和生产中的应用和防止;能够运用电磁感应的有关规律分析通、断电自感现象;了解自感电动势的计算式。
3. 知道自感系数是表示线圈本身特征的物理量,知道它的大小与哪些因素有关,知道它的单位。
【必备知识】知识点一、互感现象(1)定义:两个相互靠近的线圈,当一个线圈中的电流变化时,它所产生的变化的磁场会在另一个线圈中产生感应电动势的现象。
互感现象中,产生的电动势叫作互感电动势。
(2)应用:互感现象可以把能量由一个线圈传递到另一个线圈,变压器、收音机的“磁性天线”就是利用互感现象制成的。
(3)危害:互感现象能发生在任何两个相互靠近的电路之间,电力工程和电子电路中,有时会影响电路正常工作,这时要设法减小电路间的互感。
知识点二、自感现象(1)定义:一个线圈中的电流变化时,它所产生的变化的磁场在它本身激发出感应电动势的现象。
由于自感而产生的电动势叫作自感电动势。
(2)自感电动势大小:正比于电流(或磁通量)的变化率公式:(1)E =n ·ΔΦΔt (2)E =L ·ΔI Δt(式中L 表示自感系数)方向:遵守楞次定律,即当原电流增大时,自感电动势与原电流方向相反;当原电流减小时,自感电动势与原电流方向相同作用:总是阻碍线圈中原电流的变化,即总是起着推迟电流变化的作用(2)自感系数物理意义:表示线圈产生自感电动势本领大小的物理量大小的决定因素:与线圈的大小、形状、圈数以及是否有铁芯等因素有关单位:国际单位是亨利,简称亨,符号是H,常用的还有毫亨(mH)和微亨(μH),1H=103mH=106μH知识点三、磁场的能量(1)自感现象中的磁场能量①线圈中电流从无到有时,磁场从无到有,电源的能量输送给磁场,储存在磁场中。
②线圈中电流减小时,磁场中的能量释放出来转化为电能。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
R2
解 两圆筒之间 B I
2πr 如图在两圆筒间取一
长为 l的面 PQRS , 并将
其分成许多小面元.
则
dΦ BdSBdlr
I
R1 Q R
Ir l
ΦdΦR R122πIrldr
P
S
R2
dr
ΦdΦR R122πIrldr
Φ Il ln R2
2π R1
LΦ l lnR2
I 2π R1
I
单位长度的自感为
V2
例 如图同轴电缆,中间充以磁介质,芯线
与圆筒上的电流大小相等、方向相反. 已
知 R 1,R 2,I, ,
求单位长度同轴电缆的
I
磁能和自感. 设金属芯 2 R1
I
线内的磁场可略.
R1 R2
解 由安培环路定律可求 H
rR 1, H 0
RH0
则 R1rR2
2 R1
R1 Q R
Ir l
L ln R2
l 2π R1
P
S
R2
dr
二 互感电动势 互感
I 1 在 I 2电流回路中所产生的磁通量
Φ21M21I1
I 2 在 I 1 电流回路 中所产生的磁通量
Φ12M12I2
B1
I1
B2
I2
（1 ）互感系数
M12M21MΦ I211Φ I122
注意 互感仅与两个线圈形状、大小、匝
数、相对位置以及周围的磁介质有关.
B1
I1
B2
I2
（2）互感电动势
E12
M
dI2 dt
E2
1
M
dI1 dt
➢ 互感系数 M E21 E12
dI1dt dI2 dt
问：下列几种情况互感是否变化？
O （1）线框平行直导线移动；
（2）线框垂直于直导线移动；
C （3）线框绕 OC 轴转动；
（4）直导线中电流变化.
当
dL dt
0
时，
IB
E
L
L
dI dt
自感
L EL
dI dt
（3）自感的计算方法
例1 如图的长直密绕螺线管,已知
l,S,N,, 求其自感 L（忽略边缘效应） .
解 先设电流 I 根据安培环路定理求
得H B Φ L
nN l
S
BHnI
lE
NΦNBS
NΦNBS N N IS
l
L N2 S VlS Ln2V
I
b
求二者的互感系数.
d
l
o
x
解 设长直导线通电流 I
B I
2π x
dΦB ds I ldx
2πx
b
Φ db I ldx
d 2πx
I
d
l
Illn(bd)
2π d
o xdx
x MΦllnb(d)
I 2π d
三 磁场的能量
2r
l RE
E LdI RI dt
E IdtLdIIR2d It
tEIdt1L2ItR2Idt
例3 两同轴长直密绕螺线管的互感 有两个长度均为l，半径分别为r1和r2（ r1<r2 ）， 匝数分别为N1和N2的 同轴长直密绕螺线管. 求它们的互感 .
M
解 先设某一线圈中通以电流 I 求
出另一线圈的磁通量 Φ
M
设半径为 r1 的线
圈中通有电流 I 1 , 则
B10 Nl1I10n1I1
则穿过半径为 r2 的线圈的磁通匝数为
N 2 Φ 21 N 2B 1(πr1 2)n2lB1(πr12)
M12
N 2Φ21 I1
0n1n2l(πr12 )
代入 B 1 计算得
N2Φ21
0n1n2l(πr12)I1
例 4 在磁导率为的均匀无限大的磁
介质中, 一无限长直导线与一宽、长分别为b
和 l 的矩形线圈共面,直导线与矩形线圈的
一侧平行,且相距为 d.
基本要求 一 了解自感、互感，掌握计算自
感和互感系数的方法 .
二 了解自感磁能公式的意义，了 解磁能密度的概念 .
一 自感电动势 自感
（1）自感
ΦLI LΦ I 若线圈有 N 匝，
NΦ 磁通匝数
IB
自感 L I
注意 无铁磁质时, 自感仅与线圈形 状、磁介质及 N 有关.
（2）自感电动势
ELd d Φ t (Ld dItId dL t)
线管的自感系数越大 LN0nS
一无限长载有电流 I 的直导线旁边有一与之共面 的矩形线圈，线圈的边长分别为l和b，l边与长直导线 平行．线圈以速度 垂直离开直导线，如图所示．求当 矩形线圈与无限长直导线间的互感系数 M 0l 时，线
2
圈的位置及此时线圈内的感应电动势的大小．
wm
1( I )2
2 2π r
I
8π 2
2
r
2
I
I
R1 R2
单位长度壳层体积 d V2πrd r1
W mVwmdVV8 πI22r2dV
I 2 ln R2
4π R1
2 R1
Wm
1 2
LI 2
L ln R2
2π R1
I I
r dr R2
下列叙述哪种正确： （A）通过螺线管的电流越大，螺线管的 自感系数越大 （B）通过螺线管的电流变化率越大，螺 线管的自感系数越大 （C）螺线管的自感系数，与螺线管是否 充有磁介质无关 （D）螺线管中单位长度的匝数越多，螺
Il
（一般情况可用下式测量自感）EL
L
dI dt
S
lE
（4）自感的应用 稳流 , LC 谐振电路 滤波电路, 感应圈等
例 2 有两个同轴圆筒形导体 , 其半径分
别为 R 1 和 R 2 , 通过它们的电流均为 I,
但电流的流向相反.设在
两圆筒间充满磁导率为
R1
的均匀磁介质 , 求其自感 L.
I Ir l
0
2
0
自感线圈磁能
Wm
1 2
LI 2
电 电源反 回路电
源 抗自感 阻所放
作 功
电动势 作的功
出的焦 耳热
自感线圈磁能
Wm
1 2
LI 2
IL
Ln2V, BnI
W m1 2L2I1 2n2V(B n)2
1 2
B2
V
wmV
磁场能量密度
IL
wm2B2 12H2
1BH 2
磁场能量
Wm
VwmdV
B2 dV