大学物理 12-4 自感和互感
合集下载
互感和自感 课件
3．自感系数 (1)大小：线圈的长度越长，线圈的横截面积越大，单 位长度上的匝数越多，线圈的自感系数就越大，线圈有铁芯 时比无铁芯时自感系数大得多。 (2)单位：亨利(符号 H)，1 H＝103 mH＝106 μH。 (3)物理意义：表征线圈产生自感电动势本领大小的物 理量，数值上等于通过线圈的电流在 1 s 内改变 1 A 时产生 的自感电动势的大小。
例 3 如图所示的电路中 A1 和 A2 是两个相同的小灯 泡，L 是一个自感系数相当大的线圈，其阻值与 R 相同。在 开关 S 接通和断开时，灯泡 A1 和 A2 亮暗的顺序是( )
A．接通时 A1 先达最亮，断开时 A1 后灭 B．接通时 A2 先达最亮，断开时 A1 后灭 C．接通时 A1 先达最亮，断开时 A1 先灭 D．接通时 A2 先达最亮，断开时 A2 先灭
L1、L2 同规格，R＝ L 很大(有铁芯)，
RL，L 较大
RL≪RLA
在 S 闭合瞬间，L2 在开关 S 断开瞬间，
灯立即亮起来，L1 灯逐渐变亮，最终一
LA 灯突然闪亮一下
后再渐渐熄灭
样亮
原因
断开开关 S 前，由于 RL≪
Hale Waihona Puke 由于开关闭合时，流 过电感线圈的电流迅 速增大，使线圈产生 自感电动势，阻碍电 流的增大，使流过 L1 灯的电流比流过 L2 灯的电流增加得慢
自感现象的“三种状态”“一个特点” (1)三种状态 ①线圈通电瞬间可把线圈看成断路； ②断电瞬间自感线圈相当于电源； ③电流稳定时，自感线圈相当于导体电阻，理想线圈电 阻为零，相当于导线。 (2)一个特点 在发生自感现象时，电流不发生“突变”。
考点 对通电自感和断电自感的理解
在处理通断电自感灯泡亮度变化问题时，不能一味套用 结论，如通电时逐渐变亮，断电时逐渐变暗，或闪亮一下逐 渐变暗，要具体问题具体分析，关键要搞清楚电路连接情况。
12_4自感和互感
dI dI R L IR dt dt I L I I dI t R I0 dt I0 I 0 L R t L I I 0e , I 0 R
t
12 - 4 自感和互感
二 互感电动势 互感 1、互感现象 当线圈1中的电流变化时, 所激发的磁场会在它邻近 的另一个线圈2中产生感应 电动势。
I
写成等式：
LI
穿过闭合电流回路的磁通量
Φ LI
—自感系数为线圈中磁链 与线圈中的电流之比。
称 L为自感系数,简称自感或电感。
2、自感系数
LΦ I
自感系数
若线圈有 N 匝，磁通链数
NΦ L I
要求 : L与I 符合右手螺旋关系
12 - 4 自感和互感
第十二章 电磁感应 电磁场
R
t
0
(ln
R ln ) t L
R t L
I R dI dt 0 L I R
I0
I
I e R R
t
R t L
I (1 e R
R t L
) I 0 (1 e
)
12 - 4 自感和互感 L
第十二章 电磁感应 电磁场
B
A k
衰减过程：k与B接触， 形成RL回路。I减少， L产生与原电流方向相 同的自感电动势。
N1 B1 0 I1 0 n1 I1 l
当
dL 0 时， dt
dI L L dt
12 - 4 自感和互感
第十二章 电磁感应 电磁场
d d ( N ) dI L 若线圈有N匝 L dt dt dt
自感（动态）
L L
第四节自感与互感
Ψ N2 L= =µ S = µn 2 Sl = µn 2V I l
《大学物理》
教师：
胡炳全
二、互感现象 互感系数 1、互感现象 一个线圈的电流变化所引 起的另一线圈中的电磁感 应现象。叫互感。 2、互感系数 I1 B
1 可以证明
2
Φ m 2 = M 21 I1 Φ m1 = M 12 I 2
M 12 = M 21 = M
《大学物理》
教师：
胡炳全
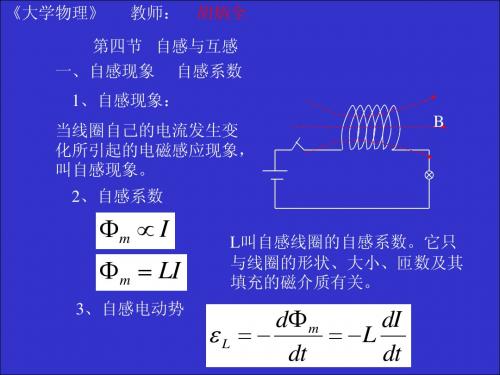
例题1、有一长直密绕螺线管，长度为l，横截面积为S，线 圈的总匝数为N，管中介质的磁导率为µ。试求其自感系数。 解：设螺线管载流为I，则有
∫ H ⋅ d l = H ⋅ ab = I f =
l
N abI l
由
N H= I l B H= 可得
µ
N B=µ I l
每匝线圈的磁通量为： Φ m = BS = µ N SI l N2 总磁通量（或磁链）为： Ψ=µ SI l 则自感系数为：
证明：设有电流I Φ m = L1 I + L2 I ± 2 MI ∴ L = L1 + L2 ± 2 M 在这里，M还可以写成 M = k L1 L2 k叫耦合系数
全耦合 : k = 1 L = L1 + L2 ± 2 L1 L2 4 L0 → 0
L1 = L2 = L0
µ 0 I1 B1 = 2πr
l r I dr h a b
三角形线圈中的磁通量为
Φ
m 2
=
∫
S
B ⋅d S = =
∫
s
B cos θ ds
∫
b a
µ 0 I1 hdr 2π r
由相似三角形关系，可得 h b−r = l b−a
大学物理 12-4 自感和互感解读
自感
2、 L的计算：可用上两式之一计算,一般由 L I 计算。 3、 L 的大小反映阻碍电流变化的能力，L 是电磁 惯性的一种表现。 4、利弊 1) 应用：镇流器，扼（抑）流圈，谐振电路，··· 2) 害处：上电迟延，断电影响，分布参数，···
自感
求自感电动势的关键，在于知道线圈的自感系数大小， 一般通过实验测得;规则线圈也可以计算得出。
Ψ NΦ LI
Ψ
磁通链数
自感
2、自感电动势： d ( NΦ ) dΦ dΨ L N dt dt dt dI dL d ( LI ) L I dt dt dt
若回路几何形状、尺寸不变，周围无铁磁性物质，则：
dL 0 dt
dI L L dt
或 12
dΨ 12 dI 2 M dt dt
互感
【讨论】
1、 M 的定义：可用下两式之一定义 (1) (2)
Φ21
Ψ 2 M I1
dI 2 1 M dt
M
2
I1
I1
1
1
I2
2
M
dI 2
dt
互感系数：在数值上等于当第二个回路电流变
化率为每秒一安培时，在第一个回路所产生的互感电 动势的大小。 2、 M 的计算：可用上两式之一计算,一般用（1）式。
E
+
1 1 2 W QU CU 2 2
Q 1 1 2 电容器贮存的电能 We QU CU 2C 2 2
2
静电场的能量密度与能量计算公式
1 S 1 2 1 2 2 ( Ed ) E Sd We CU 2 d 2 2
1 1 2 ED 电场能量密度 we E 2 2
大学物理自感和互感(二)2024
大学物理自感和互感（二）引言概述：在大学物理中，自感和互感作为电磁学的重要概念，是理解电路和电磁现象的关键。
本文将介绍自感和互感的概念、特性以及在电路中的应用。
通过对这两个概念的深入理解，我们可以更好地理解电磁学原理，并在实践中应用于电路设计和电磁设备。
正文：1. 自感的概念与特性1.1 自感的定义1.2 自感系数的计算方法1.3 自感的单位与量纲1.4 自感的特性及其影响因素1.5 自感在电路中的作用2. 互感的概念与特性2.1 互感的定义2.2 互感系数的计算方法2.3 互感的单位与量纲2.4 互感的特性及其影响因素2.5 互感在电路中的作用3. 自感与互感的数学关系3.1 自感与互感的数学定义3.2 自感与互感的表达式3.3 自感与互感的对立性及作用机制3.4 引入自感与互感的电路方程组3.5 自感与互感的联合应用实例4. 自感和互感在电路分析中的应用4.1 自感与互感对电流、电压的影响4.2 自感与互感对电路能量的转移与储存的影响4.3 自感与互感对电路振荡特性的影响4.4 自感与互感在变压器设计中的应用4.5 自感与互感在电磁传感器中的应用5. 自感和互感的实验验证及工程应用5.1 自感和互感的实验测量方法5.2 自感与互感的实验数据处理与分析5.3 自感和互感在电子工程中的应用案例5.4 自感和互感在电力工程中的应用案例5.5 自感和互感的未来发展方向总结：通过本文的阐述，我们对自感和互感的概念、特性以及在电路中的应用有了较为全面的了解。
自感和互感是电磁学的重要概念，掌握它们的原理和应用，对于电子工程和电力工程领域的学习和实践具有重要意义。
通过进一步的研究和实验，我们可以深入探索自感和互感的机理，并将其应用于更广泛的电磁设备和系统中。
大学物理,电磁感应12.4自感和互感
要求自感电动势，应先求出自感系数。
9
12.3 自感和互感
自感应用：
第12章 电磁感应
日光灯镇流器；高频扼流圈；自感线圈与电 容器组合构成振荡电路或滤波电路。 通电后，启辉器辉光放电，金属片受热形变 互相接触，形成闭合回路，电流流过，日光灯灯 丝加热释放电子。 同时，启辉器接通辉光熄灭， 金属片冷却断开，电路切断，镇流器线圈中产生 比电源电压高得多的自感电动势，使灯管内气体 电离发光。 自感危害：电路断开时，产生自感电弧。
dI 1 dI 1 dΨ21 M 21 M ε 21 dt dt dt
当线圈 2 中的电流变化时，在线圈 1 中产生的 互感电动势为：
dΨ12 dI 2 dI 2 ε12 M 12 M dt dt dt
20
12.3 自感和互感
第12章 电磁感应
ε12
dI 2 = -M dt
4
12.3 自感和互感
2、自感系数 L
根据毕奥—萨尔定律： μ0 Idl r dB 4π r 3
第12章 电磁感应
I
B
线圈中的电流在空间任意一点激发的磁感应 强度的大小与线圈中的电流强度成正比，即： 穿过线圈自身总的磁通量与电流 I 成正比，
写成：
Φ LI
L 为自感系数。
解：设长直导线中电流 I ，
矩形线圈平面上的磁链数为： dr I
N B dS
M I
0 I N ldr a 2r 0 NIl a b ln 2 a 0 Nl a b ln 2 a
s ab
r
l
a
b
24
12.3 自感和互感
思考？ 若已知矩形线圈中有电流：
9
12.3 自感和互感
自感应用：
第12章 电磁感应
日光灯镇流器；高频扼流圈；自感线圈与电 容器组合构成振荡电路或滤波电路。 通电后，启辉器辉光放电，金属片受热形变 互相接触，形成闭合回路，电流流过，日光灯灯 丝加热释放电子。 同时，启辉器接通辉光熄灭， 金属片冷却断开，电路切断，镇流器线圈中产生 比电源电压高得多的自感电动势，使灯管内气体 电离发光。 自感危害：电路断开时，产生自感电弧。
dI 1 dI 1 dΨ21 M 21 M ε 21 dt dt dt
当线圈 2 中的电流变化时，在线圈 1 中产生的 互感电动势为：
dΨ12 dI 2 dI 2 ε12 M 12 M dt dt dt
20
12.3 自感和互感
第12章 电磁感应
ε12
dI 2 = -M dt
4
12.3 自感和互感
2、自感系数 L
根据毕奥—萨尔定律： μ0 Idl r dB 4π r 3
第12章 电磁感应
I
B
线圈中的电流在空间任意一点激发的磁感应 强度的大小与线圈中的电流强度成正比，即： 穿过线圈自身总的磁通量与电流 I 成正比，
写成：
Φ LI
L 为自感系数。
解：设长直导线中电流 I ，
矩形线圈平面上的磁链数为： dr I
N B dS
M I
0 I N ldr a 2r 0 NIl a b ln 2 a 0 Nl a b ln 2 a
s ab
r
l
a
b
24
12.3 自感和互感
思考？ 若已知矩形线圈中有电流：
大学物理自感和互感(一)
大学物理自感和互感（一）引言概述：在大学物理学中，自感和互感是电磁现象中非常重要的概念。
自感和互感不仅在电路中起着关键作用，还在电磁场理论中有着广泛的应用。
本文将详细探讨自感和互感的基本概念、定义、计算方法以及它们在电路和电磁场中的应用。
正文：一、自感的概念和基本特性1. 自感的定义和原理2. 自感的单位和表示方式3. 自感的计算方法4. 自感的影响因素5. 自感与能量的关系二、自感的应用1. 自感对直流电路中的影响2. 自感对交流电路中的影响3. 自感在电磁铁和电磁感应中的应用4. 自感在变压器和电感储能中的作用5. 自感在电磁波传输中的应用三、互感的概念和基本特性1. 互感的定义和原理2. 互感的单位和表示方式3. 互感的计算方法4. 互感的影响因素5. 互感与电路传输特性的关系四、互感的应用1. 互感在变压器中的作用2. 互感在电感耦合放大器中的应用3. 互感在电波传输线中的影响4. 互感在共振电路中的应用5. 互感在电磁波传输和通信中的应用五、自感和互感的比较与总结1. 自感和互感的相同点和区别2. 自感和互感的物理意义和实际应用3. 自感和互感对电路和电磁场的影响4. 自感和互感的计算和测量方法5. 自感和互感的研究方向和未来发展趋势总结：通过本文的介绍，我们了解到了自感和互感在大学物理中的重要性及其在电路和电磁场中的应用。
自感和互感的概念、特性、计算方法以及实际应用都被深入探讨。
希望读者通过本文的阐述，对自感和互感有更加全面的理解，并能将其应用于相关领域的研究和实践中。
大学物理——12.3自感和互感
互感的应用
互感现象在电工技术中应用非常广泛， 如变压器、互感器以及用来测量电流 的钳形表，都是根据磁耦合原理制成的。
1. 互感现象
因两个载流线圈中电流变 化而在对方线圈中激起感应电 动势的现象称为互感应现象。
12
I1
I2
21
2. 互感系数(M)
21 M 21 I1
12 M12 I 2
理想条件下：若两回路几何形状、尺寸及相对 位置不变，周围无铁磁性物质。
实验和理论都可以证明：
M12 M 21 M 常数
说明：
1、理想自感元件的特点：
dI 越大， εL也越大， 对电流的阻碍作用也越大(阻交流）； dt dI 0时，εL 0， 对电流的阻碍作用为零（通直流）。 dt
2、自感、互感现象可同时存在：
εL1 ↓
↓
ε21
12
dI1 0 I 2 dt
21
3、 自感、互感的应用：
自感的应用：电焊、电弧切割技术
M 0 n1n2V
L1 μ n V
2 0 1
L2 μ n V
2 0 2
12
ψ11
I1
I2
21
22M Βιβλιοθήκη L1 L2 M K L1L2
在此例中线圈1的磁通全部通过线圈2，称为全耦合。 在一般情况下：
称K 为耦合系数 M Ψ 21 Ψ12 2 k L1 L 2 Ψ11 Ψ 22
↓ ε21
dI1 0 I 2 dt
21
dI1 若 0 则 : ε21 0, ε21与I1产生的B成右手螺旋 dt dI1 若 0 则 : ε21 0, ε21与I1产生的B不成右手螺旋 dt
互感和自感 课件
有铁芯时大得多。
（2）自感系数的单位： 亨利
简称 亨 符号是 H 常用单位：
毫亨（m H） 微亨（μH）
四、磁场的能量
问题：在断电自感的实验中，为什么开关断开 后，灯泡的发光会持续一段时间？甚至会比 原来更亮？试从能量的角度加以讨论。
开关闭合时线圈中有电流，电流产生磁场， 能量储存在磁场中.
开关断开时，线圈作用相当于电源，把磁场 中的能量转化成电能。
五、自感现象的应用与防止： 1、安全开关问题
电弧放电，烧坏开关，危及人身安全
2、精密电阻
磁通量 恒=0
｛ 3.镇流器 点燃时产生瞬时高压 工作时降压限流
日光灯启动时需要一个瞬
时高压，正常发光时又需
要一个低于220V的
自感系数较大的线圈（镇流 器）在断开时能产生瞬时高 压，可谁来充当自动开关？
二、自感现象
1、由于导体本身的电流发生变化而产 生的电磁感应现象，叫自感现象。
2、自感现象中产生的电动势 -----叫自感电动势。
自感电动势的作用： 阻碍导体中原来的电流变化。
注意： “阻碍”不是“阻止”，电流 原来怎么变化还是怎么变，只是变化变 慢了，即对电流的变化起延迟作用。
① A1、A2 使用规格完全一样的灯泡。 ② 闭合电键S，调节变阻器 R 和 R1 ，使A1、
（2）自感电动势大小： E L I 4、自感系数L：与线圈的大小、形t 状、
圈数及有无铁心有关
5、磁场具有能量
间。
接通电路，待灯泡A正常
发光。然后断开电路，观察 到什么现象？
现象 S断开时，A 灯突然闪亮一下才熄灭。
正比关系
自感电动势 正比关系 磁通量变化率 电流变化率
对同一线圈:
电流变化快,穿过线圈的磁通量变化快
（2）自感系数的单位： 亨利
简称 亨 符号是 H 常用单位：
毫亨（m H） 微亨（μH）
四、磁场的能量
问题：在断电自感的实验中，为什么开关断开 后，灯泡的发光会持续一段时间？甚至会比 原来更亮？试从能量的角度加以讨论。
开关闭合时线圈中有电流，电流产生磁场， 能量储存在磁场中.
开关断开时，线圈作用相当于电源，把磁场 中的能量转化成电能。
五、自感现象的应用与防止： 1、安全开关问题
电弧放电，烧坏开关，危及人身安全
2、精密电阻
磁通量 恒=0
｛ 3.镇流器 点燃时产生瞬时高压 工作时降压限流
日光灯启动时需要一个瞬
时高压，正常发光时又需
要一个低于220V的
自感系数较大的线圈（镇流 器）在断开时能产生瞬时高 压，可谁来充当自动开关？
二、自感现象
1、由于导体本身的电流发生变化而产 生的电磁感应现象，叫自感现象。
2、自感现象中产生的电动势 -----叫自感电动势。
自感电动势的作用： 阻碍导体中原来的电流变化。
注意： “阻碍”不是“阻止”，电流 原来怎么变化还是怎么变，只是变化变 慢了，即对电流的变化起延迟作用。
① A1、A2 使用规格完全一样的灯泡。 ② 闭合电键S，调节变阻器 R 和 R1 ，使A1、
（2）自感电动势大小： E L I 4、自感系数L：与线圈的大小、形t 状、
圈数及有无铁心有关
5、磁场具有能量
间。
接通电路，待灯泡A正常
发光。然后断开电路，观察 到什么现象？
现象 S断开时，A 灯突然闪亮一下才熄灭。
正比关系
自感电动势 正比关系 磁通量变化率 电流变化率
对同一线圈:
电流变化快,穿过线圈的磁通量变化快
互感和自感 课件
1．对互感现象的理解 (1)互感现象是一种常见的电磁感应现象，它不仅 发生于绕在同一铁芯上的两个线圈之间，而且可以发生 于任何相互靠近的电路之间。 (2)互感现象可以把能量由一个电路传到另一个电路。 变压器就是利用互感现象制成的。 (3)在电力工程和电子电路中，互感现象有时会影响 电路的正常工作，这时要求设法减小电路间的互感。
2．对自感现象的理解 (1)对自感现象的理解： 自感现象是一种电磁感应现象，遵守法拉第电磁感应 定律和楞次定律。 (2)对自感电动势的理解： ①产生原因： 通过线圈的电流发生变化，导致穿过线圈的磁通量发 生变化，因而在原线圈上产生感应电动势。
②自感电动势的方向： 当原电流增大时，自感电动势的方向与原电流方向相 反；当原电流减小时，自感电动势方向与原电流方向相同 (即：增反减同)。 ③自感电动势的作用： 阻碍原电流的变化，而不是阻止，原电流仍在变化， 只是使原电流的变化时间变长，即总是起着推迟电流变化 的作用。
体开始放电，于是日光灯管成为电流的通路开始发光。启 动器相当于一个自动开关。日光灯正常工作后处于断开状 态，启动器损坏的情况下可将连接启动器的两个线头作一 个短暂接触也可把日光灯启动。启动时电流流经途径是镇 流器、启动器、灯丝，启动后电流流经途径是镇流器、灯 丝、日光灯管。
4．日光灯正常工作时镇流器的作用 由于日光灯使用的是交流电源，电流的大小和方向做 周期性变化。当交流电的大小增大时，镇流器上的自感电 动势阻碍原电流增大，自感电动势与原电压反向；当交流 电的大小减小时，镇流器上的自感电动势阻碍原电流减小， 自感电动势与原电压同向。可见镇流器的自感电动势总是 阻碍电流的变化，正常工作时镇流器就起着降压、限流的 作用。
2．自感现象的分析思路 (1)明确通过自感线圈的电流的变化情况(增大还是减小)。 (2)根据楞次定律，判断自感电动势方向。 (3)分析线圈中电流变化情况，电流增强时(如通电时)， 由于自感电动势方向与原电流方向相反，阻碍电流增加，因此 电流逐渐增大；电流减小时(如断电时)，线圈中电流逐渐减小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
l
μ0
S
l
互感系数计算举例
M Ψ12 I2
N1 N 2 l2
lS
n1n2V
③互感 M与自感L1 ，L2 的关系。
L1 n12V
L2 n22V
M L1L2
在此例中，线圈1的磁通全部通过线圈2，称为无 磁漏。
在一般情况下： M K L1L2
称K 为耦合系数 0 < K <1
自感
2、自感电动势：
dΦ
L N dt
d (NΦ ) dΨ
dt
dt
d (LI ) L dI I dL
dt
dt dt
若回路几何形状、尺寸不变，周围无铁磁性物质，则：
dL 0 dt
L
L
dI dt
自感
【讨论】：1、 L 的定义：可用下两式之一定义
H 2r NI
I
H NI 2r
B NI 2r
dm
B dS
NI 2r
hdr
R2 R1
h
r dr
dm
B dS
NI 2r
hdr
m
dm
NIh பைடு நூலகம்
R2 dr R1 r
NIh ln(
R2
)
2
R1
Nm
N 2 Ih
Lo
L l
2
ln(
R2 R1
)
R1
R2
I
I
l
rdr
§12-4 自感和互感
二、互感
互感现象——两个独立回路，由于一回路电流发生变化，
在另一回路中产生感应电动势的现象。
1、 互感系数(M)
Φ21
设线圈1中通有电流 I1
若两回路几何形状、尺寸及相对 位置不变，周围无铁磁性物质，则第 二个线圈的磁通量为：
B 0 r R1 , r R2
R1
R2
I
I
l
dΦm
B dS
Il 2r
dr
rdr
自感系数计算举例
Φm
B
dS
Il
R2 dr
2 R1 r
Il ln( R2 ) 2 R1
L Φ l ln( R2 ) I 2 R1
单位长度的自感为：
电动势方向相反，所以
a
a' b b'
总感应电动势为：
L1
dI dt
L2
dI dt
2M
dI dt
(L1
L2
2M
)
dI dt
等效自感电动势为： L dI
dt
两式比较得，等效自感： L = L1 + L2 - 2M
§12-5 磁场的能量
一、磁能的产生和存储过程
当接通电路时，线圈中产生了磁场，也就有 了磁场能。线圈由无电到有电的过程，就是电能 转换为磁场能的过程。
N1Φ12 MI2 Ψ12
I1
N2Φ21 MI1 Ψ21
Φ 12
Φ 21
I2
2、互感电动势：
21
dΨ 21 dt
M
dI1 dt
或12
dΨ12 dt
M
dI 2 dt
互感
【讨论】
1、 M 的定义：可用下两式之一定义
Φ21
(1) Ψ2 M I1
(2)
1
M
(1) Ψ LI
(2) L dI
dt
L L IdI
dt
L 的意义：若I = 1A，则 L = Ψ
自感系数在数值上等于回路中通过单位电流 时，通过自身回路所包围面积的磁通链数。
★ 自感系数是一个与线圈大小、形状及匝数有
关的量，与线圈内通有的电流 I无关，一般由实 验确定。
自感
I1 I1 B1 Φ2 Ψ2 M
互感系数计算举例
例3. 如图所示,在磁导率为
的均匀无限大磁介质中,一无
限长直载流导线与矩形线圈
一边相距为a，线圈共N匝,
其尺寸见图示。
I
求它们的互感系数。
a
dr
l b
解: 设直导线中通有自下而上的电流I,它通过矩形 线圈的磁通链数为
Nm
N
B • dS
半径为R1 和R2 两同轴圆筒状导体组成， 内外圆筒上分别流有大小相等，方向相反
的电流I。
求：长为 l 的一段电缆内储存的磁能。
解：H I
2r
Wm
V wmdV
1 H 2dV
V2
R2 1 ( I )2 2rldr
2 R1 2r
I 2l 4
ln( R2
/
R1 )
R2 R1
I l
I
r dr
dV 2rldr
磁场的能量
磁场能量公式给出了计算自感的另一种方法：
因为
Wm
1 2
LI 2
I 2l 4
ln( R2
/
R1 )
所以
L
2Wm I2
l 2
ln( R2
/ R1)
三、电磁场的能量
w
we
wm
1 2
(E D
BH)
W We Wm
s
ab I
NIl a b
N a
ldr
ln
2r
2
a
dr
I
l
由互感系数定义可得互感为:
M
Nl ln a b
I 2
a
ab
★ 互感系数仅取决于两回路的形状,
相对位置,磁介质的磁导率．
互感系数计算举例
例4. 两共轴密绕长直螺线管，C1 和 C2 ， C1 为原线圈， 匝数为N1 ，C2 为副线圈，匝数为N2 ，两者长均为l , 线圈面
dI 2 dt
M 2
I1
I1
M 1 1
dI 2
dt
I2
2
互感系数：在数值上等于当第二个回路电流变
化率为每秒一安培时，在第一个回路所产生的互感电 动势的大小。
2、 M 的计算：可用上两式之一计算,一般用（1）式。
互感
3、 互感系数和两回路的几何形状、尺寸，它们的 相对位置，以及周围介质的磁导率有关。
We
1 CU 2
2
1 S
2d
(Ed )2
1 E 2 Sd
2
电场能量密度 we
1 E 2
2
1 2
ED
物理意义 电场是一种物质，它具有能量.
电场空间所存储的能量
We
V wedV
1 E 2dV
V2
L1
dI dt
L2
dI dt
2M
dI dt
(L1
L2
2M
)
dI dt
等效自感电动势为： L dI
dt
两式比较得，等效自感： L = L1 + L2 + 2M
互感系数计算举例
(2) a' 与 b'相联
两线圈的磁场方向
相反，彼此减弱，两线
圈的自感电动势方向相
同，互感电动势与自感
I1
1
I2
2
Φ21 I1 Φ21 M21I1
互感
同理，若线圈2中通有电流 I2
若两回路几何形状、尺寸
及相对位置不变，周围无铁磁 性物质，则第一个线圈的磁通 量为：
I1 I2
Φ 12
Φ12 I2 Φ12 M12I2
互感
实验和理论都可以证明：M 12 = M 21
若两线圈的匝数分别为N1 ,N2则有：
2、 L的计算：可用上两式之一计算,一般由 L
计算。
I
3、 L 的大小反映阻碍电流变化的能力，L 是电磁 惯性的一种表现。
4、利弊 1) 应用：镇流器，扼（抑）流圈，谐振电路，···
2) 害处：上电迟延，断电影响，分布参数，···
自感
求自感电动势的关键，在于知道线圈的自感系数大小， 一般通过实验测得;规则线圈也可以计算得出。
积均为S。管内介质的磁导率为μ，求①两螺线管的自感L1 和
L2 ；② 互感 M；③互感 M与自感L1 ，L2 的关系。
解：②计算互感系数
N1
I2 B2 Φ12 Ψ12
B2
Φ12
n2 I 2
B dS
B2S
N l
2
I2
N l
2
N
I2S
2
Ψ12
N1Φ12
N1N2 I2S
L
R
BATTERY
ε 电池
磁场的能量
分析开关合上后的一
段时间内，电路中的电流
L
增长过程。
R
由欧姆定律得：
L dI IR
dt
BATTERY
ε 电池
I
解该微分方程得：
I
Rt
(1 e L )
R
Rt
I0 (1 e L )
I0
μ0
S
l
互感系数计算举例
M Ψ12 I2
N1 N 2 l2
lS
n1n2V
③互感 M与自感L1 ，L2 的关系。
L1 n12V
L2 n22V
M L1L2
在此例中，线圈1的磁通全部通过线圈2，称为无 磁漏。
在一般情况下： M K L1L2
称K 为耦合系数 0 < K <1
自感
2、自感电动势：
dΦ
L N dt
d (NΦ ) dΨ
dt
dt
d (LI ) L dI I dL
dt
dt dt
若回路几何形状、尺寸不变，周围无铁磁性物质，则：
dL 0 dt
L
L
dI dt
自感
【讨论】：1、 L 的定义：可用下两式之一定义
H 2r NI
I
H NI 2r
B NI 2r
dm
B dS
NI 2r
hdr
R2 R1
h
r dr
dm
B dS
NI 2r
hdr
m
dm
NIh பைடு நூலகம்
R2 dr R1 r
NIh ln(
R2
)
2
R1
Nm
N 2 Ih
Lo
L l
2
ln(
R2 R1
)
R1
R2
I
I
l
rdr
§12-4 自感和互感
二、互感
互感现象——两个独立回路，由于一回路电流发生变化，
在另一回路中产生感应电动势的现象。
1、 互感系数(M)
Φ21
设线圈1中通有电流 I1
若两回路几何形状、尺寸及相对 位置不变，周围无铁磁性物质，则第 二个线圈的磁通量为：
B 0 r R1 , r R2
R1
R2
I
I
l
dΦm
B dS
Il 2r
dr
rdr
自感系数计算举例
Φm
B
dS
Il
R2 dr
2 R1 r
Il ln( R2 ) 2 R1
L Φ l ln( R2 ) I 2 R1
单位长度的自感为：
电动势方向相反，所以
a
a' b b'
总感应电动势为：
L1
dI dt
L2
dI dt
2M
dI dt
(L1
L2
2M
)
dI dt
等效自感电动势为： L dI
dt
两式比较得，等效自感： L = L1 + L2 - 2M
§12-5 磁场的能量
一、磁能的产生和存储过程
当接通电路时，线圈中产生了磁场，也就有 了磁场能。线圈由无电到有电的过程，就是电能 转换为磁场能的过程。
N1Φ12 MI2 Ψ12
I1
N2Φ21 MI1 Ψ21
Φ 12
Φ 21
I2
2、互感电动势：
21
dΨ 21 dt
M
dI1 dt
或12
dΨ12 dt
M
dI 2 dt
互感
【讨论】
1、 M 的定义：可用下两式之一定义
Φ21
(1) Ψ2 M I1
(2)
1
M
(1) Ψ LI
(2) L dI
dt
L L IdI
dt
L 的意义：若I = 1A，则 L = Ψ
自感系数在数值上等于回路中通过单位电流 时，通过自身回路所包围面积的磁通链数。
★ 自感系数是一个与线圈大小、形状及匝数有
关的量，与线圈内通有的电流 I无关，一般由实 验确定。
自感
I1 I1 B1 Φ2 Ψ2 M
互感系数计算举例
例3. 如图所示,在磁导率为
的均匀无限大磁介质中,一无
限长直载流导线与矩形线圈
一边相距为a，线圈共N匝,
其尺寸见图示。
I
求它们的互感系数。
a
dr
l b
解: 设直导线中通有自下而上的电流I,它通过矩形 线圈的磁通链数为
Nm
N
B • dS
半径为R1 和R2 两同轴圆筒状导体组成， 内外圆筒上分别流有大小相等，方向相反
的电流I。
求：长为 l 的一段电缆内储存的磁能。
解：H I
2r
Wm
V wmdV
1 H 2dV
V2
R2 1 ( I )2 2rldr
2 R1 2r
I 2l 4
ln( R2
/
R1 )
R2 R1
I l
I
r dr
dV 2rldr
磁场的能量
磁场能量公式给出了计算自感的另一种方法：
因为
Wm
1 2
LI 2
I 2l 4
ln( R2
/
R1 )
所以
L
2Wm I2
l 2
ln( R2
/ R1)
三、电磁场的能量
w
we
wm
1 2
(E D
BH)
W We Wm
s
ab I
NIl a b
N a
ldr
ln
2r
2
a
dr
I
l
由互感系数定义可得互感为:
M
Nl ln a b
I 2
a
ab
★ 互感系数仅取决于两回路的形状,
相对位置,磁介质的磁导率．
互感系数计算举例
例4. 两共轴密绕长直螺线管，C1 和 C2 ， C1 为原线圈， 匝数为N1 ，C2 为副线圈，匝数为N2 ，两者长均为l , 线圈面
dI 2 dt
M 2
I1
I1
M 1 1
dI 2
dt
I2
2
互感系数：在数值上等于当第二个回路电流变
化率为每秒一安培时，在第一个回路所产生的互感电 动势的大小。
2、 M 的计算：可用上两式之一计算,一般用（1）式。
互感
3、 互感系数和两回路的几何形状、尺寸，它们的 相对位置，以及周围介质的磁导率有关。
We
1 CU 2
2
1 S
2d
(Ed )2
1 E 2 Sd
2
电场能量密度 we
1 E 2
2
1 2
ED
物理意义 电场是一种物质，它具有能量.
电场空间所存储的能量
We
V wedV
1 E 2dV
V2
L1
dI dt
L2
dI dt
2M
dI dt
(L1
L2
2M
)
dI dt
等效自感电动势为： L dI
dt
两式比较得，等效自感： L = L1 + L2 + 2M
互感系数计算举例
(2) a' 与 b'相联
两线圈的磁场方向
相反，彼此减弱，两线
圈的自感电动势方向相
同，互感电动势与自感
I1
1
I2
2
Φ21 I1 Φ21 M21I1
互感
同理，若线圈2中通有电流 I2
若两回路几何形状、尺寸
及相对位置不变，周围无铁磁 性物质，则第一个线圈的磁通 量为：
I1 I2
Φ 12
Φ12 I2 Φ12 M12I2
互感
实验和理论都可以证明：M 12 = M 21
若两线圈的匝数分别为N1 ,N2则有：
2、 L的计算：可用上两式之一计算,一般由 L
计算。
I
3、 L 的大小反映阻碍电流变化的能力，L 是电磁 惯性的一种表现。
4、利弊 1) 应用：镇流器，扼（抑）流圈，谐振电路，···
2) 害处：上电迟延，断电影响，分布参数，···
自感
求自感电动势的关键，在于知道线圈的自感系数大小， 一般通过实验测得;规则线圈也可以计算得出。
积均为S。管内介质的磁导率为μ，求①两螺线管的自感L1 和
L2 ；② 互感 M；③互感 M与自感L1 ，L2 的关系。
解：②计算互感系数
N1
I2 B2 Φ12 Ψ12
B2
Φ12
n2 I 2
B dS
B2S
N l
2
I2
N l
2
N
I2S
2
Ψ12
N1Φ12
N1N2 I2S
L
R
BATTERY
ε 电池
磁场的能量
分析开关合上后的一
段时间内，电路中的电流
L
增长过程。
R
由欧姆定律得：
L dI IR
dt
BATTERY
ε 电池
I
解该微分方程得：
I
Rt
(1 e L )
R
Rt
I0 (1 e L )
I0