第八章方差分析预防医学
合集下载
《预防医学》方差分析课件
方差分析在预防医学中的应用
在预防医学中，方差分析常用于 研究不同干预措施对疾病预防效
果的影响。
例如，研究人员可以通过方差分 析比较不同药物对高血压患者的 降压效果，为临床治疗提供依据
。
此外，方差分析还可用于评估环 境因素对健康的影响，如空气质 量与心血管疾病发病率之间的关
系等。
02
方差分析的基本原理
空气污染研究
在空气污染研究中，方差分析可用于评估不同地区、季节和气象条件等因素对空 气质量的影响，以便找出空气污染的关键控制点。
05
方差分析的局限性及解决方法
方差分析的局限性
前提假设难以满足
方差分析基于一系列前提假设，如正态性、各组方差齐性等，但 这些假设在实际情况中往往难以完全满足。
对数据质量要求高
农业研究中的方差分析
作物产量研究
方差分析可用于研究不同种植方 法、肥料种类和施肥量等因素对 作物产量的影响，为农民提供最 佳的种植策略。
动物育种
在动物育种中，方差分析可用于 评估不同品种、饲养条件和环境 因素对动物生长和生产性能的影 响。
环境研究中的方差分析
水质监测
在水质监测中，方差分析可用于分析不同时间、地点和季节等因素对水质指标的 影响，以便制定针对性的保护措施。
02
它通过将数据组的变异分解为组 内变异和组间变异，从而确定不 同因素对总体变异的影响。
方差分析的历史与发展
方差分析始于19世纪末期，当时科学家们开始研究如何准确比较不同处理组之间的 差异。
1908年，英国统计学家费希尔提出了方差分析的基本原理，并被广泛应用于农业、 医学、工业等领域。
随着计算机技术的发展，方差分析的应用逐渐普及，成为科研人员探索数据规律的 重要工具。
《医学方差分析》PPT课件电子版本
2 ij
7.2g 组 1.98 1.74i21.16 j3.137 2.97 1.69 0.94 2.11 2.81 2.5i2130j11.97 58.99 132.13
N1.31 2.51 1.88 1.41 3.19 1.92 2.47 1.02 2.10 3.71
10
2．组间变异：各组均数与总均数的
每水平有ni=30只大白鼠，分别表示为 j=1,2,…,30
因变量用Xij表示，即第i组第j号大鼠的血
中低密度脂蛋白的含量
按完全随机化设计方法将Ｎ＝120只动物随机等
分成４个组
4
ANOVA 由英国统 计学家R.A.Fisher首 创，为纪念Fisher，
以F命名，故方差分析 又称 F 检验 （F
2
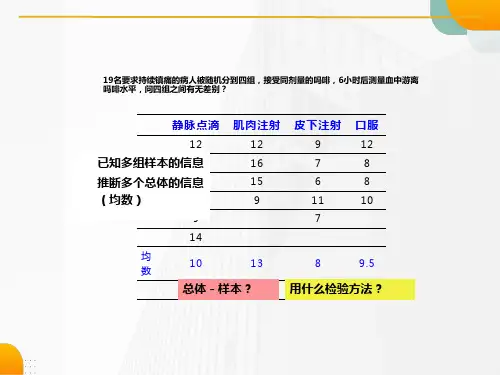
某医生为了研究一种降血脂新药的临床疗效，按统一纳入标准选择120名高血脂 患者，采用完全随机设计方法将患者等分为4组，进行双盲试验。6周后测得低 密度脂蛋白作为试验结果。问4个处理组患者的低密度脂蛋白含量总体均数有无 差别？
3
一个因素（factor）：降脂药
四个水平（level）（a=4个处理组）：A安慰剂、 Ｂ、Ｃ、D，i=1,2,3,4分别代表A、B、C、D
0 g ni
二、变异分解
X Xij / N
i1 j1
ni
Xi Xij / ni
j1
统 计 变异量 来源处 表理 4-自4效 由随 完度应 机 全+ 误 随随 机差 机 设误 计S差 资S 料 的处 方理 差效 分M析应 S 表1 F
总变异
N－1
g
ni
X ij 2
C
i1 j1
组间 组内
g－1
ni
医学统计学：方差分析课件
H1：
各组样本的总体均数不等或不全相等；
如果H0 成立，即各处理组的样本来自相同的总体，无 处理因素的作用，则组间变异同组内变异一样，只反
映随机误差作用的大小。
F值接近于l，就没有理由拒绝H0；反之，F值越大， 拒绝H0的理由越充分。
数理统计理论证明，当H0成立时，F统计量服从F分布。
F 分布曲线
方差分析步骤
单因素方差分析
1. 建立检验假设，确定检验水准 H0：4组家兔的血清ACE浓度总体均数相等，
H1：4组家兔的血清ACE浓度总体均数不等或不 全相等，各 不等或不全相等
2. 计算统计量 F 值
单因素方差分析 计算步骤
方差分析步骤
单因素方差分析 计算步骤
方差分析表
3. 确定P值，并做出统计推断
设计方法
拉丁方设计
（四）优缺点
Байду номын сангаас
拉丁方设计
❖ 优点 1、精确性高
拉丁方设计在不增加试验单位的情况下，比随机 单位组设计多设置了一个单位组因素，能将横行和 直列两个单位组间的变异从试验误差中分离出来， 因而试验误差比随机单位组设计小，试验的精确性 比随机单位组设计高。
2、试验结果的分析简便
拉丁方设计
两因素方差分析
配伍组设计资料的方差分析
例 某医师研究A、B和C 3种药物治疗肝炎的效果， 将32只大白鼠感染肝炎后，按性别相同、体重接 近的条件配成8个配伍组，然后将各配伍组中4只 大白鼠随机分配到4个组。对照组不给药物，其余3 组为实验组，分别给予A、B和C药物治疗。一定 时间后，测定大白鼠血清谷丙转氨酶浓度(IU/L)， 见下表。问4组大白鼠的血清谷丙转氨酶浓度是否 相同？
7
方差分析基本思想
医学统计学(方差分析)
03
各种变异的表示方法
04
列举存在的变异及意义
各种变异的表示方法
SS总 总 MS总
SS组内 组内 MS组内
SS组间 组间 MS组间
三者之间的关系： SS总= SS组内+ SS组间 总= 组内+ 组间
F=MS组间/MS组内
自由度： 组间=组数-1
组内=N-组数
通过这个公式计算出统计量F，查表求出对应的P值，与进行比较，以确定是否为小概率事件。
01
计算 C=(Σx) 2/N=(3309.5) 2/30=365093 SS总=Σx2-C=372974.87-365093=7881.87
α=0.05
02
SS组内=SS总-SS组间=7881.87-2384.026=5497.84
Ν总=N-1=29, Ν组间=k-1=2, Ν组内=N-k=30-3=27
159.0
111.0
115.0
合计Σxij
1160
921.5
1228
3309.5(Σx)
ni
11
9
10
30(N)
均数
105.45
102.39
122.80
110.32()
糖尿病
IGT
正常人
xij
106.5
Σ
Σxij2
123509.52
144.0
105.2
124.5
117.0
109.5
105.1
110.0
96.0
76.4
109.0
115.2
95.3
103.
95.3
各种变异的表示方法
04
列举存在的变异及意义
各种变异的表示方法
SS总 总 MS总
SS组内 组内 MS组内
SS组间 组间 MS组间
三者之间的关系： SS总= SS组内+ SS组间 总= 组内+ 组间
F=MS组间/MS组内
自由度： 组间=组数-1
组内=N-组数
通过这个公式计算出统计量F，查表求出对应的P值，与进行比较，以确定是否为小概率事件。
01
计算 C=(Σx) 2/N=(3309.5) 2/30=365093 SS总=Σx2-C=372974.87-365093=7881.87
α=0.05
02
SS组内=SS总-SS组间=7881.87-2384.026=5497.84
Ν总=N-1=29, Ν组间=k-1=2, Ν组内=N-k=30-3=27
159.0
111.0
115.0
合计Σxij
1160
921.5
1228
3309.5(Σx)
ni
11
9
10
30(N)
均数
105.45
102.39
122.80
110.32()
糖尿病
IGT
正常人
xij
106.5
Σ
Σxij2
123509.52
144.0
105.2
124.5
117.0
109.5
105.1
110.0
96.0
76.4
109.0
115.2
95.3
103.
95.3
医学统计学(课件)方差分析
要点二
原理
通过将因变量和协变量之间的关系线 性化，进行线性回归分析，并控制其 他因素的影响。
要点三
应用
医学研究中用于研究疾病与基因型、 环境因素之间的关系，社会科学中用 于研究收入和教育水平的关系等。
多重比较方法
01
定义
多重比较方法是方差分析的一种补充 方法，用于比较多个组之间的差异。
02
原理
通过比较每个组与对照组或其他组之 间的差异，推断各组之间的差异是否 具有统计学显著性。
重复测量方差分析
定义
重复测量方差分析是方差分析的另一种拓展，用于比较多次测量或重复观测的差异。
原理
通过将多次测量视为不同的观察对象，对测量误差进行控制和调整。
应用
医学研究中常用于比较不同治疗方案的效果，以及社会科学中研究时间序列数据的变化等。
协方差分析
要点一
定义
协方差分析是方差分析与其他统计方 法的结合，通过控制一个或多个协变 量对因变量的影响。
偏度检验
检查数据分布的偏斜程度。
峰度检验
检查数据分布的峰态。
正态性检验
通过图形和统计量判断数据是否符合正态分布。
方差齐性检验
• 方差齐性检验：通过Levene's Test或Bartlett's Test检验各组方差是否相等。
主效应检验
将数据按照分组变量进行分组，并 对每个分组变量的平均值进行计算 。
方差分析还可以与其他统计方法结合 使用，例如与回归分析结合可进行协 方差分析和混合线性模型分析等。
02
方差分析基本原理
数学模型
数学模型的假设
假定每个总体均数之间有差异，且每个总体均数与模型中其他变量的关系已知。
2023年专升本考试大纲 《预防医学》考试要求
《预防医学》考试要求I、考试性质为挑选专科生中优秀的学生进入普通高等学校专升本学生，特举办此考试。
该考试所包含的内容将大致稳定，试题形式多种，具有对学生把握课程的较强识别、区分能力。
II、考试内容及要求第一篇流行病学第一章绪论掌握流行病学定义及流行病学定义的诠释，流行病学的应用。
熟悉流行病学的原理。
了解流行病学发展史，流行病学的特点，流行病学与其他学科的关系，流行病学的展望。
第二章疾病的分布掌握疾病分布的概念。
熟悉疾病频率测量指标，描述疾病流行强度的常用术语。
了解疾病人群分布、地区分布和时间分布的特征与变化规律。
第三章描述性研究掌握描述性研究的概念、种类、用途；现况研究的概念及特点；普查、抽样调查的概念、用途。
熟悉生态学研究、个案调查、病例报告、病例分析的概念、用途；现况调查实施步骤、数据分析、常见偏倚及控制方法。
了解调查表的编制；生态学研究的方法和局限性。
第四章队列研究掌握队列研究的定义、基本原理和方法，队列研究的设计与资料整理分析，包括累计发病率、发病密度、相对危险度、归因危险度及人群归因危险度等指标的计算方法及其流行病学意义。
熟悉队列研究的特点、研究类型；队列研究的偏倚及其控制方法；队列研究的优缺点。
了解队列研究的实施步骤、样本大小的估计、随访方法、人年的计算、率的显著性检验。
第五章病例对照研究掌握病例对照研究的基本原理；匹配的原理和方法；病例与对照的来源与选择；资料整理和数据分析的基本方法；OR的含义及其在病例对照研究中的意义；。
熟悉病例对照研究的一般步骤；分层分析的概念及应用，病例对照研究中常见的偏倚及其控制方法；病例对照研究的优点及局限性。
了解实施病例对照研究应注意的问题。
第六章实验流行病学掌握实验流行病学的定义、基本特点、流行病学实验的类型：临床试验、现场试验、社区试验。
熟悉实验流行病学研究与队列研究优缺点的比较。
了解实验流行病学研究优缺点和应注意的问题。
第七章筛检掌握筛检的定义、评价筛检试验真实性的指标的计算及意义。
第八章方差分析1预防医学精品PPT课件
R.A.Fisher(1890~1962)
9
多个独立样本资料的方差分析
检验目的 推断多个总体均数是否相等。
10
多个独立样本资料的方差分析
应用条件
➢ 多个独立随机样本的定量资料
➢ 各样本均来自正态分布总体
➢ 各总体方差相等
X 2 ~ N( 2 , )
X1 ~ N( 1 , )
X3 ~ N(3, )
5
表 8-1 2 型糖尿病患者治疗 4 周后餐后 2 小时血糖的下降值(mmol/L)
高剂量组 (i=1)
5.6 16.3
9.5 11.8
6.0 14.6
8.7 4.9
X ij
9.2 8.1
5.0 3.8
3.5 6.1
5.8 13.2
8.0 16.5
15.5 9.2
11.8
ni
21
Xi
9.1952
卫生统计学 －方差分析
1
方差分析
定量资料
方差分析的基本思想 完全随机设计资料的方差分析** 随机区组设计资料的方差分析** 多个样本均数的两两比较* 析因设计资料的方差分析 重复测量资料的方差分析 多个样本的方差齐性检验和数据变换
2
A 完全随机分组得到多个独立样本
样本1
甲药
受试对象
合计
t检验
资料类型？ 设计类型？ 分布类型？ 总体方差相等？
20
60( N )
5.4300
6.8650( X )
12.3843
18.4176( S 2 )
6
不能用t检验的原因
检验假设： H0： 1 2 3 H1：至少有两个 总体均数不等
0.05
拒绝H0，犯一类 错误的概率是0.05
9
多个独立样本资料的方差分析
检验目的 推断多个总体均数是否相等。
10
多个独立样本资料的方差分析
应用条件
➢ 多个独立随机样本的定量资料
➢ 各样本均来自正态分布总体
➢ 各总体方差相等
X 2 ~ N( 2 , )
X1 ~ N( 1 , )
X3 ~ N(3, )
5
表 8-1 2 型糖尿病患者治疗 4 周后餐后 2 小时血糖的下降值(mmol/L)
高剂量组 (i=1)
5.6 16.3
9.5 11.8
6.0 14.6
8.7 4.9
X ij
9.2 8.1
5.0 3.8
3.5 6.1
5.8 13.2
8.0 16.5
15.5 9.2
11.8
ni
21
Xi
9.1952
卫生统计学 －方差分析
1
方差分析
定量资料
方差分析的基本思想 完全随机设计资料的方差分析** 随机区组设计资料的方差分析** 多个样本均数的两两比较* 析因设计资料的方差分析 重复测量资料的方差分析 多个样本的方差齐性检验和数据变换
2
A 完全随机分组得到多个独立样本
样本1
甲药
受试对象
合计
t检验
资料类型？ 设计类型？ 分布类型？ 总体方差相等？
20
60( N )
5.4300
6.8650( X )
12.3843
18.4176( S 2 )
6
不能用t检验的原因
检验假设： H0： 1 2 3 H1：至少有两个 总体均数不等
0.05
拒绝H0，犯一类 错误的概率是0.05
医学统计学方差分析ppt课件
24
25
方差分析步骤 ：提出检验假设，确定检验水准
26
第二节 随机区组设计的方差分析
方差分析步骤 ：计算检验统计量F 值
27
方差分析步骤 ：确定P值，做出推断结论 对于处理因素A F0.05(2，18) =3.55 F=245.79
F> F0.05(2，18) ，P<0.05，拒绝H0
方差分析
1
方差分析由英国统计 学家R.A.Fisher在1923 年提出，为纪念Fisher，
以F命名，故方差分析又 称 F 检验
2
方差分析的用途 单因素多水平组间效应分析 多因素多水平组间效应分析 回归效应分析 方差齐性分析
3
完全随机设计的方差分析 随机区组设计的方差分析 多个样本均数的两两比较 方差齐性检验
20
基本思想：各变异的平均变异，即均方
处理均方：
MS处理
SS处理
处理
区组均方：
MS区组
SS区组
区组
组内（误差）均方：
MS误差
SS误差
误差
21
基本思想：统计量F值
F处理
MS处理 MS误差
F处理>Fα （k-1,(k-1)(m-1)），P<α ，认为比较组总体均值不 全相同
F处理<Fα （k-1,(k-1)(m-1)），P>α ，尚不能认为比较组总体 均值不同
4
例 拟探讨枸杞多糖（LBP）对酒精性脂肪肝大鼠GSH （mg/gprot）的影响，将36只大鼠随机分为甲、乙、丙 三组，其中甲（正常对照组）12只，其余24只用乙醇灌 胃10周造成大鼠慢性酒精性脂肪肝模型后，再随机分为 2组，乙（LBP治疗组）12只，丙（戒酒组）12只，8周 后测量三组GSH值。试问三种处理方式大鼠的GSH值是否 相同？
25
方差分析步骤 ：提出检验假设，确定检验水准
26
第二节 随机区组设计的方差分析
方差分析步骤 ：计算检验统计量F 值
27
方差分析步骤 ：确定P值，做出推断结论 对于处理因素A F0.05(2，18) =3.55 F=245.79
F> F0.05(2，18) ，P<0.05，拒绝H0
方差分析
1
方差分析由英国统计 学家R.A.Fisher在1923 年提出，为纪念Fisher，
以F命名，故方差分析又 称 F 检验
2
方差分析的用途 单因素多水平组间效应分析 多因素多水平组间效应分析 回归效应分析 方差齐性分析
3
完全随机设计的方差分析 随机区组设计的方差分析 多个样本均数的两两比较 方差齐性检验
20
基本思想：各变异的平均变异，即均方
处理均方：
MS处理
SS处理
处理
区组均方：
MS区组
SS区组
区组
组内（误差）均方：
MS误差
SS误差
误差
21
基本思想：统计量F值
F处理
MS处理 MS误差
F处理>Fα （k-1,(k-1)(m-1)），P<α ，认为比较组总体均值不 全相同
F处理<Fα （k-1,(k-1)(m-1)），P>α ，尚不能认为比较组总体 均值不同
4
例 拟探讨枸杞多糖（LBP）对酒精性脂肪肝大鼠GSH （mg/gprot）的影响，将36只大鼠随机分为甲、乙、丙 三组，其中甲（正常对照组）12只，其余24只用乙醇灌 胃10周造成大鼠慢性酒精性脂肪肝模型后，再随机分为 2组，乙（LBP治疗组）12只，丙（戒酒组）12只，8周 后测量三组GSH值。试问三种处理方式大鼠的GSH值是否 相同？
第八讲-方差分析
x2 ij
j 1i 1
xij
N
k
2
SS B n j X j X t
i 1
2
k
j 1
nj
2
( xij)
i 1
nj
k nj
j 1i 1
xij
N
SSW SST SSB
2
nj
x k nj
x n j1 i1
k
2
ij j 1
ij i 1
j
3、确定自由度
df k 1 B
df N k W
二、（单因素）随机区组实验设计
1、模型
处理1
处理2 ……
区组1 被试1 x11 被试1 x21 ……
区组2 被试2 x12 被试2 x22 ……
处理k
被试1 xk1
被试2
xk
2
……… ……… ……
区组a 被试a x1a 被试a x2a ……
……
被试a xka
■注：每个区组内被试分配方式可以是以下 三种
T1
T2
8
39
20
26
12
31
14
45
10
40
T3
T4
17
32
工创问 具造题
21 20
23 28
教 程
丰 富 教
性 思 维
解 决 模
17
25
程教式 程教
20
29
程
T1: T2: T3: T4:CoRT
变异来源 自由度 平方和
处理 误差
总
3
1553.7
16 378.80
19 1932.55
均方
医学统计学：04 方差分析
1.4 f( F)
1.2
1.0
0.8
0.6
0.4
0.2
0.0
0
1
F 分布曲线
1 1, 2 5
1 5, 2 5
1 10,2 10
2F
3
4
F 界值表
附表4 F界值表（方差分析用，单侧界值） 上行：P=0.05 下行：P=0.01
分母自由度
υ2
1
161 1
4052
18.51 2
98.49
4.21 27
• 随机区组设计又称随机单位组设计、配伍组设计，也叫双因 素方差分析（two--way ANOVA）。是配对设计的扩展。
具体做法：
① 将受试对象按性质（如性别、年龄、病情等） （这些性质是
非处理因素，可能影响试验结果）相同或相近者组成m个单位 组（配伍组），每个单位组中有k个受试对象，分别随机地分 配到k个处理组。
2
7
33.4
18
2
8
38.3
19
2
9
38.4
20
2
10
39.8
21
3
1
32.9
22
3
2
37.9
23
3
3
30.5
24
3
4
31.1
25
3
5
34.7
26
3
6
37.6
27
3
7
40.2
28
3
8
38.1
29
3
9
32.4
30
3
10
35.6
35.51667
(Xij X )2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
随机分组
样本3
…
丙药
…
第八章方差分析预防医学 2
B 从多个总体中随机抽样得到多个独立样本
总体1 随机抽样 样本1
总体2
样本2
总体3
…
样本3
…
多个独立样本资料的方差分析
例8-1 某医生为研究一种降糖新药的疗效，以统一的 纳入标准和排除标准选择了60名2型糖尿病患者，按 完全随机设计方案将患者分为三组进行双盲临床试验。 其中，降糖新药高剂量组21人、低剂量组19人、对照 组20人。对照组服用公认的降糖药物，治疗4周后测 得其餐后2小时血糖的下降值(mmol/L)，结果如表9-1 所示。问治疗4周后，餐后2小时血糖下降值的三组总 体平均水平是否不同？
组内变异
(随机误差和处理作用) (随机误差)
总N1 组间k1
组内Nk
SS总 ＝SS组＋ 间SS组内
总
组间 组内 第八章方差分析预防医学
15
方差分析的基本思想
SS总 ＝SS组＋ 间SS组内
总组间 组内
组间均方： M组 S＝ 间S组 S间 /组间 随机误差和处理作用 组内均方： M组 S＝ 内S组 S 内 /组内 随机误差
两两比较的t检验：
H0 :1 2
H1:12 0.05
拒绝H0
H0 :1 3 H1:1 3
0.05
拒绝H0
H0:2 3
H1:2 3
0.05
拒绝H0
不能用t检验的原因
两两比较的t检验：
H0 :1 2
每次比较拒绝H0时，犯一 类错误的概率是0.05；推
H1:12 0.05 H0 :1 3 H1:1 3
4.1 7.9
X ij
9.2 8.1
-1.8 4.3
5.0 3.8
-0.1 6.4
3.5 6.1
6.3 7.0
3.9 1.5
1.6 9.4 为什么观察值之 6.4 3.8 间存在变异？
3.0 7.5
5.8 13.2
12.7 5.4
3.9 8.4
8.0 16.5
9.8 3.1
2.2 12.2
15.5 9.2
拒绝H0 拒绝H0
断正确的概率是0.95。
三次比较均推断正确的概 率是0.95×0.95×0.95。
0.05
H0:2 3
总的犯一类错误的概率是 1-0.953＝0.1426。
H1:2 3
拒绝H0
0.05
第八章方差分析预防医学 7
方差分析 （Analysis of Variance，ANOVA）
R.A第.F八i章s方h差e分r析(1预8防9医0学~1962)
8
多个独立样本资料的方差分析
检验目的 推断多个总体均数是否相等。
第八章方差分析预防医学 9
多个独立样本资料的方差分析
应用条件
➢ 多个独立随机样本的定量资料
➢ 各样本均来自正态分布总体
➢ 各总体方差相等
X2~N(2,)
X1~N(1,)
第八章方差分析预防医学 4
表 8-1 2 型糖尿病患者治疗 4 周后餐后 2 小时血糖的下降值(mmol/L)
高剂量组 (i=1)
5.6 7 4.9
X ij
9.2 8.1
5.0 3.8
3.5 6.1
5.8 13.2
8.0 16.5
15.5 9.2
11.8
表 8-1 2 型糖尿病患者治疗 4 周后餐后 2 小时血糖的下降值(mmol/L)
高剂量组 (i=1)
低剂量组 (i=2)
对照组 (i=3)
合计
5.6 16.3
-0.6 2.0
12.4 2.7
9.5 11.8
5.7 5.6
0.9 7.8
6.0 14.6
12.8 7.0
7.0 6.9
8.7 4.9
合计
t检验
资料类型？ 设计类型？ 分布类型？ 总体方差相等？
19
20
60( N )
5.8000
5.4300
6.8650( X )
18.1867 第八章方差分析预1防2医.3学843
18.4176( S 2 )
5
不能用t检验的原因
检验假设：
H0： 123
H1：至少有两个 总体均数不等
0.05
拒绝H0，犯一类 错误的概率是0.05
ni
21
Xi
9.1952
S i2
17.3605
低剂量组 (i=2)
-0.6 2.0 5.7 5.6 12.8 7.0 4.1 7.9 -1.8 4.3 -0.1 6.4 6.3 7.0 12.7 5.4 9.8 3.1 12.6
对照组 (i=3)
12.4 2.7 0.9 7.8 7.0 6.9 3.9 1.5 1.6 9.4 6.4 3.8 3.0 7.5 3.9 8.4 2.2 12.2 1.1 6.0
X3~N(3,)
1 2 3
第八章方差分析预防医学 10
方差分析的基本思想
方差，又称均方差(mean square deviation) 是描述观察值变异度的指标。
离均差平方和
S2 (XX)2
n1
(Sum of Square，SS)
自由度(degrees of freedom，df)
第八章方差分析预防医学 11
2
0
我们也用了新 药，可是剂量
太低！
我们用的是 传统降糖药！
处理作用 随机误差
-2
我也用-4了新药，
可是降的0 不多！
1
2
3
4
1=高剂量1=高，剂第量2八，章＝方2差=低低分析剂预剂量防，医量学3=对，照3＝对照
13
方差分析的基本思想
20 18
X X (X i X ) (X X i)
16
X
血 14 糖 12 XX 的 10 X1 9.195
12.6
1.1 6.0
11.8
ni
21
Xi
9.1952
S
2 i
17.3605
19
20
60( N )
5.8000
5.4300
6.8650( X )
18.1867
12.3843
18.4176( S 2 )
第八章方差分析预防医学 12
方差分析的基本思想
20
因为我们用了 最18新的降糖药！
16
血 14 糖 12 的 10 下8 降6 值4
定量资料
方差分析的基本思想 完全随机设计资料的方差分析** 随机区组设计资料的方差分析** 多个样本均数的两两比较* 析因设计资料的方差分析 重复测量资料的方差分析 多个样本的方差齐性检验和数据变换
第八章方差分析预防医学 1
A 完全随机分组得到多个独立样本
样本1
甲药
受试对象
样本2
乙药
X Xi
下8 降6 值4
Xi X X2 5.800 X3 5.430
X 6.865
处理作用
2
0
随机误差
-2
-4
0
1
2
3
4
1=高剂量1=高，剂量2，＝2=低低剂剂量，量3=，对照3＝对照
方差分析的基本思想
X X (X i X ) (X X i)
(XX)2 (XiX)2 (XXi)2
总变异
组间变异