【小初高学习】七年级数学上册第二章几何图形的初步认识2.6角的大小同步训练新版冀教版
【七年级数学】冀教版七年级数学上册第2章几何图形的初步认识同步练习题(共9套附答案)

冀教版七年级数学上册第2章几何图形的初步认识同步练习题(共9套附答案)21 从生活中认识几何图形一、选择题1.下列所述的物体中,与球形状类似的是( )A 铅笔 B.烟囱帽 c.西瓜 D.电视机2.下列图形中,不属于立体图形的是 ( )图-16-13.如图-16-2所示的几何体的面数是( )图-16-2A.3 B.4 c.5 D.64.下列几何图形中,与其他三个不是同一类的是 ( )A 正方体 B.三棱柱 c.三棱锥 D.长方体5.图-16-3是一座房子的平面图,组成这幅图的几何图形有( ) 图-16-3A 三角形、长方形B.三角形、长方形、正方形c.三角形、长方形、正方形、梯形D.长方形、正方形、梯形6.下雨时,司机会打开雨刷器,雨刷器在运动时会形成一个扇面,这是因为( )A 点动成线 B.线动成面c.面动成体 D.面面相交成线二、填空题7.长方体是一个立体图形,它有________个面,________条棱,________个顶点.8.请从数学(几何)的角度解释下列现象(1)国庆之夜,燃放的礼花在天空中留下美丽的弧线____________;(2)用一条笔直的细线切一块豆腐__________;(3)自行车辐条转动时,形成一个________,这说明了____________.三、解答题9.找朋友.图-16-4素养提升规律探究下列图形中,图(a)是正方体木块,把它切去一块,得到如图(b)(c)(d)(e)的木块.图-16-5(1)我们知道,图(a)的正方体木块有8个顶点,12条棱,6个面,请你将图(b)(c)(d)(e)中木块的顶点数、棱数、面数填入下表图号顶点数x棱数面数z(a)8126(b)(c)(d)(e)(2)上表中,各种木块的顶点数、棱数、面数之间存在一定的规律,请你写出顶点数x、棱数、面数z之间的数量关系式.1.c 2A 3c 4c 5c6.[解析] B 雨刷可以看成一条线,运动形成的扇形可以看成一个面,即线动成面.7.6 12 88.(1)点动成线(2)线动成面(3)圆面线动成面9.略[素养提升]解(1)填表如下图号顶点数x棱数面数z(a)8126(b)695(c)8126(d)8137(e)10157(2)x+z-2=2.2 点和线一、选择题1.下列各图形中,可以比较长短的是( )A 两条射线 B.两条直线 c.两条线段 D.直线与射线2.下列说法中,错误的是( )A 经过一点的直线可以有无数条B.经过两点的直线只有一条c.一条直线只能用一个字母表示D.线段cD和线段Dc是同一条线段3.下列语句中正确的个数是( )①直线N和直线N是同一条直线;②射线AB和射线BA是同一条射线;③线段PQ和线段QP是同一条线段;④直线上一点把这条直线分成的两部分都是射线.A 4 B.3 c.2 D.14.下列现象中,可以用“两点确定一条直线”解释的有( )①把弯曲的路改直,就能缩短路程;②园林工人栽一行树,先栽首尾的两棵树;③解放军叔叔打靶瞄准;④在墙上钉木条至少要两颗钉子才能牢固.A 1个 B.2个 c.3个 D.4个5.如图-17-1所示,下列说法不正确的是( )图-17-1A 直线Ac经过点AB.Bc是线段c.点D在直线Ac上D.直线Ac与线段BA相交于点A6.经过任意不重合的三点中的两点共可以画出的直线有( )A 一条或三条 B.三条c.两条 D.一条二、填空题7.如图-17-2,图中有________条直线,有________条射线,有________条线段.图-17-2三、解答题8.按下列语句画出图形①画一条直线l,在直线l上取两点A,B;②在直线l外取两点P,Q,使点P,Q在直线l的异侧,且A,B,P,Q任意三点不共线;③画直线PQ交线段AB于点;④画线段PA,PB和射线QA,QB素养提升建模思想(1)观察思考如图-17-3所示,线段AB上的点数与线段的总条数有如下关系如果线段AB上有3个点,那么线段总条数为3;如果线段AB上有4个点,那么线段总条数为6;如果线段AB上有5个点,那么线段总条数为________.3=2+1=3×(3-1)26=3+2+1=4×(4-1)2图-17-3(2)模型构建如果线段上有个点(包括线段的两个端点),那么共有________条线段.(3)拓展应用8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.1.c2.c3.[解析] B ②不正确.4.c5.[解析] c A.直线Ac经过点A,正确;B.Bc是线段,正确;c.点D在直线Ac外,不在直线Ac上,错误;D.直线Ac与线段BA相交于点A,正确.故选c6.[解析] A 当三点在同一直线上时,只能画出一条直线;当三点不在同一直线上时,每过两点可画一条直线,共可画3条.故选A 7.[答案] 1 9 12[解析] 图中有直线Ac,共1条直线;以A为端点有2条射线,B为端点有1条射线,c为端点有2条射线,E为端点有3条射线,F为端点有1条射线,共2+1+2+3+1=9(条)射线;线段有Ac,AD,AE,AF,Bc,BD,BE,BF,cD,cE,DF,EF,共12条线段.8.解如图所示[素养提升]解(1)10 (2)(-1)2(3)把8位同学看作线段上的8个点,每两位同学之间的一场比赛看作一条线段,线段上8个点所构成的线段条数就等于比赛的场数,因此一共要进行8×(8-1)2=28(场)比赛.。
2024年冀教版七年级上册第二章 几何图形的初步认识角大小的比较

课时目标1.类比线段长短的比较,经历探索角大小比较的过程,会用估测、测量、叠合的方法比较两个角的大小.特别要掌握叠合法.培养学生类比的思维能力和对知识的迁移能力.2.能用直尺和圆规作一个角等于已知角,通过动手操作感知知识形成的过程.学习重点用叠合法比较角的大小.学习难点能用尺规作一个角等于已知角.课时活动设计回顾引入线段有长短,角也有大小,类比线段长短的比较方法,如何比较两个角的大小呢?请同学说出自己的想法.学生预期回答:线段的大小比较方法有估测法、度量法,叠合法.猜想角的大小比较方法也可能有估测法、度量法,叠合法.设计意图:引导学生类比线段长短的比较方法,探究比较两个角大小的方法,巩固旧知识,引入新知识,培养学生类比的思维能力和对知识的迁移能力.探究新知探究1角大小的比较方法问题1:如图,请大家观察下面两个角∠AOB和∠A'O'B',哪个角大?你有什么方法来比较它们的大小?方法一用估测法比较两个角的大小.若角度相差较大就可以估测出大小,相差不大时,就很难观察和估测出来了.方法二用测量法比较两个角的大小.用量角器量出∠AOB和∠A'O'B'的度数,哪个角的度数较大,哪个角就较大,当度数相等时,两个角相等.追问:还有其他方法吗?类比线段的长短是怎样比较的?方法三用叠合法比较两个角的大小.将∠A'O'B'叠合到∠AOB上来,比较∠AOB和∠A'O'B'的大小,应怎样进行呢?(1)∠A'O'B'的顶点O'应放到什么位置?(2)∠A'O'B'的边O'B'应放到什么位置?(3)∠A'O'B'的另一边O'A'应放到哪一侧?(4)这时根据什么情况来判断∠A'O'B'与∠AOB的大小?总结:把∠A'O'B'叠合在∠AOB上,使顶点O'与O重合,边O'B'和OB重合,边O'A'和OA落在重合边的同侧.思考:两个角的大小一般有几种情况?师生共同归纳:(1)如果OA落在∠AOB的外部,如图1所示,那么∠A'O'B'小于∠AOB,记作∠A'O'B'<∠AOB.(2)如果O'A'与OA重合,如图2所示,那么这两个角相等,记作∠A'O'B'=∠AOB.(3)如果OA落在∠A'O'B'的内部,如图3所示,那么∠A'O'B'大于∠AOB,记作∠A'O'B'>∠AO'B.探究2作一个角等于已知角问题2:请你说说如何作一个角等于已知角?鼓励学生大胆发言,展示探究问题方法的多样性,教师给予点拨和鼓励.度量法:如图,已知∠AOB,利用量角器,可以作一个角∠CPD等于这个角.请同学们用叠合法验证∠CPD=∠AOB.还有其他方法吗?你能用尺规作出一个角等于已知角吗?如图,已知∠AOB,求作∠A'O'B',使∠A'O'B'=∠AOB.给学生动手操作的时间,鼓励学生小组之间互相交流做法,派学生代表分享自己认为简便的方法.在半透明的纸上,按下列步骤作一个角等于已知角.步骤1:画射线O'M;步骤2:以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D.步骤3:以点O'为圆心,以OC长为半径画弧,交O'M于点A'.步骤4:以点A'为圆心,以CD长为半径画弧,与已画的弧交于点B'.步骤5:作射线O'B'.∠A'O'B'即为所求.请同学们用叠合法验证∠A'O'B'=∠AOB.归纳:像这样只有直尺(无刻度)和圆规画图的方法称为尺规作图.思考:经历了刚才的作角过程,比较两个方法的优缺点.设计意图:采用类比的方法,按照“几何模型——图形——文字——符号”的学习程序,学生动手操作,自主探究.建立线段比较长短与角比较大小之间知识与方法的联系,在对比中加深理解.指出对于两个角的大小关系和有理数的大小关系一样.让学生根据实际经历,感受解决问题的方法的多样性,同时感受尺规作图的规范性.典例精讲例如图,已知∠α和∠β.(1)请用直尺和圆规作两个角,使它们分别等于∠α和∠β.(保留作图痕迹)(2)请用两种方法比较这两个角的大小.注:不写过程,保留作图痕迹,写出作图结果.解:(1)如图所示,∠1=∠α,∠2=∠β,∠1,∠2即为所求.(2)方法一测量法.经过测量得知,∠1=30°,∠2=60°,所以∠1<∠2.方法二尺规作图法.由图可知,∠1<∠2.设计意图:通过例题,巩固所学知识,规范作图要求,进一步增强对新知的理解.巩固训练1.如图,正方形网格中每个小正方形的边长都为1,则∠1与∠2的大小关系为(A)A.∠1<∠2B.∠1=∠2C.∠1>∠2D.无法比较2.老师设置了一个问题,让同学们体验“经过已知角一边上的点,做一个角等于已知角”的作法,问题:如图,用尺规过∠AOB的边OB上一点C(图1)作∠DCB=∠AOB(图2).作图步骤已打乱,请同学们寻找出正确的排序.①以点C为圆心,OM的长为半径作弧,交OB于点P;②以点O为圆心,小于OC的长为半径作弧,分别交OA,OB于点N,M;③以点P为圆心,MN的长为半径作弧,与已画的弧交于点D;④作射线CD.下列排序正确的是(D)A.①②③④B.④③①②C.③②④①D.②①③④设计意图:通过巩固训练,及时巩固本节课重点知识,加深对所学知识的理解,提高综合运用能力.课堂小结1.本节课我们学习的内容是什么?2.通过本节课的探究活动,你有什么感受?设计意图:通过小结,学生梳理本节所学内容,同学们互帮互助,解决困惑.充分发挥学生的主体意识,培养学生的语言概括能力和发散思维能力.课堂8分钟.1.教材第85页习题B组第3,4题.2.七彩作业.2.6角大小的比较1.角大小的比较方法:度量法(数)、叠合法(形).2.作一个角等于已知角.教学反思。
七年级数学上册 第二章 几何图形的初步认识 2.6 角的大小专题练习2 (新版)冀教版

BCD O2.6 角的大小1. 一个角的补角的13等于它的余角,则这个角是 度.2. 一个角的补角加上14°,等于这个角的余角的5倍,这个角的度数是 .3. 如果两个角互补,并且它们的差是30°,那么较大的角是 °.4. 若90A B ∠+∠=︒,90BC ∠+∠=︒,那么____A C ∠∠,理由是 .5. 已知:12201552'''∠-∠=︒,且122∠=∠,求1∠和2∠.6. 如图,点O 是直线AD 上的点,AOB ∠,BOC ∠,COD ∠三个角从小到大依次相差25°,则这三个角的度数是 .7. 如图,AOC BOD ∠=∠=____=.8. 内装有 只小彩灯.9. 如图,O 是直线AB OE 是COB ∠的平分线,求DOE ∠的度数.AC DEOA BCD E O A B C DE变式⑴:如图,90DOE ∠=︒,OD 平分AOC ∠,问OE 是否平分BOC ∠?变式⑵:如图,点O 在直线AB 上,且AOC BOC ∠≠∠,OD 平分AOC ∠,90DOE ∠=︒,下面四个结论,错误的有( )①图中必有3个钝角; ②图中只有3对既相邻又互补的角;③图中没有45°的角; ④OE 是BOC ∠的平分线.A.0个 B.1个 C.2个 D.3个10. 已知40AOB ∠=︒,OC 是AOB ∠的平分线,则AOC ∠的余角等于 .11. 如图,3540AOB '∠=︒,5030BOC '∠=︒,2118DOC '∠=︒,OE 平分AOD ∠,求BOE ∠的度数.12. 若把一个平角三等分,则两旁的两个角的平分线所组成的角等于( )A.13平角 B.12平角 C.23平角 D.34平角 13. 已知AOB ∠和BOC ∠之和为180︒,这两个角的平分线所成的角( ) A.一定是直角 B.一定是锐角 C.一定是钝角 D.是直角或锐角14. 如图,O 是直线AB 上一点,120AOD ∠=︒,90AOC ∠=︒,OE 平分BOD ∠,则图中和为180︒的两个角有( )A.3对 B.4对 C.5对 D.6对15. 已知:170AOB ∠=︒COD ∠的大小.16.AB CDO AE F17. 一个锐角的补角比这个角的余角大 °.18. 如图,已知2COB AOC ∠=∠,OD 平分AOB ∠,且20COD ∠=︒,求AOB ∠的度数.19. 下列说法中错误的个数是 ( ) ①线段有两个端点,直线有一个端点; ②角的大小与我们画出的角的两边的长短无关;③线段上有无数个点; ④同角或等角的补角相等; ⑤两锐角的和一定大于直角. A.1个 B.2个 C.3个 D.4个20. 如图,平原上有A ,B ,C ,D 四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.⑴不考虑其他因素,请你画图确定蓄水池H 点的位置,使它与四个村庄的距离之和最小. ⑵计划把河中的水引入蓄水池H 中,怎样开的渠最短?并说明根据.21. 下列说法中正确的是( )A.一条射线把一个角分成两个角,这条射线是这个角的角平分线B.点到直线的距离是指从直线外一点到这条直线的垂线的长度C.若2MN MC =,则点C 是线段MN 的中点D.有AB MA MB =+,AB NA NB <+,则点M 在线段AB 上,点N 在线段AB 外22. 已知线段AB ,在AB 的延长线上取一点C ,使2AC BC =,在AB 的反向延长线上取一点D ,使2DA AB =,那么线段AC 是线段DB 的 ( ) A.13 B.23 C.12 D.3223. 已知∠α与∠β互余,且∠α=40°,则∠β的补角为 度.10° 30° 60° 80°100° 120° 150° 170°24. 请你用三角板、圆规或量角器等工具,画∠POQ =60°,在它的边OP 上截取OA =50 mm ,OQ 上截取OB =70 mm ,连结AB ,画∠AOB 的平分线与AB 交于点C ,并量出AC 和OC 的长.(结果精确到1 mm ,不要求写作法)25. 已知α50∠=,那么它的补角等于.26. 图中给出的各角中,哪些互为余角?哪些互为补角?参考答案1.答案:45.2.答案:64°.E FK 3.答案:105.4.答案:=;同角的余角相等.5.答案:解:设2∠为x ︒,则1∠为2x ︒,则 2201552x x '''︒-︒=︒201552x '''︒=︒,2403144x '''︒=︒,答:2∠为201552'''︒,1∠为403144'''︒.6.答案:35°,60°,85°.7.答案:121°.8.答案:12.9.答案:解:由题意可知12DOC AOC ∠=∠,12EOC BOC ∠=∠. 因为AB 是一条直线,所以180AOB ∠=︒,也就是180AOC BOC ∠+∠=︒,119022DOE DOC EOC AOC BOC ∠=∠+∠=∠+∠=︒. ⑴解:因为180AOC BOC ∠+∠=︒,90DOE ∠=︒, 所以1()2DOE AOC BOC ∠=∠+∠1122AOC BOC =∠+∠, 而DOE DOC EOC ∠=∠+∠,12DOC AOC ∠=∠, 所以12COE BOC ∠=∠,即OE 平分BOC ∠. ⑵A.10.答案:70°11.答案:解:35405030211810728AOD AOB BOC COD ''''∠=∠+∠+∠=︒+︒+︒=︒153442AOE AOD '∠=∠=︒ 53443540184BOE AOE AOB '''∠=∠-∠=︒-︒=︒12.答案:C.13.答案:A.14.答案:D.15.答案:40°或60°或160°或180°.16.答案:4517.答案:9018.答案:120°19答案:B.20答案:解:⑴连结AD ,BC ,交于点H ,则H 为所求的蓄水池点.⑵过H 作HK EF ⊥于K “点与直线的连线中,垂线段最短”.(如图)21.答案:D.22.答案:B.23.答案:13024.答案:画出图形(基本正确即可)AC=26 mm,OC=50 mm.25.答案:130.26.答案:互余:10°和80°;30°和60°.互补:100°和80°;120°和60°;150°和30°;170°和10°.。
冀教版七年级上册数学第2章 几何图形的初步认识 角的大小(1)

【点拨】如图,连接 BC,AC,BD,AD,BE,AE. 通过测量可知∠ACB<∠ADB=∠AEB,所以最好的射点在线段 DE(异于端点) 上一点.故选 C.
【答案】C
6.如图,∠AOB=30°,用尺规作图:以 O 为顶点,射线 OA 为
一边作一个角∠AOC,使∠AOC=60°,则∠BOC 的度数为
4.已知∠A=18°20′36″,∠B=18.35°,∠C=18°21′,下列比较 正确的是( A ) A.∠A<∠B B.∠B<∠A
一
C.∠B<∠C D.∠C<∠B
5.足球射门,不考虑其他因素,仅考虑射点到球门 AB 的张角 大小时,张角越大,射门越好.在如图所示的正方形网格中, 点 A,B,C,D,E 均在格点上,球员带球沿 CD 方向进攻, 最好的射点在( ) A.点 C B.点 D 或点 E C.线段 DE(异于端点) 上一点 D.线段 CD(异于端点) 上一点
2.已知∠AOB=50°,∠AOC=60°,射线 OB,OC 在射线 OA 的同侧,则射线 OC( B ) A.在∠AOB 的内部 B.在∠AOB 的外部 C.在∠AOB 的内部或外部 D.可能与射线 OB 重合
3.(河北邯郸大名期末)若∠1=40.4°,∠2=40°4′,则∠1 与∠2 的关系是( B ) A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.以上都不对
9.用尺规作图作一个角等于已知角的示意图如图所示,则叙述 正确的个数有( B ) ①OA=O′A′;②OB=O′B′;③CD=C′D′; ④∠A′O′B′=∠AOB. A.1 B.2 C.3 D.4
10.如图,已知∠AOB,请用直尺和圆规作出一个角等于∠AOB.
解:略.
11.如图是一张跑步示意图,其中的 4 面小旗表示 4 个饮水点, 跑步者在经过某个饮水点时需要改变的方向的角度最大,这 个饮水点是( A ) A.1 B.2 C.3 D.4
七年级数学上册 2 几何图形的初步认识 2.6 角的大小同步练习 (新版)冀教版

2.6 角的大小
1.如图,∠AOB______∠AOC ,∠AOB______∠BOC(填“>”“=”或“<”)
第1题图 第2题图
2.如图,∠AOC =________+________=________-________;∠BOC=________-
________=________-________.
3.OC 是∠AOB 内部的一条射线,若∠AOC=12
________,则OC 平分∠AOB;若OC 是∠AOB 的平分线,则________=2∠AOC.
4.在∠AOB 的内部任取一点C ,作射线OC ,则一定存在 ( )
A .∠AOB>∠AOC
B .∠AO
C =∠BOC
C .∠BOC>∠AOC
D .∠AOC>∠BOC
5.角α和角β的顶点和一边重合,另一边都在公共边同侧,且α>β,那么角α的
另一边落在角β的
( )
A .另一边上
B .内部
C .外部
D .以上结论都不对
6.下列说法正确的是 ( )
A .一个钝角与一个锐角的差一定是锐角
B .一个钝角和一个直角的差一定是锐角
C .一个钝角与一个锐角的差一定是直角
D .一个钝角与一个锐角的差仍是钝角
7.已知∠AOB =58°,作射线OC 使∠AOC=30°,求∠BOC 的度数.
2.6 角的大小
1.> >
2.∠AOB ∠BOC∠AOD∠COD∠BOD∠COD∠AOC∠AOB 3.∠AOB ∠AOB 4.A 5.C 6.B 7.28°或88°。
七年级数学上册 第二章 几何图形的初步认识 2.6 角的大小专题练习1 (新版)冀教版
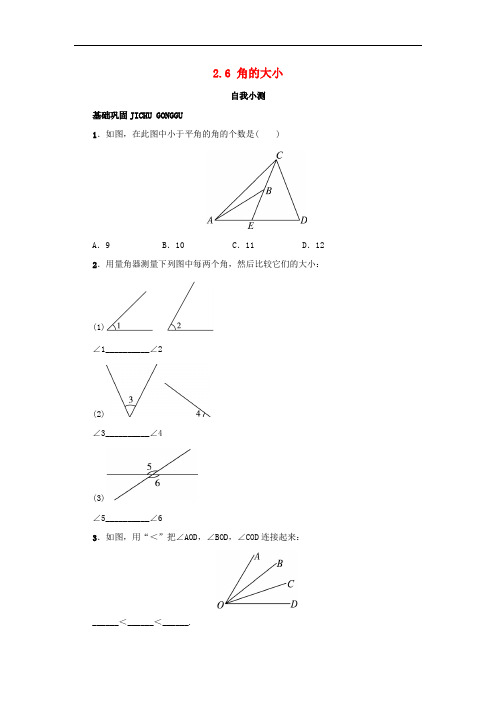
2.6 角的大小自我小测基础巩固JICHU GONGGU1.如图,在此图中小于平角的角的个数是( )A.9 B.10 C.11 D.12 2.用量角器测量下列图中每两个角,然后比较它们的大小:(1)∠1__________∠2(2)∠3__________∠4(3)∠5__________∠63.如图,用“<”把∠AOD,∠BOD,∠COD连接起来:______<______<______.4.如果∠1=4°18′,∠2=3°79′,∠3=4.4°,则∠1,∠2,∠3的大小顺序是__________.(由大到小排列)5.已知射线BC和∠α,用直尺、圆规作∠ABC,使∠ABC=∠α.[6.如图,已知O是直线AD上的点,∠AOB,∠BOC,∠COD三个角从小到大依次相差25°,求这三个角的度数.能力提升NENGLI TISHENG7.在∠AOB的内部任取一点C,作射线OC,则一定存在( )A.∠A O B>∠A O C B.∠B O C>∠A O BC.∠B O C>∠A O C D.∠A O C>∠B O C8.如图,∠AOD>∠BOC,则下列说法中正确的是( )A.∠C O D>∠A O B B.∠A O B>∠C O DC.∠C O D=∠A O B D.∠A O B与∠C O D的大小关系不能确定9.如图,在一张透明纸上画∠AOB,能否折出一条射线,使这条射线把∠AOB平均分为2份?参考答案1.C2.(1)<(2)>(3)=3.∠COD∠BOD∠AOD4.∠3>∠2>∠1点拨:∵∠2=3°79′=4°19′,∠3=4.4°=4°24′,故∠3>∠2>∠1.5.略6.解:设∠AOB的度数为x,由题意得:x+(x+25°)+(x+50°)=180°,解得x=35°,则x+25°=60°,x+50°=35°+50°=85°.即∠AOB=35°,∠BOC=60°,∠COD=85°.7.A8.B 点拨:∠AOD=∠AOB+∠BOD,∠BOC=∠COD+∠BOD,因为∠AOD>∠BOC,所以∠AOB+∠BOD>∠COD+∠BOD,所以∠AOB>∠COD.9.解:能.把∠AOB对折,使OA,OB重合,则折痕可把∠AOB平分.。
【配套K12】七年级数学上册第二章几何图形的初步认识2.7角的和与差第2课时同步训练新版冀教版
第2课时互余、互补及其性质知识点 1 互余、互补的概念1.若∠α与∠β互为余角,则∠α+∠β=________;若∠α与∠β互为补角,则∠α+∠β=________.2.[2017·常德]若一个角为75°,则它的余角的度数为( )A.285° B.105° C.75° D.15°3.若∠A=34°,则∠A的补角的度数为( )A.56° B.146° C.156° D.166°4.一个角的余角是54°38′,则这个角的补角是________.5.已知∠1与∠2互余,∠2与∠3互补.若∠1=63°,则∠3=________.6.如图2-7-17,O是直线AE上的一点,OB是∠AOC的平分线,OD是∠COE的平分线.(1)图中互余的角有哪几对?(2)图中互补的角有哪几对?图2-7-17知识点 2 互余、互补的性质7.(1)若∠1+∠2=90°,∠1+∠3=90°,则∠2________∠3(填“>”“<”或“=”),理由:________________________.(2)若∠1+∠3=90°,∠2+∠4=90°,且∠1=∠2,则∠3________∠4(填“>”“<”或“=”),理由:________________________.(3)若∠1+∠2=180°,∠1+∠3=180°,则∠2________∠3(填“>”“<”或“=”),理由:________________________.(4)若∠1+∠3=180°,∠2+∠4=180°,且∠1=∠2,则∠3________∠4(填“>”“<”或“=”),理由:________________________.8.如图2-7-18,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.(1)求出∠AOB及其补角的度数;(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.图2-7-189.将一副三角尺按如图2-7-19所示的位置摆放,其中∠α与∠β一定互余的是( )图2-7-1910.下列说法正确的是( )A .互补的两个角一个是锐角,一个是钝角B .180°的角是补角C .互余的两个角可能是等角D .只有锐角有补角11.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值等于( )A .45°B .60°C .90°D .180°12.如果一个角和它的余角的比是1∶3,那么这个角的度数为________.13.已知∠α与∠β互补,且∠α>∠β,试判断∠β与12(∠α-∠β)的数量关系.14.如图2-7-20,将两块直角三角尺的直角顶点C 叠放在一起.(1)若∠DCE =35°,求∠ACB 的度数;(2)若∠ACB =140°,求∠DCE 的度数;(3)写出∠ACB 与∠DCE 的数量关系,并说明理由.图2-7-2015.如图2-7-21,O为直线AB上的一点,∠AOE为直角,∠DOF=90°,OB平分∠COD,则图中与∠DOE互余的角有哪些,与∠DOE互补的角有哪些?图2-7-2116.如图2-7-22,∠AOB∶∠BOC∶∠COD=2∶3∶4,射线OM,ON分别平分∠AOB与∠COD,已知∠MON=90°,则∠AOB等于( )图2-7-22A.20° B.30° C.40° D.45°17.如图2-7-23①,∠AOB,∠COD都是直角.(1)试猜想,∠AOD和∠BOC在数量上是否存在相等、互余或互补的关系?你能说明你的猜想的正确性吗?(2)当∠COD绕点O旋转到图2-7-23②所示的位置时,(1)中的猜想还成立吗?图2-7-23【详解详析】1.90°180°2.D [解析] 它的余角的度数为90°-75°=15°.故选D.3.B [解析] ∠A的补角的度数为180°-34°=146°.故选B.4.144°38′[解析] 根据题意得这个角为90°-54°38′=35°22′,则这个角的补角为180°-35°22′=144°38′.5.153° [解析] 因为∠1是∠2的余角,∠3是∠2的补角,所以∠3-∠1=90°,所以∠3=90°+63°=153°.6.解:(1)∠AOB 与∠DOE ,∠AOB 与∠COD ,∠COD 与∠BOC ,∠BOC 与∠DOE 都是互余的角.(2)∠AOB 与∠BOE ,∠BOC 与∠BOE ,∠AOC 与∠COE ,∠COD 与∠AOD ,∠EOD 与∠AOD 都是互补的角.7.(1)= 同角的余角相等 (2)= 等角的余角相等 (3)= 同角的补角相等 (4)= 等角的补角相等8.解:(1)∠AOB =∠BOC +∠AOC =70°+50°=120°,其补角为180°-∠AOB =180°-120°=60°.(2)∠DOC =12∠BOC =12×70°=35°,∠AOE =12∠AOC =12×50°=25°.∠DOE 与∠AOB 互补.理由:因为∠DOE =∠DOC +∠COE =∠DOC +∠AOE =35°+25°=60°,所以∠DOE +∠AOB =60°+120°=180°,故∠DOE 与∠AOB 互补.9.C10.C.11.C12.[22.5°[解析] 根据题意,知这个角的度数是90°×14=22.5°.13.解:因为∠α与∠β互补,所以∠α+∠β=180°,所以∠β=180°-∠α,所以∠β的余角为90°-(180°-∠α)=∠α-90°=∠α-12(∠α+∠β)=12∠α-12∠β=12(∠α-∠β), 所以∠β+12(∠α-∠β)=90°. 14.解:(1)因为∠ECB =90°,∠DCE =35°,所以∠DCB =90°-35°=55°.因为∠ACD =90°,所以∠ACB =∠ACD +∠DCB =145°.(2)因为∠ACB=140°,∠ACD=90°,所以∠DCB=140°-90°=50°.因为∠ECB=90°,所以∠DCE=90°-50°=40°.(3)∠ACB+∠DCE=180°(或∠ACB与∠DCE互补).理由:因为∠ECB=90°,∠ACD=90°,所以∠ACB=∠ACD+∠DCB=90°+∠DCB,∠DCE=∠ECB-∠DCB=90°-∠DCB,所以∠ACB+∠DCE=180°.15.[解析] 本题要根据余角、补角的定义,结合图形认真观察.解:因为∠BOE=∠AOB-∠AOE=180°-90°=90°,所以∠BOD+∠DOE=90°,即∠DOE与∠BOD互余.因为OB平分∠COD,所以∠BOC=∠BOD,所以∠DOE与∠BOC互余.因为∠DOF=90°,所以∠DOE+∠EOF=90°,所以∠DOE与∠EOF互余.即与∠DOE互余的角有∠BOD,∠BOC,∠EOF.因为∠DOE+∠BOF=∠DOE+∠EOF+∠BOE=∠DOF+∠BOE=180°,所以∠DOE与∠BOF互补.因为∠DOE+∠COE=∠DOE+∠COB+∠BOE=∠DOE+∠BOD+∠BOE=∠BOE+∠BOE=180°,所以∠DOE与∠COE互补,即与∠DOE互补的角有∠BOF,∠COE.16.B17.解:(1)猜想:∠AOD与∠BOC互补.因为∠AOD=∠AOB+∠BOD=90°+∠BOD,∠BOD=90°-∠BOC,所以∠AOD=90°+90°-∠BOC,所以∠AOD+∠BOC=180°,即∠AOD与∠BOC互补.(2)(1)中的猜想仍然成立.因为∠AOB,∠COD都是直角,所以∠AOB+∠COD=180°.又因为∠AOB+∠BOC+∠COD+∠AOD= 360°,所以∠AOD+∠BOC=180°,所以∠AOD与∠BOC互补.。
七年级数学上册第二章几何图形的初步认识2.6角的大小同步训练
2.6 角的大小知识点 1 比较角的大小的方法1.射线OC,OD与∠AOB的关系如图2-6-1所示,下列各式中错误的是( )A.∠AOB<∠AOD B.∠BOC<∠AOBC.∠COD<∠AOD D.∠AOB<∠AOC2.∠α和∠β的顶点和一边都重合,另一边都在公共边的同侧,且∠α>∠β,那么∠α的另一边落在∠β的( )A.另一边上 B.内部C.外部 D.以上说法都不对图2-6-1 图2-6-23.如图2-6-2所示,其中最大的角是________,∠DOC,∠DOB,∠DOA的大小关系是________________(用“>”连接).4.如图2-6-3,直线AB和CD相交于点O.(1)分别测量∠AOC,∠AOD,∠BOD和∠BOC的度数;(2)∠AOC和∠BOD相等吗?∠AOD和∠BOC呢?图2-6-35.如图2-6-4,比较∠AOB,∠AOC,∠AOD,∠AOE的大小.图2-6-4知识点 2 角的画法6.不能用一副三角尺画出的角的度数是( )A.75° B.85° C.105° D.150°7.如图2-6-5,已知∠1,用直尺和圆规求作一个角,使它等于∠1.(不写作法,保留作图痕迹)图2-6-58.已知∠A=18°18′,∠B=18.18°,∠C=18.3°,下列说法正确的是( )A.∠A=∠B B.∠A=∠CC.∠A<∠B D.∠A>∠C图2-6-69.在图2-6-6所示的4×4的方格中,记∠ABD=∠α,∠DEF=∠β,∠CGH=∠γ,则( )A.∠β<∠α<∠γB.∠β<∠γ<∠αC.∠α<∠γ<∠βD.∠α<∠β<∠γ10.比较两个角的大小,有以下两种方法:方法一:用量角器量出两个角的度数,则度数大的角大;方法二:构造图形,若一个角包含(或覆盖)另一个角,则这个角大.对于如图2-6-7给定的∠ABC与∠DEF,用以上两种方法分别比较它们的大小.(注:构造图形时,用尺规作图作出示意图)图2-6-71.D [解析] 由图可知∠AOB<∠AOD,故A选项正确;因为射线OC在∠AOB的内部,所以∠BOC<∠AOB,故B选项正确;由图可知∠COD<∠AOD,故C选项正确;因为射线OC 在∠AOB的内部,所以∠AOB>∠AOC,故D选项错误.2.C [解析] 如图所示:故选C.3.∠AOD∠DOA>∠DOB>∠DOC4.解:(1)∠AOC=30°,∠AOD=150°,∠BOD=30°,∠BOC=150°.(2)∠AOC=∠BOD,∠AOD=∠BOC.5.解:∠AOB<∠AOC<∠AOD<∠AOE.6.B [解析] 一副三角尺的度数分别是30°,60°,90°和45°,45°,90°,所以可以拼出75°,105°,150°的角,但不能拼出85°的角.7.解:如图,∠ABC即为所求作的角.8.B.9.B10.解:方法一:测量得∠ABC=45°,∠DEF=65°,所以∠ABC<∠DEF.方法二:以E为顶点,EF为一边,作∠FEA′,使∠FEA′=∠ABC,且EA′与ED在EF 的同侧,如图,则∠FEA′<∠DEF.又因为∠FEA′=∠ABC,所以∠ABC<∠DEF.。
【优质】最新七年级数学上册第二章几何图形的初步认识2-2点和线同步训练冀教版
教学资料参考范本
【优质】最新七年级数学上册第二章几何图形的初步认识2-2
点和线同步训练冀教版
撰写人:__________________
部门:__________________
时间:__________________
知识点 1 线段、射线和直线的概念及表示方法
1.以下说法中正确的是( )
图2-2-1
A.①可表示为点a
B.②可表示为直线ab
C.③可表示为直线AB
D.④可表示为直线l
2.如图2-2-2,下列不正确的几何语句是( )
图2-2-2
A.直线AB与直线BA是同一条直线
B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
3.[2017·乐亭期中]如图2-2-3,图中射线的条数为( )
图2-2-3
A.两条 B.三条 C.四条 D.六条
4.图2-2-4所示的图形中有______条直线,分别是;以B为端点的线段有________条,分别是________________________;以A为端点的射线有______条,分别是____________________________.。
2019七年级数学上册 第二章 几何图形的初步认识 2.5 角以及角的度量同步训练 (新版)冀教版
2.5角以及角的度量知识点 1 角的定义和表示方法1.下列说法:①两条射线组成的图形是角;②角的大小与边的长短有关;③角的两边必须画得一样长;④角的两边是两条射线;⑤因为平角的两边也成一条直线,所以一条直线可以看成一个平角.其中正确的有( )A.1个 B.2个 C.3个 D.4个2.如图2-5-1,下列说法错误的是( )A.∠1与∠AOB表示同一个角B.∠β表示的是∠BOCC.图中共有三个角:∠AOB,∠AOC,∠BOCD.∠AOC也可用∠O来表示图2-5-1 图2-5-23.图2-5-2中小于平角的角有( )A.5个 B.6个 C.7个 D.8个知识点 2 角的度量单位及换算4.完成下列角度的换算.(1)65.34°=________°________′________″;(2)72°15′=________°;(3)0.2°=________′;(4)1.45°=________′.5.用度表示下列各角:(1)15°24′36″;(2)36°25′12″;(3)50°65′60″.6.已知∠A=25°12′,∠B=25.12°,∠C=25.2°,下列结论中正确的是( )A.∠A=∠B B.∠A=∠CC.∠B=∠C D.以上均不正确7.[教材练习第2题变式]当分针指向12,时针这时恰好与分针成120°的角,此时是( )A.9点钟 B.8点钟C.4点钟 D.8点钟或4点钟8.如图2-5-3所示,写出所有以点O为顶点的角:________________,写出所有以点B为顶点的小于平角的角:__________________.图2-5-39.小明利用星期天搞社会调查活动,早晨8:00出发,中午12:30到家,请说出小明到家时钟表上的时针和分针的夹角为________度.10.根据如图2-5-4 所示的图形,回答下列问题:图2-5-4(1)从一点O出发引出2条射线,可组成________个角;(2)从一点O出发引出3条射线,可组成________个角;(3)从一点O出发引出4条射线,可组成________个角;(4)从一点O出发引出5条射线,可组成________个角;(5)从一点O出发引出n(n≥2,且n为正整数)条射线,可组成________个角.【详解详析】1.A [解析] 只有说法④正确.故选A.2.D [解析] ∠AOC 不能用∠O 表示,故D 选项错误.故选D.3.C4.(1)65 20 24 (2)72.25 (3)12 (4)875.解: (1)15°24′36″=15°24′+⎝ ⎛⎭⎪⎫3660′=15°24.6′=15°+⎝ ⎛⎭⎪⎫24.660°=15.41°. (2)36°25′12″=36°25′+(1260)′=36°25.2′=36°+⎝ ⎛⎭⎪⎫25.260°=36.42°. (3)50°65′60″=50°66′=51°6′=51°+⎝ ⎛⎭⎪⎫660°=51.1°. 6.B [解析] 先将三个角的单位统一成度再进行比较,∠A =25°12′=25.2°,所以∠A =∠C .故选B.7.D [解析] 因为钟表上每相邻两个表示整点的大格之间的夹角是30°,所以当分针指向12,时针这时恰好与分针成120°的角时,时针距分针4个格,所以只有8点钟或4点钟时符合要求.故选D.8.∠AOB ,∠AOC ,∠BOC ∠ABO ,∠CBO ,∠CBE ,∠EBA9.6510.(1)1 (2)3 (3)6 (4)10 (5)n (n -1)2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.6 角的大小
知识点 1 比较角的大小的方法
1.射线OC,OD与∠AOB的关系如图2-6-1所示,下列各式中错误的是( )
A.∠AOB<∠AOD B.∠BOC<∠AOB
C.∠COD<∠AOD D.∠AOB<∠AOC
2.∠α和∠β的顶点和一边都重合,另一边都在公共边的同侧,且∠α>∠β,那么∠α的另一边落在∠β的( )
A.另一边上 B.内部
C.外部 D.以上说法都不对
图2-6-1 图2-6-2
3.如图2-6-2所示,其中最大的角是________,∠DOC,∠DOB,∠DOA的大小关系是________________(用“>”连接).
4.如图2-6-3,直线AB和CD相交于点O.
(1)分别测量∠AOC,∠AOD,∠BOD和∠BOC的度数;
(2)∠AOC和∠BOD相等吗?∠AOD和∠BOC呢?
图2-6-3
5.如图2-6-4,比较∠AOB,∠AOC,∠AOD,∠AOE的大小.
图2-6-4
知识点 2 角的画法
6.不能用一副三角尺画出的角的度数是( )
A.75° B.85° C.105° D.150°
7.如图2-6-5,已知∠1,用直尺和圆规求作一个角,使它等于∠1.(不写作法,保留作图痕迹)
图2-6-5
8.已知∠A=18°18′,∠B=18.18°,∠C=18.3°,下列说法正确的是( )
A.∠A=∠B B.∠A=∠C
C.∠A<∠B D.∠A>∠C
图2-6-6
9.在图2-6-6所示的4×4的方格中,记∠ABD=∠α,∠DEF=∠β,∠CGH=∠γ,则( )
A.∠β<∠α<∠γ
B.∠β<∠γ<∠α
C.∠α<∠γ<∠β
D.∠α<∠β<∠γ
10.比较两个角的大小,有以下两种方法:
方法一:用量角器量出两个角的度数,则度数大的角大;
方法二:构造图形,若一个角包含(或覆盖)另一个角,则这个角大.
对于如图2-6-7给定的∠ABC与∠DEF,用以上两种方法分别比较它们的大小.(注:构造图形时,用尺规作图作出示意图)
图2-6-7
1.D [解析] 由图可知∠AOB<∠AOD,故A选项正确;因为射线OC在∠AOB的内部,所以∠BOC<∠AOB,故B选项正确;由图可知∠COD<∠AOD,故C选项正确;因为射线OC 在∠AOB的内部,所以∠AOB>∠AOC,故D选项错误.
2.C [解析] 如图所示:
故选C.
3.∠AOD∠DOA>∠DOB>∠DOC
4.解:(1)∠AOC=30°,∠AOD=150°,∠BOD=30°,∠BOC=150°.
(2)∠AOC=∠BOD,∠AOD=∠BOC.
5.解:∠AOB<∠AOC<∠AOD<∠AOE.
6.B [解析] 一副三角尺的度数分别是30°,60°,90°和45°,45°,90°,所以可以拼出75°,105°,150°的角,但不能拼出85°的角.
7.解:如图,∠ABC即为所求作的角.
8.B.
9.B
10.解:方法一:测量得∠ABC=45°,∠DEF=65°,所以∠ABC<∠DEF.
方法二:以E为顶点,EF为一边,作∠FEA′,使∠FEA′=∠ABC,且EA′与ED在EF 的同侧,如图,则∠FEA′<∠DEF.又因为∠FEA′=∠ABC,所以∠ABC<∠DEF.。
