薄壁钢管无芯弯曲最小相对弯曲半径的确定
薄壁小弯曲半径弯头制造工艺探讨

薄壁小弯曲半径弯头制造工艺探讨【摘要】本文详细介绍了薄壁管子小弯曲半径弯头的一些制作要点。
针对不同弯管机,通过大量工艺试验,对设备参数调整、弯管模具改进以及弯制工艺改进等方式,来保证弯头质量。
从而为管子弯制和小R挤压提供了可以借鉴的方法。
【关键词】制造工艺;弯头制造;小弯曲前言在日趋激烈的市场竞争中,成本控制是企业生存的一个重要方面。
在保证使用性能及使用寿命的前提下,紧凑型、薄壁蛇形管可节省空间,降低锅炉总体高度;同时可节约原材料,对锅炉成本控制有着巨大的意义。
因此,薄壁管子小弯曲半径弯头的制造工艺研发迫在眉睫。
如今我们通过公司现有的弯管设备,对部分弯头的制作进行反复的工艺试验,从而发现和总结出了一些普遍性的制造方法和宝贵经验。
在此基础上,我们仍需要对影响弯管及挤压弯头的各种因素进行更深入、更精细化的研究和分析,从而找到更先进、操作性更强的工艺方法。
1 弯头成型要素及制造难点目前公司的弯管机分4种,包括114、108、89、60弯管机;弯制的管子主要为φ32~φ63.5之间,管子材质包含碳钢、合金钢及不锈钢。
弯管包含三个主要控制要点。
包括弯头的椭圆度、管子壁厚减薄量以及弯头外观成型。
这三个控制点相辅相成,相互制约。
对于薄壁小弯曲半径的弯头,弯制时最容易出现的问题在于椭圆度超差,以及弯头内侧出现褶皱。
弯管时弯头外侧为拉伸面,弯头内侧为挤压面.当管子壁厚相对较薄时,内侧会由于挤压过度产生褶皱;与之相对,外侧则会因为拉伸过渡出现壁厚达不到要求,甚至出现拉裂的情况。
对于挤压弯头,常见的缺陷有:弯头内侧内凹、挤压后弯头呈方形、偏心及椭圆度超差。
小R挤压对工人操作要求较高,包括对加热温度的控制,挤压和整形时弯头的摆放位置等。
当壁厚较薄时,更大程度增加了加热弯头随意变形的可能性,容易造成弯头不合格。
2 弯管要点介绍影响弯管质量的因素是多样化的。
在弯制管子规格φ60×4 20G,弯管半径R120,弯管角度150°的弯头过程中,弯管速度为480r/h,所用滑槽规格为φ60/R120。
钢管转弯半径

钢管转弯半径一、引言钢管是一种常见的建筑材料,广泛应用于各个行业。
在实际的钢管应用过程中,我们经常会遇到需要将钢管进行弯曲的情况。
钢管的转弯半径是一个重要的参数,它决定了钢管能否被顺利弯曲并且保持其原有的强度和形状。
本文将深入探讨钢管转弯半径的相关知识。
二、钢管转弯的方式钢管转弯的方式有很多种,常见的包括手工弯管、机械弯管和冷弯管等。
其中,手工弯管是最简单的方式,适用于一些简单的弯曲需求,但是由于操作难度大且无法保证弯曲的精度和一致性,因此在工业生产中使用较少。
机械弯管是一种自动化的弯管方式,通过机械设备实现对钢管的弯曲,具有高效、精准的特点,广泛应用于工业制造领域。
而冷弯管则是在常温下对钢管进行弯曲,具有高度的塑性变形能力,适用于各类钢管的弯曲需求。
三、钢管转弯半径的定义钢管转弯半径指的是在钢管进行转弯时曲线的半径大小。
钢管转弯半径的大小对于弯曲后的钢管质量和性能影响巨大。
一般来说,钢管转弯半径越小,弯曲后的钢管的变形程度就越大,导致钢管性能下降;反之,钢管转弯半径越大,弯曲后的钢管的变形程度越小,性能保持得更好。
因此,在实际应用中,需要根据具体要求和钢管的性能来选择合适的转弯半径。
四、钢管转弯半径的计算方法计算钢管转弯半径的方法有很多种,下面介绍两种常用的计算方法。
1. 弹性计算方法弹性计算方法是根据材料的弹性变形特性来计算钢管转弯半径的方法。
首先需要知道钢管的屈服强度和弯曲力矩,然后根据力矩和弯曲力的关系,可以计算出钢管的转弯半径。
这种计算方法适用于弯曲后钢管仍能保持良好刚度和形状的情况。
2. 塑性计算方法塑性计算方法是根据材料的塑性变形特性来计算钢管转弯半径的方法。
该方法适用于需要较大变形的情况,如冷弯管的弯曲。
在计算过程中,需要考虑到钢管的材料强度、弯曲角度、弯曲力和转弯半径等因素,并进行综合计算。
五、钢管转弯半径的影响因素钢管转弯半径的大小受多种因素的影响,下面列举几个主要的因素。
1. 钢管材料不同材料的钢管具有不同的力学性能和塑性特性,因此钢管材料是决定转弯半径的重要因素之一。
材料的最小弯曲半径

材料的最小弯曲半径
材料的最小弯曲半径是指材料在弯曲时所能承受的最小弯曲半径。
这种半径取决于材料的性质,如硬度、强度和韧性等。
一般来说,材料的最小弯曲半径越小,其弯曲的性能就越好,但在实际应用中需要根据具体情况进行选择。
例如,在钢材的制造中,钢材的最小弯曲半径较小,可以使钢材弯曲成复杂的形状,但同时也会增加钢材的应力和变形程度,因此需要在设计中考虑这些因素。
在选择材料时,应根据具体的使用要求来确定最小弯曲半径,以确保材料能够承受所需的弯曲应力。
- 1 -。
管材弯曲技术简介
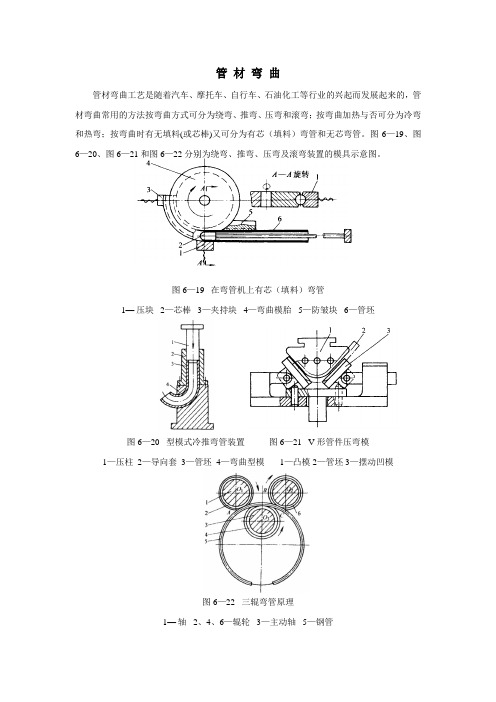
管材弯曲管材弯曲工艺是随着汽车、摩托车、自行车、石油化工等行业的兴起而发展起来的,管材弯曲常用的方法按弯曲方式可分为绕弯、推弯、压弯和滚弯;按弯曲加热与否可分为冷弯和热弯;按弯曲时有无填料(或芯棒)又可分为有芯(填料)弯管和无芯弯管。
图6—19、图6—20、图6—21和图6—22分别为绕弯、推弯、压弯及滚弯装置的模具示意图。
图6—19 在弯管机上有芯(填料)弯管1—压块2—芯棒3—夹持块4—弯曲模胎5—防皱块6—管坯图6—20 型模式冷推弯管装置图6—21 V形管件压弯模1—压柱2—导向套3—管坯4—弯曲型模1—凸模 2—管坯 3—摆动凹模图6—22 三辊弯管原理1—轴2、4、6—辊轮3—主动轴5—钢管一、管材弯曲变形及最小弯曲半径管材弯曲时,变形区的外侧材料受切向拉伸而伸长,内侧材料受到切向压缩而缩短,由于切向应力θσ及应变θε沿着管材断面的分布是连续的,可设想为与板材弯曲相似,外侧的拉伸区过渡到内侧的压缩区,在其交界处存在着中性层,为简化分析和计算,通常认为中性层与管材断面的中心层重合,它在断面中的位置可用曲率半径ρ表示(图6—23)。
管材的弯曲变形程度,取决于相对弯曲半径D R 和相对厚度D t (R 为管材断面中心层曲率半径,D 为管材外径,t 为管材壁厚)的数值大小,D R 和D t 值越小,表示弯曲变形程度越大(即D R 和D t 过小),弯曲中性层的外侧管壁会产生过度变薄,甚至导致破裂;最内侧管壁将增厚,甚至失稳起皱。
同时,随着变形程度的增加,断面畸变(扁化)也愈加严重。
因此,为保证管材的成形质量,必须控制变形程度在许可的范围内。
管材弯曲的允许变形程度,称为弯曲成形极限。
管材的弯曲成形极限不仅取决于材料的力学性能及弯曲方法,而且还应考虑管件的使用要求。
对于一般用途的弯曲件,只要求管材弯曲变形区外侧断面上离中性层最远的位置所产生的最大伸长应变m ax ε不致超过材料塑性所允许的极限值作为定义成形极限的条件。
管材最小弯曲半径

圆援苑缘 圆援苑缘 猿援圆缘 猿援圆缘 猿援缘 猿援缘 猿援苑缘 源 源
源 源 源援缘 远 远 远 远 愿 愿 员园
中国第一重型机械集团公司 圆园园8原12原01 批准
返回总目录
返回分目录
圆园园8原12原31 实施 后退 1
返回总目录
返回分目录
后退
1
中国第一重型机械集团公司标准
管材最小弯曲半径
CFHI SD 圆猿原2008 代替 YZB 223-89
皂皂 凿噪 无 缝 钢 管 远 愿 员园 员圆 员源 员源 员远 员愿 员愿 圆园 圆圆 圆缘 猿圆 猿圆 猿愿 猿愿 源源援缘 源缘 缘苑 缘苑 苑远 愿怨 员园圆 员园愿 员猿猿 员缘怨 员缘怨 员怨源 圆员怨 圆源缘 圆苑猿 猿圆缘 猿苑员 dK 壁厚 员 员 员援缘 员援缘 员援缘 猿 员援缘 员援缘 猿 员援缘 猿 猿 猿 猿援缘 猿 猿援缘 猿 猿援缘 猿援缘 源 源 源 砸 员缘 员缘 圆园 圆缘 猿园 员愿 猿园 源园 圆愿 源园 缘园 缘园 远园 远园 愿园 苑园 员园园 怨园 员员园 员缘园 员愿园 圆圆园 圆苑园 猿源园 源缘园 源圆园 缘园园 缘园园 远园园 苑园园 愿园园 怨园园 dK 不 锈 钢 管 壁厚 圆 圆 圆 圆 圆援缘 圆援缘 圆援缘 圆援缘 猿援缘 源 源 源 源 砸 员愿 圆愿 缘园 缘园 远园 苑园 怨园 员员园 圆圆缘 圆缘园 猿远园 源园园 源缘园 员源 员愿 (圆圆) 圆缘 猿圆 猿愿 源缘 缘苑 (苑远) 愿怨 员园圆 (员园愿) 员猿猿 员猿怨 不锈无缝钢管 远 愿 员园 员圆 员源 员远 员愿 圆园 圆圆 圆缘 猿圆 猿愿 源员 缘苑 苑远 愿怨 员园圆 员园愿 员猿猿 员缘怨 员怨源 圆员怨 dK 壁厚 员 员 员援缘 员援缘 员援缘 员援缘 员援缘 员援缘 员援缘 猿 猿 猿 猿 源 源 源 远 远 远 员园 员圆 砸 员缘 员缘 圆园 圆缘 猿园 猿园 源园 源园 远园 远园 愿园 愿园 员园园 员愿园 圆圆园 圆苑园 猿源园 源圆园 远园园 愿园园 怨园园 员猿援缘 员苑 圆员援圆缘 圆远援苑缘 猿猿援缘 源圆援圆5 源愿 远园 苑缘援缘 愿愿援缘 员员源 员圆缘 员缘园 dK 讕义 讈 變义 讙 讈义 讓 變义 讕 员义 员讕 讈义 员讓 讈义 圆义 圆讓 讈义 猿义 源义 缘义 远义 焊 接 钢 管 壁厚 热 源园 缘园 远缘 愿园 员园园 员猿园 员缘园 员愿园 圆圆缘 圆远缘 猿源园 源园园 缘园园 砸 冷 愿园 员园园 员猿园 员远园 圆园园 圆缘园 圆怨园 猿远园 源缘园 缘猿园 远愿园 造 最小 源园 源缘 缘园 缘缘 苑园 愿缘 员园园 员圆园 员缘园 员苑园 圆猿园
不锈钢管弯曲半径

不锈钢管弯曲半径摘要:1.不锈钢管概述2.不锈钢管弯曲半径的定义3.不锈钢管弯曲半径的计算方法4.不锈钢管弯曲半径的影响因素5.不锈钢管弯曲半径的注意事项正文:一、不锈钢管概述不锈钢管是一种具有较高耐腐蚀性能的钢管,广泛应用于石油、化工、医疗、食品等领域。
其主要成分是铁、铬、镍等元素,其中铬元素是关键的耐腐蚀元素。
根据不同的使用环境和要求,不锈钢管有多种类型和规格。
二、不锈钢管弯曲半径的定义不锈钢管弯曲半径是指在不锈钢管弯曲过程中,管道中心线与弯曲部分外侧的直线距离。
它通常用R 表示,单位为毫米。
弯曲半径的大小直接影响到管道的强度和美观度。
三、不锈钢管弯曲半径的计算方法不锈钢管弯曲半径的计算方法比较简单,一般采用以下公式:R = (D ×θ) / (2 ×β)其中,D 为管道直径,θ为弯曲角度,β为弯曲半径系数。
β值根据不同的管道类型和弯曲角度来选取,通常在0.2~0.5 之间。
四、不锈钢管弯曲半径的影响因素1.管道材料:不同材料的不锈钢管,其弯曲性能和强度不同,因此弯曲半径也会有所差异。
2.管道直径:管道直径越大,需要的弯曲半径也越大,以保证管道在弯曲过程中不破裂或变形。
3.弯曲角度:弯曲角度越大,弯曲半径就越小,但过大的弯曲角度可能导致管道强度降低。
4.弯曲方式:不同的弯曲方式对弯曲半径的要求也不同,如冷弯和热弯的弯曲半径就有所区别。
五、不锈钢管弯曲半径的注意事项1.选择合适的弯曲半径,以保证管道在弯曲过程中不破裂或变形。
2.在弯曲过程中要注意操作规范,避免因操作不当导致的管道损伤。
3.对于大型项目,需要提前进行弯曲半径的计算和试验,以确保工程质量和安全。
最小弯曲半径

最小弯曲半径
在材料不发生破坏的情况下所能弯曲半径的最小值。
最小弯曲半径定义为:软管工作时在不受损伤或不明显降低寿命的最小的弯转半径。
应检测工作中的软管的弯曲半径以保证得当的使用胶管。
软管弯曲半径应该检测弯曲部分的内面,如下所示:
推荐的最小弯曲半径
可在软管资料中或价格表中查找,对没有列出的最小弯曲半径,请查询客户服务手册。
量规上画有所有尺寸的最小弯曲半径。
要决定弯曲半径的大小,请将量规放在软管弯曲部分的内侧,找到最吻合配合曲线,然后读数。
如果内面弯曲半径没有,您可以使用外部弯曲半径,但是您必须将测得的数据减去软管的外径。
最小弯曲半径

2 板材的方向性
冷轧板具有方向性。轧制方向上的塑性 指标δρ(最大伸长率)和ψρ(最大断面收 缩率)大于垂直方向。当弯曲线垂直于 轧制方向时,最小相对弯曲半径rmin/t的 数值最小。
3 板料表面质量与剪切断面质量
板料表面有划伤、裂纹或剪切断面有毛 刺、裂口和冷作硬化等缺陷,弯曲时容 易造成应力集中,使材料过早地破坏。
rmin/t应适当增大,应将 有毛刺的表面朝向弯曲 凸模。
4 板料的宽度和厚度
相对宽度b/t大时,允许采用的相对弯曲半径 应大一些
图示是b/t对rmin/t的影响,b/t较小时影响明显, b/t>10时其影响不大。
5 板料的厚度
当板厚较小时,切向应变梯度大,从外表面到 变形中性层其数值很快由最大值衰减为零。
当材料B>3t时,可不计材料的变薄,即η=1, 最小相对弯曲半径为:
rm in 1 1 1
t
2 2 2
或 rmin 1 1 t 2
δρ——最大伸长率 ψρ——最大断面收缩率值。 δρ和ψρ值越大,则最小弯曲半径rmin/t越小。
1 零件的弯曲角α
零件的弯曲角α较小时,接近弯曲圆角的直边 部分也参与变形,使弯曲角处的变形得到一定 程度的减轻,当α<70°时,弯曲角的影响比较 显著,α>70°时,其影响不大。
最小弯曲半径
最小相对弯曲半径rmin/t
弯曲时在切向拉应力作用下,毛坯外表 面金属变形的伸长率为:
R (r t)
η—材料变薄系数
代入式
(r
1 2
t)
整理,得
2 (1 )
r 21 1 t
断面收缩率ψ和伸长率δ有如下关系
1
1
故又有
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第35卷第2期Vol 135 No 12FORGING &S TAMPING TECHNOLOGY2010年4月Apr.2010薄壁钢管无芯弯曲最小相对弯曲半径的确定杨士铁1,肖曙红1,陈署泉1,廖健棠2,林 勇2(11广东工业大学机电工程学院,广东广州510006;21天健钢家具制品厂有限公司,广东江门529159)摘要:分析了钢管弯曲应力和应变,探索了最小相对弯曲半径与管的弯曲切向主应变的关系,并确定了最小相对弯曲半径的计算方法,进一步推导出分别按照材料硬化指数、延伸率和变形几何条件计算的最小相对弯曲半径公式,再通过薄壁钢管无芯弯曲试验对其进行修正。
用此方法可在少量的钢管弯曲试验的基础上,精确地确定钢管弯曲的实际最小相对弯曲半径,具有较高的参考价值。
关键词:薄壁钢管;最小相对弯曲半径;变形几何条件;弯曲试验DOI :1013969/j 1issn 1100023940120101021033中图分类号:TG 38613 文献标识码:A 文章编号:100023940(2010)022*******Establishment of minimum relative bending radius of thin 2w alled tube no 2mandrel bendingYANG Shi 2tie 1,XIAO Shu 2hong 1,CHEN Shu 2qu an 1,L IAO Jian 2tang 2,L IN Yong 2(11Faculty of Mechanical &Electronic Engineering ,Guangdong University of Technology ,Guangzhou 510006,China ;21Tian Jian Steel Furniture Manufacturing Co.,Ltd.,Jiangmen 529159,China )Abstract :The steel tube bending stress and strain were briefly analyzed ,the relationship between the minimum relative bending radius and the tube bending tangential strains was explored ,the calculation method of the minimum relative bending radius was determined ,and then the calculated minimum relative bending radius formulas according to the ma 2terial hardening exponent ,elongation and deformation of the geometric condition were deduced respectively.It was modified f urther through the steel tube bending tests.This method can precisely determine the actual minimum relative bending radius based on the small amount of steel tube bending tests ,which has a strong reference value.K eyw ords :thin 2walled steel tube ;minimum relative bending radius ;deformation of geometric condition ;bending test收稿日期:2009209223;修订日期:2009211223作者简介:杨士铁(1982-),男,硕士研究生电子信箱:yangshitie @1261com 随着人们生活水平的不断提高和环保意识的日益增强,钢制家具越来越受到广泛欢迎,为节省材料,钢制家具普遍大量采用薄壁钢管,家具的外观和耐用性对钢管成形质量的要求越来越高,其特殊的形状结构(薄壁、中空)使得弯曲变形机理比板料成形复杂,给弯曲变形解析和弯曲成形极限的研究带来了很大困难。
目前,在冲压理论中,对于最小相对弯曲半径的研究大多数仅限于板材成形领域,而在管材弯曲成形研究领域理论中,对于最小相对弯曲半径的研究还很少,且多数为涉及到最小相对弯曲半径的管材塑性变形定性的基础理论研究或属研究展望综述性质或仅涉及到壁厚变形因素对最小相对弯曲半径的影响或仅为名义应力下且简化成平面应变时的最小相对弯曲半径,与实际的真实应力和实际的三维立体应变下的真实最小相对弯曲半径尚有一定差距。
因此,虽然现在管材弯曲成形加工较为普遍,但是在生产现场中最小相对弯曲半径的确定仍然普遍采用经验性手工操作、将样件试弯然后不断修正或者直接套用板料成形中相关理论方法,为达到管材弯曲精确的塑性成形和高效率制造的要求,本文在薄壁钢管拉伸试验和弯曲成形试验的基础上对管材弯曲成形的最小相对弯曲半径展开理论和试验研究,以期对管材弯曲成形提供合适的工艺参数[124]。
1 薄壁钢管弯曲的应力应变分析弯曲过程中,管的弯曲切向主应变εθ、径向主应变εt 和横截面圆周方向主应变εD 可表示为[5]:εθ=ln 1+r ρ;εt =ln t t 0;εD =ln r r 0(1)式中:t 0,t 为弯曲前、后的管壁厚;r 0,r 为弯曲前、后内外侧管壁上任一点的径向坐标值;ρ为上述中性层的曲率半径。
钢管弯曲的塑性加工过程满足弹塑性变形的全量理论,即管的弯曲切向主应力σθ、径向主应力σt 和横截面圆周方向主应力σD 与管的弯曲切向主应变εθ、径向主应变εt 和横截面圆周方向主应变εD 之间的关系满足[627]:σθ-σt εθ-εt =σt -σD εt -εD =σθ-σD εθ-εD=2 σ3 ε(2)εθ= ε σσθ-12(σt +σD );εt = εσσt -12(σθ+σD );εD =εσσD -12(σθ+σt )(3)2 薄壁钢管无芯弯曲最小相对弯曲半径的规律分析211 最小相对弯曲半径[ρ/d ]min 与管的弯曲切向主应变εθ的关系 薄壁钢管在无芯弯曲过程中,其外侧表面切向拉伸变形程度最大,当拉伸变形程度超过材料的极限变形程度时就会被拉裂,上述管材弯曲的极限变形程度可用最小相对弯曲半径来描述。
薄壁钢管由于其异于实心管材的中空、壁薄形状结构以及在无芯弯曲时无芯棒的支撑作用,弯曲过程中受到弯曲内、外侧管壁上切向应力在法向的合力作用,使弯曲变形区的圆管横断截面在法向受压而产生畸变,即法向半径减少、横向直径增大,而成为近似椭圆形[8]。
设管材初始半径为d ,弯曲后外侧椭圆的短轴变化率为Φd ,其短轴长度为d a ,短轴半径为r d 。
为简化分析和计算,认为在弯曲过程中应力中性层与应变中性层重合且通过断面中心[8],并用ρ表示弯曲后断面中心层的曲率半径。
弯曲后椭圆短轴处的切向应变为:εθ=ln 1+r d ρ=ln 1+(1-Φd )d2ρ(4) 由式(4)可得,管材的相对弯曲半径为:ρd=1-Φd2(e εθ-1)(5) 设管材的许用短轴变化率为[Φd ],上式中当εθ取最大值εθmax 时,即可得到最小相对弯曲半径:ρd min =1-[Φd ]2(e εθmax -1](6) 由式(6)可知,在管材的许用短轴变化率[Φd ]一定的情况下,确定最小相对弯曲半径的关键是确定εθ的最大值εθmax 。
下面分别根据材料的硬化指数、延伸率和变形几何条件来确定εθmax ,从而最终确立最小相对弯曲半径[ρ/d ]min 。
212 受硬化指数约束决定的最小相对弯曲半径为了简化分析,将弯曲过程近似为简单加载,即认为应力主轴与应变增量主轴重合,真实应力2应变服从幂指数关系[9]。
一般当实际的 σ2 ε曲线与理论 σ=B εn 曲线吻合度较好时,硬化指数n 能够比较准确的描述材料的拉伸失稳性能[10]。
一般地,钢材弹塑性大变形基本上符合 σ=B εn 曲线。
对于符合幂乘硬化规律的材料,n 值高低直接反映了材料发生颈缩前依靠硬化使材料均匀变形的能力大小。
在拉伸试验曲线σ=f (ε)中,σ是用原截面面积A 0来计算的,即σ=P/A 0,称为名义应力或条件应力,而不是真实应力。
真实应力σT 应为σT =P/A ,真实应力应变曲线应该表示为σT =f (ε),塑性变形中等效应力为:σ=12(σθ-σt )2-(σt -σD )2-(σθ-σD )2 (7) 式(7)可以把任意复杂应力状态等效为单向应力状态,在拉伸试验中σt =σD =0,由式(7)可知 σ=σθ。
为下文叙述方便,令: σ=σθ=σT 。
塑性变形中等效应变为: ε=23(εθ-εt )2+(εt -εD )2+(εθ-εD )2 (8) 在单向拉伸试验中,εθ=ε,εt =εD =-12ε,由式(8)可知: ε=εθ=ε。
实际上,根据式(3)和式(7)推出的结果同样可以得出:这样材料的真实应力2应变关系可以表示为:σT =B εn(9) 根据材料拉伸试验中体积不变的条件[11],可求出A 和A 0的关系为:l 0A 0=lA 则A 0=All 0=A (1+ε)(10)σT =P A=P A 0(1+ε)=σ(1+ε)(11) 由(9)和式(11)可得:σ=Bεn 1+ε(12) 由式(9)和式(11)比较可知,材料在拉伸试验中σT 和σ是不能等同的,但这种现象在材料达到屈服之前影响极微[11]。
根据本文试验材料Q195的管材拉伸试验结果,Q195的屈服点σS ≤220M Pa ,其弹性模量E =212GPa ,达到屈服时其应变ε≤0100104,在材料从变形开始直至达到屈服点的过程中有σT ≈σ,即可认为对两者等同;但当材料进入塑性变形阶段,随着拉伸过程的持续进行,材料的应变量逐渐增大。
在本试验中(1+ε)由小变大的范围是1100104≤(1+ε)≤1126236,真实应力σT与名义应力σ相差的倍数值(1+ε)越来越大,即331第2期杨士铁等:薄壁钢管无芯弯曲最小相对弯曲半径的确定 真实应力σT与名义应力σ的差别将越来越明显,故在塑性变形阶段σT与σ应该分别进行分析计算。
材料在发生拉伸颈缩失稳时[11]:dσdε=0(13)代入式(12)即:ε=n1-n(14) 一般管材弯曲时,管壁厚度方向和圆周方向产生的应力σT和σD都很小,在理论分析时可忽略不计,令σt=0,σD=0,此时由式(7)可知 σ=σθ。
