2016届全国通用高考数学理科二轮专题复习习题专题一函数与导数、不等式第5讲
(衡水万卷)2016届高考数学二轮复习 三十一 函数与导数(一)作业 理
衡水万卷作业(三十一) 函数与导数(一)考试时间:45分钟姓名:__________班级:__________考号:__________一、选择题(本大题共12小题,每小题4分,共48分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.下列函数中,在其定义域内既是偶函数又在(,0)-∞上单调递增的函数是( )A.2()f x x =B. ()2xf x = C. 21()log f x x= D. ()sin fx x = 2.若函数()()3,5,2,5x x f x f x x -≥⎧⎪=⎨+<⎪⎩则()2f 的值为 A.2 B.3 C.4 D.5 3.(2015安徽高考真题)函数()()2ax bf x x c +=+的图象如图所示,则下列结论成立的是( )(A )0a >,0b >,0c < (B )0a <,0b >,0c > (C )0a <,0b >,0c < (D )0a <,0b <,0c < 4.若关于x 的方程各个实根所对应的点均在直线y =x 的同侧,则实数m 的取值范围是( )A 、(-1,7)B 、(-∞,-7)U (-1,+∞)C 、(-7,1)D 、(-∞,1)U (7,+∞) 5.已知0.12a =,1n0.1,sin1,b c ==则A.a>b>cB.a>c>bC.c>a>bD.b>a>c 6.若函数b a y x +=的部分图象如图1所示,则( )A.01,10<<-<<b a B 。
10,10<<<<b a C.01,1<<->b a D 。
10,1<<>b a a>1, 0<b<17.()0,∞-∈x 时,)(x f +x '()f x <0成立 ,若,则c b a ,, 的大小关系是( ) D. c a b >>8.已知函数()f x 是定义在R 上的奇函数,在(0,2]上是增函数,且(4)()f x f x -=-,给出下列结论:①若1204x x <<<且124x x +=,则12()()0f x f x +>;②若1204x x <<<且125x x +=,则12()()f x f x >;③若方程()f x m =在[8,8]-内恰有四个不同的实根1234,,,x x x x ,则12348x x x x +++=-或8;④函数()f x 在[8,8]-内至少有5个零点,至多有13个零点其中结论正确的有 ( )A .1个B .2个C .3个D .4个9.若关于x 的方程240+-=x ax 在区间[2,4]上有实数根,则实数a 的取值范围是( )(A )(3,)-+∞ (B )[3,0]- (C )(0,)+∞ (D)[0,3]10.(2015安徽高考真题)下列函数中,既是偶函数又存在零点的是(A )y cos x = (B )y sin x = (C )y n l x = (D )21y x =+ 11.曲线y 2=|x|+1的部分图象是( )A .B .C .D .12.定义在R 上的偶函数满足()()3311,0222f x f x f f ⎛⎫⎛⎫+=--==- ⎪ ⎪⎝⎭⎝⎭且,则()()()()1232014f f f f +++⋅⋅⋅+的值为( )A.2B.1C.0D.2-图1二、填空题(本大题共6小题,每小题4分,共24分) 13.若α,β是一二次方程2x 2+x+3=0的两根,则= .14.函数)432(31sin 232sin3)(2ππ≤≤-=x x x x f 的最小值是 . 15.若f (x )为R 上的奇函数,当x <0时,f (x )=log 2(2﹣x ),则f (0)+f (2)= . 16.函数()2sin cos f x x x x x=++,则不等式()()ln 1f x f <的解集为___________.17.已知0,0x y >>,若m m yx x y 2822+>+恒成立,则实数m 的取值范围是 . 18.函数21(0)()2ln x (0)x x f x x x ⎧-≤=⎨-+>⎩的零点个数为_____________.三、解答题(本大题共2小题,共28分)19.某大型企业一天中不同时刻的用电量y (单位:万千瓦时)关于时间t (024t ≤≤,单位:小时)的函数()y f t =近似地满足()sin()(0,0,0)f t A t B A ωϕωϕπ=++>><<,下图是该企业一天中在0点至12点时间段用电量y 与时间t 的大致图象.(Ⅰ)根据图象,求A ,ω,ϕ,B 的值;(Ⅱ)若某日的供电量()g t (万千瓦时)与时间t (小时)近似满足函数关系式205.1)(+-=t t g (012t ≤≤).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1). 参考数据:20.某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路的山区边界的直线型公路,记两条相互垂直的公路为12l l ,,山区边界曲线为C ,计划修建的公路为l ,如图所示,M ,N 为C 的两个端点,测得点M 到12l l ,的距离分别为5千米和40千米,点N 到12l l ,的距离分别为20千米和2.5千米,以12l l ,所在的直线分别为x ,y 轴,建立平面直角坐标系xOy ,假设曲线C 符合函数2ay x b=+(其中a ,b 为常数)模型.(1)求a ,b 的值;(2)设公路l 与曲线C 相切于P 点,P 的横坐标为t .①请写出公路l 长度的函数解析式()f t ,并写出其定义域; ②当t 为何值时,公路l 的长度最短?求出最短长度.衡水万卷作业(三十一)答案解析一、选择题1.【答案】C 解析: 2()f x x =和()2xf x =是偶函数,在(,0)-∞上单调递减,()sin f x x =为奇函数,故选C. 【思路点拨】根据函数的性质之奇偶和增减的定义可求.2.【答案】B 解析:由题意知:(2)(4)(6)3f f f ===,故选B.【思路点拨】分段函数求值时,把自变量代入到对应的解析式即可。
2016届高考数学(浙江专用理科)二轮专题精练专题一函数不等式1-2Word版含解析

第2讲 函数与方程及函数的应用(建议用时:60分钟)一、选择题1.“a >3”是“函数f (x )=ax +3在(-1,2)上存在零点”的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析 由于“函数f (x )=ax +3在(-1,2)上存在零点”⇔f (-1)f (2)<0⇔(-a +3)(2a +3)<0⇔a <-32或a >3,则“a >3”是“函数f (x )=ax +3在(-1,2)上存在零点”的充分不必要条件. 答案 A2.函数f (x )=2ln x 的图象与函数g (x )=x 2-4x +5的图象的交点个数为( ).A .3B .2C .1D .0解析 由已知g (x )=(x -2)2+1,所以其顶点为(2,1),又f (2)=2ln 2∈(1,2),可知点(2,1)位于函数f (x )=2ln x 图象的下方,故函数f (x )=2ln x 的图象与函数g (x )=x 2-4x +5的图象有2个交点. 答案 B3.已知函数f (x )=⎩⎨⎧2x-1,x ≤1,1+log 2x ,x >1,则函数f (x )的零点为( ).A.12,0 B .-2,0 C.12 D .0解析 当x ≤1时,由f (x )=2x -1=0,解得x =0;当x >1时,由f (x )=1+ log 2 x =0,解得x =12,又因为x >1,所以此时方程无解.综上,函数f (x )的零点只有0,故选D. 答案 D4.(2015·北京卷)汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( ).A .消耗1升汽油,乙车最多可行驶5千米B .以相同速度行驶相同路程,三辆车中,甲车消耗汽油量最多C .甲车以80千米/时的速度行驶1小时,消耗10升汽油D .某城市机动车最高限速80千米/时.相同条件下,在该市用丙车比用乙车更省油解析 汽车每消耗1升汽油行驶的里程为“燃油效率”,由此理解A 显然不对;B 应是甲车耗油最少;C 甲车以80千米/时的速度行驶10 km ,消耗1升汽油,故D 正确. 答案 D5.设函数f (x )=13x -ln x (x >0),则y =f (x )( ).A .在区间⎣⎢⎡⎦⎥⎤1e ,1,(1,e)内均有零点B .在区间⎣⎢⎡⎦⎥⎤1e ,1,(1,e)内均无零点C .在区间⎣⎢⎡⎦⎥⎤1e ,1内有零点,在区间(1,e)内无零点D .在区间⎣⎢⎡⎦⎥⎤1e ,1内无零点,在区间(1,e)内有零点解析 法一 因为f ⎝ ⎛⎭⎪⎫1e =13·1e -ln 1e =13e +1>0,f (1)=13-ln 1=13>0,f (e)=e 3-ln e=e 3-1<0,∴f ⎝ ⎛⎭⎪⎫1e ·f (1)>0,f (1)·f (e)<0,故y =f (x )在区间⎣⎢⎡⎦⎥⎤1e ,1内无零点(f (x )在⎝ ⎛⎭⎪⎫1e ,1内根据其导函数判断可知单调递减),在区间(1,e)内有零点. 法二 在同一坐标系中分别画出y =13x 与y =ln x 的图象,如图所示.由图象知零点存在区间(1,e)内. 答案 D6.若a <b <c ,则函数f (x )=(x -a )(x -b )+(x -b )(x -c )+(x -c )(x -a )的两个零点分别位于区间( ).A .(a ,b )和(b ,c )内B .(-∞,a )和(a ,b )内C .(b ,c )和(c ,+∞)内D .(-∞,a )和(c ,+∞)内解析 由于a <b <c ,所以f (a )=(a -b )(a -c )>0,f (b )=(b -c )(b -a )<0,f (c )=(c -a )(c -b )>0.因此有f (a )·f (b )<0,f (b )·f (c )<0,又因f (x )是关于x 的二次函数,函数的图象是连续不断的曲线,因此函数f (x )的两零点分别位于区间(a ,b )和(b ,c )内,故选A. 答案 A7.若函数y =f (x )(x ∈R )满足f (x +1)=-f (x ),且x ∈[-1,1]时f (x )=1-x 2.函数g (x )=⎩⎪⎨⎪⎧lg x (x >0),-1x(x <0),则函数h (x )=f (x )-g (x )在区间[-5,4]内的零点的个数为( ).A .7B .8C .9D .10解析 由f (x +1)=-f (x ),可得f (x +2)=-f (x +1)=f (x ),所以函数f (x )的周期为2,求h (x )=f (x )-g (x )在区间[-5,4]内的零点,即求f (x )=g (x )在区间[-5,4]上图象交点的个数.画出函数f (x )与g (x )的图象,如图,由图可知两图象在 [-5,4]之间有7个交点,所以所求函数有7个零点,选A.答案 A 二、填空题8.一块形状为直角三角形的铁皮,两直角边长分别为40 cm 、60 cm ,现要将它剪成一个矩形,并以此三角形的直角为矩形的一个角,则矩形的最大面积是________cm 2.解析 设直角边为40 cm 和60 cm 上的矩形边长分别为x cm 、y cm ,则40-x 40=y 60,解得y =60-32x .矩形的面积S =xy =x⎝ ⎛⎭⎪⎫60-32x =-32(x -20)2 +600,当x =20时矩形的面积最大,此时S =600. 答案 6009.已知[x ]表示不超过实数x 的最大整数,如[1.8]=1,[-1.2]=-2.x 0是函数f (x )=ln x -2x 的零点,则[x 0]=________.解析 函数f (x )的定义域为(0,+∞),且易判断函数f (x )在(0,+∞)上单调递增.由f (2)=ln 2-1<0,f (e)=ln e -2e >0,知x 0∈(2,e),∴[x 0]=2. 答案 210.(2015·四川卷)某食品的保鲜时间y (单位:小时)与储藏温度x (单位:℃)满足函数关系y =e kx +b (e =2.718…为自然对数的底数,k ,b 为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是________小时.解析 由题意⎩⎨⎧e b=192,e22k +b =48,∴e 22k =48192=14,∴e 11k =12,∴x =33时,y =e 33k +b =(e 11k )3·e b =⎝ ⎛⎭⎪⎫123·e b =18×192=24.答案 2411.已知函数f (x )=⎩⎨⎧-x 2+2x ,x ≤0,ln (x +1),x >0.若|f (x )|≥ax ,则a 的取值范围是________.解析 当x ≤0时,f (x )=-x 2+2x =-(x -1)2+1≤0,所以|f (x )|≥ax ,化简为x 2-2x ≥ax ,即x 2≥(a +2)x ,因为x ≤0,所以a +2≥x 恒成立,所以a ≥-2;当x >0时,f (x )=ln(x +1)>0,所以|f (x )|≥ax 化简为ln(x +1)>ax 恒成立,由函数图象可知a ≤0,综上,当-2≤a ≤0时,不等式|f (x )|≥ax 恒成立,故填 [-2,0]. 答案 [-2,0]12.(2015·北京卷)设函数f (x )=⎩⎨⎧2x-a ,x <1,4(x -a )(x -2a ),x ≥1.(1)若a =1,则f (x )的最小值为________;(2)若f (x )恰有2个零点,则实数a 的取值范围是________. 解析 (1)当a =1时,f (x )=⎩⎨⎧2x-1,x <1,4(x -1)(x -2),x ≥1.当x <1时,2x -1>-1∈(-1,1), 当x ≥1时,f (x )=4(x 2-3x +2)= 4⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫x -322-14≥-1, ∴f (x )最小值为-1.(2)由于f (x )恰有2个零点,分两种情况讨论: 当f (x )=2x -a ,x <1没有零点时,a ≥2或a ≤0.当a ≥2时,f (x )=4(x -a )(x -2a ),x ≥1时,有2个零点; 当a ≤0时,f (x )=4(x -a )(x -2a ),x ≥1时无零点. 因此a ≥2满足题意.当f (x )=2x -a ,x <1有一个零点时,0<a <2. f (x )=4(x -a )(x -2a ),x ≥1有一个零点, 此时a <1,2a ≥1, 因此12≤a <1.综上知实数a 的取值范围是⎩⎨⎧⎭⎬⎫a 12≤a <1或a ≥2.答案 (1)-1 (2)⎣⎢⎡⎭⎪⎫12,1∪[2,+∞)三、解答题13.(2015·湖州模拟)设函数f (x )=ax 2+bx +b -1(a ≠0). (1)当a =1,b =-2时,求函数f (x )的零点;(2)若对任意b ∈R ,函数f (x )恒有两个不同零点,求实数a 的取值范围. 解 (1)当a =1,b =-2时,f (x )=x 2-2x -3, 令f (x )=0,得x =3或x =-1. ∴函数f (x )的零点为3和-1.(2)依题意,f (x )=ax 2+bx +b -1=0有两个不同实根.∴b 2-4a (b -1)>0恒成立,即对于任意b ∈R ,b 2-4ab +4a >0恒成立, 所以有(-4a )2-4(4a )<0⇒a 2-a <0, 所以0<a <1.因此实数a 的取值范围是(0,1).14.(2015·浙江卷)设函数f (x )=x 2+ax +b (a ,b ∈R ).(1)当b =a 24+1时,求函数f (x )在[-1,1]上的最小值g (a )的表达式; (2)已知函数f (x )在[-1,1]上存在零点,0≤b -2a ≤1,求b 的取值范围. 解 (1)当b =a 24+1时,f (x )=⎝ ⎛⎭⎪⎫x +a 22+1,故对称轴为直线x =-a2.当a ≤-2时,g (a )=f (1)=a 24+a +2. 当-2<a ≤2时,g (a )=f ⎝ ⎛⎭⎪⎫-a 2=1.当a >2时,g (a )=f (-1)=a 24-a +2. 综上,g (a )=⎩⎪⎨⎪⎧a 24+a +2,a ≤-2,1,-2<a ≤2,a 24-a +2,a >2.(2)设s ,t 为方程f (x )=0的解,且-1≤t ≤1, 则⎩⎨⎧s +t =-a ,st =b , 由于0≤b -2a ≤1, 因此-2t t +2≤s ≤1-2tt +2(-1≤t ≤1). 当0≤t ≤1时,-2t 2t +2≤st ≤t -2t 2t +2,由于-23≤-2t 2t +2≤0和-13≤t -2t 2t +2≤9-45,所以-32≤b ≤9-4 5.当-1≤t <0时,t -2t 2t +2≤st ≤-2t 2t +2,由于-2≤-2t 2t +2<0和-3≤t -2t 2t +2<0,所以-3≤b <0.故b 的取值范围是[-3,9-45].15.某工厂某种产品的年固定成本为250万元,每生产x 千件,需另投入成本为C (x ),当年产量不足80千件时,C (x )=13x 2+10x (万元);当年产量不小于80千件时,C (x )=51x +10 000x -1 450(万元).每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.(1)写出年利润L (x )(万元)关于年产量x (千件)的函数解析式; (2)年产量为多少千件时,该厂在这种商品的生产中所获利润最大?解 (1)因为每件商品售价为0.05万元,则x 千件商品销售额为0.05×1 000x 万元,依题意得,当0<x <80时,L (x )=(0.05×1 000x )-13x 2-10x -250=-13x 2+40x -250.当x ≥80时,L (x )=(0.05×1 000x )-51x -10 000x +1 450-250=1 200-⎝ ⎛⎭⎪⎫x +10 000x . 所以L (x )=⎩⎪⎨⎪⎧-13x 2+40x -250 (0<x <80),1 200-⎝ ⎛⎭⎪⎫x +10 000x (x ≥80).(2)当0<x <80时,L (x )=-13(x -60)2+950,此时,当x =60时,L (x )取得最大值L (60)=950(万元). 当x ≥80时,L (x )=1 200-⎝ ⎛⎭⎪⎫x +10 000x ≤1 200-2x ·10 000x =1 200-200=1000.此时,当x=10 000x,即x=100时,L(x)取得最大值1 000万元.因为950<1 000,所以,当年产量为100千件时,该厂在这种商品的生产中所获利润最大,最大利润为1 000万元.。
【热点重点难点专题透析】(新课标)2016届高考数学二轮复习 细致讲解专题1 不等式、函数与导数课件 理
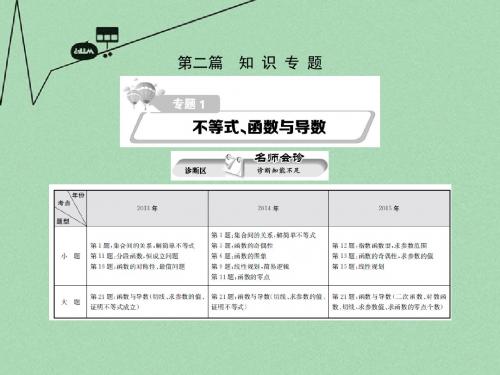
������-������ ≤ 0,
3.设变量 x、y 满足约束条件 ������ + 3������-4 ≤ 0,则 z=y-2x 的最大值
为( ).
������ + 2 ≥ 0,
A.1 B.2 C.4 D.6
������-������ ≤ 0,
【解析】作出表示约束条件 ������ + 3������-4 ≤ 0,的可行域,得 z
数若在 x=0 处有定义,则必有 f(0)=0”的灵活应用.
2.应用不等式性质时,一定要弄清楚性质成立的前提条件.
判断数式的不等关系,既可利用不等式性质,也可灵活运用函数
的单调性.利用基本不等式求最值时,要善于运用“拆、拼、配、
凑”的技巧,同时满足基本不等式中“正、定、等”的条件,多次 使用基本不等式时,要确保取得等号的条件的一致性,否则容易
1+1
1+������
-1 0
=a0<1������+(ee-)1=1e+-e2-1<1,
即 a0∈(0,1).
当 a=a0 时,有 f'(x0)=0,f(x0)=φ(x0)=0,
由(1)知,f'(x)在区间(1,+∞)上单调递增,
故当 x∈(1,x0)时,f'(x)<0,从而 f(x)>f(x0)=0;
在处理分段函数问题时,不仅要研究每段函数的性质,而且要对
整个函数性质进行研究.
7.函数导数的应用,一是利用导数的几何意义求切线方程,
此时要明确题给的已知点是“切点”还是“非切点”,以避免错 解;二是应用导数研究函数的单调性、极值与最值,此时要重视函 数的定义域,熟练掌握可导函数的单调性、极值与最值的判断方 法,利用数形结合思想;三是运用导数与函数的单调性建立不等 式求参数范围,此时不等号中切勿遗漏含等号情况;四是利用导 数研究函数的零点、求参数范围、解(证)不等式、求函数最值等 较难的综合问题,有时需构造函数,通过两次求导来解决问题,当
创新设计(全国通用)高考数学二轮复习 专题一 函数与导数、不等式 第2讲 不等式问题训练 文

专题一 函数与导数、不等式 第2讲 不等式问题训练 文一、选择题1.(2016·全国Ⅲ卷)已知a =243,b =323,c =2513,则( ) A.b <a <c B.a <b <c C.b <c <aD.c <a <b解析 a =243=316,b =323=39,c =2513=325,所以b <a <c . 答案 A2.(2016·浙江卷)已知a ,b >0且a ≠1,b ≠1,若log a b >1,则( ) A.(a -1)(b -1)<0 B.(a -1)(a -b )>0 C.(b -1)(b -a )<0D.(b -1)(b -a )>0解析 由a ,b >0且a ≠1,b ≠1,及log a b >1=log a a 可得: 当a >1时,b >a >1,当0<a <1时,0<b <a <1, 代入验证只有D 满足题意. 答案 D3.(2016·太原模拟)若点A (m ,n )在第一象限,且在直线x 3+y4=1上,则mn 的最大值是( ) A.3B.4C.7D.12解析 因为点A (m ,n )在第一象限,且在直线x 3+y 4=1上,所以m ,n ∈R +,且m 3+n4=1,所以m 3·n4≤(m 3+n42)2⎝ ⎛⎭⎪⎫当且仅当m 3=n 4=12,即m =32,n =2时,取“=”,所以m 3·n 4≤⎝ ⎛⎭⎪⎫122=14,即mn ≤3,所以mn 的最大值为3.答案 A4.已知当x <0时,2x 2-mx +1>0恒成立,则m 的取值范围为( ) A.[22,+∞)B.(-∞,22]C.(-22,+∞)D.(-∞,-22)解析 由2x 2-mx +1>0,得mx <2x 2+1, 因为x <0,所以m >2x 2+1x =2x +1x.而2x +1x =-⎣⎢⎡⎦⎥⎤(-2x )+1(-x )≤-2(-2x )×1(-x )=-2 2.当且仅当-2x =-1x ,即x =-22时取等号,所以m >-2 2. 答案 C5.(2016·唐山模拟)已知函数f (x )=⎩⎪⎨⎪⎧x 2+2x ,x ≥0,x 2-2x ,x <0,若f (-a )+f (a )≤2f (1),则实数a的取值范围是( ) A.[0,1] B.[-1,0] C.[-1,1]D.[-1,0]解析 f (-a )+f (a )≤2f (1)⇔⎩⎪⎨⎪⎧a ≥0,(-a )2-2×(-a )+a 2+2a ≤2×3或 ⎩⎪⎨⎪⎧a <0,(-a )2+2×(-a )+a 2-2a ≤2×3 即⎩⎪⎨⎪⎧a ≥0,a 2+2a -3≤0或⎩⎪⎨⎪⎧a <0,a 2-2a -3≤0, 解得0≤a ≤1,或-1≤a <0.故-1≤a ≤1. 答案 C 二、填空题6.设目标函数z =x +y ,其中实数x ,y 满足⎩⎪⎨⎪⎧x +2y ≥0,x -y ≤0,0≤y ≤k .若z 的最大值为12,则z 的最小值为________.解析 作出不等式组所表示的可行域如图所示,平移直线x +y=0,显然当直线过点A (k ,k )时,目标函数z =x +y 取得最大值,且最大值为k +k =12,则k =6,直线过点B 时目标函数z =x +y 取得最小值,点B 为直线x +2y =0与y =6的交点,即B (-12,6),所以z min =-12+6=-6. 答案 -67.(2016·合肥二模)当a >0且a ≠1时,函数f (x )=log a (x -1)+1的图象恒过点A ,若点A 在直线mx -y +n =0上,则4m +2n的最小值为________.解析 函数f (x )的图象恒过点A (2,1),∴2m -1+n =0,即2m +n =1, ∴4m+2n≥24m·2n=222m +n=22,当且仅当2m =n =12时等号成立.答案 2 28.(2016·全国Ⅰ卷)某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料.生产一件产品A 需要甲材料1.5 kg ,乙材料1 kg ,用5个工时;生产一件产品B 需要甲材料0.5 kg ,乙材料0.3 kg ,用3个工时,生产一件产品A 的利润为2 100元,生产一件产品B 的利润为900元.该企业现有甲材料150 kg ,乙材料90 kg ,则在不超过600个工时的条件下,生产产品A 、产品B 的利润之和的最大值为________元. 解析 设生产A 产品x 件,B 产品y 件,根据所耗费的材料要求、工时要求等其他限制条件,得线性约束条件为⎩⎪⎨⎪⎧1.5x +0.5y ≤150,x +0.3y ≤90,5x +3y ≤600,x ≥0,x ∈N *,y ≥0,y ∈N*目标函数z =2 100x +900y .作出可行域为图中阴影部分(包括边界)内的参数点,顶点为(60,100),(0,200),(0,0),(90,0),在(60,100)处取得最大值,z max =2 100×60+900×100=216 000(元). 答案 216 000 三、解答题9.已知f (t )=log 2t ,t ∈[2,8],对于f (t )值域内的所有实数m ,不等式x 2+mx +4>2m +4x 恒成立,求x 的取值范围.解 易知f (t )∈⎣⎢⎡⎦⎥⎤12,3,由题意,令g (m )=(x -2)m +x 2-4x +4=(x -2)m +(x -2)2>0对∀m ∈⎣⎢⎡⎦⎥⎤12,3恒成立.所以只需⎩⎪⎨⎪⎧g ⎝ ⎛⎭⎪⎫12>0,g (3)>0即可,即⎩⎪⎨⎪⎧12(x -2)+(x -2)2>0,3(x -2)+(x -2)2>0⇒x >2或x <-1. 故x 的取值范围是(-∞,-1)∪(2,+∞). 10.已知函数f (x )=2xx 2+6. (1)若f (x )>k 的解集为{x |x <-3,或x >-2},求k 的值; (2)对任意x >0,f (x )≤t 恒成立,求t 的取值范围. 解 (1)f (x )>k ⇔kx 2-2x +6k <0.由已知{x |x <-3,或x >-2}是其解集,得kx 2-2x +6k =0的两根是-3,-2. 由根与系数的关系可知(-2)+(-3)=2k ,即k =-25.(2)因为x >0,f (x )=2x x 2+6=2x +6x≤226=66,当且仅当x =6时取等号.由已知f (x )≤t 对任意x >0恒成立,故t ≥66,即t 的取值范围是⎣⎢⎡⎭⎪⎫66,+∞. 11.(1)解关于x 的不等式x 2-2mx +m +1>0; (2)解关于x 的不等式ax 2-(2a +1)x +2<0.解 (1)原不等式对应方程的判别式Δ=(-2m )2-4(m +1)=4(m 2-m -1).当m 2-m -1>0,即m >1+52或m <1-52时,由于方程x 2-2mx +m +1=0的两根是m ±m 2-m -1,所以原不等式的解集是{x |x <m -m 2-m -1,或x >m +m 2-m -1};当Δ=0,即m =1±52时,不等式的解集为{x |x ∈R ,且x ≠m };当Δ<0,即1-52<m <1+52时,不等式的解集为R .综上,当m >1+52或m <1-52时,不等式的解集为{x |x <m -m 2-m -1,或x >m +m 2-m -1};当m =1±52时,不等式的解集为{x |x ∈R ,且x ≠m };当1-52<m <1+52时,不等式的解集为R .(2)原不等式可化为(ax -1)(x -2)<0.①当a >0时,原不等式可以化为a (x -2)⎝⎛⎭⎪⎫x -1a <0,根据不等式的性质,这个不等式等价于(x -2)·⎝ ⎛⎭⎪⎫x -1a <0.因为方程(x -2)⎝ ⎛⎭⎪⎫x -1a =0的两个根分别是2,1a,所以当0<a<12时,2<1a ,则原不等式的解集是⎩⎨⎧⎭⎬⎫x |2<x <1a ;当a =12时,原不等式的解集是∅;当a>12时,1a <2,则原不等式的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1a <x <2. ②当a =0时,原不等式为-(x -2)<0,解得x >2,即原不等式的解集是{x |x >2}.③当a <0时,原不等式可以化为a (x -2)⎝⎛⎭⎪⎫x -1a <0,根据不等式的性质,这个不等式等价于(x -2)⎝ ⎛⎭⎪⎫x -1a >0,由于1a<2,故原不等式的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <1a或x >2.综上,当0<a <12时,不等式解集为⎩⎨⎧⎭⎬⎫x |2<x <1a ,当a =12时,不等式解集为∅,当a >12时,不等式解集为⎩⎨⎧⎭⎬⎫x |1a <x <2,当a =0时,不等式解集为{x |x >2}.当a <0时,不等式解集为⎩⎨⎧⎭⎬⎫x |x <1a 或x >2.。
2016年全国各地高考数学试题及解答分类汇编大全(05 不等式)

2016年全国各地高考数学试题及解答分类汇编大全(05不等式)一、选择题1.(2016北京理)若x,y满足203x yx yx-≤⎧⎪+≤⎨⎪≥⎩,则2x y+的最大值为()A.0B.3C.4D.5【答案】C【解析】考点:线性规划.【名师点睛】可行域是封闭区域时,可以将端点代入目标函数,求出最大值与最小值,从而得到相应范围.若线性规划的可行域不是封闭区域时,不能简单的运用代入顶点的方法求最优解.如变式2,需先准确地画出可行域,再将目标函数对应直线在可行域上移动,观察z的大小变化,得到最优解.2.(2016山东文、理)若变量x,y满足2,239,0,x yx yx+≤⎧⎪-≤⎨⎪≥⎩则x2+y2的最大值是()(A)4 (B)9 (C)10 (D)12【答案】C【解析】试题分析:画出可行域如图所示,点31A-(,)到原点距离最大,所以22max()10x y+=,选C.考点:简单线性规划【名师点睛】本题主要考查简单线性规划的应用,是一道基础题目.从历年高考题目看,简单线性规划问题,是不等式中的基本问题,往往围绕目标函数最值的确定,涉及直线的斜率、两点间距离等,考查考生的绘图、用图能力,以及应用数学解决实际问题的能力.3.(2016天津理)设变量x ,y 满足约束条件20,2360,3290.x y x y x y -+≥⎧⎪+-≥⎨⎪+-≤⎩则目标函数25z x y =+的最小值为( )(A )4- (B )6 (C )10 (D )17【答案】B考点:线性规划【名师点睛】线性规划问题,首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值取法、值域范围.4.(2016浙江理)在平面上,过点P 作直线l 的垂线所得的垂足称为点P 在直线l 上的投影.由区域200340x x y x y -≤⎧⎪+≥⎨⎪-+≥⎩中的点在直线x +y -2=0上的投影构成的线段记为AB ,则│AB │=( ) A .22 B .4 C .32 D .6 【答案】C 【解析】考点:线性规划.【思路点睛】先根据不等式组画出可行域,再根据题目中的定义确定AB的值.画不等式组所表示的平面区域时要注意通过特殊点验证,防止出现错误.5.(2016浙江文)若平面区域30,230,230x yx yx y+-≥⎧⎪--≤⎨⎪-+≥⎩夹在两条斜率为1的平行直线之间,则这两条平行直线间的距离的最小值是()A.35B.2C.32D.5【答案】B考点:线性规划.【思路点睛】先根据不等式组画出可行域,再根据可行域的特点确定取得最值的最优解,代入计算.画不等式组所表示的平面区域时要注意通过特殊点验证,防止出现错误.6.(2016浙江理)已知实数a,b,c()A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100 B.若|a2+b+c|+|a2+b–c|≤1,则a2+b2+c2<100 C.若|a+b+c2|+|a+b–c2|≤1,则a2+b2+c2<100 D.若|a2+b+c|+|a+b2–c|≤1,则a2+b2+c2<100 【答案】D【解析】试题分析:举反例排除法:A.令10,110===-a b c ,排除此选项,B.令10,100,0==-=a b c ,排除此选项,C.令100,100,0==-=a b c ,排除此选项,故选D . 考点:不等式的性质.【方法点睛】对于判断不等式恒成立问题,一般采用举反例排除法.解答本题时能够对四个选项逐个利用赋值的方式进行排除,确认成立的不等式.二、填空1.(2016全国Ⅰ文、理)某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料.生产一件产品A 需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B 需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A 的利润为2100元,生产一件产品B 的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A 、产品B 的利润之和的最大值为 ______ 元.【答案】216000【解析】试题分析:设生产产品A 、产品B 分别为x 、y 件,利润之和为z 元,那么目标函数2100900z x y =+.取得最大值.解方程组10390053600x y x y +=⎧⎨+=⎩,得M 的坐标(60,100).所以当60x=,100y=时,max210060900100216000z=⨯+⨯=.故生产产品A、产品B的利润之和的最大值为216000元.考点:线性规划的应用【名师点睛】线性规划也是高考中常考的知识点,一般以客观题形式出现,基本题型是给出约束条件求目标函数的最值,常见的结合方式有:纵截距、斜率、两点间的距离、点到直线的距离,解决此类问题常利用数形结合.本题运算量较大,失分的一个主要原因是运算失误.2.(2016全国Ⅱ文)若x,y满足约束条件103030x yx yx-+≥⎧⎪+-≥⎨⎪-≤⎩,则2z x y=-的最小值为__________ 【答案】5-考点:简单的线性规划.【名师点睛】利用线性规划求最值,一般用图解法求解,其步骤是:(1)在平面直角坐标系内作出可行域;(2)考虑目标函数的几何意义,将目标函数进行变形;(3)确定最优解:在可行域内平行移动目标函数变形后的直线,从而确定最优解;(4)求最值:将最优解代入目标函数即可求出最大值或最小值.3.(2016全国Ⅲ文)若,x y满足约束条件210,210,1,x yx yx-+≥⎧⎪--≤⎨⎪≤⎩则235z x y=+-的最大值为___________. 【答案】10-考点:简单的线性规划问题.【技巧点拨】利用图解法解决线性规划问题的一般步骤:(1)作出可行域.将约束条件中的每一个不等式当作等式,作出相应的直线,并确定原不等式的区域,然后求出所有区域的交集;(2)作出目标函数的等值线(等值线是指目标函数过原点的直线);(3)求出最终结果.4.(2016全国Ⅲ理)若,x y 满足约束条件1020220x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩则z x y =+的最大值为_____________.【答案】32【解析】试题分析:作出不等式组满足的平面区域,如图所示,由图知,当目标函数z x y =+经过点1(1,)2A 时取得最大值,即max 13122z =+=.考点:简单的线性规划问题.【技巧点拨】利用图解法解决线性规划问题的一般步骤:(1)作出可行域.将约束条件中的每一个不等式当作等式,作出相应的直线,并确定原不等式的区域,然后求出所有区域的交集;(2)作出目标函数的等值线(等值线是指目标函数过原点的直线);(3)求出最终结果.5、(2016上海文\理)设x ∈R ,则不等式31x -<的解集为_______. 【答案】(2,4) 【解析】试题分析:由题意得:131x -<-<,即24x <<,故解集为(2,4) 考点:绝对值不等式的基本解法.【名师点睛】解绝对值不等式,关键是去掉绝对值符号,进一步求解,本题也可利用两边平方的方法 .本题较为容易.6、(2016上海文)若,x y 满足0,0,1,x y y x ≥⎧⎪≥⎨⎪≥+⎩则2x y -的最大值为_______.【答案】2-【解析】试题分析:由不等式组画出可行域,如图,令y x z 2-=,当直线z x y 2121-=经过点)1,0(P 时,z 取得最大值,且为2-.考点:简单线性规划【名师点睛】本题主要考查简单线性规划的应用,是一道基础题目.从历年高考题目看,简单线性规划问题,是不等式中的基本问题,往往围绕目标函数最值的确定,涉及直线的斜率、两点间距离等,考查考生的绘图、用图能力,以及应用数学解决实际问题的能力.7. (2016上海文、理)设a >0,b >0. 若关于x ,y 的方程组1,1ax y x by无解,则a b 的取值范围是 . 【答案】(2,)+∞ 【解析】试题分析:方程组无解等价于直线1ax y +=与直线1x by +=平行,所以1ab =且1a b ≠≠.又a ,b 为正数,所以22a b ab +>=(1a b ≠≠),即a b +取值范围是(2,)+∞.考点:方程组的思想以及基本不等式的应用.【名师点睛】根据方程表示直线,探讨得到方程组无解的条件,进一步应用基本不等式达到解题目的.易错点在于忽视得到a b ≠.本题能较好地考查考生的逻辑思维能力、基本运算求解能力、数形结合思想等.三、解答题1. (2016天津文)某化肥厂生产甲、乙两种混合肥料,需要A,B,C 三种主要原料.生产1车皮甲种肥料和生产1车皮乙中肥料所需三种原料的吨数如下表所示:现有A 种原料200吨,B 种原料360吨,C 种原料300吨,在此基础上生产甲乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y 表示生产甲、乙两种肥料的车皮数.(Ⅰ)用x,y 列出满足生产条件的数学关系式,并画出相应的平面区域;OxyP(Ⅱ)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.【答案】(Ⅰ)详见解析(Ⅱ)生产甲种肥料20车皮,乙种肥料24车皮时利润最大,且最大利润为112万元(1)3x+10y=3004x+5y=2008x+5y=3601010yxO(2)考点:线性规划【名师点睛】解线性规划应用问题的一般步骤是:(1)分析题意,设出未知量;(2)列出线性约束条件和目标函数;(3)作出可行域并利用数形结合求解;(4)作答.而求线性规划最值问题,首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值取法.。
【5份】江苏省2016年高考理科数学二轮专题复习课件:专题一 函数与导数、不等式 共168张PPT

解析 因为函数 f(x)是周期为 2 的函数,所以 f(-1)=f(1)⇒-a 1 b+2 1 3 1 2 b+2 1 +1= ,又 f 2 =f 2 =f -2 ⇒ =- a+1,联立列成方 2 3 2 2 程组解得 a=2,b=-4,所以 a+3b=2-12=-10.
真题感悟· 考点整合
热点聚焦· 题型突破
归纳总结· 思维升华
考点整合 1.函数的性质 (1) 单调性:证明函数的单调性时,规范步骤为取值、作差、变 形、判断符号和下结论 .可以用来比较大小,求函数最值,解不 等式,证明方程根的唯一性;
(2)奇偶性:①若f(x)是偶函数,那么f(x)=f(-x);②若f(x)是奇函
解析 作出函数 y=f(x)与 y=a 的图象, 根据图象交点个数得出 a
的取值范围.作出函数 y=f(x)在[-3,4]上的图象,f(-3)=f(-2) 1 1 =f(-1)=f(0)=f(1)=f(2)=f(3)=f(4)=2,观察图象可得 0<a<2.
答案
1 0, 2
真题感悟· 考点整合 热点聚焦· 题型突破 归纳总结· 思维升华
1 f(x+a)=-f(x)或f(x+a)=f(x) ,
则 y=f(x)是周期为 2|a|的周期函数.
真题感悟· 考点整合
热点聚焦· 题型突破
归纳总结· 思维升华
2.函数的图象
对于函数的图象要会作图、识图和用图,作函数图象有两种基 本方法:一是描点法;二是图象变换法,其中图象变换有平移 变换、伸缩变换和对称变换. 3.函数的零点与方程的根
4.应用函数模型解决实际问题的一般程序 读题 建模 求解 反馈 ⇒ ⇒ ⇒ (文字语言) (数学语言) (数学应用) (检验作答) 与函数有关的应用题,经常涉及到物价、路程、产值、环保等实 际问题,也可涉及角度、面积、体积、造价的最优化问题.解答这 类问题的关键是确切的建立相关函数解析式,然后应用函数、方 程、不等式和导数的有关知识加以综合解答.
《2017参考》金版教程2016高考数学理二轮复习训练1-1-6-2利用导数解决不等式、方程解的问题Word版含解析
1.[2015·山西质监]已知函数f (x )=x ln x . (1)试求曲线y =f (x )在点(e ,f (e))处的切线方程;(2)若x >1,试判断方程f (x )=(x -1)(ax -a +1)的解的个数. 解 (1)f ′(x )=ln x +x ·1x =1+ln x ,∴f ′(e)=2,又f (e)=e ,∴切线方程为2x -y -e =0.(2)方程f (x )=(x -1)(ax -a +1)的解即为方程ln x -(x -1)(ax -a +1)x=0的解. 设h (x )=ln x -(x -1)(ax -a +1)x,x >1. 则h ′(x )=-ax 2-x -a +1x 2=-(x -1)(ax +a -1)x 2,x >1. 当a =0时,h ′(x )>0,h (x )为增函数,∴h (x )>h (1)=0,方程无解. 当a ≠0时,令h ′(x )=0得x 1=1,x 2=1-a a .当a <0,即x 2=1-aa <1时,∵x >1,∴h ′(x )>0,则h (x )为(1,+∞)上的增函数,∴h (x )>h (1)=0,方程无解.当0<a <12,即1-a a >1时,x ∈⎝⎛⎭⎪⎫1,1-a a 时,h ′(x )>0,h (x )为增函数;x ∈⎝ ⎛⎭⎪⎫1-a a ,+∞时,h ′(x )<0,h (x )为减函数. 又x →+∞时,h (x )=ln x -ax +1-ax +2a -1<0,h (1)=0, ∴方程有一个解. 当a ≥12,即1-a a ≤1时,∵x >1,∴h ′(x )<0,h (x )为减函数,而h (x )<h (1)=0,方程无解.综上所述,当a ∈(-∞,0]∪⎣⎢⎡⎭⎪⎫12,+∞时,原方程无解; 当0<a <12时,原方程有一个解.2.[2015·郑州质量预测]已知函数f (x )=ax -1+ln x ,其中a 为常数.(1)当a ∈⎝⎛⎭⎪⎫-∞,-1e 时,若f (x )在区间(0,e)上的最大值为-4,求a 的值;(2)当a =-1e 时,若函数g (x )=|f (x )|-ln x x -b2存在零点,求实数b 的取值范围.解 (1)f ′(x )=a +1x ,令f ′(x )=0得x =-1a , 因为a ∈⎝⎛⎭⎪⎫-∞,-1e ,所以0<-1a <e , 由f ′(x )>0得0<x <-1a ,由f ′(x )<0得-1a <x <e , 从而f (x )的增区间为⎝ ⎛⎭⎪⎫0,-1a ,减区间为⎝ ⎛⎭⎪⎫-1a ,e , 所以f (x )max =f ⎝ ⎛⎭⎪⎫-1a =-1-1+ln ⎝ ⎛⎭⎪⎫-1a =-4,解得a =-e 2.(2)函数g (x )=|f (x )|-ln x x -b 2存在零点,即方程|f (x )|=ln x x +b2有实数根,由已知,函数f (x )的定义域为{x |x >0},当a =-1e 时,f (x )=-x e -1+ln x ,所以f ′(x )=-1e +1x =-x -e e x , 当0<x <e 时,f ′(x )>0;当x >e 时,f ′(x )<0, 所以,f (x )的增区间为(0,e),减区间为(e ,+∞),所以f (x )max =f (e)=-1, 所以|f (x )|≥1.令h (x )=ln x x +b2,则h ′(x )=1-ln x x 2.当0<x <e 时,h ′(x )>0;当x >e 时,h ′(x )<0,从而h (x )在(0,e)上单调递增,在(e ,+∞)上单调递减, 所以h (x )max =h (e)=1e +b2, 要使方程|f (x )|=ln x x +b2有实数根, 只需h (x )max ≥1即可, 故b ≥2-2e .3.[2015·石家庄质检(二)]已知f (x )=x ln x -12mx 2-x ,m ∈R .(1)当m =-2时,求函数f (x )的所有零点;(2)若f (x )有两个极值点x 1,x 2,且x 1<x 2,求证:x 1x 2>e 2(e 为自然对数的底数).解 (1)当m =-2时,f (x )=x ln x +x 2-x =x (ln x +x -1),x >0. 设g (x )=ln x +x -1,x >0,则g ′(x )=1x +1>0,于是g (x )在(0,+∞)上为增函数.又g (1)=0,所以,g (x )有唯一零点x =1. 从而,函数f (x )有唯一零点x =1.(2)证明:欲证x 1x 2>e 2,需证ln x 1+ln x 2>2若f (x )有两个极值点x 1,x 2,即函数f ′(x )有两个零点.又f ′(x )=ln x -mx ,所以,x 1,x 2是方程f ′(x )=0的两个不同实根.于是,有⎩⎪⎨⎪⎧ln x 1-mx 1=0ln x 2-mx 2=0.解之得m =ln x 1+ln x 2x 1+x 2.另一方面,由⎩⎪⎨⎪⎧ln x 1-mx 1=0ln x 2-mx 2=0得ln x 2-ln x 1=m (x 2-x 1),从而可得ln x 2-ln x 1x 2-x 1=ln x 1+ln x 2x 1+x 2于是,ln x 1+ln x 2=(ln x 2-ln x 1)(x 2+x 1)x 2-x 1=⎝⎛⎭⎪⎫1+x 2x 1lnx 2x 1x 2x 1-1.又0<x 1<x 2,设t =x 2x 1,则t >1.因此,ln x 1+ln x 2=(1+t )ln tt -1,t >1.要证ln x 1+ln x 2>2, 即证:(t +1)ln t t -1>2,t >1.即当t >1时,有ln t >2(t -1)t +1. 设函数h (t )=ln t -2(t -1)t +1,t ≥1.则h ′(t )=1t -2(t +1)-2(t -1)(t +1)2=(t -1)2t (t +1)2≥0,所以,h (t )为(1,+∞)上的增函数.注意到,h (1)=0.因此,h (t )≥h (1)=0.于是,当t >1时,有ln t >2(t -1)t +1.所以,有ln x 1+ln x 2>2成立,即x 1x 2>e 2.4.[2015·甘肃一诊]已知函数f (x )=ax 2+ln (x +1). (1)当a =-14时,求函数f (x )的单调区间;(2)当x ∈[0,+∞)时,函数y =f (x )的图象上的点都在⎩⎪⎨⎪⎧x ≥0y -x ≤0所表示的平面区域内,求实数a 的取值范围.解 (1)当a =-14时,f (x )=-14x 2+ln (x +1)(x >-1), f ′(x )=-12x +1x +1=-(x +2)(x -1)2(x +1)(x >-1),由f ′(x )>0解得-1<x <1,由f ′(x )<0解得x >1.∴函数f (x )的单调递增区间为(-1,1),单调递减区间为(1,+∞).(2)当x ∈[0,+∞)时,函数y =f (x )的图象上的点都在⎩⎪⎨⎪⎧x ≥0y -x ≤0所表示的平面区域内,即当x ∈[0,+∞)时,不等式f (x )≤x 恒成立,即ax 2+ln (x +1)≤x 恒成立,设g (x )=ax 2+ln (x +1)-x (x ≥0), 只需g (x )max ≤0即可.由g ′(x )=2ax +1x +1-1=x [2ax +(2a -1)](x +1),①当a =0时,g ′(x )=-xx +1,当x >0时,g ′(x )<0,函数g (x )在(0,+∞)上单调递减. ∴g (x )≤g (0)=0成立.②当a >0时,由g ′(x )=x [2ax +(2a -1)](x +1)=0,因x ∈[0,+∞),∴x =12a -1.(ⅰ)若12a -1<0,即a >12时,在区间(0,+∞)上,g ′(x )>0,函数g (x )在(0,+∞)上单调递增,函数g (x )在[0,+∞)上无最大值,此时不满足.(ⅱ)若12a -1≥0,即0<a ≤12时,函数g (x )在⎝ ⎛⎭⎪⎫0,12a -1上单调递减,在区间⎝ ⎛⎭⎪⎫12a -1,+∞上单调递增,同样函数g (x )在[0,+∞)上无最大值,此时也不满足.③当a <0时,由g ′(x )=x [2ax +(2a -1)](x +1),∵x ∈[0,+∞),∴2ax +(2a -1)<0,∴g ′(x )<0,故函数g (x )在[0,+∞)上单调递减.∴g (x )≤g (0)=0成立.综上所述,实数a 的取值范围是(-∞,0]. 5.已知函数f (x )=(2a +2)ln x +2ax 2+5 (1)讨论函数f (x )的单调性;(2)设a <-1,若对任意不相等的正数x 1,x 2,恒有⎪⎪⎪⎪⎪⎪f (x 1)-f (x 2)x 1-x 2≥8,求a 的取值范围.解 (1)f (x )的定义域为(0,+∞).f ′(x )=2a +2x +4ax =2(2ax 2+a +1)x. 当a ≥0时,f ′(x )>0,故f (x )在(0,+∞)单调递增;当a ≤-1时,f ′(x )<0,故f (x )在(0,+∞)单调递减;当-1<a <0时,令f ′(x )=0,解得x =-a +12a .即x ∈⎝ ⎛⎭⎪⎫0,-a +12a 时,f ′(x )>0;x ∈⎝⎛⎭⎪⎫-a +12a ,+∞时,f ′(x )<0;故f (x )在⎝⎛⎭⎪⎫0,-a +12a 单调递增,在⎝⎛⎭⎪⎫-a +12a ,+∞单调递减;(2)解法一:不妨设x 1<x 2,而a <-1,由(1)知f (x )在(0,+∞)单调递减,从而对任意x 1、x 2∈(0,+∞),恒有⎪⎪⎪⎪⎪⎪f (x 1)-f (x 2)x 1-x 2≥8⇔|f (x 1)-f (x 2)|≥8|x 1-x 2|⇔f (x 1)-f (x 2)≥8(x 2-x 1)⇔f (x 1)+8x 1≥f (x 2)+8x 2令g (x )=f (x )+8x ,则g ′(x )=2a +2x +4ax +8原不等式等价于g (x )在(0,+∞)单调递减,即a +1x +2ax +4≤0,从而a ≤-4x -12x 2+1=(2x -1)2-4x 2-22x 2+1=(2x -1)22x 2+1-2,故a 的取值范围为(-∞,-2].解法二:a ≤⎝ ⎛⎭⎪⎫-4x -12x 2+1min ,设φ(x )=-4x -12x 2+1, 则φ′(x )=-4(2x 2+1)-(-4x -1)·4x (2x 2+1)2=8x 2+4x -4(2x 2+1)2=4(2x -1)(x +1)(2x 2+1)2,当x ∈⎝⎛⎭⎪⎫0,12时,φ′(x )<0,φ(x )为减函数,x ∈⎝⎛⎭⎪⎫12,+∞时,φ′(x )>0,φ(x )为增函数.∴φ(x )min =φ⎝ ⎛⎭⎪⎫12=-2,∴a 的取值范围为(-∞,-2].6.[2015·衡水中学一调]已知f (x )=x ln x ,g (x )=ax 22,直线l :y =(k -3)x -k +2.(1)函数f (x )在x =e 处的切线与直线l 平行,求实数k 的值; (2)若至少存在一个x 0∈[1,e]使f (x 0)<g (x 0)成立,求实数a 的取值范围;(3)设k ∈Z ,当x >1时f (x )的图象恒在直线l 的上方,求k 的最大值.解 (1)∵f ′(x )=1+ln x ,∴f ′(e)=1+ln e =k -3,∴k =5, (2)由于存在x 0∈[1,e],使f (x 0)<g (x 0), 则12ax 20>x 0ln x 0,∴a >2ln x 0x 0,设h (x )=2ln xx ,则h ′(x )=2(1-ln x )x 2, 当x ∈[1,e]时,h ′(x )≥0(仅当x =e 时取等号). ∴h (x )在[1,e]上单调递增,∴h (x )min =h (1)=0,因此a >0.(3)由题意x ln x >(k -3)x -k +2在x >1时恒成立,即k <x ln x +3x -2x -1,设F (x )=x ln x +3x -2x -1,∴F ′(x )=x -ln x -2(x -1)2,令m (x )=x -ln x -2,则m ′(x )=1-1x =x -1x >0在x >1时恒成立, 所以m (x )在(1,+∞)上单调递增,且m (3)=1-ln 3<0,m (4)=2-ln 4>0,所以在(1,+∞)上存在唯一实数x 0(x 0∈(3,4))使m (x )=0 当1<x <x 0时m (x )<0即F ′(x )<0, 当x >x 0时m (x )>0即F ′(x )>0,所以F (x )在(1,x 0)上单调递减,在(x 0,+∞)上单调递增, F (x )min =F (x 0)=x 0ln x 0+3x 0-2x 0-1=x 0(x 0-2)+3x 0-2x 0-1=x 0+2∈(5,6),故k <x 0+2,又k ∈Z ,所以k 的最大值为5.。
2016届全国通用高考数学理科二轮专题复习习题专题一函数与导数、不等式第1讲
第1讲 函数图象与性质及函数与方程一、选择题1.(2015·广东卷)下列函数中,既不是奇函数,也不是偶函数的是( )A.y =x +e xB.y =x +1xC.y =2x +12xD.y =1+x 2解析 令f (x )=x +e x ,则f (1)=1+e ,f (-1)=-1+e -1,即f (-1)≠f (1),f (-1)≠-f (1),所以y =x +e x 既不是奇函数也不是偶函数,而B ,C ,D 依次是奇函数、偶函数、偶函数,故选A.答案 A2.函数f (x )=log 2x -1x 的零点所在的区间为( )A.⎝ ⎛⎭⎪⎫0,12B.⎝ ⎛⎭⎪⎫12,1C.(1,2)D.(2,3)解析 函数f (x )的定义域为(0,+∞),且函数f (x )在(0,+∞)上为增函数.f ⎝ ⎛⎭⎪⎫12=log 212-112=-1-2=-3<0,f (1)=log 21-11=0-1<0, f (2)=log 22-12=1-12=12>0,f (3)=log 23-13>1-13=23>0,即f (1)·f (2)<0,∴函数f (x )=log 2x -1x 的零点在区间(1,2)内.答案 C3.(2014·山东卷)已知函数f (x )=|x -2|+1,g (x )=kx .若方程f (x )=g (x )有两个不相等的实根,则实数k 的取值范围是( )A.⎝ ⎛⎭⎪⎫0,12B.⎝ ⎛⎭⎪⎫12,1C.(1,2)D.(2,+∞) 解析 由f (x )=g (x ),∴|x -2|+1=kx ,即|x -2|=kx -1,所以原题等价于函数y =|x -2|与y =kx -1的图象有2个不同交点.如图:∴y =kx -1在直线y =x -1与y =12x -1之间,∴12<k <1,故选B.答案 B4.(2015·山东卷)设函数f (x )=⎩⎨⎧3x -1,x <1,2x ,x ≥1,则满足f (f (a ))=2f (a )的a 取值范围是( )A.⎣⎢⎡⎦⎥⎤23,1 B.[0,1] C.⎣⎢⎡⎭⎪⎫23,+∞ D.[1,+∞)解析 当a =2时,f (a )=f (2)=22=4>1,f (f (a ))=2f (a ),∴a =2满足题意,排除A ,B 选项;当a =23时,f (a )=f ⎝ ⎛⎭⎪⎫23=3×23-1=1,f (f (a ))=2f (a ),∴a =23满足题意,排除D 选项,故答案为C.答案 C5.(2015·全国Ⅱ卷)如图,长方形ABCD 的边AB =2,BC =1,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记∠BOP =x .将动点P 到A ,B 两点距离之和表示为x 的函数f (x ),则y =f (x )的图象大致为( )解析 当点P 沿着边BC 运动,即0≤x ≤π4时,在Rt △POB 中,|PB |=|OB |tan ∠POB=tan x ,在Rt △PAB 中,|PA |=|AB |2+|PB |2=4+tan 2x ,则f (x )=|PA |+|PB |=4+tan 2x +tan x ,它不是关于x 的一次函数,图象不是线段,故排除A 和C ;当点P 与点C 重合,即x =π4时,由上得f ⎝ ⎛⎭⎪⎫π4=4+tan 2π4+tan π4=5+1,又当点P 与边CD 的中点重合,即x =π2时,△PAO 与△PBO 是全等的腰长为1的等腰直角三角形,故f ⎝ ⎛⎭⎪⎫π2=|PA |+|PB |=2+2=22,知f ⎝ ⎛⎭⎪⎫π2<f ⎝ ⎛⎭⎪⎫π4,故又可排除D.综上,选B.答案 B二、填空题6.(2015·福建卷)若函数f (x )=⎩⎨⎧-x +6,x ≤2,3+log a x ,x >2(a >0,且a ≠1)的值域是[4,+∞),则实数a 的取值范围是________.解析 由题意f (x )的图象如图,则⎩⎨⎧a >1,3+log a2≥4,∴1<a ≤2.答案 (1,2]7.(2015·洛阳模拟)若函数f (x )=⎩⎨⎧2x -a ,x ≤0,ln x ,x >0有两个不同的零点,则实数a 的取值范围是________.解析 当x >0时,由f (x )=ln x =0,得x =1.因为函数f (x )有两个不同的零点,则当x ≤0时,函数f (x )=2x -a 有一个零点,令f (x )=0得a =2x ,因为0<2x ≤20=1,所以0<a ≤1,所以实数a 的取值范围是0<a ≤1.答案 (0,1]8.已知函数y =f (x )是R 上的偶函数,对x ∈R 都有f (x +4)=f (x )+f (2)成立.当x 1,x 2∈[0,2],且x 1≠x 2时,都有f (x 1)-f (x 2)x 1-x 2<0,给出下列命题: ①f (2)=0;②直线x =-4是函数y =f (x )图象的一条对称轴;③函数y =f (x )在[-4,4]上有四个零点;④f (2 014)=0.其中所有正确命题的序号为________.解析 令x =-2,得f (-2+4)=f (-2)+f (2),解得f (-2)=0,因为函数f (x )为偶函数,所以f (2)=0,①正确;因为f (-4+x )=f (-4+x +4)=f (x ),f (-4-x )=f (-4-x +4)=f (-x )=f (x ),所以f (-4+x )=f (-4-x ),即x =-4是函数f (x )的一条对称轴,②正确;当x 1,x 2∈[0,2],且x 1≠x 2时,都有f (x 1)-f (x 2)x 1-x 2<0,说明函数f (x )在[0,2]上是单调递减函数,又f (2)=0,因此函数f (x )在[0,2]上只有一个零点,由偶函数知函数f (x )在[-2,0]上也只有一个零点,由f (x +4)=f (x ),知函数的周期为4,所以函数f (x )在(2,4]与[-4,-2)上也单调,因此,函数在[-4,4]上只有2个零点,③错;对于④,因为函数的周期为4,即有f (2)=f (6)=f (10)=…=f (2 014)=0,④正确.答案 ①②④三、解答题9.定义在[-1,1]上的奇函数f (x ),已知当x ∈[-1,0]时,f (x )=14x -a 2x (a ∈R ).(1)写出f (x )在[0,1]上的解析式;(2)求f (x )在[0,1]上的最大值.解 (1)∵f (x )是定义在[-1,1]上的奇函数,∴f (0)=0,∴a =1,∴当x ∈[-1,0]时,f (x )=14x -12x .设x ∈[0,1],则-x ∈[-1,0],∴f (-x )=14-x -12-x =4x -2x , ∵f (x )是奇函数,∴f (-x )=-f (x ),∴f (x )=2x -4x .∴f (x )在[0,1]上的解析式为f (x )=2x -4x .(2)f (x )=2x -4x ,x ∈[0,1],令t =2x ,t ∈[1,2],g (t )=t -t 2=-⎝ ⎛⎭⎪⎫t -122+14, ∴g (t )在[1,2]上是减函数,∴g (t )max =g (1)=0,即x =0,f (x )max =0.10.(2015·太原模拟)已知函数f (x )=ax 2-2ax +2+b (a ≠0)在区间[2,3]上有最大值5,最小值2.(1)求a ,b 的值;(2)若b <1,g (x )=f (x )-2m x 在[2,4]上单调,求m 的取值范围.解 (1)f (x )=a (x -1)2+2+b -a .①当a >0时,f (x )在[2,3]上为增函数,故⎩⎨⎧f (3)=5,f (2)=2⎩⎨⎧9a -6a +2+b =5,4a -4a +2+b =2⎩⎨⎧a =1,b =0. ②当a <0时,f (x )在[2,3]上为减函数,故⎩⎨⎧f (3)=2,f (2)=5⎩⎨⎧9a -6a +2+b =2,4a -4a +2+b =5⎩⎨⎧a =-1,b =3.故⎩⎨⎧a =1,b =0或⎩⎨⎧a =-1,b =3.(2)∵b <1,∴a =1,b =0,即f (x )=x 2-2x +2,g (x )=x 2-2x +2-2m x =x 2-(2+2m )x +2.若g (x )在[2,4]上单调,则2+2m 2≤2或2m +22≥4,∴2m≤2或2m≥6,即m≤1或m≥log26.故m的取值范围是(-∞,1]∪[log26,+∞).11.已知函数f(x)=-x2+2e x+m-1,g(x)=x+e2x(x>0).(1)若g(x)=m有实根,求m的取值范围;(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.解(1)∵x>0,∴g(x)=x+e2x≥2e2=2e,等号成立的条件是x=e.故g(x)的值域是[2e,+∞),因而只需m≥2e,则g(x)=m就有实根.故m∈[2e,+∞).(2)若g(x)-f(x)=0有两个相异的实根,即g(x)=f(x)中函数g(x)与f(x)的图象有两个不同的交点,作出g(x)=x+e2x(x>0)的大致图象.∵f(x)=-x2+2e x+m-1=-(x-e)2+m-1+e2.其对称轴为x=e,开口向下,最大值为m-1+e2.故当m-1+e2>2e,即m>-e2+2e+1时,g(x)与f(x)有两个交点,即g(x)-f(x)=0有两个相异实根. ∴m的取值范围是(-e2+2e+1,+∞).。
2016届高考数学(理)二轮复习课件高考大题专讲1
重点透析 难点突破
题型一 导数与不等式问题 1. 利用导数解决不等式的恒成立问题时常采用分离参数法或 不等式转化法,通过求函数的最值加以解决. 2. 利用导数证明不等式关键是把不等式变形后构造恰当的函 数,然后用导数判断函数的单调性或求出最值,达到证明不等式 的目的.
(2015· 福建卷)已知函数 f(x)=ln(1+x),g(x)=kx(k∈R). (1)证明:当 x>0 时,f(x)<x; (2)证明:当 k<1 时,存在 x0>0,使得对任意的 x∈(0,x0), 恒有 f(x)>g(x); (3)确定 k 的所有可能取值,使得存在 t>0,对任意的 x∈(0, t),恒有|f(x)-g(x)|<x2.
[思路引导]
x
(1)转化为求 ax2+x≤0 的解集;(2)转化为函数
2 h(x)=e - -1 的零点存在问题,利用导数求解;(3)通过导数研 x 究函数 f(x)的单调性和极值,再求出 a 的范围.
[解]
(1)因为 ex>0,所以不等式 f(x)≤0 即为 ax2+x≤0,
1 xx+a ≤0,
[思路引导]
(1)欲证当 x>0 时, f(x)<x,只需构造函数 F(x)
=f(x)-x,证明当 x>0 时,F(x)<0;(2)构造函数 G(x)=f(x)-g(x), 求 G′(x),对 k 进行分类讨论,判断 G′(x)的符号,从而判断函 数 G(x)=f(x)-g(x)的单调性,即可证得结果;(3)当 k>1 时,利用 (1)的结论,构造函数,利用导数判断该函数的单调性,从而可判 断满足题意的 t 是否存在;当 k<1 时,利用(2)的结论,再构造函 数,利用导数判断该函数的单调性,从而可判断满足题意的 t 是 否存在;当 k=1 时,利用(1)的结论,构造函数,利用导数的知 识可判断是否存在满足题意的 t,从而确定 k 的取值.
函数与导数专题(理科)(2016高考真题分专题复习)
2016函数与导数专题(理)1.已知函数))((R x x f ∈满足)(2)(x f x f -=-,若函数xx y 1+=与)(x f y =图象的交点为(x 1,y 1),(x 2,y 2),…,(x m ,y m ),则=+∑=m i i i y x 1)(( ) A.0 B.m C.2m D.4m2.已知函数f (x )=(a >0,且a≠1)在R 上单调递减,且关于x 的方程|f (x )|=2﹣x 恰好有两个不相等的实数解,则a 的取值范围是( )A .(0,]B .[,]C .[,]∪{}D .[,)∪{}3.设直线21,l l 分别是函数⎩⎨⎧><<-=1,ln 10,ln )(x x x x x f 图象上点P 1,P 2处的切线,21l l 与垂直相交于点P ,且21,l l 分别与y 轴相交于点A ,B ,则△PAB 的面积的取值范围是( )A.(0,1)B.(0,2)C.(0,+∞)D.(1,+∞) 4.函数y=2x 2-e |x|在[-2,2]的图象大致为( ) A. B. C. D.5.设f (x )、g (x )、h (x )是定义域为R 的三个函数,对于命题:①f (x )+g (x )、f (x )+h (x )、g (x )+h (x )均为增函数,则f (x )、g (x )、h (x )中至少有一个增函数;②若f (x )+g (x )、f (x )+h (x )、g (x )+h (x )均是以T 为周期的函数,则f (x )、g (x )、h (x )均是以T 为周期的函数,下列判断正确的是( )A.①和②均为真命题B.①和②均为假命题C.①为真命题,②为假命题D.①为假命题,②为真命题6.已知函数f (x )的定义域为R .当x <0时,f (x )=x 3-1;当-1≤x≤1时,f (-x )=-f (x );当21>x 时,)21()21(-=+x f x f .则f (6)=( ) A.-2B.-1C.0D.2 7.若函数y=f (x )的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f (x )具有T 性质.下列函数中具有T 性质的是( )A.y=sinxB.y=lnxC.y=e xD.y=x 3 8.已知函数⎩⎨⎧>+-≤=m x m mx x m x x x f ,42,)(2,其中m >0,若存在实数b ,使得关于x 的方程f (x )=b 有三个不同的根,则m 的取值范围是 ______ .9.已知a >b >1,若a b b a b a a b ==+,25log log ,则a= ______ ,b= ______ . 10.已知函数f (x )是定义在R 上的周期为2的奇函数,当0<x <1时,f (x )=4x ,则f (25-)+f (1)= ______ .11.若直线y=kx+b 是曲线y=lnx+2的切线,也是曲线y=ln (x+1)的切线,则b= ______ .12.已知f (x )为偶函数,当x <0时,f (x )=ln (-x )+3x ,则曲线y=f (x )在点(1,-3)处的切线方程是 ______ .13.已知直线033:=-++m y mx l 与圆x 2+y 2=12交于A ,B 两点,过A ,B 分别作l 的垂线与x 轴交于C ,D 两点,若|AB|=32,则|CD|= ______ .14.已知f (x )是定义在R 上的偶函数,且在区间(﹣∞,0)上单调递增,若实数a 满足)2()2(1->-f f a ,则a 的取值范围是 .15.设函数f (x )=.①若a=0,则f (x )的最大值为 ;②若f (x )无最大值,则实数a 的取值范围是 .16.已知函数f (x )=(x-2)e x +a (x-1)2有两个零点.(Ⅰ)求a 的取值范围;(Ⅱ)设x 1,x 2是f (x )的两个零点,证明:x 1+x 2<2.17.(Ⅰ)讨论函数x e x x x f 22)(+-=的单调性,并证明当x >0时,(x-2)e x +x+2>0; (Ⅱ)证明:当a ∈[0,1)时,函数)0()(2>--=x x a ax e x g x 有最小值.设g (x )的最小值为h (a ),求函数h (a )的值域.18.设函数f (x )=acos2x+(a-1)(cosx+1),其中a >0,记|f (x )|的最大值为A . (Ⅰ)求f′(x );(Ⅱ)求A ;(Ⅲ)证明:|f′(x )|≤2A .19.已知a ∈R ,函数)1(log )(2a xx f +=. (1)当a=5时,解不等式f (x )>0;(2)若关于x 的方程f (x )-log 2[(a-4)x+2a-5]=0的解集中恰好有一个元素,求a 的取值范围.(3)设a >0,若对任意t ∈[21,1],函数f (x )在区间[t ,t+1]上的最大值与最小值的差不超过1,求a 的取值范围.20.设函数f (x )=(x ﹣1)3﹣ax ﹣b ,x ∈R ,其中a ,b ∈R .(1)求f (x )的单调区间;(2)若f (x )存在极值点x 0,且f (x 1)=f (x 0),其中x 1≠x 0,求证:x 1+2x 0=3;(3)设a >0,函数g (x )=|f (x )|,求证:g (x )在区间[0,2]上的最大值不小于.21.已知a≥3,函数F (x )=min{2|x-1|,x 2-2ax+4a-2},其中min (p ,q )=⎩⎨⎧>≤q p q q p p ,, (Ⅰ)求使得等式F (x )=x 2-2ax+4a-2成立的x 的取值范围(Ⅱ)(i )求F (x )的最小值m (a )(ii )求F (x )在[0,6]上的最大值M (a )22.设函数f (x )=xea ﹣x +bx ,曲线y=f (x )在点(2,f (2))处的切线方程为y=(e ﹣1)x+4, (Ⅰ)求a ,b 的值;(Ⅱ)求f (x )的单调区间.23.设函数f (x )=ax 2-a-lnx ,其中a ∈R . (Ⅰ)讨论f (x )的单调性;(Ⅱ)确定a 的所有可能取值,使得x e x x f -->11)(在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).24.已知212)ln ()(xx x x a x f -+-=,a ∈R . (1)讨论f (x )的单调性;(2)当a=1时,证明f (x )>f′(x )+23对于任意的x ∈[1,2]成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5讲 导数与不等式、存在性及恒成立问题一、选择题1.已知函数f (x )=13x 3-2x 2+3m ,x ∈[0,+∞),若f (x )+5≥0恒成立,则实数m 的取值范围是( ) A.⎣⎢⎡⎭⎪⎫179,+∞ B.⎝ ⎛⎭⎪⎫179,+∞ C.(-∞,2]D.(-∞,2)解析 f ′(x )=x 2-4x ,由f ′(x )>0,得x >4或x <0.∴f (x )在(0,4)上单调递减,在(4,+∞)上单调递增,∴当x ∈[0,+∞)时,f (x )min =f (4).∴要使f (x )+5≥0恒成立,只需f (4)+5≥0恒成立即可,代入解之得m ≥179. 答案 A2.若存在正数x 使2x (x -a )<1成立,则a 的取值范围是( ) A.(-∞,+∞) B.(-2,+∞) C.(0,+∞)D.(-1,+∞)解析 ∵2x (x -a )<1,∴a >x -12x . 令f (x )=x -12x , ∴f ′(x )=1+2-x ln 2>0. ∴f (x )在(0,+∞)上单调递增, ∴f (x )>f (0)=0-1=-1,∴a 的取值范围为(-1,+∞),故选D. 答案 D3.(2015·合肥模拟)当x ∈[-2,1]时,不等式ax 3-x 2+4x +3≥0恒成立,则实数a 的取值范围是( ) A.[-5,-3] B.⎣⎢⎡⎦⎥⎤-6,-98 C.[-6,-2]D.[-4,-3]解析 当x ∈(0,1]时,得a ≥-3⎝ ⎛⎭⎪⎫1x 3-4⎝ ⎛⎭⎪⎫1x 2+1x ,令t =1x ,则t ∈[1,+∞),a ≥-3t 3-4t 2+t ,令g (t )=-3t 3-4t 2+t ,t ∈[1,+∞),则g ′(t )=-9t 2-8t +1=-(t +1)·(9t -1),显然在[1,+∞)上,g ′(t )<0,g (t )单调递减,所以g (t )max =g (1)=-6,因此a ≥-6;同理,当x ∈[-2,0)时,得a ≤-2.由以上两种情况得-6≤a ≤-2,显然当x =0时也成立.故实数a 的取值范围为[-6,-2]. 答案 C4.(2015·全国Ⅱ卷)设函数f ′(x )是奇函数f (x )(x ∈R )的导函数,f (-1)=0,当x >0时,xf ′(x )-f (x )<0,则使得f (x )>0成立的x 的取值范围是( ) A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞) C.(-∞,-1)∪(-1,0) D.(0,1)∪(1,+∞)解析 因为f (x )(x ∈R )为奇函数,f (-1)=0,所以f (1)=-f (-1)=0.当x ≠0时,令g (x )=f (x )x ,则g (x )为偶函数,且g (1)=g (-1)=0.则当x >0时,g ′(x )=⎝ ⎛⎭⎪⎫f (x )x ′=xf ′(x )-f (x )x 2<0,故g (x )在(0,+∞)上为减函数,在(-∞,0)上为增函数.所以在(0,+∞)上,当0<x <1时,g (x )>g (1)=0⇔f (x )x >0⇔f (x )>0;在(-∞,0)上,当x <-1时,g (x )<g (-1)=0⇔f (x )x <0⇔f (x )>0.综上,得使得f (x )>0成立的x 的取值范围是(-∞,-1)∪(0,1),选A. 答案 A5.已知函数f (x )=2ax 3-3ax 2+1,g (x )=-a 4x +32,若任意给定的x 0∈[0,2],总存在两个不同的x i (i =1,2)∈[0,2],使得f (x i )=g (x 0)成立,则实数a 的取值范围是( )A.(-∞,-1)B.(1,+∞)C.(-∞,-1)∪(1,+∞)D.[-1,1]解析 当a =0时,显然不成立,故排除D ; 当a >0时,注意到f ′(x )=6ax 2-6ax =6ax (x -1), 即f (x )在[0,1]上是减函数,在[1,2]上是增函数, 又f (0)=1<32=g (0),当x 0=0时,结论不可能成立; 进一步,可知a <0,此时g (x )在[0,2]上是增函数, 且取值范围是⎣⎢⎡⎦⎥⎤32,-a 2+32,同时f (x )在0≤x ≤1时,函数值从1增大到1-a ,在1≤x ≤2时,函数值从1-a 减少到1+4a , 所以“任意给定的x 0∈[0,2],总存在两个不同的x i (i =1,2)∈[0,2], 使得f (x i )=g (x 0)成立”,当且仅当⎩⎨⎧f (x )的最大值>g (x )的最大值,f (x )的最小值<g (x )的最小值,即⎩⎪⎨⎪⎧1-a >-a 2+32,1+4a <32,解得a <-1.答案 A 二、填空题6.(2015·太原模拟)设函数f (x )=ax 3-3x +1(x ∈R ),若对于任意x ∈[-1,1],都有f (x )≥0成立,则实数a 的值为________.解析 若x =0,则不论a 取何值,f (x )≥0显然成立; 当x >0时,即x ∈(0,1]时,f (x )=ax 3-3x +1≥0可化为 a ≥3x 2-1x 3.令g (x )=3x 2-1x 3,则g ′(x )=3(1-2x )x 4, 所以g (x )在区间⎝ ⎛⎦⎥⎤0,12上单调递增,在区间⎣⎢⎡⎦⎥⎤12,1上单调递减.因此g (x )max =g ⎝ ⎛⎭⎪⎫12=4,从而a ≥4.当x <0时,即x ∈[-1,0)时,同理a ≤3x 2-1x 3.g (x )在区间[-1,0)上单调递增,所以g (x )min =g (-1)=4,从而a ≤4,综上可知a =4. 答案 47.(2014·江苏卷)已知函数f (x )=x 2+mx -1,若对于任意x ∈[m ,m +1],都有f (x )<0成立,则实数m 的取值范围是________.解析 作出二次函数f (x )的图象,对于任意x ∈[m ,m +1], 都有f (x )<0,则有⎩⎨⎧f (m )<0,f (m +1)<0,即⎩⎨⎧m 2+m 2-1<0,(m +1)2+m (m +1)-1<0,解得-22<m <0. 答案 ⎝ ⎛⎭⎪⎫-22,08.(2015·青岛模拟)已知函数f (x )=x -1x +1,g (x )=x 2-2ax +4,若对于任意x 1∈[0,1],存在x 2∈[1,2],使f (x 1)≥g (x 2),则实数a 的取值范围是________. 解析 由于f ′(x )=1+1(x +1)2>0,因此函数f (x )在[0,1]上单调递增,所以x ∈[0,1]时,f (x )min =f (0)=-1.根据题意可知存在x ∈[1,2],使得g (x )=x 2-2ax +4≤-1,即x 2-2ax +5≤0,即a ≥x 2+52x 能成立,令h (x )=x 2+52x ,则要使a ≥h (x )在x ∈[1,2]能成立,只需使a ≥h (x )min ,又函数h (x )=x 2+52x 在x ∈[1,2]上单调递减,所以h (x )min =h (2)=94,故只需a ≥94.答案 ⎣⎢⎡⎭⎪⎫94,+∞三、解答题9.(2015·天津卷改编)已知函数f (x )=nx -x n ,x ∈R ,其中n ∈N *,n ≥2. (1)讨论f (x )的单调性;(2)设曲线y =f (x )与x 轴正半轴的交点为P ,曲线在点P 处的切线方程为y =g (x ),求证:对于任意的正实数x ,都有f (x )≤g (x ). (1)解 由f (x )=nx -x n , 可得f ′(x )=n -nx n -1=n (1-x n -1).其中n ∈N *,且n ≥2,下面分两种情况讨论: ①当n 为奇数时.令f ′(x )=0,解得x =1,或x =-1. 当x 变化时,f ′(x ),f (x )的变化情况如下表:所以,f (x )在(-∞,-1),(1,+∞)上单调递减,在(-1,1)内单调递增. ②当n 为偶数时.当f ′(x )>0,即x <1时,函数f (x )单调递增; 当f ′(x )<0,即x >1时,函数f (x )单调递减;所以,f (x )在(-∞,1)上单调递增,在(1,+∞)上单调递减.(2)证明设点P的坐标为(x0,0),则x0=n1n-1,f′(x0)=n-n2.曲线y=f(x)在点P处的切线方程为y=f′(x0)(x-x0),即g(x)=f′(x0)(x-x0).令F(x)=f(x)-g(x),即F(x)=f(x)-f′(x0)(x-x0),则F′(x)=f′(x)-f′(x0).由于f′(x)=-nx n-1+n在(0,+∞)上单调递减,故F′(x)在(0,+∞)上单调递减,又因为F′(x0)=0,所以当x∈(0,x0)时,F′(x)>0,当x∈(x0,+∞)时,F′(x)<0,所以F(x)在(0,x0)内单调递增,在(x0,+∞)上单调递减,所以对于任意的正实数x,都有F(x)≤F(x0)=0,即对于任意的正实数x,都有f(x)≤g(x).10.(2014·新课标全国Ⅰ卷)设函数f(x)=a e x ln x+b e x-1x,曲线y=f(x)在点(1,f(1))处的切线方程为y=e(x-1)+2.(1)求a,b;(2)证明:f(x)>1.(1)解函数f(x)的定义域为(0,+∞),f′(x)=a e x ln x+ax ex-bx2ex-1+bx ex-1.由题意可得f(1)=2,f′(1)=e. 故a=1,b=2.(2)证明由(1)知,f(x)=e x ln x+2x ex-1,从而f(x)>1等价于x ln x>x e-x-2 e.设函数g (x )=x ln x ,则g ′(x )=1+ln x .所以当x ∈⎝ ⎛⎭⎪⎫0,1e 时,g ′(x )<0;当x ∈⎝ ⎛⎭⎪⎫1e ,+∞时,g ′(x )>0.故g (x )在⎝ ⎛⎭⎪⎫0,1e 上单调递减,在⎝ ⎛⎭⎪⎫1e ,+∞上单调递增, 从而g (x )在(0,+∞)上的最小值为g ⎝ ⎛⎭⎪⎫1e =-1e .设函数h (x )=x e -x -2e ,则h ′(x )=e -x (1-x ). 所以当x ∈(0,1)时,h ′(x )>0; 当x ∈(1,+∞)时,h ′(x )<0.故h (x )在(0,1)上单调递增,在(1,+∞)上单调递减, 从而h (x )在(0,+∞)上的最大值为h (1)=-1e . 综上,当x >0时,g (x )>h (x ),即f (x )>1. 11.已知函数f (x )=mxx 2+n(m ,n ∈R )在x =1处取得极值2. (1)求函数f (x )的解析式;(2)设函数g (x )=ln x +ax ,若对任意的x 1∈R ,总存在x 2∈[1,e],使得g (x 2)≤f (x 1)+72,求实数a 的取值范围. 解 (1)f ′(x )=m (x 2+n )-2mx 2(x 2+n )2=mx 2-2mx 2+mn (x 2+n )2=-mx 2+mn (x 2+n )2,由于f (x )在x =1处取得极值2, 故f ′(1)=0,f (1)=2,即⎩⎪⎨⎪⎧mn -m (1+n )2=0,m 1+n=2,解得⎩⎨⎧m =4,n =1,经检验,此时f (x )在x =1处取得极值.故f (x )=4xx 2+1.(2)由(1)知f (x )的定义域为R ,且f (-x )=-f (x ). 故f (x )为奇函数,f (0)=0. 当x >0时,f (x )>0,f (x )=4x +1x≤2,当且仅当x =1时取“=”. 故f (x )的值域为[-2,2], 从而f (x 1)+72≥32.依题意有g (x )min ≤32,x ∈[1,e], g ′(x )=1x -a x 2=x -a x 2,①当a ≤1时,g ′(x )≥0,函数g (x )在[1,e]上单调递增,其最小值为g (1)=a ≤1<32,符合题意;②当1<a <e 时,函数g (x )在[1,a ]上单调递减,在[a ,e]上单调递增, 所以函数g (x )的最小值为g (a )=ln a +1. 由ln a +1≤32,得0<a ≤e , 从而知当1<a ≤ e 时,符合题意;③当a ≥e 时,显然函数g (x )在[1,e]上单调递减,其最小值为g (e)=1+a e ≥2>32,不符合题意.综上所述,a 的取值范围为(-∞,e].。
