统计学例题-方差分析、相关分析、卡方检验和交互分析
卡方检验及交互分析-Excel计算实例
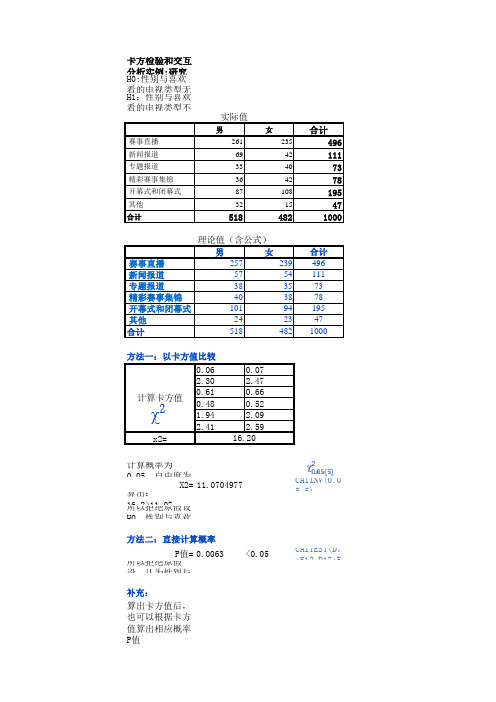
0.07 2.47 0.66 0.52 2.09 2.59 16.20
计算概率为
0.05,自由度为
算出:
X2= 11.0704977
1所6以.2拒>1绝1.原07假设
H0,性别与喜欢
方法二:直接计算概率
P值= 0.0063 所以拒绝原假 设,认为性别与
<0.05
补充:
算出卡方值后, 也可以根据卡方 值算出相应概率 P值
1000
理论值(含公式)
男
女
赛事直播
257
239
新闻报道
57
54
专题报道
38
35
精彩赛事集锦
40
38
开幕式和闭幕式
101
94
其他
24
23
合计
Hale Waihona Puke 518482合计 496 111 73 78 195 47 1000
方法一:以卡方值比较
计算卡方值
0.06 2.30 0.61 0.48 1.94
2.41
x2=
卡方检验和交互 分析实例:研究 H0:性别与喜欢 看的电视类型无 H1:性别与喜欢 看的电视类型不
赛事直播 新闻报道 专题报道 精彩赛事集锦 开幕式和闭幕式 其他 合计
实际值
男 261 69 33 36 87 32
518
女 235 42 40 42 108 15
482
合计 496 111 73 78 195 47
CHIINV(0.0 5,5)
CHITEST(D7 :E12,D17:E
P值=
0.0063
CHIDIST(16 .2,5)
统计学方差分析

水平
水平指因素的具体表现,如销售的 四种方式就是因素的不同取值等级。有 时水平是人为划分的,比如质量被评定 为好、中、差。
单元
单元指因素水平之间的组合。如销 售方式一下有五种不同的销售业绩,就 是五个单元。方差分析要求的方差齐就 是指的各个单元间的方差齐性。
元素
元素指用于测量因变量的最小单 位。一个单元里可以只有一个元素, 也可以有多个元素。
SSE ( xijk xij ) 2
i 1 j 1 k 1
有交互作用的双方差分析表 方差来源 离差平方和 SS df 均方和 MS 因素 A SSA r-1 MSA = SSA /(r-1) 因素 B SSB s-1 MSB = SSB /(s-1) 因素 A×B SSAB (r-1)(s-1) MSAB=SSAB/(r-1)(s-1) 误差 SSE rs(t-1) MSE= SSE / rs(t-1) 总方差 SST rst-1
F MSA/MSE
若 F F (r 1, n r) ,则拒绝原假设 H 0
F
MSA ~ F ( r 1, n r ) MSE
两因素方差分析
无交互作用
xij ij ij
xij i j ij , i 1,, r , j 1,, s r s i 0, i 0 ; j 1 i 1
t sp xy 1 1 n1 n2
水平均值
总均值
离差平方和
均方
判断
例题_计算1
例题_计算2
Excel操作
种类
1. 无交互作用的双因素方差分析,它假定因 素A和因素B的效应之间是相互独立的,不 存在相互关系; 2. 有交互作用的方差分析,它假定A、B两个 因素不是独立的,而是相互起作用的,两 个因素同时起作用的结果不是两个因素分 别作用的简单相加,两者的结合会产生一 个新的效应。
统计学习题答案 第7章 方差分析与试验设计

第7章 方差分析与试验设计——练习题(全免)7.1 0215.86574.401.0=<=F F (或01.00409.0=>=-αvalue P ),不能拒绝原假设。
7.2 8853.30684.1705.0=>=F F (或05.00003.0=<=-αvalue P ),拒绝原假设。
85.54.14304.44=>=-=-LSD x x B A ,拒绝原假设; 85.58.16.424.44=<=-=-LSD x x C A ,不能拒绝原假设; 85.56.126.4230=>=-=-LSD x x C B ,拒绝原假设。
7.3554131.3478.105.0=<=F F (或05.0245946.0=>=-αvalue P ),不能拒绝原假设。
7.4 有5种不同品种的种子和4种不同的施肥方案,在20快同样面积的土地上,分别采用5种种子和4种施肥方案搭配进行试验,取得的收获量数据如下表:2592.32397.705.0=>=F F 种子(或05.00033.0=<=-αvalue P ),拒绝原假设。
4903.32047.905.0=<=F F 施肥方案(或05.00019.0=<=-αvalue P ),拒绝原假设。
7.5 9443.60727.005.0=<=F F 地区(或05.09311.0=>=-αvalue P ),不能拒绝原假设。
9443.61273.305.0=<=F F 包装方法(或05.01522.0=>=-αvalue P ),不能拒绝原假设。
7.6 1432.575.1005.0=>=F F 广告方案(或05.00104.0=<=-αvalue P ),拒绝原假设。
9874.5305.0=<=F F 广告媒体(或05.01340.0=>=-αvalue P ),不能拒绝原假设。
方差分析卡方检验练习题

方差分析与卡方检验练习题本练习题涵盖了方差分析和卡方检验的基概念、方法和应用,包含不同难度等级的题目,旨在帮助学习者巩固知识,提高分析问题和解决问题的能力。
第部分:方差分析 (ANOVA)一、单因素方差分析1. 基本概念题 (500字)简述方差分析的基本思想和假设条件。
* 解释方差分析中组间方差、组内方差和总方差的概念,以及它们之间的关系。
* 说明F检的原理以及在方差分析中的应用。
* 解释方差分析结果中的P值及其意义。
* 比较方差分析与t检验的异同点。
2. 计算题 (000字)某研究者想比较三种不同肥料对小麦产量的影响。
他随机选择了三个地块,每个地块种植了相同数量的小麦,分别施用三种不同的肥料A、B、C。
收获后,测得三个地块的小麦产量如下(单位:k/亩):肥料A:15, 18, 16, 17, 19 肥料B:20, 22, 21, 19, 23 肥料C:12, 14, 13, 5, 16请根据以上数据,进行单因素方差分析,判断三种肥料对小麦产量是否有显著性差异。
(需写出详细的计算步骤,包括自由度、平方和、均方、F值、P值等,并进行结果解释。
). 应用题 (1000字)一家公司想比较四种不同广告策略对产品销量的影响。
他们随机选择了四个地区,每个地区采用一种不同的广告策略。
三个月后,测得四个地区的销售额如下(单位:万元):策略A:10, 110, 95, 105 策略B:120, 130, 115, 125 策略C:80, 90, 75,85 策略D:150, 60, 145, 155(1)请根据以上数据,进行单因素方差分析,判断四种广告策略对产品销量是否有显著性差异。
(需写出详细的计算步骤,并进行结果解释。
)(2)如果发现有显著差异,请进行事后检验(例如Tukey检验或LSD检验),找出哪些广告策略之间存在显著性差异。
(需说明所用检验方法的原理和步骤)二、双因素方差分析 (1500字)1. 基本概念题 (50字)•解释双因素方差分析的概念和应用场景。
第七讲卡方检验和方差分析

2 (观察值期望期值望值)2
D3:D5=B3:B5*$B$6
EXCEL的chitest函数计算卡方统计量 后直接报告P值。
由于P值非常 小,有足够的 信心拒绝拟定
假设。
C5:c8=binomdist(b5:b8, $b$2,$b$4,false)
处置内
差异
处置间 差异
X13 X23 X33 X43 X53
处置内
差异
如果处置间差异显著地大于处置内差异, 则认为各样本所来自的总体并非具有相等的平均数
差异的表述
绝对差异的表述:(离差)平方和 相对差异的表述:均方和=(离差)平方和
除以自由度
处置(列)间平方和 处置(列)内平方和 总平方和 总自由度:
Within Groups 427300.0
T o ta l
439835.7
包装 方式 促销 的数 据和 方差 分析 表
ANOVA
M ea n
df
Square
2 6267.857
11 38845.455
13
F .161
Si g. .853
圣地亚哥 25 31 18 23 27
洛杉矶 28 33 35 29 36
假定前提: (1)各总体都服从正态分布; (2)各总体方差相等; (3)样本间相互独立。
程序: (1)提出假设; (2)根据指定的显著水平和观察 值总数目、处置数目确定拒绝的
最小F 值; (3)求出SSC和SSE,计算样本F
值; (4)比较检验统计量,得出结论 。
SALES
Sum of Squares Between Groups 12535.714
商务统计学课件-有交互作用双因素方差分析问题描述

有交互作用双因素方差分析问题描述
因素B 因素A
B1
A1
X111, X112 ,
..., X11t
… Bj
… X1 j1, X1 j2 , ..., X1 jt
…
…
…
…
Ai
X i11, X i12 , ..., X i1t
… X ij1, X ij2 , ..., X ijt
…
…
…
…
X k11, X k12 ,
ij
ijs
ijs ~ N (0, 2 ), 各 ijs独立
i 1, 2,..., k; j 1, 2,..., r; s 1, 2,..., t
X ij
ij ai bj (ab)ij ijs
ijs ~ N (0, 2 ), 各 ijs独立
i 1, 2,..., k; j 1, 2,..., r; s 1, 2,..., t
… ..., X krt
… Tr
… Xr
…
Ti
Xi
…
…
Tk
Xk
总和 总均值
TX
有交互作用双因素方差分析问题描述
所考察的因素记为 A、B
因素 A共有 k个水平 因素B 共有 r个水平
Xijs ~ N ( ij , 2 )(i 1, 2,..., k; j 1, 2,..., r; s 1, 2,...,t) 其中,ij , 2 均未知
1r
i
r ij j1
1k
k j
ij
i1
ai
i
bj
j
i 1, 2,..., k
j 1, 2,..., r i 1, 2,..., k j 1, 2,..., r
方差分析习题及答案

方差分析习题及答案方差分析习题及答案方差分析是一种统计方法,用于比较两个或多个样本均值之间的差异。
它可以帮助我们确定是否存在显著的差异,并进一步了解这些差异的来源。
在本文中,我们将介绍一些方差分析的习题,并提供相应的答案。
习题一:某研究人员想要比较三种不同的肥料对植物生长的影响。
他随机选择了30个植物,并将它们分成三组,每组10个。
每组植物分别使用不同的肥料进行施肥。
研究人员在10天后测量了每组植物的平均生长高度(单位:厘米)。
下面是测量结果:组1:12, 14, 15, 16, 17, 13, 14, 15, 16, 18组2:10, 11, 13, 12, 14, 15, 13, 12, 11, 10组3:9, 10, 8, 11, 12, 13, 10, 9, 11, 12请使用方差分析方法,判断这三种肥料是否对植物生长有显著影响。
答案:首先,我们需要计算每组的平均值和总体平均值。
组1的平均值为15.0,组2的平均值为11.1,组3的平均值为10.5。
总体平均值为12.2。
接下来,我们计算组内平方和(SS_within),组间平方和(SS_between)和总体平方和(SS_total)。
根据公式,我们有:SS_within = Σ(xi - x̄i)^2SS_between = Σ(ni * (x̄i - x̄)^2)SS_total = Σ(xi - x̄)^2其中,xi代表第i组的观测值,x̄i代表第i组的平均值,x̄代表总体平均值,ni代表第i组的样本量。
计算得到:SS_within = 23.0SS_between = 48.6SS_total = 71.6接下来,我们计算均方(mean square):MS_within = SS_within / (n - k)MS_between = SS_between / (k - 1)其中,n代表总样本量,k代表组数。
计算得到:MS_within = 2.56MS_between = 24.3最后,我们计算F值:F = MS_between / MS_within计算得到:F = 9.49根据F分布表,自由度为2和27时,F临界值为3.35。
第八章卡方检验与交互分析

第八章卡方检验与交互分析交互分析是社会调查研究中常用方法之一,用于研究两个定类变量的关系。
交互分析中用于检验两个变量是否相关的方法叫做卡方检验,也叫独立性检验。
卡方检验是建立在观测频次和期望频次之差基础上的一种检验。
一、卡方检验的原理例:一项调查得到890个样本的与收入和所处地区的数据,希望分析收入和地区的关系。
表1要检验的H0:收入和地区之间没有相关性,即每一地区的收入分布模式应该是相同的,收入的高低不应随着地区的不同而有所差异。
也就是说,如果东部城市的四个收入类别各自比重和中西北部城市的四个收入类别各自比重一致,那么,收入和地区之间是相互独立的。
如果这个890人的样本能够反应总体的独立性特征,那么就应该能够观测到两个地区具有相同的收入分布模式,称为期望模式,样本的期望观测频次如下:表2接下来,计算观测频次f0与期望频次f e之间的偏差(f0-f e),如果这些偏差比较小,则有利于证明原假设即总体的独立性。
反之,则可能推翻原假设。
但偏差之和为0,所以对偏差进行平方。
但是,为了说明每一个偏差的相对重要性,每一偏差平方和都需要和本组中的期望频次相比较,计算相对(f0-f e)2/f e。
然后,将所有组的贡献相加,从而得到度量全部偏差的一个量,叫做卡方χ2=∑∑(fo−fe)2,fe服从自由度为(c-1)(r-1)的卡方分布。
如用c 和r 分别表示表中的列数和行数,自由度为(c-1)(r-1)。
f 0 f e(f 0-f e )(f 0-f e )2/f e计算出卡方值后,可根据已知的显著性水平和自由度查卡方分布表,找出临界值,与之作对比。
反过来,也可以计算出概值,再根据我们所希望的显著性水平做比较。
该例题中计算出χ2为31.6,查表发现对应自由度为3的那一行的所有临界值都小于χ2,因此,概值小于0.001。
由于概值如此小,检验水平可以是1%甚至更小,所以一定可以拒绝原假设。
也就是说,在总人口中,收入与地区有显著的相关性,二者并不独立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章方差分析
例1、1977年,美国的某项调查从三种受过不同教育类型的妇女中各分别抽取了50位全日制工作的妇女样本,她们的年收入(单位:千美元)数据整理后归纳如下:
完成的学历年数收入平均值X ()2)
(
∑-X
X
初中(8年)X1 高中(12年)X2 大学(16年)X3 7。
8
9.7
14。
0
1835
2442
4707
解:: =
:三组收入均值有显著差异
F =,即组间均方/组内均方
其中,组间自由度=3—1=2,组内自由度=(50—1)╳3=147
由于样本均值=(7。
8+9.7+14。
0)/3=10。
5
所以组间偏差平方和=50=50*(++)=1009
组内偏差平方和==1835+2442+4707=8984
所以,F = ≈ 8。
2548419 >(2,147)=3。
07
拒绝原假设;认为不同学历的妇女收入存在差异。
例2、月收入数据:
男:2500,2550,2050,2300,1900
女:2200,2300,1900,2000,1800
如果用Y表示收入,哑变量X表示性别(X=1为女性),计算Y对X的回归方程,并在5%的水平下检验收入是否与性别无关(先求回归系数的置信区间).
解:令Y=+X+
根据最小二乘法,可知=
(1)
VAR()=
(2)
=
(3)
计算如下:
:收入与性别无关
收入与性别不完全无关
Y 2500255020502300190022002300190020001800 X 0 0 0 0 0 1 1 1 1 1 240 290 —210 40 —360 160 260 -140 —40 -240 =2150=0。
5
根据公式1,得=—220;,即Y=—220X+
根据公式2、3,得VAR()=≈156.3549577
n=10。
,n-2=8;当df=8时,=2.306
的0。
05置信区间求解方法如下:
-2。
036〈=〈=2。
306,得140.57769。
由于原假设=0落入了这个置信区间,所以接受原假设,认为系数不显著,收入与性别无关。
第二章相关分析
例1、10对夫妇的一个随机样本给出了如下的结婚年龄数据
结婚时丈夫的年龄y 24 22 26 20 23 21 24 25 22 23
结婚时妻子的年龄x 24 18 25 22 20 23 19 24 23 22
1) 计算样本相关系数r;
2)求总体相关系数 的95%置信区间;
3)以5%的水平,检验“夫妻的结婚年龄之间没有什么线性联系”这一原假设。
解:(1)=
由于=22,=23;=≈0.3426
(2)由于se ()=,n=10,df=8
=2.306,所以:
se ()=0.332
-2。
036〈=
〈=2.306
得
1.062072
(3):夫妻的结婚年龄之间没有线性相关,
夫妻的结婚年龄之间不完全没有线性相关,≠0 根据第(2)题的计算结果,
1。
062072
由于的原假设落入了该置信区间,所以接受原假设,认为夫妻的结婚年龄之间没有线性相关关系。
第三章 卡方检验和交互分析
例1、为了研究性别和“最希望看到的有关奥运会的电视节目类型”之间的关系,2004年在10城市调查
了1000个样本,调查数据如下:
男 女 赛事直播 261 235 新闻报道 69 42 专题报道 33 40 精彩赛事集锦 36 42 开幕式和闭幕式 87 108 其他
32
15
1) 陈述0H ;
2) 计算2 和0H 的概值。
解:(1):性别与希望看到的电视节目类型无关
性别与希望看到的电视节目类型不完全无关
(2)理论频数表如下:
男 女 合计 赛事直播 257 239 496 新闻报道 57.5 53。
5 111 专题报道 37。
8 35.2 73 精彩赛事集锦 40。
4 37.6 78 开幕式和闭幕式
101
94
195
性 别
频
次
希望看到的节目类型 性 别
频
次
希望看到的节目类型
其他242347
合计518 482 1000
所以=+ +..。
≈16。
63431164>=11。
07自由度df=1*5=5;
所以拒绝原假设,备择假设成立,性别与希望看到的电视节目类型是有关联的。
