§2 格林公式及其应用
合集下载
格林公式及其应用

思考:如果L 取负向呢?
证明: 设 D 是 X 型区域,
D {( x , y ) a x b , 1 ( x ) y 2 ( x )}
P ( x , y )dx
L
L1
L2
L3
P ( x , y ) dx
L4
Pdx
L1 a b
Pdx
2( y)
1
x 1( y)
y
D
L3
L4
c
x 2( y)
[
c
D
Q ( x , y ) x
( y)
dx ]dy (把Q( x , y )看作x的函数
x dxdy .
Q
用牛顿 莱布尼兹公式)
如果D既是X型又是Y 型,则
L
P ( x , y ) dx
P y
,
则曲线积分 Pdx Qdy在该区域内与路径无关 .
L
( 2 ) 如果
Q x
P y
在复连通域内成立,则
曲线积分
不一定与路径无关。
前例,
xdy ydx x y
2 2
.
L
( 3)由定理的证明过程可知 u ( x, y)
( x, y) ( x 0 , y0 )
P ( x , y ) d x Q( x , y ) d y .
L3
( L2 , L4上 dx 0)
b a
L1 y ( x ) 2
L2
P ( x , 2 ( x )) dx
b a
P ( x , 1 ( x )) dx
证明: 设 D 是 X 型区域,
D {( x , y ) a x b , 1 ( x ) y 2 ( x )}
P ( x , y )dx
L
L1
L2
L3
P ( x , y ) dx
L4
Pdx
L1 a b
Pdx
2( y)
1
x 1( y)
y
D
L3
L4
c
x 2( y)
[
c
D
Q ( x , y ) x
( y)
dx ]dy (把Q( x , y )看作x的函数
x dxdy .
Q
用牛顿 莱布尼兹公式)
如果D既是X型又是Y 型,则
L
P ( x , y ) dx
P y
,
则曲线积分 Pdx Qdy在该区域内与路径无关 .
L
( 2 ) 如果
Q x
P y
在复连通域内成立,则
曲线积分
不一定与路径无关。
前例,
xdy ydx x y
2 2
.
L
( 3)由定理的证明过程可知 u ( x, y)
( x, y) ( x 0 , y0 )
P ( x , y ) d x Q( x , y ) d y .
L3
( L2 , L4上 dx 0)
b a
L1 y ( x ) 2
L2
P ( x , 2 ( x )) dx
b a
P ( x , 1 ( x )) dx
格林公式及其应用

L1 L2 L2
Pdx Qdy Pdx Qdy
L2
Pdx Qdy Pdx Qdy 0,
L1 L1 ( L2 ) L2
Pdx Qdy 0
此时L1 ( L2 )为有向闭曲线,故结论成立, 反之也成立.
3、定理2
设区域G是一个单连通域,函数P( x, y )、Q( x, y ) 在G内具有一阶连续偏导数,则曲线积分 Pdx Qdy
Q y2 x2 P 2 2 2 x ( x y ) y 则
L
xdy ydx x y
2 2
0
(2) 原点在D内时
选取适当小的r 0, 作位于D内的圆周l x2 y2 r 2 记L与l所围的闭区域为D1;
即D1为复连通区域,
l的方向取逆时针方向 有 , xdy ydx x y
P 因 连续,故第一式左边 y 2 ( x ) P ( x, y ) P b dy dx y dxdy a 1 ( x ) y D a Px, 2 ( x) Px,1 ( x)dx
b
第一式右边 Pdx Pdx Pdx
第三节
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径 无关的条件 三、二元函数的全微分求积
一、 格林公式
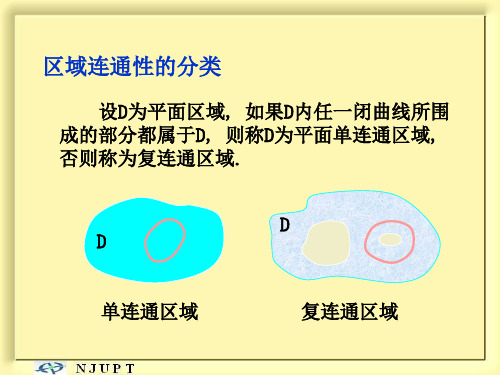
平面单连通区域: 设D为平面区域,如果D内任一闭曲线所围的部
分都属于D,则称D为平面单连通区域,否则称为复连
通区域.
通俗的说,平面单连通区域是不含有“洞”的区
域.
例如 圆形区域: x, y ) x 2 y 2 1} {(
Pdx Qdy
ABPA
Q P x y dxdy Pdx Qdy D3 BCNB
Pdx Qdy Pdx Qdy
L2
Pdx Qdy Pdx Qdy 0,
L1 L1 ( L2 ) L2
Pdx Qdy 0
此时L1 ( L2 )为有向闭曲线,故结论成立, 反之也成立.
3、定理2
设区域G是一个单连通域,函数P( x, y )、Q( x, y ) 在G内具有一阶连续偏导数,则曲线积分 Pdx Qdy
Q y2 x2 P 2 2 2 x ( x y ) y 则
L
xdy ydx x y
2 2
0
(2) 原点在D内时
选取适当小的r 0, 作位于D内的圆周l x2 y2 r 2 记L与l所围的闭区域为D1;
即D1为复连通区域,
l的方向取逆时针方向 有 , xdy ydx x y
P 因 连续,故第一式左边 y 2 ( x ) P ( x, y ) P b dy dx y dxdy a 1 ( x ) y D a Px, 2 ( x) Px,1 ( x)dx
b
第一式右边 Pdx Pdx Pdx
第三节
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径 无关的条件 三、二元函数的全微分求积
一、 格林公式
平面单连通区域: 设D为平面区域,如果D内任一闭曲线所围的部
分都属于D,则称D为平面单连通区域,否则称为复连
通区域.
通俗的说,平面单连通区域是不含有“洞”的区
域.
例如 圆形区域: x, y ) x 2 y 2 1} {(
Pdx Qdy
ABPA
Q P x y dxdy Pdx Qdy D3 BCNB
格林公式及其应用

u ( x, y)
P(x, y)dx Q(x, y)dy y
( x0 , y0 )
x
y
x0 P(x, y0 )dx
Q(x, y)dy
y0
或
u (x, y)
y
y0 Q(x0 , y)dy
x
P(x, y)dx
x0
y0
x0
x
©
格林公式及其应用
例 计算 ( x2 2xy)dx ( x2 y4 )dy.其中L为
y)dy
©
例4续
1 0
1 1+y
y
2
dy
1 1 x 1 1+x 2
dx
0 1 y 11+y2 dy
2
01 1 1+y 2
dy
1 xdx 1 1+x 2
11 11+x2 dx
4
01 11+y 2
dy
0
4(arc tan y)
0 -1
P Q y x
©
证明 (4)
(1)
设L为D中任一分段光滑闭曲线,所围区域为 D D (如图) , 因此在 D上
P Q y x
D D L
利用格林公式 , 得
L
P
d
x
Q
d
y
D
(
Q x
Q x
)dxd
y
0
证毕
©
说明: 根据定理2 , 若在某区域内 P Q , 则 y x
所以
P ( x2 y2 ) 2 y( x-y)
高等数学-格林公式及其应用.ppt

l D1
O D2
x
1
2π
d
1 2π
π
20
2
l :4x2 y2 2
法二
l
ydx xdy 4x2 y2
l
ydx
2
xdy
1
2
ydx xd y
l
格林公式
D2是由l 所围区域
4x2 y2 2
所以 I 0 π
π.
1
2
1
2
(1
D2
(2)
π
2
1)dxdy
2
π
25
10.3 格林公式及其应用
Pdx Qdy
L
(L1, L2, L3对D来说为正方向)
8
10.3 格林公式及其应用
(3) 对复连通区域证明:
对若复区连域通不区止域由D一, 格条林闭公曲式线
的右所曲端围线应成积 包.添分 括加,沿且直区边线域界段D的的A方全B向,部CE对边.区界 G D
域则DD来的说边都界是曲正线向由. AB, L2 , BA,
2π 0
格林公式
sin d(
2
(Q P )dxdy D1 x y 0
cos ) cos d(
2
2
0 sin
)
24
10.3 格林公式及其应用
l
ydx xdy 4x2 y2
2π
sin
d(
2
cos
)
2
cos
d(
sin
)
0
2
2 0
π
2
2
sin
2
2
2
2
cos2
d
y L: x2 y2 4
高等数学-格林公式及其应用

由格林公式知 xdy ydx 0 L x2 10 y 2
(2) L为正方形 x y 1 的正向.
作位于 D内圆周 l : x2 y2 a2 ,
取顺时针方向。
记 D1由 L和 l所围成, 应用格林公式,得
L
xdy x2
ydx y2
xdy ydx Ll x2 y2
xdy ydx l x2 y2
,
0 2
所围面积
1 2 (abcos2 absin2 ) d ab 20 14
例5 计算抛物线 ( x y)2 ax(a 0) 与 x 轴所围成
的面积.
解 ONA为直线 y 0.
曲线 AMO 由函数
y ax x, x [0,a]表示,
M
N
A(a,0)
1
A xdy ydx
计算
L
xdy x2
ydx , y2
(1) L为圆周(x 1)2 ( y 1)2 1的正向.
(2) L为正方形 x y 1的正向.
解 记 L所围成的闭区域为 D,
令
P
y x2 y2
,
Q
x2
x
y2
,
则当
x2 y2 0
时,有
Q x
y2 x2 ( x2 y2 )2
P .
y
(1) L为圆周(x 1)2 ( y 1)2 1的正向.
高等数学
第二十讲
第三节
第十一章
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径无关的 等价条件
一、 格林公式
区域 D 分类 单连通区域 ( 无“洞”区域 )
L
多连通区域 ( 有“洞”区域 )
D
域 D 边界L 的正向: 域的内部靠左
(2) L为正方形 x y 1 的正向.
作位于 D内圆周 l : x2 y2 a2 ,
取顺时针方向。
记 D1由 L和 l所围成, 应用格林公式,得
L
xdy x2
ydx y2
xdy ydx Ll x2 y2
xdy ydx l x2 y2
,
0 2
所围面积
1 2 (abcos2 absin2 ) d ab 20 14
例5 计算抛物线 ( x y)2 ax(a 0) 与 x 轴所围成
的面积.
解 ONA为直线 y 0.
曲线 AMO 由函数
y ax x, x [0,a]表示,
M
N
A(a,0)
1
A xdy ydx
计算
L
xdy x2
ydx , y2
(1) L为圆周(x 1)2 ( y 1)2 1的正向.
(2) L为正方形 x y 1的正向.
解 记 L所围成的闭区域为 D,
令
P
y x2 y2
,
Q
x2
x
y2
,
则当
x2 y2 0
时,有
Q x
y2 x2 ( x2 y2 )2
P .
y
(1) L为圆周(x 1)2 ( y 1)2 1的正向.
高等数学
第二十讲
第三节
第十一章
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径无关的 等价条件
一、 格林公式
区域 D 分类 单连通区域 ( 无“洞”区域 )
L
多连通区域 ( 有“洞”区域 )
D
域 D 边界L 的正向: 域的内部靠左
《格林公式及其应用》PPT课件

n (cos,cos).
v nds L
(P cos Q cos)ds
L
由格林公式
Pdy Qdx =========
(P Q )d .
L
D y x
(格林公式的另一种形式)
称函数
为平面向量场 v (P(x, y),Q(x, y))
的散度.物理意义:稳定流体通过某一闭曲线的流量,等
于其散度在该闭曲线所的区域上的二重积分之值.
(x y)dx (x y)dy
( L )
x2 y2
0dxdy 0.
D1
首页
上页
返回
下页
结束
铃
这里(L ) 表示多连通区域 D1的正向边界曲线 .这时L按 逆时针方向,而按顺时针方向.因而
(x y)dx (x y)dy
( L )
x2 y2
(x y)dx (x y)dy (x y)dx (x y)dy,
(x y)dx (x y)dy
L
x2 y2
1 r2
2 [r2 (cost sin t)(sin t) r2 (cost sin t)(cost)]dt
0
2
0 1dt 2.
例 4 设函数u(x,y)在有界闭区域D上有连续的二阶
偏导数,L 为D 的边界且逐段光滑.证明:
u
L
u n
ds
y
x
(x2 y)dx (x y2 sin3 y)dy, AO
oA
(x2 y)dx (x y2 sin3 y)dy
AO
0 x2dx 8 .
2
3
首页
上页
返回
下页
结束
铃
当曲线积分 (x2 y)dx (x y2 sin3 y)dy 与路径无 AB
格林公式及其应用 (2)45页PPT文档
D
(
Q x
P y
)dxdy
L
Pdx
Qdy
(1)
其中 L是 D的取正向的边界曲线,
公式(1)叫做格林公式.
L1
D
L2
L1
D
L2
L由 L1与 L2连成 L由 L1与 L2组成
边界曲线L的正向 当观察者沿边界行走时, 区域D总在他的左边。
y
证明 (1)
d
E y2(x)
若区域 D既是 X 型 x1(y)
L L l lD ( Q x P y)dx d l y
要求右端的二重积分及曲线l积分易于计算。l 选用直线段、折线、圆、半圆、椭圆、抛物线等。
(3)如在D上P、Q一阶偏导连续,且处处有
Q P , x y
则 L 0;
如
D
内除点
M 0(x0,y0)外均有
Q x
P y
,
则
Ll
其中 l 是包围点(x0,y0)的与 L同向的光滑的简 单闭曲线,特别地 l 是以(x0,y0)为中心的圆、椭圆 等(半径或长短半轴大小不限,只要内部没有别的
Dx
c 1(y) x
d
d
cQ (2 (y )y ) ,d y cQ (1 (y )y ) ,dy
y
Q (x ,y )d yQ (x ,y )dy
CBE
CAE
d
x1(y)
Q (x ,y )d yQ (x ,y )dy
CBE
EAC
c
LQ(x,y)dy
o
E D
C
x2(y)
x
同理可证 D P ydx dL yP(x,y)dx
由 O x 于 A d 0 ,y Bx O d 0 ,y
格林公式及其应用

P dxdy
b
dx
2 ( x) P dy
D y
a
1( x) y
y
b
a{P[ x,2( x)] P[ x,1( x)]}dx.
L2 : y 2( x)
D
Pdx Pdx Pdx
L
L1
L2
L1 : y 1( x)
Oa
bx
b
a
a P[ x,1( x)]dx b P[ x,2( x)]dx
L l
xdy ydx 4x2 y2
0,
于是I
L
xdy ydx 4x2 y2
l
xdy ydx 4x2 y2
1 a2
xdy ydx
l
2 a2
(l所围的椭圆区域的面积)
2 a2
a2π 2
π.
感谢下 载
I1 I2
由格林公式
I1
D
Q x
P y
dxdy
D
(b
a)dxdy
(b
a)
πa 2 2
由于OA在x轴上, y 0, dy 0,
故I2
2a
(bx)dx
2a 2b,
0
于是
I
I1
I2
π 2
2 a 2b
πa3. 2
(2)简化二重积分
例4 计算 e y2dxdy, D :以O(0,0), A(1,1), B(0,1)
线y 2ax x2到点O(0,0)的有向弧段.
解 Q e x cos y a, x P ex cos y b, y
y
D
O
Ax
Q x
P y
b
a,
添加辅助线OA,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 =0,从而 因为 是 基 本 解 , 所 以 ∆ M0 r rM 0 M M0M 由叠加原理, (见引 ∆R( M 0 ) = 0 。由叠加原理, ∆V ( M 0 ) = F ( M 0 ) 。 见引 (
1
力场势函数) 。 力场势函数)
1 F ( M ) 可理解为电荷体密度或质量密度。 称为体位势: 可理解为电荷体密度或质量密度。 − ∆ V ( M 0 ) 称为体位势: 4π
(2.11)
证 明: 将调和函数基本积分公式应用到Γa 上有:
1 ∂ 1 1 ∂u u( M 0 ) = − ∫∫ u r − r dS = 0 4π Γa ∂n r r ∂n
上页 下页 返回
1 1 1 ∂ 1 在Γa 上 = , r = − 2 ,所以 r a ∂n r a 1 ∂u 1 ∂u r r ∫∫ r ∂n dS = a ∫∫ ∂n dS = 0 Γa Γa
1 1 1 ∂u ∂ 1 1 ∂u − ∫∫∫ ∆udΩ = ∫∫ u r − r dS + 2 ∫∫ udS − ∫∫ r dS r ∂n r r ∂ n ε Γε ∂n ε Γε Ω\ Kε Γ
ε ε ε
上页 下页 返回
1 ∂u 1 ∂u dS , 即 u∗ 和 udS , r = 记u = 2 ∫∫ r 2 ∫∫ 4πε Γε ∂n 4πε Γε ∂n
当 u 是Ω 内的调和函数, M 0 ≠ Ω ,则由格林第二公式 有:
∂ 1 u( M ) r ∫∫ ∂n rM 0 M Γ
1 ∂u( M ) − r dS = 0 r ∂n M0M
当 u 是 Ω 内的调和函数,M 0 ∈ ∂Ω = Γ ,类似基本积分公 内的调和函数, 式的推导, 式的推导,记 Γε′ = Γε I Ω , Γ ′ = Γ \ K ε ,则有
为所给调和函数, 证明 格林第二公式中取 u 为所给调和函数, v ≡ 1, ∂u 则得 ∫∫ r dS = 0 。 □ ∂n Γ ∆u = 0 ( in Ω ) 由此定理可知,诺伊曼内问题 ∂u 有解 r ∂n = g (on Γ )
的必要条件为 ∫∫ gdS = 0 。
Γ
上页 下页 返回
Ω Γ Γ
由于 u∆v = ∇ ⋅ (u∇v ) − ∇u ⋅ ∇v ,则由高斯公式可得
∂v 格林第一公式: 格林第一公式: ∫∫∫ u(∆v)dΩ = ∫∫ u r dS − ∫∫∫ ∇u ⋅ ∇vdΩ ∂n Ω Γ Ω
∂u ∂v 格林第二公式: 格林第二公式: [u(∆v) − v(∆u)]dΩ = ∫∫ u r − v r dS ∫∫∫ ∂n ∂n Ω Γ r 的单位外法向量。 其中 n 是 Γ 的单位外法向量。
0
1 1 ∂u( M ) ∂ 1 − u( M 0 ) = − ∫∫ u( M ) r r dS M 4π Γ ∂n rM 0 M rM 0 M ∂n 1 F (M ) dΩ M − ∫∫∫ 4π Ω rM 0 M
作为 M 0 的 函数,记
基本积分公式
当 u 是 Ω 内的调和函数时,即 ∆u = 0 时,若 M 0 ∈ Ω ,则 内的调和函数时,
1 1 ∂u( M) ∂ 1 − u( M0 ) = − ∫∫ u( M) r r dS 4π Γ ∂n rM0M rM0M ∂n
调和函数基本积分公式 上页 下页 返回
上页 下页 返回
2)调和函数的积分表达式
考察函数
v( x, y, z ) =
1 rM 0 M
=
1 ( x − x0 ) 2 + ( y − y0 ) 2 + ( z − z0 ) 2
容 易 验 证 , 当 M = ( x , y , z ) ≠ M 0 = ( x0 , y0 , z0 ) 时 , 1 ∆v = 0 。 见 P73 习题 1) v = ( ) 称 为 三维拉普拉 斯 rM 0 M 方程的基本解。
设 u = u( x , y , z ) ∈ C 2 ( Ω ) I C 1 ( Ω ) , M 0 = ( x 0 , y 0 , z 0 ) 是Ω 内一定点。
上页 下页 返回
第二公式, 充分小, 为球心, 为利用 Green 第二公式, ε 充分小, 取 使得以 M 0 为球心, 不相交, 半径为 ε 的球 K ε 的球面 Γε 与 Ω 的边界 Γ 不相交, 则在复连
利用体位势, 利用体位势,可将泊松方程的求解问题通过叠加原理化为调和方 程的求解问题。 程的求解问题。
上页 下页 返回
4)调和方程的诺伊曼内问题有解的必要条件
定理 2.1 设 u ∈ C 2 ( Ω ) I C 1 ( Ω ) , ∆u = 0 ( in Ω ) ,则 ∂u r ∫∫ ∂n dS = 0。 Γ
中的有界开集, 设 Ω 是 R 中的有界开集,Γ = ∂Ω ,u ∈ C (Ω ) I C ( Ω ) ,
2
2
1
则对∀M 0 ∈ Ω ,有 1 1 1 ∂u( M) ∂ − ln u( M0 ) = − ∫ u( M) r ln r dsM 2π Γ rM0M ∂n ∂n rM0M
∗
∗
∂u ∂u 的面积, 示 Γε′ 的面积, u 和 r 分别为 u 和 r 在 Γε′ 上的 即 ∂n ∂n 平均值, 平均值,则
∗
∗
σ ( ε ) ∗ σ ( ε ) ∂u ∂ 1 1 ∂u r r r ∫∫′ u ∂n r − r ∂n dS = − ε 2 u + ε ∂n Γ σ(ε ) 1 ∗ = ,上式两边令 ε → 0 , 因为 lim u = u( M 0 ) , lim 2 ε → 0 4 πε ε→0 2 得 ∂ 1 1 ∂u r r ∫∫ u ∂n r − r ∂n dS = −2πu( M 0 ) Γ
上页 下页 返回
1 ∂ 1 R( M 0 ) = − ∫∫ u( M ) r 4π Γ ∂n rM 0 M
1 ∂u( M ) − r dS M r ∂n M0M
1 F(M ) V ( M 0 ) = − ∫∫∫ dΩ M 4π Ω rM 0 M
1 1 ∂u( M) ∂ 1 − u( M0 ) = − ∫∫ u( M) r r dSM 4π Γ ∂n rM0 M rM0 M ∂n 1 F ( M) dΩM − ∫∫∫ 4π Ω rM0 M
(2.8)
上页 下页 返回
补:二维空间上的基本积分公式以及调和函数的 基本积分公式
∗
∗
∂u ∂u r 分别为u 和 r 在Γε 上的平均值,则 ∂n ∂n ∗ 1 ∂ 1 1 ∂u ∂u ∗ − ∫∫∫ ∆udΩ = ∫∫ u r − r dS + 4πu − 4πε r r ∂n r r ∂n ∂n Ω\ Kε Γ
∗
令 ε → 0 ,则
1 ∂ 1 1 ∂u − ∫∫∫ ∆udΩ = ∫∫ u r − r dS + 4πu( M 0 ) r ∂n r r ∂n Ω Γ
上页 下页 返回
从而有: 从而有:
1 ∂u( M) 1 ∂ 1 − u( M0 ) = − ∫∫ u( M) r r dS 4π Γ ∂n rM0 M rM0 M ∂n 1 1 − ∫∫∫ ∆udΩ 4π Ω rM0 M
1 通区域 Ω \ K ε 中, ∆v = ∆ r M0 M ≡ 0。
Ω
Kε
在复连通区域 Ω \ K ε 中对上述函数 u 和
v 应用 Green 第二公式,得 第二公式,
∂ 1 1 ∂u 1 1 r r ∫∫∫ u∆ r − r ∆u dΩ = Γ∫∫ u ∂n r − r ∂n dS U Γε Ω\ Kε
1 1 ∂u ∂ 1 1 ∂u r r r ∫∫′ u ∂n r − r ∂n dS = − ε 2 ∫∫ udS + ε ∫∫ ∂n dS ′ ′ Γ Γε Γε
上页 下页 返回
1 1 ∂u ∂u ε 记u = 其中 r r ∫∫ udS , ∂n = σ(ε ) ∫∫ ∂n dS , σ(ε) 表 σ(ε ) Γε′ ′ Γε
上页 下页 返回
∗
设 综上所述, Ω 是以足够光滑的曲面 Γ 为边界的有界 区域,u = u( x , y , z ) ∈ C 2 ( Ω ) I C 1 ( Ω ) ,若 ∆u = 0 ,则:
( M0 ∉ Ω) 0 ∂ 1 1 ∂u u r dSM = 2πu( M0 ) ( M0 ∈ Γ) − − ∫∫ r ∂n rM M rM M ∂n Γ 0 4πu( M ) ( M ∈ Ω) 0 0 0 (2.7) 若 ∆ u = F ( M ) ,则当 M 0 ∈ Ω 时:
上页 下页 返回
3) 泊松方程
利用基本积分公式(2.8)很容易导得泊松方程的一个 很容易导得泊松方程的一个 利用基本积分公式 很容易导得泊松方程 特解表达式。 特解表达式。
事 实 上 , 设 有 函 数 u( M ) ∈ C 2 ( Ω ) I C 1 ( Ω ) , 满 足
ቤተ መጻሕፍቲ ባይዱ
∆u = F ,其中 F ∈ C ( Ω ) ,由(2.8),对∀M 0 ∈ Ω ,
1 1 − ∫∫ ln ∆udσM 2π Ω rM0M
内的调和函数时, 当 u 是 Ω 内的调和函数时,即 ∆u = 0 时,若 M 0 ∈ Ω ,则 有
1
力场势函数) 。 力场势函数)
1 F ( M ) 可理解为电荷体密度或质量密度。 称为体位势: 可理解为电荷体密度或质量密度。 − ∆ V ( M 0 ) 称为体位势: 4π
(2.11)
证 明: 将调和函数基本积分公式应用到Γa 上有:
1 ∂ 1 1 ∂u u( M 0 ) = − ∫∫ u r − r dS = 0 4π Γa ∂n r r ∂n
上页 下页 返回
1 1 1 ∂ 1 在Γa 上 = , r = − 2 ,所以 r a ∂n r a 1 ∂u 1 ∂u r r ∫∫ r ∂n dS = a ∫∫ ∂n dS = 0 Γa Γa
1 1 1 ∂u ∂ 1 1 ∂u − ∫∫∫ ∆udΩ = ∫∫ u r − r dS + 2 ∫∫ udS − ∫∫ r dS r ∂n r r ∂ n ε Γε ∂n ε Γε Ω\ Kε Γ
ε ε ε
上页 下页 返回
1 ∂u 1 ∂u dS , 即 u∗ 和 udS , r = 记u = 2 ∫∫ r 2 ∫∫ 4πε Γε ∂n 4πε Γε ∂n
当 u 是Ω 内的调和函数, M 0 ≠ Ω ,则由格林第二公式 有:
∂ 1 u( M ) r ∫∫ ∂n rM 0 M Γ
1 ∂u( M ) − r dS = 0 r ∂n M0M
当 u 是 Ω 内的调和函数,M 0 ∈ ∂Ω = Γ ,类似基本积分公 内的调和函数, 式的推导, 式的推导,记 Γε′ = Γε I Ω , Γ ′ = Γ \ K ε ,则有
为所给调和函数, 证明 格林第二公式中取 u 为所给调和函数, v ≡ 1, ∂u 则得 ∫∫ r dS = 0 。 □ ∂n Γ ∆u = 0 ( in Ω ) 由此定理可知,诺伊曼内问题 ∂u 有解 r ∂n = g (on Γ )
的必要条件为 ∫∫ gdS = 0 。
Γ
上页 下页 返回
Ω Γ Γ
由于 u∆v = ∇ ⋅ (u∇v ) − ∇u ⋅ ∇v ,则由高斯公式可得
∂v 格林第一公式: 格林第一公式: ∫∫∫ u(∆v)dΩ = ∫∫ u r dS − ∫∫∫ ∇u ⋅ ∇vdΩ ∂n Ω Γ Ω
∂u ∂v 格林第二公式: 格林第二公式: [u(∆v) − v(∆u)]dΩ = ∫∫ u r − v r dS ∫∫∫ ∂n ∂n Ω Γ r 的单位外法向量。 其中 n 是 Γ 的单位外法向量。
0
1 1 ∂u( M ) ∂ 1 − u( M 0 ) = − ∫∫ u( M ) r r dS M 4π Γ ∂n rM 0 M rM 0 M ∂n 1 F (M ) dΩ M − ∫∫∫ 4π Ω rM 0 M
作为 M 0 的 函数,记
基本积分公式
当 u 是 Ω 内的调和函数时,即 ∆u = 0 时,若 M 0 ∈ Ω ,则 内的调和函数时,
1 1 ∂u( M) ∂ 1 − u( M0 ) = − ∫∫ u( M) r r dS 4π Γ ∂n rM0M rM0M ∂n
调和函数基本积分公式 上页 下页 返回
上页 下页 返回
2)调和函数的积分表达式
考察函数
v( x, y, z ) =
1 rM 0 M
=
1 ( x − x0 ) 2 + ( y − y0 ) 2 + ( z − z0 ) 2
容 易 验 证 , 当 M = ( x , y , z ) ≠ M 0 = ( x0 , y0 , z0 ) 时 , 1 ∆v = 0 。 见 P73 习题 1) v = ( ) 称 为 三维拉普拉 斯 rM 0 M 方程的基本解。
设 u = u( x , y , z ) ∈ C 2 ( Ω ) I C 1 ( Ω ) , M 0 = ( x 0 , y 0 , z 0 ) 是Ω 内一定点。
上页 下页 返回
第二公式, 充分小, 为球心, 为利用 Green 第二公式, ε 充分小, 取 使得以 M 0 为球心, 不相交, 半径为 ε 的球 K ε 的球面 Γε 与 Ω 的边界 Γ 不相交, 则在复连
利用体位势, 利用体位势,可将泊松方程的求解问题通过叠加原理化为调和方 程的求解问题。 程的求解问题。
上页 下页 返回
4)调和方程的诺伊曼内问题有解的必要条件
定理 2.1 设 u ∈ C 2 ( Ω ) I C 1 ( Ω ) , ∆u = 0 ( in Ω ) ,则 ∂u r ∫∫ ∂n dS = 0。 Γ
中的有界开集, 设 Ω 是 R 中的有界开集,Γ = ∂Ω ,u ∈ C (Ω ) I C ( Ω ) ,
2
2
1
则对∀M 0 ∈ Ω ,有 1 1 1 ∂u( M) ∂ − ln u( M0 ) = − ∫ u( M) r ln r dsM 2π Γ rM0M ∂n ∂n rM0M
∗
∗
∂u ∂u 的面积, 示 Γε′ 的面积, u 和 r 分别为 u 和 r 在 Γε′ 上的 即 ∂n ∂n 平均值, 平均值,则
∗
∗
σ ( ε ) ∗ σ ( ε ) ∂u ∂ 1 1 ∂u r r r ∫∫′ u ∂n r − r ∂n dS = − ε 2 u + ε ∂n Γ σ(ε ) 1 ∗ = ,上式两边令 ε → 0 , 因为 lim u = u( M 0 ) , lim 2 ε → 0 4 πε ε→0 2 得 ∂ 1 1 ∂u r r ∫∫ u ∂n r − r ∂n dS = −2πu( M 0 ) Γ
上页 下页 返回
1 ∂ 1 R( M 0 ) = − ∫∫ u( M ) r 4π Γ ∂n rM 0 M
1 ∂u( M ) − r dS M r ∂n M0M
1 F(M ) V ( M 0 ) = − ∫∫∫ dΩ M 4π Ω rM 0 M
1 1 ∂u( M) ∂ 1 − u( M0 ) = − ∫∫ u( M) r r dSM 4π Γ ∂n rM0 M rM0 M ∂n 1 F ( M) dΩM − ∫∫∫ 4π Ω rM0 M
(2.8)
上页 下页 返回
补:二维空间上的基本积分公式以及调和函数的 基本积分公式
∗
∗
∂u ∂u r 分别为u 和 r 在Γε 上的平均值,则 ∂n ∂n ∗ 1 ∂ 1 1 ∂u ∂u ∗ − ∫∫∫ ∆udΩ = ∫∫ u r − r dS + 4πu − 4πε r r ∂n r r ∂n ∂n Ω\ Kε Γ
∗
令 ε → 0 ,则
1 ∂ 1 1 ∂u − ∫∫∫ ∆udΩ = ∫∫ u r − r dS + 4πu( M 0 ) r ∂n r r ∂n Ω Γ
上页 下页 返回
从而有: 从而有:
1 ∂u( M) 1 ∂ 1 − u( M0 ) = − ∫∫ u( M) r r dS 4π Γ ∂n rM0 M rM0 M ∂n 1 1 − ∫∫∫ ∆udΩ 4π Ω rM0 M
1 通区域 Ω \ K ε 中, ∆v = ∆ r M0 M ≡ 0。
Ω
Kε
在复连通区域 Ω \ K ε 中对上述函数 u 和
v 应用 Green 第二公式,得 第二公式,
∂ 1 1 ∂u 1 1 r r ∫∫∫ u∆ r − r ∆u dΩ = Γ∫∫ u ∂n r − r ∂n dS U Γε Ω\ Kε
1 1 ∂u ∂ 1 1 ∂u r r r ∫∫′ u ∂n r − r ∂n dS = − ε 2 ∫∫ udS + ε ∫∫ ∂n dS ′ ′ Γ Γε Γε
上页 下页 返回
1 1 ∂u ∂u ε 记u = 其中 r r ∫∫ udS , ∂n = σ(ε ) ∫∫ ∂n dS , σ(ε) 表 σ(ε ) Γε′ ′ Γε
上页 下页 返回
∗
设 综上所述, Ω 是以足够光滑的曲面 Γ 为边界的有界 区域,u = u( x , y , z ) ∈ C 2 ( Ω ) I C 1 ( Ω ) ,若 ∆u = 0 ,则:
( M0 ∉ Ω) 0 ∂ 1 1 ∂u u r dSM = 2πu( M0 ) ( M0 ∈ Γ) − − ∫∫ r ∂n rM M rM M ∂n Γ 0 4πu( M ) ( M ∈ Ω) 0 0 0 (2.7) 若 ∆ u = F ( M ) ,则当 M 0 ∈ Ω 时:
上页 下页 返回
3) 泊松方程
利用基本积分公式(2.8)很容易导得泊松方程的一个 很容易导得泊松方程的一个 利用基本积分公式 很容易导得泊松方程 特解表达式。 特解表达式。
事 实 上 , 设 有 函 数 u( M ) ∈ C 2 ( Ω ) I C 1 ( Ω ) , 满 足
ቤተ መጻሕፍቲ ባይዱ
∆u = F ,其中 F ∈ C ( Ω ) ,由(2.8),对∀M 0 ∈ Ω ,
1 1 − ∫∫ ln ∆udσM 2π Ω rM0M
内的调和函数时, 当 u 是 Ω 内的调和函数时,即 ∆u = 0 时,若 M 0 ∈ Ω ,则 有
