岩石非线性黏弹塑性蠕变模型研究及其参数识别_蒋昱州

合集下载

不同浸润时间下煤岩蠕变力学模型研究

不同浸润时间下煤岩蠕变力学模型研究
张智敏
【期刊名称】《粉煤灰综合利用》
【年(卷),期】2024(38)2
【摘要】以煤岩为研究对象,进行不同浸润时间下的单轴压缩蠕变试验。

试验表明:煤岩在轴向应力加载瞬间,产生瞬时弹性应变,接着出现衰减、稳定蠕变,当加载应力高于长期强度时,表现出加速蠕变行为;通过等时应力-应变曲线求拐点的方式,确定
煤岩长期强度,随着浸润时间的增长而递减。

基于煤岩蠕变的黏弹塑性,确定基础蠕
变模型,利用考虑损伤的Hooke体描述煤岩瞬时弹性应变,分数阶黏滞体表征黏弹
性应变,分数阶黏塑性体反映黏塑性应变,构建一个新的改进后的煤岩蠕变力学模型。

结果表明:改进后模型对煤岩蠕变曲线具有良好模拟效果,能较为准确反映煤岩在不
同浸润时间下的蠕变力学行为。

【总页数】6页(P39-44)
【作者】张智敏
【作者单位】中铁一院集团陕西铁道工程勘察有限公司
【正文语种】中文
【中图分类】TD315
【相关文献】
1.高填方碳酸盐岩块石地基蠕变特性及蠕变力学模型研究
2.不同瓦斯压力下煤岩三轴加载时蠕变规律及模型
3.含瓦斯煤岩三维蠕变特性及蠕变模型研究
4.不同含水率孔周煤岩体蠕变试验及蠕变模型研究
因版权原因，仅展示原文概要，查看原文内容请购买。

基于分数阶导数的岩石非线性蠕变损伤模型

基于分数阶导数的岩石非线性蠕变损伤模型王晴;仇晶晶;朱其志;刘思利;余健【摘要】利用Riemann-Liouville分数阶理论,给出一种分数阶软体元件及其本构方程,阶数取值不同,可分别模拟蠕变的三个阶段.采用两个分数阶软体元件与虎克体进行组合,引入岩石硬化函数、损伤变量,提出一种新的含分数阶导数的非线性蠕变损伤模型,并推导出该模型的本构方程.利用砂岩的蠕变试验数据进行验证,发现该模型能有效描述砂岩的蠕变特性.【期刊名称】《河南科学》【年(卷),期】2019(037)003【总页数】5页(P406-410)【关键词】分数阶;软体元件;非线性蠕变【作者】王晴;仇晶晶;朱其志;刘思利;余健【作者单位】河海大学岩土力学与堤坝工程工程教育部重点实验室,南京 210098;河海大学江苏省岩土工程技术工程研究中心,南京 210098;江苏纬信工程咨询有限公司,南京 210014;河海大学岩土力学与堤坝工程工程教育部重点实验室,南京210098;河海大学江苏省岩土工程技术工程研究中心,南京 210098;河海大学岩土力学与堤坝工程工程教育部重点实验室,南京 210098;河海大学江苏省岩土工程技术工程研究中心,南京 210098;河海大学岩土力学与堤坝工程工程教育部重点实验室,南京 210098;河海大学江苏省岩土工程技术工程研究中心,南京 210098【正文语种】中文【中图分类】TU45在工程实际中，岩石蠕变特性是岩石材料重要力学性质之一，与岩体工程的安全性、稳定性密切相关，因此，岩石蠕变研究越来越被人们重视［1］.国内外研究者多采用元件模型来研究蠕变本构关系，代表性的有Burgers模型、Maxwell模型等，其中的胡克元件仅可描述纯弹性行为，可模拟蠕变线弹性阶段；牛顿体元件仅可描述材料的黏滞性，用以模拟蠕变稳定阶段.基于此，国内外很多学者引进非线性元件来模拟蠕变加速阶段，并适当组合非线性元件和线性元件，从而能更好地模拟蠕变的三个阶段［2-11］.为更好地模拟，必须使用多个元件，导致了模型参数增加.由此，一些学者提出了含参数少、方程简洁的分数阶软体元件.殷德顺等［12］基于分数阶微积分理论，提出一种介于理想固体和流体之间的分数阶软体元件，将该软体元件与弹簧元件分别进行串联和并联得到两种模型，推导出本构方程，与土的试验数据进行比较，发现模型能有效描述蠕变特性；何志磊等［13］改进了西原模型，将西原模型中的牛顿黏壶替换为分数阶Abel黏壶，克服了西元模型不能描述蠕变加速阶段的缺点，得到分数阶非定常蠕变模型；吴斐等［14］引入了分数阶非线性黏壶元件，提出了参数少且可描述蠕变三个阶段的新的岩石蠕变模型；郭佳奇［15］等将Kelvin-Voigt蠕变模型中的牛顿体元件替换为分数阶软体元件，得到分数阶Kelvin-Voigt蠕变模型，与实验数据拟合后，比较发现分数阶Kelvin-Voigt蠕变模型不仅参数更少，且拟合效果比整数阶5参数开尔文蠕变模型和整数解Kelvin-Voigt蠕变模型好.在上述研究基础上，本文讨论了阶数取值对分数阶软体元件的影响，提出了一种新的含有分数阶导数的非线性蠕变损伤模型，利用两个不同阶数的分数阶软体元件，同时引入岩石硬化函数和损伤变量，最后结合砂岩蠕变试验进行验证.1 分数阶非线性蠕变损伤模型建立1.1 含分数阶导数的非线性蠕变损伤模型分数阶微积分定义有多种，本文采用Riemann-Liouville型分数阶微积分算子理论，Riemann-Liouville积分形式为式中：为Gamma函数［15-16］.Riemann-Liouville微分形式为函数 f(t)的r阶Riemann-Liouville分数阶微分［15-16］.将应力-应变关系用分数阶微分形式进行表示，如式（3）：式中：ξ和β均为材料常数.可知，当β=0，式（3）可表示理想固体的应力-应变关系：σ(t)-ε(t)，满足胡克定律；当β=1，式（3）可表示理想流体的应力-应变关系：σ(t)-d1ε(t)/dt1，满足牛顿黏性定律.当σ(t)=const应力恒定时，可描述蠕变现象.对式（3）两边进行积分，可得软体元件的蠕变方程为［17-18］：如图1和图2所示，应力水平保持恒定，当β采用不同值时，由式（4）表示的一系列蠕变曲线.可知，随着β取值的增大，软体元件应力-应变的非线性增加，这与理想固体保持不变的状态和理想流体线性增加的状态不同.从图1可以看出，当0＜β＜1时，随着β增加，软体元件的应力应变关系线性特征逾明显，可以用来描述蠕变的线性、稳态阶段；从图2可以看出，当β＞1时，随着β增加，软体元件的应力应变曲线的斜率越来越大，可以描述蠕变加速阶段.图1 分数阶软体元件的蠕变曲线图（0＜β＜1）Fig.1 Creep curves of fractionalsoftware components（0＜β＜1）由此发现，可以通过调整分数阶的阶数来模拟蠕变的不同阶段，故提出如图3所示模型：第I部分为引入硬化函数的虎克体元件；第II部分为黏弹性分数阶软体元件，其阶数小于1；第III部分为引入损伤变量、阶数大于1的黏塑性分数阶软体元件和应力阈值开关元件并联组成.图2 分数阶软体元件的蠕变曲线图（β＞1）Fig.2 Creep curves of fractional software components（β＞1）图3 含分数阶导数的非线性蠕变损伤模型Fig.3 Nonlinear creep damage model with fractional derivatives1.2 蠕变本构方程对于第I部分，引入硬化函数，由陈化理论［19］可知，材料强度H(σ,t)可表示为式中：H(σ ,t)为材料强度；σ、t分别为应力、时间；H0为初始强度；λ、n为材料常数.本文为方便计算，取n=0.则第I部分的本构方程为对于第II部分，使用黏弹性分数阶软体元件，其阶数小于1，本构方程为式中：γ1,α分别为材料常数和分数阶阶数，且0＜α＜1.对式（7）两边积分，可得第II部分本构方程为对于第III部分，引入损伤变量.根据能量损伤的方法，定义损伤变量为：式中：D(σ,t)表示t时刻材料的损伤变量；E(σ,t)表示任意t时刻的弹性模量，其值与t时刻对应的应力水平有关；E0表示材料初始弹性模量.由经典蠕变损伤模型可定义E(σ,t)为式中：e为自然常数；θ表示材料常数.将式（10）代入式（9），可得由式（11）可知：t→∞时，D=1，表示材料已经完全损伤.易知，随时间t和应力σ增长，试样弹性模量逐渐减小，损伤慢慢变大.Kachanov定义有效应力为式中：为有效应力；σ为名义应力.将式（11）带入式（12），得当σ＞σs（长期强度）时，进入蠕变损伤阶段，则本构方程为式中：γ2,β分别为软体元件的材料常数和阶数，且β＞1.对式（14）积分，并将式（13）代入，得第III部分本构方程为综上，当σ＜σs时，蠕变无加速阶段，模型中仅存在第I、II部分，此时本构方程为当σ＞σs时，蠕变会进入加速阶段，此时模型包含第I、II、III部分，本构方程为2 蠕变实验及模型验证2.1 实验准备及实验结果试验采用全自动岩石三轴伺服仪，如图4所示.试样为砂岩（如图5所示），标准圆柱形，尺寸为50 mm×100 mm（直径×高度）.图4 全自动岩石三轴伺服仪Fig.4 Automatic three-axis rock servo试验室温度控制在（21±0.5）℃内，以减小温度对试验数据的影响.试验期间，先将围压加载至目标值10 MPa，并保持恒定，加载速率3 MPa/min.待围压、温度稳定后，采用轴向应力控制方法加载偏压至目标值（分别为：118、119 MPa），加载速率为0.3 MPa/min.保持温度、偏压稳定，直到试样破坏.蠕变试验曲线如图6所示.图5 砂岩试样Fig.5 Sandstone sample2.2 模型验证及参数识别利用以上蠕变试验数据验证模型，对实验数据进行非线性拟合，得模型参数见表1.由于试样之间的差异性，所得参数存在一定差异.如图7所示，根据拟合结果可知，本文提出的非线性蠕变损伤模型能较好地模拟蠕变试验的全过程.图6 不同强度下的蠕变试验应力-应变曲线Fig.6 Stress-strain curve of creep test under different strength图7 非线性蠕变损伤模型的拟合曲线Fig.7 Fitting curve of nonlinear creep damage model表1 模型参数Tab.1 Parameters of model应力水平/MPa 118 119 λ α β θ0.484 0.456 γ1/（h·MPa-1）0.726×103 0.789×103 0.245 0.286 γ2/（h·MPa-1）3.967×1011 2.177×1011 8.121 9.152 0.301 0.6713 结论1）基于Riemann-Liouville分数阶微积分理论，给出了分数阶软体元件及其本构关系，并发现当分数阶阶数取值小于1时，软体元件可模拟瞬时弹性和稳定蠕变阶段，当阶数取值大于1时，软体元件可以模拟加速蠕变阶段.2）通过两个软体元件与虎克体进行组合，引入硬化函数和损伤变量，增加应力阈值开关，提出含分数阶导数的非线性蠕变损伤模型，并推导出该模型的本构方程.由砂岩试验数据进行验证，提出的非线性蠕变损伤模型能较好地描述蠕变全过程.【相关文献】［1］徐平，杨挺青.岩石流变试验与本构模型辨识［J］.岩石力学与工程学报，2001，20（S1）：1739-1744.［2］徐卫亚，杨圣奇，杨松林，等.绿片岩三轴流变力学特性的研究（I）：试验结果［J］.岩土力学，2005，26（4）：531-537.［3］徐卫亚，杨圣奇，谢守益，等.绿片岩三轴流变力学特性的研究（II）：模型分析［J］.岩土力学，2005，26（5）：23-28.［4］杨广雨，王伟，熊德发，等.岩石非线性黏弹塑性蠕变模型研究［J］.河北工程大学学报（自然科学版），2017，34（4）：23-26.［5］蒋昱州，张明鸣，李良权.岩石非线性黏弹塑性蠕变模型研究及其参数识别［J］.岩石力学与工程学报，2008，27（4）：832-839.［6］赵延林，曹平，文有道，等.岩石弹黏塑性流变试验和非线性流变模型研究［J］.岩石力学与工程学报，2008，27（3）：477-486.［7］张英.岩石流变的一种非线性黏弹塑性流变模型研究［J］.湖南工业大学学报，2015，29（3）：10-14.［8］蒋海飞，胡斌，刘强，等.一种新的岩石黏弹塑性流变模型［J］.长江科学院院报，2014，31（7）：44-48.［9］马明军，钟时猷.一个软弱岩石的粘弹塑性流变力学模型［J］.中南矿冶学院学报，1990，21（3）：236-241.［10］ LIU L，WANG G，CHEN J，et al.Creep experiment and rheological model of deep saturated rock［J］.Transactions of Nonferrous Metals Society of China，2013，23（2）：478-483.［11］ MARANINI E，YAMAGUCHI T.A non-associated viscoplastic model for the behaviour of granite in triaxial compression［J］.Mechanics of Materials，2001，33（5）：283-293.［12］殷德顺，任俊娟，和成亮，等.一种新的岩土流变模型元件［J］.岩石力学与工程学报，2007，26（9）：1899-1903.［13］何志磊，朱珍德，朱明礼，等.基于分数阶导数的非定常蠕变本构模型研究［J］.岩土力学，2016，37（3）：737-744.［14］吴斐，刘建锋，武志德，等.盐岩的分数阶非线性蠕变本构模型［J］.岩土力学，2014，35（S2）：162-167.［15］郭佳奇，乔春生，徐冲，等.基于分数阶微积分的Kelvin-Voigt流变模型［J］.中国铁道科学，2009，30（4）：1-6.［16］何明明，李宁，陈蕴生，等.基于分数阶微积分岩石的动态变形行为研究［J］.岩土工程学报，2015，37（S1）：178-184.［17］宋勇军，雷胜友.基于分数阶微积分的岩石非线性蠕变损伤力学模型［J］.地下空间与工程学报，2013，9（1）：91-95.［18］王学彬.拉普拉斯变换方法解分数阶微分方程［J］.西南师范大学学报（自然科学版），2016，41（7）：7-12.［19］穆霞英.蠕变力学［M］.西安：西安交通大学出版社，1990.。

岩石试件非线性黏弹塑性蠕变模型研究

Ｆｂｕｒ２０ｅｒａｙ０８
岩石试件非线性黏弹塑性蠕变模型研究
刘玉春，赵扬锋
（．辽宁工程技术大学理学院，辽宁阜新１３０１２００；２．辽宁工程技术大学力学与工程科学系，辽宁阜新１３０）２００
［摘
要］蠕变是岩石的重要力学特征之一。根据岩石全过程应力一应变曲线的特征，建立非线
性黏弹塑性蠕变模型，并建立了模型的状态方程、本构方程、恒应力状态下的蠕变方程和恒速率应力
状态下的蠕变方程。通过引入岩石的流变指数建立的非线性黏弹塑性蠕变模型，较好地反映了岩石试
件的３阶段蠕变过程，充分描述岩石加速蠕变特性；同时，得出岩石试件蠕变变形、蠕变速率和蠕变加速度的解析表达式。通过分析，岩石试件在恒应力速率下，只要应力大于岩石的长期强度，岩石试
ＡｂｔａｔＣｅｐｉｎｆｉｏｔｎｏｋｍｅｈｎｃｈｒｃｅｉｔｓａｅｎｒｃｔｅｓｓｒｉｕｖｌｎｏｌｔｐｔｓｒｃ：ｒｅｓｏｅｏｍｐｒｔｃｃａｉｓｃａａｔｒｉ．Ｂｓｄｏｏｋｓｒｓ —ｔａｎｃｒｅａｏｇｃｍｐｅｅａｈ，ａｎｎｌｅａｒｓｃｏ — ｎ — ｉａｉｃｕｌｓｉ— ｌｓｉａｄｃｅｐｍｏｅｓｓｔｐｔｔｅｕｔｎ，ｈｓｃｌｑａｉｎａｄｃｅｐｒｇｌｒｔｉｏｓａｔｔｓｎｅ — ｔｖｓｏｓｅａｔｐａｔｎｒｅｄｌｃｃｗａｅ．Ｓａｅｑａｉｕｏｐｙｉａｅｕｔｎｒｅｅｕａｙｎｃｎｔｎｒｓａｄｐｒｏｉｓｅｍａｅｔａｅｓｒｓｅｅｏｔｉｅ．Ｗｉｏｋｒｅｌｇｃｅｐｎｎｉｌｈｓｃｅｐｍｏｅｏｌｅｔｒｂｈｖ－ｔｇｒｅｒｃｅｉｇｓｎｎｔｔｓｗｒｂａｎｄｒｅｔｒｃｈｏｏｉｘｏｅｔ，ｔｉｒｅｄｌｕｄｂｔｅａｅ３ｓａｅｃｅｐｐｏｅｄｎ，ｅ — ｈａｃｅｐｃａｌｃｅｅａｉｇｃｅｐｓａｅｅｉｌａｃｌｒｔｒｅｔｇ。Ａｎｌｔｘｒｓｉｎｆｃｅｐｄｆｒｔｎ，ｃｅｐｓｅｄａｄｃｅｐａｃｌｒｔｎｏｏｋｓｍｐｅｗｒｙｎａｙｉｅｐｅｓｓｏｒｅｅｏｍａｉｃｏｏｒｅｐｅｎｒｅｃｅｅａｉｆｒｃａｌｅｅｏｇｖｎｉｅ．Ａｎｌｓｓｒｓｌｅｅｓｏｓｆｌｗ．Ｉｅｍａｅｔａｅｓｒｓ，ｏｃｔｓｆｏｋｓｍｐｅｗｓｇｅｔｒｔａｏｇｔｒｔｎｔａｙｉｅｕｔｗｒｈｗｎａｏｌｓｏｎｐｒｎｎｔｔｓｎｅｓｅｓｏｃａｌａｒａｅｈｎｌｎ — ｒｓｒｇｈｒｅｒｒｅａｅｏｃｆｏｋ，ｒｃａｌｏｌｅｃｃｅｅａｉｎｃｅｐｓａｅＨｏｅｅ，ｉｏｓａｔｓｒｓ，ｒｃａｌｏｌｅｃｃｅｅａｉｎｃｅｐｒｏｋｓｍｐｅｗｕｄｒａｈａｃｌｒｔｒｅｔｇ．ｏｗｖｒｎｃｎｔｎｔｓｏｋｓｍｐｅｃｕｄｒａｈａｃｌｒｔｒｅｅｏｓａｅｏｌｆｅｅｔｉｉ。Ｔｉｔｍｅｗｓｍｕｈｒｌｔｄｔｏｋｍｅｈｎｃｈｒｃｅｓｉ。ｔｇｎｙａｔｒｃｒｎｔａｍｅｈｓｉａｃｅａｅｏｒｃｃａｉｓｃａａｔｒｔｉｃＫｅｒｓｒｃｃａｉｓｏ — ｎａｉｏｓｅａｔ — ｌｓｉｒｅｙｗｏｄ：ｏｋｍｅｈｎｃ；ｎｎｌｅｒｖｓｕｌｓｉｐａｔｃｃｅｐ；ｓａｉｔｉｃｃｔｂｌｙｉ

一种用来预测岩石蠕变的流变硬化新模型

后应用到如文献所述的一系列的三轴和单轴测试试验中。我们通过对不同应力下瞬态变形
和蠕变变形的预测检验了模型的潜在应用性。本文还针对数值结果和样品测试结果作了对比性讨论。
１．引言
岩体的时效变形特点对边坡和地下结构的稳定性影响很大（Ｔｓａｉ，２００７）。关于岩土材料
一
种用来预测岩石蠕变的流变硬化新模型
Ｍ．ＫａｒａｍｉＡ．Ｆａｈｉｍｉｆａｒ
ＤｅｐａｒｔｍｅｎｔｏｆＣｉｖｉｌａｎｄＥｎｖｉｒｏｎｍｅｎｔａｌＥｎｇｉｎｅｅｒｉｎｇ，ＡｍｉｒｋａｂｉｒＵｎｉｖｅｒｓｉｔｙｏｆＴｅｃｈｎｏｌｏｇｙ，Ｔｅｈｒａｎ，Ｉｒａｎ
与粘弹模型形成对比并假设蠕变曲线的第一、二、三阶段为完全不可逆形变，一些研究者提出了粘塑模型来评价地下岩石开挖过程中的岩石（主要是岩盐）的长期稳定性（Ｍａｌａｎ，１９９９；Ｗａｌｌｎｅｒ，１９８０４：Ｅｒｉｃｈｓｅｎ，２００３）。但是，完全弹塑性模型的缺点是通过包括卸载和重加载的蠕变试验来研究的，试验中出现了可逆的岩石蠕变变形
２．模型描述
对于多数岩石和地质材料，尤其是在土壤和软岩中，都可观测到硬化蠕变现象

岩石流变的一种非线性黏弹塑性流变模型研究

岩石流变的一种非线性黏弹塑性流变模型研究张英【摘要】将黏滞系数视为非定常量,建立黏滞系数的非线性函数关系,提出一种能描述岩石蠕变全过程的非线性流变力学模型,且在一定条件下模型可蜕变为Burgers 模型或西原正夫模型.推导了岩石在常应力和常应变条件下的流变方程;研究了岩石的非线性蠕变特性和松弛特性.对不同应力条件下的岩石蠕变试验结果进行拟合,并将本文的非线性岩石流变力学模型与试验结果进行比较.结果表明,试验曲线与理论曲线较吻合,从而证明了本模型的正确性与合理性.【期刊名称】《湖南工业大学学报》【年(卷),期】2015(029)003【总页数】5页(P10-14)【关键词】非线性流变模型;流变特性;弹黏塑性【作者】张英【作者单位】重庆地质矿产研究院外生成矿与矿山环境重庆市重点实验室,重庆400042;煤炭资源与安全开采国家重点实验室重庆研究中心,重庆400042【正文语种】中文【中图分类】TU451在外部环境作用下，岩石类材料的应力应变表现出随时间变化而发生变化的现象称为流变。

作为常用的工程材料，岩石的流变力学特性对工程应用影响深远。

工程实例和理论分析表明，岩土工程的变形破坏与时间有密不可分的关系。

流变模型是流变力学理论的研究基础，但由于实际试验条件的限制，岩石流变力学模型研究并不深入，特别是非线性流变力学模型的研究至今尚未有统一共识。

目前对衰减蠕变和稳态蠕变的认识较成熟，多种力学模型如广义凯尔文模型、Burgers模型等，都能较好地描述岩体衰减蠕变和稳态蠕变，而不能对岩体加速蠕变进行准确描述。

关于非线性流变力学模型的研究，人们常对线性流变元件进行改进，通过非线性函数的流变元件来建立非线性流变力学模型，或者基于损伤力学理论、内时理论等新的理论建立流变力学模型。

孙钧[1-2]将黏滞系数视为变量，表示为应力与持续时间的函数。

陈沅江等[3]建立2种非线性元件，并将它们和开尔文体及虎克体相结合，得到了一种新的可较好描述软岩加速蠕变特性的复合流变力学模型。

关于“对‘岩石非线性黏弹塑性流变模型(河海模型)及其应用’的讨论”答复

维普资讯
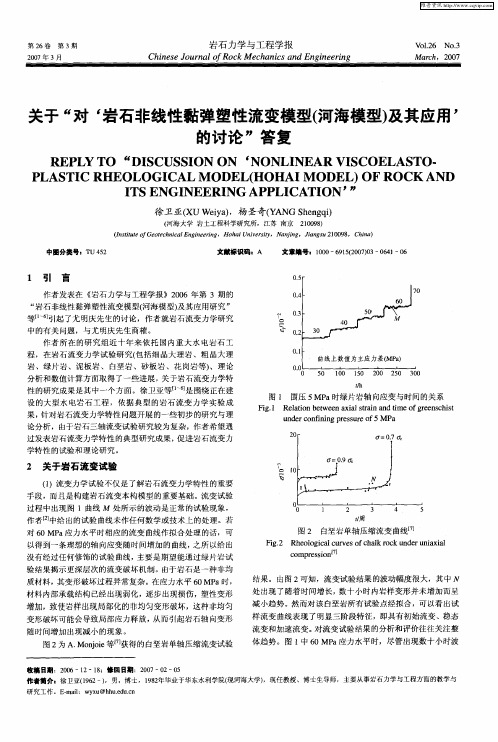
第２６卷
第３期
２００７年３月
岩石力学与工程学报ＣｉｅｅｏｒａＲｃｃａｉｎｎｉｅｒｇｈｎｓｕｎｌｆｏｋＪｏＭｅｈｎｃａｄＥｇｎｅｉｓｎ
、ＩＮＥＥＲＩＮＧＡＰＰＬＩＣＡＴＩＯＮ ’’ ’
徐卫亚（ｕＷｅａ，杨圣奇（ＡＧＳｅｇｉｘｉ）ｙＹＮｈｎｑ）
（河海大学岩土工程科学研究所，江苏南京２０９）１０８
（ｓｔｅｆＧｏｅｈｉｌｎｉｅｒｇＩｔｕｅｔｎｃＥｇｎｅｉ，Ｈｏａｎｖｒｉ，Ｎｎｉｇｉｎｓ１０８ｈｎ）ｎｉｔｏｃａｎｈｉｉｅｓｙａｊ，Ｊｇｕ２０９，ＣｉＵｔｎａａ
中圈分类号：Ｔ５ｕ４２
文献标识码ｌＡ
文章号ｌ００—６１（０７００４～６１０９５２０）３— ６１０
１引
言
作者发表在《岩石力学与工程学报》２００６年第３期的 “ 岩石非线性黏弹塑性流变模型（河海模型）及其应用研究 ” 等Ｉ６１￣引起了尤明庆先生的讨论，作者就岩石流变力学研究中的有关问题，与尤明庆先生商榷。作者所在的研究组近十年来依托国内重大水电岩石工
程，在岩石流变力学试验研究（括细晶大理岩、粗晶大理包岩、绿片岩、泥板岩、白垩岩、砂板岩、花岗岩等）、理论
分析和数值计算方面取得了一些进展，关于岩石流变力学特性的研究成果是其中一个方面。徐卫亚等［６１］－是围绕正在建设的大型水电岩石工程，依据典型的岩石流变力学实验成果，针对岩石流变力学特性问题开展的一些初步的研究与理论分析，由于岩石三轴流变试验研究较为复杂，作者希望通过发表岩石流变力学特性的典型研究成果，促进岩石流变力

基于应变屈服临界的岩石黏弹塑性蠕变模型研究

基于应变屈服临界的岩石黏弹塑性蠕变模型研究蒋昱州;王奔;王瑞红;卢波;李聪;朱杰兵【期刊名称】《长江科学院院报》【年(卷),期】2017(034)011【摘要】为了研究岩石的非线性加速蠕变特性,依据岩石蠕变变形不同阶段的力学特征,划分出了岩石由变形发展至破裂需经历的不同黏弹塑性状态,并给出了相应状态的蠕变力学特性.假定岩石在三轴压缩试验条件下,发生延性剪切破坏,推导了应变空间Drucker-Prager准则的临界状态转化的最大剪应变判别式.基于Perzyna黏塑理论,考虑后继屈服硬化作用,引入统计损伤因子,构建了能描述非线性加速蠕变特性的黏弹塑性损伤演化模型;采用岩石全自动伺服三轴蠕变试验机对三峡库区典型砂岩试样开展了蠕变试验,得到了岩石试样在不同应力水平作用下的蠕变变形曲线.结果表明:蠕变试验中,岩样力学性质的时效特征显著,在最后一级应力水平作用下发生了非线性加速蠕变现象.基于提出的黏弹塑性蠕变模型对试验曲线进行拟合,拟合结果说明模型能够较好地反映砂岩蠕变3个阶段变形的规律特征,拟合效果较好.【总页数】7页(P89-95)【作者】蒋昱州;王奔;王瑞红;卢波;李聪;朱杰兵【作者单位】长江科学院水利部岩土力学与工程重点实验室,武汉430010;长江科学院信息中心,武汉430010;三峡大学三峡库区地质灾害教育部重点实验室,湖北宜昌443002;长江科学院水利部岩土力学与工程重点实验室,武汉430010;长江科学院水利部岩土力学与工程重点实验室,武汉430010;长江科学院水利部岩土力学与工程重点实验室,武汉430010【正文语种】中文【中图分类】TU452【相关文献】1.岩石非线性黏弹塑性蠕变模型研究 [J], 杨广雨;王伟;熊德发;冯晓伟2.岩石试件非线性黏弹塑性蠕变模型研究 [J], 刘玉春;赵扬锋3.水岩耦合作用下岩石黏弹塑性分析及屈服准则研究 [J], 吕洪淼;林晓楠4.基于应变能的岩石黏弹塑性损伤耦合蠕变本构模型及应用 [J], JIANG Peng;PAN Pengzhi;ZHAO Shankun;WU Zhenhua;CHEN Gang5.考虑黏弹塑性应变分离的岩石复合蠕变模型研究 [J], 张亮亮;王晓健因版权原因，仅展示原文概要，查看原文内容请购买。

盐岩蠕变特性及其非线性本构模型

盐岩蠕变特性及其非线性本构模型王军保;刘新荣;郭建强;黄明【摘要】为了研究盐岩的蠕变特性,利用RLW-2000岩石流变试验机对盐岩试件进行了三轴压缩分级加载蠕变试验.试验结果表明:在围压一定的情况下,随着轴向应力增大,盐岩瞬时应变、蠕变应变以及蠕变速率等均随之增大,同时进入稳态蠕变阶段所需要的时间逐渐延长;等时应力-应变曲线显示,盐岩蠕变具有非线性特征,且其非线性程度与蠕变时间和应力水平有关,蠕变时间越长、应力水平越高,非线性程度越高.基于非线性流变力学理论,提出了一种非线性黏滞体,其黏滞系数是所加应力水平和蠕变时间的函数,将非线性黏滞体替换常规Burgers模型中的线性黏滞体,建立了可描述盐岩非线性蠕变特性的MBurgers模型,并根据盐岩蠕变试验结果,采用曲线拟合法对MBurgers模型的参数进行了反演识别.拟合曲线和试验曲线对比显示,两者吻合良好,误差较小,说明该模型可以描述盐岩的蠕变特性.【期刊名称】《煤炭学报》【年(卷),期】2014(039)003【总页数】7页(P445-451)【关键词】盐岩;蠕变特性;非线性模型;参数识别【作者】王军保;刘新荣;郭建强;黄明【作者单位】西安建筑科技大学土木工程学院,陕西西安710055;重庆大学土木工程学院,重庆400045;西安建筑科技大学土木工程学院,陕西西安710055;重庆大学土木工程学院,重庆400045;重庆大学土木工程学院,重庆400045;福州大学土木工程学院,福建福州350108【正文语种】中文【中图分类】TD313;TU45Key words:salt rock;creep properties;nonlinear model;parameters identification蠕变特性作为盐岩典型的力学性质之一,是影响盐岩地下储存库长期稳定性、安全性以及可用性的关键因素。

由于盐岩在能源地下储存方面的重要地位,近年来国内外学者对盐岩蠕变特性及其本构模型进行了较多研究。

岩石非线性黏弹塑性流变模型(河海模型)及其应用

ｍａｅｉ１ｔｒａ．Ｔｈｈｅｏｉａｅｕａｉｎｓｏｏｋａｈｏｓａｔｓｒｓｎｔａｎａｅｅｕｅｅｒｏｌｇｃｌｑｔｏｆｒｃｔｔｅｃｎｔｎｔｅｓａｄｓｒｉｒｄｄｃｄ．Ｔｈｅｎｎｉａｒｅｏｌｎｅｃｅｐｒ
ＭＯＤＥ）ＬＯＦＲＯＣＫＡＮＤＴＮＧＩＥＲＩＡＰＬＣＩＩＳＥＮＥＮＧＰＩＡＴＯＮ
ＸＵＷｅｙ，ＹＮＧＳｅｇｑ，ＣｉｉｎｉａＡｈｎ—ｉＨＵＷｅ－ａｇ — ｊ
（ｓｔｔｏＧｏｃｎｃｌｎｉｅｒｇＩｔｕｅｔｈｉａＥｇｎｅｉ，Ｈｏａｎｖｒｉ，Ｎａｊｎ，Ｊｎｓ１０８ｈｎ）ｎｉｅｆｅｎｈｉｉｅｓｙＵｔｎｉｇｉｇｕ２０９，Ｃｉａａ
缩算例，进。步验证提出的非线性流变模型的正确性与合理性。采ｆ研制的非线性流变数值程序，对锦屏－｝｛Ｉ＝级
水电站坝基岩石工程进行三维流变数值模拟，分析结果为锦屏一级水电站坝基岩石Ｔ程的长期稳定与安全性提
供了合理建议与评价。
ｆｅｃｍｐｎｎｉｃｐａｔｄｌｉｅｉｓａｎｗｅｅ — ｏｏｅｔｎｎｉｅｒｖｓｏｌｓｏｐａｔｈｏｏｉａｉ — ｏｏｅｔｖｓｏｌｓｉｍｏｅｎｓｒｅ，ｅｓｖｎｃｍｐｎｎｏｌａｉｃｅａｔ．ｌｓｃｒｅｌｇｃｌｖｃｎｉ
维普资讯
第２．．．．．
岩石力学与工程学报

对“岩石非线性黏弹塑性流变模型(河海模型)及其应用”的讨论

中圈分类号ｌＵ４８Ｔ５．３
文献标识码ｌＡ
文章缩号ｌ００— ９５２０）３０３０１０６１（０７０ — ６７— ４
１引
言
体表示岩石的理想塑性特征，当应力
时变形为０。
到某一极限值
后，承载能力保持恒定而变形可以持续增大；而应力小于笔者从未进行过岩石流变力学的研究，只是近年讲授岩石力学课程，需要学习相关知识，阅读研究该方面论文。某些论文的试验结果似乎不太可信，对流变模型和模型参数或许有所误解。自认为这是研究生因时间仓促而疏忽所致，但学习了徐卫亚等【的研究成果之后，笔者失去了自信。须ｌ
对“ 岩石非线性黏弹塑性流变模型（河海模型）及其应用 ’的讨论 ’
ＤＩＳＣＵＳＯＮＮ “ ＳＩＯＮＯＮＬＩＮＥＡＲＳＶＩＣＯＥＬＡＳＴＯ．ＰＬＡＳＣＴＩ
ＲＨＥｏＬｏＧＩＣＡＬＭｏＤＥＬＨｏＨＡＩｏＤＥＬ）ＭｏＦＲｏＣＫＡＮＤＴＳＩ
维普资讯
第２卷６
第３期
２００７年３月
岩石力学与工程学报ＣｉｅｅｏｒａＲｃＭｅｈｎｃｎｎｉｅｒｇｈｎｓｕｎｌｆｏｋｃａｉａｄＥｇｎｅｉＪｏｓｎ
、０．６Ｎ０３，２１．Ｍａｃ，２０ｒｈｏ７
理意见。答复是，已将我的文章节录转告作者；作者也予以
图１西原流变模型
Ｆｇ１Ｎｉｈｈｒｅｌｇｃｌｄｌｉ．ｓｉａａｒｏｏｉａｈｍｏｅ

岩石非线性黏弹塑性蠕变模型研究-河北工程大学学报

第34卷第4期河北工程大学学报（自然科学版）V ol.34 No.42017年12月Journal of Hebei University of Engineering (Natural Science Edition)Dec.2017岩石非线性黏弹塑性蠕变模型研究杨广雨1，2，王伟1，2，熊德发1，2，冯晓伟1，2(1.河海大学岩土力学与堤坝工程教育重点实验室，江苏南京 210098；2.河海大学岩土工程科学研究所，江苏南京 210098)摘要：提出一种新的非定常粘滞系数的流变元件，然后将提出的非线性流变元件引进到Poyting-Thomson 模型中，从而建立了新的非线性黏弹塑性流变模型，该模型不但可以较好地模拟岩石蠕变三个阶段，而且模型参数较少。

推导出模型的本构方程及蠕变方程，并探讨了模型参数的辨识方法，最后利用本文建立的非线性流变模型所得到的理论曲线与砂岩蠕变试验曲线进行对比分析。

结果表明：本文建立的非线性流变模型具有较高的准确性及合理性。

关键词：岩石流变；非线性元件；加速蠕变；饱依丁-汤姆逊模型中图分类号：TU43 文献标志码：AStudy on nonlinear viscoelasto-plastic creep model of rockYANG Guangyu 1，2，WANG Wei 1，2，XIONG Defa 1，2，FENG Xiaowei 1，2(1.Key Laboratory of Ministry of Education For Geotechnical & embankment Engineering ，Hohai University ，Nanjing 210098，China ；2.Geotechnical Research Institute ，Hohai University ，Nanjing 210098，China)Abstract ：In this paper ，a new rheological component with unsteady viscous coefﬁcient is proposed ，then connecting the proposed nonlinear rheological component with the Poyting-Thomson model ，a new nonlinear viscoelastic-plastic rheological model is established. The model can not only simulate the three stages of rock creep ，but also has less model parameters. In this paper ，the constitutive equation and creep equation of the model are deduced ，and the identiﬁcation method of the model parameters is discussed. Finally ，the theoretical curves obtained by the nonlinear rheological model established in this paper and the sandstone creep test curves is compared and analyzed. The results show that the nonlinear rheological model established in this paper has good accuracy and rationality.Key words ：rock rheology ；nonlinear component ；accelerative creep ；Poyting-Thomson model收稿日期：2017-07-14基金项目：国家自然科学基金资助项目(11672343，51679069)；中央高校基本科研业务费专项资金资助项目(2016B20214)作者简介：杨广雨(1993-)男，河南驻马店人，硕士，从事岩石力学与工程方面的研究。

一种非定常参数的岩石蠕变本构模型

一种非定常参数的岩石蠕变本构模型罗润林;阮怀宁;孙运强;朱昌星【摘要】在前人的研究基础上提出了一种新的非定常参数的岩石蠕变模型,该模型由一个牛顿体和一个类似于开关的SO元件并联后与一个广义Kelvin体串联,通过SO元件的作用,新模型可以在Burgers模型与广义Kelvin模型之间切换,并将Burgers模型中牛顿体的粘滞系数η1看成与时间有关的非定常参数,使得模型不仅可以反映稳态蠕变过程也可以反映加速蠕变过程.【期刊名称】《桂林理工大学学报》【年(卷),期】2007(027)002【总页数】4页(P200-203)【关键词】非定常参数;蠕变;本构模型;Burgers模型;Kelvin 模型【作者】罗润林;阮怀宁;孙运强;朱昌星【作者单位】河海大学,岩土工程研究所,南京,210098;河海大学,岩土工程研究所,南京,210098;新疆石油管理测井公司研究所,新疆,克拉玛依,834000;河海大学,岩土工程研究所,南京,210098【正文语种】中文【中图分类】TU452大量的试验数据和工程实践表明，岩石的流变破坏普遍存在，许多岩体工程的破坏都因岩石流变破坏而引起，并在破坏前都有加速流变过程.根据目前的研究结果，描述岩石蠕变的本构模型主要有经验模型、元件组合模型、内时理论模型和屈服面模型等［1］. 元件模型是用模型元件线性组合来模拟岩土的流变行为，可以描述岩石的定常蠕变和衰减蠕变［2］. 但是，其力学性质单一，通过参数调整仍然无法定量模拟实测的应力－应变－时间曲线，特别是无法表现岩石的破坏特性，也即不能描述岩石的加速蠕变. 于是，研究人员将目光投向非线性理论，采用非线性元件( 如非线性弹性元件、非线性粘性元件等) 代替传统模型中部分或者全部线性元件. 金丰年等［3］基于试验结果，结合传统线性粘弹性模型的分析，提出了非线性粘弹性模型. 邓荣贵等［4］引进一种非线性粘滞阻尼器，该阻尼器所受应力与其蠕变加速度大小成正比，将该元件与其他元件组合形成一种新的复合元件，并在工程中得到了应用. 韦立德［5］等根据粘聚力在流变中的作用，建议采用一个类似于开关的SO 元件，并由此建立了一维粘弹塑性本构模型. G. N. Boukharov［6］于1995 年提出了一种具有一定质量的延迟阻尼器元件，该元件有一应变门槛值，当应变大于该值时，模型发生加速运动. 徐卫亚［7］提出了一个考虑粘聚力与内摩擦系数的岩石非线性粘塑性体，并与五元件粘弹性模型串联建立非线性粘弹塑性流变模型. 陈沅江［8］等引入一种变截面积的阻尼器来模拟岩石的加速蠕变. 曹树刚等［9］采用非牛顿体粘性元件构成五元件的改进西原正夫模型，探讨了与时间有关的软岩一维和三维本构方程和蠕变方程. 张向东［10］等基于泥岩的三轴蠕变试验结果，建立了泥岩的非线性蠕变方程，并以此分析了围岩的应力场和位移场. 王来贵等［11］以改进的西原正夫模型为基础，利用岩石全程应力-应变曲线与蠕变方程中参数的对应关系，建立了参数非线性蠕变模型.许宏发［12］通过对等时应力－应变曲线分析认为，弹模与时间符合指数的关系. 受此启发，丁志坤［13］提出了一种非定常参数的H－K 模型，与定常参数的模型对比发现，非定常模型能够更为准确地反映岩石的粘弹性变形性能. 本文为了能够同时描述岩石的稳态蠕变和加速蠕变过程，提出一种新的非定常参数岩石蠕变模型.1 岩石的定常参数蠕变模型大量的试验显示，岩石在不同应力下的蠕变特性可以归纳为图1 的3 种曲线. 曲线I 和曲线II为应力较低时的岩石的稳态蠕变曲线，曲线I 在初始蠕变后进入速率为零的稳态蠕变，曲线II 在初始蠕变后进入速率为一常数的稳态蠕变. 曲线III具有初始蠕变、稳态蠕变和加速蠕变3 个阶段.对于曲线I 和曲线II，已有传统的元件组合模型可以描述，如Burgers 模型可以描述曲线II 的蠕变过程.Burgers 模型是一种粘弹性蠕变模型，由一个广义Kelvin 体和一个牛顿体串联而成 ( 图2) .Burgers 模型的蠕变方程可以表示为［14］：从图3 的Burgers 模型的蠕变曲线可以看出，该模型描述图1 中的曲线Ⅱ时，稳态蠕变速率趋于σ0/η1，也就是说，稳态蠕变速率的大小取决于牛顿体的粘滞系数η1. 由于该模型有串联牛顿体元件，所以不能反映I 型曲线. 同样，由于牛顿体的粘滞系数η1是一常数，从而限制了Burgers 模型对加速蠕变过程描述.图1 3 种典型的岩石蠕变曲线Fig.1 3 kinds of typical creep curves图2 Burgers 模型Fig.2 Burgers model图3 Bugers 模型的蠕变曲线Fig.3 Creep curve of Burgers model2 非定常参数的Burgers 蠕变模型前人的研究结果表明，岩石在不同荷载下都存在图1 中的3 种曲线，当荷载较小时蠕变过程如曲线I 所示，当荷载大于某一门槛值σs 时，岩石的蠕变过程可以由图1 中的曲线II 来描述. 如上所分析，由于串联有牛顿体元件，传统的Burgers模型不能描述图1 中稳态速率为0 的蠕变曲线I.然而广义Kelvin 可以很好地描述稳态蠕变过程［14］.从图2 及式( 1) 可以看出Burgers 模型是由广义Kelvin 模型和一个牛顿体串联而成. 因此，可以采用一个开关元件与牛顿体并联：当荷载σ ＞σs时，开关开，牛顿体起作用，模型变成Burgers 模型，可以描述II 型曲线;σ≤σs 时开关关闭，牛顿体不起作用，模型变成广义Kelvin，可以描述I型曲线. SO 元件就是这样一个开关元件［5］，元件图形如图4 所示.图4 SO 元件Fig.4 SO component其应力应变关系：当σ≤σs 时，元件的应变为0; 当σ ＞σs 时，元件的应变为任意值. 该元件与圣维南体有点类似，所不同的是，圣维南体的σ's 是达到塑性应变时的应力，并且分担大小为σ's 的荷载. 而SO 元件的σs 则是一个门槛值，反映蠕变进入II 型曲线时的应力值，可能会小于σ's，且不分担荷载.将SO 模型与Burgers 模型组合形成的新模型如图5 所示. 该模型的数学表示为图5 本文提出的非定常参数的蠕变模型Fig.5 Non-stationary parameters creep model当σ ≤σs 时，新模型为广义Kelvin 体当σ ＞σs 时，模型为式(1) 的Burgers 体.这样，新模型可以反映岩石蠕变过程的I 型曲线和II 型曲线.丁志坤等［13］为了更好反映岩石的粘弹性变形性能，将广义Kelvin 体的E2参数采用与时间有关的非定常参数E2( t) 来表示，并取得了很好的效果.本文中E2( t) 仍然采用此表述，即从上一节分析知道，由于Burgers 模型中的η1为一常数而不能描述岩石蠕变的加速过程( 图1中曲线III) ，如果将η1 也采用与时间有关的非定常参数η1( t) 即可以解决这一问题.由于粘滞系数随时间不断减小，初始减小不明显，而当应变大于某一值时，粘滞系数突然加速减小，最终导致粘滞力为0 使得岩石破坏［6，8，13］，楼志文［15］、金丰年［16］指出岩石的损伤变量D 与时间t呈指数型关系. 由此，可以假设η1( t) 符合指数衰减的规律，即由式(2) 、(5) 和(6) 可以得到图5 模型的表达式H( σ－σs) 的含义与式(3) 一致.3 模型应用研究图6 中的虚线是某泥质板岩的单轴压缩蠕变试验结果［12］. 在不同荷载下，岩石出现不同的蠕变过程，在该试验中出现了图1 的3 种类型曲线.采用粒子群算法［17］，利用本文提出的模型( 式(7) ) 对该试验数据进行参数识别. 参数识别时，根据先验知识给出模型的范围，在此范围随机生成20 个粒子形成粒子群，当全局最优粒子的拟合误差小于1%或者迭代40 次，辨识完成. 如果没有先验知识，可以通过试算的方法进行辨识，即先给出模型的范围，如果某个模型参数与其边界接近，那么可以放宽模型的边界( 如果与下界接近，减小下界; 如果跟上界接近，则增大上界)再进行识别. 从拟合结果( 图6) 看出，本文提出的非定常参数蠕变模型与试验结果非常吻合，表明该蠕变模型不仅可以反映岩石的稳态蠕变过程，也能很好地反映岩石的加速蠕变过程. 从拟合误差( 表1) 来看，不同荷载下的拟合误差都很小，最大的拟合误差只有1.22%，最小拟合误差为0.56%.图6 蠕变试验曲线和理论曲线Fig.6 Curves of experiment vs. theory表1 参数识别结果Table 1 Identified results of parameters荷载/MPa E1/Gpa p1/GPa p2/GPa p3/1·d－1 η2/( GPa·d－1)η10/( GPa·d－1) a/10－5 b/( d－1)拟合误差/%5.08 4.46 2.24 6.55 0.627 58.60 0.66 7.06 4.82 2.14 8.29 0.617 61.49 1.20 10.10 4.82 2.11 8.24 0.604 61.19 1.07 13.16 4.19 2.53 7.56 0.17158.54 2 007.52 1.79 1.268 0.56 14.29 4.05 2.36 7.27 0.158 57.57 2 302.840.015 9 1.66 1.16 15.82 4.39 1.85 6.42 0.118 54.74 2 189.94 0.010 3 1.7551.22从拟合所得的参数( 表1) 看出，E1、p1、p2 和η10 与荷载大小基本无关，而与岩石的特性及试件的状态有关.在σ ≤σs 时，η2 也与荷载大小无关，这与文献［7］的结果一致，p3 随着荷载的增加而减小，也即随时间增大，E2( t) 的减小速度减慢，说明在荷载较小时，岩石蠕变初始时间较短，容易过渡到稳态蠕变( 图6) ，荷载越大，由初始蠕变过渡到稳态蠕变的时间越长，即越不容易达到稳态流变，说明该模型也能很好地反映岩石由初始蠕变进入稳态蠕变的过程.当σ ＞σs 时，p3和η2 都随着荷载的增大而减小，p3 的减小尤为明显.b 随荷载的增大而增大，由式(3) 和式(6) 看出，b 是主要反映加速蠕变的系数，b 越大，加速蠕变过程的蠕变加速度就越大.而a 则随荷载的增大而减小.4 结论(1) 通过类似于开关的SO 元件与牛顿体并联后与广义Kelvin 体串联形成一个新的岩石蠕变模型，该模型通过SO 元件的作用，可以实现Burgers模型与广义Kelvin 模型之间的切换，当σ ＞σs 时，新模型成为Burgers 模型，以描述速率不为0 的稳态蠕变. σ≤σs 时新模型转化为广义Kelvin 模型，以反映速率为0 的稳态蠕变.(2) 将牛顿体的粘滞系数假设为与时间有关并满足式( 7) 的关系式，与SO 并联后与文献［13］的非定常参数的广义Kelvin 体串联形成新的非定常参数的蠕变模型，根据以上分析，该模型可以很好地反映岩石的3 种蠕变过程.(3) 经过分析，参数p3、a、b 对荷载反映较为敏感.η2 只有在σ ＞σs 时随荷载的增加而减小.而其余参数受荷载的影响很小. 分析结果还表明，本文提出的新模型能很好地反映不同荷载下岩石由初始蠕变进入稳态蠕变的过程.【相关文献】［1］袁静，龚晓南，益德清. 岩土流变模型的比较研究［J］. 岩石力学与工程学报，2001，20(6) ：772－ 779.［2］夏才初，孙钧.蠕变试验中流变模型辨识及参数确定［J］. 同济大学学报，1996，24(5) ：498－503.［3］金丰年，浦奎英. 关于粘弹性模型的讨论［J］. 岩石力学与工程学报，1995，14(4) ：335－361.［4］邓荣贵，周德培，张倬元，等.一种新的岩石流变模型［J］.岩石力学与工程学报，2001，20(6) ： 780－784.［5］韦立德.岩石力学损伤和流变本构模型研究［D］.南京：河海大学，2003.［6］Boukharov G N，Chanda M W. The three processes of brittle crystalline rock creep ［J］. Int. J. Rock Mech. Min. Sci. ＆Geomech.Abstr.，1995，32(4) ：325－335.［7］徐卫亚，杨圣奇，褚卫江.岩石非线性粘弹塑性流变模型( 河海模型) 及其应用［J］. 岩石力学与工程学报，2006，25(3) ：433-447.［8］陈沅江，潘长良，曹平，等. 软岩流变的一种新力学模型［J］.岩土力学，2003，24(2) ：209－214.［9］曹树刚，边金，李鹏. 岩石蠕变本构关系及改进的西原正夫模型［J］. 岩石力学与工程学报，2002，21(5) ：632-634.［10］张向东，李永靖，张树光，等. 软岩蠕变理论及其工程应用［J］. 岩石力学与工程学报，2004，23(10) ：1635-1639.［11］王来贵，何峰，刘向峰，等. 岩石试件非线性蠕变模型及其稳定性分析［J］. 岩石力学与工程学报，2004，23(10) ：1640-1642.［12］许宏发.软岩的强度和弹模时间效应研究［J］.岩石力学与工程学报，1997，16(3) ：246－251.［13］丁志坤，吕爱钟. 岩石粘弹性非定常蠕变方程的参数识别［J］.岩土力学，2004，25( S) ：37－40.［14］蔡美峰，何满潮，刘东燕. 岩石力学与工程［M］. 北京：科学出版社，2002.［15］楼志文. 损伤力学基础［M］. 西安：西安交通大学出版社，1990.［16］金丰年，范华林，浦奎源. 岩石蠕变损伤模型研究［J］. 工程力学，2001( S) ：227－231. ［17］Kennedy J，Eberhart R C. Particle swarm optimization［C］//IEEE International Conference on Neural Networks，Perth，1995：1942－1948.。

岩石流变损伤本构模型

石众多的流变模型中，粘弹塑性元件模型由于参数物理意义明确、能够把岩石复杂的力学性质直观的表现
ＭａｘｗｅＵ体并联组成，其力学模型如图１所示。
的出来，近年来在实际工程中得到了广泛应用。但传
统的原件模型是一种线性模型，通常无法反映岩石的
一
和损伤演化方程引入到Ｍａｘｗｅｎ蠕变模型中，提出了可以较好地描述岩石蠕变３个阶段的新模型。本文通过将Ｋａｃｈａｎｏｖ蠕变损伤理论引入到常规粘塑性体中对其进行了改进，并将改进后的粘塑性体与Ｐｏｙｔｉｎｇ—Ｔｈｏｍｓｏｎ体进行串联，建立了一个
较好的反映岩石蠕变全过程，且拟合结果和试验结果吻合的较为理想，从而也证明了其合理性。关键词：岩石；损伤；流变模型
文章编号：１００８— ０８３Ｘ（２０１３）１０— ００７４— ０３中图分类号：ＴＵ２７文献标志码：Ｂ
谢文光
（贵阳市水利交通发展投资（集团）有限公司，贵州贵阳５５０００２）
摘
要：将Ｋａｃｈａｎｏｖ蠕变损伤理论引入到常规粘塑性体中对其进行了改进，将改进后的粘塑性体与Ｐｏｙｔｉｎｇ－Ｔｈｏｍ－
ｓｏｎ体进行串联，建立了一个岩石流变损伤模型，并利用砂岩蠕变试验结果对其进行了验证。结果表明：该模型能够

基于分数阶微积分的岩石非线性蠕变本构模型研究及其在Flac3D中的二次开发

3、引入损伤变量。当蠕变变形达到一定程度时，岩石内部会产生微裂纹，因此需要在模型中引入损伤变量来描述这一过程。损伤变量的变化可以通过引入一个损伤演化方程来描述。
4、结合损伤演化方程和分数阶微分方程，构建完整的非线性蠕变损伤力学模型。
五、应用和展望
基于分数阶微积分的岩石非线性蠕变损伤力学模型可以广泛应用于岩石工程中的稳定性分析、预测和优化设计。例如，它可以用于预测隧道、大坝和桥梁等基础设施在长期运营过程中可能出现的蠕变损伤问题。此外，该模型还可以为采取有效的预防和补救措施提供理论支持。
3、优化材料的加工和使用性能。通过该模型可以深入了解材料的微观结构和性能之间的关系，为材料的优化设计和加工提供理论指导。
讨论与结论
基于分数阶微积分的非线性黏弹塑性蠕变模型是一种有效的工具，在描述材料的非线性黏弹塑性行为方面具有广泛的应用前景。然而，该模型仍存在一些挑战和限制：
1、模型的参数确定需要大量的实验数据，而且某些参数可能难以获得；
2、分数阶微积分的计算比整数阶微积分更加复杂，需要采用数值方法进行求解，这可能会增加计算成本；
3、尽管该模型能够描述许多材料的非线性行为，但并不能适用于所有材料，特别是一些具有非常复杂行为的材料。
未来研究方向
为了更好地应用基于分数阶微积分的非线性黏弹塑性蠕变模型，以下几个方面值得深入研究：
模型应用
该模型在解决实际问题中具有广泛的应用，例如：
1、描述材料的蠕变和松弛行为。在高温或高应力的长期作用下，材料的形状和大小会发生变化，该模型可以描述这种变化的行为；
2、描述材料的疲劳行为。材料的疲劳失效是一个复杂的过程，受到许多因素的影响，如循环应力、温度和环境介质等，该模型可以描述这种失效的过程；

岩石蠕变模型及蠕变参数识别研究综述

Open Access
1. 引言
蠕变是正常应力作用下变形(应变)随时间发展而增加的现象。大量工程实践和研究表明，岩体的失稳破坏与时间之间密切相关[1]。不同岩体表现出不同的蠕变特性，差异也很大。目前，对于岩石蠕变的研究已广泛开展起来，1939 年 Griggs 在对砂岩、泥板岩和粉砂岩等进行了大量蠕变试验后，发现了岩石蠕变的荷载范围[2]。Okubo 完成了大理岩、砂岩、花岗岩和灰岩等岩石的压缩试验，获得了岩石加速蠕变阶段的应变-时间曲线[3]。Hayano K 等进行了沉积软岩的长期蠕变试验[4]。对于岩石蠕变模型的研究，众多学者提出了多个阶段的岩石蠕变模型和蠕变本构关系。这些蠕变模型主要分为经验模型、元件组合模型和断裂损伤模型。对于蠕变模型参数的识别也是研究的一大重点，各位学者和研究人员根据不同实际情况，提出许多有实用价值的参数识别方法。经过多年的研究，关于蠕变模型和参数识别方面的研究十分多样，本文在前人研究结果的基础上，对岩石蠕变模型和蠕变参数识别的方法进行分类和总结，希望能对接下来的岩石蠕变研究提供有意义的帮助和借鉴。
2. 岩石蠕变模型
2.1. 经验模型
蠕变经验模型是在蠕变试验结果基础上，使用数理拟合的方法，对岩体的应力、应变与时间建立函数关系式，也即为岩石蠕变经验方程。经验蠕变模型中主要有老化、流动、硬化和继效等理论，范广勤对其进行了详细的总结[5]。不同的岩石在不一样的条件下，可得出不相同的蠕变经验模型。岩石蠕变经验方程的通常形式为：
3. 蠕变模型参数识别
蠕变实验作为研究岩石蠕变力学性质的一大方法，受到了研究者的广泛关注。根据蠕变试验提供的实验数据，建立了合适的蠕变模型，并给出了相应的蠕变参数，这一直是岩石蠕变领域的一个重要课题。一种好的技术方法对参数辨识有着深远的影响。目前，蠕变模型参数识别的常用方法有回归反演法、最小二乘法，流变曲线分解法和极大似然法，其中回归反演法和最小二乘法最为常用。识别方法有数值方法和解析方法。

基于FLAC^(3D)岩石黏弹塑性流变模型的二次开发研究

基于FLAC^(3D)岩石黏弹塑性流变模型的二次开发研究褚卫江;徐卫亚;杨圣奇;周维垣
【期刊名称】《岩土力学》
【年(卷),期】2006(27)11
【摘要】由于岩土介质的复杂多样性,通用分析软件所提供的岩石流变本构模型往往不能满足工程实际数值分析的需要。

依据FLAC3D(Version2.1)所提供的二次开发程序接口,结合西原黏弹塑性流变模型分析了二次开发程序运行的基本原理,给出了西原流变模型具体实施的程序框图和代码编写中应该注意的几个关键技术。

通过一个简单的算例验证了程序编制的正确性与可靠性。

由于采用了面向对象的程序技术,FLAC3D二次开发接口更加简单实用,提供的研究思路可为其他流变本构模型的二次开发提供参考。

【总页数】6页(P2005-2010)
【关键词】岩石力学;黏弹塑性流变模型;拉格朗日元法;二次开发;面向对象技术【作者】褚卫江;徐卫亚;杨圣奇;周维垣
【作者单位】河海大学岩土工程研究所,南京210098;清华大学水利水电工程系,北京100084
【正文语种】中文
【中图分类】TU485.3
【相关文献】
1.岩石流变的一种非线性黏弹塑性流变模型研究 [J], 张英
2.软土弹粘塑性模型在FLAC3D中的二次开发及其应用 [J], 谢秀栋;苏燕
3.考虑黏聚力与内摩擦系数的岩石黏弹塑性流变模型 [J], 杨圣奇;朱运华;于世海因版权原因，仅展示原文概要，查看原文内容请购买。

基于Matlab的岩石蠕变模型参数辨识算法设计

基于Matlab的岩石蠕变模型参数辨识算法设计张华宾;闵小东;张顷顷【摘要】为减少岩石蠕变模型参数辨识的繁冗计算,探讨一种可靠、高效的岩石蠕变模型辨识方法.以M-K(伯格斯)蠕变模型为例,给出蠕变模型参数辨识方法,并编写Matlab算法函数通过COM组件从而剥离出程序,借助VB环境下编制面向对象的可视化计算软件.结果表明,该软件用于岩石蠕变模型参数辨识的计算过程同样有较好的效果并提高了计算效率,为实现其他岩石力学参数计算问题提供了可供借鉴的快速处理方法.%The reliable and efficient identify method of rock creep model was discussed, in order to re-duce the onerous calculation of parameter identification of rock creep model . Take M-K creep mod-el for example ,Algorithm was writed use Matlab and then it'''' s spun off the Matlab by mean of COM. The object-oriented visualization software was writed based on VB. The results suggest that the soft-ware used on calculation of parameter identification of rock creep model show up more efficient and worked well , which provide fast process method that can be used for reference in parameter calcula-tions of the others rock mechanics.【期刊名称】《河北工程大学学报（自然科学版）》【年(卷),期】2016(033)003【总页数】4页(P29-32)【关键词】蠕变模型;算法设计;面向对象;可视化【作者】张华宾;闵小东;张顷顷【作者单位】辽宁工程技术大学力学与工程学院,辽宁阜新123000;辽宁工程技术大学力学与工程学院,辽宁阜新123000;辽宁工程技术大学力学与工程学院,辽宁阜新123000【正文语种】中文【中图分类】TG333.17岩石蠕变力学性质模型大致可以分为以下4类：经验模型、元件组合模型、基于损伤力学的蠕变本构模型和基于热力学理论的蠕变本构模型。

岩石非线性黏弹塑性蠕变模型研究及其参数识别

σ 1 = E1ε1
(6)
dt
Bt + C
(3)
根据式(6)，消去方程中的下标获得系统总的应力、应变本构方程为 + ( E1η1 + E2η1 + E1η2 )σ + E1 E2σ = η1η2σ + E1 E2η1ε + E1 E2σ S2 E1η1η2ε (7)
⎛σ ⎞ ⎟ ⎝ A⎠
第 27 卷第 4 期 2008 年 4 月
岩石力学与工程学报 Chinese Journal of Rock Mechanics and Engineering
Vol.27 No.4 April，2008
岩石非线性黏弹塑性蠕变模型研究及其参数识别
蒋昱州，张明鸣，李良权
(河海大学岩土工程研究所，江苏南京 210098)
STUDY ON NONLINEAR VISCOELASTO-PLASTIC CREEP MODEL OF ROCK AND ITS PARAMETER IDENTIFICATION
JIANG Yuzhou，ZHANG Mingming，LI Liangquan
(Institute of Geotechnical Engineering，Hohai University，Nanjing，Jiangsu 210098，China)
，ε )ε = A[ f (ε )] Bt + C = A(ε ) Bt + C σ = η N (ε
1 1
认为，黏滞阻尼器所受应力的大小
[11]
与蠕变加速度大小成简单的正比关系，提出了能模拟非线性加速蠕变的模型；曹树刚等采用一个二次函数非线性牛顿体黏性元件构成五元件的改进西原正夫模型，探讨了与时间有关的软岩一维和三维本构方程和蠕变方程；韦立德等[12]根据岩石黏聚力在流变中的作用提出了一个新的 SO 非线性元件模型，建立了新的一维黏弹塑性本构模型；陈沅江等 [13]提出了蠕变体和裂隙塑性体 2 种非线性元件，并将它们和描述衰减蠕变特性的开尔文体及描述瞬时弹性的虎克体相结合，建立了一种可描述软岩的新的复合流变力学模型。刘江等