②非线性弹性本构关系全量型增量型③弹塑性本构
钢筋混凝土非线性分析讲解

参考教材: 1、钢筋混凝土结构非线性有限元理论与应用(同济,1995)
(吕西林、金国芳、吴晓涵) 2、钢筋混凝土非线性分析(同济,1984)
(朱伯龙、董振祥)
3、钢筋混凝土非结构线性分析(哈工大,2007) (何政、欧进萍)
学习要求: 1、认识混凝土材料的非线性性能 2、学习非线性分析基本方法 3、学习科学研究的方法和思路
(可作为:研究工具、计算工具、模拟现场过程)
三、钢筋混凝土结构有限元数值分析的特点 (与其它固体材料有限元分析的不同)
1、模拟混凝土的开裂和裂缝发展(包括裂缝闭合)过程 2、模型中反映钢筋与混凝土间的粘结、滑移 3、模拟混凝土材料应力峰值后和钢筋屈服后的性能 4、材料非线性和几何非线性并存 5、分析结果强烈依赖于钢筋、混凝土材料的本构关系和
拔出试验:假定s1→τ1→σs2、σc2→εs2、εc2→s2→τ2→
σs3、σc3→εs3、εc3→······→sn→τn→σsn=σs0(?)
3、拔出试验和拉伸试验的粘结-滑移全过程分析方法 2)反复加载下的粘结-滑移全过程分析 •用反复荷载下的τ-s关系 •裂缝或构件边缘处局部τ-s关系过渡区域处理
4、反复加载:周期性静力荷载作用下交替产生拉、压应力 重复加载:周期性静力荷载作用下仅产生单向应力
第二章:钢筋混凝土材料的本构关系
一、本构关系的理论模型 1、线弹性模型 2、非线性弹性模型 3、弹塑性模型(理想弹塑性、线性强化弹塑性、刚塑性) 4、粘弹性和粘塑性的流变模型
1)流变学的三个简单流变元件:
曲线形状基本不变 峰值应变基本不变。
4)设备刚度的影响:(下降段的影响)
5)加载时间的影响:徐变问题
基本概念:【朱】Page17 基本徐变(εbc):内部水分不变时 干徐变(εdc):总徐变-基本徐变 徐变度(εsp):单位应力下的徐变 徐变系数(φc ):徐变值/弹性变形
7.弹塑性力学--塑性本构关系

F
ij
2 f f
3 kl k2l2
2. 硬化材料的增量塑性本构关系
混合强化模型
f ij ,ij , k p F ij ij k p
f F
f F
ij ij
ij
ij
h
f kl
ij
p ij
f ij
f k
k p
f 1 k
2 f f 3 ij ij
h
4
1.理想塑性材料的增量本构关系
二、塑性理论
应力状态 多值关系、过程相关 应变状态
描述方法:过程跟踪 本构形式:增量型(应力增量、应变增量)
全量型(只在比例加载条件下可用)
5
1.理想塑性材料的增量本构关系
1)一般形式
d ij
d
e ij
d
p ij
d ij
Cijkl
d
e kl
d ij
Cijkl
d
kl
df
f
ij
d ij
f
ij
d ij
f k
dk
加载面的演化 内变量的演化
d
p ij
d
f
ij
dhijpdd
p
ij
fdijd2 ijf ijkfdf ikj
0
如果hd以kd累积pkf塑2ij d性p d32应ijdk变ijpddkfd2dijppkdpf作32p0为df内2变hd量f ij
2)Prandtl-Reuss模型(J2理论)
K
K
4
3 2
G G
K 2G 3
K 4G
K 2G 3
K 2G
0 0
0 0
0
第11章-弹塑性力学--本构关系
xy c41 x c42 y c43 z
y y
图4-2
(a)
z
x
x
z
现在引进坐标系 Ox’y’z’, 原坐 标系 Oxyz 绕 y 轴转动 1800 后可与之重合 (图4-2)
新旧坐标轴间的方向余弦
l11 l33 cos180
1 0 0 1 l22 cos 0 1 0 0 l21 l31 l12 l32 l13 l23 cos 90 0
(11-13)
平面应力问题 用应变分量表示 应力分量
E y x 1 2 x E (11-14) y y x 1 2 G
ij ije 2 ij
(11-3’)
以上证明了各向同性的均匀弹性体的弹性常数只有 两个。
现在考虑一种物体各边平行于坐标轴的特殊情况,并 由此导出工程上常用的弹性常数和广义胡克定律。当物 体边界法线方向与 z 轴重合的两对边上有均匀的σz 作 用,其他边均为自由边时,则由材料力学知道
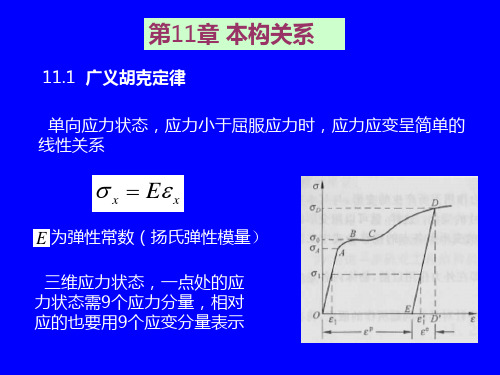
第11章 本构关系
11.1 广义胡克定律 单向应力状态,应力小于屈服应力时,应力应变呈简单的 线性关系
x E x
E 为弹性常数(扬氏弹性模量)
三维应力状态,一点处的应 力状态需9个应力分量,相对 应的也要用9个应变分量表示
弹塑性_塑性力学基本方程和解法

在加载过程中物体各点处的偏应力分量 sij 保持比例不变。在工程允许精度下,也可推
广应用于稍为偏离简单加载的情况。
以上各种理论中涉及的一些假设,例如:塑性应变偏量的增在单一的函数关系等假设,都得到了常用金属材
料大量试验的验证。
z 强化规律 对于理想弹塑性材料,材料一旦屈服,其应力状态点在主应力空间中就落在屈服
变形, Hα 也不变,于是
∂f ∂σ ij
除等向强化外,有些强化材料表现为随动强化(图 7.7b),即,在强化过程中,屈
服面的大小和形状保持不变,只随塑性变形的发展而在应力空间中平移。还有些材料
在强化过程中随动强化与等向强化同时发生,称为混合强化。
由于在应力和强化参数空间中,表示应力状态的应力点只可能位于后继屈服面
(或加载面)上或其内,不可能位于曲面之外,若加载面是一个正则曲面,则有
⎯2⎯
研究生学位课弹塑性力学电子讲义
姚振汉
⎧ε = 0 ⎨⎩σ = σ s
当 σ <σs 当 ε >0
(2)
图 7.5 理想弹塑性和刚塑性
当考虑材料强化性质时,可在理想弹塑性模型的基础上加以改进,采用线性强化 弹塑性模型来近似:
⎧σ = Eε
⎨⎩σ = σ s +E1 (ε − εs )
当 ε ≤εs 当 ε >εs
(5)
⎯3⎯
第七章 塑性力学的基本方程与解法
其中 k 可由单向拉伸或其它材料试验测得的σ s 确定, k = σ s 2 。当不能确定主应力的 排序时,在以三个主应力为坐标轴的应力空间中,由特雷斯卡条件所包围的弹性状态 的应力空间为
σ1 −σ 2 ≤ 2k, σ 2 −σ 3 ≤ 2k, σ 3 −σ1 ≤ 2k
塑性力学总结

塑性力学大报告1、绪论1.1 塑性力学的简介尽管弹塑性理论的研究己有一百多年,但随着电子计算机和各种数值方法的快速发展,对弹塑性本构关系模型的不断深入认识,使得解决复杂应力条件、加载历史和边界条件下的塑性力学问题成为可能。
现在复杂应力条件下塑性本构关系的研究,已成为当务之急。
弹塑性本构模型大都是在整理和分析试验资料的基础上,综合运用弹性、塑性理论建立起来的。
建立弹塑性材料的本构方程时,应尽量反映塑性材料的主要特性。
由于弹塑性变形的现象十分复杂,因此在研究弹塑性本构关系时必须作一些假设。
塑性力学是研究物体发生塑性变形时应力和应变分布规律的学科.是固体力学的一个重要分支。
塑性力学是理论性很强、应用范围很广的一门学科,它既是基础学科又是技术学科。
塑性力学的产生和发展与工程实践的需求是密不可分的,工程中存在的实际问题,如构件上开有小孔,在小孔周边的附近区域会产生“应力集中”现象,导致局部产生塑性变形;又如杆件、薄壳结构的塑性失稳问题,金属的压力加工问题等,均是因为产生塑性变形而超出了弹性力学的范畴,需要用塑性力学理论来解决的问题,另一方面,塑性力学能为更有效的利用材料的强度并节省材料、金属压力加工工艺设计等提供理论依据。
正是这些广泛的工程实际需要,促进了塑性力学的发展。
1.2 塑性力学的发展1913年,Mises提出了屈服准则,同时还提出了类似于Levy的方程;1924年,Hencky采用Mises屈服准则提出另一种理论,用于解决塑性微小变形问题很方便;1926年,Load证实了Levy-Mises应力应变关系在一级近似下是准确的;1930年,Reuss依据Prandtl的观点,考虑弹性应变分量后,将Prandtl所得二维方程式推广到三维方程式;1937年,Nadai研究了材料的加工硬化,建立了大变形的情况下的应力应变关系;1943年,伊柳辛的“微小弹塑性变形理论”问世,由于计算方便,故很受欢迎;1949年,Batdorf和Budiansky从晶体滑移的物理概念出发提出了滑移理论。
弹塑性力学本构关系1资料.

在
平面上任取一点,坐标为 (1, 2 , 3 )
它代表一个应力状态,对应的应力张量分量为 ij
相应的平均应力为 m 易见有
m
1 2
3
3
0
将应力张量分解为应力球张量和应力偏张量,即
ij m ij sij sij
上式表明,与此应力状态相应的应力球张量为零,应力张量
等于应力偏张量。 平面上每一点对应的应力张量是应力偏张量。
• Drucker把它引伸到复杂应力 情况,这就是Drucker公设.
0 d p 0
ij
0 ij
d
p ij
0
d d p 0
第二式中的等号适用于理想 塑性材料.
d
ij
d
p ij
0
Drucker公设在塑性力学中有
重要意义.
屈服面的外凸性和塑性应变增量的法向性
•我们如将塑性应变空间与应力空间重合起来,由Drucker公 设的第一式, 把它看成是两个矢量的点积.
在应力空间中代表一曲面,此曲面称为屈服曲面。
屈服曲面内的点满足不等式
f (1, 2,3) c 时,代表弹性状态。 屈服曲面上及屈服曲面外的点满足 f (1, 2,3) c
时,代表塑性状态。因此,屈服曲面是弹、塑性状态的分界面。
4.2.3 等倾线与 平面
1.等倾线 在应力空间中,过坐标原点与三个坐标轴成相同倾角的直线 叫等倾线。
PR线上每一点都代表一个应力状态。 PR线上的点有相同的应力偏张量和不同的应力球张量。
因为应力球张量不影响屈服,所以如果P点在屈服曲面上, 那么PR线上所有点都应该在屈服面上。因此屈服曲面实际上 是一个柱面,并且柱面的母线平行于等倾线OL
P
材料力学中的非线性本构模型
材料力学中的非线性本构模型材料力学是许多工程领域的基础,它研究材料受力后的力学行为,包括力的大小、方向、分布和变形等问题。
不同材料的力学行为需要采用不同的本构模型来描述,常见的材料本构模型有线性弹性模型、非线性本构模型等。
本文将重点介绍材料力学中的非线性本构模型。
一、非线性本构模型的概念在材料力学中,当受力材料的变形与施加的力之间呈非线性关系时,就需要采用非线性本构模型来描述其力学行为。
非线性本构模型可以分为弹塑性模型、粘弹塑性模型、本质非线性模型等不同类型,其中弹塑性模型在实际应用中被广泛采用。
二、弹塑性模型弹塑性模型又称弹塑性本构模型,它是一种介于线性弹性模型和塑性本构模型之间的模型。
弹塑性模型假设材料的力学行为在一定范围内是线性弹性的,但在超出一定应力范围后就会出现不可逆变形,这种不可逆变形称为塑性变形。
弹塑性模型可分为单轴应力状态下的本构模型和多轴应力状态下的本构模型。
其中单轴应力状态下的本构模型包括拉伸本构模型、压缩本构模型等,多轴应力状态下的本构模型包括Mises本构模型、Drucker-Prager本构模型等。
三、拉伸本构模型拉伸本构模型是弹塑性模型中最简单的模型之一,它假设材料的力学行为在拉伸状态下是线性弹性的,且材料的强度随着应力增大而增大。
在达到材料的屈服点后,材料的强度就不再随应力增大而增大了,这时材料开始出现塑性变形。
拉伸本构模型将材料的应力-应变曲线分为弹性阶段和塑性阶段来描述材料的力学行为。
四、Mises本构模型Mises本构模型也称为圆锥形模型,它是多轴应力状态下最常用的弹塑性模型之一。
该模型假设材料的塑性行为是由等效应力和应力状态判据决定的,等效应力可以通过应力张量得到,应力状态判据则基于材料力学的实验性质,通过外部应力来得到。
Mises本构模型能够较为准确地描述材料在多轴应力状态下的力学行为,并在应用中获得广泛的应用。
五、Drucker-Prager本构模型Drucker-Prager本构模型是一种常用的粘塑性模型,它假设材料有两种塑性机制:一种是塑性流动,另一种是摩擦滑移。
弹塑性力学——精选推荐
弹塑性⼒学应⼒应变关系应⼒应变都是物体受到外界载荷产⽣的响应。
物体由于受到外界载荷后,在物体内部各部分之间要产⽣互相之间的⼒的作⽤,由于受到⼒的作⽤就会产⽣相应的变形;或者由于变形引起相应的⼒的作⽤。
则⼀定材料的物体其产⽣的应⼒和应变也必然存在⼀定的关系。
在⼒学上由于平衡⽅程仅建⽴了⼒学参数(应⼒分量与外⼒分量)之间的关系,⽽⼏何⽅程也仅建⽴了运动学参数(位移分量与应变分量)之间的连系。
所以平衡⽅程与⼏何⽅程是两类完全相互独⽴的⽅程,它们之间还缺乏必要的联系,这种联系即应⼒和应变之间的关系。
有了可变形材料应⼒和应变之间关系和⼒学参数及运动学参数即可分析具体的⼒学问题。
由平衡⽅程和⼏何⽅程加上⼀组反映材料应⼒和应变之间关系的⽅程就可求解具体的⼒学问题。
这样的⼀组⽅程即所谓的本构⽅程。
讨论应⼒和应变之间的关系即可变为⼀定的材料建⽴合适的本构⽅程。
⼀.典型应⼒-应变关系图1-1 典型应⼒-应变曲线1)弹性阶段(OC段)该弹性阶段为初始弹性阶段OC(严格讲应该为CA’),包括:线性弹性分阶段OA段,⾮线性弹性阶段AB段和初始屈服阶段BC 段。
该阶段应⼒和应变满⾜线性关系,⽐例常数即弹性模量或杨⽒模量,记作:εσE =,即在应⼒-应变曲线的初始部分(⼩应变阶段),许多材料都服从全量型胡克定律。
2)塑性阶段(CDEF 段)CDE 段为强化阶段,在此阶段如图1中所⽰,应⼒超过屈服极限,应变超过⽐例极限后,要使应变再增加,所需的应⼒必须在超出⽐例极限后继续增加,这⼀现象称为应变硬化。
CDE 段的强化阶段在E 点达到应⼒的最⾼点,荷载达到最⼤值,相应的应⼒值称为材料的强度极限(ultimate strength ),并⽤σb 表⽰。
超过强度极限后应变变⼤应⼒却下降,直到最后试件断裂。
这⼀阶段试件截⾯积的减⼩不是在整个试件长度范围发⽣,⽽是试件的⼀个局部区域截⾯积急剧减⼩。
这⼀现象称为“颈缩”(necking )。
弹塑性力学本构关系
—— Green公式
U 0 U 0 U 0 U 0 U 0 U 0 x , y , z , xy , yz , zx x y z xy yz zx
由
同理
x U 0 c12 y x c31 c14 c41
横观各向异性材料,其独立的弹性常数为13个;正应变会 产生切应力,切应变也会产生正应力 工程上,单斜晶体(如正长石)可简化为横观各向异性弹 性体。
二. 正交各向异性材料
z
具有三个相互垂直弹性对 称面的材料称为正交各向异性 材料。 设三个弹性对称面分别为 Oxy、Oyz和Ozx平面,材料沿 x、 y、 z 三方向弹性性质各异。
对 称
1 c22 c33 , c44 c66 , c55 c22 c23 2
0 0 0 0 1 c11 c12 2
x y z 0 xy yz 0 zx 1 c11 c12 2 0 0 0
c12 c21 c15 c51
c56 c65
即
cmn cnm
x c11 c12 c22 y z xy 对 yz zx
c13 c23 c33
称
m、n ij、kl 1 11 2 22 3 33 4 12 5 23 6 31
如,c22 c2222 , c56 c2331 广义胡克定律的一般形式最广泛地描述了材料的线弹性性 质,但未能描述物体外部环境条件和内部物理特征。
§4-2 线弹性体的本构关系
如果材料在变形过程中处于等温绝热过程。 根据热力学第一定律和相应数学推导, ij f ij 有势, 其势函数U0(ij) 为物体单位体积的变形能(应变能)。
弹塑性本构关系
F p d kk 3d S;deijp d ij e p p d d G K kk ij 2G eij kk mn 2 mn Sij k
(2) Druker-Prager 模型
Druker-Prager模型采用广义的 Mises屈服函数,其表达式为:
m
3K
ij
弹性变形 + 塑性变形 又可写成:
ij Sij m ij K kk ij 2G eij d d d d e d e
K kk d kk ij 2G eij eijp p d d d F F K kk ij 2G eij d 3K ij 2G d d kk Sij
F σ ij J 2 I1 k 0 +
由
F kk
F Sij 2 Sij J2
得 d ij dSij d m ij d F 2G 3K
F ij Sij kk
Sij m Sij d d d ij 2G 3K ij 2 J2
2G
m为对应于 m体应变
拉梅常数 E (1 )(1 2 )
xy
2
x 3 m 2G x y 3 m 2G y z 3 m 2G z xy 2G xy G xy
yz zx
2 2
2G
G
E 2(1 )
2G
基本方程 yz 2G yz G yz zx 2G zx G zx
张量形式
张量形式
ij ij
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各种非线性本构关系的理论概念、数学表达式和计算参数取值等差别较大,计算结果也不相同。进行结构非线 性分析时,应慎重选择混凝土本构模型,重要结构应进行理论的或试验的验证。
Nonlinear analysis of concrete structures
Chapter 3 Constitutive law — mathematical description of constitutive law curve
三、常用钢筋、混凝土本构关系有:
(1)混凝土的单轴受压和受拉应力-应变关系; (2)混凝土多轴应力-应变关系; (3)多种环境和受力条件下的混凝土应力-应变关系,包括反复加卸载,多次重复荷载(疲劳),快速(毫秒 或微秒级)加载和变形,高温(>l00oC)和低温<0oC)状况下的加卸载,……; (4)与时间有关的混凝土受力性能,如徐变(松弛)、收缩、……; (5)钢材(筋)的应力-应变关系和反复应力作用的Bauschinger效应;
清华大学教授过镇海建议分段式曲线方程:
x 1
y a0 a1x a2 x2 a3x3
⑴
x
x 1
y b0 b1x b2 x2
⑵
上升段⑴式满足条件1、2、3、7,下降段⑵式满足条件3~7。
将条件1和3中的三个边界条件代入⑴式,可解得:
a0 0 , a2 3 2a1 , a3 a1 2
3.1 混凝土受压应力-应变全曲线(Stress-strain curve of concrete in compression)
Stress-strain curve of concrete in compression is desoordinates as ( 将混凝土受压应力-应变全曲线用无量纲坐标表示):
(N/mm 2 )
f cu ,k
Nonlinear Analysis of Concrete Structures Chapter 3 Constitutive law — mathematical description of constitutive law curve 对参数取αa 和αd 赋予不等的数值,可得变化的理论曲线。
d2 y dx 2
2d [x3 3x [d (x 1)2
(2 1
d
x ]3
)]
0
可解得拐点inflexion位置xD(>1.0)
同理,由数学条件5满足:
d3 y dx3
6
d
[
2 d
x
4
6
2 d
x
2
(8
2 d
4 d
[d (x 1)2 x
)x ]3
(3
2 d
4 d
1)]
0
可解得最大曲率点point of the maximum curvature的位置 xE>xD
对不同强度等级的结构混凝土或约束混凝土,选用合适的参数值,可得到与试验结果 相符的理论曲线。过镇海等建议的参数值见上表。
混凝土受压应力应变试验曲线的数 学函数曲线有:多 项式、指数式、三 角函数、有理分式、 分段式等
Compressive stress-strain relation of concrete
Chapter 3 Constitutive law — mathematical description of constitutive law curve 二、确定本构关系的三种方法:
⑴ 用与工程结构相同的混凝土,通过棱柱体试件试验测定; ⑵ 选定适合该结构的本构模型,其数学表达式中的参数由少量试验标定; ⑶ 采用经过试验验证或工程经验证明可行的具体本构(数学)模型。 混凝土材料施工工艺和质量控制不够精细,混凝土力学试验结果变异性和离散度较大。结构分 析的本构关系应根据结构重要性、计算精度、试验条件等慎重地选择。
上升段曲线方程为:
x 1 y a x (3 2a )x2 (a 2)x3
⑶
上升段曲线方程,满足条件7,由条件2的不等式,可得αa值的范围:
1.5 a 3.0
Nonlinear Analysis of Concrete Structures
Chapter 3 Constitutive law — mathematical description of constitutive law curve
Nonlinear Analysis of Concrete Structures
Chapter 3 Constitutive law — mathematical description of constitutive law curve
故d的取值范围为: 0 d
Nonlinear Analysis of Concrete Structures
Chapter 3 Constitutive law — mathematical description of constitutive law curve
此外,由数学条件 4 满足:
b1 1 2b0 ,
b2 b0
式中b0为独立参数,规范称其为下降段参数,
即 αd= b0 将其代入⑵式,并简化可得:
x 1 y
x
⑷
d (x 1)2 x
x 1
y
x
d (x 1)2 x
⑷
上式满足条件6、7。
当d 0时,y 1,峰点后为水平线(全塑性); d 时,y 0,峰点后为垂直线(脆性)。
Chapter 3 Constitutive law — mathematical description of constitutive law curve
x 1
y a0 a1x a2 x2 a3x3
⑴
x 1
y
b0
x b1x
b2 x2
⑵
下降段曲线方程含三个参数,将条件3 的两个边界条件代入,可解得:
NNoonnlliinneeaarr aAnnaalylyssisisofocfoCnocnrectreetsetruSctrtuurcetsures
Chapter 3 Constitutive law — mathematical description of constitutive law curve
7. 全部曲线x 0, 1 y 0.
下降段曲线可无限延长,收敛于横坐标轴,但不相交
Nonlinear Analysis of Concrete Structures
Chapter 3 Constitutive law — mathematical description of constitutive law curve
Nonlinear Analysis of Concrete Structures
Chapter 3 Constitutive law — mathematical description of constitutive law curve
下降段曲线上两个特征点D、E的位置随参数αd 值而变化,按式
testing stress-strain curve of concrete column under compression
Nonlinear Analysis of Concrete Structures
Chapter 3 Constitutive law — mathematical description of constitutive law curve
d2 y
2 d [x3
3x (2 1
d
)]
0
dx 2
[ d (x 1)2 x ]3
d3 y dx3
6
d
[
2 d
x
4
6
2 d
x
2
(8
2 d
4 d
[d (x 1)2 x
)x ]3
(3
2 d
4 d
1)]
0
计算结果如图,与试验数据一致
Nonlinear Analysis of Concrete Structures
一、本构关系分类: types of constitutive laws ①线弹性本构关系:虎克定律
②非全线量性型弹:性本构{关系c }: [Ec ]{} 增量型: {d c } [Ec ]{d }
③弹塑性本构关系: 变形理论:简称为弹塑性小变形理论 增量理论:用增量形式描述材料处于塑性状态时的应力应变关系
1. x 0, y 0;
2.
0
x
1,
d2y dx 2
0,即曲线斜率(dy
/
dx)单调减小,无拐点;
3. x 1时, y 1, dy / dx 0,即单峰值;
4.
当d2y dx2
0时,xD
1,即下降段有一拐点(D);
5.
当d3y dx3
0时,xE
1,即下降段上的最大曲率点(E);
6. 当x , y 0时, dy 0, dx
Chapter 3 Constitutive law — mathematical description of constitutive law curve
初始弹性模量测定方法testing method of elastic modulus
s
ε ce εcp
0.5fc
5~10 次
e
Ec
2.2
105 34.74
④损伤本构关系 ⑤其它本构理论:粘弹性与粘塑性本构关系、内时理论
