高考文科数学试题分类汇编训练三视图
完整word版三视图历年高考真题x
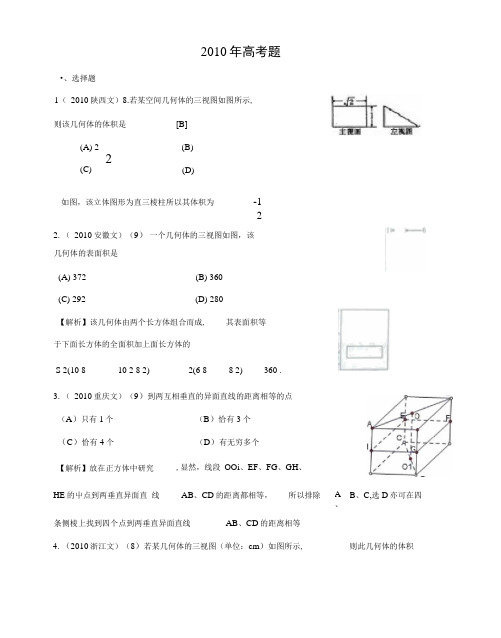
•、选择题2010年高考题1(2010陕西文)8.若某空间几何体的三视图如图所示,则该几何体的体积是[B](A) 22 (C) (B) (D)如图,该立体图形为直三棱柱所以其体积为-122. (2010安徽文)(9)一个几何体的三视图如图,该几何体的表面积是(A) 372 (B) 360(C) 292 (D) 280【解析】该几何体由两个长方体组合而成, 其表面积等于下面长方体的全面积加上面长方体的S 2(10 8 10 2 8 2) 2(6 8 8 2) 360 .3. (2010重庆文)(9)到两互相垂直的异面直线的距离相等的点(A)只有1个(B)恰有3个(C)恰有4个(D)有无穷多个【解析】放在正方体中研究,显然,线段OOi、EF、FG、GH、HE的屮点到两垂直异面直线AB、CD的距离都相等,所以排除A、B、C,选D亦可在四条侧棱上找到四个点到两垂直异面直线AB、CD的距离相等4. (2010浙江文)(8)若某几何体的三视图(单位:cm)如图所示, 则此几何体的体积面ABC且3 AA= 3- BB =CC =AB,则多面体△ ABC ・ABC的正视图(也称主视图)2是【答案】D6. (2010福建文)3.若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于()C・ 3 D. 6三棱柱是以底面边长为2,高为1的正三棱柱,选D.7. ( 2010广东文)(A)352320 224 160 cm cm【解析】选B(B) ------ cm(C)(D) ---------- cm3 5. ( 2010广东理) 6.如图1, △ ABC为三角形,AA// BB // CC , CC丄平餐题则四面体ABCD 的体积的最大值为二、填空题【答案】96【解析】考查棱锥体积公式V 丄36 89632. ( 2010湖南文)13.图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图,贝ij h=cm则多囱体的正视图f 电称三视图)是・总丕三角影.平面且■B.自由"软氏”垒点辻知.<0D 四点,若 AB=CD=2,C、8. ( 2010全国卷1文)(12)已知在半径为2的球面上有A 、B 、(A)(B)丁3(C(D)【解析】过V四面体ABCDCD 作平面PCD, 故 V m ax 12-134厂3使AB 丄平面PCD,交AB 与P,设点P 到CD 的距离为h ,则有2 _ h — h , "1直径通过AB 与CD 的中点时,hmax ”2/ 1 ? 2点,31. ( 2010 上海文)6.已知四棱椎P ABCD 的底面是边长为6的正方形,侧棱PA 底面 ABCD ,且 PA8,则该四棱椎的体积是3. (2010浙江理)(12)若某几何体的三视图(单位: cm)如图所示, 则此几何体的体积是______________ cm3 .解析:图为一四棱台和长方体的组合体的三视图,由卷中所给公式计算得体积为144,4.(2010天津文)(12)—个几何体的三视图如图所示,则这个几何体的体积为_________________ o由俯视图可知该几何体的底面为直角梯形,则正视图和俯视图可知该几何体的高为1,结合三个试图可知该几何体是底面为直角梯形的直四棱柱,所以该几何题的体积为1—(1+2) 2 1=325.(2010天津理)(12)一个几何体的三视图如图所示,则这个几何体的体积为________________【解析】由三视图可知,该几何体为一个底面边长为1,高为2的正四棱柱与一个底面边长为2,高为1的正四棱锥组成的组合体,因为正巳灵珠的体积为2,正四棱1 4 10,肪以该儿何体的体积 V=2+- =—3 3三、解答题(II )连接,过E 作//交 于点,则 丄平面,且=-1 . 2在APAB 中,AD=AB,PAB° ,BP=2, ・・・ AP=AB=72 ,EG^J G .21 11 1r/. S AABC = _ AB • BC= _ XX 2=/",/. V E ・ABC 二 _S A ABC • EG = _ x^/2 1 . 2 23 3232. ( 2010安徽文)19.(本小题满分13分) 如图,在多面体 ABCDEF44,四边形ABCD 是 正 方 形, AB=2EF=2 , EF^AB,EF±FB,ZBFC=90° , BF=FC,H 为 BC 的屮点,(I )求证:FH 〃平面EDB; (II )求证:AC 丄平面EDB;(III)求四面体 B —DEF 的体积;【解题指导】(3)证明BF 丄平面CDEF,得BF 为四面体B-DEF 的高,进而求体积1. ( 2010陕西文) 18.(本小题满分 12分)如图,在四棱锥 P —ABCD 中,底面ABCD 是矩形PA 丄平面ABCD, 分别是PB, PC 的中点.(I )证明:EF 〃平面PAD ; (II )求三棱锥E — ABC 的体积V.解(I )在APBC 中,E, F 分别是PB, 又 BC 〃 AD, A EF// AD,又T AD・・・EF 〃平面PAD.AP 二 AB, BP=BC=2, E, F平面PAD,E FPC 的中点,・・・EF// BC.平而锥的体积为一4 3(l)ffi:设AC与BD交于点G,则G为AC的中点,连EG, GH,由于H为BC的中点, 故卜carr AB,2又EFT/"1 AB,四边形EFGH为平行四边形(f®/ iHH由四进形ABCD加鹹肠4 /有AB丄E&B文EF//A3…EF丄BC。
高考文科数学试题分类汇编训练:三视图20180328

高考文科数学试题分类汇编训练:空间几何体的三视图、表面积体积1.【2017课标II ,文6】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为A.90πB.63πC.42πD.36π2.【2017课标3,文9】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( ) A .πB .3π4C .π2D .π43.【2017北京,文6】某三棱锥的三视图如图所示,则该三棱锥的体积为(A )60 (B )30 (C )20 (D )104.【2017课标1,文16】已知三棱锥S-ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S-ABC 的体积为9,则球O 的表面积为________.5.【2017课标II ,文15】长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为6.【2017江苏,6】 如图,在圆柱12,O O 内有一个球O ,该球与圆柱的上、下面及母线均相切.记圆柱12,O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是 ▲ .O O 1O 2(第6题)⋅⋅ ⋅7.【2017山东,文13】由一个长方体和两个1 4圆柱构成的几何体的三视图如图,则该几何体的体积为.8、【2016高考新课标1卷】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是()(A)(B)(C)(D)9.【2016高考新课标2文数】下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()(A)(B)(C)(D)10.【2016年高考北京文数】某三棱锥的三视图如图所示,则该三棱锥的体积为()283π17π18π20π28π20π24π28π32πA. B.C. D. 11.【2016高考山东文数】一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( )(A )(B ) (C ) (D ) 12.(2015·新课标全国Ⅱ,9)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点,若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π16131211233+π133+π136+π16+π。
2015-2019全国卷高考数学分类汇编——三视图
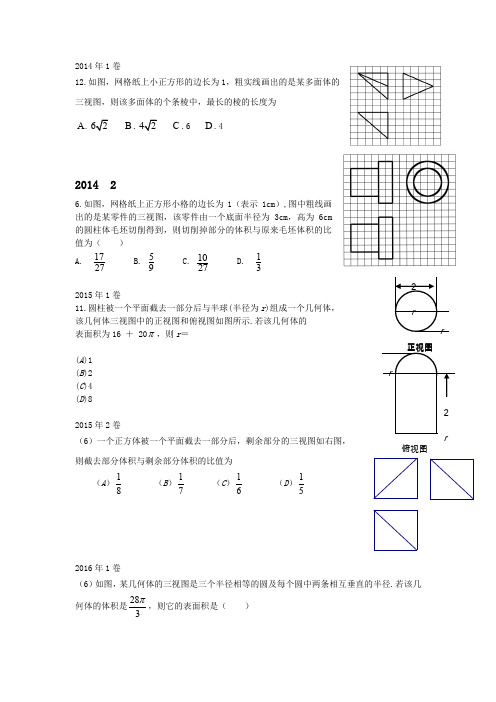
2014年1卷12.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A. B.C .6 D .42014 26.如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A. 1727B. 59C. 1027D. 132015年1卷11.圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体, 该几何体三视图中的正视图和俯视图如图所示.若该几何体的 表面积为16 + 20π,则r = (A )1 (B )2 (C )4 (D )82015年2卷(6)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图, 则截去部分体积与剩余部分体积的比值为(A )81 (B )71 (C )61 (D )512016年1卷(6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是( )2016-2(6)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A)20π(B)24π(C)28π(D)32π2016-3(9)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,学.科.网则该多面体的表面积为()(A)18+(B)54+(C)90(D)812017-17.某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A .10B .12C .14D .162017-24.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π2018-17.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .172B .52C .3D .22018-33.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是。
三视图专项训练题(简单适用于文科)
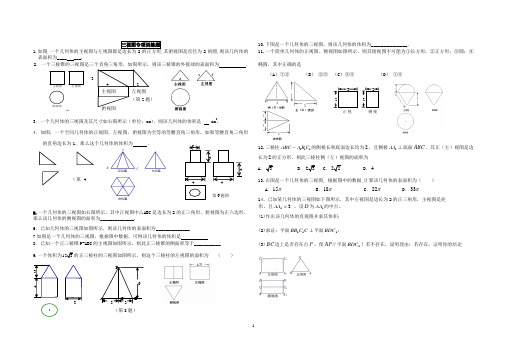
11.如图,其俯视图是直径为2的圆,则该几何体的表面积为____ ___.2.一个三棱锥的三视图是三个直角三角形,如图所示,则该三棱锥的外接球的表面积为 .3.一个几何体的三视图及其尺寸如右图所示(单位:cm ),则该几何体的体积是 cm 3.4.如图,一个空间几何体的正视图,左视图,俯视图为全等的等腰直角三角形,如果等腰直角三角形的直角边长为1,那么这个几何体的体积为 .5.一个几何体的三视图如右图所示,其中正视图中△ABC 是边长为2的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为______________.6.已知几何体的三视图如图所示,则该几何体的表面积为______________7如图是一个几何体的三视图,根据图中数据,可得该几何体的体积是8.已知一个正三棱锥P-ABC 的主视图如图所示,则此正三棱锥的侧面积等于___________ 9.一个体积为 ( )10.下图是一个几何体的三视图,则该几何体的体积为_______________.11.一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为....①长方形;②正方形;③圆;④椭圆. 其中正确的是(A )①② (B ) ②③ (C )③④ (D ) ①④12.三棱柱111ABC A B C -的侧棱长和底面边长均为2,且侧棱1AA⊥底面ABC ,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为 A...413.右图是一个几何体的三视图, 根据图中的数据,计算该几何体的表面积为( ) A .15πB .18πC .22πD .33π14、已知某几何体的三视图如下图所示,其中左视图是边长为2的正三角形,主视图是矩 形,且31=AA ,设D 为1AA 的中点。
(1)作出该几何体的直观图并求其体积; (2)求证:平面⊥C C BB 11平面1BDC ;(3)BC边上是否存在点P ,使//AP 平面1BDC ?若不存在,说明理由;若存在,证明你的结论(第2题)第6题图3 4 2 俯视图主视图 左视图俯视图左视图主视图第(第4题题)(第8题)。
高中数学三视图--原卷
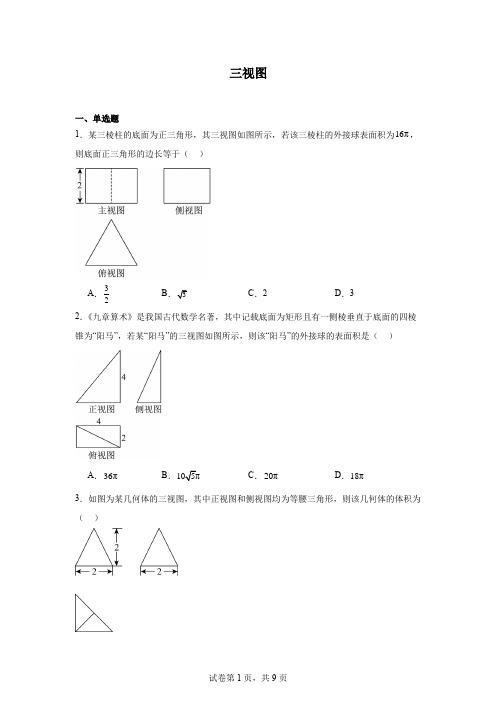
三视图一、单选题1.某三棱柱的底面为正三角形,其三视图如图所示,若该三棱柱的外接球表面积为16π,则底面正三角形的边长等于()A.32B C.2D.32.《九章算术》是我国古代数学名著,其中记载底面为矩形且有一侧棱垂直于底面的四棱锥为“阳马”,若某“阳马”的三视图如图所示,则该“阳马”的外接球的表面积是()A.36πB.C.20πD.18π3.如图为某几何体的三视图,其中正视图和侧视图均为等腰三角形,则该几何体的体积为()A .4B .43C .23 D .134.某几何体的三视图如图所示,则该几何体的表面积为( )A .π32B .π32+C .π32D .π322+ 5.已知一个长方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则该几何体的表面积为( )A B .452+ C .992+D 6.已知一个三棱锥的三视图如图,正视图为边长为3的正方形,侧视图和俯视图均为等腰直角三角形,则此几何体的外接球的表面积为( )A .6πB .12πC .17πD .27π7.如图,网格纸上的小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )A .488π+B .4816π+C .648π+D .6416π+8.如图是某几何体的三视图,已知网格纸上小正方形的边长为1,则该几何体中最长的棱长等于( )A B C D 9.某几何体的三视图如图所示,其中每个网格是由边长为1的小正方形组成,则该几何体的侧面积为( )A.B.C.D.10.某几何体的三视图如图所示,则该几何体的体积为()A.2πB.5π3C.4π3D.π11.某几何体的三视图如图所示,则该几何体的体积为()A.16π3B.20π3C.40π3D.5π12.如图,网格纸中小正方形的边长为1,粗实线绘制的是一个几何体的三视图,则该几何体的表面积为()A .(204π++B .(166π++C .(206π++D .(164π++ 13.已知某几何体的三视图如图所示,则该几何体的体积为( )A .22B .24C .26D .2814.如图,网格纸上绘制了一个几何体的三视图,若网格中小正方形的边长为1,则该几何体的体积为( )A .16π3B .28π3C .64π3D .112π315.若一个几何体的三视图如图所示,则该几何体的体积为( )A B C D16.一个几何体的三视图如图所示,如果该几何体的顶点都在球O的球面上,那么球O的表面积是().A.2πB.4πC.8πD.16π17.如图,网格纸上绘制的是某几何体的三视图,网格小正方形的边长为1,则该几何体的体积为().A.15πB.20πC.26πD.30π18.如图,网格纸中小正方形的边长为10cm,粗线画出的是某体育比赛领奖台三视图,则该领奖台除去下底面的所有面的面积之和为()A.216400cm B.218400cm C.220800cm D.223200cm 19.已知三棱锥的三视图如图所示,则该三棱锥中最长棱的长度为()A.4B.C.D.20.已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,则这个几何体的体积是()A.3π2B.5π3C.7π3D.9π221.某几何体的三视图如图所示,则该几何体的体积为()A.9B.263C.8D.23322.已知某简单组合体的三视图如图所示,则其表面积为()A .12π36+B .12π48+C .10π36+D .10π48+ 23.某几何体的三视图如图所示,则该几何体的体积为( )A .π4B .3π4C .3π2D .2π24.如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为( )A .2B .1C .12D .1325.将长方体截去一个四棱锥后,得到的几何体如图所示,则该几何体的俯视图为( )A.B.C.D.试卷第10页,共1页。
立体几何三视图(高考题精选)

三视图强化练习(13 北京)10.某四棱锥的三视图如图所示,则该四棱锥的体积为。
(12 北京)7. 某三棱锥的三视图如图所示,该三梭锥的表面积是()A. 28+6 5B. 30+6 5C. 56+ 12 5D. 60+12 5(11 北京理)7.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是A.8 B.6 2 C.10 D.8 2(11 北京文)5.某四棱锥的三视图如图所示,该四棱锥的表面积是A.32 B.16+16 2 C.48 D.16+32 2(13 辽宁)(13)某几何体的三视图如图所示,则该几何体的体积是. (13 重庆)5、某几何体的三视图如题 5 图所示,则该几何体的体积为()A、5603B、5803C、200 D 、240(13 湖北)8、一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V,V ,V ,V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为1 2 3 4多面体,则有()A. V1 V2 V4 V3B. V1 V3 V2 V4C. V2 V1 V3 V4D. V2 V3 V1 V4(13 全国新课标1)8、某几何体的三视图如图所示,则该几何体的体积为(A )16 8π(B)8 8π(C)16 16π(D)8 16π(13 全国新课标2)7、一个四面体的顶点在空间直角坐标系O xyz中的坐标分别是(1,0,1) ,(1,1,0),(0,1,1),(0,0,0) ,画该四面体三视图中的正视图时,以zOx平面为投影面,则得到正视图可以为()(A) (B) (C) (D)(12 天津)(10)一个几何体的三视图如图所示(单位:m),则该几何体的体积 3m .(11 东城二模)(4)如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为2,那么这个几何体的体积为(A)43 (B)83(C)4 (D) 8正视侧视俯视(11 海淀)11. 一个几何体的三视图如图所示,则这个几何体的体积为____________.1 11 11 1 1 12 2 2 21 1正视图左视图11俯视图(12 辽宁)(13)一个几何体的三视图如图所示,则该几何体的表面积为______________。
高考真题分类汇总之三视图(小题,09-18年)
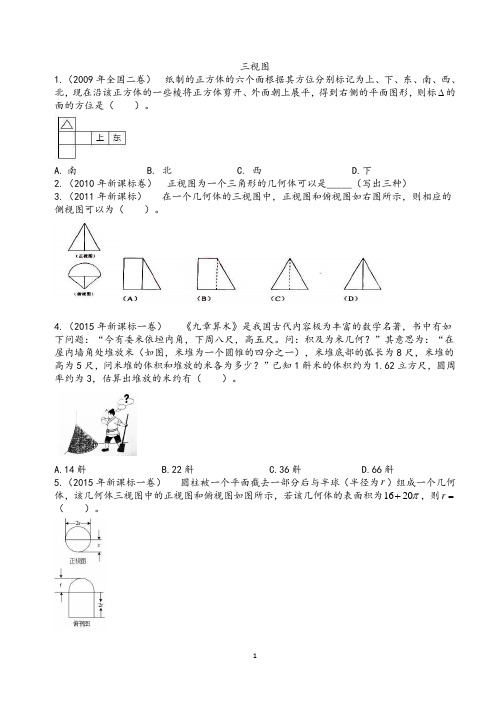
三视图1.(2009年全国二卷)纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北,现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到右侧的平面图形,则标∆的面的方位是()。
A.南B. 北C. 西D.下2.(2010年新课标卷)正视图为一个三角形的几何体可以是_____(写出三种)3.(2011年新课标)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为()。
4.(2015年新课标一卷)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。
问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()。
A.14斛B.22斛C.36斛D.66斛5.(2015年新课标一卷)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为π16+,则=20r ()。
A.1B.2C.4D.86.(2015年新课标二卷) 一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为( )。
A.81B.71C.61D.51 7.(2016年新课标一卷)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径。
若该几何体的体积是328π,则它的表面积是( )。
A. π17B.π18C.π20D.π288.(2016年新课标二卷)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )。
A. π20B.π24C.π28D.π329.(2016年新课标三卷)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A.53618+B.51854+C.90D.8110.(2017年新课标一卷)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形、该多面体的各个面中有若干是梯形,这些梯形的面积之和为A .10B .12C .14D .1611.(2017年新课标二卷)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90π B.63πC.42π D.36π。
三年高考(2017-2019)各地文科数学高考真题分类汇总:空间几何体的三视图、表面积和体积

空间几何体的三视图、表面积和体积1.(2019全国II 文16)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)2.(2019全国II 文17)如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥11E BB C C -的体积.3.(2019全国III 文16)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体1111ABCD A B C D -挖去四棱锥O −EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为0.9 g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为___________g.4.(2019江苏9)如图,长方体1111ABCD A B C D 的体积是120,E 为1CC 的中点,则三棱锥E -BCD 的体积是 .5.(2019天津文12.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________.6.(2019北京文12)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.7.(2019浙江4)祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体体积公式V 柱体=Sh ,其中S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示,则该柱体的体积是A .158B .162C .182D .328.(2018全国卷Ⅰ)已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A.B .12πC.D .10π9.(2018全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A.B. C .3 D .210.(2018全国卷Ⅰ)在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C所成的角为30︒,则该长方体的体积为 A .8B.C.D.11.(2018全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是BA12.(2018全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为,则三棱锥D ABC 体积的最大值为 A.B.C.D.13.(2018浙江)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是A .2B .4C .6D .814.(2018北京)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为A .1B .2C .3D .415.(2017新课标Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球俯视图正视图俯视图侧(左)视图正(主)视图面上,则该圆柱的体积为 A .π B .34π C .2π D .4π 16.(2017北京)某三棱锥的三视图如图所示,则该三棱锥的体积为A .60B .30C .20D .1017.(2017浙江)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是A .12π+ B .32π+ C .312π+ D . 332π+ 18.(2017新课标Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为俯视图侧视图正视图A .90πB .63πC .42πD .36π19.(2018天津)如图,已知正方体1111ABCD A B C D -的棱长为1,则四棱锥111A BB D D -的体积为__.20.(2018江苏)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .21.(2017新课标Ⅰ)已知三棱锥S ABC -的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA AC =,SB BC =,三棱锥S ABC -的体积为9,则球O 的表面积为________.22.(2017新课标Ⅱ)长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为 .23.(2017天津)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,D 1C 1B 1A 1D CBA则这个球的体积为 . 24.(2017山东)由一个长方体和两个14圆柱体构成的几何体的三视图如图,则该几何体的体积为 .25.(2017江苏)如图,在圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考文科数学试题分类汇编训练:空间几何体的三视图、表面积体积
1.【2017课标II ,文6】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为
A.90π
B.63π
C.42π
D.36π
2.【2017课标3,文9】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( ) A .π
B .
3π4
C .
π2
D .
π4
3.【2017北京,文6】某三棱锥的三视图如图所示,则该三棱锥的体积为 (A )60 (B )30 (C )20 (D )10
4.【2017课标1,文16】已知三棱锥S-ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S-ABC 的体积为9,则球O 的表面积为________.
5.【2017课标II ,文15】长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为
6.【2017江苏,6】 如图,在圆柱12,O O 内有一个球O ,该球与圆柱的上、下面及母线均相切.记圆柱
12,O O 的体积为1V ,球O 的体积为2V ,则
1
2
V V 的值是 ▲ .
7.【2017山东,文13】由一个长方体和两个1
4
圆柱构成的几何体的三视图如图,则该几何体的体积为 .
8、【2016高考新课标1卷】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是()
(A)(B)(C)(D)
9.【2016高考新课标2文数】下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()
(A)(B)(C)(D)
10.【2016年高考北京文数】某三棱锥的三视图如图所示,则该三棱锥的体积为()
A. B. .
11.【2016高考山东文数】一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为()
(A)(B)(C)(D)
12.(2015·新课标全国Ⅱ,9)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π C.144π D.256π。
