第二章对偶理论与灵敏度分析练习题答案
运筹学02对偶理论(2)对偶单纯形法,灵敏度与参数分析

3.3 对偶单纯形法 Dual Simplex Method
Chapter3 对偶理论 Dual Theory
注:当模型的数据发生变化后,不必对线性规划问题
重新求解,而用灵敏度分析方法直接在原线性规划取
得的最优结果的基础上进行分析或求解 . 线性规划的参数分析(Parametric Analysis)是研究和分
析目标函数或约束中含有的参数μ在不同的波动范围内 最优解和最优值的变化情况.这种含有参数的线性规划
3.3 对偶单纯形法 Dual Simplex Method
Chapter3 对偶理论 Dual Theory
X XB σ
b
B-1A B-1b C-CBB-1A -CBB-1b 若上表为最优单纯形表,则下列两个式子同时成立:
(1) B1b 0 (可行性条件,又叫对偶最优性条件)
(2) C CB B 1 A 0 (最优性条件,又叫对偶可行性条件)
4.最优解、无可行解的判断。
作业:教材P81 1.12 (2)
下一节:灵敏度分析与参数分析
3.4 灵敏度与参数分析
Sensitivity and Parametric Analysis
3.4 灵敏度与参数分析 Sensitivity and Parametric Analysis
Chapter3 对偶理论 Dual Theory
3.3 对偶单纯形法 Dual Simplex Method
max z 7 x1 3x 2
运筹(第二章对偶与灵敏度分析)(1)

5x2 3x3 30
x1 0, x2无约束,x3 0
2023/2/22
17
解:将原问题模型变形, 令x1 x1
min z 7x1 4x2 3x3
4x1 2x2 6x3 24
3x1 6x2 4x3 15 5x2 3x3 30
y1 y2 y3
x1 0, x2无约束,x3 0
则对偶问题是
max w 24 y1 15y2 30 y3
4 y1 3y2
7
x1
2 y1 6 y2 5 y3 4
x2
6 y1 4 y2 3x3 3
x3
y1, y2 0, x3无约束
2023/2/22
18
小结:对偶问题与原问题的关系:
目标函数:MAX
原 约束条件:m个约束
对
问
y1 y2
ym
2023/2/22
12
类似于前面的资源定价问题,每一个约束条件对 应一个“ 对偶变量”,它就相当于给各资源的单 位定价。于是我们有如下的对偶规划:
min W b1 y1 b2 y2 bm ym
a11 y1 a21 y2 am1 ym c1 a12y1 a22y2 am2ymc2 a1n y1 a2n y2 amn ym cn y1, y2 ,, ym 0
分别是原问题和对偶问题的可行解,则恒有
n
m
c j x j bi yi
j 1
i 1
m
n
考虑利用 c j aij yi 及
aij x j bi
i 1
j 1
代入。
2、无界性 如果原问题(对偶问题)有无界解,则
其对偶问题(原问题)无可行解。
2023/2/22
第二章线性规划的对偶理论和灵敏度分析自测题key

i i ii第二章 线性规划的对偶理论和灵敏度分析自测题1. 判断下述说法是否正确(1) 任何线性规划问题存在并具有唯一的对偶问题。
(2) 线性规划原问题的对偶问题的对偶是原问题本身。
(3) 原问题的任一可行解对应的目标函数值都不超过其对偶问题的任一可行解对应的目标函数值。
(4) 已知对偶问题的最优解中, y * > 0 ,则原问题中在资源最优配置下,第i 种资源已完全消 耗殆尽。
(5) 已知对偶问题的最优解中, y * = 0 ,则原问题中在资源最优配置下,第 i 种资源一定未 完全消耗。
(6) 影子价格就是市场价格。
(7) 若第 i 种资源的影子价格为 y * > 0 ,则在保持原问题中其它条件不变时,在资源最优配置下,当第i 种资源增加10个单位时,最优值将一定增加10 y * .(8) 在应用对偶单纯形法计算时,若在某一个单纯形表中,出现某行除该行对应的基变量值小于0外,该行其余元素全部大于或等于0,则可以判断该线性规划问题无最优解。
(9) 在应用对偶单纯形法计算时,若在某一个单纯形表中,出现某行除该行对应的基变量值小于0外,该行其余元素全部小于或等于0,则可以判断该线性规划问题的对偶问题无最优解。
(10)线性规划的原问题和其对偶问题的最优值如果存在,则必然相等。
(11)线性规划问题的最终单纯形表中,当仅某一非基变量在目标函数中的系数变化时,线性规划问题的最优解一定不改变。
(12)线性规划问题的最终单纯形表中,当仅有某一基变量在目标函数中的系数变化时,线性规划问题的最优解一定不改变。
(13)线性规划问题的最终单纯形表中,当仅有某一非基变量在系数矩阵中的列变化时,线性规划问题的最优解一定不改变。
(14)线性规划问题的最终单纯形表中,当仅有某一基变量在系数矩阵中的列变化时,线性规划问题的最优解一定不改变。
(15)线性规划问题的最终单纯形表中,当仅有某种资源的数量变化时,线性规划问题的最优值一定改变。
第二章对偶问题与灵敏度分析
a22 y2 a23 y2
a32 y3 a33 y3
c2 c3
对 a14 y1 a24 y2 a34 y3 c4
称 y1无符号限制,y2 0,y3 0
原问题(P)
max
型 对偶问题(D)
相
min
变量约束:
似
方程约束:
变量≥
方程≥
变量无限制
方程=
变量≤
方程≤
方程约束:
方程=
方程≤
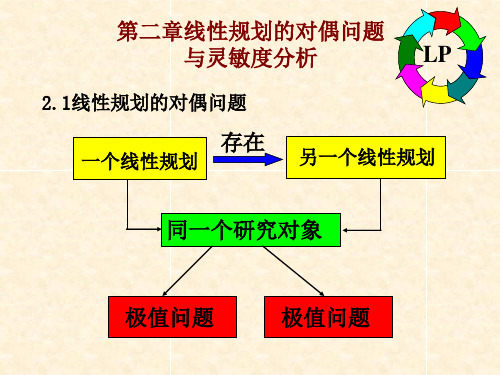
第二章线性规划的对偶问题
与灵敏度分析
LP
2.1线性规划的对偶问题
存在
一个线性规划
另一个线性规划
同一个研究对象
极值问题
极值问题
2.1.1问题的引入: 生产计划问题
LP
资源价格问题
甲 y1 A 1 y2 B 2
y3 C 1 利润 4
乙 资源量
1
45
1
80
3
90
5
2.1.1.1资源价格问题的数学模型
Max Z(X)=4x1+5x2 x1 + x2 ≤ 45
原问题
Max Z(X)= c1x1+c2x2+…+cnxn
y1
a11x1 + a12x2+…+a1n xn ≤ b1
.y.2. ym
a21x1 + a22x2+…+a2n xn ≤ b2
………………………………………………….
am1x1 + am2x2+…+amn xn ≤ bm
x1,x2,…,xn ≥0
2、求下列问题的对偶问题
变量个数n 约束方程个数m1
运筹学习题答案(1)

第一章 线性规划及单纯形法(作业)1.4 分别用图解法和单纯型法求解下列线性规划问题,并对照指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。
(1)Max z=2x 1+x 2St.⎪⎩⎪⎨⎧≥≤+≤+0,24261553212121x x x x x x 解:①图解法:由作图知,目标函数等值线越往右上移动,目标函数越大,故c 点为对应的最优解,最优解为直线⎩⎨⎧=+=+242615532121x x x x 的交点,解之得X=(15/4,3/4)T 。
Max z =33/4. ② 单纯形法:将上述问题化成标准形式有: Max z=2x 1+x 2+0x 3+0x 4St. ⎪⎩⎪⎨⎧≥≤++≤++0,,,242615535421421321x x x x x x x x x x其约束条件系数矩阵增广矩阵为:P 1 P 2 P 3 P 4⎥⎦⎤⎢⎣⎡241026150153 P 3,P 4为单位矩阵,构成一个基,对应变量向,x 3,x 4为基变量,令非基变量x 1,x 2为零,找到T 优解,代入目标函数得Max z=33/4.1.7 分别用单纯形法中的大M 法和两阶段法求解下列线性规划问题,并指出属哪一类。
(3)Min z=4x 1+x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 解:这种情况化为标准形式: Max z '=-4x 1-x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 添加人工变量y1,y2Max z '=-4x 1-x 2+0x 3+0x 4-My 1-My 2⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x(2) 两阶段法: Min ω=y 1+y 2St.⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x第二阶段,将表中y 1,y 2去掉,目标函数回归到Max z '=-4x 1-x 2+0x 3+0x 4第二章 线性规划的对偶理论与灵敏度分析(作业)2.7给出线性规划问题:Max z=2x 1+4x 2+x 3+x 4⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤++≤++≤+≤++)4,3,2,1(096628332143221421j x x x x x x x x x x x x j要求:(1)写出其对偶问题;(2)已知原问题最优解为X *=(2,2,4,0),试根据对偶理论,直接求出对偶问题的最优解。
线性规划问题及其数学模型(最新整理)

试根据对偶问题性质证明上述线性规划问题目标函数值无界。
7. 给出线性规划问题
2
max z 2x1 4x2 x3 x4
2xx12x13xxx322xx64 468
x1
x2
x3
9
x j 0 ( j 1,,4)
要求:(1)写出其对偶问题;(2)已知原问题最优解为 X*=(2,2,4,0),试根据
每捆原稿纸用白坯纸 3 1 kg, 每打日记本用白坯纸 13 1 kg, 每箱练习本用白坯纸
3
3
26 2 kg。 已知生产各种产品的赢利为:每捆原稿纸 1 元,每打日记本 2 元,每箱练 3
习本 3 元。试决定:(1)在现有生产条件下使该厂赢利最大的方案;(2)如白坯纸
供应量不变,而工人数量不足时可从市场上招收临时工,临时工费用为每人每天 15
(4)
n
aij x j
bi
(i 1,, m1 m)
j1
n
aij x j
bi
(i m1 1, m2 2,, m)
j1
x
j
0无约束
( j 1,, n1,, n)
2. 判断下列说法是否正确,为什么?
(1)如果线性规划的原问题存在可行解,则其对偶问题也一定存在可行解;
(2)如果线性规划的对偶问题无可行解,则原问题也一定无可行解;
变;
(3)约束条件右端项由
13
变为
2 3
;
(4)增加一个新的变量 x6 , P6 11, c6 7 ;
4
(5)增添一个新的约束 x1+2x2+x3≤4。 13. 分析下列线性规划问题中,当且变化时最优解的变化,并画出 z(λ)对 λ 的 变化关系图。
第2章 对偶理论和灵敏度分析-习题
理解原问题与对偶问题的关系. 论述对偶问题的基本性质并证明. 掌握对偶单纯形法. 掌握灵敏度分析及参数线性规划.
应用灵敏度分析原理讨论管理实践中的经 济决策问题.
1 写出下列线性规划问题的对偶问题
max Z = 5 x1 + 6 x 2 + 3x 3 x1 + 2 x 2 + 2 x 3 = 5 x1 + 5 x 2 x3 ≥ 3 s.t. 4 x1 + 7 x 2 + 3x 3 ≤ 8 x1无约束,x 2 ≥ 0, x3 ≤ 0
b
1 2
x1 1 0 0
-3-2+λ -5+-4λ -1+λ-
σ j′ = (c j z j )′ = C j′ C B′ B 1 Pj
= C j ′ C B ′ P j′
3 2 5 + 1 +λ
令=0
+λ
≤0 ≤0
4λ ≤ 0
-5/4≤λ≤1, 故 3/4≤c1≤3
令λ=0 -1≤≤5, 故 2≤c2≤8
b
1/3 2
X 故最优解为: * = (0, 2, 0, 0, 0,1/ 3)
(5) 增添一个新的约束 x1+2x2+x3 ≤4
Cj CB 2 3 0 XB x1 x2 x6 b
1 2 4
2 x1 1 0 1 0
3 x2 0 1 2 0
1 x3 -1 2 1 -3
0 x4 4 -1 0 -5
0 x5 -1 1 0 -1
(1)求线性规划的最优解.(20分) (2)写出对偶问题并求出对偶问题的最优解.( 5分) (3)当△b3=-150时最优基是否发生变化?为什 么?(5分) (4)求c2的灵敏度变化范围.(5分) (5)如果x3的系数由[1,3,5]变化到[1,3,2]最 优基是否改变?若改变求新的最优解.(5分)
《运筹学》课堂作业及相应答案解析
第一部分绪论第二部分线性规划与单纯形法1 判断下列说法是否正确:(a)图解法同单纯形法虽然求解的形式不同,但从几何上理解,两者是一致的;(b)线性规划模型中增加一个约束条件,可行域的范围一般将缩小,减少一个约束条件,可行域的范围一般将扩大;(c)线性规划问题的每一个基解对应可行域的一个顶点;(d)如线性规划问题存在可行域,则可行域一定包含坐标的原点;(e)对取值无约束的变量x i,通常令其中,在用单纯形法求得的最优解中有可能同时出现(f)用单纯形法求解标准型的线性规划问题时,与对应的变量都可以被选作换入变量;(g)单纯形法计算中,如不按最小比值原则选取换出变量,则在下一个解中至少有一个基变量的值为负;(h)单纯形法计算中,选取最大正检验数δk对应的变量x k作为换入变量,将使目标函数值得到最快的增长;(i)一旦一个人工变量在迭代中变为非基变量后,则该变量及相应列的数字可以从单纯形表中删除,而不影响计算结果;(j)线性规划问题的任一可行解都可以用全部基可行解的线性组合表示;(k)若x1,x2分别是某一线性规划问题的最优解,则也是该线性规划问题的最优解,其中λ1,λ2可以为任意正的实数;(1)线性规划用两阶段法求解时,第一阶段的目标函数通常写为X ai为人工变量),但也可写为,只要所有k i均为大于零的常数;(m)对一个有n个变量、m个约束的标准型的线性规划问题,其可行域的顶点恰好为个;(n)单纯形法的迭代计算过程是从一个可行解转转换到目标函数值更大的另一个可行解;(o)线性规划问题的可行解如为最优解,则该可行解一定是基可行解;(p)若线性规划问题具有可行解,且其可行域有界,则该线性规划问题最多具有有限个数的最优解;(q)线性规划可行域的某一顶点若其目标函数值优于相邻的所有顶点的目标函数值,则该顶点处的目标函数值达到最优;(r)将线性规划约束条件的“≤”号及“≥”号变换成“=”号,将使问题的最优目标函数值得到改善;(s)线性规划目标函数中系数最大的变量在最优解中总是取正的值;(t)一个企业利用3种资源生产4种产品,建立线性规划模型求解得到的最优解中,最多只含有3种产品的组合;(u)若线性规划问题的可行域可以伸展到无限,则该问题一定具有无界解;(v)一个线性规划问题求解时的迭代工作量主要取决于变量数的多少,与约束条件的数量关系相对较小。
第二章对偶理论与灵敏度分析练习题答案
第二章 对偶理论与灵敏度分析练习题答案1.判断下列说法是否正确:(1) 任何线性规划问题存在并具有惟一的对偶问题;(✓)(2) 根据对偶问题的性质,当原问题为无界解时,其对偶问题无可行解,反之,当对偶问题无可行解时,其原问题具有无界解;(✗)(3) 设j ˆx ,i ˆy 分别为标准形式的原问题与对偶问题的可行解,*j x ,*i y 分别为其最优解,则恒有n n m m**j j j j i i i i j 1j 1i 1i 1ˆˆc x c x b y b y ====≤=≤∑∑∑∑;(✓)(4) 若线性规划的原问题有无穷多最优解,则其对偶问题也一定具有无穷多最优解;(✓)(5) 已知*i y 为线性规划的对偶问题的最优解,若*i y 0>,说明在最优生产计划中第i 种资源已完全耗尽;(✓)(6) 已知*i y 为线性规划的对偶问题的最优解,若*i y 0=,说明在最优生产计划中第i 种资源一定有剩余;(✗)(7) 若某种资源的影子价格等于k ,在其他条件不变的情况下,当该种资源增加5个单位时,相应的目标函数值将增大5k ;(✗)(8) 应用对偶单纯形法计算时,若单纯形表中某一基变量i x 0<,又x i 所在行的元素全部大于或等于零,则可以判断其对偶问题具有无界解;(✓)(9) 若线性规划问题中的b i ,c j 值同时发生变化,反映到最终单纯形表中,不会出现原问题与对偶问题均为非可行解的情况;(✗)(10) 在线性规划问题的最优解中,如某一变量x j 为非基变量,则在原来问题中,无论改变它在目标函数中的系数c j 或在各约束中的相应系数a ij ,反映到最终单纯形表中,除该列数字有变化外,将不会引起其他列数字的变化。
(✓)2.下表是某一约束条件用“≤”连接的线性规划问题最优单纯形表格,其中x 4、x 5为松弛变量。
要求:(1)(3)其它条件不变时,约束条件右端项b 1在何范围内变化,上述最优基不变。
第二章 对偶问题和灵敏度分析1
1
1 2
2
y1 y3
x 2x 2 可直接寫出此問題的對偶問題如下:
1 2
7 x1 6 x2 42 y2
x1 0, x2 0
D:Max y0 32 y1 42 y2 2 y3 可直接寫出此問題的對偶問題如下: :Max y x 32 s.t. 4 y1 7 y2 y3 D10 1 y 42 y 2 y
W = 30y1 + 60 y2 + 24y3
根据原则2 ,对方能够接受的价格显然是越低越好,因此 此问题可归结为以下数学模型:
目标函数 Min W = 30y1 + 60 y2 + 24y3 y1 + 3y2 约束条件 s.t y1 , y2 , y3 0 原线性规划问题称为原问题,此问题为对偶问题, y1 , y2 , y3 称为影子价格
y,,v v))是 行解, , ((y 是D D的可行解。 的可行解。 这两个 x,,s s) )是 令 令((x 是P P 的可 的可行解 这两个 可行 且只当 只当 可行解均为 解均为最佳 最佳解当 解当且 0 ii yi sii 0
x jjv jj 0 0 jj
原始问题的变量
极个别(B)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 对偶理论与灵敏度分析练习题答案
1.判断下列说法是否正确:
(1) 任何线性规划问题存在并具有惟一的对偶问题;()
(2) 根据对偶问题的性质,当原问题为无界解时,其对偶问题无可行解,反之,当对偶问题无可行解时,其原问题具有无界解;()
(3) 设j ˆ
x ,i ˆy 分别为标准形式的原问题与对偶问题的可行解,*j x ,*i y 分别为其最优解,则恒有n n m m
**j j j j i i i i j 1
j 1
i 1
i 1
ˆˆc x c x b y b y ====≤=≤∑∑∑∑;()
(4) 若线性规划的原问题有无穷多最优解,则其对偶问题也一定具有无穷多最优解;() (5) 已知*i y 为线性规划的对偶问题的最优解,若*i y 0>,说明在最优生产计划中第i 种资源已完全耗尽;()
(6) 已知*i y 为线性规划的对偶问题的最优解,若*i y 0=,说明在最优生产计划中第i 种资源一定有剩余;()
(7) 若某种资源的影子价格等于k ,在其他条件不变的情况下,当该种资源增加5个单位时,相应的目标函数值将增大5k ;()
(8) 应用对偶单纯形法计算时,若单纯形表中某一基变量i x 0<,又x i 所在行的元素全部大于或等于零,则可以判断其对偶问题具有无界解;() $
(9) 若线性规划问题中的b i ,c j 值同时发生变化,反映到最终单纯形表中,不会出现原问题与对偶问题均为非可行解的情况;()
(10) 在线性规划问题的最优解中,如某一变量x j 为非基变量,则在原来问题中,无论改变它在目标函数中的系数c j 或在各约束中的相应系数a ij ,反映到最终单纯形表中,除该列数字有变化外,将不会引起其他列数字的变化。
()
2.下表是某一约束条件用“≤”连接的线性规划问题最优单纯形表格,其中x 4、x 5为松弛变量。
X B b x 1 x 2 x 3 x 4 x 5 — x 3 5/2 0 1/2 1 1/2 0 x 1
5/2
1
— -1/2 0
-1/6
1/3
σj 0 -4
0 -4 -2
;
要求:(1)写出原线性规划问题及其对偶问题的数学模型;(2)直接由表写出对偶问题的最优解; (3)其它条件不变时,约束条件右端项b 1在何范围内变化,上述最优基不变。
(4)若以单价购入
第一种资源是否值得,为什么若有人愿意购买第二种资源应要价多少,为什么 答案:
(1)注:该问题得解法非唯一,以下解法只是其中一种(各解法原理相同)。
由题意已知原线性规划问题目标函数为Max (因σj ≤0为最优),且c 4、c 5为0(松弛变量目标函数系数为0)。
根据1j j B j c C B P σ-=-知:2313111
1c c c 4
221
10c c 42610c 23⎧⎛⎫-⋅-⋅=- ⎪⎪⎝⎭⎪⎪⎛⎫-⋅-⋅=-⎨ ⎪⎝⎭⎪
⎪⎛⎫
-⋅=-⎪
⎪⎝⎭⎩
,得:123
c 6c 2c 10=⎧⎪=-⎨⎪=⎩
根据()51122
2
1
511126
3
2010
B A|b 10-⎛⎫=
⎪--⎝⎭,得:()012105A|b 3110110⎛⎫= ⎪-⎝⎭
则原线性规划问题的数学模型为: 12323123123
MaxZ 6x 2x 10x x 2x 53x x x 10s.t.x ,x ,x 0=-++≤⎧
⎪
-+≤⎨⎪≥⎩
其对偶问题的数学模型为:
12
21
21212Min 5y 10y 3y 6y y 2s.t.2y y 10y ,y 0
ω=+≥⎧
⎪-≥-⎪⎨+≥⎪⎪≥⎩ :
(2)直接由表写出对偶问题得最优解为:()*Y 4,2= (3)令原解()()-1i B i i i x X B b b ===,得
b r 的变化范围为:
{}{}i ir ir r i ir ir i
i
Max b /a |a 0b Min b /a |a 0∆->≤≤-<,其中:()1ir ir
a B -=。
则:
{}{()}15151
Max b Min 2226
∆-÷≤≤-÷-,即15b 15∆-≤≤,则10b 20≤≤
(4)以单价购入第一种资源是值得的,因其小于该资源“影子价格”(即<4),可盈利;第二种资源应要价至少为2(影子价格),否则不如自己组织生产。
