一次函数知识点及典型例题

一次函数知识点
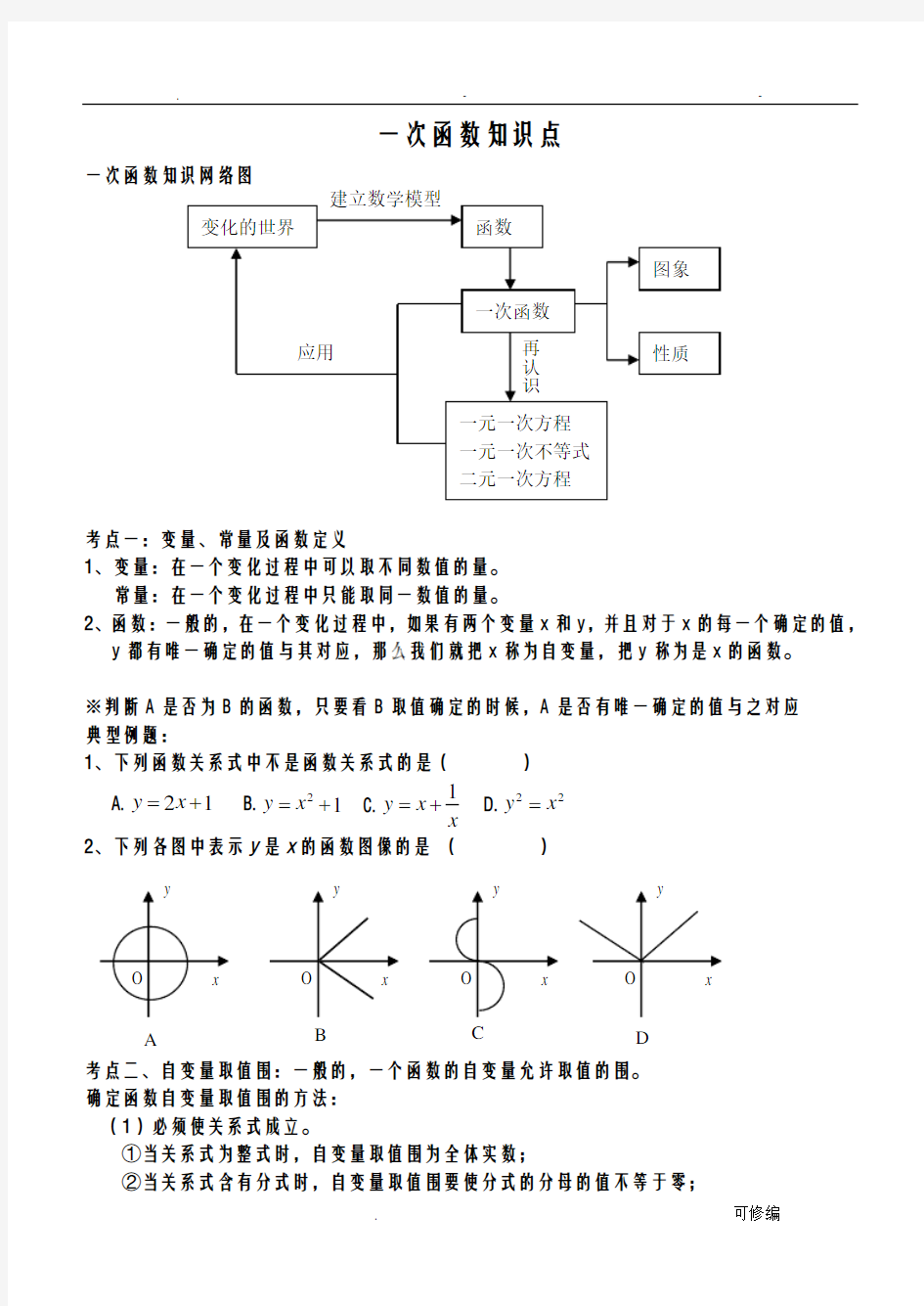
一次函数知识网络图
考点一:变量、常量及函数定义
1、变量:在一个变化过程中可以取不同数值的量。 常量:在一个变化过程中只能取同一数值的量。
2、函数:一般的,在一个变化过程中,如果有两个变量x 和y ,并且对于x 的每一个确定的值,
y 都有唯一确定的值与其对应,那么我们就把x 称为自变量,把y 称为是x 的函数。
※判断A 是否为B 的函数,只要看B 取值确定的时候,A 是否有唯一确定的值与之对应 典型例题:
1、下列函数关系式中不是函数关系式的是( ) A.21y x =+ B.2
1y x =+ C.1y x x
=+
D.22y x = 2、下列各图中表示y 是x 的函数图像的是 ( )
考点二、自变量取值围:一般的,一个函数的自变量允许取值的围。 确定函数自变量取值围的方法: (1)必须使关系式成立。
①当关系式为整式时,自变量取值围为全体实数;
②当关系式含有分式时,自变量取值围要使分式的分母的值不等于零;
A B D
③关系式含有二次根式时,自变量取值围必须使被开方的式子不小于零;
④当关系式中含有指数为零或负数的式子时,自变量取值围要使底数不等于零;
(2)当函数关系表示实际问题时,自变量的取值围还要符合实际情况,使之有意义。 (3)当函数关系表示一个图形的变化关系时,自变量的取值围必须使图形存在。 典型例题: 1、函数3
1
-=x y 的自变量x 的取值围是 2、函数3-=
x y 的自变量x 的取值围是
3、函数()
2
20x y x -=++的自变量x 的取值围是
4、小强在劳动技术课中要制作一个周长为10cm 的等腰三角形.请你写出底边长y (cm )与一腰长x (cm )的函数关系式,并写出自变量的取值围.
考点三、函数的图像与解析式的关系 1、函数的表示方法
(1)列表法:一目了然,使用起来方便,但列出的对应值是有限的,不易看出自变量与函数之间的对应规律。
(2)解析式法:简单明了,能够准确地反映整个变化过程中自变量与函数之间的相依关系,但有些实际问题中的函数关系,不能用解析式表示。
(3)图象法:形象直观,但只能近似地表达两个变量之间的函数关系。 函数的三种表示方法各有优、缺点,有时可以相互转化。 2、分段函数的解析式及图像 注意把握:(1)始点、终点、拐点的坐标及实际意义
(2)每条线段(射线)的解析式、取值围、实际意义 (3)每个解析式中K 的实际意义
典型例题:
1、 如图反映的过程是:晓明从家跑步到体育馆,在那里锻炼了一阵后又走到新华书店去买书,
然后散步走回家。其中t 表示时间(分钟),S 表示晓明离家的距离(千米),那么晓明在体育馆锻炼和在新华书店买书共用去时间是_______________分钟.你还能分析出什么?
2、如图,已知蚂蚁以均匀的速度沿台阶A →B →C →D →E 爬行,那么蚂蚁爬行的高度h 随时间t 变化的图像大致是( )
D E
C B
A
t
h
A
h B
h C
h
D
3、如图,平面直角坐标系中,在边长为1的正方形ABCD 的边 上有一动点P 沿A B C D A →→→→运动一周,则P 的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是( )
4、小强骑自行车去郊游,右图表示他离家的距离y (千米)与所用的时间x (小时)之间关系的函数图象,小强9点离开家,15点回家,根据这个图象,请你回答下列问题: (1)小强到离家最远的地方需要几小时?此时离家多远? (2)若第一次只休息半小时,则第一次休息前的平均速度是多少? (3)返回时平均速度是多少?
5、某学校组织团员举行宣传活动,从学校骑车出发,先上坡到达A
地后,宣传8分钟;然后下坡到B 地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A 地仍要宣传8分钟,那么他们从B 地返回学校用的时间是( ) A.45.2分钟 B.48分钟 C.46分钟 D.33分钟
1 2 3 4
1 2 y s
O 1 2 3 4
1 2 y s O s 1 2 3 4
1 2 y s
O 1 2 3 4
1 2 y O A .
B .
C .
D .
第10题图
6、如图表示,一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象)根据图象解答下列问题:
(1)请分别求出表示轮船和快艇行驶过程的函数解析式(写出自变量的取值围);
(2)轮船和快艇的行驶速度分别是多少? (3)问快艇出发多长时间赶上轮船?
考点四、一次函数和正比例函数的定义 1、 正比例函数定义:
一般地,形如y=kx(k 是常数,k ≠0)的函数叫做正比例函数,其中k 叫做比例系数. 注:正比例函数一般形式 y=kx ① k ≠0② x 的指数为1 2、 一次函数定义:
一般地,形如y=kx +b(k,b 是常数,k ≠0),那么y 叫做x 的一次函数.当b=0时,y=kx +b 即y=kx ,所以说正比例函数是一种特殊的一次函数.
注:一次函数一般形式 y=kx+b ① k ≠0②x 指数为1 ③ b 取任意实数
典型例题
1、 函数2
(1)1k y k x k =++-是一次函数,则k 值为_______________
2、 函数是1
2
()m y m m x
+=-正比例函数,则m 值为_______________
3、函数是22
(4)(2)2y k x k x k =-+-++正比例函数,则k 值为_______________
考点五、待定系数法——求函数解析式
基本思路(1)根据已知条件写出含有待定系数的函数关系式;
(2)将x 、y 的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知
数的方程;
(3)解方程得出未知系数的值;
(4)将求出的待定系数代回所求的函数关系式中得出所求函数的解析式.
特殊的:(1)已知直线y kx b =+过11(,)x y 和22(,)x y 则 k=_____________
(2)直线y kx b =+与x 轴的交点A 坐标为__________与y 轴交点B 坐标为_________ (3)已知直线过点(M,0)(0,N) 则函数解析式为__________________ 典型例题
1、已知一次函数的图象过(3,-3)点,并且与直线相交于x 轴上一点,求此一次
函数的解析式。
2.声音在空气中传播的速度y (m/s )是气温x (℃)的一次函数,下表列出了一组不同气温的
(1)请求y 与x 之间的函数关系式;
(2)当气温23x =℃时,某人看到烟花燃放2s 后才听到声响,那么此人与烟花燃放地约相距
多远?(光的传播时间忽略不计)
3、如图,一次函数图象经过点A ,且与正比例函数y x =-的图象 交于点B ,则该一次函数的表达式为( ) A .
2y x =-+
B .2y x =+
C .2y x =-
D .2y x =--
4、已知一个正比例函数与一个一次函数交与点P (-2, 2)与x 轴、y 轴交与A 、B 两点,且B (0,6) (1)求两个函数的解析式 (2)求△AOP 的面积
5、已知直线AB :1
52
y x =-
+与x 轴、y 轴分别交与点A 、B ,y 轴上点C 坐标为(0,10) 且△≌△AOB ,求直线CM 的解析式
6、如图,直线y=2x+4与x 轴、y 轴分别交于点C 、A ,B 交OA 于点H.
请求直线BD 的解析式
考点六、一次函数图像的位置
k>0,图象经过第一、三象限;k<0,图象经过第二、四象限
b>0,图象经过第一、二象限;b<0,图象经过第三、四象限
??
??>>00
b k 直线经过第一、二、三象限 ??
??<>00
b k 直线经过第一、三、四象限 ???
?><0
b k 直线经过第一、二、四象限 ????<<0
b k 直线经过第二、三、四象限 典型例题:
1、若一次函数y kx b =+的图象经过第一象限,且与y 轴负半轴相交,那( ) A .0k >,0b >
B .0k >,0b <
C .0k <,0b >
D .0k <,0b <
2.一次函数1y kx b =+与2y x a =+的图象如图,则下列结论①0k <;②0a >;③当3x <时,12y y <中,正确的个数是( )A .0 B .1
C .2
D .3
a
b +
3、若一次函数y kx b =+的图象不经过第一象限,则K_______b_______
考点七、一次函数的增减性
k>0,y 随x 的增大而增大,x 最大y 最大,x 最小y 最大; k<0,y 随x 的增大而减小,x 最大y 最小,x 最小y 最大. 典型例题:
1、在函数 y =kx (k <0)的图象上有A (1,y 1)、B (-1,y )、C (-2,y )三个点,则下列各式中正确( )
A 、y 1<y 2<y 3
B 、y 1<y 3<y 2
C 、y 3<y 2<y 1
D 、y 2<y 3<y 2、已知一次函数1y ax =-,y 随x 的增大而减小,则它的大致图像为 ( )
A B C D
3、若一次函数时,当62,≤≤-+=x b kx y 函数值的围为911≤≤-y ,则此一次函数的解析式为
4、一次函数y=(2a-3)x+a+2的函数在-2≤x ≤1的一段都在x 轴的上方,求a 的取值围. 考点八、倾斜度——K 的作用
|k|越大,图象越接近于y 轴;|k|越小,图象越接近于x 轴. 典型例题
1、结合图像,试说明三条直线K 值之间的大小关系________________
考点九、两直线的位置关系
(1)相交:两直线相交,则可将解析式联立形成方程组,方程组的解就是_______________ (2)平行:两直线平行,则K 值_____________
X
Y N
B
C
O A M 特殊的:垂直: 两直线平行,则K 值之积=_____________ 典型例题:
1、已知直线AB :1
52
y x =-
+与x 轴、y 轴分别交与点A 、B ,y 轴上点C 坐标为(0,10) 且△≌△AOB ,求点N 坐标
2、已知直线相交于第四象限,求k 的取值围。
3、如图,直线y =-
43x +4与y 轴交于点A ,与直线y =45x +45交于点B ,且直线y =4x +4与x 轴交于点C ,则△ABC 的面积为___.
4、将直线32y x =-向下平移m 个单位得到的直线是( )
A. 32y x m =-+ B . 32y x m =-- C . 3()2y x m =+- D .3()2y x m =--
5、已知直线111:b x k y l +=经过点(-1,6)和(1,2),它和x 轴、y 轴分别交于B 和A ;直线212:b x k y l +=经过点(2,-4)和(0,-3),它和x 轴、y 轴的交点分别是D 和C 。
(1)求直线1l 和2l 的解析式;(2)求四边形ABCD 的面积;
(3)设直线1l 与2l 交于点P ,求△PBC 的面积。
C
B
A x
O
y
y =ax +b
y =cx +d
ax+b=cx+d
ax+b ax+b>cx+d 考点十、用函数的观点看方程(组)、不等式 (1)一元一次方程与一次函数的关系 任何一元一次方程到可以转化为ax+b=0(a ,b 为常数,a ≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值. 从图象上看,相当于已知直线y=ax+b 确定它与x 轴的交点的横坐标的值. (2)一次函数与一元一次不等式的关系 任何一个一元一次不等式都可以转化为ax+b>0或ax+b<0(a ,b 为常数,a ≠0)的形式,所以解一元一次不等式可以看作:当一次函数值大(小)于0时,求自变量的取值围. (3)一次函数与二元一次方程组 ①以二元一次方程ax+by=c 的解为坐标的点组成的图象与一次函数y=b c x b a +- 的图象相同. ②二元一次方程组???=+=+2 22111c y b x a c y b x a 的解可以看作是两个一次函数y=1111b c x b a +-和 典型例题 1、如图,一次函数y ax b =+的图象经过A 、B 两点,则关于x 的不等式0ax b +<的解 集是 2、直线11:l y k x b =+与直线22:l y k x =在同一平面直角坐标中图像的位置如图所示,则关于x 的不等式21k x k x b ≥+的解集为 综合练习 1.如图,直线y=2x+4与x 轴、y 轴分别交于点C 、A ,B 点坐标为(4,0),过点B 作BD ⊥AC 于D,BD 交OA 于点H. (1) 请求直线BD 的解析式; (2) 有两个动点P 和Q 分别从点C 和点O 同时沿x 轴正方向匀速运动,速度分别为2个单位每秒 和1个单位每秒,设△PQD 的面积为S ,点P 、点Q 的运动时间为t 秒,请求S 与t 之间的函数关系式.(请直接写出相应的自变量t 的取值围); (3)请问t 为何值时,△PQD 的面积是△BCD 的面积的6 1. 2、已知直线AB :1 52 y x =- +与x 轴、y 轴分别交与点A 、B ,y 轴上点C 坐标为(0,10) (1)求A 、B 两点坐标 (2)动M 从A 点出发,以每秒1单位长度的速度,沿x 轴向左运动,连接CM. 设点M 的运动时间为t ,△的面积为S ,求S 与t 的函数关系式.(并标出自变量的取值围) (3)直线AB 与直线CM 相交于点;点P 为y 轴上一点,且始终保持PM+PN 最短, 第16题图 x y 3-1l 2 l 1 O y x H O C D B A y x H O C D B A 当t为何值时,△≌△AOB,并求出此时点P的坐标 二次函数知识点总结及典型例题和练习(极好) 知识点一:二次函数的概念和图像 1、二次函数的概念 一般地,如果)0,,(2≠++=a c b a c bx ax y 是常数,,特别注意a不为零,那么y叫做x 的二次函数。)0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。 2、二次函数的图像 二次函数的图像是一条关于a b x 2-=对称的曲线,这条曲线叫抛物线。 抛物线的主要特征: ①有开口方向;②有对称轴;③有顶点。 3、二次函数图像的画法--------五点作图法: (1)先根据函数解析式,求出顶点坐标,在平面直角坐标系中描出顶点M,并用虚线画出对称轴 (2)求抛物线c bx ax y ++=2与坐标轴的交点: 当抛物线与x 轴有两个交点时,描出这两个交点A,B 及抛物线与y 轴的交点C,再找到点C 的对称点D。将这五个点按从左到右的顺序连接起来,并向上或向下延伸,就得到二次函数的图像。 当抛物线与x 轴只有一个交点或无交点时,描出抛物线与y 轴的交点C 及对称点D。由C 、M 、D 三点可粗略地画出二次函数的草图。如果需要画出比较精确的图像,可再描出一对对称点A 、B,然后顺次连接五点,画出二次函数的图像。 【例1】 已知函数y=x 2-2x-3, (1)写出函数图象的顶点、图象与坐标轴的交点,以及图象与 y 轴的交点关于图象对称轴的对称点。然后画出函数图象的草图; (2)求图象与坐标轴交点构成的三角形的面积: (3)根据第(1)题的图象草图,说 出 x 取哪些值时,① y=0;② y <0;③ y>0 知识点二:二次函数的解析式 二次函数的解析式有三种形式: (1)一般式:)0,,(2≠++=a c b a c bx ax y 是常数, (2) 交点式:当抛物线c bx ax y ++=2与x 轴有交点时,即对应的一元二次方程 02=++c bx ax 有实根1x 和2x 存在时,根据二次三项式的分解因式))((212x x x x a c bx ax --=++,二次函数c bx ax y ++=2可转化为两根式))((21x x x x a y --=。如果 没有交点,则不能这样表示。 (3)顶点式:)0,,()(2≠+-=a k h a k h x a y 是常数, 当题目中告诉我们抛物线的顶点时,我们最好设顶点式,这样最简洁。 【例1】 抛物线c bx ax y ++=2与x 轴交于A (1,0),B(3,0)两点,且过(-1,16),求抛物线的解析式。 【例2】 如图,抛物线c bx ax y ++=2与x 轴的一个交点A 在点(-2,0)和(-1,0)之间(包括这两点),顶点C 是矩形DEFG 上(包括边界和内部)的一个动点,则: (1)abc 0 (>或<或=) (2)a 的取值范围是 ? 【例3】 下列二次函数中,图象以直线x = 2为对称轴,且经过点(0,1)的是 ( ) A.y = (x ? 2)2 + 1 B .y = (x + 2)2 + 1 C .y = (x ? 2)2 ? 3 D.y = (x + 2)2 – 3 第十八章 函数 一次函数 (一)函数 1、变量:在一个变化过程中可以取不同数值的量。 常量:在一个变化过程中只能取同一数值的量。 2、函数:一般的,在一个变化过程中,如果有两个变量x 和y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就把x 称为自变量,把y 称为因变量,y 是x 的函数。 *判断Y 是否为X 的函数,只要看X 取值确定的时候,Y 是否有唯一确定的值与之对应 3、定义域:一般的,一个函数的自变量允许取值的范围,叫做这个函数的定义域。 4、确定函数定义域的方法: (1)关系式为整式时,函数定义域为全体实数; (2)关系式含有分式时,分式的分母不等于零; (3)关系式含有二次根式时,被开放方数大于等于零; (4)关系式中含有指数为零的式子时,底数不等于零; (5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。 5、函数的解析式:用含有表示自变量的字母的代数式表示因变量的式子叫做函数的解析式 6、函数的图像 一般来说,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象. 7、描点法画函数图形的一般步骤 第一步:列表(表中给出一些自变量的值及其对应的函数值); 第二步:描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点);第三步:连线(按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来)。 8、函数的表示方法 列表法:一目了然,使用起来方便,但列出的对应值是有限的,不易看出自变量与函数之间的对应规律。 解析式法:简单明了,能够准确地反映整个变化过程中自变量与函数之间的相依关系,但有些实际问题中的函数关系,不能用解析式表示。 图象法:形象直观,但只能近似地表达两个变量之间的函数关系。 (二)一次函数 1、一次函数的定义 一般地,形如y kx b =+(k ,b 是常数,且0k ≠)的函数,叫做一次函数,其中x 是自变量。当0b =时,一次函数y kx =,又叫做正比例函数。 ⑴一次函数的解析式的形式是y kx b =+,要判断一个函数是否是一次函数,就是判断是否能化成以上形式. ⑵当0b =,0k ≠时,y kx =仍是一次函数. ⑶当0b =,0k =时,它不是一次函数. ⑷正比例函数是一次函数的特例,一次函数包括正比例函数. 初中数学函数知识点大全+典型例题 知识点一、二次函数的概念和图像 1、二次函数的概念 一般地,如果特)0,,(2≠++=a c b a c bx ax y 是常数,,特别注意a 不为零 那么y 叫做x 的二次函数。 )0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。 2、二次函数的图像 二次函数的图像是一条关于a b x 2- =对称的曲线,这条曲线叫抛物线。 抛物线的主要特征: ①有开口方向;②有对称轴;③有顶点。 3、二次函数图像的画法 五点法: (1)先根据函数解析式,求出顶点坐标,在平面直角坐标系中描出顶点M ,并用虚线画出对称轴 (2)求抛物线c bx ax y ++=2与坐标轴的交点: 当抛物线与x 轴有两个交点时,描出这两个交点A,B 及抛物线与y 轴的交点C ,再找到点C 的对称点D 。将这五个点按从左到右的顺序连接起来,并向上或向下延伸,就得到二次函数的图像。 当抛物线与x 轴只有一个交点或无交点时,描出抛物线与y 轴的交点C 及对称点D 。由C 、M 、D 三点可粗略地画出二次函数的草图。如果需要画出比较精确的图像,可再描出一对对称 点A 、B ,然后顺次连接五点,画出二次函数的图像。 知识点二、二次函数的解析式 二次函数的解析式有三种形式:口诀----- 一般 两根 三顶点 (1)一般 一般式:)0,,(2≠++=a c b a c bx ax y 是常数, (2)两根 当抛物线c bx ax y ++=2与x 轴有交点时,即对应二次好方程02=++c bx ax 有实根1x 和2x 存在时,根据二次三项式的分解因式))((212x x x x a c bx ax --=++,二次函数c bx ax y ++=2可转化为两根式))((21x x x x a y --=。如果没有交点,则不能这样表示。 a 的绝对值越大,抛物线的开口越小。 (3)三顶点 顶点式:)0,,()(2≠+-=a k h a k h x a y 是常数, 知识点三、二次函数的最值 如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当 a b x 2-=时,a b a c y 442-=最值。 如果自变量的取值范围是21x x x ≤≤,那么,首先要看a b 2-是否在自变量取值范围21x x x ≤≤内,若在此范围内,则当x=a b 2-时,a b a c y 442-=最值;若不在此范围内,则需要考虑函数在21x x x ≤≤范围内的增减性,如果在此范围内,y 随x 的增大而增大,则当2x x =时, c bx ax y ++=222最大,当1x x =时,c bx ax y ++=121最小;如果在此范围内,y 随x 的增大而减 小,则当1x x =时,c bx ax y ++=121最大,当2x x =时,c bx ax y ++=222 最小。 知识点四、二次函数的性质 1、二次函数的性质 第二讲:函数的单调性 一、定义: 1.设函数)(x f y =的定义域为I ,如果对于定义域I 内的某个区间D 内的任意两个自变量的值21,x x ,当21x x <时,都有),()(21x f x f <那么就说)(x f 在区间D 上是增函数.区间D 叫)(x f y =的单调增区间. 注意:增函数的等价式子:0) ()(0)]()()[(2 1212121>--?>--x x x f x f x f x f x x ; 难点突破:(1)所有函数都具有单调性吗? (2)函数单调性的定义中有三个核心①21x x <②)()(21x f x f <③ 函数)(x f 为增函数,那么①②③中任意两个作为条件,能不能推出第三个? 2. 设函数)(x f y =的定义域为I ,如果对于定义域I 内的某个区间D 内的任意两个自变量的值21,x x ,当21x x <时,都有),()(21x f x f >那么就说)(x f 在区间D 上是减函数.区间D 叫)(x f y =的单调减区间. 注意:(1)减函数的等价式子:0) ()(0)]()()[(21212121<--? <--x x x f x f x f x f x x ; (2)若函数)(x f 为增函数,且)()(,2121x f x f x x <<则. 题型一:函数单调性的判断与证明 例 1.已知函数)(x f 的定义域为R ,如果对于属于定义域内某个区间I 上的任意两个不同的自变量21,x x 都有 .0) ()(2 121>--x x x f x f 则( ) A.)(x f 在这个区间上为增函数 B.)(x f 在这个区间上为减函数 C.)(x f 在这个区间上的增减性不变 D.)(x f 在这个区间上为常函数 二次函数知识点总结及典型例题 一、二次函数的概念和图像 1、二次函数的概念 一般地,如果)0,,(2 ≠++=a c b a c bx ax y 是常数,,那么y 叫做x 的二次函数。 )0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。 2、二次函数的图像 二次函数的图像是一条关于a b x 2-=对称的曲线,这条曲线叫抛物线。 抛物线的主要特征: ①有开口方向;②有对称轴;③有顶点。 3、二次函数图像的画法---五点法: 二、二次函数的解析式 二次函数的解析式有三种形式: (1)一般式:)0,,(2 ≠++=a c b a c bx ax y 是常数, (2)顶点式:)0,,()(2 ≠+-=a k h a k h x a y 是常数, (3)当抛物线c bx ax y ++=2 与x 轴有交点时,即对应二次好方程0 2=++c bx ax 有实根1x 和2x 存在时,根据二次三项式的分解因式))((212 x x x x a c bx ax --=++,二次函数c bx ax y ++=2 可转化为两根式))((21x x x x a y --=。如果没有交点,则不能这 样表示。 三、抛物线c bx ax y ++=2 中,c b a ,,的作用 (1)a 决定开口方向及开口大小,这与2 ax y =中的a 完全一样. (2)b 和a 共同决定抛物线对称轴的位置.由于抛物线c bx ax y ++=2 的对称轴是直线 a b x 2- =,故:①0=b 时,对称轴为y 轴所在直线;②0>a b (即a 、b 同号)时,对称轴在y 轴左侧;③0 函数知识点总结 知识点一、平面直角坐标系 1、平面直角坐标系 在平面内画两条互相垂直且有公共原点的数轴,就组成了平面直角坐标系。 其中,水平的数轴叫做x 轴或横轴,取向右为正方向;铅直的数轴叫做y 轴或纵轴,取向上为正方向;两轴的交点O (即公共的原点)叫做直角坐标系的原点;建立了直角坐标系的平面,叫做坐标平面。 为了便于描述坐标平面内点的位置,把坐标平面被x 轴和y 轴分割而成的四个部分,分别叫做第一象限、第二象限、第三象限、第四象限。 注意:x 轴和y 轴上的点,不属于任何象限。 2、点的坐标的概念 点的坐标用(a ,b )表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒。平面内点的坐标是有序实数对,当b a ≠时,(a ,b )和(b ,a )是两个不同点的坐标。 知识点二、不同位置的点的坐标的特征 1、各象限内点的坐标的特征 点P(x,y)在第一象限0,0>>?y x 点P(x,y)在第二象限0,0>?y x 2、坐标轴上的点的特征 点P(x,y)在x 轴上0=?y ,x 为任意实数 点P(x,y)在y 轴上0=?x ,y 为任意实数 点P(x,y)既在x 轴上,又在y 轴上?x ,y 同时为零,即点P 坐标为(0,0) 3、两条坐标轴夹角平分线上点的坐标的特征 点P(x,y)在第一、三象限夹角平分线上?x 与y 相等 点P(x,y)在第二、四象限夹角平分线上?x 与y 互为相反数 4、和坐标轴平行的直线上点的坐标的特征 位于平行于x 轴的直线上的各点的纵坐标相同。 位于平行于y 轴的直线上的各点的横坐标相同。5、关于x 轴、y 轴或远点对称的点的坐标的特征 点P 与点p ’关于x 轴对称?横坐标相等,纵坐标互为相反数 点P 与点p ’关于y 轴对称?纵坐标相等,横坐标互为相反数 一次函数知识点 考点一:变量、常量及函数定义 1、变量:在一个变化过程中可以取不同数值的量。 常量:在一个变化过程中只能取同一数值的量。 2、函数:一般的,在一个变化过程中,如果有两个变量x 和y ,并且对于x 的每一个确定的值, y 都有唯一确定的值与其对应,那么我们就把x 称为自变量,把y 称为是x 的函数。 ※判断A 是否为B 的函数,只要看B 取值确定的时候,A 是否有唯一确定的值与之对应 1、下列函数关系式中不是函数关系式的是( ) A. 21y x =+ B. 21y x =+ C. 1y x x =+ D. 22y x = 2、下列各图中表示y 是x 的函数图像的是 ( ) 考点二、自变量取值围:一般的,一个函数的自变量允许取值的围。 确定函数自变量取值围的方法: (1)必须使关系式成立。 ①当关系式为整式时,自变量取值围为全体实数; ②当关系式含有分式时,自变量取值围要使分式的分母的值不等于零; ③关系式含有二次根式时,自变量取值围必须使被开方的式子不小于零; ④当关系式中含有指数为零或负数的式子时,自变量取值围要使底数不等于零; (2)当函数关系表示实际问题时,自变量的取值围还要符合实际情况,使之有意义。 (3)当函数关系表示一个图形的变化关系时,自变量的取值围必须使图形存在。 1、函数31-= x y 的自变量x 的取值围是 2、函数3-=x y 的自变量x 的取值围是 3、函数()220x y x -=++的自变量x 的取值围是 4、小强在劳动技术课中要制作一个周长为10cm 的等腰三角形.请你写出底边长y (cm )与一腰长x (cm )的函数关系式,并写出自变量的取值围. 考点三、函数的图像与解析式的关系 1、函数的表示方法 (1 )列表法:一目了然,使用起来方便,但列出的对应值是有限的,不易看出自变量与函数A B D 函数的概念与表示 知识领航 1.函数的定义 一般地:设A,B是非空的数集,如果按照某种确定的对应关系,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数() f x和它对应,那么就称(): f x A B →为从集合A到集合B的一个函数,记作:(), y f x x A =∈. 注意:函数概念中的关键词 (1) A,B是非空数集. (2)任意的x∈A,存在唯一的y∈B与之对应. 2. 函数的定义域、值域 其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{()|} f x x A ∈叫做函数的值域. 3. 函数的三要素 定义域、值域和对应法则. 4. 相等函数 如果两个函数的定义域和对应法则完全一致,则这两个函数相等; 这是判断两函数相等的依据. 5. 区间的概念 设,a b是两个实数,而且a b<.我们规定: (1)满足不等式a x b ≤≤的实数x的集合叫做闭区间,表示为[,] a b. (2)满足不等式a x b <<的实数x的集合叫做开区间,表示为(,) a b. (3)满足不等式a x b ≤<或a x b <≤的实数x的集合叫做半开半闭区间,分别表示为[,) a b,(,] a b. 这里的实数都叫做相应区间的端点. 实数R可以用区间表示为(,) -∞+∞.“∞”读作“无穷大”,“-∞”读作“负无穷大”,“+∞”读作“正无穷大”,我们可以把满足x a≥,x a>,x b≤,x b<,的实数x的集合分别表示为[,) a+∞,(,) a+∞,(,]b -∞,(,)b -∞. 6. 函数的表示法 (1)解析法:用数学表达式表示两个变量之间的对应关系的方法. (2)列表法:列出表格来表示两个变量之间的对应关系的方法. (3)图像法: 用图象表示两个变量之间的对应关系的方法. 用描点法画函数图象的一般步骤:列表、描点、连线(视其定义域决定是否连线). 7.求函数的解析式的方法 (1)待定系数法: 适用于已知函数的模型(如一次函数、二次函数、反比例函数等. (2)换元法: 适用于已知(()) f g x的解析式,求() f x. (3)消元法: 适用于同时含有() f x和1() f x ,或() f x和() f x-. 智立方教育高一函数知识点及典型例题 一、函数的概念与表示 1、映射 (1)映射:设A、B是两个集合,如果按照某种映射法则f,对于集合A中的任一个元素,在集合B 中都有唯一的元素和它对应,则这样的对应(包括集合A、B以及A到B的对应法则f)叫做集合A到集合B的映射,记作f:A→B. 注意点:(1)对映射定义的理解.(2)判断一个对应是映射的方法.一对多不是映射,多对一是映射2、函数 构成函数概念的三要素①定义域;②对应法则;③值域. 两个函数是同一个函数的条件:三要素有两个相同 例1、例2、}3 0| { }, 2 0| {≤ ≤ = ≤ ≤ =y y N x x M给出下列四个图形,其中能表示从集合M到集合N的函数关系的有( C ) A、 0个 B、 1个 C、 2个 D、3个 由题意知:M={x|0≤x≤2},N={y|0≤y≤3}, 对于图①中,在集合M中区间(1,2]的元素没有象,比如f( 3 2 )的值就不存在,所以图①不符合题意; 对于图②中,对于M中任意一个元素,N中有唯一元素与之对应,符合函数的对应法则,故②正确; 对于图③中,对于M中任意一个元素,N中有唯一元素与之对应,且这种对应是一一对应,故③正确; 对于图④中,集合M的一个元素对应N中的两个元素.比如当x=1时,有两个y值与之对应,不符合函数的定义,故④不正确 x x x x 1 2 1 1 1 2 2 2 1 1 1 1 2 2 2 2 y y y y 3 O O O O 二、函数的解析式与定义域 1、求函数定义域的主要依据: (1)分式的分母不为零; (2)偶次方根的被开方数不小于零,零取零次方没有意义; (3)对数函数的真数必须大于零; (4)指数函数和对数函数的底数必须大于零且不等于1; 例1、y = 函数的定义域为 根号下的数必须为正数,又当底数为大于0小于1的数时,只有当真数大于0小于1时,才能保证根号下的数为正数。所以让0<4X 的平方-3X<1,解0<4X 的平方-3X 得X<0或3/4 初三下学期锐角三角函数知识点总结及典型习题 1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。 2 3 5、30°、45°、 6 当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。 7、正切、的增减性: 当0°<α<90°时,tan α随α的增大而增大, 1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。 依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法) 2、应用举例: (1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。 A 90 B 90∠-?=∠? =∠+∠得由B A 对边 邻边 (2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。用字母i 表示,即h i l =。坡度一般写成1:m 的形式,如1:5i =等。 把坡面与水平面的夹角记作α(叫做坡角),那么tan h i l α= =。 3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。 4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。 例1:已知在Rt ABC △中,3 90sin 5 C A ∠==°,,则tan B 的值为( ) A .43 B .45 C .54 D . 34 【解析】本题考查三角函数的定义和勾股定理,在RT ΔABC 中,∠C=90°,则sin a A c = ,tan b B a =和222a b c +=;由3s i n 5A =知,如果设3a x =,则5c x =,结合222a b c +=得4b x =;∴44 tan 33 b x B a x ===, 所以选A . 例2 :104cos30sin 60(2)2008)-??+--=______. 【解析】本题考查特殊角的三角函数值.零指数幂.负整数指数幂的有关运算, 104cos30sin 60(2)2008)-??+-- =134122 ??--= ???,故填3 2. 1. 某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为( C ) A .8米 B . C D 米 :i h l =h l α 09级高三数学总复习讲义——基本函数1 知识清单: 1.一元一次函数:)0(≠+=a b ax y ,当0>a 时,是增函数;当0a 时: 为增函数; 为减函数; 当0a 时:在顶点处取得最小值,最大值在距离对称轴较远的端点处取得;当0a 时:最小值在距离对称轴较近的端点处取得,最大值在距离对称轴较远的端点处取得;当0?=0 )(0 )(q f a p f (检 一次函数知识点 一次函数知识网络图 考点一:变量、常量及函数定义 1、变量:在一个变化过程中可以取不同数值的量。 常量:在一个变化过程中只能取同一数值的量。 2、函数:一般的,在一个变化过程中,如果有两个变量x 和y ,并且对于x 的每一个确定的值, y 都有唯一确定的值与其对应,那么我们就把x 称为自变量,把y 称为是x 的函数。 ※判断A 是否为B 的函数,只要看B 取值确定的时候,A 是否有唯一确定的值与之对应 典型例题: 1、下列函数关系式中不是函数关系式的是( ) A.21y x =+ B.2 1y x =+ C.1y x x =+ D.22y x = 2、下列各图中表示y 是x 的函数图像的是 ( ) 考点二、自变量取值围:一般的,一个函数的自变量允许取值的围。 确定函数自变量取值围的方法: (1)必须使关系式成立。 ①当关系式为整式时,自变量取值围为全体实数; ②当关系式含有分式时,自变量取值围要使分式的分母的值不等于零; A B D ③关系式含有二次根式时,自变量取值围必须使被开方的式子不小于零; ④当关系式中含有指数为零或负数的式子时,自变量取值围要使底数不等于零; (2)当函数关系表示实际问题时,自变量的取值围还要符合实际情况,使之有意义。 (3)当函数关系表示一个图形的变化关系时,自变量的取值围必须使图形存在。 典型例题: 1、函数3 1 -=x y 的自变量x 的取值围是 2、函数3-= x y 的自变量x 的取值围是 3、函数() 2 20x y x -=++的自变量x 的取值围是 4、小强在劳动技术课中要制作一个周长为10cm 的等腰三角形.请你写出底边长y (cm )与一腰长x (cm )的函数关系式,并写出自变量的取值围. 考点三、函数的图像与解析式的关系 1、函数的表示方法 (1)列表法:一目了然,使用起来方便,但列出的对应值是有限的,不易看出自变量与函数之间的对应规律。 (2)解析式法:简单明了,能够准确地反映整个变化过程中自变量与函数之间的相依关系,但有些实际问题中的函数关系,不能用解析式表示。 (3)图象法:形象直观,但只能近似地表达两个变量之间的函数关系。 函数的三种表示方法各有优、缺点,有时可以相互转化。 2、分段函数的解析式及图像 注意把握:(1)始点、终点、拐点的坐标及实际意义 (2)每条线段(射线)的解析式、取值围、实际意义 (3)每个解析式中K 的实际意义 典型例题: 1、 如图反映的过程是:晓明从家跑步到体育馆,在那里锻炼了一阵后又走到新华书店去买书, 然后散步走回家。其中t 表示时间(分钟),S 表示晓明离家的距离(千米),那么晓明在体育馆锻炼和在新华书店买书共用去时间是_______________分钟.你还能分析出什么? 高一函数主要知识点和解决方法及典型例题 一、函数的概念与表示 1、函数 构成函数概念的三要素 ①定义域;②对应法则;③值域. 两个函数是同一个函数的条件:三要素有两个相同 例1、下列各对函数中,相同的是( ) A 、x x g x x f lg 2)(,lg )(2== B 、)1lg()1lg()(,1 1lg )(--+=-+=x x x g x x x f C 、 v v v g u u u f -+=-+=11)(,11)( D 、f (x )=x ,2)(x x f = 例2、}30|{},20|{≤≤=≤≤=y y N x x M 给出下列四个图形,其中能表示从集合M 到集合N 的函数关系的有( ) A 、 0个 B 、 1个 C 、 2个 D 、3个 二、函数的定义域 1、求函数定义域的主要依据: (1)分式的分母不为零; (2)偶次方根的被开方数不小于零,零取零次方没有意义; (3)对数函数的真数必须大于零; (4)指数函数和对数函数的底数必须大于零且不等于1; 例1、(05 卷)函数y =的定义域为 . 2、抽象函数定义域问题的几种题型及求法. (1)、已知()f x 的定义域,求[]()f g x 的定义域 其解法是:若()f x 的定义域为a x b ≤≤,则在[]()f g x 中,()a g x b ≤≤,从中解得x 的取值围即为[]()f g x 的定义域. 已知函数()f x 的定义域为[] 15-,,求(35)f x -的定义域. 分析:该函数是由35u x =-和()f u 构成的复合函数,其中x 是自变量,u 是中间变量,由于()f x 与()f u 是同一个函数,因此这里是已知15u -≤≤,即1355x --≤≤,求x 的 智立方教育高一函数知识点及典型例题 一、函数的概念与表示 1、映射 (1)映射:设A 、B 是两个集合,如果按照某种映射法则f ,对于集合A 中的任一个元素,在集合B 中都有唯一的元素和它对应,则这样的对应(包括集合A 、B 以及A 到B 的对应法则f )叫做集合A 到集合B 的映射,记作f :A→B. 注意点:(1)对映射定义的理解.(2)判断一个对应是映射的方法.一对多不是映射,多对一是映射 2、函数 构成函数概念的三要素 ①定义域;②对应法则;③值域. 两个函数是同一个函数的条件:三要素有两个相同 例1 、 例2、}30|{},20|{≤≤=≤≤=y y N x x M 给出下列四个图形,其中能表示从集合M 到集合N 的函数关系的有( C ) A 、 0个 B 、 1个 C 、 2个 D 、3个 由题意知:M={x|0≤x ≤2},N={y|0≤y ≤3}, 对于图①中,在集合M 中区间(1,2]内的元素没有象,比如f ( 3 2 )的值就不存在,所以图①不符合题意; 对于图②中,对于M 中任意一个元素,N 中有唯一元素与之对应,符合函数的对应法则,故②正确; 对于图③中,对于M 中任意一个元素,N 中有唯一元素与之对应,且这种对应是一一对应,故③正确; 对于图④中,集合M 的一个元素对应N 中的两个元素.比如当x=1时,有两个y 值与之对应,不符合函数的定义,故④不正确 x x x x 1 2 1 1 1 2 2 2 1 1 1 1 2 2 2 2 y y y y 3 O O O O 二、函数的解析式与定义域 1、求函数定义域的主要依据: (1)分式的分母不为零; (2)偶次方根的被开方数不小于零,零取零次方没有意义; (3)对数函数的真数必须大于零; (4)指数函数和对数函数的底数必须大于零且不等于1; 例1、20.5log (43)y x x = -函数的定义域为 根号下的数必须为正数,又当底数为大于0小于1的数时,只有当真数大于0小于1时,才能保证根号下的数为正数。所以让0<4X 的平方-3X<1,解0<4X 的平方-3X 得X<0或3/4 对数与对数函数 1.对数 (1)对数的定义: 如果 a b=N(a>0,a≠1),那么 b叫做以 a为底 N的对数,记作log a N=b. (2)指数式与对数式的关系: a b=N log a N=b ( a>0,a≠1,N>0). 两个式子表示的 a、b、N 三个数之间的关系是一样的,并且可以互化. ( 3)对数运算性质 : ①log a(MN)=log a M+log a N. ②log a M =log a M -log a N. N ③log a M n=nlog a M.(M>0,N>0,a>0,a≠1) ④对数换底公式: log b N= log a N(a>0, a≠1,b>0,b≠1,N>0). log a b 2.对数函数 (1)对数函数的定义 函数 y=log a x(a>0,a≠1)叫做对数函数,其中 x 是自变量,函数的定义域是( 0,+∞) . 注意:真数式子没根号那就只要求真数式大于零 ,如果有根 号 ,要求真数大于零还要保证根号里的式子大于零,底数则要大于 0 且不为 1 在一个普通对数式里 a<0, 或=1 的时候是会有相应 b 的值的。但是,根据对数定义 : log a a=1 ;如果 a=1 或=0 那么 log a a 就可以等于一切实数(比如 log1 1 也可以等于 2,3,4,5,等等)第二,根据定义 运算公式:log a M^n = nlog a M 如果 a<0, 那么这个等式两边就不会成立(比如, log(-2)4^(-2)就不等于(-2) *log (-2)4 ;一个等于 1/16,另一个等于 -1/16 ) (2)对数函数的图象 y=l og a x(a>1) y=l og a x(0 一次函数 基本概念 1、变量:在一个变化过程中可以取不同数值的量。常量:在一个变化过程中只能取同一数值的量。 例题:在匀速运动公式vt s =中,v 表示速度,t 表示时间,s 表示在时间t 内所走的路程,则变量是________,常量是_______。在圆的周长公式C=2πr 中,变量是________,常量是_________. 2、函数:一般的,在一个变化过程中,如果有两个变量x 和y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就把x 称为自变量,把y 称为因变量,y 是x 的函数。 *判断Y 是否为X 的函数,只要看X 取值确定的时候,Y 是否有唯一确定的值与之对应 例题:下列函数(1)y=πx (2)y=2x-1 (3)y=1x (4)y=2-1-3x (5)y=x 2 -1中,是一 次函数的有( ) (A )4个 (B )3个 (C )2个 (D )1个 3、函数的图像 一般来说,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象. 4、函数解析式:用含有表示自变量的字母的代数式表示因变量的式子叫做解析式。 5、描点法画函数图形的一般步骤 第一步:列表(表中给出一些自变量的值及其对应的函数值); 第二步:描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点);第三步:连线(按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来)。 6、函数的表示方法 列表法:一目了然,使用起来方便,但列出的对应值是有限的,不易看出自变量与函数之间的对应规律。 解析式法:简单明了,能够准确地反映整个变化过程中自变量与函数之间的相依关系,但有些实际问题中的函数关系,不能用解析式表示。 图象法:形象直观,但只能近似地表达两个变量之间的函数关系。 7、正比例函数及性质 一般地,形如y=kx(k 是常数,k≠0)的函数叫做正比例函数,其中k 叫做比例系数. 注:正比例函数一般形式 y=kx (k 不为零) ① k 不为零 ② x 指数为1 ③ b 取零 当k>0时,直线y=kx 经过三、一象限,从左向右上升,即随x 的增大y 也增大;当k<0时,?直线y=kx 经过二、四象限,从左向右下降,即随x 增大y 反而减小. (1) 解析式:y=kx (k 是常数,k ≠0) (2) 必过点:(0,0)、(1,k ) (3) 走向:k>0时,图像经过一、三象限;k<0时,?图像经过二、四象限 (4) 增减性:k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小 (5) 倾斜度:|k|越大,越接近y 轴;|k|越小,越接近x 轴 例题:.正比例函数(35)y m x =+,当m 时,y 随x 的增大而增大. 函数知识点 一.图像及性质 1.一次函数 ① 图 像 : y=kx+b(k ≠ 0) y=kx(k ≠0,b=0) ①k>0 增 k<0 减 ②b ≠0一次函数,b=0正比例函数 2.二次函数 ①图像: ②a>0 开口向上,a<0开口向下 ③a>0最小值,a<0最大值 ④X 对称=-b 2a ⑤顶点坐标:(-b 2a ,244ac a b -) ⑥三种表达 形 式 222 (1)(2)4()24y a x x x x b ac b y a x a a y ax bx c =--?? ?? -?? =++ ??????=++??两点式顶点式一般式 3指数函数 ①图像:y=x a (a>0且a ≠1) ②0 6对勾函数 ①图像:y=x+ p x (p>0) ②顶点坐标- 二.定义域 1.给定解析式 (1) 1 2x - (2 ) 2 () x x y - =(3 ) cos l x y g = 2.已知f(x)定义域,求f(g(x))定 义域 (1)已知f(x)定义域为[-1 2 ,1 2 ],求 y=f(2x-x-1 2 )定义域 3.已知f(g(x))的定义域。求f(x)的定义 域 (1)若f(2x)的定义域为[-1,1],求f(x) 的定义域 (一)求函数定义域 例:(21) f x-的定义域为[] 0,1,求(13) f x -的 定义域 1.求下列函数定义域 ① x x x y - - + = 2 )1 (2 ②) 4 5( log )1 ( x x y- = + 2.已知 6 lg )3 ( 2 2 2 - = - x x x f,则() f x的定义域 是 3.(2013陕西理1)设全集为R,函数 2 1 ) (x x f- =的定义域为M,则M C R 为 ( ) .A]1,1 [- .B)1,1 (- .C) ,1[ ]1 , (+∞ - -∞ .D) ,1( )1 , (+∞ - -∞ 4.(2013江西理2)函数) 1 ln(x x y- =的 定义域为( ) .A)1,0(.B)1,0[二次函数知识点总结及典型例题和练习(极好)
初二函数知识点及经典例题.
中考攻略:初中数学函数知识点大全+典型例题
函数的单调性知识点汇总及典型例题(高一必备)
二次函数知识点总结及典型例题
高中数学 函数知识点总结与经典例题与解析
一次函数知识点及典型例题复习
函数的概念与表示知识点与经典题型归纳
高中函数部分知识点及典型例题分析
初中三角函数知识点总结及典型习题(含答案)
届高三数学基本函数知识点及典型例题
一次函数知识点及典型例题
高中一年级函数主要知识点和解决方法及典型例题
高中函数部分知识点及典型例题分析
(完整版)高中数学对数与对数函数知识点及经典例题讲解
一次函数知识点及其典型例题
函数知识点及典型例题
