【优选整合】人教版数学七年级下册第9章第8课第9章小结与复习练习(学生版)
最新人教版七年级数学下册第九章《不等式与不等式组》单元小结(含答案解析)

人教版七年级数学下第九章不等式与不等式组复习检测试题(有答案)人教版七年级数学下册第九章不等式与不等式组单元测试题复习检测试卷(有答案)一、选择题1.以下式子:① -2<0;② 2x+3y<0;③ x=3;④ x+y 中,是不等式的个数有A.1个B.2个C.3个D. 4 个2.若 m> n,则以下不等式中必定建立的是()A. m+2<n+3B. 2 m< 3nC. a- m<a- n22 D. ma>na3.数 a、 b 在数轴上的地点如下图,则以下不等式建立的是()A. a>bB. ab> 0C. a+b> 0D. a+b< 04.若对于 x 的一元一次不等式组的解集是 x<5,则 m的取值范围是()A. m≥5B. m>5C. m≤5D. m< 55.某商品的标价比成本价高m%,依据市场需要,该商品需降价n%销售,为了不赔本,n 应知足()A.≤B. ≤C.n ≤ D.n≤n m n6.某种记事本零售价每本 6 元,凡一次性购置两本以上赐予优惠,优惠方式有两种,第一种:“两本按原价,其他按七折优惠”;第二种:所有按原价的八折优惠,若想在购置同样数目的状况下,要使第一种方法比第二种方法获取的优惠多,最少要购置记事本()A.5 本B.6 本C.7 本D.8 本7. 不等式组的解集在数轴上表示正确的选项是()A. B.C. D.8. 不等式组的解集是()A. x>4B.x≤3C. 3≤x<4D. 无解9. 假如不等式组只有一个整数解,那么 a 的范围是()A. 3<a≤4B. 3≤a<4C. 4≤a<5D. 4< a≤510. 现有三种不一样的物体:“甲、乙、丙”,用天平称了两次,状况如下图,那么“甲、乙、丙”这三种物体按质量从大到小的次序摆列为A. 丙甲乙B. 丙乙甲C. 乙甲丙D. 乙丙甲二、填空题1. 不等式组:的解集是2. 某采石场爆破时,点燃引火线的甲工人要在爆破前转移到400m 之外的安全地区甲工人在转移过程中,前40m只好步行,以后骑自行车。
2020人教版七年级数学下册第九章不等式与不等式组小结与复习课件

列不等式,得 2 x 4(2 2) ,解得x≥16.
3
3
答:小亮的速度至少为16千米/时.
例5、一堆玩具分给若干个小朋友,若每人分3件,
则剩余4件;若前面每人分4件,则最后一人得到的
玩具不足3件,求小朋友的人数与玩具数。
解: 设小朋友总共有x人,由此可得不等式组
3x+4-4(x-1)≥0, 3x+4-4(x-1)<3;
例4、小明上午8时20分出发去郊游,10时20分时,小 亮乘车从同一地点出发,已知小明每小时走4千米,那么 小亮要在11时追上或超过小明,速度至少应是多少?
【分析】从路程下手找不等关系: 即小亮40分钟行进路程≥小明从8时20分到11时行进路程.
解:设小亮的速度为x千米/时,40分= 2 小时,
3
解:设小明答对了x道题,则 4x-(25-x) ≥85
解得 x≥22 所以,小明到少答对了22道题,他可能答对22,23,24或 25道题。
通过本课学 习,你收获 了什么?
课后作业:
完成教科书中相关练习题。
即 10x>220
解得
x> 22
答:商店每天需要出售23件或23件以上这样的商品,才 能保证商店每天的净利润在100元以上(不包括100元)
我们已经站在了人生 的起跑线上,为了实现心 中的远大目标,我们正努 力拼搏着。成功属于不畏 困难、勇往直前的人。相 信自己!
题组五:一元一次不等式的应用
• 1. 一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题 扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对 了几道题?
m+2=0的解是负数,则m的取值范
【人教版七年级数学下册教案】第九章小结与复习

第九章复习教课设计一、教课内容:不等式与不等式组二、教课目标1、知识与技术:可以依据详尽问题中的大小关系认识不等式的意义,并探究不等式的基天性质。
会解简单的一元一次不等式,并能在数轴上表示出解集。
会解由两个一元一次不等式构成的不等式组,并会用数轴确立解集。
2、方法与过程 :可以依据详尽问题中的数目关系,列出一元一次不等式和一元一次不等式组,解决简单的实质问题。
3、感情、态度与价值观:会运用数形结合、分类等数学思想方法解决问题,会“逆向”地思虑问题,灵巧的解答问题 .三、教课要点:能熟练的解一元一次不等式与一元一次不等式组四、教课难点:能熟练的解一元一次不等式( 组 ) 并领悟数形结合、分类谈论等数学思想。
五、教课过程(一)知识梳理1.知识结构图不等式的定义看法不等式的解集基天性质不等式一元一次不等式的解法不等式的解实质应一元一次不等式组2.知识点回顾( 1)、不等式用不等号连接起来的式子叫做不等式.常有的不等号有五种:“≠”、“>” 、“<” 、“≥”、“≤”.(2)、不等式的解与解集不等式的解:使不等式成立的未知数的值,叫做不等式的解.不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.不等式的解集可以在数轴上直观的表示出来,详尽表示方法是先确立界限点。
解集包括界限点,是实心圆点;不包括界限点,则是空心圆圈;再确立方向:大向右,小向左。
说明:不等式的解与一元一次方程的解是有区其余,不等式的解是不确立的,是一个范围,而一元一次方程的解则是一个详尽的数值.( 3)、不等式的基天性质A、不等式的两边都加上 ( 或减去 ) 同一个数或同一个整式.不等号的方向不变.假如 a>b ,则 a+c>b+c,a-c>b-cB、不等式的两边都乘以 ( 或除以 ) 同一个正数,不等号的方向不变.假如 a>b ,而且 c>0 ,那么则 ac>bc (或 a/c>b/c)C、不等式的两边都乘以 ( 或除以 ) 同一个负数,不等号的方向改变.假如 a>b ,而且 c<0 ,那么则 ac<bc( 或 a/c<b/c)说明:任意两个实数 a、b 的大小关系:①a-b>O a>b;②a-b=O a=b;③ a-b<O a<b.(4)、一元一次不等式只含有一个未知数,且未知数的次数是1.系数不等于 0 的不等式叫做一元一次不等式.注:一元一次不等式的一般形式是ax+b>O或 ax+b<O(a≠O,a,b 为已知数 ) .(5)、解一元一次不等式的一般步骤解一元一次不等式的一般步骤:(1)去分母; (2) 去括号; (3) 移项; (4) 合并同类项; (5) 化系数为 1.说明:解一元一次不等式和解一元一次方程近似.不一样的是:一元一次不等式两边同乘以 ( 或除以 ) 同一个负数时,不等号的方向一定改变,这是解不等式时最简单出错的地方.(6).一元一次不等式组含有同样未知数的几个一元一次不等式所构成的不等式组,叫做一元一次不等式组.说明:判断一个不等式组是一元一次不等式组需满足两个条件:①构成不等式组的每一个不等式一定是一元一次不等式,且未知数同样;②不等式组中不等式的个数最少是 2 个,也就是说,可以是 2 个、 3 个、 4 个或更多.( 7).一元一次不等式组的解集一元一次不等式组中,几个不等式解集的公共部分.叫做这个一元一次不等式组的解集.一元一次不等式组的解集平时利用数轴来确立.( 8) .不等式组解集的确定方法,可以归纳为以下四各种类(设a>b)不等式组图示解集x a x a x a(同大取大)1b x bx>axb ax b (同小取小)x a x bx a x bb x a(大小交织取中间)b a无解(大小分别解为空)ba(9).解一元一次不等式组的步骤(1)分别求出不等式组中各个不等式的解集;(2)利用数轴求出这些解集的公共部分,即这个不等式组的解集.3.课堂练习 ( 一)1. 解不等式 2 x 15x 5,34并把它的解集在数轴上表示出来.解:去分母,得:4(2x-1)≥12(5/4x-5)去括号,得:8x-4≥15x-60移项,得:8x-15x≥-60+4合并同类项得:-7x≥-56系数化为1,得:x≤82.解不等式组:2 x1 5 x5342 ( x 4 )3 x3解:解不等式①得: x≤ 8解不等式②得: x ≥5把不等式①的解集和不等式②的解集在数轴上表示以下:∴原不等式组的解集为 :5 ≤x≤83、求不等式(组)的特别解:(1)求不等式 3x+1 ≥ 4x-5 的正整数解解:移项,得:3x-4x≥-5-1合并同类项,得:-x≥-6系数化为1,得:x≤6因此不等式的正整数解为: 1、 2、 3、 4、 5、 62 x 15(2)求不等式组1 ( x2)3的整数解2解:由不等式①得 : x > 2由不等式②得 : x ≤ 4把不等式①的解集和不等式②的解集在数轴上表示以下:∴不等式组的解集为 :2 < x≤ 4∴不等式组的整数解为:3、 4.4.不等式 ( 组 ) 在实质生活中的应用当应用题中出现以下的要点词 , 如大 , 小 , 多 , 少 , 不小于 , 不大于 , 最少 , 至多等 , 应属列不等式 ( 组) 来解决的问题 , 而不可以列方程 ( 组) 来解 .(1)我市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间住宅 . 假如每间住 5 人,那么有 12 人安排不下;假如每间住 8 人,那么有一间房还余一些床位,问该校可能有几间住宅可以安排学生住宿?住宿的学生可能有多少人?解:设可能有x间住宅安排学生住宿,则依据题意可得:8x>5x+12解这个不等式,得:x>4当x=5时,住宿的学生可能有37人,吻合题意;当x=6时,住宿的学生可能有42人,吻合题意;当x=7时,住宿的学生可能有47人,不吻合题意.答:该校可能有5间或6间住宅,当有5间住宅时,住宿学生有37人;当有6间住宅时,住宿学生有42人.(2)学校要到体育用品商场购买篮球和排球共100只.已知篮球、排球的单价分别为 130 元、 100 元。
数学人教版七年级下册第九章 一元一次不等式及不等式组小结与复习

岑巩县第四中学2016-2017学年第二学期数学学科导学案
引
用
图
知识点。
6.为了保护环境,某企业决定购买10台污水处理设备;现有A 、B 两种型号的设备,其中每
台的价格、月处理污水量及年消耗费如下表:
经预算,该企业购买设备的资金不高于105万元. (1)请你设计该企业有几种购买方案;(2)若该企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案; (3)在第(2)问的条件下,若每台设备的使用年限为10年,污水厂处理污水为每吨10元,请你计算,该企业自己处理污水与将污水排到污水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费
用包括购买设备的资金和消耗费)。
人教版数学七年级下册教案 第九章 小结与复习
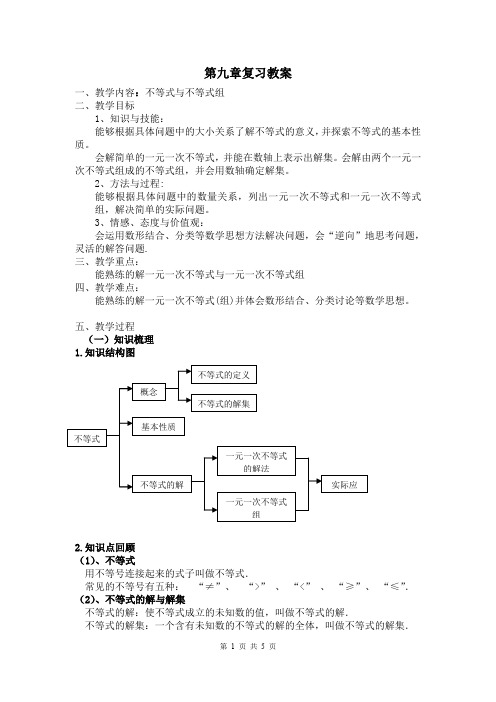
第九章复习教案一、教学内容:不等式与不等式组二、教学目标1、知识与技能:能够根据具体问题中的大小关系了解不等式的意义,并探索不等式的基本性质。
会解简单的一元一次不等式,并能在数轴上表示出解集。
会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集。
2、方法与过程:能够根据具体问题中的数量关系,列出一元一次不等式和一元一次不等式组,解决简单的实际问题。
3、情感、态度与价值观:会运用数形结合、分类等数学思想方法解决问题,会“逆向”地思考问题,灵活的解答问题.三、教学重点:能熟练的解一元一次不等式与一元一次不等式组四、教学难点:能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想。
五、教学过程(一)知识梳理1.知识结构图2.知识点回顾(1)、不等式用不等号连接起来的式子叫做不等式.常见的不等号有五种:“≠”、“>” 、“<” 、“≥”、“≤”.(2)、不等式的解与解集不等式的解:使不等式成立的未知数的值,叫做不等式的解.不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。
解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.(3)、不等式的基本性质A、不等式的两边都加上(或减去)同一个数或同一个整式.不等号的方向不变.如果a>b,则a+c>b+c,a-c>b-cB、不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.如果a>b,并且c>0,那么则ac>bc(或a/c>b/c)C、不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.如果a>b,并且c<0,那么则ac<bc(或a/c<b/c)说明:任意两个实数a、b的大小关系:①a-b>O⇔a>b;②a-b=O⇔a=b;③a-b<O⇔a<b.(4) 、一元一次不等式只含有一个未知数,且未知数的次数是1.系数不等于0的不等式叫做一元一次不等式.注:一元一次不等式的一般形式是ax+b>O或ax+b<O(a≠O,a,b为已知数).(5)、解一元一次不等式的一般步骤解一元一次不等式的一般步骤:(1)去分母;(2)去括号;(3)移项; (4)合并同类项;(5)化系数为1.说明:解一元一次不等式和解一元一次方程类似.不同的是:一元一次不等式两边同乘以(或除以)同一个负数时,不等号的方向必须改变,这是解不等式时最容易出错的地方.(6).一元一次不等式组含有相同未知数的几个一元一次不等式所组成的不等式组,叫做一元一次不等式组.说明:判断一个不等式组是一元一次不等式组需满足两个条件:①组成不等式组的每一个不等式必须是一元一次不等式,且未知数相同;②不等式组中不等式的个数至少是2个,也就是说,可以是2个、3个、4个或更多.(7).一元一次不等式组的解集一元一次不等式组中,几个不等式解集的公共部分.叫做这个一元一次不等式组的解集.一元一次不等式组的解集通常利用数轴来确定.(1)分别求出不等式组中各个不等式的解集;(2)利用数轴求出这些解集的公共部分,即这个不等式组的解集. 3.课堂练习(一)解:去分母,得:4(2x-1)≥12(5/4x-5) 去括号,得:8x-4≥15x-60 移项,得: 8x-15x≥-60+4 合并同类项得:-7x≥-56 系数化为1,得:x≤8 2.解不等式组:解:解不等式①得:x ≤8解不等式②得:x ≥5把不等式①的解集和不等式②的解集在数轴上表示如下:∴ 原不等式组的解集为:5≤x ≤83、求不等式(组)的特殊解:(1)求不等式 3x+1≥4x-5的正整数解解:移项,得:3x-4x≥-5-1 合并同类项,得:-x≥-6 系数化为1,得:x≤6所以不等式 的正整数解为:1、2、3、4、5、6(2)求不等式组 的整数解2151.5,34.x x -≥-解不等式并把它的解集在数轴上表示出来 33)4(2545312+≤+-≥-x x x x 2151(2)32x x +>⎧⎪⎨+≤⎪⎩解:由不等式①得: x>2由不等式②得: x≤4把不等式①的解集和不等式②的解集在数轴上表示如下:∴不等式组的解集为:2<x≤4∴不等式组的整数解为:3、4.4.不等式(组)在实际生活中的应用当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.(1)我市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间住房. 如果每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位,问该校可能有几间住房可以安排学生住宿?住宿的学生可能有多少人?解:设可能有x间住房安排学生住宿,则根据题意可得:8x>5x+12解这个不等式,得:x>4当x=5时,住宿的学生可能有37人,符合题意;当x=6时,住宿的学生可能有42人,符合题意;当x=7时,住宿的学生可能有47人,不符合题意.答:该校可能有5间或6间住房,当有5间住房时,住宿学生有37人;当有6间住房时,住宿学生有42人.(2)学校要到体育用品商场购买篮球和排球共100只.已知篮球、排球的单价分别为130元、100元。
人教版七年级下册数学第九章教案小结与复习

人教版七年级下册数学教案第九章小结与复习教学内容:不等式与不等式组教学目标1.知识与技能能够根据具体问题中的大小关系了解不等式的意义,并探索不等式的基本性质。
会解简单的一元一次不等式,并能在数轴上表示出解集。
会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集。
2.方法与过程能够根据具体问题中的数量关系,列出一元一次不等式和一元一次不等式组,解决简单的实际问题。
3.情感、态度与价值观会运用数形结合、分类等数学思想方法解决问题,会“逆向”地思考问题,灵活的解答问题.重点能熟练的解一元一次不等式与一元一次不等式组难点能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想。
教学过程(一)知识梳理1.知识结构图不等式概念不等式的解集基本性质一元一次不等式的解法不等式的解一元一次不等式组实际应不等式的定义2.知识点回顾(1)不等式用不等号连接起来的式子叫做不等式.常见的不等号有五种:“≠”、“>”、“<”、“≥”、“≤”.(2)不等式的解与解集不等式的解:使不等式成立的未知数的值,叫做不等式的解.不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。
解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.(3)不等式的基本性质A.不等式的两边都加上(或减去)同一个数或同一个整式.不等号的方向不变.如果a>b,则a+c>b+c,a-c>b-cB.不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.如果a>b,并且c>0,那么则ac>bc(或a/c>b/c)C.不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.如果a>b,并且c<0,那么则ac<bc(或a/c<b/c)说明:任意两个实数a、b的大小关系:①a-b>O⇔a>b;②a-b=O⇔a=b;③a-b<O⇔a<b.(4)一元一次不等式只含有一个未知数,且未知数的次数是1.系数不等于0的不等式叫做一元一次不等式.注:一元一次不等式的一般形式是ax+b>O或ax+b<O(a ≠O,a,b为已知数)。
【优选整合】数学七年级下册第9章第8课 第9章小结与复习 导学案
•不等式(组)在实际生活中的应用
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
四、当堂反馈
1.下列不等式是一元一次不等式的是()
4.在解不等式(2+X)/3 >(2X-1)/5的变形过程中,出现错误的步骤是()
(A)5(2+x)>3(2x-1) (B)10+5x>6x-3
(C)5x-6x>-3-10 (D) x>13
5.x取哪些整数值时,代数式(9x + 2)/7与(3x-14/)2
的差大于6且小于8
五.小结
六.作业:课本P148 T4,T5,T8,T9选做:T10,7,11
自我评价专栏(分优良中差四个等级)
自主学习:合作与交流:书写:综合:
(A)2(1-y)>4y+2 (B)x(2-x) ≥1
(C) 2 + 3 > 4 (D)x+1<y+2
2.不等式(X-2)/2 < 0的解集是()
(A)x>2 (B) x>-2 (C) x<-2 (D) x<2
3.不等式2x-2≥3x-4的正整数解的个数为()
(A)1个(B) 2个(C) 3个(D) 4个
(借助于数轴)得到不等式组的解集.
(四)基本练习
1.不等式x-2<3的解集是
2.不等式x-2≤3x+5的负整数解有
-x≤1
3.不等式组{x-2<3的解集是
2X-1>1
人教版七年级数学 下册 第九章 不等式与不等式组 小结与复习 课件(共31张PPT)
不等式的性质2 不等式两边乘(或除以)同一个正数, 不等号的方向不变.
不等式的性质3 不等式两边乘(或除以)同一个负数,不 等号的方向改变.
例1、 如果 a b,那么下列不等式中
不成立的是( B) (A)
(B) a 3 b 3
(C) 2 3a 2 3b (D) a b
33
a b 0
分析:运用不等式的性质.
• 判断下列式子哪些是不等式? (1) 3>2 是 (2) a2+1>0 是 (3) 3x2+2x
(4) x<2x+1 是 (5) x=2x-5 (6)x2+4x<3x+1 是 (7)a+b≠c 是
自己举出几个不等式的例子(至少两个)
提示:解不等式x-a≥0,得x≥a;解不等式-
2x>-4,得x<2.因为不等式组有解,故2在a的右边, 即a<2.
不等式的应用情况很多,但解所有的题目关键 在于找准表示不等关系的语句,并能够列出不等式, 再利用不等式的性质解不等式,这样问题才能得以 解决.
当应用题中出现以下的关键词,如大,小,多,少, 不小于,不大于,至少,至多等,应属于通过列不等式 (组)来解决的问题,而不属于通过列方程(组)来解 决的问题.
3
②不等式组的解集是x≥9.
• 9. 一次环保知识竞赛共有25道题,规定答对一 道题得4分,答错或不答一道题扣1分,在这次竞赛 中,小明被评为优秀(85分或85分以上),小明至 少答对了几道题?
实际问题 的答案
设未知数, 列不等式(组)
数学问题 (一元一次不 等式(组))
2020春人教版数学七年级下册习题课件:第9章 第8课时 本章小结 课后巩固课件
(2)现要购买 A,B 两种奖品共 100 件,总费用不超过 900 元, 那么 A 种奖品最多购买多少件?
解:设 A 种奖品购买 a 件.由题意得 16a+4(100-a)≤900,解得 a≤1325. ∵a 为正整数,∴a≤41. 答:A 种奖品最多购买 41 件.
13
.
3
3.解不等式组x3+ x-2≥ 1<-5,1,并将解集在数轴上表示出来. 解:解不等式 x+2≥-1,得 x≥-3. 解不等式 3x-1<5,得 x<2.
∴不等式组的解集是-3≤x<2.
4
2(x-1)≥3x-4,① 4.解不等式组x+2 1≥3-4 x-1,② 并将其解集在数轴上表示 出来.
第九章 不等式与不等式组
第8课时 本章小结
1.下列不等式变形正确的是( D ) A.由 a>b,得 ac>bc B.由 a>b,得 a-2<b-2 C.由-12>-1,得-a2>-a D.由 a>b,得 c-a<c-b
2
2.关于 x 的不等式 2x-a≤-1 的解集如图所示,则 a 的值
是 -1
10
8.某校拟举办“创文知识”抢答赛,欲购买 A,B 两种奖品 以鼓励抢答者.如果购买 A 种 20 件,B 种 15 件,共需 380 元; 如果购买 A 种 15 件,B 种 10 件,共需 280 元.
(1)A,B 两种奖品每件各多少元?
11
解:设 A 种奖品每件 x 元,B 种奖品每件 y 元. 由题意得2105xx+ +1150yy= =328800, , 解得xy==41.6, 答:A 种奖品每件 16 元,B 种奖品每件 4 元.
8
7.小兰准备用 27 元买钢笔和笔记本,已知一支钢笔 4.5 元, 一本笔记本 3 元.若钢笔和笔记本共买了 8 件,每一种至少买一 件,则她有多少种购买方案?
【人教版】七年级数学下册:第九章 小结与复习教案
第九章复习教案一、教学内容:不等式与不等式组二、教学目标1、知识与技能:能够根据具体问题中的大小关系了解不等式的意义,并探索不等式的基本性质。
会解简单的一元一次不等式,并能在数轴上表示出解集。
会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集。
2、方法与过程:能够根据具体问题中的数量关系,列出一元一次不等式和一元一次不等式组,解决简单的实际问题。
3、情感、态度与价值观:会运用数形结合、分类等数学思想方法解决问题,会“逆向”地思考问题,灵活的解答问题.三、教学重点:能熟练的解一元一次不等式与一元一次不等式组四、教学难点:能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想。
五、教学过程(一)知识梳理1.知识结构图2.知识点回顾(1)、不等式用不等号连接起来的式子叫做不等式.常见的不等号有五种:“≠”、“>” 、“<” 、“≥”、“≤”.(2)、不等式的解与解集不等式的解:使不等式成立的未知数的值,叫做不等式的解.不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。
解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.(3)、不等式的基本性质A 、不等式的两边都加上(或减去)同一个数或同一个整式.不等号的方向不变.如果a>b ,则a+c>b+c ,a-c>b-cB 、不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.如果a>b ,并且c>0,那么则ac>bc (或a/c>b/c )C 、不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.如果a>b ,并且c<0,那么则ac<bc(或a/c<b/c)说明:任意两个实数a 、b 的大小关系:①a -b>O ⇔a>b ;②a -b=O ⇔a=b ;③a-b<O ⇔a<b .(4) 、一元一次不等式只含有一个未知数,且未知数的次数是1.系数不等于0的不等式叫做一元一次不等式.注:一元一次不等式的一般形式是ax+b>O 或ax+b<O(a ≠O ,a ,b 为已知数). (5)、解一元一次不等式的一般步骤解一元一次不等式的一般步骤:(1)去分母;(2)去括号;(3)移项; (4)合并同类项;(5)化系数为1. 说明:解一元一次不等式和解一元一次方程类似.不同的是:一元一次不等式两边同乘以(或除以)同一个负数时,不等号的方向必须改变,这是解不等式时最容易出错的地方.(6).一元一次不等式组含有相同未知数的几个一元一次不等式所组成的不等式组,叫做一元一次不等式组.说明:判断一个不等式组是一元一次不等式组需满足两个条件:①组成不等式组的每一个不等式必须是一元一次不等式,且未知数相同;②不等式组中不等式的个数至少是2个,也就是说,可以是2个、3个、4个或更多.(7).一元一次不等式组的解集一元一次不等式组中,几个不等式解集的公共部分.叫做这个一元一次不等式组的解集.一元一次不等式组的解集通常利用数轴来确定. 不等式组 图示 解集x a x b>⎧⎨>⎩ x a >(同大取大) x>ax b <(同小取小)a b (){a x b x >>1x ax b<⎧⎨>⎩b ab x a<<(大小交叉取中间)x ax b>⎧⎨<⎩b a无解(大小分离解为空)(1)分别求出不等式组中各个不等式的解集;(2)利用数轴求出这些解集的公共部分,即这个不等式组的解集.3.课堂练习(一)解:去分母,得:4(2x-1)≥12(5/4x-5)去括号,得:8x-4≥15x-60移项,得:8x-15x≥-60+4合并同类项得:-7x≥-56系数化为1,得:x≤82.解不等式组:解:解不等式①得:x≤8解不等式②得:x≥5把不等式①的解集和不等式②的解集在数轴上表示如下:∴原不等式组的解集为:5≤x≤83、求不等式(组)的特殊解:(1)求不等式 3x+1≥4x-5的正整数解解:移项,得:3x-4x≥-5-1合并同类项,得:-x≥-6系数化为1,得:x≤6所以不等式的正整数解为:1、2、3、4、5、6 (2)求不等式组的整数解2151.5,34.xx-≥-解不等式并把它的解集在数轴上表示出来33)4(2545312+≤+-≥-xxxx2151(2)32xx+>⎧⎪⎨+≤⎪⎩解:由不等式①得: x>2由不等式②得: x≤4把不等式①的解集和不等式②的解集在数轴上表示如下:∴不等式组的解集为:2<x≤4∴不等式组的整数解为:3、4.4.不等式(组)在实际生活中的应用当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.(1)我市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间住房. 如果每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位,问该校可能有几间住房可以安排学生住宿?住宿的学生可能有多少人?解:设可能有x间住房安排学生住宿,则根据题意可得:8x>5x+12解这个不等式,得:x>4当x=5时,住宿的学生可能有37人,符合题意;当x=6时,住宿的学生可能有42人,符合题意;当x=7时,住宿的学生可能有47人,不符合题意.答:该校可能有5间或6间住房,当有5间住房时,住宿学生有37人;当有6间住房时,住宿学生有42人.(2)学校要到体育用品商场购买篮球和排球共100只.已知篮球、排球的单价分别为130元、100元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章单元练习
一、选择题(每题4分,共40分)
1、下列各式:(1)5x -≥;(2)30y x -<;(3)
50x π+<;(4)23x x +≠; (5)333x x
+≤;(6)20x +<是一元一次不等式的有( ) A. 2个 B. 3个 C. 4个 D. 5个
2、下列命题正确的是( )
A. 若a b >,b c <,则a c >
B. 若a b >,则ac bc >
C. 若a b >,则22ac bc >
D. 若22ac bc >,则a b >
3、若点P(21m +,
312
m -)在第四象限,则m 的取值范围是( ) A.14m < B.12m > C.1123m -<< D.1123m -≤≤ 4、如图,A ,B 两点在数轴上表示的数分别为a ,b ,下列式子成立的是( )
A.0ab >
B.0a b +<
C.(1)(1)0b a -+>
D.(1)(1)0b a -->
5、不等式组1(1)
2,233
1
x x x ⎧
+
≤⎪⎨
⎪
-<+
⎩的解集在数轴上表示正确的是( )
6、已知2x =是不等式(5)(32)0x ax a --+≤的解,且1x =不是这个不等式的解,则实数a 的取值范围是( )
A.1a > B .2a ≤ C.12a <≤ D.12a ≤≤
7、若0a b +<,且0b <,则a ,b ,a -,b -的大小关系为( )
A.a b b a -<-<<
B.a b b a -<<-< C .a b a b -<-<< D.a b b a <<-<-
8、已知4,221
x y k x y k +=⎧⎨+=+⎩且10x y -<-<,则k 的取值范围为( )
A.112k -<<-
B.102k <<
C. 01k <<
D.112k <<
9、若不等式组1,1
x x m <⎧⎨>-⎩恰有两个整数解,则m 的取值范围是( )
A.10m -≤<
B.10m -<≤
C. 10m -≤≤
D.10m -<<
10、若人要完成2.1千米的路程,并要在18分钟内到达,已知他每分钟走90米,若跑步每分钟可跑210米,问这人完成这段路程,至少要跑多少分钟?设要跑x 分钟,则列出的不等式为( )
A. 21090(18)2100x x +-≥
B. 90210(18)2100x x +-≤
C. 21090(18) 2.1x x +-≤
D. 21090(18) 2.1x x +->
二、填空题(每题5分,共20分)
11、若不等式组0,122
x a x x +≥⎧⎨->-⎩有解,则a 的取值范围是___________.
12、已知实数x ,y 满足234x y -=,并且1x ≥-,2y <,现有k x y =+,则k 的取值范围是____________.
13、若不等式组20,0
x b x a -≥⎧⎨+≤⎩的解集为34x ≤≤,则不等式ax b +<0的解集为____________.
14、某商品的标价比成本价高m%,根据市场需要,该商品需降价n%出售,为了不亏本,n 应满足________________.
三、解答题(15—18,每题8分;19、20每题10分;21、22每题12分;23题14分)
15、解不等式(组),并把解集在数轴上表示.
(1)
122362x x x -+-<- (2)53362
x -≤<
16、已知实数a 是不等于3的常数,解不等式组233,11(2)022
x x a x -+≥-⎧⎪⎨-+<⎪⎩,并依据a 的取值情况写出其解集.
17、已知关于x ,
y 的方程组2,2324x y m x y m -=⎧⎨+=+⎩的解满足不等式组30,50x y x y +≤⎧⎨+>⎩求满足条件的m 的整数值.。
