数学建模(合)大作业
数学建模大作业

数学建模大作业姓名1:魏家蓉学号:201100414 姓名2:何嘉琪学号:201100415 姓名3:向歆学号:201100418 姓名4:牟宇宇学号:201100420 姓名4:曾朝忠学号:201100431 专业:交通工程班级:交工1101指导老师:张仲荣2014年5 月22 日直升机运输公司问题问题提出一家运输公司正考虑用直升机从某城市的一摩天大楼运送人员。
你被聘为顾问,现在要确定需要多少架飞机。
按照建模过程仔细分析,建模。
为了简化问题,可以考虑升机运输公司问题。
基本假设如下:假设运载的直升机为统一型号; 假设每架飞机每次载人数相同;假设飞机运送的人员时互不影响;假定人员上了飞机就安全,因此最后一次运输时,只考虑上飞机所花时间。
1、按照数学建模的全过程对本题建立模型,并选用合理的数据进行计算(模型求解); 2、本问题是否可以抽象为优化模型;除了考虑建立优化模型之外,是否可以采用更简单的方法建立模型。
注意考虑假设条件。
甚至基于不同的假设建立多个模型。
模型假设:(H1)所有飞机的飞行高度度均为10 000m ,飞行速度均为800km/h 。
(H2)飞机飞行方向角调整幅度不超过6,调整可以立即实现;(H3)飞机不碰撞的标准是任意两架飞机之间的距离大于8km; (H4)刚到达边界的飞机与其他飞机的距离均大于60km; (H5)最多考虑N 架飞机;(H6)不必考虑飞机离开本区域以后的状况. 符号说明:D 为飞行管理区域的边长;S 为飞行管理区域取直角坐标系使其为[0,D ]×[0,D]; v 为飞机飞行速度,v=800km/h; (x 0i ,y i)第i 架飞机的初始位置;()(),(t t y x ii )为第i 架飞机在t 时刻的位置;θ0i为第i 架飞机的原飞行方向角,即飞行方向与x 轴夹角,0≤θ≤2π;θi ∆第i 架飞机的方向角调整,-6π≤i θ∆≤6π; i θ﹦i 0i θθ∆+为第i 架飞机调整后的飞行方向角;模型建立一、两架飞机不碰撞的条件1、两架飞机距离大于8km 的条件设第i 架和第j 架飞机的初始位置为(0i 0i y x ,),(0j 0j y x ,),飞行方向角分别为和,他们的位置为(t)=vtcos +(t)=vtsin+和(t)=vtcos + 0j x(t)=vtsin+0j y若记时刻t 他们距离为(t),则他们之间距离的平方为2ijr (t )=(x i (t )-x j (t))2+(y i (t)-y j (t ))2经简单计算可得2ijr (t )=v 2 [(cos i θ-cos j θ)2+(sin i θ-sin j θ)2] t 2+2v[(0i x -0j x )(cos i θ-cos j θ)+(0i y -0j y )(sin i θ-sin j θ)]t+(0i x -0j x )2+(0i y -0j y )2引入ij a = v 2 [(cos i θ-cos j θ)2+(sin i θ-sin j θ)2]ij b =2v[(0i x -0j x )(cos i θ-cos j θ)+(0i y -0j y )(sin i θ-sin j θ)]那么2ij r (t )=ij a t 2+ij b t+ 2ij r (0)由此可见,两架飞机不碰撞的条件为2ij r (t )=ij a t 2+ij b t+ 2ij r (0) >642、由假设(6),我们不必理会飞机飞离区域Ω的状况,因此,在考虑两架飞机是否在区域内发生碰撞时,只需考察两架飞机有一架到达边界之前(7-7)式是否成立就可以了。
数学建模大作业.

《数学实验》报告实验名称数学建模与 MATLAB 学院材料学院专业班级材料 1014姓名徐萌孔德成戴思雨学号 41071046 41030400 410303992012年 6月一、问题的提出。
传染病是当今世界最严重的疾病之一, 2009年 4月 26日世界卫生组织以确认, 美国和墨西哥发生了甲型 H1N1流感, 随后疫情迅速蔓延, 截止 8月中旬, 全球感染人数约 5万人。
因此,运用传染病的数学模型来描述传染病甲型 H1N1流感的传播过程, 分析受感染人数的变化规律, 探索制止甲型 H1N1蔓延的手段是值得关注的。
二、模型的建立。
考查中国内地疫情变化,在疾病传播期间不考虑人口的出生率和死亡率, 人口总数不变, 为常量。
中国的疫情研究发现易感染人数多为 20~50岁的青壮年, 故保守估计在此传染病系统的人数 N=50000人。
甲型 HINI 流感的传播途径是与病源的直接接触, 患者与健康者接触时, 都使健康者感染病变. 故将人群分为 3类:健康者(易感染者人群、患者 (已被感染人群、治愈者 (研究期间 6月 14日~8 月 14日间中国内地感染病毒死亡人数为 0, 故此处不考虑死亡者 . 三者在总人数中的比例分别为 :s(t,i(t,r(t且 s(t+i(t+r(t=1,io,So分别为患者人数, 健康人数的比例初始值.设每个患者每日感染健康者的平均人数为日感染率,记为λj ,则λj=j日新增病例数 /(j-1日(累计确诊人数 -累计出院人数 ;每日被治愈的患者人数占其总数的比例为日治愈率,记为μj ,则Μj=j日被治愈的人数 /j日累计确诊病人数 ;定义整个传染期内每个患者有效接触的平均人数为接触数σ,由 s(t+i(t+r(t=1可知, 对于病愈免疫的治愈者而言应有dr/dt=μi, 因此考虑 SIR 传染模型,该模型的方程为2λsi-μi;λsi (1三、模型的求解1、数值运算由于在方程 (1中无法求出 s(t和 i(t的解析解,故先做数值运算.据来自中国卫生部网站公布的 2009年 6月 14日~8月 14日的疫情数据 (见表1[包括日累计确诊病例、日累计治愈病例等. 其中缺失的部分数据, 将以通过给定的数据拟合得到 .表 1疫情原始数据日期新增病例确诊病例累计治愈累计新增治愈数6月 14日 20 185 736月 15日 41 226 86 136月 16日 11 237 97 11 6月 17日 27 264 114 17 6月 18日 33 297 135 21 6月 19日 31 328 160 25 6月 20日 28 356 185 25 6月 21日 58 414 199 14 6月 22日 27 441 227 28 6月 23日 49 490 251 24 6月 24日 38 528 275 24 6月 25日 42 570 321 46 6月 26日 48 618 338 17 6月 27日 60 678 373 35 6月 28日 51 729 401 28 6月 29日 37 766 445 44 6月 30日 44 810 496 51 7月 1日 56 866 554 58 7月 2日 49 915 612 58 7月 3日 45 960 660 48 7月 4日 40 1000 704 4437月 5日 40 1040 749 45 7月 6日 57 1097 793 44 7月 7日 54 1151 870 77 7月 8日 36 1187 927 57 7月 9日 36 1223 985 58 7月 10日 40 1263 1035 50 7月 11日 39 1302 1085 50 7月 12日 26 1328 1110 25 7月 13日 26 1354 1134 24 7月 14日 45 1399 1166 32 7月 15日 45 1444 1197 31 7月 16日 41 1485 1230 33 7月 17日 52 1537 1263 33 7月 18日 44 1581 1293 30 7月 19日 44 1625 1323 30 7月 20日 43 1668 1355 32 7月 21日 52 1720 1404 49 7月 22日 52 1772 1454 50 7月 23日 38 1810 1529 75 7月 24日 42 1852 1604 75 7月 25日 26 1878 1663 59 7月 26日 26 1904 1722 59 7月 27日 26 1930 1781 59 7月 28日 37 1967 1817 36 7月 29日 36 2003 1853 36 7月 30日 43 2046 1883 30 7月 31日 44 2090 1912 29 8月 1日 20 2110 1937 25 8月 2日 21 2131 1962 25 8月 3日 21 2152 1988 26 8月 4日 29 2181 2031 43 8月 5日 29 2210 2074 43 8月 6日 27 2237 2098 24 8月 7日 27 2264 2122 24 8月 8日 28 2292 2137 15 8月 9日 28 2320 2152 15 8月 10日 28 2348 2167 15 8月 11日 38 2386 2203 36 8月 12日 39 2425 2240 37 8月 13日 57 2482 2261 21 8月 14日 55 2537 2283 22注:2009年疫情效据见文献 [8]4以 6月 15日为基日,当日累计确诊病例 226例,累计出院者 86例,故s(0=(50000-226+86/50000=0.9972;I(0=(226-86/50000=0.0028;在研究期间,平均日感染率λ和平均日治愈率μ由每天相应数据平均求得. 设计程序为:新增病例 A 确诊病例累计 B 治愈累计 C 新增治愈数 D>>A=[41 11 27 33 31 28 58 27 49 38 42 48 60 51 37 44 56 49 45 40 40 57 54 36 3640 39 26 26 45 45 41 52 44 44 43 52 52 38 42 26 26 26 37 36 43 44 20 21 21 29 29 27 27 28 28 28 38 39 57 55]>>B=[226 237 264 297 328 356 414 441 490 528 570 618 678 729 766 810 866 915 9601000 1040 1097 1151 1187 1223 1263 1302 1328 1354 1399 1444 1485 1537 1581 1625 1668 1720 1772 1810 1852 1878 1904 1930 1967 2003 2046 2090 2110 2131 2152 2181 2210 2237 2264 2292 2320 2348 2386 2425 2482 2537]>>C=[86 97 114 135 160 185 199 227 251 275 321 338 373 401 445 496 554 612 660704 749 793 870 927 985 1035 1085 1110 1134 1166 1197 1230 1263 1293 1323 1355 1404 1454 1529 1604 1663 1722 1781 1817 1853 1883 1912 1937 1962 1988 2031 2074 2098 2122 2137 2152 2167 2203 2240 2261 2283]>>D=[13 11 17 21 25 25 14 28 24 24 46 17 35 28 44 51 58 58 48 44 45 44 77 57 5850 50 25 24 32 31 33 33 30 30 32 49 50 75 75 59 59 59 36 36 30 29 25 25 26 43 43 24 24 15 15 15 36 37 21 22]>>E=A./(B-C %日感染率>>e=sum(E/61 %平均日感染率>>F=D./(B-C %日治愈率>>f=sum(F/61 %平均日治愈率运行结果:A =Columns 1 through 1641 11 27 33 31 28 58 27 49 38 42 48 60 51 37 44Columns 17 through 3256 49 45 40 40 57 54 36 36 40 39 26 26 45 45 41552 44 44 43 52 52 38 42 26 26 26 37 36 43 44 20 Columns 49 through 6121 21 29 29 27 27 28 28 28 38 39 57 55B =Columns 1 through 8226 237 264 297 328 356 414 441Columns 9 through 16490 528 570 618 678 729 766 810 Columns 17 through 24866 915 960 1000 1040 1097 1151 1187 Columns 25 through 321223 1263 1302 1328 1354 1399 1444 1485 Columns 33 through 40 1537 1581 1625 1668 1720 1772 1810 1852 Columns 41 through 48 1878 1904 1930 1967 2003 2046 2090 2110 Columns 49 through 56 2131 2152 2181 2210 2237 2264 2292 2320 Columns 57 through 61 2348 2386 2425 2482 2537C =Columns 1 through 886 97 114 135 160 185 199 227 Columns 9 through 16251 275 321 338 373 401 445 496 Columns 17 through 24554 612 660 704 749 793 870 927 Columns 25 through 32985 1035 1085 1110 1134 1166 1197 1230 Columns 33 through 40 1263 1293 1323 1355 1404 1454 1529 1604 Columns 41 through 48 1663 1722 1781 1817 1853 1883 1912 1937 Columns 49 through 56 1962 1988 2031 2074 2098 2122 2137 2152 Columns 57 through 61 2167 2203 2240 2261 2283D =Columns 1 through 1613 11 17 21 25 25 14 28 24 24 46 17 35 28 44 5158 58 48 44 45 44 77 57 58 50 50 25 24 32 31 33Columns 33 through 4833 30 30 32 49 50 75 75 59 59 59 36 36 30 29 25Columns 49 through 6125 26 43 43 24 24 15 15 15 36 37 21 22e =0.173970451885603 %平均日感染率λ=0.173970451885603 f =0.164030384929960 %平均日治愈率μ=0.164030384929960 接触数:σ=λ/μ=0.173970451885603/0.164030384929960=1.060598936958463 可得模型方程为:;然后用 Matlab 软件编程,解常微分方程做出患者人数比例 i(t--时间 t/d关图, 健康者比例 s(t--时间 t/d关系图 ,患者人数比例 i-健康者比例 s 图。
数学建模通识课大作业题目
数学建模通识课大作业题目注意事项:(1) 大型作业由学生组队完成,每队不超过3人;(2) 在17个题目中任选一题完成;(3) 答卷包括问题复述、建模假设与建立、模型求解与计算等部分组成,引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出;(4) 答卷必须具有原创性,如发现抄袭和雷同,成绩计0分;(5) 答卷以电子版的形式发给各任课老师指定的邮箱,交卷截止时间为2012年12月20日晚上9:30。
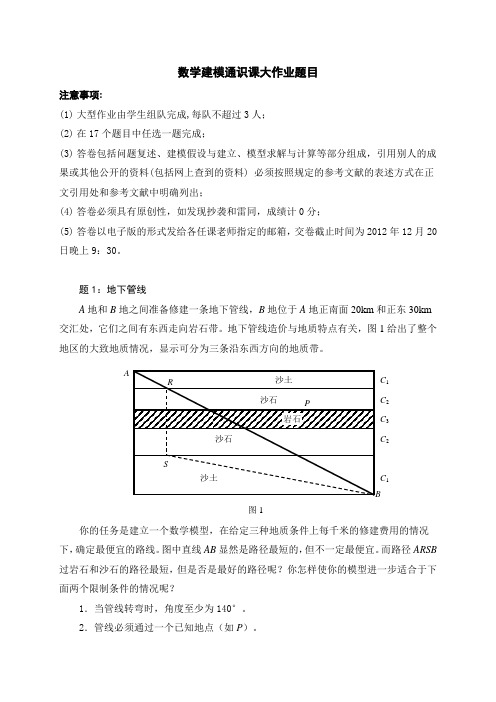
题1:地下管线A 地和B 地之间准备修建一条地下管线,B 地位于A 地正南面20km 和正东30km 交汇处,它们之间有东西走向岩石带。
地下管线造价与地质特点有关,图1给出了整个地区的大致地质情况,显示可分为三条沿东西方向的地质带。
你的任务是建立一个数学模型,在给定三种地质条件上每千米的修建费用的情况下,确定最便宜的路线。
图中直线AB 显然是路径最短的,但不一定最便宜。
而路径ARSB 过岩石和沙石的路径最短,但是否是最好的路径呢?你怎样使你的模型进一步适合于下面两个限制条件的情况呢?1.当管线转弯时,角度至少为140°。
2.管线必须通过一个已知地点(如P )。
AC 1 C 1C 2 C 2C 3 图1题2:电子游戏中的数学近年来,随着电子游戏的日益普及,电子游戏业已成为横跨信息技术和文化的重要产业。
对电子游戏中的一些数学问题进行研究,成为数学界和相关人士的一个热门话题。
在某电子游戏中,玩家每次下注一元,由机器随机分配给玩家五张扑克牌,然后允许玩家有一次换牌的机会,即可以放弃其中的某几张牌,放弃的牌留下的空缺由机器在剩下的47张牌中再次随机分配。
玩家的奖金依据其最后所持有的牌型而定。
下面是一份典型的奖金分配表:牌型奖金(元)同花大顺(10到A)800同花顺50四张相同点数的牌25满堂红(三张同点加一对)8同花 5顺子 4三张相同点数的牌 3两对 2一对高分对(J及以上) 1其它0在上表中,玩家的牌型属于某一类型且不属于任何更高的类型,则赢得该牌型相应的奖金。
数学建模 大作业1

N
( 1, 2 ,..... N )= i 的极小值。通常表示为 i 1
N
min F( 1, 2 ,..... N )= i , i 1
s.t. rij2 (t)>64 ,t tij ,i,j=1,2,….N,i≠j
i
6
,i=1,2,….N.
由于在这个及消化问题中目标函数可约束条件关于变量 1, 2 ,..... N 均为非 线性的,因此上述方程组是一个有约束的非线性的规划模型。
数学建模大作业
姓名 1:廉文秀 学号:200904745 姓名 2:沙吾列 学号:200903952 姓名 3:索海娟 学号:200903951 专业:车辆工程 班级:094 指导老师:张仲荣
2012 年 5 月 22 日
升机运输公司问题
一家运输公司正考虑用直升机从某城市的一摩天大楼运送人员。你被聘为顾 问,现在要确定需要多少架飞机。按照建模过程仔细分析,建模。为了简化问题, 可以考虑升机运输公司问题。 基本假设如下:
由于约束条件 ri2j (t)>64, t t ij ,i,j=1,2,…N,i j
有较强的非线性,特别是 tij 的表达式比较复杂,我们可以将问题进一步简化。注
(t)=vtcos
+
x
0 j
(t)=vtsin
+
y
0 j
若记时刻 t 他们距离为 (t),则他们之间距离的平方为
ri2j (t)=(xi(t)-xj(t))2+(yi(t)-yj(t))2
经简单计算可得
ri2j ( t ) =v2 [(cos i -cos j )2+(sin i -sin j )2] t2
i
架飞机的方向角调整,-
数学建模大作业

兰州交通大学数学建模大作业学院:机电工程学院班级:车辆093学号:200903812 姓名:刘键学号:200903813 姓名:杨海斌学号:200903814 姓名:彭福泰学号:200903815 姓名:程二永学号:200903816 姓名:屈辉高速公路问题1 实验案例 (2)1.1 高速公路问题(简化) (2)1.1.1 问题分析 (3)1.1.2 变量说明 (3)1.1.3 模型假设 (3)1.1.4 模型建立 (3)1.1.5 模型求解 (4)1.1.6 求解模型的程序 (4)1实验案例1.1 高速公路问题(简化)A城和B城之间准备建一条高速公路,B城位于A城正南20公里和正东30公里交汇处,它们之间有东西走向连绵起伏的山脉。
公路造价与地形特点有关,图4.2.4给出了整个地区的大致地貌情况,显示可分为三条沿东西方向的地形带。
你的任务是建立一个数学模型,在给定三种地形上每公里的建造费用的情况下,确定最便宜的路线。
图中直线AB显然是路径最短的,但不一定最便宜。
而路径ARSB过山地的路段最短,但是否是最好的路径呢?AB图8.2 高速公路修建地段1.1.1 问题分析在建设高速公路时,总是希望建造费用最小。
如果要建造的起点、终点在同一地貌中,那么最佳路线则是两点间连接的线段,这样费用则最省。
因此本问题是一个典型的最优化问题,以建造费用最小为目标,需要做出的决策则是确定在各个地貌交界处的汇合点。
1.1.2 变量说明i x :在第i 个汇合点上的横坐标(以左下角为直角坐标原点),i =1,2,…,4;x 5=30(指目的地B 点的横坐标)x=[x 1,x 2,x 3,x 4]Tl i :第i 段南北方向的长度(i =1,2, (5)S i :在第i 段上地所建公路的长度(i =1,2, (5)由问题分析可知,()()()()25425524324423223322122221211x x l S x x l S x x l S x x l S x l S -+=-+=-+=-+=+=C 1:平原每公里的造价(单位:万元/公里)C 2:高地每公里的造价(单位:万元/公里) C 3:高山每公里的造价(单位:万元/公里)1.1.3 模型假设1、 假设在相同地貌中修建高速公路,建造费用与公路长度成正比;2、 假设在相同地貌中修建高速公路在一条直线上。
数学建模大作业习题答案

数学建模大作业习题答案数学建模大作业习题答案作为一门应用数学课程,数学建模在现代科学研究和工程技术中具有重要的地位和作用。
通过数学建模,我们可以将实际问题转化为数学模型,从而利用数学方法进行分析和求解。
在数学建模的学习过程中,我们经常会遇到一些习题,下面我将为大家提供一些数学建模大作业题目的答案,希望能对大家的学习有所帮助。
1. 题目:某城市的交通拥堵问题解答:针对这个问题,我们可以采用图论的方法进行建模和求解。
首先,我们将城市的道路网络抽象为一个图,图的节点表示交叉口,边表示道路。
然后,我们可以给每条边赋予一个权重,表示道路的通行能力。
接着,我们可以使用最短路径算法,比如Dijkstra算法,来计算从一个交叉口到另一个交叉口的最短路径,从而找到最优的交通路线。
此外,我们还可以使用最小生成树算法,比如Prim算法,来构建一个最小的道路网络,以减少交通拥堵。
2. 题目:某工厂的生产调度问题解答:对于这个问题,我们可以采用线性规划的方法进行建模和求解。
首先,我们可以将工厂的生产任务抽象为一个线性规划模型,其中目标函数表示最大化生产效益,约束条件表示生产能力、物料供应和市场需求等方面的限制。
然后,我们可以使用线性规划求解器,比如Simplex算法或内点法,来求解这个线性规划模型,得到最优的生产调度方案。
此外,我们还可以引入一些启发式算法,比如遗传算法或模拟退火算法,来寻找更好的解决方案。
3. 题目:某股票的价格预测问题解答:对于这个问题,我们可以采用时间序列分析的方法进行建模和求解。
首先,我们可以将股票的价格序列抽象为一个时间序列模型,比如ARIMA模型。
然后,我们可以使用历史数据来拟合这个时间序列模型,并进行参数估计。
接着,我们可以利用这个时间序列模型来预测未来的股票价格。
此外,我们还可以引入其他的预测方法,比如神经网络或支持向量机,来提高预测的准确性。
通过以上的例子,我们可以看到,在数学建模的过程中,我们需要将实际问题抽象为数学模型,然后利用数学方法进行分析和求解。
数模大作业报告
草原生态建模问题草原生态建模问题一、问题重述:二十世纪二十年代,在美国西部,狼和羊的数量一直保持平衡。
狼吃羊,羊吃草,草原生态系统一直保持平衡。
但是由于美国人觉得羊数量由于狼一直得不到提升。
于是当局政府下令,让猎人进入山区,捕杀狼群。
几年后,狼的数量大幅减少,并在三十年代一度灭绝,羊的数量呈指数增长。
但是随着时间的推移,羊没有了天敌,把草原的草都吃完了,且没有天敌,羊体质明显下降。
羊的数量不升反降,不久,羊也大幅度减少。
生态学家研究这种现象,提出了生态平衡的概念。
这个模型以狼吃羊问题为出发点,模拟生态平衡。
二、问题分析:1、狼吃羊,羊吃草,草场生长,符合一定的生长规律。
如果把这种规律找到,就为后面分析问题提供了方便。
2、当狼、羊、草场有一定合理初值情况下,按照分析1找到的规律分析是否在一定的时间范围内,一直保持生态平衡。
3、在有外界干预的情况下:人为捕杀狼群、草原大火、羊物种入侵,是否还能保持稳定。
三、模型假设:1、假设1(草场假设):(1)草场总面积1000平方公里;(2)每平方公里在供养50只一下黄羊情况下,草场不退化;(3)当黄羊数量平均每平方公里超过50只时,草场面积减小率与黄羊超过50只的数量成正比,比例系数0.0001.2、假设2(羊群假设):(1)当前黄羊总群数量60000只;(2)草场充足,没有狼群情况下,黄羊群净增长率0.1;(3)草场不充足会导致总群繁殖率下降,下降率与每平方公里平均黄羊数量减50长比例,比例系数为0.001.(4)狼群存在会减少黄羊的数量。
3、假设3(狼群假设):(1)当前狼群总数100只;(2)黄羊总群数量与狼群数量之比超过300:1时,狼群净增长率0.01.(3)之比低于300:1时,会导致狼群繁殖率下降,下降与狼群总量与黄羊总量值比成比例,比例系数0.5。
(4)每只狼平均每年吃掉20只黄羊。
四、模型分析及求解:生态系统一般性分析:由上述模型假设分析得:goat1=60000lawn1=1000当 0<goat i/lawn i<=50时goat i+1=1.1*goat i-20*wolf ilawn i+1=lawn i当goat i/lawn i>=50时goat i+1=(1-0.001*(goat i/lawn i-50))*goat i-20*wolf i lawn i+1=(1-0.0001*(goat i/lawn i-50))*lawn i当goat i/wolf i>=300时wolf i+1=(1+0.01)*wolf i当0<goat i/wolf i <=300时wolf i+1=(1-0.5*wolf i/goat i)*wolf i建立如下程序:clc;clear;lawn(1)=1000;goat(1)=60000;wolf(1)=100;i=1;k=200;figure(1);t=1:1:k;while i<kx1=goat(i);x2=wolf(i);x0=lawn(i);if x1/x0<=50goat(i+1)=1.1*x1-20*x2;lawn(i+1)=x0;elsegoat(i+1)=(1-0.001*(x1/x0-50))*x1-20*x2;lawn(i+1)=(1-0.0001*(x1/x0-50))*x0;endif x1/x2>=300wolf(i+1)=(1+0.01)*x2;elsewolf(i+1)=(1-0.5*x2/x1)*x2;endi=i+1;endsubplot(2,2,1);plot(goat,wolf,'b');title('羊和狼的数量变化');xlabel('羊的数量/只');ylabel('狼的数量/只');axis([40000 70000 100 175]); subplot(2,2,2);plot(t,goat,'b');grid on;title('羊的数量变化');xlabel('时间/年');ylabel('羊的数量/只');axis([0 200 0 60000]);subplot(2,2,3);plot(t,wolf,'b');grid on;title('狼的数量变化');xlabel('时间/年');ylabel('狼的数量/只');subplot(2,2,4);plot(t,lawn,'b');grid on;title('草场的数量变化');xlabel('时间/年');ylabel('草场的数量/公亩');由matlab编程可得:当goat1=60000wolf1=100lawn1=1000时:羊最终数量为:goat=48000只狼最终数量为:wolf=168只草场的最终数量为:lawn=992公亩模型结果分析:图一羊数量随时间变化由图一可得,当t=7年时,羊的数量就保持稳定且t=200年时,羊的数量一直保持在4.8万只左右。
2023年数学建模大作业题.大案
2023年数学建模大作业题-大案1. 引言在2023年的数学建模大作业中,我们将研究一个题为“大案”的问题。
本文档将详细介绍该问题的背景和目标,并提供相关的数学模型和求解方法。
2. 问题背景和目标在我们的城市中,发生了一个严重的犯罪案件,被称为“大案”。
警方已经掌握了一些证据,包括嫌疑人的信息、嫌疑人之间的联系和一些可能的犯罪地点。
然而,由于数量庞大的数据和复杂的关系网络,警方无法准确判断嫌疑人之间的关联以及他们可能的行动轨迹。
我们的目标是根据已有的证据,建立一个数学模型,并通过模型求解,揭示嫌疑人之间的关联和可能的行动轨迹。
我们希望通过这个模型,为警方提供行动指导,并帮助他们尽快破案。
3. 数学模型为了建立一个准确且实用的数学模型,我们需要考虑以下几个因素:3.1 数据预处理首先,我们需要对已有的证据进行数据预处理。
这包括数据清洗、数据转换和数据统计等步骤。
通过对数据的预处理,我们可以去除噪声和异常值,并提取出有用的特征。
3.2 嫌疑人关联网络模型基于已有的证据,我们可以构建一个嫌疑人关联网络模型。
在该模型中,每个嫌疑人都被表示为一个节点,而嫌疑人之间的联系则被表示为边。
我们可以使用图论的方法来研究和分析这个网络模型,例如通过计算节点的中心度来评估嫌疑人的重要性或通过社区发现算法来发现潜在的犯罪团伙。
3.3 行动轨迹预测模型为了预测嫌疑人的行动轨迹,我们可以建立一个行动轨迹预测模型。
在该模型中,我们需要考虑时间因素、地理位置和其他相关因素。
我们可以使用时间序列分析方法来预测嫌疑人在不同时间点的行动,使用地理信息系统(GIS)技术来分析嫌疑人的活动范围,并使用机器学习算法来预测嫌疑人可能的下一步行动。
3.4 优化算法为了求解模型,我们需要设计和应用一种有效的优化算法。
这个优化算法可以考虑多个因素,包括时间效率、精确度和可扩展性。
我们可以使用线性规划、整数规划或遗传算法等方法来求解模型。
4. 求解方法基于上述的数学模型,我们可以提出以下的求解方法:1.对数据进行预处理,包括数据清洗、数据转换和数据统计等步骤。
数学建模大作业题目
(1) 用起泡法对10个数由小到大排序. 即将相邻两个数比较,将小的调到前头. (10个数字自己选择,方法要一般)(2)有一个45⨯矩阵,编程求出其绝对值最大值及其所处的位置. (用abs 函数求绝对值)(3)编程求201!n n =∑ ( 分别用for 和while 循环)(4)一球从100米高度自由落下,每次落地后反跳回原高度的一半,再落下. 求它在第10次落地时,共经过多少米?第10次反弹有多高? (5)有一函数2(,)sin 2f x y x xy y =++,写一程序,输入自变量的值,输出函数值,并画出其图像,加上图例和注释. (区间自理) (6) 建立一个脚本M 文件将向量a,b 的值互换。
(7) 某商场对顾客所购买的商品实行打折销售,标准如下(商品价格用price 来表示): price<200 没有折扣; 200≤price<500 3%折扣; 500≤price<1000 5%折扣; 1000≤price<2500 8%折扣; 2500≤price<5000 10%折扣;5000≤price 14%折扣;输入所售商品的价格,求其实际销售价格。
(用input 函数) (8) 已知y ,22221111123y n=++++,当n=100时,求y 的值。
(9)画出分段函数2221y 1 122 1 2x x x x x x x ⎧<⎪=-≤<⎨⎪-+≥⎩的图像,并求分段函数在任意几点的函数值。
(用hold on 函数)(10) 给定5阶方阵,求方阵的行列式、特征值、迹、上三角元素的和。
(11) 输入40个数字,按照从小到大的顺序排列输出。
(12) 把当前窗口分成四个区域,在每个区域中分别用不同的颜色和线形画sin ;tan y x y x==,x y e =和31y x x =++的图像。
(区间自理)(13) 对于,AXB YA B==,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,,求解X,Y ;(14) 如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,242679836B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,求1122,*,.*,,,,T A B A B A B AB A B A A ---。
数学建模(合)大作业
学生实验报告实验时间:2017 学年第 2 学期专业班级:信息与计算科学1502班____ (学号):庞云杰(20155653)_______2017年 03月21日通过N(t)=N0e rt其中r=0.0202(1/年),N0 =6.0450(百万);我们可以预测美国2010,2020,2030,2040,2050年的人口;通过计算,我们可以得出2010年 514.28(百万)2020年629.39(百万) 2030年770.26(百万) 2040年942.66(百万)2050年1153.65(百万)误差分析利用指数增长模型预测美国人口变化状况,其预测结果与真实值比较,相对误差在1%-55%之间,预测模型明显不可靠。
模型2利用MATLAB进行曲线拟合,首先在平面上绘出已知数据的分布图,通过直观观察,猜测人口随时间的变化规律,再用函数拟合的方法确定其中的未知参数,从而估计出2010 2020 2030 2040 2050年的美国人口。
利用MATLAB作出美国人口统计数据的连线图如图1。
1美国人口统计数据连线图2建模方法2拟合效果图由图1可以发现美国人口的变化规律曲线近似为一条指数函数曲线,因此我们假设美国的人口满足函数关系x=f(t), f(t)=ea+bt,a, b为待定常数,根据最小二乘拟合的原理,a, b是函数的最小值点。
其中xi是ti时刻美国的人口数。
利用MATLAB中的曲线拟合程序“curvefit”,编制的程序如下:首先创建指数函数的函数M——文件用最小二乘拟合求上述函数中待定常数,以及检验拟合效果的图形绘制程序m-function, fun1.mfunction f=fun1(a,t)f=exp(a(1)*x + a(2));t=1790:10:2000;图3误差分析观察误差和图像,模型2对过去的统计数据吻合得较好,但也存在问题,即人口是呈指数规律无止境地增长,此时人口的自然增长率随人口的增长而增长,这不可能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学生实验报告实验时间:2017 学年第 2 学期专业班级:信息与计算科学1502班____ (学号):庞云杰(20155653)_______2017年 03月21日实验名称实验一:用MATLAB求解线性规划问题实验地点信息楼121 实验日期2017.03.21学时2一、实验目的1.了解线性规划的基本容2.熟悉MATLAB软件求解线性规划问题的基本命令3.学习灵敏分析问题的思维方法二、实验容三、实验作业P226,1和3任选一1.问题分析:确定种植最佳土地分配,即每种等级耕地分别种植水稻、大豆、玉米的面积2.模型建立:1)令分别为I II III三等耕地上种植的水稻面积,令分别为III III三等耕地上种植的大豆面积,令分别为I II III三等耕地上种植的玉米面积且令为xi(1<=i<=9)面积的耕地上的产量为ci.2)目标函数:总产量最大,即max=3)约束条件非负条件:最低产量限制:耕地面积恒定:综上数学模型为:在MATLAB中调试>>clc>>c=[11 9.5 9 8 6.8 6 14 12 10];A=[-11 -9.5 -9 0 0 0 0 0 00 0 0 -8 -6.8 -6 0 0 00 0 0 0 0 0 -14 -12 -10];b=[-190;-130;-350];F=[1 0 0 1 0 0 1 0 00 1 0 0 1 0 0 1 00 0 1 0 0 1 0 0 1];>>FF=[100;300;200];>>G=[0;0;0;0;0;0;0;0;0];>>GG=[];>> [x,fval]=linprog(c,A,b,F,FF,G,GG) Optimization terminated.x =17.27270.000082.7273300.0000165.00000.00000.000035.0000fval =4.2318e+003即:值分别17.27270.00.082.7273300.0165.00.00..0,此时才能使总产量最大。
2)根据题(1),当要求得产值最大时,目标函数只需变成max =1.2(11+9.5+9)+1.5(8+6.8+6)+0.8(14+12+10) =1 3.2+11.4+10.8+12+10.2+9+11.2+9.6+8在MATLAB中调试>>c=[13.2 11.4 10.8 12 10.2 9 11.2 9.6 8];>> [x,fval]=linprog(c,A,b,F,FF,G,GG)Optimization terminated.x =17.27270.00000.000019.11760.000082.7273280.8824200.0000所以:值分别为17.27270.00.00.019.11760.082.7273280.8824200.0,此时才能使总产值最大。
实验名称实验二:用MATLAB求解整数规划问题实验地点信息楼121 实验日期2017.03.28学时 2一、实验目的1.了解整数规划的基本容2.熟悉MATLAB软件求解整数规划问题的基本命令3.学习灵敏分析问题的思维方法二、实验容三.实验作业第三题1.问题分析合理安排人去干不同的任务,使指派总耗时最少。
2.模型建立引入0-1变量设工人甲乙丙丁分别为A1,A2,A3,A4;任务A,B,C,D分别为B1,B2,B 3,B4。
S表示完成所有任务所需的总工时,则该问题的数学模型为:(1)目标函数min s=+++(2)约束条件在MATLAB中调试>>clc>> c=[3 3 5 3;3 2 5 2;1 5 1 6;4 6 4 10]c =3 3 5 33 2 5 21 5 1 64 6 4 10>>Aeq=[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 1 1 1 1 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 1 1 1 1 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 1 1 1 11 0 0 0 1 0 0 0 1 0 0 0 1 0 0 00 1 0 0 0 1 0 0 0 1 0 0 0 1 0 00 0 1 0 0 0 1 0 0 0 1 0 0 0 1 00 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1]Aeq =Columns 1 through 141 1 1 1 0 0 0 0 0 0 0 0 0 00 0 0 0 1 1 1 1 0 0 0 0 0 00 0 0 0 0 0 0 0 1 1 11 0 00 0 0 0 0 0 0 0 0 0 00 1 11 0 0 0 1 0 0 0 1 0 0 0 1 00 1 0 0 0 1 0 0 0 1 0 0 0 10 0 1 0 0 0 1 0 0 0 1 0 0 00 0 0 1 0 0 0 1 0 0 01 0 0Columns 15 through 160 0此可以假定美国人口总量是一个连续变化、可导的实函数。
(2)人口增长率(人口的相对增长率,即单位时间单位人口的增长数量)是常数,或者单位时间人口的增长量与当时的人口成正比。
建立模型记为第年的美国人口总数(单位:百万);r为人口增长率,是定常数;=为初始时刻时的人口数(单位:百万)所以建立模型为>> y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 123.2 131.7 150.7 179.3 103.2 226.5 149.6 281.4];>> t=1790:10:2000;>> t=t-1790;>> Y=log(y);>> a=polyfit(t,Y,1)a =0.0191 1.8636>> r=a(1);>> NO=exp(a(2));>>r,NOr =0.0191NO =6.4470>> P=NO.*exp(r*t);>> PP =Columns 1 through 86.44707.8025 9.4430 11.4285 13.8314 16.739520.2591 24.5187Columns 9 through 1629.6738 35.9129 43.4638 52.6023 63.6622 77.0476 93.2472 112.8530Columns 17 through 22136.5809 165.2978 200.0525 242.1146 293.0205 354.6297>> plot(t,y,'+k',t,P,'-k')>> legend('Monitoring','predictde') >>xlabel('t'),ylabel('US Population') 模型参数估计结果为r=0.0202(1/年),N 0=6.0450(百万)50100150200250050100150200250300350400tU S P o p u l a t i o nMonitoring predictde通过 其中r=0.0202(1/年),N 0 =6.0450(百万);我们可以预测美国2010,2020,2030,2040,2050年的人口;通过计算,我们可以得出2010年 514.28(百万)2020年629.39(百万) 2030年770.26(百万) 2040年942.66(百万)2050年1153.65(百万)误差分析利用指数增长模型预测美国人口变化状况,其预测结果与真实值比较,相对误差在1%-55%之间,预测模型明显不可靠。
模型2利用MATLAB进行曲线拟合,首先在平面上绘出已知数据的分布图,通过直观观察,猜测人口随时间的变化规律,再用函数拟合的方法确定其中的未知参数,从而估计出2010 2020 2030 2040 2050年的美国人口。
利用MATLAB作出美国人口统计数据的连线图如图1。
1美国人口统计数据连线图2建模方法2拟合效果图由图1可以发现美国人口的变化规律曲线近似为一条指数函数曲线,因此我们假设美国的人口满足函数关系, ,a, b为待定常数,根据最小二乘拟合的原理,a, b是函数的最小值点。
其中xi是ti时刻美国的人口数。
利用MATLAB中的曲线拟合程序“curvefit”,编制的程序如下:首先创建指数函数的函数M——文件用最小二乘拟合求上述函数中待定常数,以及检验拟合效果的图形绘制程序m-function, fun1.mfunction f=fun1(a,t)f=exp(a(1)*x + a(2));t=1790:10:2000;图3误差分析观察误差和图像,模型2对过去的统计数据吻合得较好,但也存在问题,即人口是呈指数规律无止境地增长,此时人口的自然增长率随人口的增长而增长,这不可能。
一般说来,当人口较少时增长得越来越快,即增长率在变大;人口增长到一定数量以后,增长就会慢下来,即增长率变小这是因为,自然资源、环境条件等因素不允许人口无限制地增长,它们对人口的增长起着阻滞作用,而且随着人口的增加,阻滞作用越来越大。
而且人口最终会饱和。
实验名称实验七:综合实验实验地点信息楼121 实验日期2015/5/2学时 4一、实验目的1.掌握分析问题和解决问题的过程2.掌握前几章学习过的利用MATLAB求解方法3.综合利用所学方法建立模型,并用MATLAB进行求解二、实验容浴缸问题编程实现两种不同的加水策略下的水龙头流速,并做敏感性分析,画出相应的图形。
一、持续加水情形我们通过各种数据分析得到其中流速u的微分方程。
首先我们做的是流速与时间的关系在MATLAB中t=0:10:1200;u=182.4658./tplot(t,u)2004006008001000120002468101214161820我们可以算出在时的流速时,供应825s 水,二、 间歇加水情形我们经过分析可以得到在间歇加水情形时的微分方程我们可以看出流速与一个周期供水时间与供水温度均成反比,我们可以算出温度与流速u 的关系Th=0:2:50;u=1.334./(Th-36.5) plot(Th,u)05101520253035404550-3-2.5-2-1.5-1-0.500.51我们可以得出在供水温度 ,流速得出为,经过225 s 升温,耗水量为由此可知,持续加水方式耗水多。
