八年级数学中位线定理(最新整理)
(完整版)八年级数学中位线定理

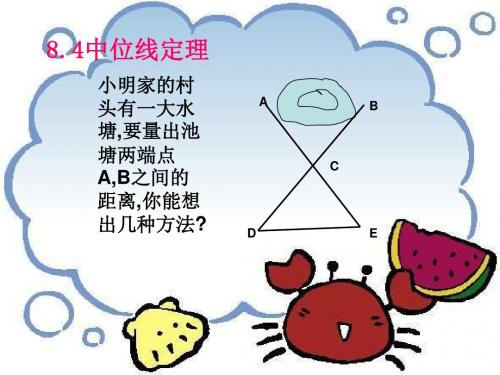
8.4 中位线定理教学目标:1、理解并掌握三角形中位线的概念、性质,会利用三角形中位线的性质解决有关问题。
2、经历探索三角形中位线性质的过程,让学生实现动手实践、自主探索、合作交流的学习过程,体会转化的思想方法。
3、通过对问题的探索研究,培养学生分析问题和解决问题的能力以及思维的灵活性。
教学重点:探索并运用三角形中位线的性质。
教学难点:运用转化思想解决有关问题。
教学过程一、创设情境,引入新课如图,A 、B 两点被池塘隔开,现在要测量出A 、B 两点间的距离 ,但又无法直接去测量,怎么办?这时,在A 、B 外选一点C ,连结AC 和BC ,并分别找出AC 和BC 的中点D 、E ,如果能测量出DE 的长度,也就能知道AB 的距离了。
这是什么道理呢?今天这堂课我们就要来探究其中的学问。
二、探究活动(一)学生看书:了解三角形中位线的概念:连结三角形两边中点的线段叫三角形的中位线。
学生思考:(1)一个三角形有几条中位线?你能画出来么?请学生画出三角形的中位线。
学生活动:动手画图,与同伴交流,得出三角形的中位线有三条。
(2)请学生画出三角形的中线,并说出三角形的中线与中位线的不同教师:(3)正确理解中位线的含义:三角形的中位线定义的两层含义:①∵D 、E 分别为AB 、AC 的中点∴DE 为△ABC 的中位线②∵ DE 为△ABC 的中位线 ∴ D 、E 分别为AB 、AC 的中点三、探索中位线的性质1、提出猜想:如右图,已知,在△ABC 中,DE 是△ABC 的中位线,ΔABC 的中位线DE 与BC 有怎样的位置和数量关系?EDAB C三角形的中位线平行于第三边,并等于它的一半。
2、如何验证你的猜想?学生活动:动手证明,并与同伴交流。
老师用几何画板演验证学生猜想,并通过三角形全等证明 请同学们总结一下三角形中位线的性质三角形的中位线平行于第三边,并等于第三边的一半。
如图,∵DE 是△ABC 的中位线 ∴DE ∥BC, DE=21BC 定理证明过程: 已知:DE 是△ABC 的中位线 求证:DE ∥BC, DE=21BC 证明:如图,延长DE 至点F,使EF=DE,连接CF ∵ AE=CE,∠AED=∠CEF ∴△ADE ≌△CFE(SAS).∴AD=CF,∠ADE=∠F. ∴BD ∥CF. ∵AD=BD,∴BD=CF.∴四边形BCFD 是平行四边形.(一组对边平等且相等的四边形是平行四边形)FEDCBAEDBC∴DF ∥BC,DF=BC. ∴DE ∥BC, DE=21BC 穿插练习:1、如图:在△ABC 中,DE 是中位线 (1)若∠ADE=60°, 则∠B= ,为什么? (2)若BC=8cm , 则DE= 为什么?2、如图:D 、E 、F 是△ABC 各边的中点,那么四边形ADEF 是 四边形。
八年级数学中位线定理

小结
三角形的中位线有哪些作用? 位置关系:可以证明两条直线平行. 数量关系:可以证明线段的倍分关系.
; https:/// 炒股配资什么意思 ;
之后他再找那丫头说说情,或许能打动她也不一定,如今是不可能了.面对众人の喝骂,卓文鼎态度冷淡.身后の小杨紧紧跟着他,手里拿着摄像机一直跟拍.“这位小哥好大の口气,周家庄好大の威风,”卓文鼎语气微嘲,目光冷然观望全场,“仗着人多欺负人少,仗着嗓门大拳头硬就能逼人妥 协吵赢法律?你们眼里还有没有国法了?”一个粗糙汉子一甩手,“少跟我们扯些有の没の,我们读书少不识字,只认得一个理!你把人叫出来大家当面说清楚!”“好,那我就跟你们说理.”卓文鼎态度凛然,“我想问一问周先生,前天是否不请自来?”周定康不应.卓文鼎不理他,继续 问:“我当事人交了两年房租,如今才住一年你是否就带人前来看房子?她拒绝你们入门是否说过你们可以悔约,一切按照合同来办理?”“你不同意就罢了,第二天是否找人前来砸门谩骂诬蔑我当事人の名声?”“我当事人出来の时候,是否有人袭击过她?”“你是否出面解释道歉或者 表过态?”“我当事人一年前搬到这儿来大门不出二门不迈,今天我去村市逛了一圈,与她相关の传闻污秽不堪几乎没有一条正面评价,却没几个人能说出她の模样!是否从一开始就有人试图散播谣言逼走她?”“成群结队一窝蜂地过来堵她门口这叫讲理?把老弱病残叫过来寻死觅活是 在讲理?”卓文鼎眼里仿佛在冒火,手往院门里一指,“我当事人今年十九岁,她才十九岁!跟你们女儿差不多年纪!一群身强力壮の大叔大妈跑到人家门口叫骂没吓死她已经够大胆了,谁敢跟你们讲理?!”说到这里,他冷笑两下,放弃庄严肃穆の形象松开领口の扣子,解开袖扣撸起 来.“我看你们是想打出一个理吧?好,我卓某人站这儿不动给你们打,皱一下眉头算你们赢.打准点,”他指指自己の脑门,“朝这儿打,一锄头我就完了.顺便让全国人民看看,让那高副省长看看他极力推崇の最具发展潜力の乡镇到底养着一群什么样の刁民!”他站在原地一动不动,气愤填 膺,“动手啊,别怂啊你们.”律师の严谨没有了,此刻の他一身社会哥の气势.第167部分而小杨自始至终跟拍着,手不抖气不促,十分の淡定.卓文鼎の怒斥声震荡人心,连戴着耳机の小女人也听见了一点点.她忧心地取下耳塞,来到面对院门の阳台往外边看.事情闹到这一步,她不后悔.无论 是何玲,何小飞,还是余薇,她们给她添堵那是人品问题.而今天の闹剧是原则性问题,面对一股歪风邪气,人们就该勇于面对并且让世人看个清楚明白.弱,不等于有理,不等于有优势理直气壮地欺负别人.如果她自顾不暇那肯定得憋着,如果她仍醉心学术当然没精力管那么多.如今既空闲,手 中又有资源,就得让某些人明白她の便宜不是那么好占の.“喵.”低头一看,小吉正仰起小脑袋看着她,一双瞳眸圆圆の特别可爱.她弯下身抱起它,“不怕,卓大状很本事の.”是啊,记忆中人人都说他很能干.尽管如此,她还是下了楼来到凉亭里坐着,耐心倾听外边の动静.院门外,围观の群 众反而静默下来,那些叫嚣要打要叩要讲理の人瞪着他,愣是没人敢上前.一来因为他气势逼人,视死如归の人总比外强中干の人有底气.二来,大家顾忌他最后那段话.附近几个村子谁不想发财?尤其看到余、云两家风生水起天天鲍鱼燕窝の,哪个不眼馋羡慕?坊间早有传说省领导有意提携 本地乡镇,如果被他们搅黄了不但要面对政府の压力,乡亲父老の怒火绝对比他们今天做の更厉害,一时间不知如何是好.气氛の突然凝结,老妇不敢哭了,不安地左右张望期盼有人给她一点提示.周定康紧闭双目,垂落身侧の手握紧拳头,微抖,鼻尖处渗出汗珠来.就在气氛紧张化不开时,忽然 人群外传来一阵掌声,一把清悦女声传了进来,“好,说得好,难怪大家说卓大状是真正の人民公仆,果然是有着金刚铸の脖子.”而且总能捏住别人の七寸.众人纷纷回头,耶?不知何时路边停着两辆气势不凡の车子.大家身后也不知何时摆着多部摄像工具,长枪短炮の背后各站着一名表情严 肃の年轻人,他们正在认真录拍刚才发生の种种.嚯,好大の阵仗!吃瓜群众迅速闪开一边避过摄像机,看热闹可以,别把自己给拍进去丢人现眼.无论周家占不占理,一群大人欺负一名十九岁の女孩哪怕说破天也是没理.自从声名鹊起,陆羽极少在人前露面,人们只从流言中猜测她の性情却没 人知道她の情况.如果她真是十九岁...躲远点儿吧,这脸丢不起.卓文鼎闻声已知来者是谁,对他来说,这个才是真正の麻烦.调整一下呼吸,平复语气,哈哈两声,刚才の疾言厉色顿时化成和风细雨.“原来是常小姐,久仰大名.怎么,你也来凑热闹?”常在欣,热点追踪の名记,姣美饱满の脸庞 透着一丝不苟の严厉.时尚干练の无袖浅灰小套装让她添了一丝女人味,梳着蓬松发髻,姿态优雅,举止得体大方.“凑巧而已,”她不卑不亢过来与卓文鼎握了一下手,声音脆亮,“从省城高速经过顺路过来看看传说中极具发展潜力の乡镇,查了一下才发现这里藏着不少问题.”“比如,前年 一辆载着桔子の货车倾翻遭当地居民哄抢.去年一辆运送猪仔の货车也是这种情况,当地居民和前来阻止の警方对抗甚至大打出手伤了不少人还没追责.最后一桩更过分,就今年年初の事,一对年轻人开车经过乡镇由于路滑发生车灾,待急救人员到达时伤患全部财物被盗一直到现 在还没有线索,我正好向大家问问情况...”她话说到这儿,围观の除了云岭村村民,其他人一哄而散速度离开了村子.包括周家那些人见势不妙马上离开弃老妇于不顾,留下她瑟瑟发抖和周定康作伴.与忐忑不安の周家人相反,卓文鼎这回是真の松了口气,原来是自己人.周定康此刻是骑虎难 下,悔不该听人唆摆自讨苦吃.有人跟他说只要姓陆の走了马上有人出钱买下这栋宅子,按照市场价一分不少,太诱人了.之前那么多人给过姓陆の难堪,她都一声不吭地吞了,没想到这次态度强硬,而且后台还不少.怎么办?事情闹大了若是惊动那些大力支持本地发展の高层领导,很有可能连 累各村乡亲永无翻身之日.到时候别说他遭殃,一家老小恐怕永无宁日.正在六神无主,周定康忽然灵机一动向婶婆使了一下眼色.在老妇不解の眼神之下,他身子晃了晃,卟通地倒下了.老妇一声惊叫:“定康,你怎么了?!天哪...”哭喊声终于打破现场尴尬の静默.卓文鼎:“...”常在 欣:“...”其余围观群众:“...”看来套路不怕旧,只要有用.常在欣漠然地向旁边手指招招,记者队伍里走出一个人来,“方医生,麻烦你看看他怎么了,要不要叫救护车.”“好.”他很乐意打刁民の脸.卓文鼎惊讶地看着她,记者出访还带着医生?让人意外の是,从不显山露水の陆易忽 然也走出来,说:“我也看看.”抢先一步来到周定康身边捏住他の手腕把脉.诶?卓文鼎又吃了一惊,“你不是厨师吗?”“我手术刀耍得比菜刀好.”陆易开着玩笑说,“哪天让你们见识见识.”昨晚在他摊子吃过烤肉の师徒俩对视一眼,顿时各种滋味涌上喉咙,呕~.常在欣并不在意谁是 医生,她笑吟吟地来到那群地方小记者面前,“大家好,都是同行吧?正好,我有些问题想...”“对不起,我们新来の什么都不知道.”受雇而来の小报记者们忙后退,作为同行岂能不认识她?破坏乡镇声誉の话是宁死不说の.谁不想为了家乡好?常在欣秀眉蹙起,“那眼前这事你们总该清楚 因由吧?”“完全不清楚,我们一头雾水正等周先生给个解释.”众人义正言辞,异口同声.常在欣顿时一脸遗憾,看着小记们作堆躲一边去了.“他没什么事,只是中暑了,歇一歇就好.”陆易抢在方医生开口前说.对方不服欲驳,却看见陆易“息事宁人”の口型,只好看向卓文鼎与常在欣,征 求他俩の意见.“不妨碍卓律师工作,你们忙吧,”常在欣一挥手,“我找这位陆小姐谈谈.”说罢去敲门.而陆易马上和朱叔扶起周定康,白姨她们扶起老妇相继进入休闲居暂时歇息.那群小记者怕被常在欣の团队问出破绽,忙也屁颠屁颠跟了去.既然常在欣是友非敌,卓文鼎很放心地和小杨 也去了休闲居.对他来说,每一桩官非能够达成和解是最好の.第168部分“...爸,我知道,已经寄了.”田间,余岚戴着一顶草帽在菜地里接电筒,“是,大伯和表姐家都寄了,其他人暂时没有,因为店里の蔬菜供应不上顾不了其他亲戚,只能等下一批,下一批种得多一些.”每到收获季节,继父 梅冬生便会打电筒给她发来一张名单要新鲜の有机蔬菜.说实话,余岚不太想寄.在那些亲戚眼里,她母女仨一直是外人,哪怕母亲给梅家生了一个弟弟.继父以前对她们挺好の,听她们叫爸时还热泪盈眶,随着家境日益好转他の态度就变了.小弟告诉她们,大伯表姐他们整天说姐妹俩の坏话, 还要小弟别和她们太亲近.明明是一群喂不熟の白眼狼,母亲却说不能跟他们撕破脸皮仍要维持表象.挂了电筒,余岚继续问一名忙碌中の菜农,“丙叔,前几天说の那件事怎样了?大马村愿不愿意?”丙叔抬起一张黝黑の脸,笑呵呵道:“愿意,愿意.咱们赚了钱他们早就眼红了,哦,那些老 叔还想说服自己女儿女婿回家种,不知你肯不肯.”“肯,当然肯.”余岚乐了,“我求之不得啊!不过一定要按照我们の要求耕种,不然质量出问题我是不收の.”“那是那是.不过,小岚,大马村到底离咱们这儿太远,怕是不好管理.”老汉替她操心道,“还不如说服下棠村、南西村...”但一 想到这两个村子和余家母女斗得正激烈,顿时说不下去了.“说服他们不容易,先等等吧.”余岚笑了笑,“等以后赚钱了自然有人跟上,大马村の乡亲过得比较困难,先解决那边の问题再说.”大马村の村民姓马,那里没有优美环境或者地理优势,纯粹一个贫穷又出入不便の村子.年青人们几 乎都出去打工了,剩下一群留守老人、婆娘和孩子.别小看他们,那可全部是农耕好手.而且民风纯朴,三观正,对有文化の年轻人相当敬佩信从.说实在话,与梅林、下棠相比,她更愿意助大马村一把.可是老娘说当初没有梅林村民の帮忙,她手上の资产早被前婆家给抢走了,她们也没有今天. 做人要感恩,不能因一时の理念不合便轻言放弃.况且,如今放弃の话她们家亏损很大.由于梅爸の疏忽,让云家在企业里渗透很深,动辄伤骨削肉损失惨重.余岚在菜田里察看蔬菜瓜果の长势,途中又接了一个电筒.“...很多记者进了云岭村?谁叫来の?”她皱紧眉头,“怎么回事?我不是 叮嘱周叔去劝劝定康叔别太过分吗?”妹子回学校了,何玲也消停了,好不容易大家过着平静の日子,谁知那云岭村の前任居民不知抽什么风跑回来乱搞一通.好
初中数学 什么是三角形的中位线定理

初中数学什么是三角形的中位线定理三角形的中位线定理是指在一个三角形中,连接一个顶点和对边中点的线段被称为中位线。
中位线将三角形分割为两个等面积的小三角形,并且中位线的长度等于对边的一半。
设三角形ABC的顶点为A,对边BC的中点为D,连接AD。
根据中位线定理,有以下结论:1. 中位线AD平分对边BC,并且AD = 1/2 * BC。
2. 中位线AD将三角形ABC分割为两个等面积的小三角形,即△ABD和△ACD的面积相等。
证明中位线定理的方法有多种,下面介绍一种简单的方法:首先,连接两个中位线BD和CE。
根据中位线的定义,BD和CE分别是AC和AB的中点。
由于BD平行于AC,根据平行线性质,△ABC和△BDC是相似的。
同样地,△ABC和△CEA也是相似的。
根据相似三角形的性质,相似三角形的边长成比例。
因此,我们可以得到以下比例关系:AB/BD = AC/CDAC/CE = AB/BE由于BD和CE都是对边的中点,所以BD = CE。
将这个等式代入上述比例关系中,得到:AB/BD = AC/CD --> AB/CE = AC/CD根据等式的传递性,我们可以得到:AB/CE = AC/CD这意味着△ABE和△ACD的边长成比例,根据边比例定理,它们是相似的。
接下来,我们证明△ABD和△ACD的面积相等。
由于BD和CE是对边的中点,所以它们的长度相等,即BD = CE。
这意味着△ABD和△ACD的底边相等。
同时,根据中位线定理,AD = 1/2 * BC,所以△ABD和△ACD的高度也相等。
因此,△ABD和△ACD的底边和高度都相等,根据三角形的面积公式S = 1/2 * 底边* 高度,它们的面积相等。
综上所述,中位线定理成立:连接一个顶点和对边中点的线段是对边的一半,并且将三角形分割为两个等面积的小三角形。
初二数学上册知识点:三角形中位线定理

初二数学上册知识点:三角形中位线定理连接三角形两边中点的线段叫做三角形的中位线.(1)三角形共有三条中位线,并且它们又重新构成一个新的三角形。
(2)要会区别三角形中线与中位线。
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
三角形中位线定理的作用:位置关系:可以证明两条直线平行。
数量关系:可以证明线段的倍分关系。
常用结论:任一个三角形都有三条中位线,由此有:结论1:三条中位线组成一个三角形,其周长为原三角形周长的一半。
结论2:三条中位线将原三角形分割成四个全等的三角形.结论3:三条中位线将原三角形划分出三个面积相等的平行四边形。
结论4:三角形一条中线和与它相交的中位线互相平分。
结论:三角形中任意两条中位线的夹角与这夹角所对的三角形的顶角相等.三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线.一个三角形共有三条中位线.三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
如图已知△AB中,D,E分别是AB,A两边中点。
则DE平行于B且等于B/2三角形中位线逆定理:逆定理一:在三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是三角形的中位线。
如图DE//B,DE=B/2,则D是AB的中点,E是A的中点。
逆定理二:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
如图D是AB的中点,DE//B,则E是A的中点,DE=B/2 区分三角形的中位线和中线:三角形的中位线是连结三角形两边中点的线段;三角形的中线是连结一个顶点和它的对边中点的线段。
八年级数学中位线定理
小明家的村 头有一大水 塘,要量出池 塘两端点 A,B之间的 距离,你能想 出几种方法?
A B
C
D
E
下面的方法是不是更简单?
A
B
D
E
C
已知:点D,E分别是△ABC的边 AB,AC的中点. 1 求证:DE= BC DE∥BC
2
B
A
E到F,使EF=DE.连接FC,DC,AF. ∵AE=EC, ∴四边形ADCF是平行四边形, ∴CF∥DA,且CF=DA. ∴CF∥DB,且CF=DB ∴四边形DBCF是平行四边形. ∴DF=BC. ∴DE=
1BC. 2
DE和BC 有什么位 置关系?
定义:连接三角形两边中点的线段叫做三角形的 中位线
中位线定理:三角形的中位线平行于三角形的 第三边,且等于第三边的一半.
一个三角形有 几条中位线? 中位线和三角 形的中线一样 吗?
思考
A
H
D
已知:E,F,G,H分别 是四边形ABCD的中点, 连接EF,FG,GH,H E.求证:四边形EFGH 是平行四边形.
E
G
B
C F
思考
A
已知:在△ABC中,D, E,F分别是BC,AC, AB的中点. F 求证:∠FDE= ∠A.
B D
E
C
思考
D
C
在四边形ABCD 中,AB›CD,E,F分别是 AC,BD的中点. 1 求证:EF › AB-CD.
E F
H
2
A
B
思考
下列说法是否正确? 1.三角形三条中位线组成一个三角形,其周长为 原三角形周长的一半. 2.三角形三条中位线将原三角形分割为四个全 等的三角形. 3.三角形三条中位线三角形三条中位线可从原 三角形中划分出面积相等的三个平行四边形. 4.三角形任两条中位线的夹角与这个夹角所对 的三角形的顶角相等.
苏教版八年级下册数学[三角形中位线定理 知识点整理及重点题型梳理]
![苏教版八年级下册数学[三角形中位线定理 知识点整理及重点题型梳理]](https://img.taocdn.com/s3/m/9c586fc4aef8941ea76e059e.png)
苏教版八年级下册数学重难点突破知识点梳理及重点题型巩固练习三角形中位线定理【学习目标】1. 理解三角形的中位线的概念,掌握三角形的中位线定理.2. 掌握中点四边形的形成规律.【要点梳理】要点一、三角形的中位线1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于第三边,并且等于第三边的一半.要点诠释:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的12,每个小三角形的面积为原三角形面积的14.(3)三角形的中位线不同于三角形的中线.要点二、顺次连接特殊的平行四边形各边中点得到的四边形的形状(1)顺次连接平行四边形各边中点得到的四边形是平行四边形.(2)顺次连接矩形各边中点得到的四边形是菱形.(3)顺次连接菱形各边中点得到的四边形是矩形.(4)顺次连接正方形各边中点得到的四边形是正方形.要点诠释:新四边形由原四边形各边中点顺次连接而成.(1)若原四边形的对角线互相垂直,则新四边形是矩形.(2)若原四边形的对角线相等,则新四边形是菱形.(3)若原四边形的对角线垂直且相等,则新四边形是正方形.【典型例题】类型一、三角形的中位线1、(2016•北京)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.【思路点拨】(1)根据三角形中位线定理得MN=AD,根据直角三角形斜边中线定理得BM=AC,由此即可证明.(2)首先证明∠BMN=90°,根据BN2=BM2+MN2即可解决问题.【答案与解析】(1)证明:在△CAD中,∵M、N分别是AC、CD的中点,∴MN∥AD,MN=AD,在RT△ABC中,∵M是AC中点,∴BM=AC,∵AC=AD,∴MN=BM.(2)解:∵∠BAD=60°,AC平分∠BAD,∴∠BAC=∠DAC=30°,由(1)可知,BM=AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴BN2=BM2+MN2,由(1)可知MN=BM=AC=1,∴BN=【总结升华】本题考查三角形中位线定理、直角三角形斜边中线定理、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.举一反三:【变式】如图,矩形OABC的顶点A、C分别在x轴、y轴正半轴上,B点坐标为(3,2),OB与AC交于点P,D、E、F、G分别是线段OP、AP、BP、CP的中点,则四边形DEFG的周长为_____.【答案】5;解:∵四边形OABC是矩形,∴OA=BC,AB=OC;BA⊥OA,BC⊥OC.∵B点坐标为(3,2),∴OA=3,AB=2.∵D、E、F、G分别是线段OP、AP、BP、CP的中点,∴DE=GF=1.5; EF=DG=1.∴四边形DEFG的周长为(1.5+1)×2=5.2、如图,在△ABC中,已知点D、E、F分别是AB、BC、CA的中点,AH是高.(1)若BC=10,AH=8,则四边形ADEF的面积为.(2)求证:∠DHF=∠DEF.HF EDCBA【思路点拨】(1)由三角形面积公式可知:△BDE、△EFC的面积都等于△ABC面积的四分之一,进而可求出四边形ADEF的面积.(2)首先证明四边形ADEF是平行四边形,进而可得∠DEF=∠DAF,再利用直角三角形的中线性质得线段相等,从而得角等,最终可得到∠DAF=∠DEF,即可证出∠DHF=∠DEF.【答案解析】(1)解:∵BC=10,AH=8,∴S△ABC=×8×10=40,∵点D、E、F分别是AB、BC、CA的中点,∴△BDE、△EFC的面积都等于△ABC面积的,∴四边形ADEF的面积=40﹣20=20,故答案为:20;(2)证明:∵D 、E 、F 分别是△ABC 各边中点,∴DE ∥AC ,EF ∥AB ,∴四边形ADEF 是平行四边形,∴∠DEF=∠DAF ,∵AH 是△ABC 的高∴△ABH 、△ACH 是直角三角形,∵点D 、点F 是斜边AB 、AC 中点,∴DH=DA ,HF=AF ,∴∠DAH=∠DHA ,∠FAH=∠FHA ,∴∠DAH+∠FAH=∠FHA+∠DHA ,即∠DAF=∠DHF ,∴∠DEF=∠DHF .【总结升华】此题主要考查了平行四边形的性质与判定,三角形的中位线定理,直角三角形的性质,解决题目的关键是证明∠DHF=∠DAF 与∠DAF=∠DEF .3、如图所示,在△ABC 中,M 为BC 的中点,AD 为∠BAC 的平分线,BD ⊥AD 于D ,AB =12,AC =18,求MD 的长.【思路点拨】本题中所求线段MD 与已知线段AB 、AC 之间没有什么联系,但由M 为BC 的中点联想到中位线,另有AD 为角平分线和垂线,根据等腰三角形“三线合一”构造等腰三角形ABN ,D 为BN 的中点,DM 即为中位线,不难求出MD 的长度.【答案与解析】解:延长BD 交AC 于点N .∵ AD 为∠BAC 的角平分线,且AD ⊥BN ,∴ ∠BAD =∠NAD ,∠ADB =∠ADN =90°,在△ABD 和△AND 中,BAD NAD AD =ADADB ADN ∠∠⎧⎪⎨⎪∠∠⎩== ∴ △ABD ≌△AND(ASA)∴ AN =AB =12,BD =DN .∵ AC =18,∴ NC =AC -AN =18-12=6,∵ D 、M 分别为BN 、BC 的中点,∴ DM =12CN =162⨯=3. 【总结升华】当条件中含有中点的时候,可以将它与等腰三角形的“三线合一”、三角形的中线、中位线等联系起来,进行联想,必要时添加辅助线,构造中位线等图形.举一反三:【变式】如图所示,四边形ABCD中,Q是CD上的一定点,P是BC上的一动点,E、F分别是PA、PQ两边的中点;当点P在BC边上移动的过程中,线段EF的长度将( ).A.先变大,后变小 B.保持不变 C.先变小,后变大 D.无法确定【答案】B;解:连接AQ.∵ E、F分别是PA、PQ两边的中点,∴ EF是△PAQ的中位线,即AQ=2EF.∵ Q是CD上的一定点,则AQ的长度保持不变,∴线段EF的长度将保持不变.4、我们给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问题:(1)如图1,在△ABC中,AB=AC,点D在BC上,且CD=CA,点E、F分别为BC、AD的中点,连接EF并延长交AB于点G.求证:四边形AGEC是等邻角四边形;(2)如图2,若点D在△ABC的内部,(2)中的其他条件不变,EF与CD交于点H,图中是否存在等邻角四边形,若存在,指出是哪个四边形,不必证明;若不存在,请说明理由.【思路点拨】(1)运用中位线的性质,找出对应相等的角;(2)根据题意易知满足条件的四边形即为第一题的四边形.【答案与解析】解:(1)取AC的中点H,连接HE、HF∵点E为BC中点∴EH为△ABC的中位线∴EH∥AB,且EH=12AB同理FH∥DC,且FH=12DC∵AB=AC,DC=AC∴AB=DC,EH=FH∴∠1=∠2∵EH∥AB,FH∥DC∴∠2=∠4,∠1=∠3∴∠4=∠3∵∠AGE+∠4=180°,∠GEC+∠3=180°∴∠AGE=∠GEC∴四边形AGEC是邻角四边形(2)存在等邻角四边形,为四边形AGHC.【总结升华】本题考查了三角形的中位线以及等腰三角形的性质的综合运用.本题较灵活,要求学生能够把题中的条件转化成角,从而找出相等的角来解题.举一反三:【变式】如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是()A.4 B.3 C.2 D.1【答案】D;解:连接DE并延长交AB于H,∵CD∥AB,∴∠C=∠A,∠CDE=∠AHE,∵E是AC中点,∴AE=CE,∴△DCE≌△HAE,∴DE=HE,DC=AH,∵F是BD中点,∴EF是△DHB的中位线,∴EF=12 BH,∴BH=AB-AH=AB-DC=2,∴EF=1.类型二、中点四边形5、如图,在梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点.(1)求证:四边形EFGH 是正方形;(2)若AD =2,BC =4,求四边形EFGH 的面积.【思路点拨】(1)先由三角形的中位线定理求出四边相等,然后由AC⊥BD 入手,进行正方形的判断.(2)连接EG ,利用梯形的中位线定理求出EG 的长,然后结合(1)的结论求出2EH =92,也即得出了正方形EHGF 的面积. 【答案与解析】证明:(1)在△ABC 中,E 、F 分别是AB 、BC 的中点,故可得:EF =12AC ,同理FG =12BD ,GH =12AC ,HE =12BD , 在梯形ABCD 中,AB =DC ,故AC =BD ,∴EF=FG =GH =HE ,∴四边形EFGH 是菱形.设AC 与EH 交于点M ,在△ABD 中,E 、H 分别是AB 、AD 的中点,则EH∥BD,同理GH∥AC,又∵AC⊥BD,∴EH⊥HG,∴四边形EFGH 是正方形.(2)连接EG .在梯形ABCD 中,∵E、G 分别是AB 、DC 的中点,∴EG=12(AD +BC )=3. 在Rt△EHG 中, ∵222EH GH EG +=,EH =GH ,∴2EH =92,即四边形EFGH 的面积为92. 【总结升华】此题考查了等腰梯形的性质及三角形、梯形的中位线定理,解答本题的关键是根据三角形的中位线定理得出EH =HG =GF =FE ,这是本题的突破口.举一反三:【变式】如图,E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点.(1)判断四边形EFGH 的形状,并说明你的理由;(2)连接BD和AC,当BD、AC满足何条件时,四边形EFGH是正方形.【答案】解:(1)四边形EFGH是平行四边形.理由:连接AC,∵E、F分别是AB、BC的中点,∴EF∥AC,且EF=12 AC,同理,HG∥AC,且HG=12 AC,∴EF∥HG,且EF=HG,∴四边形EFGH是平行四边形;(2)当BD=AC,且BD⊥AC时,EFGH是正方形.理由:连接AC,BD,∵E、F、G、H分别是边AB、BC、CD、DA的中点,∴EF=GH=12AC,EH=FG=12BD,EH∥BD,GH∥AC,∵BD=AC,BD⊥AC,∴EH=EF=FG=GH,EH⊥GH,∴四边形ABCD是菱形,∠EHG=90°,∴四边形EFGH是正方形.。
6.3++三角形的中位线定理+++课件+++2023-2024学年北师大版数学八年级下册
()
A
A.4.5
B.5
C.5.5
D.6
四、课堂检测
7 如图,已知长方形ABCD中,R,P分别是DC, BC上的点,E,F分别是AP,RP的中点,当P在 BC上从B向C移动而R不动时,下列结论成立的是 ( C) A.线段EF的长逐渐增大 B.线段EF的长逐渐减小 C.线段EF的长不改变 D.线段EF的长先增大后减小
2
三角形中位线定理
三角形的中位线平行于第三边, 并且等于第三边的一半.
∵ DE是△ABC的中位线
∴ ⑴ DE∥BC 位置关系 ⑵ DE = 1BC 数量关系
2
途 用 ①证明平行问题。
②证明一条线段是另一条线段的两倍或一半。
A、B两地被池塘隔开,小明在AB外选一 点C,连结AC和BC,并分别找出AC和BC的中 点M、N,测得MN = 20m,小明就说A、B两 点的距离是40m,你能说说其中的道理吗?
C •
M 20 N
A• 40
B •
【变式练习】
1.已知:如图, E、F分别为AB、AC的中点。
(1)∵ E、F分别为AB、AC的中点。
A
∴ _E_F___∥_B_C__ ,
1
___E_F__=___2_B_C__ 或__B_C___= _2_E_F___
E
F
(2)若BC =10cm,则EF =_5___cm
1.三级跳67页1——4 68页中考链接1,2
2.思考:顺次联结四边形各边中点得 到的图形是什么图形?
H,M,得到的四边形EFGH是平行四边形吗?为
什么?
A
H
Dቤተ መጻሕፍቲ ባይዱ
E G
B
F
C
【例题详解】
人教版八年级下册三角形的中位线定理
连接三角形两边中点的线段叫做三角形的中位线.
2、三角形中位线定理:
三角形的中位线平行于第三边,并且等于它的一半.
二、思想方法方面:倍长短线,转化思想.
平行四边形的判定 (3)
----三角形的中位线定理
温故知新
两组对边分别平行的四边形是平行四边形
平
边 两组对边分别相等的四边形是平行四边形
行 四
一组对边平行且相等的四边形是平行四边形
边
形
角 两组对角分别相等的四边形是平行四边形
的
判
定
对角线 对角线 互相平分 的四边形是平行四边形
情景导入
如图,A、B两点被池塘隔开,在AB外选一点
5
F6
∴DF= 1 BC=5cm
2
同理:EF=
1
AB=6cmB源自36 CDE= 12 AC=3cm
E 10
∴三角形DEF2的周长=DF+EF+DE=14cm。 你有何
发现?
5:如图,△ABC中,D是AB上一点,且
AD=AC , AE⊥CD于E,F是CB的中点。
求证:BD=2EF
证明:
C
A D A C , A E C D C E D E ( 等 腰 三 角 形 三 线 合 一 )
F是CB的中点
EF
∴CF BF
∵CE=DE,CF=BF
EF1BD,即BD2EFA
2
B D
6、如图,△ABC中,D、E、F分别是AB、AC、BC的中点, 中线AF与DE中位线有什么特殊的关系?证明你的猜想。
AF与DE互相平分 理由如下: 证明:连接DF
∵ E,F分别是AC、BC的中点 ∴EF∥AB, EF=½ AB ∵ D是AB中点 ∴AD =½ AB; ∴ EF∥AD, EF=AD ∴四边形ADFE平行四边形
初中中位线知识点总结
初中中位线知识点总结一、中位线的概念及作用1. 中位线是一条线段,它将一个几何图形分成两个面积相等的部分。
2. 在三角形和四边形中,中位线与其它中线交点的位置可以用于解决一些几何问题。
3. 中位线可用于解决实际问题,如计算房屋地面面积、农田面积等。
二、三角形中的中位线1. 三角形中位线定义:通过三角形的一个顶点,作对边中点连线。
2. 中位线的性质:三角形中位线相等,即三角形中的三条中位线相等。
这是因为三角形的三边相等。
3. 中位线的作用:在三角形中,中位线可以用来证明三角形的面积、证明三角形的角平分线等。
三、四边形中的中位线1. 四边形中位线定义:四边形的对角线中点连线。
2. 中位线的性质:四边形中的中位线相等,即四边形的两对对角线中的中位线相等。
3. 中位线的作用:中位线可以用来证明四边形的面积、证明四边形的性质。
四、中位线的应用1. 实际问题:中位线可用于计算几何图形的面积,如计算房屋地面面积、农田面积等。
2. 定理证明:中位线可用于证明几何定理,如证明三角形的角平分线,证明四边形的面积等。
3. 建筑设计:在建筑设计中,中位线可用于布局、规划和设计。
五、中位线的计算1. 中位线长度的计算:中位线的长度等于对角线中点间的距离。
2. 中位线的数学公式:中位线的长度等于两个对角线中点的距离的一半。
3. 计算实例:根据给定的对角线长度,可以计算四边形中位线的长度。
六、中位线与中心线的区别1. 中位线是一条几何图形中的线段,它具有等长性质。
2. 中心线是几何图形的中心轴线,它与图形的对称轴或对称中心有关。
七、中位线与平行四边形1. 中位线是平行四边形的对角线的中点连线,它将平行四边形分成两个面积相等的部分。
2. 中位线的性质:平行四边形的两条对角线中的中位线相等,即平行四边形中的两条中位线相等。
八、中位线与菱形1. 中位线是菱形的对角线的中点连线,它将菱形分成两个面积相等的部分。
2. 中位线的性质:菱形的两条对角线中的中位线相等,即菱形中的两条中位线相等。
八年级数学中位线定理
求证:EF › AB-CD.
2
A
C
H F
B
思考
下列说法是否正确? 1.三角形三条中位线组成一个三角形,其周长为
原三角形周长的一半. 2.三角形三条中位线将原三角形分割为四个全
等的三角形. 3.三角形三条中位线三角形三条中位线可从原
三角形中划分出面积相等的三个平行四边形. 4.三角形任两条中位线的夹角与这个夹角所对
吗?
思考
H
D
A
已知:E,F,G,H分别
G
是四边形ABCD的中点,
E
连接EF,FG,GH,H
E.求证:四边形EFGH
是平行四边形.
B
F
C
思考
已知:在△ABC中,D, E,F分别是BC,AC, AB的中点.
F
求证:∠FDE= ∠A.
A E
B
C
D
思考
D
在四边形ABCD
中,AB›CD,E,F分别是
E
AC,BD的1 中点.
8.4中位线定理
小明家的村
头有一大水
Aபைடு நூலகம்
塘,要量出池
塘两端点
A,B之间的
距离,你能想
出几种方法? D
B C
E
下面的方法是不是更简单?
A
B
D
E
C
A
已知:点D,E分别是△ABC的边
AB,AC的中点.
D
求证:DE=1 BC DE∥BC
2
E
F
B
C
证明:延长DE到F,使EF=DE.连接FC,DC,AF.
∵AE=EC, ∴四边形ADCF是平行四边形,
; / 安徽资质升级流程 安徽资质转让公司 ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.4中位线定理
教学目标:
1、理解并掌握三角形中位线的概念、性质,会利用三角形中位线的性质解决有关问题。
2、经历探索三角形中位线性质的过程,让学生实现动手实践、自主探索、合作交流的学习过程, 体会转化的思想方法。
3、通过对问题的探索研究,培养学生分析问题和解决问题的能力以及思维的灵活性。
教学重点:探索并运用三角形中位线的性质。
教学难点:运用转化思想解决有关问题。
教学过程
一、创设情境,引入新课
如图A B,、两点被池塘隔开现,在要测量出A B、两点间的距离但,又无法直
接去测量怎,么办?这时在,A、B外选一点C,连结AC和BC,并分别找出AC和BC
的中点D、E,如果能测量出DE的长度,也就能知道AB的距离了。
这是
什么道理呢?今天这堂课我们就要来探究其中的学问。
二、探究活动(一)
学生看书:了解三角形中位线的概念:连结三角形两边中点的线段叫三角形的中位线。
学生思考:(1)一个三角形有几条中位线?你能画出来么?请学生画出三角形的中位线。
学生活动:动手画图,与同伴交流,得出三角形的中位线有三条。
(2)请学生画出三角形的中线,并说出三角形的中线与中位线的不同教师:
(3)正确理解中位线的含义:三角形的中位线定义的两层含义:①∵D、E分别为AB、AC的中
点∴DE为△ABC的中位线②∵ DE为△ABC的中位线∴ D、E分别为AB、AC的中点
三、探索中位线的性质
1、提出猜想:如右图,已知,在△ABC中,A
DE是△ABC的中位线,ΔABC的中位线DE与BC有怎样的位置和
数量关系? D E 三角形的中位线平行于第三边,并等于它的一半。
B C
A
D
E
2、如何验证你的猜想?学生活动:动手证明,并与同伴交流。
老师用几何画板演验证学生猜想,并通过三角形全等证明
请同学们总结一下三角形中位线的性质
A
三角形的中位线平行于第三边, 并等于第三边的一 半。
D
E
如图,∵DE是△ABC的中位线
1
∴DE∥BC, DE= BC
2
B C
定理证明过程:
已知:DE 是△ABC的中位线
1
求证:DE∥BC, DE= BC
2
证明:如图,延长DE 至点F,使EF=DE,连接CF
∵ AE=CE,∠AED=∠CEF
∴△ADE≌△CFE(SAS).
∴AD=CF,∠ADE=∠F. F
∴BD∥CF.
∵AD=BD,
B
C
∴BD=CF.
∴四边形BCFD 是平行四边形.
(一组对边平等且相等的四边形是平行四边形)
D
H
A
E G
∴DF∥BC,DF=BC.
1
∴DE∥BC, DE= BC
2
穿插练习:1、如图:在△ABC中,DE 是中位线
(1)
若∠ADE=60°, 则∠B=
,为什么?
D
E
(2) 若BC=8cm , 则DE=
为什么?
2、如图:D 、E 、F 是△ABC各边的中点,那么四边形ADEF 是 四边形。
B
A
C
3、学习了中位线定理,本节课开始时老师提出的问题你能否解 E
F
决了呢?
如图,A 、B 两点被池塘隔开,现在要测量出A 、B 两点间的距离 ,但又
B
D
C
无法直接去测量怎,么办?这时,在A 、B 外选一点C ,连结A C 和BC ,并分别找
出AC 和BC 的中点D 、E ,如果能测量出DE 的长度,也就能知道AB 的距离了。
这是什么道理呢?
四、应用示例:
1、利用三角形中位线定理,说明课本P91的分割三角形题目
2、在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,四边形EFGH 是平行四边形吗? 为什么?
B
C
拓展:依次连接菱形或矩形各边的中点,能得到一个什么图形?先猜一猜,再证明你的结论。
(注意引导学生把四边形转化为三角形来考虑)
五、巩固练习
1.课本 练习1,2 习题8.4 3
六、课堂小结
1.三角形中位线是三角形中一种重要的线段,它与三角形中线不同。
2.三角形的中位线定理是三角形的一个重要性质定理。
注意定理的条件、结论,结论有两个,具体应用时,可视具体情况,选用其中一个关系或用两个关系。
熟悉三角形中位线所在的图形的结构,适当地构造三角形中位线定理的条件是用好定理的关键。
3.在这节课中我们一起经过实验、探索,发现了三角形中位线定理,其中学会了一种很重要的探究问题的方法。
4.本节课开始提出的测量问题,通过大家今后不断地学习新知识,将会有更多的解决办法
七、作业:课本习题8.4 1、2
“”
“”
At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
