焦耳-汤姆孙实验真实气体内能
焦耳汤姆孙效应原理

焦耳汤姆孙效应原理
"焦耳汤姆孙效应"(Joule Thomson effect)是指当气体或液体在一个封闭的系统中通过绝热节流装置(如阀门或孔隙)时,由于节流装置的局部压力降低,使得流体的温度下降的现象。
这个效应是以英国物理学家詹姆斯·焦耳(James Prescott Joule)和威廉·汤姆孙(William Thomson,也被称为开尔文勋爵)的名字命名的,因为他们对这一现象做
出了重要贡献。
焦耳汤姆孙效应的原理可以用以下几个步骤来解释:
1. 流体在节流装置前后的压力发生变化,根据伯努利原理,流速增加的同时,压力降低。
2. 由于节流装置处压力降低,流体分子的平均动能增加,导致温度升高。
然而,由于节
流过程是绝热的,即没有热量交换,流体的内能不变。
3. 根据热力学第一定律,系统内能的变化等于外界对系统做的功加上系统吸收的热量。
在绝热节流过程中,系统内能不变,因此外界对系统做的功必须转化为系统的冷量,即流体的温度下降。
4. 这个冷量表现为节流后流体的温度低于节流前的温度。
这个现象在制冷技术中非常有用,是制冷循环中的一个重要过程。
焦耳汤姆孙效应在工程应用中非常广泛,尤其是在制冷和空调技术中,它被用来解释制冷剂在压缩机和节流装置(如膨胀阀)中的温度变化。
此外,这个效应也是喷气发动机工作原理的一部分。
第五章 热力学第一定律

注意是绝热过程有Q=0
由热力学第一定律可得出
U2 U1 p1V1 p2V2
或者 U1 p1V1 U2 p2V2
即 H1 H2
所以气体经绝热节流过程后焓不变。
3.节流膨胀后气体温度的变化
节流膨胀后压强降低,温度改变。 为定量描述这种变化,定义焦汤系数α:
lim
p0
T p
H
T p
dA pdV
在一个有限小的准静态过程中,系统的 体积由V1变为V2,外界对系统所做的总功 为
A V2 pdV V1
上式适用于任意形状容器(p.132习题 11的结论)。
三.P-V图上体积膨胀功的表示
画斜线的小长方形面积=负的元功 曲线p1 p2下的总面积=-A
体积膨胀功不是系统状态的特征 而是过程的特征
奠基人:迈耶、焦耳、赫姆霍兹。 焦耳是通过大量的定量实验去精确测定热功 当量,从而证明能量守恒定律。 迈耶从哲学思辩方面阐述能量守恒概念。 赫姆霍兹认证了在各种运动中的能量是守 恒的,第一次以数学的方式提出了定律。
还有他们的贡献:
18世纪初纽可门发明了蒸汽机。后由瓦特做 了重大改进。
1800年伏打化学电池的发明。
深度分析:
1、内能是一种宏观热力学的观点,不考虑微观 的本质。
2、内能是一个相对量。 3、热学中的内能不包括物体整体运动的机械能。
4、内能概念可以推广到非平衡态系统。 5、有些书上提到的热能实质上是指物体的内能。
20
三、热力学第一定律的表达式
考虑系统与外界间的作用有做功与传 热两种方式
设经某一过程系统由平衡态1→平衡态2 此过程中外界对系统做功为A,系统从外界吸收 热量为Q,由此引起的内能增量为
早期最著名的一个永动机设计方案,是十三世纪的法国 人亨内考(Villard de Honnecourt)设计的。如下图(左)所示。
气体的节流过程和绝热膨胀过程[1]
![气体的节流过程和绝热膨胀过程[1]](https://img.taocdn.com/s3/m/d41e8913d1f34693dbef3eac.png)
绵阳师范学院本科生毕业论文(设计)题目气体的绝热膨胀和节流过程探讨专业物理学院部物理与电子工程学院学号 04姓名李飞指导教师廖碧涛讲师答辩时间 2011年5月论文工作时间: 2010 年 11 月至 2011 年 05 月气体的绝热膨胀过程和节流过程探讨学生: 李飞指导教师: 廖碧涛摘要:目前低温技术越来越受到人们的关注,低温制冷技术已经广泛应用于气象,军事,航空航天,低温电子技术,低温医学领域等。
气体的绝热膨胀和节流过程是获得低温的两种途径。
在绝热的条件下高压气体经过多孔塞或节流阀流到低压一边的稳定流动过程称为节流过程。
测量气体在多孔塞或节流阀两边的温度表明,在节流过程前后,气体的温度发生了变化,这效应称为焦耳-汤姆逊效应,简称焦-汤效应。
这是焦耳和汤姆逊在1852年用多孔塞实验研究气体内能时发现的。
绝热膨胀是指与外界没有热量交换,但气体对外界做功,气体膨胀。
根据热力学第一定律,可证明这是等熵过程,在这个过程中气体体积增大,压强降低,因而温度降低。
所以绝热膨胀经常用于降低气体的温度,起到冷冻的效应。
本篇文章主要是对理想气体和范德瓦耳斯气体在节流过程和绝热膨胀两种过程中热力学特征以及各状态函数变化的研究,得出各状态参量的变化情况。
加深对节流过程和绝热膨胀过程的理解和认识。
节流过程和绝热膨胀过程制冷都有着各自的优点和缺点,将节流过程和绝热膨胀过程结合使用可以充分弥补各自的缺点,发挥优点,达到极好的制冷效果,获得低至1K的低温。
目前节流过程和绝热膨胀过程被广泛运用与化工生产中。
关键词低温;绝热膨胀;节流过程;焦耳一汤姆孙效应The Insulation the Expansion Process and inThe Throttling process toUndergraduate: Li feiSupervisor: Liao BitaoAbstract:At present technology has been getting refrigeration technology is widely applied to meteorological, military, the cooler the air space and technology, medicine, etc. low temperatures.Of hot gas expands and throttling process is a low temperature two ways.In the insulation of high pressure gas after the plug or throttling the valve to the stability of the low side of the current process is called the throttling process. the gas or throttling the valve in the plug on the temperature that, in the throttling process, the temperature of the gas has changed, the effect is called joule - thompson, short dark - soup joule and effect. thompson is in the membrane in the plug experimental research on the gas can find. insulation expansion is from outside world and no calories But gas to do work, expansion of gases. according to law of thermodynamics to the first, but that this is the process of entropy, volume of gas, lower pressure and temperature is lower. therefore, the insulation is often used for lowering the temperature of the gas, to freeze effect. this article is in an ideal gas and vande gas in the throttling process and the insulation the expansion process thermodynamics characteristics and the condition function That the state the throttling process and the insulation. the expansion process of refrigeration have their respective advantages and disadvantages, will the throttling process and the insulation the expansion process can be used for their faults and virtues, a chilling effect, the low temperatures. in addition, 1k in temperatures constant concern and to explore technology, The throttling process and the insulation the expansion process was widely used and chemical production.Key words:Temperatures;Insulation expansion;The throttling process Joule and tom effect.目录引言 (1)1节流过程和绝热膨胀过程 (1)节流过程 (1)节流过程的定义及特征 (1)焦耳-汤姆逊效应 (2)绝热膨胀过程 (4)绝热膨胀的定义 (4)绝热膨胀的特征 (5)2理想气体的绝热膨胀和节流过程 (6)理想气体的绝热膨胀过程 (6)理想气体的节流过程 (8)3范德瓦尔斯气体的绝热膨胀和节流过程 (8)范德瓦耳斯气体的绝热膨胀 (8)范德瓦耳斯气体的节流过程 (9)4绝热膨胀与节流过程的比较和应用 (11)绝热膨胀与节流过程的比较 (11)两种过程获得低温的优缺点 (11)绝热膨胀和节流过程的应用 (12)结束语......................................................................12参考文献 (13)致谢 (14)引言低温制冷技术在已经在各领域的到广泛应用;有研究表明,寿命与环境温度的关系非常密切,如青蛙生活在2℃的水中的寿命,比它在21℃的水中高出960倍。
焦耳汤姆生实验及节流膨胀的热力学特征
H H dH = dT + p d p = 0 T p T (H/p )T T = J -T = (H/T ) p p H
H = C p; T p
JT =
(U / p )T
x y z H = U + pV y z x = 1 y x z + { ( pV ) / p }T Cp 2
焦耳—汤姆生系数及其正负号的热力学分析
J -T
T = p ( U / p ) T { ( pV ) / p }T = Cp Cp H
节流过程体积增大, 克服分子间引力需吸收能量, 而使热 力学势能增加, 即 (U/p)T < 0. 若 {(pV)/p}T < 0, 则 2.5 J-T > 0 , 产生致冷效应;
2.0 1.5 1.0 0.5 0.0 0
p/10 kPa 相同温度下不同气体的 Z - p等温线
若 {(pV)/p}T > 0 , 则当 H2 |(U/p)T | >| {(pV)/p}T | 时, 理想气体 J-T 为正值; 当 |(U/p)T | < CH4 |{(pV)/p}T | 时为负值. 究竟 NH3 是正是负要看气体的性质及 200 400 600 800 1000 所处温度, 压力而定. 2 理想气体 J-T = 0 .
焦耳—汤姆生实验及节流膨胀的热力学特征
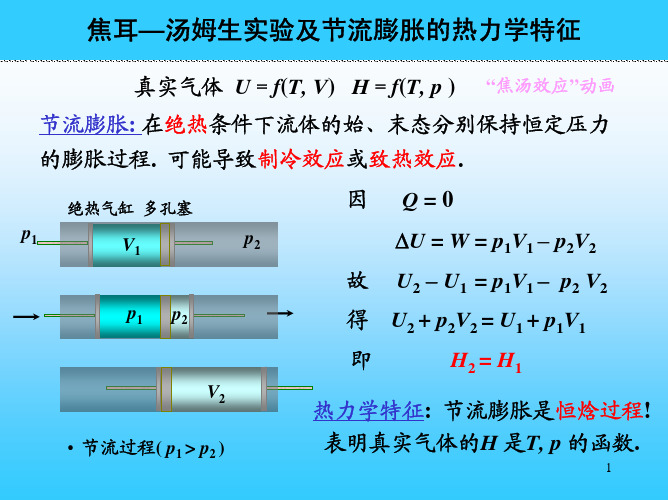
真实气体 U=f(T, V) H=f(T, p ) 的膨胀过程. 可能导致制冷效应或致热效应.
绝热气缸 多孔塞
“焦汤效应”动画
节流膨胀: 在绝热条件下流体的始、末态分别保持恒定压力 因
p2
Q=0 U = W = p1V1 p2V2 U2 U1 = p1V1 p2 V2 U2 + p2V2 = U1 + p1V1 H2 = H1
joule thomson实验原理

joule thomson实验原理Joule-Thomson实验原理是一种用来研究气体在膨胀过程中温度变化的实验方法。
它是由英国物理学家詹姆斯·普雷斯科特·焦耳和苏格兰物理学家威廉·汤姆逊共同发现并提出的。
在Joule-Thomson实验中,首先需要将高压气体通过细小的孔或阀门进行膨胀,使得气体从高压区域流向低压区域。
在这个过程中,气体的温度会发生变化,有的气体在膨胀过程中温度会升高,有的气体则会降低。
这种现象被称为Joule-Thomson效应。
Joule-Thomson效应的原理是基于气体的内能和势能之间的转化。
当气体膨胀时,气体的内能会减少,导致气体的温度下降。
而在Joule-Thomson实验中,如果气体在膨胀过程中温度升高,那么气体的内能就会增加,从而导致温度的上升。
Joule-Thomson实验可以通过实验装置来实现。
实验装置一般包括高压气体的容器、细小的孔或阀门、压力计和温度计等仪器。
通过调节气体的压力和温度,可以观察到气体在膨胀过程中的温度变化,从而验证Joule-Thomson效应。
Joule-Thomson实验在实际应用中具有重要的意义。
例如,工业上的制冷过程就是利用Joule-Thomson效应来实现的。
此外,Joule-Thomson实验还有助于研究气体的物理性质和热力学过程,对于深入理解气体的行为和特性具有重要的意义。
总的来说,Joule-Thomson实验原理是研究气体在膨胀过程中温度变化的重要方法,通过实验验证Joule-Thomson效应,可以深入理解气体的特性和热力学过程,对于工业和科研领域具有重要的应用价值。
焦耳—汤姆逊阀制冷原理

焦耳—汤姆逊阀制冷原理节流膨胀(Throttling Expansion)也叫焦耳—汤姆逊膨胀,即较高压力下的流体(气或液)经多孔塞(或节流阀)向较低压力方向绝热膨胀过程。
1852年,焦耳和汤姆逊设计了一个节流膨胀实验,使温度为T1的气体在一个绝热的圆筒中由给定的高压p1经过多孔塞(如棉花、软木塞等)缓慢地向低压p2膨胀。
多孔塞两边的压差维持恒定。
膨胀达稳态后,测量膨胀后气体的温度T2。
他们发现,在通常的温度T1下,许多气体(氢和氦除外)经节流膨胀后都变冷(T2<T1)。
如果使气体反复进行节流膨胀,温度不断降低,最后可使气体液化。
调节阀在管道中起可变阻力的作用。
它改变工艺流体的紊流度或者在层流情况下提供一个压力降,压力降是由改变阀门阻力或“摩擦”所引起的。
这一压力降低过程通常称为“节流”。
对于气体,它接近于等温绝热状态,偏差取决于气体的非理想程度(焦耳一汤姆逊效应)。
在液体的情况下,压力则为紊流或粘滞摩擦所消耗,这两种情况都把压力转化为热能,导致温度略为升高。
根据热力学原理,在焦耳-汤姆逊实验中系统对环境做功-W=p2V2-p1V1,V1及V2分别为始态和终态的体积。
Q=0,故ΔU=-(p2V2-plV1);U2+p2V2=U1+p1V1;即H2=H1。
所以焦耳-汤姆孙实验的热力学实质是焓不改变,或者说它是一个等焓过程。
由于理想气体的焓值只是温度的函数,即焓值不变温度不变,故理想气体节流前后温度不变。
对于实际气体,其比焓是温度和压力的函数,即比焓受温度和压力的共同影响,又节流过程焓值不变,则压力降低,温度就会变化。
焦耳-汤姆逊(开尔文)系数可以理解为在等焓变化的节流膨胀中(或是焦耳-汤姆逊作用下)温度随压力变化的速率。
μJT的国际单位是K/Pa,通常用°C/bar。
当μJ.T是正数是,则气体降温,反之则升温。
大气压下焦耳汤姆逊效应中氦气和氢气通常为升温性质的气体,而大多数气体则是降温,对于理想气体焦耳汤姆逊系数为零,在焦耳汤姆逊效应中既不升温也不降温。
§5 热容量与焓
二、理想气体宏观特性
到现在为止,可把理想气体宏观特性总结为: 到现在为止,可把理想气体宏观特性总结为: 关系; 满足道耳顿分压定律; 1 、满足 pV = ν RT 关系;2、 满足道耳顿分压定律; 满足阿伏伽德罗定律; 满足焦耳定律。 3、 满足阿伏伽德罗定律;4、 满足焦耳定律。 注意:对于一般的气体(即非理想气体) 注意:对于一般的气体(即非理想气体),内能还是V 的 函数,所以气体向真空自由膨胀时温度是要变化的。 函数,所以气体向真空自由膨胀时温度是要变化的。
利用右图讨论节流的热力学过程: 利用右图讨论节流的热力学过程: 两端开口绝热气缸中心有多孔塞, 两端开口绝热气缸中心有多孔塞, 两侧维持 维持不同压强 使两侧维持不同压强 p1 >p2 以活塞左边气体为研究对象 ,当 气体全部穿过多孔塞以后, 气体全部穿过多孔塞以后,它的 状态参量从V1 变为V2 ,p1变为 p2 ,T1变为T2 。 设气体都在左边时的内能为U1 ,气体都在右边时的内能 气体穿过多孔塞过程中,左边活塞对它作功, 为U2 。 气体穿过多孔塞过程中,左边活塞对它作功, 气体推动右边活塞作功: 气体推动右边活塞作功:
∆U = Q + W
U 2 − U 1 = p1V1 − p 2V 2
H1 = H 2
可见,节流膨胀过程前后的焓不变,是一个等焓过程。 可见,节流膨胀过程前后的焓不变,是一个等焓过程。 膨胀过程前后的焓不变 实验表明, 所有的理想气体, 实验表明,对所有的理想气体,在节流过程前后 的温度都不变。可知理想气体的内能仅是温度的函数。 的温度都不变。可知理想气体的内能仅是温度的函数。
二、定压热容与焓 定压热容与焓 对于定压过程,dU = dQ – p dV 可改写为 (ΔQ)p = Δ( U + pV )
【高中物理】优质课件:焦耳汤姆孙实验
解:
0
1 T2 T1
1 300 1000
70%
(1)
1
1 300 1100
73.3%
(2)
2
1 200 1000
80%
1 0 4.7% 0
2 0 14.3% 0
若采取(2)方案将低温热源温度降低到环境温度
以下,又必需使用致冷机。因此,实用上,从节能方
面综合考察,以方案(1)为好。
例 : 1mol 理想气体在 400K 与 300K 之间完成一 卡诺循环,在等温线上,起始体积为 1L ,最后体 积为5L,试计算在此循环中所作的功,以及高温热 源吸收的热量和传给低温热源的热量。
高中物理
焦耳 汤姆孙实验
焦耳-汤姆孙 ( Thomson )实验
A
绝 热 套
T 1
T2 B
多孔塞
例 :1mol 氧气作如图所示的循环。 求:循环效率
解:Q
ab
=
M M
mol
C
P
(T
b
T)
a
P
Q
bc
=
M M
C (T
Vc
mol
T
)
P 0
b
Q
ca
=
M M
R
mol
T ln
c
V 2V0
0
0
Q a ab
等 温
例:一台家用冰箱,放在室温为27C的房 间里,做一 盘零下13度的冰块需从冰室取走 2.09105 J 的热量,设冰箱为理想卡诺制冷 机,问:(1)做一盘冰块需作多少功?(2) 若此冰箱以2.09 102 的速率取出热量,要求 的电功率多少kw ?(3)作冰块需多少时间?
利用焦耳-汤姆逊系数估算实际气体焦耳膨胀的温度变化
利用焦耳 -汤姆逊系数估算实际气体焦耳膨胀的温度变化摘要为了进一步研究和观测真实气体的焦耳膨胀过程(即自由膨胀),并研究绝热节流膨胀同焦耳膨胀之间的联系,得到较为准确的真实气体焦耳系数,本文在焦耳实验的基础上,利用精度为0.01K的温度传感器和精度为0.2kPa的数显压力表,设计了一套简单的实验仪器并用其观测了真空(粗真空)中,氦气在不同温度压强条件下的绝热自由膨胀前后的压强和温度变化情况,实验结果表明在较小的温度压强范围内,节流膨胀系数和焦耳系数存在某种特定的关系,可以利用焦-汤系数在压强变化范围较小的情况下对实际气体焦耳膨胀前后的温度变化进行精确计算.关键词焦耳膨胀;焦耳汤姆逊系数;氦气引言焦耳-汤姆逊膨胀(以下简称焦-汤膨胀以及焦-汤系数)与焦耳膨胀是两种完全不同的热力学过程,二者都是热力学中研究气体变化的经典案例,其中焦耳膨胀实验是焦耳于1845年所做,是热力学史上最为著名的实验之一,其过程可以简化为图1所示:一个绝热密闭容器分为左右两个部分,中间用一个阀门封闭,将该容器的右侧抽成真空,左侧充有一定量的理想气体。
当阀门开启,容器左侧的气体向右侧膨胀。
(a)(b)图1 焦耳膨胀(a)打开阀门前;(b)打开阀门后焦耳-汤姆逊膨胀(以下简称焦汤膨胀)实验是焦耳与汤姆逊为了进一步研究气体内能,于1852年所做,其过程可表示为下图:在一个定常流过程中,绝热活塞强迫具有高压的气体由高压区(左侧)通过一个多孔塞流至低压区(右侧),随着气体穿越到低压区一侧,其体积发生膨胀(a)(b)图2 焦汤膨胀(a)推动活塞前;(b)推动活塞后这两个实验分别是研究体积、压强变化对气体内能变化的影响,因此,关于气体的体积和温度存在一个系数:用来描述气体体积变化对温度变化的影响;同理对于气体的压强和温度亦存在一个系数:用来描述气体压强变化对温度变化的影响,这两个系数分别被称为焦耳系数和焦-汤系数.后文提到的定压、定容比热容(、)是指压强(体积)不变的情况下,单位质量的某种物质温度升高1K所需吸收的热量,标况下温度指0摄氏度下的热力学温度(=273.15K),摩尔体积()是指一摩尔气体在空间中所占的体积以及气体常数(R=8.314J/(mol·K))等与气体有关的基本热力学常量,在文中讨论时均视为常数,相关的热力学计算过程例如摄氏温标转换为开氏温标为简化论述在此不再赘述[1][2] .1 焦耳、焦汤系数与第二位力系数之间的关系1.1第二位力系数分别于焦耳、焦汤系数之间的关系在研究实气体时,可取理想气体状态方程并用1/Vm (Vm是摩尔体积),P的幂级数进行修正,展开为以下两种形势:这样的气体状态方程被称为昂尼斯(Onne's)方程,期中A',B',C',D'均为系数,B'依序被称为第二位力系数(Second virial coefficient),研究表明B'与温度和分子种类相关:其中T表示气体温度,u(r)表示气体分子势能,其与分子间距离r关系如图3[3][4]图3 两个分子之间势能与分子距离之间的函数关因此根据焦耳、焦-汤系数的定义式,利用热力学基本定律展开并代入昂尼斯方程[5],有:此处的μ,J为略去了除包含第二位力系数的其它高阶项形式,其中CV ,CP表示定容、定压比热容.当针对同态同种气体时,有B=RTB’.1.2焦耳、焦汤系数二者之间的关系考虑标况下(273.15K)1mol某真实气体由初始状态P1,V1经过一个非常轻微的膨胀过程来到P2,V2,其温度,压强,体积变化分别为 , ,,设此时的气体体积为,温度为,定压与定容比热容分别为代入(3)(4)两式,有:(5)(6)对于(8)式,通过文献[6]中的相关数据知,大小可以忽略不计,因此有:(7)假设较小,以至于温度变化前后没有明显变化.由于可以近似为:则对于(5)(7)两式有:(8)(9)而又可以写为:(10)(11)将(12)(13)代入(10)(11)中并联立两式,有:(12)通常情况下,若很小,和的变化也不会太大,因此为了方便后续计算,可将和近似计算为和 ,经过整理我们有其中代表焦耳系数,代表焦汤系数,和分别代表气体的定容比热容和定压比热容,表示气体的气压变化,表示气体的体积变化:这样就能够在不知道真实气体焦耳系数但知道气体焦汤系数的情况下,计算气体经过焦耳膨胀的温度变化,例如1mol氦气在标况下发 k生焦耳膨胀,压强由101Kpa减小为50Kpa时,其温度变化为:(为方便查询和确保计算准确,使用了美国国家标准与技术研究院NIST数据库里的数据[7]:μ=-0.62563K/MPa;CV =12.472J/mol*K; CP=20.786J/mol*K;表示标况下的气体体积,取22.41L;表示标况下温度,取273.15K;R为气体常数,取8.314Jˑmol-1ˑK-1)2 实验部分2.1实验原理图4 实验装置原理图实验装置原理如图4所示,该设备通过PU管连接两个相互独立的玻璃容器A和F,并通过容器A上的泄压阀实现A与F之间的隔离,根据需要将容器A左侧的主泄压阀(接I)接氦气罐接口或旋叶式真空泵,通过SMC负压表(图三中D)监测A、F中的压力,通过I接入真空泵抽气或接入氦气罐充入氦气来控制F中气体的初压,先通过恒温水浴锅将F中的加热到实验前所需的温度,当F中的温度和压强时达到实验所需的初温初压时,即可关闭A与F之间的次级泄压阀,此时D上显示的是F中的压强,在关闭A、F之间的次泄压阀后,将主泄压阀转接至真空泵,并将A中气体抽空,直至A所带的真空表指针指向0时,利用主泄压阀(I)迅速切断A与外界环境的联系,保持A中近乎真空的环境。
焦耳实验及其推论
H = f (T , p),
∆U =
∫T
T2
1
nCV ,m dT
∆H =
∫T
T2
1
nC p,m dT
不受恒容 或恒压限制
∆H = ∆U + nR ∆T ∆U= 0 ; ∆H = 0
C p ,m = CV ,m + R
( 理想气体恒温过程 )
注意: 非恒容时∆U ≠ Q , 非恒压时 ∆H ≠ Q. 如: 压缩绝热气缸内的理想气体, Q = 0; 而 ∆T > 0, ∆U > 0, ∆H > 0.
理想气体无分子间力不存在分子间相互作用的势而分子的平动能转动能和振动能又仅是温度的函因此分子间距离亦即气体体积的大小对理想气体的热力学能无影响
焦耳实验及其推论
实验结果: 解释: 理想气体无分子间力, 气体膨胀前后, 水浴温度未变. 解释: 理想气体无分子间力, 结果分析: Q=0 ; 不存在分子间相互作用的势 水温T 不变, 不存在分子间相互作用的势 空气自由膨胀, W=0 ; 能, 而分子的平动能、转动 能, 而分子的平动能、转动 可知 ∆U = 0 . 能和振动能又仅是温度的函 能和振动能又仅是温度的函 ⎛ ∂U ⎞ ⎛ ∂U ⎞ 数, 因此分子间距离亦即气 = ⎜ 因 dU ( n 一定 ) ⎟ dT + ⎜ ⎟ dV 数, 因此分子间距离亦即气
2
⎝ ∂ T ⎠V 体体积的大小对理想气体的 U ⎞ 体体积的大小对理想气体的 ⎛∂ 得 ⎜ ⎟ = 0, 热力学能无影响. ⎝ ∂V ⎠ T 热力学能无影响. ⎝ ∂V ⎠ T ⎛ ∂U ⎞ ⎜ 及 ⎜ ∂p ⎟ = 0 ⎟ ⎝ ⎠T
推论一: 一定量理想气体的热力学能 只是温度的函数. U = f(T) (理想气体) 推论二: 一定量理想气体的焓也仅是温度的函数. H = U + pV = f (T) ( 理想气体 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*焦耳-汤姆孙实验、真实气体的内能●焦耳实验●焦耳定律•焦耳-汤姆孙实验•真实气体的内能§3 循环过程卡诺循环3.1循环过程3.2理想气体的卡诺循环及效率作业:8-6,7 , 8气体真空A BC1845年焦耳用自由膨胀实验研究了气体的内能。
实验结果表明:水温不变!焦耳-汤姆孙实验真实气体的内能右图为其实验装置的示意图。
容器A 充满气体,容器B 为真空。
AB 相连处用一活门C 隔开,将它们全部浸在水中。
将活门打开后,气体将自由膨胀并充满A 和B 。
焦耳测量了自由膨胀前后水温的变化。
焦耳实验说明:(诚然,在膨胀过程中,后进到容器B 的气体将对先进入B 的气体作功,但此功是气体系统内部各部分之间进行的,不是外界对气体系统所作的功。
)把热力学第一定律应用于此过程:Q=0 A=0因为所以D U=0 即U(T,V)=恒量即气体绝热自由膨胀过程是一个等内能过程。
*膨胀前后气体的温度没有改变。
*水和气体没有发生热交换。
Q=0,即气体的自由膨胀是绝热过程。
气体向真空自由膨胀过程中不受外界阻力,所以外界不对气体作功,即气体对外界不作功A=0。
体积改变,内能不变体积改变,温度不变焦耳实验结果气体的内能只是温度的函数,与体积无关。
}U=U(T,V)dU=( )V dT+( )T dV dT=0 (焦耳实验结果)dU=( )T dVdU=0 (自由膨胀前后内能不变)且dV 0( )T =0TU ∂∂V U ∂∂VU∂∂VU∂∂≠Q Q \\数学表达式:焦耳实验的结果是否正确?事实上,焦耳的实验并不精确,原因是水的热容比气体要大上千倍,气体膨胀前后即使会有微小的温度变化,也不足以引起水的温度发生可观察的变化,焦耳无法检测到水温变化。
后来,在1852年焦耳和汤姆逊做了节流过程实验,才较好的测得气体的内能。
焦耳的结果只适用于理想气体。
只有在实际气体密度趋于零的极限情形下,气体的内能才只是温度的函数而与体积无关。
焦耳定律U=U(T)或()T =oV U/∂∂理想气体没有节流效应。
•焦耳-汤姆孙(Joule-Thomson) 实验焦耳-汤姆孙过程(绝热节流过程),x 1x 2T 1T 2F 1F 2p 1p 2A A'B'B 多孔塞焦耳-汤姆孙效应反转温度多孔塞使气体维持恒定的压差且形成稳定的流动。
结论是:气体经过绝热节流过程后一般会有温差,但焓不变。
PVU H def+≡焓致冷区致温区t o C200-2000200400atmN 2的温度转换曲线)(lim 0≠D D =→D H P PTαα>0致冷效应•真实气体的内能真实气体内能中应含有来自分子间相互作用的势能.α≠0说明内能不仅与温度有关,而且也与体积有关。
真实气体的焦耳汤姆孙效应说明分子间存在有相互作用力,相互作用势能与分子间距离有关。
体积变化时反映分子间势能的贡献部分也就变化。
对于理想气体,分子间无相互作用能α=0。
探索真实气体内能有无分子间势能的问题,结果导致了一个实际应用—节流致冷效应可以使气体降温、液化,这是目前低温工程中重要手段之一。
例如高压CO 2(30 atm) 从钢瓶的阀口喷向阀上的布袋中,因节流膨胀温度从室温降到-78o C 形成干冰。
U(T,V)例题 3 求大气垂直温差大气垂直方向的对流进行的比较缓慢,可近似看作准静态过程。
另外,干燥的空气导热能力很差,因此该准静态对流过程可当作是绝热过程来处理。
作用在单位面积上的上下压强差:PdPP +dzgρSD gdzdP ρ-=AN n /μρ=Q kTP n /=Q μ是平均摩尔质量P RTg g dz dP μρ-=-=\常量=--γγTP 1Q TP dT dP 1-=\γγdzdT T P dz dT dT dP dz dP 1-==\γγkm gK g dT /101-≈--=\μγ大气每上升一公里常量=--γγTP1Q dTTPdP T P112)1(-----=-\γγγγγγγγγγγγ------=\TP T P dT dP 2111TP dT dP 1-=\γγ历史上,热力学理论最初是在研究热机工作过程的基础上发展起来的。
在热机中被用来吸收热量并对外作功的物质叫工质。
工质往往经历着循环过程,即经历一系列变化又回到初始状态。
若循环的每一阶段都是准静态过程,则此循环可用P-V 图上的一条闭合曲线表示。
箭头表示过程进行的方向。
工质在整个循环过程中对外作的净功等于曲线所包围的面积。
沿顺时针方向进行的循环称为正循环或热循环。
沿反时针方向进行的循环称为逆循环或制冷循环。
§3 循环过程卡诺循环PVQA =0=D E 3.1循环过程正循环的特征:一定质量的工质在一次循环过程中要从高温热源吸热Q 1,对外作净功|A|,又向低温热源放出热量Q 2。
而工质回到初态,内能不变。
如热电厂中水的循环过程(示意如图)。
实用上,用效率表示热机的效能以η表示Q A =ηT 1 Q 1T 2 Q 2泵|A|气缸Q 1、Q 2、|A|均表示数值大小。
工质经一循环|A|= Q 1-Q 2abV V RT Q ln11ν=PV 图Op VV a ap a 绝热线等温线p b p C p d V bV cV d b c d Q 2Q 11824年卡诺(法国)提出了一个能体现热机循环基本特征的理想循环−卡诺循环。
由4个准静态过程(两个等温、两个绝热)组成。
a →b :与温度为T 1的高温热源接触,T 1不变,体积由V a 膨胀到V b ,从热源吸收热量为:=Q b →c :绝热膨胀,体积由V b 变到V c ,吸热为零。
PV 图Op VV a ap a 绝热线等温线p b p C p d V bV cV d b c d Q 2Q 1c →d :与温度为T 2的低温热源接触,T 2不变,体积由V c 压缩到V d ,从热源放热为:dcV V RT Q ln22ν=PV 图Op VV a ap a 绝热线等温线p b p C p d V bV cV d b c d Q 2Q 1=Q d →a :绝热压缩,体积由V d 变到V a ,吸热为零。
PV 图Op VV a ap a 绝热线等温线p b p C p d V bV cV d b c d Q 2Q 1在一次循环中,气体对外作净功为|A|= Q 1-Q 2 (参见能流图)高温恒温热源1T 低温恒温热源2T 热机1Q 2Q21Q Q A -=热机效率为:ab d CV V T V V T Q Q Q Q Q Q A lnln1212121111-=-=-==η21T T -=\η热机效率为:ab d CV V T V V T Q Q Q Q Q Q A lnln1212121111-=-=-==η由绝热方程b →c 、d →a2111T V T V c b --=γγ2111T V T V d a --=γγdca b V V V V =−→−比理想气体卡诺循环的效率只与两热源的温度有关Op VV a ap a 绝热线等温线p b p Cp d V bV cV d b c d Q 2Q 1后面将证明在同样两个温度T 1和T 2之间工作的各种工质的卡诺循环的效率都由上式给定,而且是实际热机可能效率的最大值。
21Q Q A -=高温恒温热源1T 低温恒温热源2T 热机21Q A Q +=2Q 逆向循环反映了制冷机的工作原理,循环方向a →d →c →b ;其能流图如右图所示。
2122Q Q Q A Q -==εaV d V bV C V Pabc dAaP bP CP dP 1T 2T V1Q 2Q 致冷系数:定义为2122Q Q Q A Q -==ε212T T T -=ε这是在T 1和T 2两温度间工作的各种制冷机的制冷系数的最大值工质把从低温热源吸收的热量和外界对它所作的功以热量的形式传给高温热源,其结果可使低温热源的温度更低,达到制冷的目的。
吸热越多,外界作功越少,表明制冷机效能越好。
用制冷系数ε表示[实例] 冰箱热泵aV d V bV C V Pab c dAaP bP CP dP 1T2T V1Q 2Q卡诺致冷机致冷系数212T T T -=ε压缩机低温吸热高温放热高压液体高压气体节流过程Op VV aap a p b p C p d V b V C V d b cd Q 2Q 1。
