使用状态方程计算天然气焦耳-汤姆逊系数
第一章 热力学第一、二定律试题及解答

第一章 热力学第一定律一、选择题1.下述说法中,哪一种正确( )(A)热容C 不是状态函数; (B)热容C 与途径无关;(C)恒压热容C p 不是状态函数;(D)恒容热容C V 不是状态函数。
2.对于内能是体系状态的单值函数概念,错误理解是( )(A) 体系处于一定的状态,具有一定的内能;(B) 对应于某一状态,内能只能有一数值不能有两个以上的数值;(C) 状态发生变化,内能也一定跟着变化;(D) 对应于一个内能值,可以有多个状态。
3.某高压容器中盛有可能的气体是O 2 ,Ar, CO 2, NH 3中的一种,在298K 时由5dm3绝热可逆膨胀到6dm3,温度降低21K ,则容器中的气体( )(A) O 2 (B) Ar (C) CO 2 (D) NH 34.戊烷的标准摩尔燃烧焓为-3520kJ·mol -1,CO 2(g)和H 2O(l)标准摩尔生成焓分别为-395 kJ·mol -1和-286 kJ·mol -1,则戊烷的标准摩尔生成焓为( )(A) 2839 kJ·mol -1 (B) -2839 kJ·mol -1 (C) 171 kJ·mol -1 (D) -171 kJ·mol -15.已知反应)()(21)(222g O H g O g H =+的标准摩尔反应焓为)(T H m r θ∆,下列说法中不正确的是( )。
(A).)(T H m r θ∆是H 2O(g)的标准摩尔生成焓 (B). )(T H m r θ∆是H 2O(g)的标准摩尔燃烧焓 (C). )(T H m r θ∆是负值 (D). )(T H m r θ∆与反应的θm r U ∆数值相等 6.在指定的条件下与物质数量无关的一组物理量是( )(A) T , P, n (B) U m , C p, C V(C) ΔH, ΔU, Δξ (D) V m , ΔH f,m (B), ΔH c,m (B)7.实际气体的节流膨胀过程中,下列那一组的描述是正确的( )(A) Q=0 ΔH=0 ΔP< 0 ΔT≠0 (B) Q=0 ΔH<0 ΔP> 0 ΔT>0(C) Q>0 ΔH=0 ΔP< 0 ΔT<0 (D) Q<0 ΔH=0 ΔP< 0 ΔT≠08.已知反应 H 2(g) + 1/2O 2(g) →H 2O(l)的热效应为ΔH ,下面说法中不正确的是( )(A) ΔH 是H 2O(l)的生成热 (B) ΔH 是H 2(g)的燃烧热(C) ΔH 与反应 的ΔU 的数量不等 (D) ΔH 与ΔH θ数值相等9.为判断某气体能否液化,需考察在该条件下的( )(A) μJ-T > 0 (B) μJ-T < 0 (C) μJ-T = 0 (D) 不必考虑μJ-T 的数值10.某气体的状态方程为PV=RT+bP(b>0),1mol 该气体经等温等压压缩后其内能变化为( )(A) ΔU>0 (B) ΔU <0 (C) ΔU =0 (D) 该过程本身不能实现11.均相纯物质在相同温度下C V > C P的情况是()(A) (∂P/∂T)V<0 (B) (∂V/∂T)P<0(C) (∂P/∂V)T<0 (D) 不可能出现C V>C P12.理想气体从相同始态分别经绝热可逆膨胀和绝热不可逆膨胀到达相同的压力,则其终态的温度,体积和体系的焓变必定是()(A) T可逆> T不可逆, V可逆> V不可逆, ΔH可逆>ΔH不可逆(B) T可逆< T不可逆, V可逆< V不可逆, ΔH可逆<ΔH不可逆(C) T可逆< T不可逆, V可逆> V不可逆, ΔH可逆<ΔH不可逆(D) T可逆< T不可逆, V可逆< V不可逆, ΔH可逆>ΔH不可逆13.1mol、373K、1atm下的水经下列两个不同过程达到373K、1atm下的水汽:(1)等温可逆蒸发,(2)真空蒸发。
第一章 热力学第一、二定律试题及答案

第一章 热力学第一定律一、选择题1.下述说法中,哪一种正确( )(A )热容C 不是状态函数; (B )热容C 与途径无关;(C )恒压热容C p 不是状态函数;(D )恒容热容C V 不是状态函数。
2.对于内能是体系状态的单值函数概念,错误理解是( )(A) 体系处于一定的状态,具有一定的内能;(B ) 对应于某一状态,内能只能有一数值不能有两个以上的数值;(C ) 状态发生变化,内能也一定跟着变化;(D) 对应于一个内能值,可以有多个状态.3.某高压容器中盛有可能的气体是O 2 ,Ar , CO 2, NH 3中的一种,在298K 时由5dm3绝热可逆膨胀到6dm3,温度降低21K ,则容器中的气体( )(A ) O 2 (B) Ar (C ) CO 2 (D ) NH 34.戊烷的标准摩尔燃烧焓为—3520kJ·mol -1,CO 2(g)和H 2O(l )标准摩尔生成焓分别为—395 kJ·mol —1和-286 kJ·mol —1,则戊烷的标准摩尔生成焓为( )(A ) 2839 kJ·mol —1 (B ) -2839 kJ·mol —1 (C) 171 kJ·mol -1 (D ) —171 kJ·mol —15.已知反应)()(21)(222g O H g O g H =+的标准摩尔反应焓为)(T H m r θ∆,下列说法中不正确的是( ).(A )。
)(T H m r θ∆是H 2O (g )的标准摩尔生成焓 (B)。
)(T H m r θ∆是H 2O (g)的标准摩尔燃烧焓 (C)。
)(T H m r θ∆是负值 (D ). )(T H m r θ∆与反应的θm r U ∆数值相等 6.在指定的条件下与物质数量无关的一组物理量是( )(A ) T , P , n (B ) U m , C p, C V(C) ΔH, ΔU , Δξ (D) V m , ΔH f,m (B ), ΔH c,m (B )7.实际气体的节流膨胀过程中,下列那一组的描述是正确的( )(A ) Q=0 ΔH=0 ΔP< 0 ΔT≠0 (B ) Q=0 ΔH<0 ΔP 〉 0 ΔT>0(C) Q 〉0 ΔH=0 ΔP 〈 0 ΔT 〈0 (D ) Q<0 ΔH=0 ΔP 〈 0 ΔT≠08.已知反应 H 2(g) + 1/2O 2(g ) →H 2O (l)的热效应为ΔH ,下面说法中不正确的是( )(A ) ΔH 是H 2O (l)的生成热 (B ) ΔH 是H 2(g)的燃烧热(C) ΔH 与反应 的ΔU 的数量不等 (D ) ΔH 与ΔH θ数值相等9.为判断某气体能否液化,需考察在该条件下的( )(A) μJ —T > 0 (B ) μJ-T < 0 (C ) μJ-T = 0 (D) 不必考虑μJ —T 的数值10.某气体的状态方程为PV=RT+bP (b>0),1mol 该气体经等温等压压缩后其内能变化为( )(A) ΔU>0 (B) ΔU <0 (C)ΔU =0 (D)该过程本身不能实现11.均相纯物质在相同温度下C V 〉C P的情况是()(A) (∂P/∂T)V<0 (B) (∂V/∂T)P〈0(C)(∂P/∂V)T〈0 (D)不可能出现C V〉C P12.理想气体从相同始态分别经绝热可逆膨胀和绝热不可逆膨胀到达相同的压力,则其终态的温度,体积和体系的焓变必定是()(A)T可逆> T不可逆,V可逆〉V不可逆,ΔH可逆〉ΔH不可逆(B)T可逆< T不可逆, V可逆< V不可逆,ΔH可逆〈ΔH不可逆(C) T可逆〈T不可逆, V可逆> V不可逆, ΔH可逆<ΔH不可逆(D) T可逆〈T不可逆,V可逆< V不可逆, ΔH可逆〉ΔH不可逆13.1mol、373K、1atm下的水经下列两个不同过程达到373K、1atm下的水汽:(1)等温可逆蒸发,(2)真空蒸发。
天然气物性参数及管线压降与温降的计算

整个计算过程的公式包括三部分:一. 天然气物性参数及管线压降与温降的计算 二. 天然气水合物的形成预测模型 三. 注醇量计算方法.天然气物性参数及管线压降与温降的计算 20 C 标准状态1y i M i24.055任意温度与压力下Y i M i式中厂混合气体的密度,P —任意温度、压力下i 组分的密度,kg/m 3; y i — i 组分的摩尔分数; M i —i组分的分子量, V i —i 组分摩尔容积, 天然气密度计算公式pMW gZRT天然气相对密度天然气相对密度△的定义为:在相同温度,压力下,天然气的密度与空气密 度之比。
天然气分子量标准状态下,Ikmol 天然气的质量定义为天然气的平均分子量,Y i M iM式中 M —气体的平均分子量,kg/kmol ; y i —气体第i 组分的摩尔分数;M —气体第i 组分的分子量,kg/kmol天然气密度混合气体密度指单位体积混合气体的质量。
0 °C 标准状态按下面公式计算:1 22.414y i M i简称分子量。
(1)kg/m 3;kg/kmol;⑹式中 △—气体相对密度;厂气体密度,kg/m 3;p —空气密度,kg/m 3,在 P o =1O1.325kPa, T o =273.15K 时,p =1.293kg/m 3;在 P o =1O1.325kPa T O =273.15K 时,p =1.293kg/m 3。
因为空气的分子量为28.96,固有28.96假设,混合气和空气的性质都可用理想气体状态方程描述,则可用下列关系 式表示天然气的相对密度天然气的虚拟临界参数任何气体在温度低于某一数值时都可以等温压缩成液体,但当高于该温度时, 无论压力增加到多大,都不能使气体液化。
可以使气体压缩成液态的这个极限温 度称为该气体的临界温度。
当温度等于临界温度时,使气体压缩成液体所需压力 称为临界压力,此时状态称为临界状态。
混合气体的虚拟临界温度、虚拟临界压 力和虚拟临界密度可按混合气体中各组分的摩尔分数以及临界温度、临界压力和 临界密度求得,按下式计算。
2.11节流膨胀与焦耳—汤姆逊效应

显然,在点3左侧,
J-T 0
在点3右侧, J-T 0 在点3处,
J-T 0 。
2.11 节流膨胀与焦耳—汤姆逊效应 思考题:
1. 将置于室内的一电冰箱的箱门打开,使其致冷机运转,能 否降低全室温度?设该机在 0℃ 与室温(25℃)作理想可 逆循环每小时能冻出 1Kg 的冰,如房间的总热容为 150KJ· K-1,估算电冰箱工作 10 小时后室内温度的变化?
但 H 和 He 等气体在常温下, J-T 0,经节流过程, 2 温度反而升高。若降低温度,可使它们的 J-T 0 。 当 J-T 0 时的温度称为转化温度,这时气体经焦 -汤实验,温度不变。
2.11 节流膨胀与焦耳—汤姆逊效应 为了求 J-T 的值,必须 作出等焓线,这要作若干个 节流过程实验。 实验1,左方气体为 p1T1 ,经 节流过程后终态为 p2T2 ,在 T-p图上标出1、2两点。
开始,环境将一定量气体压缩时所作功(即以 气体为体系得到的功)为:
W1 p1V pV1 1
(V =0 V1 V1)
气体通过小孔膨胀,对环境作功为:
W2 p2V p2V2
(V =V2 0 V2 )
2.11 节流膨胀与焦耳—汤姆逊效应 在压缩和膨胀时体系净功的变化应该是两个功 的代数和。
J-T是体系的强度性质。因为节流过程的dp 0 ,
所以当:
J-T >0 J-T <0 J-T =0
经节流膨胀后,气体温度降低。 经节流膨胀后,气体温度升高。 经节流膨胀后,气体温度不变。
2.11 节流膨胀与焦耳—汤姆逊效应
在常温下,一般气体的 J-T 均为正值。例如,空 气的 J-T 0.4 K /101.325 kPa ,即压力下降 101.325 kPa , 气体温度下降 0.4 K 。
第五版物理化学第三章习题答案

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载第五版物理化学第三章习题答案地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容第三章热力学第二定律3.1 卡诺热机在的高温热源和的低温热源间工作。
求(1)热机效率;(2)当向环境作功时,系统从高温热源吸收的热及向低温热源放出的热。
解:卡诺热机的效率为根据定义3.2 卡诺热机在的高温热源和的低温热源间工作,求:(1)热机效率;(2)当从高温热源吸热时,系统对环境作的功及向低温热源放出的热解:(1) 由卡诺循环的热机效率得出(2)3.3 卡诺热机在的高温热源和的低温热源间工作,求(1)热机效率;(2)当向低温热源放热时,系统从高温热源吸热及对环境所作的功。
解:(1)(2)3.4 试说明:在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时,若令卡诺热机得到的功等于不可逆热机作出的功-W。
假设不可逆热机的热机效率大于卡诺热机效率,其结果必然是有热量从低温热源流向高温热源,而违反势热力学第二定律的克劳修斯说法。
证:(反证法)设不可逆热机从高温热源吸热,向低温热源放热,对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等,即总的结果是:得自单一低温热源的热,变成了环境作功,违背了热力学第二定律的开尔文说法,同样也就违背了克劳修斯说法。
3.5 高温热源温度,低温热源温度,今有120KJ的热直接从高温热源传给低温热源,求此过程。
解:将热源看作无限大,因此,传热过程对热源来说是可逆过程3.6 不同的热机中作于的高温热源及的低温热源之间。
求下列三种情况下,当热机从高温热源吸热时,两热源的总熵变。
天然气物性参数及管线压降与温降的计算

整个计算过程的公式包括三部分:一.天然气物性参数及管线压降与温降的计算 二.天然气水合物的形成预测模型 三.注醇量计算方法一.天然气物性参数及管线压降与温降的计算 天然气分子量标准状态下,1kmol 天然气的质量定义为天然气的平均分子量,简称分子量。
∑=ii M y M(1) 式中 M —气体的平均分子量,kg/kmol ;y i —气体第i 组分的摩尔分数;M i —气体第i 组分的分子量,kg/kmol 。
天然气密度混合气体密度指单位体积混合气体的质量。
按下面公式计算: 0℃标准状态∑=i i M y 14.4221ρ (2) 20℃标准状态∑=i i M y 055241.ρ (3) 任意温度与压力下∑∑=ii ii V y M y ρ(4)式中 ρ—混合气体的密度,kg/m 3;ρi —任意温度、压力下i 组分的密度,kg/m 3; y i —i 组分的摩尔分数;M i —i 组分的分子量,kg/kmol ; V i —i 组分摩尔容积,m 3 /kmol 。
天然气密度计算公式gpMW ZRTρ= (5)天然气相对密度天然气相对密度Δ的定义为:在相同温度,压力下,天然气的密度与空气密度之比。
aρρ∆=(6) 式中 Δ—气体相对密度;ρ—气体密度,kg/m 3; ρa —空气密度,kg/m 3,在P 0=101.325kPa ,T 0=273.15K 时,ρa =1.293kg/m 3;在P 0=101.325kPa ,T 0=273.15K 时,ρa =1.293kg/m 3。
因为空气的分子量为28.96,固有28.96M∆=(7) 假设,混合气和空气的性质都可用理想气体状态方程描述,则可用下列关系式表示天然气的相对密度28.96gg ga a pMW MW MW RT pMW MW RT∆===(8) 式中 MW a —空气视相对分子质量;MW g —天然气视相对分子质量。
天然气的虚拟临界参数任何气体在温度低于某一数值时都可以等温压缩成液体,但当高于该温度时,无论压力增加到多大,都不能使气体液化。
天然气物理化学性质
海底天然气物理化学性质第一节海底天然气组成表示法一、海底天然气组成海底天然气是由多种可燃和不可燃的气体组成的混合气体。
以低分子饱和烃类气体为主,并含有少量非烃类气体。
在烃类气体中,甲烷(CH4)占绝大部分,乙烷(C2H6)、丙烷(C3H8)、丁烷(C4H10)和戊烷(C5H12)含量不多,庚烷以上(C5+)烷烃含量极少。
另外,所含的少量非烃类气体一般有氮气(N2)、二氧化碳(CO2)、氢气(H2)、硫化氢(H2S)和水汽(H2O)以及微量的惰性气体。
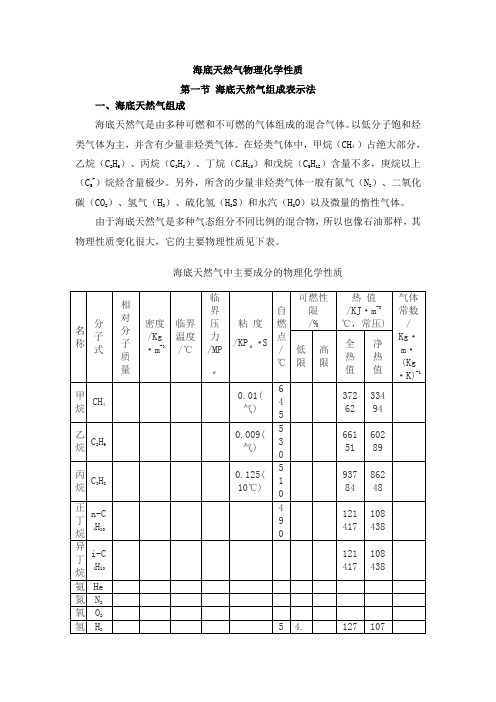
由于海底天然气是多种气态组分不同比例的混合物,所以也像石油那样,其物理性质变化很大,它的主要物理性质见下表。
海底天然气中主要成分的物理化学性质二、海底天然气容积分数和摩尔分数定义混合物中各组分的容积为V i ,总容积V ;摩尔分数y i :i 组分的摩尔数n i 与混合物总摩尔数n 的比值。
∑=='ii i i V VV V y ; 1='∑i y ;∑==i i i i n n n n y ; 1=∑i y由分压定律,存在P i V= n i R M T ;P i V=n R M T 由分容定律,存在PV i = n i R M T ;PV=n R M Tpp n n y ii i ==; i i i i y n n V V y ===' 结论:对于理想气体混合物,任意组分的摩尔分数可以用该组分的分压与混合物总压的比值表示,且摩尔分数与容积分数相等。
三、海底天然气分子量标准状态下,1kmol 天然气的质量定义为天然气的平均分子量,简称分子量。
∑=i i M y M 四、海底天然气密度(1)平均密度混合气体密度指单位体积混合气体的质量。
按下面公式计算:0℃标准状态 ∑=i i M y 414.221ρ; 20℃标准状态 ∑=i i M y 055.241ρ 任意温度与压力下 i i i i V y M y ∑∑=/ρ (2)相对密度在标准状态下,气体的密度与干空气的密度之比称为相对密度。
第五版物理化学第三章习题答案

第三章热力学第二定律3.1 卡诺热机在的高温热源和的低温热源间工作。
求(1)热机效率;(2)当向环境作功时,系统从高温热源汲取的热及向低温热源放出的热。
解:卡诺热机的效率为依据定义3.2 卡诺热机在的高温热源和的低温热源间工作,求:(1)热机效率;(2)当从高温热源吸热时,系统对环境作的功及向低温热源放出的热解:(1) 由卡诺循环的热机效率得出(2)3.3 卡诺热机在的高温热源和的低温热源间工作,求(1)热机效率;(2)当向低温热源放热时,系统从高温热源吸热及对环境所作的功。
解:(1)(2)3.4 试说明:在高温热源和低温热源间工作的不行逆热机与卡诺机结合操作时,若令卡诺热机得到的功r W 等于不行逆热机作出的功-W 。
假设不行逆热机的热机效率大于卡诺热机效率,其结果必定是有热量从低温热源流向高温热源,而违背势热力学第二定律的克劳修斯说法。
证: (反证法) 设 r ir ηη>不行逆热机从高温热源吸热,向低温热源放热,对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不行逆热机从高温热源汲取的热相等,即总的结果是:得自单一低温热源的热,变成了环境作功,违背了热力学第二定律的开尔文说法,同样也就违背了克劳修斯说法。
3.5 高温热源温度,低温热源温度,今有120KJ的热干脆从高温热源传给低温热源,求此过程。
解:将热源看作无限大,因此,传热过程对热源来说是可逆过程3.6 不同的热机中作于的高温热源及的低温热源之间。
求下列三种状况下,当热机从高温热源吸热时,两热源的总熵变。
(1)可逆热机效率。
(2)不行逆热机效率。
(3)不行逆热机效率。
解:设热机向低温热源放热,依据热机效率的定义因此,上面三种过程的总熵变分别为。
3.7 已知水的比定压热容。
今有1 kg,10℃的水经下列三种不同过程加热成100 ℃的水,求过程的。
(1)系统与100℃的热源接触。
(2)系统先与55℃的热源接触至热平衡,再与100℃的热源接触。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使用状态方程计算天然气焦耳-汤姆逊系数YUAN Weimin;WANG Hui;CHEN Xueyan;WANG Le;LEI Jiangkai;ZHANG Xiaohui;CHEN Li【摘要】当气体在管道中流动时,遇到阀门、孔板等节流元件,由于压力显著降低形成节流现象,需要通过焦耳-汤姆逊系数预测温度的变化.对具有代表性的立方型状态方程,即Redlich-Kwong(RK)、Soave-Redlich-Kwong(SRK)、Peng-Robinson(PR)状态方程,以及多参数状态方程即Benedict-Webb-Rubin-Starling(BWRS)状态方程和对比态原理状态方程即Lee-Kesler-Plocker(LKP)状态方程进行了焦耳-汤姆逊系数相关偏导数的推导,并给出了计算过程中涉及到的温度的一阶导数da/dT和Tda/dT公式及其单组分计算公式和多组分的混合规则.由具有代表性的状态方程推导出焦耳-汤姆逊系数公式,便于工程设计计算中使用.【期刊名称】《石油工程建设》【年(卷),期】2019(045)001【总页数】5页(P22-26)【作者】YUAN Weimin;WANG Hui;CHEN Xueyan;WANG Le;LEI Jiangkai;ZHANG Xiaohui;CHEN Li【作者单位】;;;;;;【正文语种】中文1 焦耳-汤姆逊系数及其基本关联式高压流体经节流膨胀后,由于压力变化而引起温度的变化,被称为节流效应或者焦耳-汤姆逊(Joule-Thomson)效应[1]。
节流膨胀可近似看作敞开系统稳流过程,并且是绝热又无轴功,如略去动能、位能变化,焓差为零,是恒焓过程。
节流膨胀时,微小的压力变化引起温度变化的关系称为微分节流效应系数或焦耳-汤姆逊(Joule-Thomson)效应系数[2],以μJ来表示,它代表在等焓的情况下节流过程中温度随压力的变化率。
式中:μJ为焦耳-汤姆逊系数,K/kPa;p为系统压力,kPa;T为系统温度,K;H为气体的焓,J/mol。
由热力学关系式:式中:V为气体的摩尔体积,m3/kmol;Cp为气体的定压比热容,J/(mol·K)。
对于实际气体:当dH=0,可得:式中:ρ为气体摩尔密度,kmol/m3。
焦耳-汤姆逊系数中的偏微分项可通过实际状态方程来求解,常用的气体状态方程有Redlich-Kwong(RK)、Soave-Redlich-Kwong(SRK)、Peng-Robinson (PR)、Benedict-Webb-Rubin-Starling(BWRS)、Lee-Kesler-Plocker (LKP)方程。
本文将一一进行求解各状态方案下的焦耳-汤姆逊系数。
2 Redlich-Kwong(RK)状态方程2.1 方程的形式及混合规则Redlich和Kwong于1949年提出的两参数状态方程原始形式如下[3]:采用Soave给定的混合规则[4],a和b的系数采用修正过的数值[5-15]:其中,a和b的混合规则见下式:式中:Tci为临界温度,K;yi为纯组分i的摩尔分数;n为组分总数。
2.2 焦耳-汤姆逊系数采用RK方程推导式(4)中可得:将式(9)~(10)代入式(4)可得:3 Soave-Redlich-Kwong(SRK)状态方程3.1 方程的形式及混合规则1972年Soave提出了改进的RK状态方程(简称SRK方程)[4],将RK方程中a/T0.5项改用较具普遍意义的温度函数α(T)来代替,a和b的系数采用修正过的数值[6-15],即:α是与气体温度和偏心因子ω有关的无因次因子,α按下式计算:对于混合气体,除了考虑各组分i的常数ai和摩尔分数yi外,为了改进对非烃-烃体系的预测,Soave模型在参数a的混合规则中引入经验校正因子Kij,混合规则如下式:式中:Tri为对比温度,Tri=T/Tci,无量纲;i、j代表流体组成,n为流体组分总数,yi、yj为纯组分的摩尔分数。
3.2 焦耳-汤姆逊系数采用 SRK方程推导式(4)中4 Peng-Robinson(PR)状态方程4.1 方程的形式及混合规则1976年,Peng-Robinson在SRK模型基础上进行了修正,提出了PR状态方程[16]:混合规则同式(16)。
4.2 焦耳-汤姆逊系数采用PR方程推导式(4)中偏微分将式(21)、(22)代入式(4)可得:5 SRK方程和PR方程中的温度导数SRK方程和PR方程中的温度导数形式一致,温度的一阶导数da/dT和Tda/dT 用下式计算。
对于单一组分:对于混合物:6 Benedict-Webb-Rubin-Starling(BWRS)状态方程6.1 方程的形式及混合规则1972年Starling和Han提出了BWRS方程,该方程是修正BWR方程而得到的,它保留了BWR方程中与密度关联的系数项,改变了与温度关联的系数项。
BWRS 方程包含了计算轻烃组分的系数,决定烃类混合物气体系数的混合规则,可以用于热力学性质计算和气液平衡计算。
BWRS状态方程是一个多参数状态方程,其基本形式[10,17]为:方程中的11 个参数(A0,B0,C0,D0,E0,a,b,c,d,α,γ)可以通过参考文献[10]得到。
6.2 焦耳-汤姆逊系数采用BWRS方程推导式(5)中偏微分将式(29)~(30)代入式(5)即可得到焦耳-汤姆逊系数计算公式。
7 L ee-Kesler-Plocker(L KP)状态方程7.1 方程的形式及混合规则1978年Plocker等人在Lee-Kesler(LK)状态方程[18]基础上提出了Lee-Kesler-Plocker(LKP)状态方程[19],将该方程推广到小分子(如N2、CO、CH4和H2)和大分子(如高沸点的烷烃、芳烃和稠环化合物)组成的不对称混合物的气液平衡和焓的计算中,保留了LK方程的原型,修改了混合规则,增加了两个参数kij和η,其中二元交互系数kij可由纯组分的临界参数关联得到;虚拟临界温度混合规则中的通用指数η为:对称混合物η=0,稍稍不对称混合物η=1,严重不对称混合物η=0.25。
kij和η的引入提高了方程的精确度。
LKP方程及其混合规则如下:式中:Z为压缩因子,ω为偏心因子,pr为对比压力,Vr为对比摩尔体积,上标(0)表示简单流体的相应参数,上标(r)表示参考流体的相应参数,其余参数为常数。
对于混合物,虚拟临界性质表达式[19]:式中:M代表混合物;η取值0.25。
7.2 焦耳-汤姆逊系数采用 LKP方程推导式(4)中将式(33)~(34)代入式(4)可得到LKP方程求解简单流体和参考流体的焦耳-汤姆逊系数,代入式(35)得到流体的焦耳-汤姆逊系数。
8 结论(1)使用RK、SRK、PR、BWRS和LKP状态方程对流体的焦耳-汤姆逊公式进行了推导,给出了焦耳-汤姆逊公式。
(2)由于大多数文献没有温度导数的相关公式,对SRK、PR方程的温度一阶导数进行了推导,给出了单一流体和混合物的表达式。
(3)将立方方程、多参数方程和对比态原理方程具有代表性的状态方程进行归纳讨论,便于设计、科研人员使用和进一步研究。
参考文献【相关文献】[1]冯新,宣爱国,周彩荣,等.化工热力学[M].北京:化学工业出版社,2009:278-283.[2]张乃文,于志家.化工热力学[M].2版.大连:大连理工出版社,2014:275-280.[3]REDICH O,KWONG J N.On the thermodynamics of solutions.V-An equation of state.Fugacities of gaseous solutions[J].ChemicalReviews,1949,44(1):233-244. [4] SOAVE G. Equilibrium constants from a modified Redlich-Kwong equation ofstate[J].Chemical Engineering Science,1972,27(6):1 197-1 203.[5]童景山,李敬.流体热物理性质的计算[M].北京:清华大学出版社,1982:13-94.[6]白执松,罗光熹.石油及天然气物性预测[M].北京:石油工业出版社,1995:20-52.[7]骆赞椿,徐汛.化工节能热力学原理[M].北京:烃加工出版社,1990:36-63.[8]童景山.流体的热物理性质[M].北京:中国石化出版社,1996:20-103.[9]童景山.流体热物性学——基本理论与计算[M].北京:中国石化出版社,2008:24-102.[10]李长俊,汪玉春,陈祖泽,等.天然气管道输送[M].2版.北京:石油工业出版社,2008:25-40.[11]陈新志,蔡振云,胡望明,等.化工热力学[M].3版.北京:化学工业出版社,2009:13-46.[12]陈钟秀,顾飞燕,胡望明.化工热力学[M].3版.北京:化学工业出版社,2012:7-50.[13]施云海,王艳莉,彭阳峰等.化工热力学[M].2版.上海:华东理工大学出版社,2013:10-56.[14]石玉冰.真实气体等压热容的关联[J].化肥设计,2010,48(3):11-13.[15]陈漓,莫小梅.Excel在SRK方程中计算纯流体饱和热力学性质的应用[J].山东化工,2016,45(19):119-121.[16]PENG D Y,ROBINSON D B.A new two-constant equation of state[J].Minerva Ginecologica,1976,12(11-12):3 069-3078.[17]STARLING K E,SLIEPCEVICH C M,FISH L W,et al.Development of working fluid thermodynamic properties information for geothermal cycles:phase 1 [R].Oklahoma:The University of Oklahoma,1977:1-55.[18]LEE B I,KESLER M G.A generalized thermodynamic correlation based on three-parameter corresponding states[J].AIChE Journal,1975,21(3):510-527.[19]PLOCKER U,KNAPP H,PRAUSNITZ J.Calculation of highpressure vapor-liquid equilibria from a corresponding-states correlation with emphasis on asymmetric mixtures[J].Industrial& Engineering Chemistry Process Design &Development,1978,17(3):324-332.。
