初中数学竞赛专题选讲-线段、角的和差倍分
证题技巧之三——证明线段或角的和差倍分(推荐文档)

证题技巧之三一一证明线段或角的和差倍分一、证明线段或角的倍分1、方法:①长(或大)折半 ②短(或小)加倍2、判断:两种方法有时对同一个题都能使用,但存在易繁的问题,因此,究竟是折半还是加倍要以有利于利用已知条件为准。
3、添线:①为折半或加倍而添;②为折半或加倍后创造条件或利于利用已知条件而添。
4、传递:在加倍或折半后,还不易或不能证明结论,则要找与被证二量有等量关系的量来传递,或者添加这个量来传递。
此时,添 线从两方面考虑:①造等量②为证等量与被证二量相等而添。
参考例4、例5、例6。
例1 AD 是^ ABC 的中线,ABEF 和ACGH 是分别以AB 和AC 为边向形外作的正方形。
求证:FH=2AD/ BAC+ / ACN=180证明:延长AD 至N 使AD=DN则ABNC 是平行四边形CN=AB=FA AC=AH又/ FAH+ / BAC=180 •••△ FAHY NCA ••• FH=AN例 2、△ ABC 中,/ B=2 / C ,AD 是高,M 是BC 边上的中点。
$•••1求证:DM=2 AB/ 2=Z B •••/ 2=2Z 1•••/ 1 = / DNM 又 AN=DN=ND • DM=2 A B1贝J BFAC••• BF=AE•••△ AEC 心 BFD •DF 二CE 二 CD=2CE作业:1、在△ABC 中,D 为BC 的中点,E 为AD 的中点,BE 的延长 1线交AC 于F ,求证:AF=2 FC2、AB 和AC 分别切© O 于B 和C, BD 是直径。
求证/ BAC 二Z CBD3、圆内接△ ABC 的AB=AC ,过C 作切线交AB 的延长线于D , DE 垂直于AC 的延长线于E 。
求证:BD=2CE例4从平行四边形的钝角顶点 A 向BC 边作垂线,垂足为E ,证明:取AB 的中点N ,连接MN 、DN贝J MN // AC / 1 = / C••• DM=DN例 3 △ ABC 中,AB=AC , E 是AB 的中点,D 在AB 的延长线上,且 DB=AC 。
初中数学竞赛和差倍分问题

和差倍分问题基础知识:一、掌握利用线段图解和差倍分应用题的方法;二、掌握好设单位1,设份数的方法:可以直接将题目中的某些量设成为“1”份或者是多份;三、解题时需要注意认真审题,多注意观察题目中的隐含条件,特别是对于题目中的不变量,要十分注意。
根据倍数关系将不变量设为多份往往可以大大简化解题的过程;四、对于涉及到3个以上的对象并且给出了部分对象之和的题目,通常利用将条件累加或者对条件进行比较的方法来解题。
基本类型:1. 和倍问题是已知大小两个数的和与它们的倍数关系,常采用画线段图的方法来表示两种量间的这种关系,以便于找到解题的途径。
和÷(倍数+1)=小数(1倍数)小数×倍数=大数和-小数=大数2.“差倍问题”就是已知两个数的差和它们的倍数关系,求这两个数。
差倍问题的解题思路与和倍问题一样,先要在题目中找到1倍量,再画图确定解题方法。
被除数的数量和除数的倍数关系要相对应,相除后得到的结果是一倍量,然后求出另一个数,最后再写出验算和答题。
差÷(倍数-1)=小数(1倍数)小数×倍数=大数小数+差=大数例1.爸爸和小明一起搬砖,爸爸所搬的砖头是小明的6倍。
后来父子二人每个人又搬了18块砖头,于是爸爸所搬的砖头变成了小明的4倍。
那么最终爸爸和小明共搬了多少块砖?[答疑编号0518430101]【答案】225【解答】分析:“图解法”是解决这类问题最经典的方法。
注意到原来和后来父子二人所搬砖头数的差是一个“不变量”,可以利用这个特点来解题。
原来爸爸所搬的砖头是小明的6倍,因此两个人的差应为5的倍数;后来爸爸所搬的砖头变成了小明的4倍,因此两个人的差又应该是3的倍数。
综合起来看这两个条件,差既是5的倍数又是3的倍数,因此这个差应该是15的倍数,它可能是15、30、45、60……。
所以可以假设爸爸和小明的差为“15”份。
解法1:如图,画出线段图表示题目条件的含义。
小明原来搬了“1”,后来又搬了18块。
线段与角的和差倍分计算

线段与角的和差倍分计算
在几何学中,我们经常遇到线段与角之间的和、差和倍分计算问题。
这些计算方法是为了帮助我们更好地理解图形的性质和关系。
本文将详细
介绍线段与角之间的和、差和倍分计算方法。
一、线段的和、差计算
1.线段的和计算:给定线段AB和线段BC,我们需要计算出两个线段
的和,即线段AB+BC。
计算方法是将线段AB和BC的长度相加,即AB+BC。
2.线段的差计算:给定线段AB和线段BC,我们需要计算出两个线段
的差,即线段AB-BC。
计算方法是将线段AB的长度减去线段BC的长度,
即AB-BC。
二、角的和、差计算
1.角的和计算:给定角α和角β,我们需要计算出两个角的和,即
角α+角β。
计算方法是将两个角的度数相加,即α+β。
2.角的差计算:给定角α和角β,我们需要计算出两个角的差,即
角α-角β。
计算方法是将角α的度数减去角β的度数,即α-β。
三、线段与角的倍分计算
1.线段的倍分计算:给定线段AB,我们需要计算出线段AB的一半或
一四分之一的长度。
计算方法是将线段AB的长度除以2或4,即AB/2或AB/4
2.角的倍分计算:给定角α,我们需要计算出角α的一半或一四分
之一的度数。
计算方法是将角α的度数除以2或4,即α/2或α/4
以上是线段与角的和、差和倍分计算的基本方法。
在实际应用中,我们还可以利用一些几何定理和性质来简化计算,例如角的补角、互补角和对应角等关系。
微专题八线段及角的和差倍分计算人教版七年级数学上册课件

微专题八线段及角的和差倍分计算人 教版七 年级数 学上册 课件
解:(1)(i)∵∠AOC=30°, ∴∠BOC=180°-∠AOC=150°, ∵OM 平分∠BOC, ∴∠COM=∠BOM=12∠BOC=75°, ∠AON=180°-90°-75°=15°, ∴t=155°°=3; (ii)由(i)知∠AON=15°, ∴∠CON=30°-15°=15°, ∴∠AON=∠CON,即 ON 平分∠AOC;
微专题八线段及角的和差倍分计算人 教版七 年级数 学上册 课件
微专题八线段及角的和差倍分计算人 教版七 年级数 学上册 课件
微专题八线段及角的和差倍分计算人 教版七 年级数 学上册 课件
解:(1)∵∠COD=90°,
∴∠AOC+∠BOD=90°,
∵OE 平分∠AOC,OF 平分∠BOD,
∴∠EOC=12∠AOC,∠DOF=12∠BOD,
∴∠EOF
= ∠COD + ∠EOC + ∠DOF =
微专题八线段及角的和差倍分计算人 教版七 年级数 学上册 课件
二 角的和差倍分计算 (教材 P140 习题 4.3 第 9 题) 如图 5,OB 是∠AOC 的平分线,OD 是∠COE 的平分线. (1)如果∠AOB=40°,∠DOE=30°,那么∠BOD 是多少度? (2)如果∠AOE=140°,∠COD=30°,那么∠AOB 是多少度?
微专题八线段及角的和差倍分计算人 教版七 年级数 学上册 课件
图5
微专题八线段及角的和差倍分计算人 教版七 年级数 学上册 课件
解:(1)∵OB 是 ∠AOC 的平分线, ∴∠BOC=∠AOB=40°, ∵OD 是∠COE 的平分线, ∴∠COD=∠DOE=30°, ∴∠BOD=∠BOC+∠COD=70°; (2)∠AOB=12∠AOC=12(∠AOE-∠COE)=12(∠AOE-2∠COD)=12×(140° -2×30°)=40°. 【思想方法】 解这种题的方法主要是寻找出要求的角与相关的角之间的和差 倍分关系,通过求出相关的角,从而求出所求的角.
八年级数学尖子班线段的和、差、倍、分问题
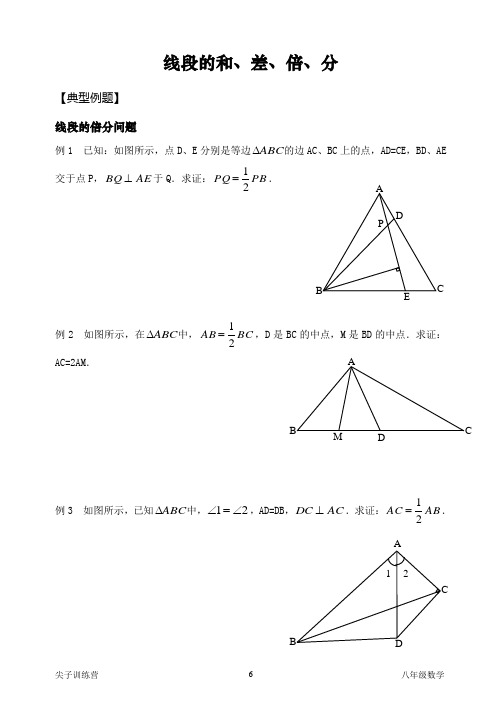
线段的和、差、倍、分【典型例题】 线段的倍分问题例1 已知:如图所示,点D 、E 分别是等边ABC ∆的边AC 、BC 上的点,AD=CE ,BD 、AE 交于点P ,AE BQ ⊥于Q .求证:PB PQ 21=.例2 如图所示,在ABC ∆中,BC AB 21=,D 是BC 的中点,M 是BD 的中点.求证:AC=2AM .例3 如图所示,已知ABC ∆中,21∠=∠,AD=DB ,AC DC ⊥.求证:AB AC 21=.A DPCBA DBC1 2ADBCM例 4 已知:如图所示,在ABC Rt ∆中,BAC CAD B ∠=∠︒=∠21,90,过点D 作AC DE ⊥,DE 恰好是ADC ∠的平分线.求证:DC BD 21=.例5 已知:如图所示,D 是ABC ∆的边BC 上一点,且CD=AB ,BAD BDA ∠=∠,AE 是ABD ∆的中线.求证:AC=2AE .例6 已知:如图所示,在ABC ∆中,AB=AC ,︒=∠120BAC ,D 是BC 的中点,AB DE ⊥于E .求证:EB=3EA .ABDECABEDEC EA EBC例7 已知:如图所示,锐角ABC ∆中,C B ∠=∠2,BE 是角平分线,BE AD ⊥,垂足是D .求证:AC=2BD .例8 已知:如图所示,在ABC ∆中,BD 是AC 边上的中线,BH 平分BH AF CBD ⊥∠,,分别交BD 、BH 、BC 于E 、C 、F .求证:2DE=CF .例9 如图所示,在ABC ∆中,AB=AC ,︒=∠90BAC ,BE 平分ABC ∠,交AC 于D ,BE CE ⊥于E 点,求证:BD CE 21=.ADEBA E G BDHCFAB EDC线段和差例10 如图所示,已知ABC ∆中,B A ∠=∠2,CD 是ACB ∠的平分线,求证:BC=AC+AD .例11 如图所示,在等腰三角形ABC 中,P 是底边BC 上的任意一点.(1)求证:P 点到两腰的距离之和等于腰上的高.(2)若P 点在BC 的延长线上,那么点P 到两腰的距离与腰上的高三者之间存在什么关系?例12 如图所示,若E 为正方形ABCD 的边BC 上一点,AF 为DAE ∠的平分线,AF 与CD 相交于F 点.求证:AE=BE+DF .ADCB M PBFDAE ABCDF例13 如图所示,已知ABC ∆和ADE ∆均为等边三角形,B 、C 、D 在一直线上,求证:CE=AC+CD .例14 如图所示,等腰三角形ABC 中,AB=AC ,︒=∠108A ,BD 平分ABC ∠.求证:BC=AB+DC . 例15 如图所示,在A B C ∆中,AB=AC ,D为ABC ∆外的点,BDC ADB ABD ∠-︒=∠︒=∠2190,60,求证:AB=BD+DC .例16 如图所示,在等腰直角三角形ABC 中,︒=∠90BAC ,AD=AE ,BE AF ⊥交BC 于F ,过点F 作CD FG ⊥于M ,交BE 延长线于点G ,求证:BG=AF+FG .ABCDABDCABCD A DEMCBG【大展身手】1 已知:如图所示,在ABC ∆中,AB=AC ,︒=∠120A ,AB 的垂直平分线MN 分别交BC 、AB 于点M 、N .求证:CM=2BM .2 已知:如图所示,ABC ∆是等边三角形,D 是AB 的中点,且BC DE ⊥于E .求证:BC BE 41=.3 如图所示,在ABC ∆中,︒=∠90ACB ,P 是AC 的中点,过A 过BP 的垂线交BC 延长线于点D ,E 是垂足.若︒=∠30DBE ,求证:BP=4PE . AMNBCADEBCAPECBD4 已知:如图所示,在ABC ∆中,AB=AC ,︒=∠120BAC ,P 是BC 上一点,且︒=∠90BAP .求证:PB=2PC .5 如图所示,已知ABC ∆是等腰三角形,AB=AC ,︒=∠45BAC ,AD 和CE 是高,它们相交于H ,求证:AH=2BD .6 如图所示,已知ABC ∆中,︒=∠60A ,BD 、CE 分别平分ABC ∠和ACB ∠,BD 、CE 交于点O .求证:BE+CD=BC . ABCAEHBDAOEBCFD7 如图所示,已知在ABC ∆中,︒=∠90C ,AC=BC ,AD 是BAC ∠的平分线,求证:AB=AC+CD .8 如图所示,等边ABC ∆和等边BDE ∆,点A 在DE 的延长线上,求证:BD+DC=AD .9 如图所示,在ABC ∆中,AB=AC ,︒=∠100A ,BE 平分ABC ∠,求证:AE+BE=BC .AD BCAEBDCAEB。
7年级-上册-数学-第6章《图形的初步知识》专题讲解-线段、角的和差倍分计算-分节好题挑选
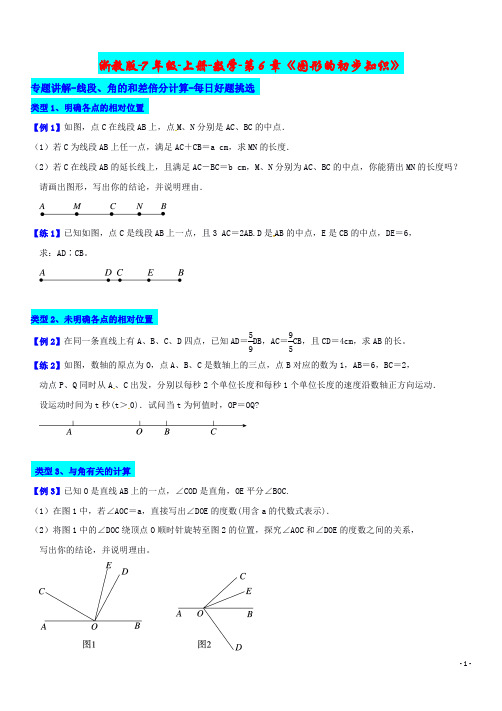
浙教版-7年级-上册-数学-第6章《图形的初步知识》专题讲解-线段、角的和差倍分计算-每日好题挑选类型1、明确各点的相对位置【例1】如图,点C在线段AB上,点M、N分别是AC、BC的中点.(1)若C为线段AB上任一点,满足AC+CB=a cm,求MN的长度.(2)若C在线段AB的延长线上,且满足AC-BC=b cm,M、N分别为AC、BC的中点,你能猜出MN的长度吗?请画出图形,写出你的结论,并说明理由.【练1】已知如图,点C是线段AB上一点,且3AC=2AB.D是AB的中点,E是CB的中点,DE=6,求:AD∶CB。
类型2、未明确各点的相对位置【例2】在同一条直线上有A、B、C、D四点,已知AD=59DB,AC=95CB,且CD=4cm,求AB的长。
【练2】如图,数轴的原点为O,点A、B、C是数轴上的三点,点B对应的数为1,AB=6,BC=2,动点P、Q同时从A、C出发,分别以每秒2个单位长度和每秒1个单位长度的速度沿数轴正方向运动.设运动时间为t秒(t>0).试问当t为何值时,OP=OQ?类型3、与角有关的计算【例3】已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.(1)在图1中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示).(2)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由。
【练3】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将三角板的直角顶点放在点O处.(1)如图1,将三角板MON的一边ON与射线OB重合时,则∠MOC=;(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON=,∠CON=。
【巩固专题练习】1、如图,AB=24,点C为AB的中点,点D在线段AC上,且AD∶CB=1∶3,则DB的长度为。
2、两根木条,一根长18cm,一根长22cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为.3、如图,点A、B、O在同一条直线上,∠COE和∠BOE互余,射线OF和OD分别平分∠COE和∠BOE,则∠AOF+∠BOD与∠DOF之间的等量关系是.4、如图,线段AD=6cm,线段AC=BD=4cm,E、F分别是线段AB、CD的中点,则EF=.5、已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD=.6、如图,在2×2的方格中,连结AB,AC,AD,则∠1+∠2+∠3=.7、点A,B在线段EF上,EA∶AB∶BF=1∶2∶3,M、N分别为EA、BF的中点,且MN=8cm,求EF的长。
证题技巧之三——证明线段或角的和差倍分
证题技巧之三——证明线段或角的和差倍分一、证明线段或角的倍分1、方法:①长(或大)折半②短(或小)加倍2、判断:两种方法有时对同一个题都能使用,但存在易繁的问题,因此,究竟是折半还是加倍要以有利于利用已知条件为准。
3、添线:①为折半或加倍而添;②为折半或加倍后创造条件或利于利用已知条件而添。
4、传递:在加倍或折半后,还不易或不能证明结论,则要找与被证二量有等量关系的量来传递,或者添加这个量来传递。
此时,添线从两方面考虑:①造等量②为证等量与被证二量相等而添。
参考例4、例5、例6。
例1 AD是△ABC的中线,ABEF和ACGH是分别以AB和AC 为边向形外作的正方形。
求证:FH=2AD证明:延长AD至N使AD=DN则ABNC是平行四边形∴CN=AB=FA AC=AH又∠FAH+∠BAC=180°∠BAC+∠ACN=180°∴△FAH≌△NCA ∴FH=AN ∴FH=2AD例2、△ABC中,∠B=2∠C,AD是高,M是BC边上的中点。
求证:DM=12AB 证明:取AB 的中点N ,连接MN 、DN 则 MN ∥AC ∠1=∠C ∠2=∠B ∴∠2=2∠1 ∴∠1=∠DNM ∴DM=DN又 AN=DN=ND ∴DM=12AB 例3 △ABC 中,AB=AC ,E 是AB 的中点,D 在AB 的延长线上,且DB=AC 。
求证:CD=2CE证明:过B 作CD 的中线BF则 BF ∥12AC ∠A=∠DBF ∵AB=AC ,E 是AB 的中点∴BF=AE又DB=AC ∴△AEC ≌△BFD ∴DF=CE ∴CD=2CE作业:1、在△ABC 中,D 为BC 的中点,E 为AD 的中点,BE 的延长线交AC 于F ,求证:AF=12FC 2、AB 和AC 分别切⊙O 于B 和C ,BD 是直径。
求证∠BAC=2∠CBD3、圆内接△ABC 的AB=AC ,过C 作切线交AB 的延长线于D ,DE 垂直于AC 的延长线于E 。
七年级数学竞赛培优第四讲线段和角(最新整理)
7、我们知道:平面上有一个点,过这一点可以画无数条直线.
若平面上有两个点,则过这两点可以画的直线的条数是
;
若平面上有三个点,过每两点画直线,则可以画的直线的条数是
;
若平面上有四个点,过每两点画直线,则可以画的直线的条数是
.
8、如图,已知∠AOB=90°,∠BOC=30°,OM 平分∠AOB,ON 平分∠BOC.
(1)三点整时时针与分针所夹的角是度
.
(2)7 点 25 分时针与分针所夹的角是度
.
(3)一昼夜(0 点到 24 点)时针与分针互相垂直的次数有多少?
6、α 为锐角,β 为钝角,甲、乙、丙、丁四人在计计算 1 时结果依次为 10°,23°,46°,51°,其中
6 只有一个是正确的,你知道四人中谁的结果正确吗?
暑假精英训练
第四讲 线段和角 典型例题: 1、下图是某一立方体的侧面展开图,则该立方体是( )
2012.07
A
B
C
D
2、由下列条件一定能得到“P.是线段 A.B 的中点.”的是(. )
A、AP= 1 AB 2
B、AB=2PB
C、AP=PB
D、AP=PB= 1 AB 2
3、将长为 10 厘米的一条线段用任意方式分成 5 小段,以这 5 小段为边可以围成一个五边形.问其中最
2 其中能表示 B 是线段 AC 的中点的有( )
A.1 个 B.2 个 C.3 个 D.4 个
4、如图所示,B、C 是线段 AD 上任意两点,M 是 AB 的中点,N 是 CD 中点,若 MN=a,BC=b,则线
段 AD 的长是(
)
A
M
B
A 2(a-b) B 2a-b C a+b D a-b
线段及角的和差倍分计算
线段及角的和差倍分计算
首先我们来介绍线段的和、差计算方法。
1.线段的和计算:
设线段AB的长度为a,线段BC的长度为b,那么线段AC的长度为
a+b。
2.线段的差计算:
设线段AB的长度为a,线段BC的长度为b,那么线段AC的长度为,
a-b,即两个线段长度的差的绝对值。
接下来我们来介绍角的和、差计算方法。
1.角的和计算:
设角A的度数为α,角B的度数为β,那么角A和角B的度数和为
α+β。
2.角的差计算:
设角A的度数为α,角B的度数为β,那么角A和角B的度数差为,α-β,即两个角度数的差的绝对值。
--------------------------------------------
下面我们来介绍线段和角的倍数计算方法。
1.线段的倍数计算:
设线段AB的长度为a,倍数为n,那么线段AB的n倍长度为na。
2.角的倍数计算:
设角A的度数为α,倍数为n,那么角A的n倍度数为nα。
需要注
意的是,角度的n倍有时候不是一个具体的度数,而是一种表示角度大小
关系的相对概念。
线段和角的等分计算方法:
1.线段的等分计算:
设线段AB的长度为a,要将其等分成n份,那么每一份的长度为a/n。
例如,要将线段AB等分成3份,那么每一份的长度为a/3
2.角的等分计算:
设角A的度数为α,要将其等分成n份,那么每一份的度数为α/n。
例如,要将角A等分成2份,那么每一份的度数为α/2。
人教七下线段的和差倍分计算专题
线段的和差倍分计算一.和差问题1.线段上有1个点。
如线段AB上有一点M和:AB=+差:AM=—BM=—2.线段上有2个点。
如点M、N是线段AB上的两个点。
和:AB=++;AN=+;MB=+差:AM=AB—;AM=AN—;MN=AB——;MN=AN—MN=MB—;NB=AB—;NB=MB—。
2.如图,若线段AC=4cm,BC=3.5cm,求线段AB的长.思路指引:(1)已知条件有哪些?求什么?(2)利用线段的和还是差来求线段AB的长?(3)在右边的框里填写推理步骤。
3.如图,若线段AC=4,AB=7,求线段CB的长.4、已知线段AB=8点C在线段AB上,且BC=3,求线段AC的长.二.线段中点的图形及符号语言:线段中点的三种表示方法:如图(1)∵C 是线段AB 中点∴=(2)∵C 是线段AB 中点∴=2或=2(3)∵C 是线段AB 中点∴=12或=12三应用新知1:已知:如图线段AB=6cm,点C 是线段AB 的中点,求线段BC 的长解:∵C 是线段AB 中点∴=12又∵AB=6∴=12=12=答:线段BC 的长是________2已知:如图,若线段CA=5cm,点C 是线段AB 的中点,求线段BC 的长3已知:如图,若线段CB=7cm,点C 是线段AB 的中点,求线段BA 的长C A练习:A 层1、已知点M 是线段AE 的中点,则AM=______,AE=____MEAM=_____AE2已知,点F 是线段AB 的中点,线段BF=6cm ,求线段AB 的长B 层1.如图:AB=4cm ,BC=3cm ,如果O 是线段AC 的中点,求线段OB 的长度.解:∵AB=4,BC=3,AC=______+______=4+3=7又∵O 为AC 的中点,∴OC=______AC=______=______∴OB=OC-BC=_____-______=__________2.已知:如图,AB=16cm ,点C 为AB 的中点,点D 为CB 的中点,求线段CD 的长3、如图,C 为线段AB 的中点,D 在线段CB 上,DA=8,DB=6,求CD 的长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学竞赛专题选讲
线段、角的和差倍分
一、内容提要
证明线段、角的和,差,倍,分,常用两种方法:一是转化为证明线段或角的相等关系;一是用代数恒等式的证明方法。
一.转化为证明相等的一般方法
㈠通过作图转化
1.要证明一线段(角)等于两线段(角)的和(用截长补短法)
⑴分解法――把大量分成两部分,证它们分别等于两个小量
⑵合成法――作出两个小量的和,证它与大量相等
2.要证明一线段(角)等于另一线段(角)的2倍
⑴折半法――作出大量的一半,证它与小量相等
⑵加倍法――作出小量的2倍,证它与大量相等
㈡应用有关定理转化
1.三角形中位线等于第三边的一半,梯形中位线等于两底和的一半
2.直角三角形斜边中线等于斜边的一半
3.直角三角形中,含30度的角所对的直角边等于斜边的一半
4.三角形的一个外角等于和它不相邻的两个内角和
5.等腰三角形顶角的外角等于底角的2倍
6.三角形的重心(各中线的交点)分中线为2∶1
7.有关比例线段定理
二.用代数恒等式的证明
1.由左证到右或由右证到左
2.左右两边分别化简为同一个第三式
3.证明左边减去右边的差为零
4.由已知的等式出发,通过恒等变形,到达求证的结论
二、例题
例1.已知:△ABC中,∠B=2∠C,AD是高
求证:DC=AB+BD
分析一:用分解法,把DC分成两部分,分别证与AB,BD相等。
可以高AD为轴作△ADB的对称三角形△ADE,再证EC=AE。
∵∠AEB=∠B=2∠C且∠AEB=∠C+∠EAC,∴∠EAC=∠C
辅助线是在DC上取DE=DB,连结AE。
分析二:用合成法,把AB,BD合成一线段,证它与DC相等。
仍然以高AD为轴,作出DC的对称线段DF。
为便于证明,辅助线用延长DB到F,使BF=AB,连结AF,则可得
∠ABD =2∠F =2∠C 。
例2.已知:△ABC 中,两条高AD 和BE 相交于H ,两条边BC 和AC
的中垂线相交于O ,垂足是M ,N
求证:AH =2MO , BH =2NO 证明一:(加倍法――作出OM ,ON 的2倍) 连结并延长CO 到G 使OG =CO 连结AG ,BG 则BG ∥OM ,BG =2MO ,AG ∥ON ,AG =2NO
∴四边形AGBH 是平行四边形, ∴AH =BG =2MO ,BH =AG =2NO
证明二:(折半法――作出AH ,BH
分别取AH ,BH 的中点F ,G 连结FG ,MN
则FG =MN =21AB ,FG ∥MN ∥AB 又∵OM ∥AD ,
∴∠
OMN =∠HGF (两边分别平行的两锐角相等)
同理∠ONM =∠HFG ∴△OMN ≌△HFG ……
例3. 已知:在正方形ABCD 中,点E 在AB 上且CE =AD +AE ,F
是AB 的中点
求证:∠DCE =2∠BCF
分析:本题显然应着重考虑如何发挥CE =AD +AE 条件的作用,如果
只想用加倍法或折半法,则脱离题设的条件,难以见效。
我们可将AE (它的等量DG )加在正方形边CD 的延长线上(如左图)
也可以把正方形的边CD (它的等量AG )加在AE 的延长线上(如右图)
后一种想法更容易些。
辅助线如图,证明(略)自己完成
A B D F B C D G
例4.已知:△ABC 中,∠B 和∠C 的平分线相交于I ,
求证:∠BIC =90 +2
1∠A 证明一:(由左到右)
∠BIC =180 -(∠1+∠2)=180 -2
1(∠ABC +∠ACB ) =180 -21(∠ABC +∠ACB +∠A )+2
1∠A =90 +2
1∠A
证明二:(左边-右边=0) ∠BIC -(90 +2
1∠A ) =180 -21(∠ABC +∠ACB )-90 -2
1∠A =90 -2
1(∠ABC +∠ACB +∠A )=…… 证明三:(从已知的等式出发,进行恒等变形)
∵∠A +∠ABC +∠ACB =180 ∴∠A =180 -(∠ABC +∠ACB ) 21∠A =90 -2
1(∠ABC +∠ACB ) 90 +21∠A =180 -21(∠ABC +∠ACB ),即∠BIC =90 +2
1∠A 三、练习
1. △ABC 中,∠B =2∠C ,AD 是角平分线,求证:AC =AB +BD
2. △ABC 中,∠B =2∠C ,AD 是高,M 是BC 的中点,则AB =2DM
3. △ABC 中,∠B 的平分线和∠C 的外角平分线交于E ,则∠A =2∠E
4. △ABC 的AB =AC ,CD 是中线,延长AB 到E 使BE =AB ,连结EC ,
则CE =2CD
5. 已知:等腰直角三角形ABC 中,∠A =Rt ∠,BD 是角平分线
求证:BC =AB +AD
6. 已知:△ABC 中,AB <AC ,AD 是高,AE 是角平分线
求证 :∠DAE =2
1(∠B +∠C ) 7. 已知:△ABC 中,AB =AC ,点D 在AC 的延长线上,
求证:∠CBD =2
1(∠ABD -∠D )
8. 已知:AD 是△ABC 的中线,E 是AD 的中点,BE 延长线交AC 于F
求证:BF =4EF
9. 已知:在正方形ABCD 中,E 是BC 边上的一点,AF 平分∠DAE ,交
CD 于F
求证:AE =BE +DF
10. 在△ABC 中,∠BAC =Rt ∠,BC 的中垂线MN 交AB 于M ,交BC 于
N ,角平分线AD 延长线交MN 于E ,则BC =2NE
(1987年泉州市双基赛题)
11. 以Rt △ABC 两直角边AC ,BC 为边向形外作正方形ACDE 和BCFG ,
分别过E ,G 作斜边AB 所在直线的垂线段EE ,,GG ,则AB =EE ,+GG ,
12. 已知:△ABC 中,AB =AC ,AD 是高,CE 是角平分线EF ⊥BC 于F ,
GE ⊥CE 交CB 延长线于G ,
求证:FD =4
1CG (提示:以CE 为轴作△CEG 的对称三角形) 13. 已知:△ABC 中,∠A =100 ,AB =AC ,BD 是角平分线
求证:BC =BD +AD
14. 已知:正方形ABCD 中,AE 平分∠BAC 交BC 于E ,交BD 于F ,O
是对角线的交点
求证:CE =2FO
15. 已知:如图AC ,BD 都垂直于AB ,且CD 交AB 于E ,CE =2AD
求证:∠ADE =2∠BDE
16. 已知:△ABC 中,AB <AC <BC ,点D 在BC 上,点E 在BA 的延长
线上,且BD =BE =AC ,△BDE 的外接圆和△ABC 的外接圆交于点F 求证:BF =AF +FC (1991年全国初中数学联赛题)
(提示:在BF 上取BG =CF )
(15)
练习题参考答案
1.以AD轴作轴对称三角形
2.取AB中点N,再证明DN=DM
3.利用外角性质,分别用两角差表示∠A和∠E
4.有多种证明方法,注意三角形中位线性质
5.在BC上取BE=BD,则△EDC等腰,作DF∥BC交AB于F,可证△
ECD≌△ADF
6.∠B+(∠BAE-∠DAE)=90,∠C+(∠EAC+∠DAE)=90
7.∠ABC=∠ACB=∠D+∠CBD,两边同加上∠CBD
10.作高AH
12延长GE交AC于M,则E是GM的中点,作EP∥BC交AC于P,则EP被AD平分
16.在BF上截取BG=FC,△BGE≌△CFA,再证GE=GF
[文章来源:教师之家/转载请保留出处] [相关优质课视频请访问:教学视频网/]。
