第3章 恒定磁场
恒定电流与真空中的恒定磁场
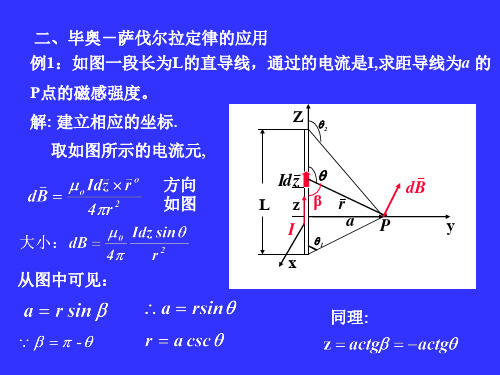
例1:如图一段长为L的直导线,通过的电流是I,求距导线为a 的
P点的磁感强度。
解: 建立相应的坐标. 取如图所示的电流元, 方向 如图
从图中可见:
Z 2
Idz L z β r
I
a
1
x
dB
P
y
同理:
β
在此坐标系下写成矢量式
注意: θ 1θ2 分别是导线的起点 和终点处的电流元与该处
1、无限长载流直导线 :
2、无限长均匀通电
B=
圆柱体 :
3、无限长均匀通电圆柱体 面:
练习题:
16-1;16 -2;16-3;
16-5 ;16- 7.
4、密绕通电螺绕环
5、无限大均匀载流平面
§11-10 磁力及其应用 一.带电粒子在磁场中受力 1.洛仑兹力
方向用左手定则 综合考虑 :
注意 :电荷为负计算时, 代入符号,即方向与上方 向相反。
1、 r < R ;作一与磁力线同心 的回路如图所示,则有:
而:
2、r >R ;同理作如图的所示回路,则: 则有:
B=
例:无限大的金属板,电流方向如图所示,单位长度的电流
为I ,求离板为L 处的磁感强度。
解:由对称性可知:磁力
B
线平行于板面,如图所示。
取如图所示的回路,则:
例:导体横截面如图所示,半径均为R,两圆心距离OO‘ 为1.6R,沿轴向通以反向电流 ,电流密度为j ,求在其所围 的缺口中任一点的磁感强度。
2.应用之一
霍耳效应
1879年美国物理学家霍耳发现
1879年美国物理学家霍耳发 现: 对应图中沿Z方向有电势差
第三章 静磁场

二、磁偶极子的场与标势
由磁偶极子的势 可计算出磁偶极子的场,
(其中, , )
由于
所以
如果定义 为磁偶极子的磁标势。
则 ,
总之,一个小范围内的电流分布在远处产生的磁场的最初级近似为磁偶极近似,
矢势的最初级近似 。
磁场的最初级近似 。
三、小区域电流在外场中的能量
1、电流分布 在外场中的相互作用能
当研究介质中的磁场时,必须考虑介质的磁化对场的影响。自由电流产生磁场,磁场作用于介质产生磁化电流,又激发磁场,场再作用于介质……也必须象静电学问题一样,求解反映场与介质相互作用的微分方程(在一定边界条件下求解)。
我们先引入静磁场的矢势,导出矢势满足的微分方程,然后再讨论磁标势及其微分方程,最后讨论磁多极展开。
球内磁场是
铁球内外的 和 。 线总是闭合的,而 线则不然。 线从右半球面的正磁荷发出,止于左半球的负磁荷。在铁球内部, 和 反向,说明磁铁内部的 和 是有很大的差异。
代表磁铁内的总宏观磁场,即在物理小体积内对微观磁场的平均值,而 仅为一辅助场量。
静电场
静磁场
无旋场
无源场
(由此,历史上人们错误地认为 与 相对应)
2、矢势的一级近似
恒定电流可以分成许多闭合电流管,我们就一个电流管计算上式。若线圈电流为 ,则有
由于 为线圈上各点的坐标,因此 ( 表示对带撇的变量微分)。利用全微分绕闭合回路的线积分等于零,得
因此
则
其中 ,是电流体系的磁偶极矩。电流分布是一个小线圈,则 , 是线圈的面积矢量, , 为线圈法线方向单位向量, 与电流方向满足右手螺旋关系。
若考虑外场变化的情况,设外场是由另一带有电流 的线圈 产生。
恒定磁场环路定理物理意义

恒定磁场环路定理物理意义恒定磁场环路定理就像是一场神秘的磁场旅行中的魔法规则。
想象一下,磁场就像一个超级复杂的迷宫,里面到处都是看不见的磁力线在穿梭。
这个定理说的是,在恒定磁场中,磁感应强度沿任何闭合路径的线积分,等于这个闭合路径所包围的电流的代数和乘以真空磁导率。
这就好比是在磁场迷宫里,沿着特定的路线走一圈,所积累的某种神秘力量(线积分)和路线中间包围的电流宝藏(电流的代数和)有着紧密的联系。
电流就像是磁场迷宫里的能量小精灵,有的小精灵带来正向的力量,有的带来负向的力量,它们综合起来通过乘以真空磁导率这个魔法系数,就决定了沿着闭合路径走一圈感受到的磁场的那种积累效果。
如果把磁场比作是一场盛大的无形舞会,磁力线就是舞者们的舞步轨迹。
恒定磁场环路定理就像是规定了这个舞会上,当你沿着某个特殊的环形舞步路径走的时候,你所感受到的舞步的总体旋转力度(线积分)和在这个环形舞步中间那些发电小站(电流)的总和有关。
那些发电小站就像一个个小电池,它们输出的电量有正有负,就像电池的正负极一样,不同方向的电流就像性格不同的小精灵在磁场里捣乱或者帮忙。
从更宏观的角度看,这个定理就像是磁场世界的一本账本。
每一个闭合回路就像一个账目单元,而包围的电流就像这个单元里的收支情况。
磁场的线积分就是这个账目单元最后的结余,它反映了这个单元内部电流收支平衡后的结果。
如果把电流想象成是一群调皮的小怪兽在磁场这个大森林里到处跑,那么定理就是在计算小怪兽们在某个特定区域内活动所造成的磁场森林的整体变化。
恒定磁场环路定理还像是一个磁场美食配方。
闭合路径是装美食的盘子,电流是食材,不同方向的电流就像酸甜苦辣各种味道的食材。
真空磁导率就是烹饪的火候或者调味料的比例。
按照这个配方,你就能算出这盘磁场美食(线积分)最终的味道和效果。
它也像是磁场交通规则中的一条重要法则。
磁力线在磁场空间里穿梭,就像车辆在道路上行驶。
闭合路径是一条特殊的环形道路,电流就是在道路中间区域那些影响交通流(磁场)的特殊因素。
《电磁波与电磁场》4-恒定磁场

外加磁场时,磁场力使带电粒子的运动方向发生变化或产生 新的电流,使磁矩重新排列,宏观的合成磁矩不再为零,这 种现象称为磁化。
媒质磁化 B
B
B'
磁化结果出磁偶现极的子 合成磁矩产生二次磁场BS,这种二次 磁场影响外加磁场Ba,导致磁化状态发生改变,从而又使J’S
Chapter 4 恒定磁场
磁场是由运动电荷或电流产生的;当产生磁场 的电流恒定时,它所产生的磁场不随时间变化, 这种磁场称为恒定磁场。
4.1 磁感应强度 4.3 磁场的基本方程 4.5 电感 4.7 磁路
4.2 安培环路定律 4.4 磁场位函数 4.6 磁场能量
第4章 恒定磁场
1. 磁场是由运动电荷或电流产生的。 2. 运动电荷或载流导线在磁场中要受到磁场的作用力。 3. 检验磁场是否存在的一种方法是改变载流导线在磁
抗磁性。媒质正常情况下,原子中的合成磁矩为零。当外 加磁场时,电子进动产生的附加磁矩方向总是与外加磁场 的方向相反,导致媒质中合成磁场减弱。如银、铜、铋、 锌、铅及汞等属抗磁性媒质。 顺磁性。媒质在正常情况下,原子中的合成磁矩并不为零, 只是由于热运动结果,宏观的合成磁矩为零。在外加磁场的 作用下,磁偶极子的磁矩方向朝着外加磁场方向转动。使合 成磁场增强。如铝、锡、镁、钨、铂及钯等属顺磁性媒质。
但是,无论抗磁性或者顺磁性媒质,其磁化现象均很微弱,因此,可 以认为它们的相对磁导率基本上等于1。铁磁性媒质的磁化现象非常 显著,其磁导率可以达到很高的数值。值得注意的是,近年来研发的 新型高分子磁性材料,其相对磁导率可达到与介电常数同一数量级。
媒质 金 银 铜
大学物理稳恒磁场理论及习题

结果:
1.
F
v,
B组
成
的
平
面.
2. F 大小正比于v, q0,sin.
q0沿磁场方向运动, F 0.
q0 垂直磁场方 向运动, F Fmax .
NIZQ 第4页
大学物理学 恒定磁场
在垂直磁场方向改变速率v,改变点电荷 电量q0 .
结论: 场中同一点, Fmax/q0v有确定值. 场中不同点, Fmax/q0v量值不同.
大学物理学 恒定磁场
从毕-萨定律导出运动电荷的磁场
S: 电流元横截面积
n: 单位体积带电粒子数
q: 每个粒子带电量
v: 沿电流方向匀速运动
电流元 Idl产生的磁场:
大学物理学 恒定磁场
一.磁场 磁感应强度
• 磁性起源于电荷的运动 磁铁的磁性: 磁性: 能吸引铁、钴、镍等物质的性质.
磁极: 磁性最强的区域, 分磁北.
磁力: 磁极间存在相互作用, 同号相斥,
异号相吸.
问题: 磁现象产生的原因是什么?
司南勺
北宋沈括发明 “指南针(罗盘
1.在任何磁场中每一条磁感线都
是环绕电流的无头无尾的闭合线, 条形磁铁周围的磁感线 即没有起点也没有终点,而且这些
闭合线都和闭合电路互相套连.
2.在任何磁场中,每一条闭合的磁
感线的方向与该闭合磁感线所包围
的电流流向服从右手螺旋法则.
直线电流的磁感线
NIZQ 第6页
大学物理学 恒定磁场
二.毕澳-萨伐尔定律
r a
sin
B
l
dB
2 1
0I
4π
a
sin 2
sin 2
a2
sin d
《电磁场与电磁波》复习纲要(含答案)

S
第二类边值问题(纽曼问题) 已知场域边界面上的位函数的法向导数值,即 第三类边值问题(混合边值问题) 知位函数的法向导数值,即
|S f 2 ( S ) n
已知场域一部分边界面上的位函数值,而其余边界面上则已
|S1 f1 ( S1 )、 | f (S ) S 2 2 n 2
线处有无限长的线电流 I,圆柱外是空气(µ0 ),试求圆柱内 外的 B 、 H 和 M 的分布。 解:应用安培环路定理,得 H C dl 2 H I I H e 0 磁场强度 2π I e 0 a 2 π 磁感应强度 B I e 0 a 2 π 0 I B e 2π M H 磁化强度 0 0 0
C
F dl F dS
S
5、无旋场和无散场概念。 旋度表示场中各点的场量与旋涡源的关系。 矢量场所在空间里的场量的旋度处处等于零,称该场为无旋场(或保守场) 散度表示场中各点的场量与通量源的关系。 矢量场所在空间里的场量的散度处处等于零,称该场为无散场(或管形场) 。 6、理解格林定理和亥姆霍兹定理的物理意义 格林定理反映了两种标量场 (区域 V 中的场与边界 S 上的场之间的关系) 之间满足的关系。 因此,如果已知其中一种场的分布,即可利用格林定理求解另一种场的分布 在无界空间,矢量场由其散度及旋度唯一确定 在有界空间,矢量场由其散度、旋度及其边界条件唯一确定。 第二章 电磁现象的普遍规律 1、 电流连续性方程的微分形式。
D H J t B E t B 0 D
D ) dS C H dl S ( J t B E dl dS S t C SB dS 0 D dS ρdV V S
电磁场与电磁波7-1pdf
学时:5学时
电磁场与电磁波
第一节 波动方程及其解
电磁波 波动方程 波动方程的解 解的物理意义
电磁场与电磁波
电磁波
回忆麦克斯韦第一方程:
H
J
D
t
回忆麦克斯韦第二方程:
E
B
t
电磁场与电磁波
电磁波
H
J
D
t
E
B
t
从麦克斯韦第一方程可以看出,若电场对时间
E
H
t
消去一个变量,直接代入不容易,考虑把
E
H
t
两边做运算
根据矢量恒等式 E E 2 E
所以 E E 2 E 2 E
电磁场与电磁波
H
t
0
电磁场与电磁波
波动方程的解
2
E
2 E t 2
0
分析无源区域E在直角坐标系中的解
2
e
x
Ex
ey
Ey
ez
Ez
2
e
x
Ex
e y Ey
t 2
ez
Ez
第五-恒定磁场【共42张PPT】
B0 J
此式表明,真空中某点恒定磁场的磁感应强度的旋度等于该点的电流密度与真空 磁导率的乘积。
另外,由高斯定理获知
SBdSVBdV
那么,根据磁通连续性原理求得
VBdV0
由于此式处处成立,因此被积函数应为零,即
B0 此式表明,真空中恒定磁场的磁感应强度的散度处处为零。
综上所述,求得真空中恒定磁场方程的微分形式为
可见,无源区中磁感应强度B 是无旋的。
无
考虑到
,求得
关。为了计算方便起见,令所求的场 对于大多数媒质,磁化强度 M 与磁场强度 H 成正比,即
a 为物理无限小体积。
r - r' y 可见,矢量磁位 A 满足矢量泊松方程。
r' 当两者垂直时,受到的力矩最大。
e 点位于xz 平面,即 ' 在设小外电加流磁环场为四的根作长用度下为,l 的除电了流引元围起成电的子平进面方动框以,外电,流磁方' 向偶如极左子下的图示磁。矩方向朝着外加磁场方向转动。
例1 计算无限长的,电流为I 的线电流产生的磁感应强度。
z
dl
r′ r - r′
o
y
r e
x
I
解 取圆柱坐标系,如图示。令 z 轴沿电 流方向。 dl(rr)的方向为B 的方向。那 么,由图可见,这个叉积方向为圆柱坐标 中的 e 方向。因此,磁感应强度 B 的方 向为 e 方向,即
B Be
此式表明,磁场线是以 z 轴为圆心的一系列的同心圆。显然,此时磁场分布以 z 轴 对称,且与 无关。又因线电流为无限长,因此,场量一定与变量 z 无关,所 以,以线电流为圆心的磁场线上各点磁感应强度相等。因此,沿半径为r 的磁场线上 磁感应强度的环量为
恒定磁场分析
7
求证:
证 明:
∫
ur r B ds = 0
Q
ur µ B= 0 4π
∫
r ur Id l × R R3
r r u r r µ0 Idl × eR r ∴ ∫ B ds = ∫ ∫ c R2 d s s 4π
又Q
uv ur uv uv ur uv A× B C = A B×C
23
2、磁偶极子的标量位(解释P116) 磁偶极子的标量位(解释 ) 在无源区域( 在无源区域(只有无源 ∇ × H = J=0 uu r 区域才定义标量位): 区域才定义标量位): ∇×H =0 uu r H = −∇ ϕ m 由下面式子
P ( r ,θ , 0 )
µ0 µ0 1 A = p m × e r = − p m × ∇ 2 4πr 4π r B、幂级数近似) 与求电偶极子类似的方法(余弦定理、幂级数近似)可以得到 磁偶极子的矢量位和标量位: 磁偶极子的矢量位和标量位:
µ0 µ0 1 A= p m × er = − p m × ∇ 2 4πr 4π r
的距离,是标量。 其中 r 为场点 P 到磁偶极子中心 O 的距离,是标量。
这表明恒定磁场是无散有旋场, 这表明恒定磁场是无散有旋场, 无散有旋场 传导电流是其旋涡源。 传导电流是其旋涡源。
13
5-2、内、外半径分别为 a、b 的无限长空心圆柱中,均匀 - 、 、 的无限长空心圆柱中, 分布着轴向电流 求柱内、外的磁场强度。 I ,求柱内、外的磁场强度。
解:使用圆柱坐标系。电流密度沿轴线方向为 使用圆柱坐标系。
12
3、真空(介质)中磁场的基本方程: 真空(介质)中磁场的基本方程:
∫sB • d s = 0 , ∇•B =0 , ∇×H = J ∫c H • d l = I B = µ0H B = µH
恒定磁场基本方程的微分形式
恒定磁场基本方程的微分形式
恒定磁场基本方程的微分形式是指表达磁场变化率的一种方程形式,其中包括了磁场的旋度和磁场随时间变化的导数。
在电磁学领域中,磁场是一种非常重要的物理量,它与电场一起构成了电磁场,是电磁学理论的基础之一。
恒定磁场指的是磁场在时间上不发生改变的情况,因此可以将磁场看做是一个恒定的场。
对于恒定磁场,其基本方程可以表示为:
∇×B = μ0J
其中,B是磁场,J是电流密度,μ0是真空中的磁导率,∇×表示旋度运算符。
这个方程表达了磁场的旋度与电流密度之间的关系,可以通过旋度运算符来求解。
旋度运算符是一个矢量运算符,用于计算一个矢量场的旋度。
它将一个矢量场的偏导数进行了组合,并给出了一个新的矢量场。
在这个方程中,磁场的旋度表示了磁场的变化率,而电流密度则表示了磁场的来源。
这个方程告诉我们,如果我们知道了磁场的变化率和电流密度,就可以求解出磁场的分布情况。
如果我们考虑磁场随时间的变化,那么可以将上述方程进行扩展,得到恒定磁场基本方程的微分形式:
∇×E = -∂B/∂t
其中,E是电场,B是磁场,∂/∂t表示对时间的偏导数。
这个方程表示了电场的旋度与磁场随时间变化的导数之间的关系。
它告诉我们,如果我们知道了磁场随时间的变化率和电场的旋度,就可以求解出电场的分布情况。
恒定磁场基本方程的微分形式是电磁学中非常重要的一个方程形式。
它将磁场的变化率和电流密度联系起来,以及将电场的旋度和磁场随时间的变化联系起来,为电磁学理论的研究提供了重要的基础。
