河北省邢台一中2013—2014学年高二下学期第三次月考数学理试题
河北省唐山一中2013-2014学年高二下学期开学调研考试数学理试卷Word版含答案

唐山一中高二年级第二学期第一次调研考试 数学试题(理科)第Ⅰ卷 选择题(共60分)一.选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项符合题目要求,将正确答案填涂在答题卡上。
1.不等式21ax <解集为Q ,{}0p x x =≤,若104R Q C P x x ⎧⎫=<<⎨⎬⎩⎭,则a 等于 A.14 B.12C.4D. 2 ( ) 2.设复数21i z i=-,则z = ( ) A .1i + B .1i - C .1i -+ D .1i -- 3.设S n 为等比数列{a n }的前n 项和,若0852=-a a ,则=24S S ( ) A.8- B.5 C. 8 D. 154. 已知直线l ⊥平面α,直线m ⊂平面β,则“α//β”是“l ⊥m ”的 ( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件5.已知命题p :∀x ∈(0,∞+),3x >2x ,命题q :∃x ∈(∞-,0),x x ->2,则下列命题为真命题的是 ( )A . p ∧qB .(¬p )∧q C.(¬p )∧(¬q ) D.p ∧(¬q )6. 直线x -2y -3=0与圆C :(x -2)2+(y+3)2=9交于E 、F 两点,则△ECF 的面积为( )A .23 B.52 C. 553 D. 437.已知向量(sin(),1),(4,4cos 6παα=+=a b ,若⊥a b ,则4sin()3πα+等于( )A. B. 14- C. D. 148. 已知双曲线22221x y a b-= (0,0)a b >>的左、右焦点分别为12,F F ,以12||F F 为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为 ( ) A .221916x y -= B .22134x y -= C . 221169x y -= D .22143x y -=9. 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图可能为()10.函数3sin(2)3y xπ=-的图像为C,如下结论中错误的是()A.图像C关于直线1112xπ=对称B.图像C关于点2(,0)3π对称C.函数()f x在区间)127,12(ππ-内是增函数D.由xy2cos3=得图像向右平移125π个单位长度可以得到图像C11. 已知函数()(f x x∈R)是偶函数,且(2)(2)f x f x+=-,当[0,2]x∈时,()1f x x=-,则方程1()1||f xx=-在区间[10,10]-上的解的个数是()A.8 B.9 C.10 D.1112. △ABC内接于以O为圆心,1为半径的圆,且02=-+OCOBOA ,则的值为()A.1- B.1 C. 2- D. 2第Ⅱ卷非选择题(共90分)二.填空题:本大题共4小题,每小题5分,共20分,将答案填在答题卡上相应位置。
河北省邢台一中高二数学下学期第一次月考试题 理 新人教A版

河北省邢台一中2013-2014学年高二数学下学期第一次月考试题 理新人教A 版第Ⅰ卷 (选择题共60分)一、选择题(每小题5分,共60分)1.如果随机变量),1(~2σξ-N ,且4.0)13(=-≤≤-ξP ,则=≥)1(ξP ( ) A .4.0 B . 3.0 C . 2.0 D .1.02 )A .1B . 4πC . 2312+π D .216+π 3.一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X 是一个随机变量,其分布列为)(X P ,则)4(=X P 的值为( )A . 2201B . 5527C . 22027D .25214.过点)1,1(-且与曲线x x y 23-=相切的直线方程为( ) A . 014502=-+=--y x y x 或 B . 02=--y x C .015402=++=--y x y x 或 D . 02=+-y x5.已知函数32()2(0)f x x ax x a =+++>的极大值点和极小值点都在区间(1,1)- 内,则实数a 的取值范围是( )A .(0,2]B .(0,2)C 6.甲乙两人进行羽毛球比赛,比赛采取五局三胜制,无论哪一方先胜三局则比赛结束,假定甲每局比赛获胜的概率均为32,则甲以1:3的比分获胜的概率为( ) A . 278 B . 8164 C . 94 D .987.已知箱中共有6个球,其中红球、黄球、蓝球各2个.每次从该箱中取1个球 (有放回,每球取到的机会均等),共取三次.设事件A :“第一次取到的球和第二次取到的球颜色相同”,事件B :“三次取到的球颜色都相同”,则P(B|A)=( )A.18.设函数在上可导,其导函数,且函数在处取得极小值,则函数的图象可能是( )9.现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙、丙不会开车但能从事其他三项工作,丁、戊都能胜四项工作,则不同安排方案的种数是( ) A .240 B .126 C .78 D .7210.使nxx x )13(+()*N n ∈的展开式中含有常数项的最小的n 为( ) A .4 B .5 C .6 D .711.函数1)(23+-=bx x x f 有且仅有两个不同的零点,则b 的值为( ) A .243B .223C .3223D .不确定12.设函数()y f x =在(0,+∞)内有定义,对于给定的正数K ,定义函数(),()(),()K f x f x K f x K f x K ≤⎧=⎨>⎩,取函数ln 1()x x f x e +=,恒有()()Kf x f x =,则 A .K 的最大值为1e B .K 的最小值为1e C .K 的最大值为2 D .K 的最小值为2第Ⅱ卷 (非选择题共90分) 二、填空题:(每小题5分,共20分)13.有编号分别为1,2,3,4,5的5个红球和5个黑球,从中随机取出4个,则取出球的编号互不相同的概率为_______________14.已知函数223)(a bx ax x x f +++=在1=x 处有极值10,则)2(f 等于_______15.箱中装有标号为1,2,3,4,5,6且大小相同的6个球,从箱中一次摸出两个球,记下号码并放回,如果两球号码之积是4的倍数,则获奖.现有4人参与摸奖,恰好有3人获奖()f x R()f x '()f x 2x =-()y xf x '=的概率是________________16. 定义在R 上的函数()f x 满足:(1)1f =,且对于任意的x R ∈,都有1'()2f x <,则不等式22log 1(log )2x f x +>的解集为 __________________三、解答题:(第17题满分10分,第18~22题满分各12分)17.(1)求921⎪⎪⎭⎫⎝⎛-x x 的展开式中的常数项;(2)已知1010221010)2(...)2()2(+++++++=x a x a x a a x ,求10321...a a a a ++++的值.18.生产A ,B 两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为(1)试分别估计元件A 、元件B 为正品的概率;(2)生产一件元件A ,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B ,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下, (i )求生产5件元件B 所获得的利润不少于300元的概率;(ii )记X 为生产1件元件A 和1件元件B 所得的总利润,求随机变量X 的分布列和数学期望.19.用0,1,2,3,4这五个数字组成无重复数字的自然数. (1)在组成的三位数中,求所有偶数的个数;(2)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;(3)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数. 20.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸.呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为53.(1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;(3)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为ξ,求ξ的分布列,数学期望以及方差.下面的临界值表供参考:(参考公式 其中)21.“蛟龙号”从海底中带回的某种生物,甲乙两个生物小组分别独立开展对该生物离开恒温箱的成活情况进行研究,每次试验一个生物,甲组能使生物成活的概率为31,乙组能使生物成活的概率为21,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的.甲小组做了三次试验,求至少两次试验成功的概率;如果乙小组成功了4次才停止试验,求乙小组第四次成功前共有三次失败,且恰有两次连续失败的概率;若甲乙两小组各进行2次试验,设试验成功的总次数为ξ,求ξ的期望. 22. 已知函数()()2ln 1f x ax x =++.(1时,求函数()f x 的单调区间;(2)若函数()f x 在区间[)1,+∞上为减函数,求实数a 的取值范围;(3)当[)0,x ∈+∞时,不等式()0f x x -≤恒成立,求实数a 的取值范围.邢台一中2013—2014学年下学期第一次月考2)若个位数为2或4,则共有(种)所以,共有30个符合题意的三位偶数. (Ⅱ)将这些“凹数”分为三类: (1)若十位数字为0,则共有(种);18332=⨯⨯1224=A(2)若十位数字为1,则共有(种);(3)若十位数字为2,则共有(种),所以,共有20个符合题意的“凹数”(Ⅲ)将符合题意的五位数分为三类:(1)若两个奇数数字在一.三位置,则共有(种); (2)若两个奇数数字在二.四位置,则共有(种); (3)若两个奇数数字在三.五位置,则共有(种),所以,共有28个符合题意的五位数.20.试题分析:(Ⅰ)解:列联表补充如下 (Ⅱ)解:因为,所以>7.879那么,我们有99.5%的把握认为是否患心肺疾病是与性别有关系的. (Ⅲ)解:ζ的所有可能取值:0,1,2,3;;;;则623=A 222=A 123322=⋅A A 8221222=⋅⋅A C A 8221222=⋅⋅A C A22. (1)当14a =-时,()()()21ln 114f x x x x =-++>-,解()0f x '>得11x -<<;解()0f x '<得1x >,故()f x 的单调递增区间是()1,1-,单调递减区间是()1,+∞;(2)由题知(3)因为当[)0,x ∈+∞时,不等式()0f x x -≤恒成立,即()2ln 10ax x x ++-≤恒成立,设()()()2ln 10g x ax x x x =++-≥,只需()max 0g x ≤即可21①当0a =时,当0x >时,()0g x '<,函数()g x 在()0,+∞上单调递减故()()00g x g ≤=成立;②当0a >时,令,因为0x ≥,所以解得。
【数学】河北省唐山市一中2013-2014学年高二下学期期中考试(理)

第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设复数z 满足1+2,ii z=则z 等于 ( ) A.2i -+ B.2i -- C. 2i - D.2i + 2.已知函数()ln ,f x x x =-则()f x 的单调减区间是( )A.()1,-∞B.()01,C.()()01,,-∞+∞和D.()1+∞, 3.设x0f x tdt ()sin ,=⎰ 则[()]f f 2π的值等于 ( )A.1cos1-B.1C.cos1-D.1- 4.函数3()2f x x ax a =-+在(0,1)内有极小值,则实数a 的取值范围为 ( )A.(0,3)B.(,3)-∞C.(0,)+∞ 302.(,)D 5.设111(1)(1)(1),1(,,)M a b c a b c a b c=---++=且均为正数,由综合法得M 的取值范围是 ( )A. 108⎡⎤⎢⎥⎣⎦,B. 118⎡⎫⎪⎢⎣⎭,C. []18,D. [)+8∞, 6.已知2()(1),(1)1(),()2f x f x f x N f x *+==∈+猜想()f x 的表达式为 ( )A.4()22x f x =+B.2()1f x x =+C. 1()1f x x =+D.2()21f x x =+ 科网7.由6个座位连成一排,现有3人就坐,则恰有两个空座位相邻的不同坐法有( ).36种A .48种B .72种C .96种D 8.若20112011012011(12)(),x a a x a x x R -=+++∈则20111222011222a a a +++的值为( ).2A .0B .1C - .2D -9.从混有5张假钞的20张百元钞票中任意抽取两张2张,将其中一张在验钞机上检验发现是假钞,问这2张都是假钞的概率是 ( ) A.215 B.217 C.119 D.173810.对于变量y x 与的10组统计数据的回归模型中,相关指数20.95R =,又知残差平方和为.51203,那么1021()ii yy =-∑的值为 ( )A..62410B..02416C..02538D. .8253018.已知随机变量X 服从正态分布(3,1),(24)0.6826,(4)且则N P X P X ≤≤=>=( ) A..10585 B..10586 C..10587 D..0341312.已知函数()ln f x x =,21()()2g x x a a =+为常数,直线l 与 函数(),()f x g x 的图像都相切,且l 与函数()f x 图像的切点的横坐标为1,则a 的值为( )A. 1B. 12-C. 1-D.2 第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分.把正确答案填在题中横线上) 13.已知实数,m n 满足11mni i=-+,则复数z m ni =+的模z = _______________ 14. 小李练习射击,每次击中目标的概率为13,用ξ表示小李射击5次击中目标的次数,则ξ的均值E ξ与方差D ξ的值分别是______________________.15.定积分1-=⎰___________.16.当012,,a a a 成等差数列时,有01220;a a a -+=当0123,,,a a a a 成等差数列时,有0123330;a a a a -+-=当01234,,,,a a a a a 成等差数列时,有+012344640;a a a a a -+-=由此归纳,当 012,,,,n a a a a 成等差数列时,有012012(1)0n nn n n n n C a C a C a C a -+-+-=.如果012,,,,n a a a a 成等比数列,类比上述方法归纳出的等式为______________.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)一机器可以按各种不同的速度运转,其生产物件有一些会有缺点,每小时生产有缺点物件的多少随机器运转速度而变化,用x 表示转速(单位转/秒),用18.( 本小题满分12分)已知2()(1)1x x f x a a x -=+>+ (Ⅰ)证明函数()f x 在()1,-+∞上是增函数; (Ⅱ)用反证法证明方程()0f x =没有负数根.19.(本小题满分12分)已知数列{}n a 是首项11a =,公比为q 的等比数列, (Ⅰ)证明:11(,,).kk n n kC nC k n N k n -*-=∈≤ (Ⅱ)计算:12311212312()()()().nn n n n n a C a a C a a a C a a a C n N *++++++++++∈20.(本小题满分12分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为12与p ,且乙投球2次均未命中的概率为116. (Ⅰ)求乙投球的命中率p ;(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为ξ,求ξ的分布列和数学期望.21.(本小题满分12分)由下列各个不等式:11,21111,23111131,23472111112,23415>++>+++++>+++++>你能得到一个怎样的一般不等式?并加以证明.22.(本小题满分12分)设211()()ln()(),f x x x ax x a R =++--∈ (Ⅰ)若0,a =求函数()f x 的极值点及相应的极值;(Ⅱ)若对任意00(,),()x f x ∈+∞<恒成立,求实数a 的取值范围.参考答案三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分) 【解】(1)设回归直线方程为y bx a =+,125825.,.x y ==,44211660438,.ii i i i x x y ====∑∑于是2438412582551660412570..,.b -⨯⨯==-⨯ 516825125707..a y bx =-=-⨯=- 所以所求的回归直线方程为516707y x =-. 6分(2)由516707y x =-≤10,得76051x ≤, 即机器的速度不得超过14转/秒.10分18.(本小题满分12分) 【证明】(Ⅰ)23()ln (1)x f x a a x '=++,且已知1,1a x >>-, 2ln 0,(1)0,x a a x ∴>+>()0f x '∴>,故函数()f x 在()1,-+∞上是增函数.(注:也可以用单调性定义证明) 6分(Ⅱ)假设存在000(1)x x <≠-使0()0f x =,则0002.1x x a x -=-+ 00001,x x a<<<由得故002011x x -<-<+,解得:012,2x <<显然与00x <矛盾,所以使0()0f x =的0x 不存在,即方程()0f x =没有负数根.12分(ii)当1q ≠时,111,111kk kk k k n n n q b C C q C q q q-==---- 1212211()()11n n nn n n n n n C C C qC q C q C q q∴=+++-+++--原式 =112(1)(21)[(1)1].111n n n nq q q q q-+--+-=---11分故=12, 1.2(1), 1.1n n n n q q q q -⎧⋅=⎪⎨-+≠⎪-⎩原式12分20.(本小题满分12分)【解】(Ⅰ)P (乙投球2次均未命中)=p (乙投球2次命中0次)()()2002210116P C p p ==-=,∴()21116p -=,114p -=,∴34p =. 4分(Ⅱ)ξ可取0,1,2,3,则()() 0 0 0P P ξ⋅==甲中次乙中次020213111124421632C ⎛⎫⎛⎫=⨯⋅⋅=⨯= ⎪ ⎪⎝⎭⎝⎭, ()()() 0 1 1 0 1P P P ξ⋅⋅==+甲中次乙中次甲中次乙中次 1121022131131317244244163232C C ⎛⎫⎛⎫⎛⎫⎛⎫=⨯⋅⋅+⨯⋅⋅=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, ()()() 0 2 1 1 2P P P ξ⋅⋅==+甲中次乙中次甲中次乙中次201121221311313915244244163232C C ⎛⎫⎛⎫⎛⎫⎛⎫=⨯⋅⋅+⨯⋅⋅=+=⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭, ()() 1 2 3P P ξ⋅==甲中次乙中次222131924432C ⎛⎫⎛⎫=⨯⋅⋅= ⎪ ⎪⎝⎭⎝⎭, ∴ξ的分布列为:10分∴171590123232323232E ξ=⨯+⨯+⨯+⨯=. 12分21.(本小题满分12分)【解】根据给出的几个不等式可以猜想第n 个不等式,即一般不等式为: 11111().234212nnn N *+++++>∈- 4分用数学归纳法证明如下: (1)当n =1 时112>,猜想成立. 5分 (2)假设当时n k =猜想成立,即11111,234212k k+++++>-6分 则当1n k =+时,11111123421k ++++++-=1111123421k +++++-+111122121k k k +++++-2k >+111122121k k k +++++-2k >+ 1112111222k k k k ++++++个=121,222k k k k +++= 10分这就说明n k =猜想也成立,由(1)(2)知,猜想对一切n N *∈都成立.12分 22.(本小题满分12分) 【解】(Ⅰ)()f x 的极值点为0,相应的极小值为00().f =(过程略)4分(Ⅱ)12()ln(),f x x ax '=+- 设()()m x f x '=则1212211(),ax am x a x x -+-'=-=++ ① 当0a ≤时,0(),m x '>则()()m x f x '=在0(,)+∞上为增函数,所以00()(),f x f ''>=所以()f x 在0(,)+∞上为增函数,00()(),f x f ∴>=与0()f x <恒成立矛盾.② 当0a >时,12221()ax a m x a x --'=-⋅+, 若11202,a a -≤≥即时,0(),m x '<则()()m x f x '=在0(,)+∞上为减函数, 所以00()(),f x f ''<=所以()f x 在0(,)+∞上为减函数,00()(),f x f ∴<=满足题意.若120a ->,即102a <<时,若1202(,)ax a-∈,则0(),m x '> 则()()m x f x '=在1202(,)aa-上为增函数,从而有00()(),f x f ''>= 所以()f x 在1202(,)aa-上为增函数,00()(),f x f ∴>=与0()f x <恒成立矛盾. 综上所述,实数a 的取值范围.是12,.⎡⎫+∞⎪⎢⎣⎭12分。
河北省邢台一中2013-2014学年高一下学期第四次月考数学(理)试题

第I 卷(选择题共60分)一.选择题:(每小题5分,共60分)1.已知某几何体的三视图如图所示,则该几何体的体积为( )A.8π3 B .3π C.10π3 D .6π2. 直线1l :ax+3y+1=0, 2l :2x+(a+1)y+1=0, 若1l ∥2l ,则a=( )A .-3B .2C .-3或2D .3或-23. 设m 、n 是两条不同的直线,,,αβγ是三个不同的平面,给出下列四个命题: ①若m ⊥α,n //α,则m n ⊥ ②若αβ//,βγ//,m ⊥α,则m ⊥γ③若m //α,n //α,则m n // ④若αγ⊥,βγ⊥,则//αβ其中正确命题的序号是 ( )(A )①和② (B )②和③ (C )③和④ (D )①和④4.在△ABC 中,a =5,b =15,A =30°,则c 等于( )A .25 B. 5 C .25或 5 D .3 55.设变量x ,y 满足约束条件⎩⎪⎨⎪⎧ x ≥0,x -y ≥0,2x -y -2≤0,则z =3x -2y 的最大值为( )A .0B .2C .4D .66.已知各项均为正数的等差数列{a n }的前20项和为100,那么a 3·a 18的最大值是() A .50 B .25 C .100 D .2207. 已知直线l 过点(2,1),且在两坐标轴上的截距互为相反数,则直线l 的方程为()A . 10x y --= B. 30x y +-=或20x y -=C. 10x y --=或20x y -= D .30x y +-=或10x y --=8.在三棱柱ABC -A 1B 1C 1中,各棱长相等,侧棱垂直于底面,点D 是侧面BB 1C 1C 的中心,则AD 与平面BB 1C 1C 所成角的大小是( )A .30°B .45°C .60°D .90°9.若数列{x n }满足lg x n +1=1+lg x n (n ∈N *),且x 1+x 2+x 3+…+x 100=100,则lg(x 101+x 102+…+x 200)的值为( )A .102B .101C .100D .9910.过点M(-2,4)作圆C :(x -2)2+(y -1)2=25的切线l ,且直线l 1:ax +3y +2a =0与l 平行,则l 1与l 间的距离是( )A.85B.25C.285D.12511.如图,平面PAD ⊥平面ABCD ,ABCD 为正方形,090=∠PAD ,且F E AD PA ,,2==分别是线段CD PA ,的中点,则异面直线EF 与BD 所成角的余弦值为( ) A.33 B.23 C.43 D.6312.如图,四棱锥ABCD P -中,⊥PA 平面ABCD ,底面ABCD 是直角梯形,且CD AB //, 90=∠BAD ,2===DC AD PA ,4=AB .则点A 到平面PBC 的距离是( ) A.36 B.26 C.362 D.62 第II 卷(非选择题共90分)二.填空题:(每小题5分,共20分)13.如图所示,Rt △A ′B ′C ′为水平放置的△ABC 的直观图,其中A ′C ′⊥B ′C ′,B ′O ′=O ′C ′=1,则△ABC 的面积为________.14.△ABC 中,a 、b 、c 分别为A 、B 、C 的对边,如果a ,b ,c 成等差数列,B =30°,△ABCB的面积为32,那么b =15. 已知数列{}n a 中,11,a =前n 项和为n S ,且点*1(,)()n n P a a n N +∈在直线10x y -+= 上,则1231111nS S S S ++++= 16.将正方形ABCD 沿对角线BD 折成直二面角A -BD -C ,有如下四个结论:①AC ⊥BD ;②△ACD 是等边三角形;③AB 与平面BCD 成60°的角;④AB 与CD 所成的角是60°.其中正确结论的序号是________ .三.解答题:(其中17小题题10分,其它每小题12分,共70分)17. 已知圆C 同时满足下列三个条件:①与y 轴相切;②在直线y=x 上截得弦长为27;③圆心在直线x -3y=0上. 求圆C 的方程.18. 在ABC ∆中,已知角A ,B ,C的对边分别是a ,b ,c ,且222a b c +-=. (1)求角C 的大小;(2)如果203A π<≤,22cos sin 12A m B =--,求实数m 的取值范围.19、已知数列{}n a 是等差数列,且12a =,12312a a a ++=.⑴ 求数列{}n a 的通项公式;⑵ 令n n n b a =⋅3*(N )n ∈,求数列{}n b 的前n 项和. 20.森林失火,火势以每分钟100 m 2的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火5分钟到达现场开始救火,已知消防员在现场平均每人每分钟可灭火50 m 2,所消耗的灭火材料、劳务津贴等费用平均每人每分钟125元,所消耗的车辆、器械和装备等费用平均每人100元,而每烧毁1 m 2的森林损失费为60元,设消防队派x 名消防队员前去救火,从到现场把火完全扑灭共用n 分钟.(1)求出x 与n 的关系式;(2)求x 为何值时,才能使总损失最少.21. 如图,在矩形ABCD 中,AB=33,BC=3,沿对角线BD 将BCD折起,使点C 移到点C ˊ,且C ˊ在平面ABD 的射影O 恰好在AB 上(1)求证:BC ˊ⊥面ADC ˊ;BA CB A(2)求二面角A —BC ˊ—D 的正弦值。
河北省邢台一中2012—2013学年高二下学期第一次月考数学(文)试题

命题人:贺磊第Ⅰ卷(选择题共60分)一、选择题(每小题5分,共60分)1. 点M 的直角坐标为)3,1(-,则点M 的极坐标为( ) A. ⎪⎭⎫⎝⎛6,2π B. ⎪⎭⎫ ⎝⎛3,2π C. ⎪⎭⎫ ⎝⎛32,2π D.)(23,2Z ∈⎪⎭⎫⎝⎛+k k ππ 2. 以下各点坐标与点)3,5(π-M 不同的是( )A. )3,5(π-B. )34,5(π C. )32,5(π- D. )35,5(π-- 3. 若直线的参数方程为⎩⎨⎧+=-=t y tx 3241)(为参数t ,则直线的斜率为( ) A.34 B. 34- C. 43 D. 43- 4. 曲线⎩⎨⎧==θθsin 5cos 4y x )(为参数θ的焦点坐标为( )A. )0,1(±B. )1,0(±C. )0,3(±D. )3,0(± 5. 极坐标方程θρsin =和参数方程⎩⎨⎧+=--=ty tx 31)(为参数t 所表示的图形分别是( )A. 直线、直线B. 直线、圆C. 圆、圆D. 圆、直线6. 与参数方程⎪⎩⎪⎨⎧=+=θθ22sin sin 2y x )(为参数θ等价的普通方程为( ) A. 2-=x y B. 2+=x y C. )32(2≤≤-=x x y D. )10(2≤≤+=y x y 7. 直线αθ=与1)cos(=-⋅αθρ的位置关系( )A. 平行B. 垂直C. 相交不垂直D. 与α有关 8. 极坐标方程0cos 2=-ρθρ的直角坐标方程为( )A. 022=+y x 或1=x B. 1=x C. 022=+y x 或1=y D. 1=y9. 直线⎪⎪⎩⎪⎪⎨⎧+-=+=t y t x 2333211)(为参数t 和圆1622=+y x 交于A ,B 两点,则AB 的中点坐标为( )A. )3,3(-B. )3,3(-C. )3,3(-D. ()3,3-10. 在极坐标系中,过点),2(π且与极轴的倾斜角为45°的直线的极坐标方程是( ) A .2)4cos(=+⋅πθρ B .2)4cos(-=+⋅πθρC . 2)4cos(=-⋅πθρ C .2)4cos(-=-⋅πθρ 11.设P(x ,y)是曲线C :⎩⎨⎧=+-=θθsin cos 2y x )20(πθθ<≤为参数,上任意一点,则x y的取值范围是( ) A .[]3,3- B .(][)+∞-∞-,33,C .⎥⎦⎤⎢⎣⎡-33,33D .⎪⎪⎭⎫⎢⎣⎡+∞⎥⎦⎤ ⎝⎛-∞-,3333, 12. 参数方程⎪⎪⎩⎪⎪⎨⎧-==1112t t y tx )(为参数t 所表示的曲线是( )第Ⅱ卷(非选择题共90分)二、填空题(每小题5分,共20分)13. 若点M 的柱坐标为)1,65,2(-π,则它的直角坐标为 ;14. 曲线⎩⎨⎧+==θθsin 1cos y x )(为参数θ的极坐标方程为 ;15. 在极坐标系中,点)3,4(πP 到圆θρcos 4=的圆心距离为 ;16. 已知圆θρcos 2=与直线0sin 4cos 3=++a θρθρ相切,则实数a = ;三、解答题(17小题10分,18—22题每小题12分,共70分)17. 在平面直角坐标系中,(1)求曲线x y 22=经过伸缩变换⎪⎩⎪⎨⎧-==yy xx 23:''ϕ后得到的曲线的方程;(2)曲线C 经过伸缩变换⎪⎩⎪⎨⎧==yy xx ''3:ϕ后得到的曲线的方程为992'2'=+y x ,求曲线C 的方程。
河北省邢台一中2013—2014学年高二下学期第三次月考化学试题
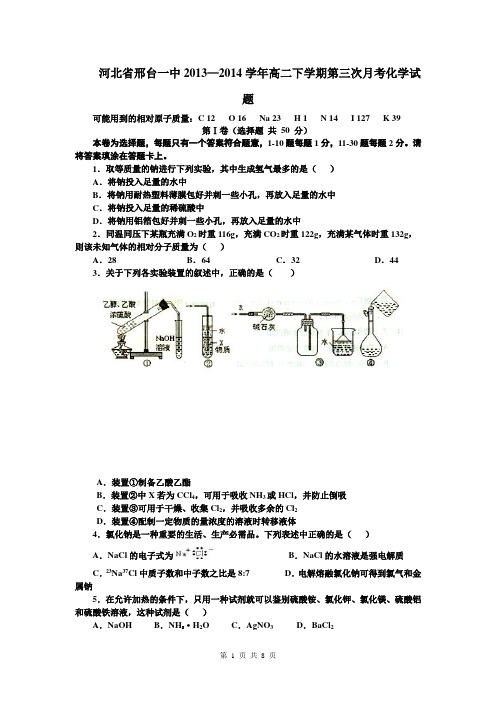
河北省邢台一中2013—2014学年高二下学期第三次月考化学试题可能用到的相对原子质量:C 12 O 16 Na 23 H 1 N 14 I 127 K 39第Ⅰ卷(选择题共50 分)本卷为选择题,每题只有一个答案符合题意,1-10题每题1分,11-30题每题2分。
请将答案填涂在答题卡上。
1.取等质量的钠进行下列实验,其中生成氢气最多的是()A.将钠投入足量的水中B.将钠用耐热塑料薄膜包好并刺一些小孔,再放入足量的水中C.将钠投入足量的稀硫酸中D.将钠用铝箔包好并刺一些小孔,再放入足量的水中2.同温同压下某瓶充满O2时重116g,充满CO2时重122g,充满某气体时重132g,则该未知气体的相对分子质量为()A.28 B.64 C.32 D.443.关于下列各实验装置的叙述中,正确的是()A.装置①制备乙酸乙酯B.装置②中X若为CCl4,可用于吸收NH3或HCl,并防止倒吸C.装置③可用于干燥、收集Cl2,并吸收多余的Cl2D.装置④配制一定物质的量浓度的溶液时转移液体4.氯化钠是一种重要的生活、生产必需品。
下列表述中正确的是()A.NaCl的电子式为B.NaCl的水溶液是强电解质C.23Na37Cl中质子数和中子数之比是8:7 D.电解熔融氯化钠可得到氯气和金属钠5.在允许加热的条件下,只用一种试剂就可以鉴别硫酸铵、氯化钾、氯化镁、硫酸铝和硫酸铁溶液,这种试剂是()A.NaOH B.NH3·H2O C.AgNO3 D.BaCl26.下列除杂质的方法中正确的是()A.乙醇中混有乙酸,加入NaOH溶液后,用分液漏斗分液B.乙烷中混有乙烯,通入H2,在一定条件下反应使乙烯完全转化成乙烷C.苯甲醛中混有苯甲酸,加入生石灰后,再加热蒸馏D.溴苯中含有单质溴加入KI溶液后用分液漏斗分液7.能使溴水褪色,发生取代反应的是()A.乙烯B.乙炔C.乙醇D.苯酚8.碳酸钠(Na2CO3)俗称纯碱,是一种重要的基础化工原料,广泛应用于玻璃、造纸等工业。
河北省邢台一中2013-高一上学期第三次月考数学试题
邢台一中2013—2014学年上学期第三次月考高一年级数学试题第Ⅰ卷(选择题共60分)一、选择题. (每小题5分,共60分) 1、集合{2ππ4ππ|+≤≤+k k αα,∈k Z}中的角所表示的范围(阴影部分)是( )(A )(B ) (C ) (D )2.将分针拨慢5分钟,则分钟转过的弧度数是( )A.3π B . 3π-C .6π D . 6π-3 已知sin 2cos 5,tan 3sin 5cos ααααα-=-+那么的值为 ( )A .-2B .2C .2316D .-23164、若函数y =x 2+(2a -1)x +1在(-∞,2]上是减函数,则实数a 的取值范围是 ( )A. ),23[+∞-B. ]23,(--∞C. ),23[+∞D.]23,(-∞ 5、满足函数x y sin =和x y cos =都是增函数的区间是( )A .]22,2[πππ+k k , Z k ∈ B .]2,22[ππππ++k k , Z k ∈ C .]22,2[ππππ--k k , Z k ∈ D .]2,22[πππk k -Z k ∈6、已知x x f 3cos )(cos =,则)(sin x f 等于( )(A )x 3sin (B )x 3cos (C )x 3sin - (D )x 3cos -7、设函数211()21x x f x x x⎧+≤⎪=⎨>⎪⎩,则((3))f f =( )A .15B .3C .23D .1398,若函数()(()0)f x f x ≠为奇函数,则必有 ( ) (A )()()0f x f x ⋅-> (B )()()0f x f x ⋅-< (C )()()f x f x <- (D )()()f x f x >-9、要得到函数)42sin(3π+=x y 的图象,只需将函数x y 2sin 3=的图象( )(A )向左平移4π个单位 (B )向右平移4π个单位 (C )向左平移8π个单位 (D )向右平移8π个单位10 函数()f x 是定义在[6,6]-上的偶函数,且(3)(1)f f >,则下列各式一定成立的是( )A 、(0)(6)f f <B 、(1)(3)f f -<C 、(3)(2)f f >D (2)(0)f f > 11 1sin ()lgcos xf x x+=是 ( )A 、奇函数B 、偶函数C 非奇函数非偶函数D 、奇且偶函数 12、已知01a <<,则函数|||log |x a y a x =-的零点的个数为( ).A 、1B 、2C 、3D 、4第Ⅱ卷(非选择题共90分)二、填空题:(每小题5分,共20分)13、满足条件{0,1}∪A={0,1}的所有集合A 的个数是 个 14 .若lg2 = a ,lg3 = b ,则lg 54=_____________.15、函数x x f cos 21)(-=的定义域是__________________________ 16、函数π()3sin 23f x x ⎛⎫=-⎪⎝⎭的图象为C ,则如下结论中正确的序号是 _____①、图象C 关于直线11π12x =对称; ②、图象C 关于点2π03⎛⎫⎪⎝⎭,对称;③、函数()f x 在区间π5π1212⎛⎫-⎪⎝⎭,内是增函数; ④、由3sin 2y x =的图角向右平移π3个单位长度可以得到图象C . 三.解答题(本大题共6小题,共70分)17(10分) 已知函数f (x )=log 2(ax +b ),若f (2)=1,f (3)=2,求f (5)18 化简求值 (12分).(1)232021)5.1()833()6.9()412(--+---(2)︒--︒︒︒-170sin 1170sin 10cos 10sin 212;19. (12分)已知sin α是方程06752=--x x 的根,求)cos()2cos()2cos()2(tan )23sin()23sin(2απαπαπαπαππα-+--•-•--的值.20. (12分)求函数y=-x 2cos +x cos 3+45的最大值及最小值,并写出x 取何值时函数有最大值和最小值。
河北省邢台市第一中学2016-2017学年高二下学期3月月考数学理试题 含答案 精品
邢台一中2016—2017学年下学期第一月考高二年级数学(理科)试题第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、在复平面内,复数(1)i i -对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限2、1234566666C C C C C ++++的值为 A .61 B .62 C .63D .643、在独立性检验中,统计量2χ有两个临界值,3.841和6.635,当2 3.841χ>时,有95%的把握说明两个事件有关,当2 6.635χ>时,有99%的把握说明两个事件有关,当2 3.841χ<时,认为两个事件无关,在一项打鼾与患心脏病的调查中,共调出来2000人,经计算220.87χ>,根据这一数据分析,认为打鼾与患心脏病之间A .有95%的把握认为两者有关B .约有95%的打鼾者患心脏病C .有99%的把握认为两者有关D .约有95%的打鼾者患心脏病4、已知在10件产品中有2件次品,现从中任意抽取2件产品,则至少抽出1件次品的概率为 A .415 B .25 C .1745 D .28455、5(12)(2)x x -+的展开式中3x 的项的系数是 A .120 B .-120 C .100 D .-1006、已知随机变量ξ服从正态分布2(2,)N σ,且(4)0.8p ξ<= ,则(02)P ξ<<=A .0.6B .0.4C .0.3D .0.27、在国乒“直通莫斯科”比赛中共那女运动员5人,从这10名运动员中选出6人进行男女混合双打比赛,由于排名世界第一,男队的马龙,女队的丁宁自动入选,组队方案有A .225()AB .22242()C A C .22353()C AD .22343()C A8、在10个球中有6个红球和4个白球(各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第2次也摸到红球的概率为A .35 B .25 C .110 D .59 9、若随机变量η的分布列如下:则当()0.8P x η<=时,实数x 的取值范围是10、若2013220130122013(21)()x a a x a x a x x R -=++++∈,则32013223201311112222a a a a a a ++++=A .12013 B .12013- C .14026 D .14026- 11、鸡年春节期间,国人发微信拜年已成为一种时尚,若小李的40名同事中,给其发微信拜年的概率为1,0.8,0.5,0的人数分别为8,15,14,3(人),则通常情况下,小李应收到同事的拜年的微信数为 A .27 B .37 C .38 D .812、一袋中装有5个白球,3个红球,现从袋中往外取球,每次任取一个,取出后记下颜色,若为红色停止,若为白色则继续抽取,停止时袋中抽取的白球的个数为随机变量ξ,则(P ξ≤= A .914 B .2556 C .3756 D .2328第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上。
河北省邢台二中2013-2014学年高二数学下学期第二次月考试题 理 新人教A版
高二下学期第二次月考数学(理)试题一、选择题(60分)1.复数2i 1i -3⎪⎭⎫⎝⎛+=( )A .-3+4iB .-3-4iC .3-4iD .3+4i2曲线3x y =在点)1,1(处的切线与x 轴、直线2=x 所围成的三角形的面积为( )A.34 B.37 C.35 D.38 3、已知直线kx y =是x y ln =的切线,则k 的值为( )A.e 2 B.e 1- C.e 1 D.e2- 4.设集合{}{}21,2,,M N a ==则 “1a =”是“N M ⊆”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分又不必要条件8. 设,,x y R ∈ 则“2x ≥且2y ≥”是“224x y +≥”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 9、设常a R ∈,集合A ={|(1)()0x x x a --≥},B ={|1x x a ≥-},若AB =R ,则a 的取值范围为( )A .(-∞,-2)B .(-∞,2]C .(2,+∞)D .[2,+∞)10.已知f (x )=x 3+x ,若a ,b ,c ∈R ,且a +b >0,a +c >0,b +c >0,则f (a )+f (b )+f (c )的值( ) A .一定大于0 B .一定等于0 C .一定小于0 D .正负都有可能11.若点P 在曲线y =x 3-3x 2+(3-3)x +34上移动,经过点P 的切线的倾斜角为α,则角α的取值范围是( )A .[0,π2)B .[0,π2)∪[2π3,π)C .[2π3,π)D .[0,π2)∪(π2,2π3]12.等比数列{a n }中a 1=2,a 8=4,函数f (x )=x (x -a 1)(x -a 2)…·(x -a 8),则f ′(0)=( )A .26B .29C .212D .215二、填空题(20分)13、函数13)(3+-=x x x f 在闭区间]0,3[-上的最大值与最小值分别为: 14.由曲线2y x =与2x y =所围成的曲边形的面积为________________ 15.观察下列不等式213122+< 353121122<++474131211222<+++……照此规律,第五个...不等式为 . 16. 函数g (x )=ax 3+2(1-a )x 2-3ax 在区间⎝ ⎛⎭⎪⎫-∞,a 3内单调递减,则a 的取值范围是________.三、解答题(共6题,70分)17.(10分)已知集合P ={x |x 2-8x -20≤0}, S ={x |1-m ≤x ≤1+m }(1)是否存在实数m ,使”x ∈P ”是”x ∈S ”的充要条件?若存在,求m 的取值范围;若不存在说明理由;(2)是否存在实数m ,使”x ∈P ”是”x ∈S ”的必要条件?若存在,求m 的取值范围。
河北省邢台一中2013-2014学年高一下学期第四次月考数学(理)试题Word版含答案
高一下学期第四次月考数学(理)试题第I 卷(选择题共60分)一.选择题:(每小题5分,共60分)1.已知某几何体的三视图如图所示,则该几何体的体积为( )A.8π3 B .3π C.10π3D .6π2. 直线1l :ax+3y+1=0, 2l :2x+(a+1)y+1=0, 若1l ∥2l ,则a=( ) A .-3 B .2 C .-3或2 D .3或-23. 设m 、n 是两条不同的直线,,,αβγ是三个不同的平面,给出下列四个命题: ①若,,则 ②若,,,则③若,,则④若αγ⊥,βγ⊥,则//αβ其中正确命题的序号是 ( )(A )①和② (B )②和③(C )③和④ (D )①和④4.在△ABC 中,a =5,b =15,A =30°,则c 等于( )A .25 B. 5 C .25或 5 D .3 5 5.设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x ≥0,x -y ≥0,2x -y -2≤0,则z =3x -2y 的最大值为( )A .0B .2C .4D .66.已知各项均为正数的等差数列{a n }的前20项和为100,那么a 3·a 18的最大值是( )A .50B .25C .100D .2207. 已知直线l 过点(2,1),且在两坐标轴上的截距互为相反数,则直线l 的方程为( ) A . 10x y --=B. 30x y +-=或20x y -=C. 10x y --=或20x y -=D .30x y +-=或10x y --=8.在三棱柱ABC -A 1B 1C 1中,各棱长相等,侧棱垂直于底面,点D 是侧面BB 1C 1C 的中心,则AD 与平面BB 1C 1C 所成角的大小是( ) A .30° B .45° C .60° D .90°9.若数列{x n }满足lg x n +1=1+lg x n (n ∈N *),且x 1+x 2+x 3+…+x 100=100, 则lg(x 101+x 102+…+x 200)的值为( ) A .102 B .101 C .100D .9910.过点M(-2,4)作圆C :(x -2)2+(y -1)2=25的切线l ,且直线l 1:ax +3y +2a =0与l平行,则l 1与l 间的距离是( ) A.85 B.25 C.285 D.125 11.如图,平面PAD ⊥平面ABCD ,ABCD 为正方形,090=∠PAD ,且F E AD PA ,,2==分别是线段CD PA ,的中点,则异面直线EF 与BD 所成角的余弦值为( )A.33 B.23 C.43 D.6312.如图,四棱锥ABCD P -中,⊥PA 平面ABCD ,底面ABCD 是直角梯形,且CD AB //,90=∠BAD ,2===DC AD PA ,4=AB .则点A 到平面PBC 的距离是( )A.36 B.26 C.362 D.62第II 卷(非选择题共90分)BD二.填空题:(每小题5分,共20分)13.如图所示,Rt △A ′B ′C ′为水平放置的△ABC 的直观图,其中A ′C ′⊥B ′C ′,B ′O ′=O ′C ′=1,则△ABC 的面积为________.14.△ABC 中,a 、b 、c 分别为A 、B 、C 的对边,如果a ,b ,c 成等差数列,B =30°,△ABC 的面积为32,那么b =15. 已知数列{}n a 中,11,a =前n 项和为n S ,且点*1(,)()n n P a a n N +∈在直线10x y -+=上,则1231111nS S S S ++++= 16.将正方形ABCD 沿对角线BD 折成直二面角A -BD -C ,有如下四个结论:①AC ⊥BD ;②△ACD 是等边三角形; ③AB 与平面BCD 成60°的角; ④AB 与CD 所成的角是60°.其中正确结论的序号是________ .三.解答题:(其中17小题题10分,其它每小题12分,共70分) 17. 已知圆C 同时满足下列三个条件:①与y 轴相切;②在直线y=x 上截得弦长为27;③圆心在直线x -3y=0上. 求圆C 的方程.18. 在ABC ∆中,已知角A ,B ,C的对边分别是a ,b ,c ,且222a b c +-=.(1)求角C 的大小; (2)如果203A π<≤,22cos sin 12A mB =--,求实数m 的取值范围.19、已知数列{}n a 是等差数列,且12a =,12312a a a ++=.BA CB A⑴ 求数列{}n a 的通项公式; ⑵ 令nnn b a =⋅3*(N )n ∈,求数列{}n b 的前n 项和. 20.森林失火,火势以每分钟100 m 2的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火5分钟到达现场开始救火,已知消防员在现场平均每人每分钟可灭火50 m 2,所消耗的灭火材料、劳务津贴等费用平均每人每分钟125元,所消耗的车辆、器械和装备等费用平均每人100元,而每烧毁1 m 2的森林损失费为60元,设消防队派x 名消防队员前去救火,从到现场把火完全扑灭共用n 分钟. (1)求出x 与n 的关系式;(2)求x 为何值时,才能使总损失最少.21. 如图,在矩形ABCD 中,AB=33,BC=3,沿对角线BD 将BCD 折起,使点C 移到点C ˊ,且C ˊ在平面ABD 的射影O 恰好在AB 上(1)求证:BC ˊ⊥面ADC ˊ;(2)求二面角A —BC ˊ—D 的正弦值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北省邢台一中2013—2014学年高二下学期第三次月考数学理试题第Ⅰ卷(选择题共60分)一、选择题:(每小题5分,共60分)1. 已知22{|1},{|1},M x y x N y y x M N ==-==-则等于 ( )A .NB .MC .RD .Φ2.i 是虚数单位,则复数ii-12的虚部为 ( ) A .i - B. 1 C.1 D. i 3. 一个学生能够通过某种英语听力测试的概率是12,他连续测试2次,那么其中恰有一次获得通过的概率是 ( )A .14 B .13 C .12 D .344.命题P :若,,R b a ∈则1>+b a |是1>+b a 的充分不必要条件;命题q :不等式1|1|->-x xx x 的解集为}10|{<<x x ,则 ( ) A .“p 或q ” 为假命题 B.“p 且q ” 为真命题 C.“┒p 或q ” 为假命题 D.“┒p 且q ” 为真命题5. 103)1)(1(x x +-的展开式中,5x 的系数是 ( ) A.297- B.252- C.297 D.2076.下列函数中,在[-1,0]上单调递减的是 ( )A .cos y x =B .|1|y x =--C .xxy -+=22lnD .x x y e e -=+ 7.一位母亲纪录了儿子3~9岁的身高数据(略),她根据这些数据建立的身高y (cm )与年龄x 的回归模型为y =7.19x +73.93,用此模型预测孩子10岁时的身高,则有 ( ) A .身高一定是145.83cm B .身高在145.83cm 左右C .身高在145.83cm 以上D .身高在145.83cm 以下8.()=⎪⎭⎫ ⎝⎛---⎰dx x x 10211 ( ) . A 、218-π B 、214-π C 、8π D 、41π-9.设ABC ∆的三边长分别为a 、b 、c ,ABC ∆的面积为S ,内切圆半径为r ,则r =2Sa +b +c;类比这个结论可知:四面体P -ABC 的四个面的面积分别为4321,,,S S S S 内切球的半径为r ,四面体P -ABC 的体积为V ,则r = ( )A .4321S S S S V +++ B . 43212S S S S V+++C .43213S S S S V +++ D .43214S S S S V+++ 10.某校在一天的6节课中随机安排语文、数学、英语三门文化课和音乐、体育、美术三种艺术课各一节,则在课表上的相邻2节文化课之间至少间接一节艺术课的概率为:( ) A.101 B. 51 C. 274 D. 9211.已知函数1(1)(),()(,)(23)36(1)x a x f x f x a x a x ⎧-≤=-∞+∞⎨--+>⎩若在上是增函数,则实数a 的取值范围是( )A .3{|2}2a a <≤ B .{|2}a a ≥ C .3{|}2a a >D .{|2}a a =12.已知函数⎪⎩⎪⎨⎧>-≤<=)(ln 2)0(ln )(e x x e x x x f 若c b a ,,互不相等,且),()()(c f b f a f ==则c b a ++的取值范围为 ( )A.)1,1(2e e e +++B. )2,21(2e e e++ C.)2,12(22e e ++ D.)21,12(2e ee ++第Ⅱ卷(非选择题共90分)二、填空题(每小题5分,共20分)13. 函数2()3'(1),f x x xf =+在点(2,(2))f 处的切线方程为_______________.14. 已知随机变量X 服从正态分布),0(2σN 且4.0)02(=≤≤-X P 则=>)2(X P __________________.15. 若对任意的实数)(,,c a c b a ≠,都有ca cb b a x --+-≤-12恒成立,则x 的取值范围是_______________________________. 16.已知数列{}a n 为等差数列,则有,02321=+-a a a 0334321=-+-a a a aa a a a a 123454640-+-+=写出第四行的结论__________________________ 三、解答题(共70分) 17.(本小题满分10分) 已知函数()|21||23|.f x x x =++- (I )求不等式()6f x ≤的解集;(Ⅱ)若关于x 的不等式()|1|f x a <-的解集不是空集,求实数a 的取值范围。
18. (本小题满分12分)设{}{}.01)1(2,04222=-+++==+=a x a x x B x x x A (1)若,B B A = 求a 的值; (2)若,B B A = 求a 的值. 19.(本小题满分12分)用数学归纳法证明:当n 为正整数时,4)1(321223333+=++++n n n20. (本小题满分12分)某商场决定从3种服装,2种家电,3种日用品中,选出3种商品进行促销活动。
(1)试求选出的3种商品中至少有一种是家电的概率;(2)商场对选出的某商品采用抽奖的方式进行促销,即在该商品现价的基础上将价格提高100元,规定购买该商品的顾客有3次抽奖的机会:若中一次奖,则获得数额为m 元的奖金;若中两次奖,则共获得数额为m 3元的奖金;若中三次奖,则共获得数额为m 6元的奖金.假设顾客每次抽奖中奖的概率都是31,请问:商场将奖金数额m 最高定为多少元,才能使促销方案保证商场不亏? 21.(本小题满分12分) 已知函数).,()(223R b a a bx ax x x f ∈+++= (1)若函数)(x f 在1=x 出取得极值10,求,a b 的值;(2)若对任意的[))(,,4x f a +∞-∈在[]2,0∈x 上单调递增,求b 的最小值。
22. (本小题满分12分)已知函数x ax x f ln )(+=,其中a 为常数. (1)当1a =-时,求)(x f 的最大值;(2) 若)(x f 在区间(0,e ]上的最大值为-3,求a 的值; (3) 当1a =- 时,试推断方程()f x =ln 12x x +是否有实数解.邢台一中2013——2014学年下学期第三次月考高二年级数学(理科)试题 答案一、选择题:(每小题5分,共60分)二、填空题(每小题5分,共20分)13.____04=--y x __ 14. ___0.1________15. ___[0,1]______________ 16.____0510105654321=-+-+-a a a a a a _____ 三、解答题(共70分) 17.(本小题满分10分)18.解答:{}.4,0-=A(1)A B B B A ⊆∴=, ----- 1分 ①若,0B ∈则,1,012±==-a a 当1=a ,时{},042A x x x B ==+= 当,1-=a 时{},0A B ⊂= ----- 3分②若,4B ∈-则,0782=+--a a 则7=a 或,1=a当7=a ,时{}{}4,12048162--==++=x x x B 舍去。
------ 5分 ③若Φ=B ,则(4=∆2)1+a ,0)1(42<--a 解得,1-<a ----- 7分 综上,,1-≤a 或.1=a ------ 8分 (2)B A B B A ⊆∴=,又{}.4,0-=A 而B 中最多有两个元素,,B A =∴即.1=a ------- 12分19.证明:(1)当n =1时,左边=1,右边=22124⨯=1,∴等式成立. ····································································································································· 2分 (2)假设当n =k 时,等式成立,即13+23+33+……+k 3=22(1)4k k +. ··························································································· 4分那么,当n =k +1时,有13+23+33+……+k 3+(k +1)3=22(1)4k k ++(k +1)3. ······················································· 6分=(k +1)2(24k +k +1)=(k +1)22444k k ++=22(1)(2)4k k ++=2(1)[(1)1]4k k +++. ·················································································································· 9分这就是说,当n =k +1时,等式也成立. ················································································· 10分 根据(1)和(2),可知对n ∈N *等式成立. ··········································································· 12分 20.解:(1)设选出的3种商品中至少有一种是家电为事件A ,从3种服装、2种家电、3种日用品中,选出3种商品,一共有C 38种不同的选法,选出的3种商品中,没有家电的选法有C 36种.所以,选出的3种商品中至少有一种是家电的概率为P (A )=1-C 36C 38=914. 4分(2)设顾客三次抽奖所获得的奖金总额为随机变量X ,其所有可能的取值为0,m ,3m ,6m (单位:元).X =0表示顾客在三次抽奖都没有获奖,所以P (X =0)=(1-13)3=827;同理,P (X =m )=C 13×(1-13)2×13=49;P (X =3m )=C 23×(1-13)1×(13)2=29; P (X =6m )=C 33×(13)3=127. 所以奖金总额的分布列为8分顾客在三次抽奖中所获得的奖金总额的期望值是E (X )=0×827+m ×49+3m ×29+6m ×127=43m . 10分 由43m ≤100,解得m ≤75. 故m 最高定为75元,才能使促销方案对商场有利. 12分21,解析(1) ,23)(2b ax x x f ++='由题意可得⎩⎨⎧=+++==++='101)1(023)1(2a b a f b a f 解得⎩⎨⎧-==114b a 或⎩⎨⎧=-=33b a 2分当⎩⎨⎧-==114b a 时,0,1183)(2>∆-+='x x x f 有极值点,满足题意;当⎩⎨⎧=-=33b a 时,0)1(3)(2≥-='x x f 函数无极值点,舍去。
