05-5对定轴的角动量守恒
合集下载
定轴转动的角动量定理 角动量守恒定律

Iz
( 1 ml 2 12
mr 2 )
代入得 mgr cos 2mr dr
dt
v
dr dt
g cos 2
g
2
cos
t
7 lg 24v 0
cos(12v 7l
0t
)
L 0 J 常量
即:合外力为对转轴的力矩为零时,刚体的角动量守恒
讨论:
a.对于绕固定转轴转动的刚体,因J保持不变, 当合外力矩为零时,其角速度恒定。
当M z 0时, J =恒量 =恒量
b.若系统由若干个刚体构成,当合外力矩为零时,系
统的角动量依然守恒。J 大→ 小, J 小→ 大。
当M z 0时, Lz J11 J22 恒量
。这样,棒与物体相撞时,它们组成的系统所受的对
转轴O的外力矩为零,所以,这个系统的对O轴的角
动量守恒。我们用v表示物体碰撞后的速度,则
1
ml 2
mvl
1
ml 2
3
3
(2)
式中’为棒在碰撞后的角速度,它可正可负。
’取正值,表示碰后棒向左摆;反之,表示向右
摆。
第三阶段是物体在碰撞后的滑行过程。物体作匀减 速直线运动,加速度由牛顿第二定律求得为
例12、如图所示,长为L,质量为m1的均匀细棒 能绕一端在铅直平面内转动。开始时,细棒静止于
垂直位置。现有一质量为m2的子弹,以水平速度v0
射入细棒下断而不复出。求细棒和子弹开始一起运 动时的角速度?
题意分析:由于子弹射入细棒的时间极为短促,我们 可以近似地认为:在这一过程中,细棒仍然静止于垂 直位置。因此,对于子弹和细棒所组成的系统(也就 是研究对象)在子弹射入细棒的过程中,系统所受的 合外力(重力和轴支持力相等)对转轴O的力矩都为 零。根据角动量守恒定律,系统对于O轴的角动量守 恒。
第5章 大学普物

§5-3 转动惯量的计算
Computation of Moment of inertia
意义:转动惯量是对刚体转动时惯性大小的量度。
1J M z 产生 。对一定的 M z , z
特性:(1)与质量有关。 J (2)与质量对轴的分布有关。 (3)与转轴的位置有关。 计算:(1)质点系
解得
m2 m1 a g m1 m2 m 2 m1 (2m2 m 2) T1 g m1 m2 m 2 m2 (2m1 m 2) T2 g m1 m2 m 2
[例2] 一个飞轮的质量为60kg,半径为0.25 m, 正在以每分1000转 的转速转动。现在要制动飞轮,要求在5.0秒内使它均匀减速而最后停下 来。求闸瓦对轮子的压力N为多大?设闸瓦与飞轮之间的 k 0.8 。
O
l
g m
60°
§5-5 对定轴的角动量守恒
Conservation of Angular Momentum about a Fixed Axis
dL z 质点系的角动量定理: M z dt
如果 M z 0 , Lz 常量。
守恒
对定轴的角动量守恒定律:如果一个质点系对某一固
定轴的合外力矩为零,则对该定轴的总角动量保持不变。
角动量: Lz J z
对轴定义的力矩、角动量:
z
M iz ri Fi sin i Liz ri pi mi ri2
与 OR在轴 上何处无关
M z ——对z轴的力矩 Lz ——对z轴的角动量
O ri riR
OR
刚体定轴转动定律: M d ( J ) J z z z dt
看运动
查受力
角动量守恒定律五
实际: 因为对质心存 在“质心运动定理” 所以: 基点就选质心
A’ D’ B’
D
A B
图示基点任选
3
二、刚体的定轴转动
1.各点运动的特点
在自己的转动平面内作圆周运动
2.描述的物理量
任一质点圆周运动的线
量和角量的关系
r
r
an r 2 at r
EK
i
12mii2
1 2
J 2
自证
19
2) 用角量表示的力作功的形式
dA
F
ds
Md
自证
A内 0
3) 刚体定轴转动的动能定理形式
A
1 2
J 2
1 2
J02
2.重力场中,机械能守恒定律
系统-- 刚体 + 地球
E
mghc
1 2
J
2
20
例1 质点与质量均匀的细棒相撞(如图)
i
z
i
mi
ri
9
进一步 化简
L (
miri2 )
i
定义刚体对定
轴的转动惯量
J miri2
i
则刚体对定 轴的角动量
或写为
L
J
L J
z
L
mi
ri
10
2.刚体定轴M转动ddLt的转J 动ddt定律
M
J
z
L
mi
ri
应用转动
F
L
Lz
^z
A’ D’ B’
D
A B
图示基点任选
3
二、刚体的定轴转动
1.各点运动的特点
在自己的转动平面内作圆周运动
2.描述的物理量
任一质点圆周运动的线
量和角量的关系
r
r
an r 2 at r
EK
i
12mii2
1 2
J 2
自证
19
2) 用角量表示的力作功的形式
dA
F
ds
Md
自证
A内 0
3) 刚体定轴转动的动能定理形式
A
1 2
J 2
1 2
J02
2.重力场中,机械能守恒定律
系统-- 刚体 + 地球
E
mghc
1 2
J
2
20
例1 质点与质量均匀的细棒相撞(如图)
i
z
i
mi
ri
9
进一步 化简
L (
miri2 )
i
定义刚体对定
轴的转动惯量
J miri2
i
则刚体对定 轴的角动量
或写为
L
J
L J
z
L
mi
ri
10
2.刚体定轴M转动ddLt的转J 动ddt定律
M
J
z
L
mi
ri
应用转动
F
L
Lz
^z
刚体定轴转动的角动量角动量守恒定律

v0
m v
典型例题分析
因, 由两式得
请问:
1.子弹和棒的总动量守恒吗? 为什么? 2.总角动量守恒吗?若守恒, 其方程应如何写?
典型例题分析
谢 谢
二、刚体定轴转动的角动量定理
2、刚体定轴转动的角动量定理 (1)微分形式
Mdt dL d( J)
表明:合外力矩 M 在时间 dt 内的累积效应使得刚体定轴
d ( J ) 的变化。 转动的角动量发生了
(2)积分形式
t2
t1
M dt L2 L1 J2 J1
当 J 增大时, 减小; 增大。 当 J 减小时,
Mdt dL L J 常矢量
实际中的一些现象
空中抱膝 入水展开
空中收拢腿和双臂: J 减小, 增大,完成空翻; 入水时打开腿和双臂: 增大, 减小,垂直入水, J 减小水花。
实际中的一些现象
质容
刚体定轴转动的角动量
刚体定轴转动的角动量定理 刚体定轴转动的角动量守恒定律
应用举例
一、刚体定轴转动的角动量 刚体绕定轴转动时,各质元某一瞬时均
以相同的角速度绕该定轴作圆周运动.
对刚体中质元 m i 的角动量大小:
ri
L
Li mi vi ri mi ri 2
原因
二、刚体定轴转动的角动量定理
1、转动定律的另一形式
转动定律: M J d dL 简单变形: M J J dt dt
dL M dt
作定轴转动的刚体所受的合外力矩等于刚体的角 动量随时间的变化率。 ——与质点转动情形一致,适用范围更广!
m v
典型例题分析
因, 由两式得
请问:
1.子弹和棒的总动量守恒吗? 为什么? 2.总角动量守恒吗?若守恒, 其方程应如何写?
典型例题分析
谢 谢
二、刚体定轴转动的角动量定理
2、刚体定轴转动的角动量定理 (1)微分形式
Mdt dL d( J)
表明:合外力矩 M 在时间 dt 内的累积效应使得刚体定轴
d ( J ) 的变化。 转动的角动量发生了
(2)积分形式
t2
t1
M dt L2 L1 J2 J1
当 J 增大时, 减小; 增大。 当 J 减小时,
Mdt dL L J 常矢量
实际中的一些现象
空中抱膝 入水展开
空中收拢腿和双臂: J 减小, 增大,完成空翻; 入水时打开腿和双臂: 增大, 减小,垂直入水, J 减小水花。
实际中的一些现象
质容
刚体定轴转动的角动量
刚体定轴转动的角动量定理 刚体定轴转动的角动量守恒定律
应用举例
一、刚体定轴转动的角动量 刚体绕定轴转动时,各质元某一瞬时均
以相同的角速度绕该定轴作圆周运动.
对刚体中质元 m i 的角动量大小:
ri
L
Li mi vi ri mi ri 2
原因
二、刚体定轴转动的角动量定理
1、转动定律的另一形式
转动定律: M J d dL 简单变形: M J J dt dt
dL M dt
作定轴转动的刚体所受的合外力矩等于刚体的角 动量随时间的变化率。 ——与质点转动情形一致,适用范围更广!
5.5 角动量守恒定律
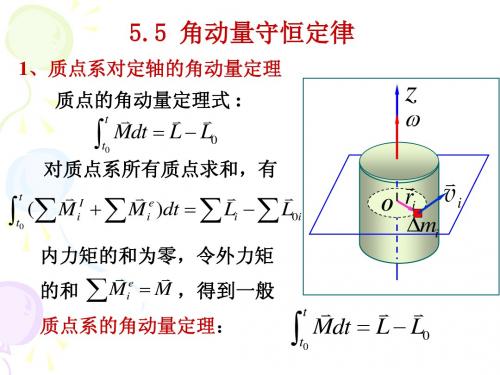
例题1 : 一粒子弹水平射入一静止悬杆的下端,穿出 后速度损失 3 / 4,求子弹穿出后棒的角速度 。已知轴处自由 。
解:以 f 代表杆对子弹的阻力,对子弹有: fdt m(v v0 ) 3mv0 / 4
子弹对杆的冲量矩为:
l f dt J f ldt
若 M 0 ,则
L J 常量
——刚体定轴转动的角动量守恒定律
讨论
内力矩不改变系统的角动量.
在冲击等问题中
M内 M外 L 常量
角动量守恒定律是自然界的一个基本定律. 刚体(或刚体组系统)角动量守恒的三种情况: ①J 不变(刚体),角速度ω的大小和方向均不变 ②J 可变(质点系),ω亦可变,但Jω乘积不变 ③刚体组的角动量守恒
a
v
m
3mva 2 2 m' l 3ma
射入竿后,以子弹、细杆和 地球为系统 ,机械能守恒 .
o
30
a
1 1 2 2 2 ( ml ma ) 2 3 l mga(1 cos 30) mg (1 cos 30) 2
2 2 v g (2 3 )( m l 2ma )( m l 3ma ) 6 ma
质点系的角动量定理:
t
t0
Mdt L L0
质点系的角动量定理:
t
t0
Mdt L L0
O
ri
mi
z
该矢量式向固定转轴(如 z轴) 的投影,得一个标量式,即
vi
t
t0
M z dt Lz L0 z
相对某固定轴,质点系所受的角冲量等于系统 角动量的增量。——质点系对定轴的角动量定理。
刚体定轴转动的角动量定理 角动量守恒定律

典型例子
[例题]如图(a)表示半径为R的放水弧形闸门,可绕图中
左方质点转动,总质量为m,质心在距转轴
7 9
2 处,闸 R 3
门及钢架对质点的总转动惯量为 I mR 2 ,可用钢丝 绳将弧形闸门提起放水,近似认为在开始提升时钢架 部分处于水平,弧形部分的切向加速度为a=0.1g,g为 重力加速度,不计摩擦,不计水浮力.
图(a)
(1)求开始提升时的瞬时,钢丝绳对弧形闸门的拉力 和质点对闸门钢架的支承力. (2)若以同样加速度提升同样重量的平板闸门[图(b)]
需拉力是多少?
FT
W
图(b)
[解](1)以弧形闸门及钢架 为隔离体,受力如图(a)所示. 建立直角坐标系Oxy, 根据质心运动定理 FT FN W mac 向x及y轴投影得
考虑到
t
12v0 dr g 7lg v cos t cos( t) dt 2 24v0 7l
例:圆盘(R,M),人(m)开始静止,人
走一周,求盘相对地转动的角度.
1 I 2 MR 2 2
解: 系统对转轴 角动量守恒
M=0
I11 () I 22 0
I1 mR
2
人— ,盘— (对地的角位移) d d m 1 2 dt dt
I1d I 2 d
1 2 0
2
1 M 2
I d I d
0
2m 2 2m M
例:
圆盘质量M,半径R,J=MR2/2, 转轴光滑,人的质量m,开始时, 两者静止.求:人在盘上沿边 缘走过一周时,盘对地面转过 的角度.
in ex
角动量守恒定律是自然界的一个基本定律.
《大学物理》3.4刚体定轴转动的角动量定理 角动量守恒定律
我国第一颗人造地球卫星沿椭圆轨道绕地球运动, 例:我国第一颗人造地球卫星沿椭圆轨道绕地球运动,地心为该椭圆 的一个焦点。 的一个焦点。已知地球半径 R ,卫星的近地点到地面距离 l ,卫星的远 地点到地面距离 l 。若卫星在近地点速率为 v1 ,求它在远地点速率 v2 。
1 2
卫星在运动过程中,所受力主要是万有引力, 解:卫星在运动过程中,所受力主要是万有引力,其它力忽 略不计,故卫星在运动过程中对地心角动量守恒。 略不计,故卫星在运动过程中对地心角动量守恒。 m
0
r
A
θ = 90
0
mv
质点作圆周运动的角动量
θ
L = rmv = mr ω
2
2.2刚体的角动量 刚体的角动量 刚体对 oz轴的角动量为
z
ω
v
2
i
L = ∑ m r ω = (∑ m r )ω
2 i i i i
o
r
i
m
i
∑ m r 刚体绕 oz 轴的转动惯量
2 i i
L = Jω
L = Jω
刚体对转轴的角动量等于其转动惯量与角速度乘积。 刚体对转轴的角动量等于其转动惯量与角速度乘积。
1 m v 0 a = ( ML2 + ma 2 )ω 3
子弹射入后一起摆动的过程只有重力做功,故系统机 械能守恒。
1 1 L 2 2 2 ( ML + ma )ω = mga (1 cos60°) + Mg (1 cos60°) 2 3 2
ω=
3(2ma + ML)g 2(3ma 2 + ML2 )
二、角动量定理和角动量守恒定理
1× mv 对时间求导 = r × (mv ) + × mv dt dt dt dr d dL ∵ = v , F = (mv ) M = dt dt dt dL 质点所受合外力矩等于质 ∴ = r × F + v × mv dt 点角动量对时间的变化率
角动量 守恒(2011)
称为质点系所受合外力矩 称为质点系所受合外力矩 对i , j 两个质点,内力矩之和为 两个质点,
Mij + M ji = ri × f ij + r j × f ji = ri − r j × f ij = 0
(
)
(r
i
− rj
)
与 f ij 共线, 共线,
Mij + M ji = ri × f ij + r j × f ji = ri − r j × f ij = 0
角动量定理
Fdt = dP
t2 t2
dL M= dt M t = dL d
∫ Fdt =ΔP
t1
∫ Mdt =ΔL
t1
F = 0 P = 常矢量
F P
t2
M = 0 L = 常矢量
M L
t2
力 动量
力矩或角力 角动量 或动量矩
∫ Fdt 合力的冲量
t1
Mdt 合力矩的冲量 或冲量矩 ∫
t1
例
讨论行星运动
1 GMm 1 2 GMm 2 mv0 − = mv − 2 r0 2 R v0r0sinθ v= = 4v0sinθ mv0r0sinθ = mvR R
1 3GM sinθ = 1+ 2 4 2Rv0
1/ 2
3GM v = v01+ 2 2Rv 0
L
3、行星近地点速度大,在远地点速度小 、行星近地点速度大 地点速度小
在近日点与远日点
r ⊥v
v近
m r远
v远 =m r近 v近
v
v远 r远
r近
∴ v远 < v近
的光滑圆环置于竖直平面内.一质量为 例5-1 一半径为 R 的光滑圆环置于竖直平面内 一质量为 m 的小球穿在圆环上 并可在圆环上滑动 小球开始时静 的小球穿在圆环上, 并可在圆环上滑动. 止于圆环上的点 A (该点在通过环心 O 的水平面上 然后 该点在通过环心 的水平面上),然后 点开始下滑.设小球与圆环间的摩擦略去不计 设小球与圆环间的摩擦略去不计.求小球 从 A 点开始下滑 设小球与圆环间的摩擦略去不计 求小球 的角动量和角速度. 滑到点 B 时对环心 O 的角动量和角速度 解 小球受重力和支持力作 支持力的力矩为零,重力 用, 支持力的力矩为零 重力 矩垂直纸面向里
Mij + M ji = ri × f ij + r j × f ji = ri − r j × f ij = 0
(
)
(r
i
− rj
)
与 f ij 共线, 共线,
Mij + M ji = ri × f ij + r j × f ji = ri − r j × f ij = 0
角动量定理
Fdt = dP
t2 t2
dL M= dt M t = dL d
∫ Fdt =ΔP
t1
∫ Mdt =ΔL
t1
F = 0 P = 常矢量
F P
t2
M = 0 L = 常矢量
M L
t2
力 动量
力矩或角力 角动量 或动量矩
∫ Fdt 合力的冲量
t1
Mdt 合力矩的冲量 或冲量矩 ∫
t1
例
讨论行星运动
1 GMm 1 2 GMm 2 mv0 − = mv − 2 r0 2 R v0r0sinθ v= = 4v0sinθ mv0r0sinθ = mvR R
1 3GM sinθ = 1+ 2 4 2Rv0
1/ 2
3GM v = v01+ 2 2Rv 0
L
3、行星近地点速度大,在远地点速度小 、行星近地点速度大 地点速度小
在近日点与远日点
r ⊥v
v近
m r远
v远 =m r近 v近
v
v远 r远
r近
∴ v远 < v近
的光滑圆环置于竖直平面内.一质量为 例5-1 一半径为 R 的光滑圆环置于竖直平面内 一质量为 m 的小球穿在圆环上 并可在圆环上滑动 小球开始时静 的小球穿在圆环上, 并可在圆环上滑动. 止于圆环上的点 A (该点在通过环心 O 的水平面上 然后 该点在通过环心 的水平面上),然后 点开始下滑.设小球与圆环间的摩擦略去不计 设小球与圆环间的摩擦略去不计.求小球 从 A 点开始下滑 设小球与圆环间的摩擦略去不计 求小球 的角动量和角速度. 滑到点 B 时对环心 O 的角动量和角速度 解 小球受重力和支持力作 支持力的力矩为零,重力 用, 支持力的力矩为零 重力 矩垂直纸面向里
定轴转动的角动量定理 角动量守恒定律
返回
退出
r 对于定轴转动, 对于定轴转动, L 对沿定轴的分量 Lz 为
Lz = ∑ ∆Li cosθ = ∑ ∆mi Ri vi cosθ = ∑ ∆mi ri vi = (∑ ∆mi ri )ω
2
称刚体绕定轴转动的角动量。 称刚体绕定轴转动的角动量。 刚体转动惯量: 刚体转动惯量
I = ∑ ∆mi ri
ml 2 ω ′2 23 l h = + 3 µ s − 6 µ sl 2 mgh =
返回
退出
返回
退出
3、物体系的角动量守恒 、 若系统由几个物体组成, 若系统由几个物体组成,当系统受到的外力对 轴的力矩的矢量和为零,则系统的总角动量守恒: 轴的力矩的矢量和为零,则系统的总角动量守恒:
如:直升机机尾加侧向旋叶,是为防止机身的反转。 直升机机尾加侧向旋叶,是为防止机身的反转。
返回
退出
飞轮1: 摩擦轮 : 例4-7 摩擦离合器 飞轮 :I1、 ω1 摩擦轮2: I2、 静止,两轮沿轴向结合, 静止,两轮沿轴向结合,求结合后两轮达到的共同角 速度。 速度。 解:两轮对共同转轴的角动量守恒
返回
退出
角动量定理比转动定律的适用范围更广,适用于 角动量定理比转动定律的适用范围更广, 刚体,非刚体和物体系。 刚体,非刚体和物体系。 对几个物体组成的系统, 对几个物体组成的系统,如果它们对同一给 定轴的角动量分别为 I ω , I 2 ω 2 ,L
1 1
系统对该轴的角动量为 且系统满足角动量定理
Lz = ∑ I i ω i
i
dLz d = ∑ I iω i Mz = dt dt i
返回
退出
三、定轴转动刚体的角动量守恒定律
角动量守恒定律的公式
角动量守恒定律的公式
1. 角动量守恒定律公式。
- 对于质点,角动量L = r× p(其中r是质点相对于某参考点的位矢,p = mv 是质点的动量,×表示矢量叉乘)。
- 在合外力矩M = 0时,角动量守恒,即L_1 = L_2。
- 对于定轴转动的刚体,角动量L = Iω(其中I是刚体对轴的转动惯量,ω是刚体的角速度)。
当合外力矩M = 0时,I_1ω_1=I_2ω_2。
2. 相关知识点(人教版教材相关内容补充)
- 转动惯量。
- 对于离散质点系,I=∑_im_ir_i^2,其中m_i是第i个质点的质量,r_i是该质点到转轴的垂直距离。
- 对于质量连续分布的刚体,I = ∫ r^2dm。
不同形状的刚体转动惯量有不同的计算公式,例如,对于质量为m、半径为R的均匀圆盘绕通过圆心且垂直于盘面的轴转动,其转动惯量I=(1)/(2)mR^2;对于质量为m、长为l的细棒绕通过中心且垂直于棒的轴转动,I=(1)/(12)ml^2。
- 角动量定理。
- 对于质点,M=(dL)/(dt)(M是合外力矩),这表明质点所受合外力矩等于它的角动量对时间的变化率。
- 对于刚体定轴转动,M = Iα(α是角加速度),结合L = Iω也可推导出
M=(dL)/(dt)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m0
v0
子弹射入细杆后,子弹随细杆一起绕轴O转动 转动。 子弹射入细杆后,子弹随细杆一起绕轴 转动。 在整个过程中只有保守内力做功, 在整个过程中只有保守内力做功 , 因此系统的机 械能守恒。 械能守恒。 选取细杆处在竖直位置时子弹的位置为重力 势能零点, 势能零点,系统的始末态的机械能分别为
1 l 2 E0 = Jω + mg (a − ) 2 2 l E = m0 ga(1 − cosθ ) + mg (a − cosθ ) 2 由机械能守恒有 E0 = E
解:
ω0
A 角动量守恒 l 1 2 1 2 2 Ml ω0 = ( Ml + ml )ω 3 3 机械能守恒 1 1 2 2 1 1 2 2 1 2 ⋅ Ml ω0 = ⋅ Ml ω + mv 2 3 2 3 2
m M
v
θ
ω0
vτ
A
m M l
θ
v
M ω= ω0 M + 3m
lω0 v= M( 2M + 3m) M + 3m Ml vτ = ωl = ω0 M + 3m
a
θ
m0
v0
L0 = m0 v0 a
L = Jω
子弹射入杆后系统对转轴O的转动惯量 子弹射入杆后系统对转轴 的转动惯量
1 2 J = ml + m0 a 2 3 1 2 L = Jω = ( ml + m0 a 2 )ω 3
O a
θ
角动量守恒:L0=L 角动量守恒: 1 2 ( ml + m0 a 2 )ω = m0 v0 a 3
5.5 对定轴的角动量守恒
5.5.1 刚体的角动量
一、 刚体对定点的角动量 L Z Li mi Ri O
质点m 质点 i的动量 Pi = mi vi = mi ω × Ri = mi ω × ri mi对O点的角动量 点的角动量 Li = Ri × Pi 刚体对O点的角动量: 刚体对 点的角动量: 点的角动量 L = ∑ Ri × Pi 一般情况下角动量L的方向与角速度ω方向 并不一致。 并不一致。
可变, 乘积不变 (2)J 可变,Jω乘积不变 减小时, 增加; 增加时 减小。 当 J减小时, ω 增加 ; 当 J增加时 , ω 减小 。 减小时 增加 例如跳水、芭蕾舞、茹可夫斯基凳等。 例如跳水、芭蕾舞、茹可夫斯基凳等。 演示实验: 演示实验:茹可夫斯基凳 (3)物体组的角动量守恒 演示实验: 演示实验:直升机
解得
1 1 − cosθ v0 = (ml + 2m0 a)(ml 2 + 3m0 a 2 ) g m0 a 3
例题3 质量为m的小圆环套在一长为 , 例题3 质量为 的小圆环套在一长为 l,质量为 M的光滑均匀杆AB上,杆可以绕过其A端的固定轴 杆可以绕过其A 的光滑均匀杆 在水平面上自由旋转。 在水平面上自由旋转。 开始时杆旋转的角速度为 ω0 , 而小环位于 A 点处 。 试求小环脱离杆时的速 而小环位于A 点处。 表示) 度(方向用与杆的夹角 θ 表示)
思考题
一个学生手持一绕竖直轴转动的车轮,站在一个可以 一个学生手持一绕竖直轴转动的车轮, 自由转动的静止平台上。如果她将车轮上下颠倒, 自由转动的静止平台上。如果她将车轮上下颠倒,将会出 现什么情况? 现什么情况?
例题1 如图所示,一质量为 的子弹以水平速 例题1、如图所示,一质量为m的子弹以水平速 度射入一静止悬于顶端长棒的下端, 度射入一静止悬于顶端长棒的下端,穿出后速 度损失3/4 3/4。 度损失3/4。求子弹穿出后棒的角速度ω。已知 棒长为l 质量为M 棒长为 ,质量为 。 代表棒对子弹的阻力, 解:以f 代表棒对子弹的阻力,对子弹 3 f d t = m ( v − v 0 ) = − mv 0 M ∫ 4 子弹对棒的反作用力 f′ 对棒的冲 量矩 v0
ω
二、 刚体对定轴的角动量
Z L Lz ri Li
Liz = Li cos θ = mi Ri vi cos θ
= mi ri vi
Liz = mi ri ω
2
θ
O
θ
Ri
mi
Lz = Σ( mi ri ω ) = (Σmi ri 2 )ω
2
LZ = Jω
ω
5.5.2 定轴转动刚体的角动量定理 刚体绕固定轴 的角动量为 刚体绕固定轴Z的角动量为 绕固定轴
vτ M θ = arcsin = arcsin v M (2M + 3m)
小 结 1、定轴转动刚体的角动量定理 、
∫M
0
t
Z
dt = Jω − Jω 0
2、角动量守恒定律 、
当MZ = 0时择题:6, 8 填空题: 填空题:4 计算题: , 计算题:6,10
5.5.2 角动量守恒定律 当MZ = 0时
LZ = Jω = 常量
角动量守恒定律: 当作用在刚体( 或几个刚体 角动量守恒定律 : 当作用在刚体 ( 组成的系统) 组成的系统 ) 上的外力对固定转轴的合力矩为 零时, 这刚体( 或几个刚体组成的系统) 零时 , 这刚体 ( 或几个刚体组成的系统 ) 对该 轴的角动量守恒。 轴的角动量守恒。 角动量守恒的三种情况: 角动量守恒的三种情况: 不变, (1) J不变,角速度ω的大小和方向均不变 不变 演示:地球自转角速度的大小方向均不变 演示:
Lz = Jω
刚体定轴转动定律
dω d ( Jω ) dLZ M Z = Jβ = J = = dt dt dt
∫M
0
t
Z
dt = ∫ dLZ = LZ − LZ 0 = Jω − Jω 0
L0
L
作用于固定轴的外力矩在某段时间内的累积 效果,称为冲量矩 冲量矩。 效果,称为冲量矩。 刚体受到的冲量矩等于刚体角动量的增量。 刚体受到的冲量矩等于刚体角动量的增量。
l
∫
f ′ ld t = l ∫ f ′ d t = J ω
1 2 J = Ml 3
m v
f′=−f
9mv0 ω= 4Ml
例题2 一长为l、质量为m的均质细杆 的均质细杆, 例题 一长为 、质量为 的均质细杆,可绕光滑轴 O在铅直面内摆动。当杆静止时,一颗质量为 0的 在铅直面内摆动。 在铅直面内摆动 当杆静止时,一颗质量为m 子弹水平射入与轴相距为a处的杆内 并留在杆中, 处的杆内, 子弹水平射入与轴相距为 处的杆内,并留在杆中, 求子弹的初速率v 使杆能偏转到角度θ。求子弹的初速率 0。 子弹射入细杆的过程时间极短 极短, 解 : 子弹射入细杆的过程时间 极短 , O 可以认为细杆仍处于竖直位置。 可以认为细杆仍处于竖直位置。 考虑子弹和细杆所组成的系 系统的外力为子弹、 统 , 系统的外力为子弹 、 细杆所 受重力及轴的支撑力, 受重力及轴的支撑力 , 但这些力 对转轴O均无力矩 均无力矩, 对转轴 均无力矩 , 故系统的角 动量守恒。 子弹射入细杆前后, 动量守恒 。 子弹射入细杆前后 , 系统的角动量分别为
