贵州省2018年普通高等学校招生适应性考试理科数学
贵阳市2018年高三适应性考试(一)理科数学问题详解

贵阳市2018年高三适应性考试(一)理科数学答案一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)答案:C 解析:由得,所以,又因为,故31228x ->=3x >-{}|3A x x =>-{}3,2,1B =---.{}2,1A B =-- (2)答案:B解析:由,因此.()()()41444221112i i i i z i i i i -+====+++-z z ===(3)答案:D解析:由题知这10个数按照大小排序为:10、30、30、40、40、50、60、60、60、70;所以这组数据的众数为:60,中位数为:;平均数为:4050452+=,因此所求的和为:1030240250603704510+⨯+⨯++⨯+=604545150++=(4)答案:C解析:如上图,画出可行域,表示斜率为2的一组平行线,当过点B y x z -=2y x z -=2(3.-4)时,目标函数取得最大值,故选C.10)4(32max =--⨯=z解析:由题知()111111111211311+-+2112231117k S S S k k k k k k k k +=+=+-=+-+-=-==+++++ 即,解得,此时,即()()721131k k +=+6k =1k a +>7a <(6)答案:D解析:由题可设甲、乙、丙、丁、戊所得分别为: ,由11111,,2,3,4x x d x d x d x d ++++已知可得,解得 ,因此111111111112345105234x x d x d x d x d x d x x d x d x d x d ++++++++=+=⎧⎨++=+++++⎩14316x d ⎧=⎪⎪⎨⎪=-⎪⎩丙所得为: 14122136x d ⎛⎫+=+⨯-= ⎪⎝⎭(7)答案:D 解析:函数图象上各点的横坐标缩短为原来的倍的函数为14y x π⎛⎫=++ ⎪⎝⎭12,由得变化后的函数的对称轴为:214y x π⎛⎫=++ ⎪⎝⎭()242x k k Z πππ+=+∈,()82k x k Z ππ=+∈(8)答案:A解析:设等比数列的公比为,由题知可化为,q ()26482a a a =-()2631182a q a q =-①又因为,所以①式化简为,解得,即 ,所以112a =6316640q q -+=38q =2q =()()2018201812017201811211221122a qS q--===---(9)答案:B解析:因为函数为奇函数,则,又()f x ()33311log log log 101010a f f f ⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭,,且函数为 减函数,因此333log 10log 9.1log 92>>=0.822<()f x ,即.()()()0.8332log 9.1log 10f f f >>c b a >>解析:根据三视图,作长为4,高为4,宽为2的长方体。
贵州省贵阳市2018届高三5月适应性考试(二)数学理试题 (11)
【题文】
甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
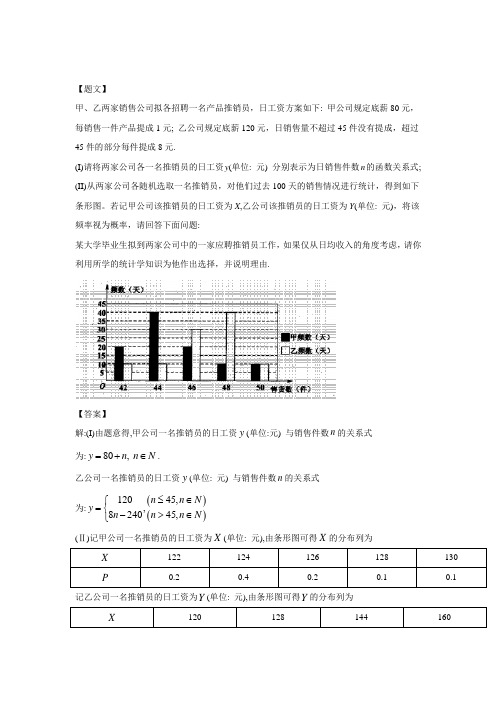
(I)请将两家公司各一名推销员的日工资y (单位: 元) 分别表示为日销售件数n 的函数关系式; (II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。
若记甲公司该推销员的日工资为X ,乙公司该推销员的日工资为Y (单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
【答案】
解:(I)由题意得,甲公司一名推销员的日工资y (单位:元) 与销售件数n 的关系式
为:80, y n n N =+∈.
乙公司一名推销员的日工资y (单位: 元) 与销售件数n 的关系式
为:()()
45,120,45,8240n n N y n n N n ≤∈⎧=⎨>∈-⎩ (Ⅱ)记甲公司一名推销员的日工资为X (单位: 元),由条形图可得X 的分布列为
记乙公司一名推销员的日工资为Y (单位: 元),由条形图可得Y 的分布列为
∵ 125,136EX EY ==,所以仅从日均收入的角度考虑,我会选择去乙公司
【解析】
【标题】贵州省贵阳市2018届高三5月适应性考试(二)数学理试题
【结束】。
贵阳第一中学2018届高考适应性月考卷(六)理数-答案

由于 x [1,2],不等式可化为 x3 x2 2x ≤ t,
理科数学参考答案·第 6 页(共 7 页)
令 h(x) x3 x2 2x ,
……………………………………………………(10 分)
h(x) 3x2 2x 2 ,当 x [1,2] 时, h(x) ≥ h(1) 3 0, h(x) 在 x [1,2] 上单调递增,
y2
4m ①,
y1 y2
4
②,
又由 |
FA |
2|
FB
| ,得
y1
2 y2
③,联立①②③可得
m
32 4
,故选
C.
7.整个电路共 6 个开关,所以共 26 64 种闭合方式,每一条支线有 3 个开关,共 23 8 种
闭合方式,其中有 3 种闭合方式可以使支线接通,则有 5 种方式使支线不通,两条支线至
1,
T199 (a100 )199 1 ,故选 C.
2017
12.由题可知函数 f (x) 和函数 y x3 sin x a 均关于点 (0,a) 对称,所以有 (xi yi ) i 1
2017
2017
xi yi 0 2017a 2017 ,则 a 1,故选 B.
i 1
少有一条接通则电路接通,所以共 64 5 5 39 种闭合方式,故选 A.
理科数学参考答案·第 1 页(共 7 页)
8.该题为几何概型,即求落入如图 2 所示阴影区域的概率,则
P
π 4
1
1 2
π
4
2
,故选
D.
9.可将该三棱锥放入如图 3 所示的长方体中,则 AB CD ,A 选
项正确;作 AB 的中点 E ,连接 DE,CE ,则 DEC 即二面角
贵州省贵阳市2018届高三数学上学期适应性月考试题(一)理

2018届高三上学期适应性月考(一)理科数学试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{A x y ==,2{0}2x B xx +=≤-,则A B = ( ) A .[2,1]-- B .[1,2]- C .[1,1]- D .[1,2)2.复数32(1)(1)i i +-在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.已知()f x 在其定义域[1,)-+∞上是减函数,若(2)()f x f x ->,则( ) A .1x > B .11x -≤< C .13x <≤ D .13x -≤≤4.双曲线方程为2221x y -=,则它的右焦点坐标为( )A .(2 B .(2 C. (2D . 5.某市国际马拉松邀请赛设置了全程马拉松、半程马拉松和迷你马拉松三个比赛项目,4位长跑爱好者各自任选一个项目参加比赛,则这4人中三个项目都有人参加的概率为( ) A .89 B .49 C. 29 D .8276.若方程2(1)10x k x --+=有大于2的根,则实数k 的取值范围是( ) A .7(,)2-∞ B .7(,]2-∞ C. 7(,)2+∞ D .7[,)2+∞ 7.已知,αβ都是锐角,且sin cos cos (1sin )αβαβ=+,则( ) A .32παβ-=B .22παβ-=C. 32παβ+=D .22παβ+=8.如图,由曲线21y x =-,直线0,2x x ==和x 轴围成的封闭图形的面积是( )A .220(1)x dx -⎰B .220(1)x dx -⎰C. 2201x dx -⎰D .122211(1)(1)x dx x dx --+-⎰⎰9.设直线2a x =与椭圆22221(0)x y a b a b+=>>交于,A B 两点,若OAB ∆是直角三角形,则椭圆的离心率为( )A B .1210.已知数列{}n a 满足:11a =,121n n a a -=+(2n ≥),为求使不等式123n a a a a k ++++< 的最大正整数n ,某人编写了如图所示的程序框图,在框图的判断框中的条件和输出的表达式分别为( )A .,S k i <B .,1S k i <- C. ,S k i ≥ D .,1S k i ≥-11.为得到函数22()2sin cos cos )f x x x x x =-的图象,可以把函数()2cos(2)3g x x π=-的图象( )A . 向左平移4π个单位 B .向左平移2π个单位C. 向右平移4π个单位D .向右平移2π个单位12.如图是某几何体的三视图,则该几何体的各个棱长中,最长的棱的长度为( )A..第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13. 61(12)()x x x-+展开式的常数项是 .(用数字作答)14.已知变量,x y 满足条件23029x y x y x y ≥⎧⎪+-≥⎨⎪≤-⎩,则23x y -的最小值等于 .15.如图,在ABC ∆中,D 是AB 上一点,2AD DB =,若CD CA ⊥,2CD = ,则CD CB ∙=.16. 已知,,a b c 分别为锐角ABC ∆的三个内角,,A B C 的对边,2a =,且(2)(sin sin )()sin b A B c b C +-=-,则ABC ∆周长的取值范围为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知数列{}n a 满足:11a =,1121n n n a a a --=+(2n ≥).(1)求数列{}n a 的通项公式;(2)设数列{}1n n a a +的前n 项和为n T ,求证:12n T <. 18. 为了解学生完成数学作业所需时间,某学校统计了高三年级学生每天完成数学作业的平均时间介于30分钟到90分钟之间,图5是统计结果的频率分布直方图.(1)数学教研组计划对作业完成较慢的20%的学生进行集中辅导,试求每天完成数学作业的平均时间为多少分钟以上的学生需要参加辅导?(2)现从高三年级学生中任选4人,记4人中每天完成数学作业的平均时间不超过50分钟的人数为X ,求X 的分布列和期望.19. 如图,在三棱锥K ABC -中,,,D E F 分别是,,KA KB KC 的中点,平面KBC ⊥平面ABC ,AC BC ⊥,KBC ∆是边长为2的正三角形,3AC =.(1)求证:BF ⊥平面KAC ; (2)求二面角F BD E --的余弦值.20. 已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12,12,F F 是椭圆的左、右焦点,P 是椭圆上一点,12PF PF ∙的最小值为2.(1)求椭圆C 的方程;(2)过点2F 且与x 轴不重合的直线l 交椭圆C 于,M N 两点,圆E 是以1F 为圆心椭圆C 的长轴长为半径的圆,过2F 且与l 垂直的直线与圆E 交于,P Q 两点,求四边形MPNQ 面积的取值范围.21. 设2()(ln 1)(2)f x x x a x x =-+-,a R ∈. (1)令'()()g x f x =,求()g x 的单调区间;(2)已知()f x 在1x =处取得极大值,求实数a 的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程已知极坐标的极点在平面直角坐标系的原点O 处,极轴与x 轴的非负半轴重合,且长度单位相同,直线l 的极坐标方程为:2sin()33πρθ+=,曲线C 的参数方程为:3cos 23sin x y αα⎧=⎪⎨=+⎪⎩,(α为参数),其中[0,2)απ∈. (1)写出直线l 的直角坐标方程及曲线C 的普通方程; (2)若,A B 为曲线C 与直线l 的两交点,求AB . 23.选修4-5:不等式选讲 设()231f x x x =-++.(1)求不等式()4f x x <+的解集;(2)若函数()()g x f x ax =+有两个不同的零点,求实数a 的取值范围.理科数学参考答案一、选择题(本大题共12小题,每小题5分,共60分)【解析】1.函数y 的定义域为(1][3+)A =-∞-∞ ,,,不等式202x x +-≤的解集为[22)B =-,,所以[21]A B =-- ,,故选A.2.复数32(1i)(1i)+-1i =--,对应点为(11)--,,位于第三象限,故选C.3.由单调性及定义域得12x x --<≤,解得13x <≤,故选C.4.双曲线焦点在x 轴上,22213122a b c ==⇒=,,右焦点为0⎫⎪⎪⎝⎭,故选C. 5.23434C A 3643819P ===,故选B. 6.问题等价于方程11x k x +=-在(2)+∞,有解,而函数1y x x=+在(2)+∞,上递增,值域为52⎛⎫+∞ ⎪⎝⎭,,所以k 的取值范围是72⎛⎫∞ ⎪⎝⎭,+,故选C. 7.πsin cos cos (1sin )sin()cos sin 2αβαβαβαα⎛⎫=+⇒-==- ⎪⎝⎭,即2αβπ-=2,故选B.8.阴影部分面积为12221[(1)]d (1)d x x x x ⎰--+⎰-,而222101|1|112x x x x x ⎧--=⎨-<⎩,,,,≤≤≤ 故选C.9.2a x =代入椭圆方程得y =2223()2a c a c a a =⇒-=⇒=,故选C.10.判断的条件为S k <;输出的结果为1i -,故选B. 11.ππ()2sin 22sin 236f x x x ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,π()2sin 26g x x ⎛⎫=+ ⎪⎝⎭π2sin 212x ⎛⎫=+ ⎪⎝⎭,故选C .12.几何体ABCD 为图1中粗线所表示的图形,最长棱是AC ,AC C .二、填空题(本大题共4小题,每小题5分,共20分)【解析】13.61x x ⎛⎫+ ⎪⎝⎭展开式的通项为6216C r rr T x -+=,6203621r r r -=⇒=-=-;无解,所以展开式的常数项为36C 20=.15.由已知3122CB CD CA =- ,0CD CA =,231622CD CB CD CDCA =-=.16.由已知()()()a b a b c b c +-=-,即2221c os 2b c a bc A +-=⇒=得60A =︒,由正弦定理,三角形的周长为π24sin 26B C B ⎛⎫++=++ ⎪⎝⎭,ππ62B ⎛⎫∈ ⎪⎝⎭,,πsin 16B ⎤⎛⎫+∈⎥ ⎪⎝⎭⎦⎝,周长的取值范围为(26]+. 三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分) (Ⅰ)解:111112111(2)2(2)21n n n n n n n a a a n n a a a a -----+=⇒==++≥≥,所以1n a ⎧⎫⎪⎨⎬⎪⎭⎩是以2为公差的等差数列,11111a a =⇒=, 所以121nn a =-, 所以数列{}n a 的通项公式为121n a n =-. (Ⅱ)证明:由(Ⅰ)得111111212122121n n a a n n n n +⎛⎫=⋅=- ⎪-+-+⎝⎭,11112212n T n ⎛⎫=-< ⎪+⎝⎭.18.(本小题满分12分)解:(Ⅰ)设每天完成作业所需时间为x 分钟以上的同学需要参加辅导,则 (70)0.02(9070)0.0050.2x -⨯+-⨯=,得65x =(分钟),所以,每天完成数学作业的平均时间为65分钟以上的同学需要参加辅导.(Ⅱ)把统计的频率作为概率,则选出的每个学生完成作业的时间不超过50分钟的概率为0.2~(40.2)X B ,, 44()C 0.20.8(01234)k k k P X k k -=== ,,,,, 0.8EX =.19.(本小题满分12分)(Ⅰ)证明:如图,建立空间直角坐标系,则(10K ,302BF CK ⎛=-= ⎝⎭,,(10(030)CA =- ,,,, 0BF CK = ,BF CK ⊥得BF CK ⊥, 0BF CA = ,BF CA ⊥得BF CA ⊥,CA ,CK 是平面KAC 内的两条相交直线,所以BF ⊥平面KAC.(Ⅱ)解:平面BDF的一个法向量(10m =,, 平面BDE (即平面ABK)的一个法向量为(32n =-,,3cos 4m n 〈〉= ,,所以二面角F BD E --的余弦值为34. 20.(本小题满分12分) 解:(Ⅰ)已知12c a =,12PF PF的最小值为222b c -=, 又222a b c =+,解得2243a b ==,,所以椭圆方程为22143x y +=.(Ⅱ)当l 与x 轴不垂直时,设l 的方程为1122(1)(0)()()y k x k M x y N x y =-≠,,,,. 由22(1)143y k x x y =-⎧⎪⎨+=⎪⎩,得2222(43)84120k x k x k +-+-=.则221212228412+4343k k x x x x k k -==++,.所以212212(1)|||43k MN x x k +=-=+.过点2(1)F ,0且与l 垂直的直线1(1)m y x k =--:,1F 到m,所以||PQ == 故四边形MPNQ的面积1||||2S MN PQ == 可得当l 与x 轴不垂直时,四边形MPNQ面积的取值范围为(12,.当l 与x 轴垂直时,其方程为1||3||8x MN PQ ===,,,四边形MPNQ 的面积为12. 综上,四边形MPNQ面积的取值范围为[12,. 21.(本小题满分12分)解:(Ⅰ)由()ln 22f x x ax a '=-+, 可得()ln 22(0)g x x ax a x =-+∈+∞,,, 则112()2axg x a x x-'=-=, 当0a ≤时,(0)x ∈+∞,时,()0g x '>,函数()g x 单调递增,当0a >时,102x a ⎛⎫∈ ⎪⎝⎭,时,()0g x '>,函数()g x 单调递增,12x a ⎛⎫∈+∞ ⎪⎝⎭,时,()0g x '<,函数()g x 单调递减.所以当0a ≤时,函数()g x 的单调递增区间为(0)+∞,,当0a >时,函数()g x 的单调递增区间为102a ⎛⎫ ⎪⎝⎭,,单调递减区间为12a ⎛⎫+∞⎪⎝⎭,.(Ⅱ)由(Ⅰ)知,(1)0f '=. ①当a ≤0时,()f x '单调递增,所以当(01)x ∈,时,()0()f x f x '<,单调递减, 当(1+)x ∈∞,时,()0()f x f x '>,单调递增, 所以()f x 在1x =处取得极小值,不合题意.②当102a <<时,112a >,由(Ⅰ)知()f x '在102a ⎛⎫ ⎪⎝⎭,内单调递增, 可得当(01)x ∈,时,()0f x '<,112x a ⎛⎫∈ ⎪⎝⎭,时,()0f x '>, 所以()f x 在(0,1)内单调递减,在112a ⎛⎫ ⎪⎝⎭,内单调递增,所以()f x 在1x =处取得极小值,不合题意. ③当12a =时,即112a =,()f x '在(0,1)内单调递增,在(1)+∞,内单调递减, 所以当(0)x ∈+∞,时,()0f x '≤,()f x 单调递减,不合题意. ④当12a >时,即1012a <<, 当112x a ⎛⎫∈ ⎪⎝⎭,时,()0f x '>,()f x 单调递增, 当(1)x ∈+∞,时,()0f x '<,()f x 单调递减, 所以()f x 在1x =处取得极大值,合题意. 综上可知,实数a 的取值范围为12a >.22.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)∵π2sin 33ρθ⎛⎫+= ⎪⎝⎭,∴sin cos 3ρθθ=,直线l 的直角坐标方程:30y +-=.曲线C :3cos 23sin x y αα⎧=⎪⎨=+⎪⎩(α为参数),消去参数可得曲线C 的普通方程为:22(()29x y -+=.(Ⅱ)由(Ⅰ)可知,22(()29x y -+=的圆心为D (2),半径为3. 设AB 中点为M ,连接DM ,DA , 圆心到直线l 的距离|323|22d -+-==,所以2D M =,又因为3DA =,所以MA =||AB =23.(本小题满分10分)【选修4−5:不等式选讲】解:(Ⅰ)分段讨论得不等式解集为(0,3).(Ⅱ)利用图象可得533a-<<-.11。
贵阳第一中学2018届高考适应性月考卷(三)理数-答案

不超过 14,均可保证最后一次循环时得到的计算结果是 2 4 6 8 10 12 ,故选 A.
5.
171,
4 ,P(167
179)
0.9544
2
0.6826
0.6826
0.8185 , 0.8185
20000
16370 ,故选 B.
6. AD
AF
FD
2 AF
CA
2 AF
x
y12 4
,
令x
1 ,得
yR
y1
y2 2
y12 y2 8
y1
2
y2
,
所以
R
是
PQ
的中点,
|PR| |RQ|
1.
……………………………………(5 分)
(Ⅱ)设 M (b ,0) 为满足条件的点, A(x1,y1) ,B(x2 ,y2 ) ,直线 MA,MB 的斜率分别为
k1,k2 ,直线 l 的方程为 x my a ,
1 x0
x
ln
x0
1 ,①
设直线 l 与曲线 y g(x) 相切于点 (x1,ex1 ) ,
∵ g(x) ex ,∴切线 l 的方程为 y ex1 ex1 (x x1) ,
即 y ex1 x ex1 (1 x1) ,②
由①②得 ex1
1 x0
, ex1 (1 x1) ln x0
1,
所以 Tn 3Tn 3 32 33 … 3n n 3n1 ,
故
Tn=
(2n 1)3n1 4
3
(n N* )
.
18.(本小题满分 12 分)
………………………………………(12 分)
解:(Ⅰ)
[小初高学习]贵州省贵阳市2018届高三数学适应性考试试题(二)理(含解析)
![[小初高学习]贵州省贵阳市2018届高三数学适应性考试试题(二)理(含解析)](https://img.taocdn.com/s3/m/8920bb8afd0a79563d1e7211.png)
贵阳市2018年高三适应性考试(二)理科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. )( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】A,从而可得复数出.故选A.点睛:本题考查复数的运算法则及几何意义.求解此类问题要能够灵活准确的对复平面内的.2. 那么)B. C. D.【答案】C,且故选C.点睛:本题考查了交集的定义与应用问题,意在考查学生的计算求解能力.3. 中,的中线,()【答案】B【解析】分析:利用向量的共线定理、平行四边形法则即可得出.是边的中点故选B.点睛:本题考查了平面向量的基本定理的应用.在解答此类问题时,熟练掌握向量的共线定理、平行四边形法则是解题的关键.4. 甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获得冠军,乙队需要再贏两局才能得到冠军,若两队每局获胜的概率相同,则甲队获得冠军的概率为()【答案】D【解析】解法一:以甲再打的局数分类讨论,若甲再打一局得冠军的概率为p1,则p1甲打两局得冠军的概率为p2,则p2p1+p2 D.解法二:设乙获得冠军的概率p1,则p1p=1-p1选D.考点:相互独立事件的概率.5. ,则)B. C. D.【答案】A诱导公式化简,即可得解.,则故选A.点睛:本题主要考查了同角三角函数关系式,诱导公式的应用,熟练掌握基本关系及诱导公式是解题的关键,诱导公式的口诀:“奇变偶不变,符号看象限”.6.)【答案】D【解析】分析:在A平行或B CDAA错误;在B B错误;在C C错误;在D D正确.故选D.点睛:本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,解答时需注意空间中线线、线面、面面间的位置关系的合理运用.空间几何体的线面位置关系的判定与证明:①对于异面直线的判定,要熟记异面直线的概念(把不平行也不想交的两条直线称为异面直线);②对于异面位置关系的判定中,熟记线面平行于垂直、面面平行与垂直的定理是关键.7. 则下列不等式恒成立的是()C. D.【答案】C【解析】分析:作出不等式组对应的平面区域,利用线性规划的知识进行判断即可.详解:作出不等式组对应的平面区域如图所示:故选C.点睛:本题主要考查线性规划的应用,利用数形结合是解决本题的关键.8.()B.【答案】B【解析】分析:根据函数奇偶性和单调性的性质,作出函数的草图,利用数形结合进行求解即可.详解:∴对应的函数图象如图(草图)所示:故选B.点睛:本题主要考查不等式的求解,利用函数奇偶性和单调性的关系及数形结合进行求解是解决本题的关键.解这种题型往往是根据函数所给区间上的单调性,根据奇偶性判断出函数在对称区间上的单调性(偶函数在对称区间上的单调性相反,奇函数在对称区间上的单调性相同),然后再根据单调性列不等式求解.9. )【答案】C【解析】分析:由图象求出函数解析式,然后利用定积分求得图中阴影部分的面积..∴图中的阴影部分面积为故选C.点睛:本题考查了导数在求解面积中的应用,关键是利用图形求解的函数解析式,在运用积分求解.定积分的计算一般有三个方法:①利用微积分基本定理求原函数;②利用定积分的几何意义,利用面积求定积分;③利用奇偶性对称求定积分,奇函数在对称区间的定积分值为0.10. 元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图()【答案】B【解析】分析:建立方程求出自变量的值即可.故选B.点睛:本题考查算法框图,解答本题的关键是根据所给的框图,得出函数关系,然后通过解方程求得输入的值,当程序的运行次数不多或有规律时,可采用模拟运行的办法解答.11.)D.【答案】A【解析】分析:-的最小值,即可求得实数.恒成立恒成立,即,当且仅当时取等号故选A.点睛:本题综合考查了二次函数、导数、基本不等式. 对于函数恒成立或者有解求参的问题,常用方法有:变量分离,参变分离,转化为函数最值问题;或者直接求函数最值,使得函数最值大于或者小于0;或者分离成两个函数,使得一个函数恒大于或小于另一个函数.12. ,; )【答案】B的垂直平分线为详解:建立如图所示的坐标系:.,则,,则代入到双曲线的方程可得,即.故选B.点睛:本题考查了双曲线的几何性质,离心率的求法,考查了转化思想以及运算能力,双曲线的离心率是双曲线最重要的几何性质,求双曲线的离心率(或离心率的取值范围),常见有,代入公式的方程(不等式),解方程(不等式),).第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)____.(用数字作答).【答案】844.,解得故答案为点睛:求二项展开式有关问题的常见类型及解题策略(1)求展开式中的特定项.可依据条件写出第.(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,由特.14. 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的.【解析】分析:由已知中的三视图,可知该几何体右边是四棱锥,即“阳马”,左边是直三棱柱,即“堑堵”,该几何体的体积只需把“阳马”,和“堑堵”体积分别计算相加即可.;左边是直三棱柱,即“堑堵”,其底面边长为1,其体积为∵该几何体的体积为点睛:本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响,对简单组合体三视图问题,先看俯视图确定底面的形状,根据正视图和侧视图,确定组合体的形状.15. 的右焦点,且圆截得的弦长等于2,则的值为__________.得的弦长等于2,求出,且双曲线的渐近线的方程为与此双曲线的渐近线相切截得的弦长等于2点睛:本题主要考查椭圆与双曲线的几何性质,直线的方程,直线与圆的位置关系以及点到直线的距离公式等基础知识.当直线与圆相切时,其圆心到直线的距离等于半径是解题的关键,当直线与圆相交时,弦长问题属常见的问题,最常用的方法是弦心距,弦长一半,圆的半径构成直角三角形,运用勾股定理解题.16. ,__________.【答案】3,由余弦定理可解得..面积的最大值为点睛:本题主要考查了正弦定理,余弦定理,同角三角函数基本关系式,三角形面积公式在解三角形中的综合应用.解答本题的关键是熟练掌握公式和定理,将三角形面积问题转化为二次函数.转化思想是高中数学最普遍的数学思想,在遇到复杂的问题都要想到转化,将复杂变简单,把陌生的变熟悉,从而完成解题目标.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)(I)【答案】(I),得,再根据(I)详解:(I)∴②-点睛:本题主要考查递推公式求通项的应用以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1(2)(4);此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.18. 已知如图1所示,在边长为12且分别交折叠,合,构成如图2 上有一点满足请在图2 中解决下列问题:(I)求证:;与平面所成角的正弦值为.【答案】(I)见解析;【解析】分析:(I作交行四边形,.详解:(I)解:又,(II)的坐标为点睛:本题主要考查线面平行的判定定理利用空间向量求线面角.利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求向量关”,求出平面的法向量;第五,破“应用公式关”.19. 甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.(I)请将两家公司各一名推销员的日工资单位: 元)式;(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下乙公司该推销员的日工资为单位: 元),将该频率视为概率,请回答下面问题:某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.【答案】(I)见解析;(Ⅱ)见解析.【解析】分析:(I)依题意可得甲公司一名推销员的工资与销售件数的关系是一次函数的关系式,而乙公司是分段函数的关系式,由此解得;(Ⅱ)分别根据条形图求得甲、乙公司一名推销员的日工资的分布列,从而可分别求得数学期望,进而可得结论.详解:(I)由题意得,单位:元)为单位: 元)单位: 元),的分布列为单位: 元),∴仅从日均收入的角度考虑,我会选择去乙公司.点睛:求解离散型随机变量的数学期望的一般步骤为:第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;第二步是“探求概率”,即利用排列组合,枚举法,概率公式,求出随机变量取每个值时的概率;第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值20. 已知椭圆在第一象限的交点,且(I)(II)求三角形.【答案】【解析】分析:(I)根据右焦点,式,即可求出三角形的面积.的坐标为,代入椭圆方程得,联立可解得.,所以直线联立直线方程和椭圆方程可得联立直线方程相抛物线方程可得到直线的距离为.点睛:本题考查直线与椭圆的位置关系.因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.21. 己知函数(Ⅱ)在(Ⅲ)求证:【答案】,增区间为.;(Ⅱ)(Ⅲ)见解析.【解析】分析:(Ⅰ)先对函数求导,再分别解与,即可得函数间;(Ⅲ)根据(Ⅰ)和(Ⅱ)可知当时,即. 详解:的定义域为,.的减区间为,增区间为.,变化时,的变化情况如下表:即(Ⅲ)由(Ⅰ)和(Ⅱ)可知当时,即..点睛:本题难点在第三问,解答第三问要根据第一问和第二问的结合,首先要知赋值,令.对此类不等式的证明,要先观察不等式的特点,结合已解答的问题把要证的不等式变形,并运用已证结论进行放缩,然后再化简或者进一步利用导数证明即可.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22. 选修4-4:坐标系与参数方程,.(I)(II)上两点,且.【解析】分析:设点,根据曲线上任意一点到极点的距离等于它到直线的距离,即可求得曲线的极坐标方程;(II)根据可设,利用极坐标方程求出,再根据三角函数的图象及性质即可求得最大值......................(II)点睛:本题主要考查求极坐标方程及极坐标方程的应用.在参数方求最值问题中,可根据题设条件列出三角函数式,借助于三角函数的图象与性质,即可求最值,注意求最值时,取得的条件能否成立.23. 选修4-5:不等式选讲(I)的最小值(II)求证【答案】见解析.【解析】试题分析:(1(2)由(1,原不等式左边加上组分别利用基本不等式求得最小值,相加后可证得原不等式成立.试题解析:(1(2)据(1)小初高试卷教案习题集小初高试卷教案习题集即,当且仅当时,取“=” 所以。
贵阳第一中学2018届高考适应性月考卷(八)理数-答案
解:(Ⅰ)椭圆
Γ
的方程可化为
x2 3
y2
1,
∴长轴端点 F1( 3,0) , F2 ( 3,0) ,
∵ | AF1 | | AF2 | 4 | F1F2 | ,由椭圆的定义可得动点 A 的轨迹 C 是以 F1 ,F2 为焦点,长轴
长为 2a 4 的椭圆,
∴ a 2 , c 3 , b a2 c2 1 ,
x
π 3
,∴向右平移
m(m
0)
个单位长度后得
y
2 sin
x
m
π 3
,又因为平移后的图象关于
y
轴对称,所以
y
2 sin
x
m
π 3
是偶函
数,∴ m
π 3
kπ
π,∴m 2
kπ
5π , 6
∵m
0,∴ k
1
时, m
取得最小值
π 6
,故选
B.
理科数学参考答案·第 1 页(共 9 页)
9.设 R 为外接球的半径, r 为底面三角形外接圆的半径, d 为球心到底面三角形外接圆圆心
3 sin x cos x cos2 x
3 2
sin
2
x
1 2
cos
2x
1 2
sin
2x
6
1 2
,
所以
f
(x)
的最大值为
3 2
.
由
2k
≤2x
6
≤2k
,得
k
6
≤x≤k
,
所以
f
(x)
的单调递减区间为
k
6
,k
,k
Z
【高三英语试题精选】2018年贵阳市高三数学理科适应性考试试卷二(含答案)
120188144160
02030401
∵,所以仅从日均收入的角度考虑,我会选择去乙司
20解(I)∵也为抛物线的焦点,∴,
由线段,得,∴的坐标为,代入椭圆方程得
又,联立可解得,
所以椭圆的方程为
(Ⅱ)由(Ⅰ)知,所以直线方程为,
联立直线方程和椭圆方程可得
2018年贵阳市高三数学理科适应性考试试卷二(含答案)
w
贵阳市4坐标系与参数方程
在极坐标系中,直线,曲线上任意一点到极点的距离等于它到直线的距离
(I)求曲线的极坐标方程;
(I)若是曲线上两点,且,求的最大值
23选修4-5不等式选讲
已知函数
(I)求的最小值;
(II)若均为正实数,且满足,求证
贵阳市10DCBCB 11、12AB
令,则,,所以
由得的坐标为
∵直线与平面所成角的正弦值为,
解得或
19解(I)由题意得,甲司一名推销员的日工资(单位元)与销售数的关系式为
乙司一名推销员的日工资(单位元)与销售数的关系式为
(Ⅱ)记甲司一名推销员的日工资为(单位元),由条形图可得的分布列为
122124126128130
0204020181
∴当时,,
令时,
即
∴
22解(Ⅰ)设点是曲线上任意一点,则,即
(II)设,则
23解(I)当时,
当时,,当时,综上 Nhomakorabea的最小值
(II)证明均为正实数,且满足,
∵
(当且仅当时,取“=”)
∴,即
w
∴
联立直线方程相抛物线方程可得,
∴
∴
∵到直线的距离为,
2018届贵州省贵阳市第一中学高三第五次适应性月考数学(理)试题(图片版)
贵阳第一中学2018届高考适应性月考卷(五)理科数学参考答案一、选择题(本大题共12小题,每小题5分,共60分)【解析】1.,其共轭复数为,故选A.2.A,C,D都不正确(类比推理的结论不一定正确;平面中的三角形与空间中的四面体、平行四边形与平行六面体作为类比对象较为合适;演绎推理是在大前提、小前提和推理形式都正确时,得到的结论一定正确),故选B.3.作出可行域,如图1,当目标等直线过点时,,过点时,,故选B.4.由已知,,故选C.5.如图2,在棱长为2的正方体中作出该几何体为棱锥P−ABCD,据此求出体积为1,故选C.6.区域F的面积为,区域E的面积为,所求概率为,故选A.7.如图3,在正方体中,异面直线与BM所成角为60°,故选D.8.判断时,所以要结束循环,故选B.9.由已知,在R上递减且,所以当时,满足条件;当时,,综上,a的取值范围是,故选B.10.设,则△OAB是边长为2的等边三角形,C在以AB为直径的圆上,,故选C.11.依题意,(舍去负值),故选D.12.,的图象与直线的交点横坐标即的根,相邻两根差的最小值为,从而,在上递增,在上递减,值域为,故选A.二、填空题(本大题共4小题,每小题5分,共20分)【解析】13.,展开式没有x的奇数次方,只需求其展开式的项的系数和,.14.余弦定理计算,设AC的中点为E,在△ADE中计算.15.由已知,作出的图象(函数周期为4,只需考虑),如图4,观察图象得. 16.如图5,假设圆心O到AC,BD的距离分别为,则,且,,所以当且仅当(即)时,四边形ABCD的面积取最大值10.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)解:(Ⅰ)当时,;……………………………(2分)当;……………………(4分)所以是以为公比、首项为的等比数列,所以.……………………………………………………(6分)(Ⅱ)……………………………………(7分),当时,;当时,,…………………………(10分)即,所以的最大项为.……………………(12分)18.(本小题满分12分)解:(Ⅰ)由题知,一套设备在五年内需更换的易坏元件数为4,5,6,7的概率分别为0.2,0.4,0.2,0.2,…………………………………………(1分)从而;;;;;;.∴的分布列为:……………………(5分)(Ⅱ)由(Ⅰ)知,,故的最小值为. ……………………(8分)(Ⅲ)记表示2套设备在购买易坏元件上所需的费用(单位:万元).当时,;当时,;可知当时所需费用的期望值小于时所需费用的期望值,故应选. ……………………………………(12分)19.(本小题满分12分)(Ⅰ)证明:在梯形ABCD中,由已知条件及勾股定理可证,………(2分)平面CDEF⊥平面ABCD,交线为CD,在矩形CDEF中,DE⊥CD,由面面垂直性质得,……………………(4分)AD与DE是平面ADE内两条相交直线,所以BD⊥平面ADE,…………………………………………(5分),所以平面BDF⊥平面ADE.……………………(6分)(Ⅱ)解:建系如图6,设,,则,,得,即,…………………………………………(8分),平面BDF的一个法向量为,平面BEF的一个法向量为,……………………………………………………(10分),……………………(11分)所以二面角的余弦值为.……………………(12分)20.(本小题满分12分)解:(Ⅰ)由题设知,,可设椭圆方程为,………………(2分)把点代入,,……………(4分)故椭圆的方程为.……………………(5分)(Ⅱ)由于对称性,可令.将直线的方程代入椭圆方程,得,由,得,则.………………(8分)再将直线的方程代入椭圆方程,得,由,得,则.故四边形的面积为.由于,且在上单调递增,故,从而有,当且仅当,即,也就是点的坐标为时,四边形的面积取最大值6.……………(12分)21.(本小题满分12分)(Ⅰ)解:的定义域为,,且,当在上递减,当时,不满足条件;当时,上递减,当时,不满足条件;当时,上递增,当时,不满足条件;若,上递减,上递增,故,综上,.………………………………………………………………………(6分)(Ⅱ)证明:由(Ⅰ)知.设,则,当时,;当时,,所以在上单调递减;在上单调递增;又,所以在上有唯一零点,在上有唯一零点1,且当时,;当时,;当时,.因为,所以是的唯一极大值点.由得,故,由得,因为是在的最大值点,由得,所以.………………………………………………(12分)22.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)C 的普通方程为,l 的直角坐标方程为.…………………………………………(5分)(Ⅱ).………………………………………………(10分)23.(本小题满分10分)【选修4−5:不等式选讲】解:(Ⅰ)当时,,,当时,,当时,,∴的最小值为4.……………………………………………………(5分)(Ⅱ)原式等价于不存在实数使得不等式成立.设,当时,,,当时,,,当时,,,∴,∴.………………………………………………………………(10分)页11第。
贵州省2018年普通高等学校招生适应性考试理科综合能力测试(word)
贵州省2018年普通高等学校招生适应性考试理科综合能力测试可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Zn 65 Te 128一、选择题:此题共13小题,每题6分,共78分。
在每题给出的四个选项中,只有一项是符合题目要求的。
1.在人体内,由某些细胞合成分泌并能使其他细胞生理活动发生变化的一组物质是A.信使RNA、抗体B.胰蛋白酶、DNA聚合酶C.胰岛素、淋巴因子D.乳糖、乙酰胆碱2.将甲、乙两种植物的块茎切成形状、大小相同的细条,分别置于质量浓度为0.3gmL蔗糖溶液中,对其失水量进行测量后绘制了如下曲线。
以下表达错误的选项是3.2017年11月我国爆发了较严重的流感。
某流感病毒是一种负链RNA病毒,侵染宿主细胞后会发生-RNA→+RNA→-RNA和-RNA→+RNA→蛋白质的过程,再组装成子代流感病毒。
“-RNA”表示负链RNA,“+RNA”表示正链RNA。
以下表达错误的选项是B.+RNA具有信使RNA的功能4.以下关于人体下丘脑的表达,正确的选项是B.下丘脑与生物节律有关,呼吸中枢也位于下丘脑C.下丘脑分布有某些反射弧的感受器、神经中枢、效应器5.以下关于哺乳动物细胞有丝分裂的表达,错误的选项是6.荠菜的果实形状有三角形和卵圆形两种。
用甲、乙、丙(三者基因型各不相同)3株果实为三角形的植株与果实为卵圆形的植株进行杂交实验,结果如下表所示。
以下说法错误的选项是三角形果实中纯合子占1/52的基因型均有3种2×丙得到的F2中表现型及比例约为3:17.化学与社会、生活密切相关。
以下说法中不正确的选项是A.有些能源比较丰富而淡水短缺的国家,常利用蒸馏法大规模地将海水淡化为可饮用水B.铝是地壳中含量最高的金属元素,因此人类很早就开始大量使用铝制器皿C.“真金不怕火炼”,说明有些金属(如金)即使在高温下也不与氧气发生反应D.存在于污水中的胶体物质,可加明矾和硫酸铁等电解质来处理8.以下对实验现象的解释与结论,正确的选项是为阿伏加德罗常数的值,以下表达正确的选项是A.2gSO2与足量O2在一定条件下反应,生成SO3的分子数为0.05N AB.100 ML PH=2的CH3×10-3N AC.常温常压下,13g苯和苯乙烯混合物中所含原子数为2N Al2与足量的NaOH稀溶液反应,转移电子数为0.2N AA.可用新制的Cu(OH)2悬浊液鉴别乙酸溶液、蔗糖溶液、葡萄糖溶液B. 中所有碳原子一定处于同一平面C.苯乙烯、植物油和苯都能与氢气发生加成反应,是因为其结构中都含有碳碳双键D.有机物(C4H10)的一溴代物有六种结构11.第三代混合动力车目前一般使用镍氢电池(M表示储氢合金;汽车在刹车或下坡时,电池处于充电状态)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
`
Word文档
省2018年普通高等学校招生适应性考试
理科数学
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.已知集合)2)(5(,55xxyxBxxA,则BA( )
A.]2,5[ B.5,5 C.5,5 D.2,5
2.在复平面,复数iiz1的共轭复数z对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.阅读如下框图,运行相应的程序,若输入n的值为8,则输出n的值为( )
A.0 B.1 C.2 D.3
4.已知函数(),0()21,0gxxfxxx是R上的偶函数,则(3)g( )
A.5 B.-5 C.7 D.-7
5.已知直线30xy与抛物线212yx的一个交点为A(不与原点重合),则直线到抛物线焦点的距离
为( )
A.6 B.7 C.9 D.12
6.为了提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设原信息
为123aaa,传输信息为11232haaah,其中112haa,213hha,运算规则为:000,011,
101,110
.例如:原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致
接收信息出错,则下列接收信息出错的是( )
A.01100 B.11010 C.10110 D.11000
7.将函数xxf2cos)(的图像向右平移0个单位,得到的图像恰好关于原点对称,则的一个可
能取值为
`
Word文档
A.6 B.4 C.3 D.2
8.在平行四边形ABCD中,3,1,2BADADAB,点E满足BEBC2,则ABAE的值为
( )
A.29 B.23 C.234 D.231
9.在正方体1111ABCDABCD中,过对角线1AC的一个平面交1BB于E,交1DD于F得四边形1AECF,
则下列结论正确的是( )
A.四边形1AECF一定为菱形
B.四边形1AECF在底面ABCD的投影不一定是正方形
C.四边形1AECF所在平面不可能垂直于平面11ACCA
D.四边形1AECF不可能为梯形
10.甲、乙两队进行一场排球比赛,根据以往经验,单局比赛甲队胜乙队的概率均为53.本场比赛采用五局
三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响.现已知前两句双方站成平手,则甲
队获得这场比赛胜利的概率为( )
A.259 B.12563 C.12581 D.125101
11.已知双曲线0,01:2222babyaxE的左、右焦点分别为21,FF,半焦距为4,P是E左支上的一
点,2PF与y轴交于点A,1PAF的切圆与边1AF切于点Q,若2AQ,则E的离心率是( )
A.2 B.3 C. D.5
12.设函数()(12)xfxexax,其中1a,若存在唯一负整数0x,使得0()fxa,则实数a的取值
围是( )
A.253(,)32ee B.3(,1)2e C.3[,1)2e D.253[,)32ee
`
Word文档
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.若x,y满足约束条件001xyxyy,则21zxy的最大值为 .
14.二项式6211xxx展开式中的常数项为 .
15.如图,网格纸上正方形小格的边长为1,图中粗线画出的是一个几何体的三视图,则这个几何体外接球
的表面积为 .
16.平面四边形ABCD中,3ADAB,602DBCBCD,当BAD变化时,对角线AC的
最大值为 .
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.已知na是等比数列,16,252aa.数列nb满足5,221bb,且nnab是等差数列.
(1)分别求na,nb的通项公式;
(2)记数列nnnaab2211log1的前n项和为nS,求证:21nS.
18.共享单车是指企业在校园、地铁站点、公共站点、居民区、商业区、公共服务区等提供自行车单车共享
服务,是一种分时租赁模式,是共享经济的一种新形态.某共享单车企业在A城市就“一天中一辆单车的平
均成本与租用单车数量之间的关系”进行了调查,并将相关数据统计如下表:
租用单车数量x(千辆) 2 3 4 5 8
每天一辆车平均成本y(元)
3.2 2.4 2 1.9 1.5
根据以上数据,研究人员设计了两种不同的回归分析模型,得到两个拟合函数:
模型甲:$14.80.8yx,模型乙:$226.41.6yx.
(1)为了评价两种模型的拟合效果,完成以下任务:
`
Word文档
①完成下表(计算结果精确到0.1元)(备注:$iiieyy$,ie$称为相应于点(,)iixy的残差);
租用单车数量x(千辆) 2 3 4 5 8
每天一辆车平均成本y(元)
3.2 2.4 2 1.9 1.5
模型甲
估计值$1iy
2.4 2 1.8 1.4
残差1ie$
0 0 0.1 0.1
模型乙
估计值$2iy
2.3 2 1.9
残差2ie$
0.1 0 0
②分别计算模型甲与模型乙的残差平方和1Q及2Q,并通过比较1Q,2Q的大小,判断哪个模型拟合效果
更好.
(2)这家企业在A城市投放共享单车后,受到广大市民的热烈欢迎并供不应求,于是该企业决定增加单
车投放量.根据市场调查,市场投放量达到1万辆时,平均每辆单车一天能收入8元;6元的概率分别为
0.6,0.4;市场投放量达到1.2万辆时,平均每辆单车一天能收入8元,6元的概率分别为0.4,0.6.若按(1)
中拟合效果较好的模型计算一天中一辆单车的平均成本,问该企业投放量选择1万辆还是1.2万辆能获得
更多利润?请说明理由.(利润=收入-成本)
19.在三棱锥SABC中,60SABSACo,SBAB,SCAC.
(1)求证:BCSA;
(2)如果2SA,2BC,AC的中点为D,求二面角CBDS的余弦值.
`
Word文档
20.在圆4:221yxC上任取一点P,过点P作xPQ轴,垂足为Q.当点P在圆1C上运动时,线段
PQ
的中点M的轨迹为曲线C.
(1)求曲线C的方程,并说明曲线C是什么图形;
(2)21,ll是过点)1,0(T且互相垂直的两条直线,其中1l与1C相交于BA,两点,2l与C的一个交点为
D
(与T不重合),求ABD面积取得最大值时直线1l的方程.
21.如图,在矩形ABCD中,)0,1(),0,1(xBA且Dx,0在曲线xy1上,BC与曲线xy1交于E,
四边形ABEF为矩形.
(1)用x分别表示矩形ABCD,曲线梯形ABED及矩形ABEF的面积,并用不等式表示它们的大小关
系;
(2)设矩形ABEF的面积为)(xf,若)1(2ln)(xaxxxf对任意的1,0x恒成立,数a的取值围;
(3)求证:e201820172018(e为自然对数的底数).
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.[选修4-4:坐标系与参数方程]
在直角坐标系xOy中,曲线1C的参数方程为1cos23sin2xy(为参数),以坐标原点为极点,x轴
的正半轴为极轴建立极坐标系,曲线2C的方程为23sin()3.
(1)求1C与2C交点的直角坐标;
(2)过原点O作直线l,使l与1C,2C分别相交于点A,B(A,B与点O均不重合),求AB的最大
值.
`
Word文档
23.[选修4-5:不等式选讲]
已知函数1()fxxxaa.
(1)若2a,求不等式9()2fx的解集;
(2)若对任意的xR,任意的(0,)a恒有()fxm,数m的取值围.
