晶体学基础知识点小节
第二节 晶体学基本
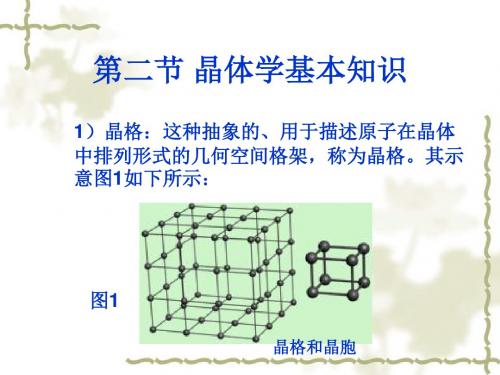
4)晶面和晶向
①晶面:晶格中由一系列原子组成的平面称 为晶面。
晶面用晶面指数来表示: 现以图3立方晶格中晶面A为例,说明确定晶面
指数的方法.
a.以晶胞的三条棱边为空间坐标轴 OX、OY、OZ,坐标轴的原点O应选 在待定晶面以外,以免截距为零。
b.晶胞棱边长a、b、c分别为OX、 OY、OZ轴上的度量单位,求出待定 晶面在三个坐标轴上的截距。A晶面 在三个坐标轴上的截距分别为∞、1、 1。
图2
晶胞的棱边长度a、b、 c和棱边夹角α、β、γ 称为晶格常数。度量单 位均为Å(1Å=10-10m) 和度。当棱边长度 a=b=c,棱边夹角 α=β=γ=90°时,这种 晶胞称为简单立方晶胞。 由简单立方晶胞组成的 晶格称为简单立方晶格。 在简单立方晶格中,晶 格常数常用边长a、b、 c来表示。
倒易点阵的本质
图4 立方晶格中的三种重要晶面 a)(110)面; b)(100)面 c)(111)面
②晶向:在晶体中,通过两个以上原子中心的直线构成一 个原子列,各种原子列的位向称为晶向。
晶向用晶面指数来表示:
晶向指数:现以图3立方体晶格中晶向OE 为例,说明晶向指数的确定方法。 a.在晶格中设空间坐标轴OX、OY、OZ, 坐标轴的原点O应在所求晶向的直线上。
三斜 Triclinic
abc ===90°
多晶体结构
如果一块晶体内部的晶格位向(即原子排列的方向) 完全一致,称这块晶体为单晶体。实际使用的金属 材料,目前只有采用特殊的方法才能得到单晶体。 实际使用的金属材料,哪怕是在很小体积中也包含 有许多外型不规则的小晶体,每个小晶体内部的晶 格位向都是一致的,而各小晶体之间位向却不相同, 如图所示。
图 单晶体与多晶体示意图 a)单晶体 b)多晶体
晶体学基础

晶体多面体上任一晶面至少同属于两个晶带(在晶体多面 体上,彼此相交于平行晶棱的一组晶面,称为晶带 )。
晶体几何理论发展简况
二.最早提出的晶体结构几何理论
布拉菲于1855年确定了晶体结构 有14种布拉菲格子即14种布拉菲 点阵
费多洛夫于1889年第一个推导出 230种空间群(费多洛夫群)
晶胞
维格纳—赛兹晶胞作为一个初基晶胞只包含一个点阵点 当它沿点阵的任一平移矢量平移时,必然充满整个空间而
没有重迭 因为维格纳—赛兹晶胞没有涉及任何基矢的选择,所以这
种晶胞具有和点阵相同的对称性
图1-9 体心立方点阵的维格纳-赛 兹晶胞
图1-10 面心立方点阵的维格纳-赛 兹晶胞
第七节 典型晶体结构举例 一、铜(Cu)型晶体结构(面心立方结构)
结构基元:点阵结构中被平移 重复的结构单元称为该点阵结 构的结构基元
点阵结构=点阵+结构基元 点阵结构的特点是具有周期性
晶体的点阵结构
二.晶体的点阵结构
晶体:凡原于、分子、离子或基 团按点阵结构作周期性地排列而 成的物质都叫晶体。
特点:
• 晶体的最大特点就是其空间点阵结 构(它决定了晶体的许多共同的基 本特征)
Tmnp ma nb pc, m, n, p 0,1,2 (1.3)
图1-5 空间点阵单位
点阵
空间格子:空间点阵按确定的 平行六面体单位划分后所形成 的格子称为空间格子 。
基本单位:每个平行六面体格 子单位只分摊到1个点阵点, 称为空间点阵的基本单位 。
我们把所有阵点可用位矢(1.1)、(1.2)或(1.3) 来描述的点阵称为布拉菲点阵。
图1-11 fcc结构的初基晶胞 是惯用晶胞内的一个平行六
第一章晶体学基础

1
2020/11/26
1.1 晶体结构的周期性
•1.1.1 晶体结构的周期性与点阵 1、晶体的周期性:晶体是一种内部粒子或粒子集团在空间按一定规律周期性重复排列而成的固体。 结构基元和大小方向为二个要素。 2、点阵结构与点阵:将晶体结构中的每个结构基元抽象成一个点,将这些点按照周期性重复的方 式排列,就可构成点阵。
晶体在一定温度下原子在振动过程中可能克服其势垒,离开其平衡位置而挤入间隙位置,形成一对 空位和间隙原子的缺陷,这类缺陷称为Frenkel缺陷。而一对正负离子同时离开其平衡位置在而迁移到 晶体表面,出现了正负离子空位并存的现象称为Schottky缺陷。
晶体中含有微量杂质原子时,当杂质原子取代了正常原子的位置时,则形成杂质原子缺陷。
晶体的线缺陷的主要形式是各种形式的位错。从而导致晶体中点阵结构的不严格。线缺陷严重 时可使实际晶体变为多晶,即晶体是由许多微小的晶块组成。
面缺陷和体缺陷是涉及平面点阵和空间点阵的缺陷。面缺陷是指晶体中可能缺少某一层的粒子, 形成了层错现象。体缺陷则指在晶体中出现空洞、气泡、包裹物和沉积物等。
层错现象
3、点阵的基本性质:凡是能够抽取出点阵的结构可称为点阵结构;点阵结构可以被与它相对 应的平移群所重复。
一个点阵点中只有一个基本 结构的点阵称为素单元点阵。 如上述直线点阵。
一个点阵点中含有二个或二 个以上基本结构的点阵你复合 点阵,如石墨晶体。
3.点阵的基本性质: 按连接任意两点所得的向量平移拮能够复原的一组点为点阵。
实际晶体偏离理想晶体的原因: (1)实际晶体中的微粒数量是有限的; (2)晶体中所有的微粒并非处在晶格中相应位置静止不动,而是在其平衡位置附近不停的振动; (3)实际晶体中多少存在一定的缺陷。这些缺陷是指偏离理想的点阵结构情况。
第一章 晶体学基础

例:
X 轴坐标 —— 1 Y 轴坐标 —— 1 Z 轴坐标 —— ∞
11∞ ( 1 1 0)
绘出( 3 3 4 ) 和 ( 1 1 2 ) 晶面
取倒数
111
化简
3
( 334 )
(-
)
( -1 1 )
334
4
(11 2)
( 1 -1 1 ) 2
请绘出下列晶向: [001] [010] [100]
[110] [1 1 0] [10 1] [112] 请绘出下列晶面: (001) (010) (100) (110) (1 1 0) (10 1) (112)
单胞
晶体结构与点阵的关系
-Fe
CsCl bcc
a a
a
a
simple cubic
a a
-Fe
Cu3Au
CuAu
fcc
a
a
c
a
a simple cubic
a a Simple tetragonal
aa
-Fe
NaCl
a a
a fcc
CaF2
ZnS
a a
a fcc
晶体结构是晶体的直接表达; 点阵是对晶体结构的数学抽象。
数学抽象
晶体法则结:构的周期性和对称性,
1. 一个或几个小球合并成一个数学点
由于2. 高各度阵对称点的的几何周关围系 环境相同, 它只结原果子能:或有原子1群4中具有类相型同的环境
得到
数学点的集合
得到
空间点阵
原子的具体排列方式
直接表达
数学抽象
晶体结构
空间点阵
提取
有代表性的、基本的单元
提取
第一章晶体学基础

隋性气体无规则排列
表示有些材料包括水蒸气和玻璃的短程有序
表示有些材料包括水蒸气和玻璃的短程有序 金属及其他许多材料的长程有序排列
图 材料中原子的排列
二氧化硅结构示意图
a)晶态
b)非晶态
3. 晶体的特征
(1)周期性(不论沿晶体的哪个方向看去,总是相隔一定 的距离就出现相同的原子或原子集团。这个距离称为周期 ) 液体和气体都是非晶体。 (2)有固定的凝固点和熔点. (3)各向异性(沿着晶体的不同方向所测得的性能通常是 不同的 :晶体的导电性、导热性、热膨胀性、弹性、强度、 光学性质 )。
(a)
Z
βα
Xb
(b) 简单立方晶体 (a) 晶体结构 (b) 晶格 (c) 晶胞
γ (c)
c aY
2.晶胞的选取原则:
(1)晶胞几何形状能够充分反映空间点阵的对称性; (2)平行六面体内相等的棱和角的数目最多; (3)当棱间呈直角时,直角数目应最多; (4)满足上述条件,晶胞体积应最小。
图 晶胞的选取
立方晶系 ( Cubic)
Simple
Body centered
Face centered
a
a
a
a a
a a
a a
a = b = c, a = b = = 90
正方晶系 ( Tetragonal )
Simple
Body centered
c
c
a a
a a
a = b c, a = b = = 90
1.2 晶体学基础 Fundamentals of crystallogphy
(完整版)第1章 晶体学基础

第一篇 X射线衍射分析(15万字)1 晶体学基础1.1 晶体结构的周期性与点阵晶体是由原子、离子、分子或集团等物质点在三维空间内周期性规则排列构成的固体物质,这种周期性是三维空间的。
晶体中按周期重复的原子、分子或离子团称为结构基元,也就是重复单元。
为了描述晶体内部原子排列的周期性,总是把一个结构基元抽象地看成为一个几何点,而不考虑它的实际内容(指原子、离子或分子)。
这些几何点按结构周期排列,这种几何点的集合就称为点阵,将点阵中的每个点叫阵点。
要构成点阵,必须具备三个条件:(1)点阵点数无限多;(2)各点阵点所处的几何环境完全相同;(3)点阵在平移方向的周期必须相同。
凡是能够抽取出点阵的结构可称为点阵结构或晶体点阵。
点阵中每一阵点对应于点阵结构中的一个结构基元,在晶体中则是一些组成晶体的实物粒子,即原子、分子或离子等,或是这些微粒的集团。
这样,晶体结构与晶体点阵是两个不同的概念,其关系如图1-1所示,晶体结构可以表示为:晶体结构= 晶体点阵+ 结构基元图1-1晶体结构与点阵的关系根据点阵的性质,把分布在同一直线上的点阵称为直线点阵或一维点阵,分布在同一平面内的点阵称为平面点阵或二维点阵,分布在三维空间中的点阵称为空间点阵或三维点阵。
1.1.1 一维周期性结构与直线点阵图1-2(a)是聚乙烯分子链的结构示意图,具有一维周期结构,其结构基元(CH2CH2)周期性地排列在一个方向上。
每一个结构基元的等同位置抽象成一个几何点,可形成一条直线点阵,是等距离分布在一条直线上的无限点列,如图1-2(b)所示。
取任一阵点作为原点O ,A 为相邻的阵点,则矢量a=OA 表示重复的大小和方向,称为初基(单位)矢量或基矢,若以单位矢量a 进行平移,必指向另一阵点,而矢量的长度a a =ρ称为点阵参数。
图1-2晶体结构与点阵的关系(a )聚乙烯分子链的结构示意图;(b )等效的一维直线点阵直线点阵中任何两阵点的平移矢量称为矢径,可表示为T p = p a (0, ±1, ±2……)矢径T p 完整而概括地描述了一维结构基元排列的周期性。
金属的晶体结构知识点总结

金属的晶体结构知识点总结一、晶体结构的基本概念1. 晶体及其性质晶体是由原子、离子或分子按一定的顺序排列而成的,具有周期性结构的固体。
晶体内部的原子、离子或分子按照规则排列,形成了晶体的结晶面、晶格点、结晶方位等。
晶体具有明显的外部形状和内部结构,具有特定的物理、化学性质。
晶体根据其结构的不同可以分为同质晶体和异质晶体。
2. 晶体结构晶体结构是指晶体内部的原子、离子或分子的排列方式和规律。
根据晶体内部原子、离子或分子的排列方式的不同,晶体结构可以分为点阵型、面心立方型、体心立方型等。
3. 晶体的组成晶体的组成通常是由晶格单元和晶格点构成的。
晶格单元是晶体的最小重复单元,晶格点是晶体内部原子、离子或分子所占据的位置。
4. 晶体的晶格晶格是晶体内部原子、离子或分子排列形成的几何形状。
晶格可以分为点阵型、面心立方型、体心立方型等。
5. 晶体的晶系晶体根据晶体中晶格的对称性可将其分为七个晶系,包括三角晶系、四方晶系、正交晶系、单斜晶系、菱形晶系、正菱形晶系和立方晶系。
6. 晶体的晶向和晶面晶体中的晶向和晶面是用来描述晶体内部结构的概念。
晶向是晶体内部原子排列的方向,晶面是晶体内部原子排列的平面。
7. 晶格常数晶格常数是用来描述晶体晶格尺寸大小的物理量。
晶格常数通常表示为a、b、c等,表示晶体中晶格点之间的距离。
二、金属的晶体结构1. 金属的结晶特点金属是一类具有典型金属性质的固体物质,具有较好的导电性、热导性、延展性和塑性等。
金属的晶体结构对其性质有着显著的影响。
2. 金属的晶体结构类型根据金属晶体内部原子排列的方式和规律,金属的晶体结构可分为面心立方结构、体心立方结构和密堆积结构等。
3. 面心立方结构(FCC)面心立方结构是一种典型的金属晶体结构类型,其中晶格点位于立方体的六个面的中心和顶点。
面心立方结构的晶体具有较好的密度和变形性能,常见于铜、铝、银、金等金属中。
4. 体心立方结构(BCC)体心立方结构是一种典型的金属晶体结构类型,其中晶格点位于立方体的顶点和中心。
晶体学基础_2

2023/10/12
45
1.6 倒易点阵
具体说来,要求从新点阵原点O
至任一节点P h,k,l的矢量OP
正好沿着正点阵中(hkl)面的法线方向, 而OP的长度就等于晶面间距的倒数,
即 OP
1
/
d
(
hkl
。
)
这样的新点阵就叫倒易点阵。
2023/10/12
46
1.6.2 倒易点阵
倒易点阵的构建方法:
c
24
1.1.4 典型晶体结构
3.面心立方晶格
Cu、Ag、Au、Al具有面心立方晶格结构
2023/10/12
25
1.1.4 典型晶体结构
4. 六角密排晶格
排列方式: ABABAB (六方密堆积)
Be、Mg、Zn、Cd具有六角密排晶格结构
2023/10/12
26
1.1.4 典型晶体结构
5.金刚石结构
分数坐标分别为:
Cs
+
:
1 2
1 2
1 2
CI : 000
由于点在晶胞内, x、y、z≤1 11
1.1.3 布拉菲阵胞
为了同时反应晶体结构的周期性和对称性,通常按照以下 原则选取晶胞: 1. 反应晶体的宏观对称性; 2. 相等的棱边和夹角尽可能多; 3. 平行六面体的棱与棱之间有尽可能多的直角; 4. 平行六面体的体积尽可能小。
<100>=[100]+[010]+[001]+[100]+[010]+[001]
2023/10/12
38
1.2.2 晶面及其表征
晶面指数(hkl)
现在广泛使用的用来表示晶面指数的是密勒指数,密勒指标是 指平面和三个晶轴相交截数的倒数的互质比,代表一族相互平 行的平面点阵。确定晶面指数的具体步骤如下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 第一章 晶体与非晶体 ★相当点(两个条件:1、性质相同,2、周围环境相同。) ★空间格子的要素: 结点、行列、面网
★晶体的基本性质: 自限性: 晶体能够自发地生长成规则的几何多面体形态。 均一性:同一晶体的不同部分物理化学性质完全相同。晶体是绝对均一性,非晶体是统计的、平均近似均一性。 异向性:同一晶体不同方向具有不同的物理性质。例如: 蓝晶石的不同方向上硬度不同. 对称性:同一晶体中,晶体形态相同的几个部分(或物理性质相同的几个部分)有规律地重复出现. 最小内能性:晶体与同种物质的非晶体相比,内能最小。 稳定性:晶体比非晶体稳定。 ■本章重点总结: 本章包括3组重要的基本概念:
1) 晶体、格子构造、空间格子、相当点;它们之间的关系。 2) 结点、行列、面网、平行六面体; 结点间距、面网间距与面网密度的关系. 3) 晶体的基本性质:自限性、均一性、异向性、对称性、最小内能、稳定性,并解释为什么。 第二章 晶体生长简介
2.1 晶体形成的方式 ★液-固结晶过程:⑴溶液结晶: ①降温法 ②蒸发溶剂法 ③沉淀反应法 ⑵熔融结晶: ①熔融提拉 ②干锅沉降 ③激光熔铸 ④区域熔融 ★固-固结晶过程: ①同质多相转变②晶界迁移结晶③固相反应结晶④重结晶⑤脱玻化 2。2 晶核的形成 ●思考:怎么理解在晶核很小时表面能大于体自由能,而当晶核长大后表面能小于体自由能?
因为成核过程有一个势垒:能越过这个势垒的就可以进行晶体生长了,否则不行。 ★均匀成核:在体系内任何部位成核率是相等的。 ★非均匀成核:在体系的某些部位(杂质、容器壁)的成核率高于另一些部位. ●思考:为什么在杂质、容器壁上容易成核?为什么人工合成晶体要放籽晶?
2。3 晶体生长 ★层生长理论模型(科塞尔理论模型) 层生长理论的中心思想是:晶体生长过程是晶面层层外推的过程。 ★ 螺旋生长理论模型(BCF理论模型) ● 思考:这两个模型有什么联系与区别? 联系:都是层层外推生长; 区别:生长新的一层的成核机理不同。 ●思考:有什么现象可证明这两个生长模型? 环状构造、砂钟构造、晶面的层状阶梯、螺旋纹
2。4 晶面发育规律 ★★布拉维法则(law of Bravais):晶体上的实际晶面往往平行于面网密度大的面网。
为什么?面网密度大-面网间距大—对生长质点吸引力小—生长速度慢—在晶形上保留— 生长速度快—尖灭
★PBC(周期性键链)理论: 晶面分为三类:F面(平坦面,两个Periodic Bond Chain PBC)晶形上易保留。 S面(阶梯面,一个PBC)可保留或不保留。 K面(扭折面,不含PBC),晶形上不易保留 . ★居里-吴里弗原理(最小表面能原理):晶体上所有晶面的表面能之和最小的形态最稳定。 ●思考:以上三个法则-理论-原理的联系? 2
面网密度大-PBC键链多-表面能小 ■2.5 影响晶体生长的因素 涡流、温度、杂质、粘度、组分相对浓度、结晶速度 2。6 晶体的溶解与再生 ■本章重点总结: 1.成核的条件; 2。晶体生长的两个模型及其相互联系; 3。影响晶体形态的内因:布拉维法则、PBC理论及其相互联系。 第三章 晶体的测量与投影
★面角守恒定律:同种矿物的晶体,其对应晶面间角度守恒。 面角守恒定律的意义:结晶学发展的奠基石。 ★晶体的投影:将晶面的空间分布转化为平面图。 极射赤平投影、心射极平投影 对于晶体上的对称面我们通常不将之转化为点,而是直接投影成一条弧线. ■本章总结: 1。 面角守恒定律及其意义; 2.晶面的投影过程, 3. 吴氏网的构成与应用, 4. 方位角与极距角的概念, 5. 投影图的解读,即从投影图上点的分布规律能看出晶体上晶面的空间分布规律 第四章 晶体的宏观对称
4。1 对称的概念和晶体对称的特点 ★概念:对称就是物体相同部分有规律的重复. ★晶体对称的特点:1)由于晶体内部都具有格子构造,通过平移,可使相同质点重复,因此,所有的晶体结构都是对称的。 2)晶体的对称受格子构造规律的限制,因此,晶体的对称是有限的,它遵循“晶体对称定律” . 3)晶体的对称不仅体现在外形上,同时也体现在物理性质. 由以上可见:格子构造使得所有晶体都是对称的,格子构造也使得并不是所有对称都能在晶体中出现的。 4。2 晶体的宏观对称要素对称操作 ★使对称图形中相同部分重复的操作,叫对称操作。 ★在进行对称操作时所应用的辅助几何要素(点、线、面),称为对称要素。 ★对称面—P 操作为反映. 可以有多个对称面存在,如3P、6P等. ★晶体中对称面可能出现的位置有:(1)垂直并平分晶面。(2)垂直晶棱并通过它的中点。 (3)包含晶棱。 ★对称轴—Ln 操作为旋转 。其中n 代表轴次,意指旋转360度相同部分重复的次数。旋转一次的角度为基转角 ,关系为:n=360/ 。 名称 符号 基转角 作图符号
一次对称轴 L1 360. 二次对称轴 L2 180
三次对称轴 L3 120 ▲ 四次对称轴 L4 90 ■ ◆ 3
六次对称轴 L6 60 ★晶体中对称轴可能出现的位置有:(1)晶面中心;(2)晶棱中点;(3)角顶。 ★晶体的对称定律 由于晶体是具有格子构造的固体物质,这种质点格子状的分布特点决定了晶体的对称轴只有n = 1,2,3,4,6这五种,不可能出现n = 5, n 〉6的情况。 为什么呢?直观形象的理解:垂直五次及高于六次的对称轴的平面结构不能构成面网,且不能毫无间隙地铺满整个空间, 即不能成为晶体结构。 ★对称中心—C 操作为反伸。只可能在晶体中心,只可能一个。 ★总结:凡是有对称中心的晶体,晶面总是成对出现且两两反向平行、同形等大. ★旋转反伸轴 –Li 操作为旋转+反伸的复合操作。
4.3。1 对称要素组合定理 ★定理1 如果有一个对称面P包含Ln,则必有n个P同时包含此Ln, Ln +P= Ln nP,且任二相邻的P之间的夹角等于360o/2n。或 :Ln +P// LnnP//(P与P夹角为Ln基转角的一半); ★逆定理:两个P相交,其交线必为一Ln,其基转角为P夹角的两倍,并导出其他n个包含Ln的P. ●思考:两个对称面相交60°,交线处会产生什么对称轴? ★定理2:Ln+L2LnnL2 (L2与L2的夹角是Ln基转角的一半) ★逆定理: L2与L2相交,在其交点且垂直两L2会产生Ln,其基转角是两L2夹角的两倍.并导出其他n个在垂直Ln平面内的L2。 ●思考: 两个L2相交30°,交点处并垂直L2所在平面会产生什么对称轴? ★定理3:Ln +P LnP C (n为偶数) ★逆定理:Ln +C LnP C (n为偶数) P +C LnP C (n为偶数) ★这一定理说明了L2、P、C三者中任两个可以产生第三者. ★定理4:Lin + P// =Lin L2 Lin n/2 L2 n/2 P// (n为偶数) Lin n L2 nP//(n为奇数) 4
本章重点总结: 1) 对称要素:P, Ln, C, Lin; 2) 对称要素组合:4个定理; 3) 对称型:要学会用组合定理判断正确与否; 4) 晶体的对称分类:3个晶族,7个晶系,32个晶类。 第五章 晶体的定向与结晶符号 5。1 结晶轴和晶体几何常数 5。1。1 结晶轴的概念和选择原则 (1)结晶轴的概念 晶轴是几条假想沿着与晶体对称有关的限定方向穿过理想晶体的直线,相交在晶体中心。 5。1.2 轴单位(轴长)和轴率 (1)轴单位:晶轴的度量单位称为轴单位,轴单位是与相应晶轴平行的行列上的结点问距,x、y、z轴上的结点间距用以a、b、c表示. (2)轴率:将轴单位进行连比,记为a:b:c,称为轴率。轴率通常以易的长度作为单位长度,写成以易为1的连比式,例如橄榄石的轴率是0.46575:1:0.58651。 5。2 各晶系结晶轴的选择及其晶体几何常数特点 5。2.1 等轴晶系 (1)对称特点:必有三个互相垂直的L4或Li4 或L2,这三个方向呈等长,这三个方向可以借助于L3的作用互相重复,性质相同,结点间距相等。 (2)选轴原则:以互相垂直的3L4或3Li4 为x、y、z轴;没有4次轴时选择互相垂直的3L2为x、y、z轴,并使z轴直立,y轴左右,x轴前后。 (3)晶体几何常数: a:b:c=1:1:l, ===90 二、晶面指数与晶面相对空间位置的关系(注意填空题) (1)如果晶面与某结晶轴平行,则晶面在该结晶轴上的截距和截距系数为∞,相应的晶面指数为0。 (2)如果晶面与结晶轴截于负端,相应晶面指数为负,把负号写在相应晶面指数的上端如 。 (3)在同一晶体上,如果有两个晶面,晶面指数的绝对值全部对应相等,符号全部对应相反,则这两晶面互相平行, 如。 (4)如果仅知道晶面与结晶轴是相交的,但无法确定晶面指数的具体数值,这类晶面符号用一般式来表示,如(hkl)、(hhk)、(hkk)等。 (5)在同一晶面符号中,晶面指数的绝对值越大,表示晶面在相应结晶轴上的截距系数越小,在轴单位相同的情况下,还表示晶面在该结晶轴上的截距越小,如(1120),晶面在U轴上的截距是X、Y轴上的1/2。 5.4 晶棱符号和晶带符号 一、晶棱符号:晶棱符号是表征晶棱方向的符号,所有平行的晶棱具有同一个晶棱符号. 二、晶带: 交棱相互平行的一组晶面的组合,称为一个晶带。 5。5 对称型的国际符号 见书本
