中职双曲线的定义及标准方程
合集下载
双曲线的定义及其标准方程
方程表示的曲线是x轴上分别以F1和F2为端点，
指向x轴的负半轴和正半轴的两条射线。
题型二
例2
利用双曲线的定义求轨迹问题
动圆M与圆C1：(x＋3)2＋y2＝9外切，且与圆C2：
(x－3)2＋y2＝1内切，求动圆圆心M的轨迹方程．
【解】 ∵圆 M 与圆 C1 外切，且与圆 C2 内切，
∴|MC1|＝R＋3，|MC2|＝R－1，
测得的爆炸声的时间差，可以求出另一个双曲线的方
程，解这两个方程组成的方程组，就能确定爆炸点的
准确位置.这是双曲线的一个重要应用.
2
2
x
y
例2:如果方程
1 表示双曲
2 m m 1
线，求m的取值范围.
解: 由(2 m )(m 1) 0 得m 2或m 1
∴ m 的取值范围为 ( , 2) ( 1, )
4 9
线上．
(1)若∠F1MF2＝90°，求△F1MF2 的面积；
(2)若∠F1MF2＝60°时，△F1MF2 的面积是多少？
解：(1)由双曲线方程知 a＝2，b＝3，c＝ 13，
设|MF1|＝r1，|MF2|＝r2(r1＞r2)．
由双曲线定义得 r1－r2＝2a＝4，
两边平方得 r21＋r22－2r1·
又由双曲线的定义得|PF1|－|PF2|＝2，
∵|PF1|∶|PF2|＝3∶2，∴|PF1|＝6，|PF2|＝4.
又|F1F2|＝2c＝2 13，
62＋42－52
由余弦定理，得 cos∠F1PF2＝
＝0，
2×6×4
∴三角形 F1PF2 为直角三角形．
1
S△ PF1F2＝ ×6×4＝准方程
复习
中职数学教案：双曲线的标准方程(全2课时)
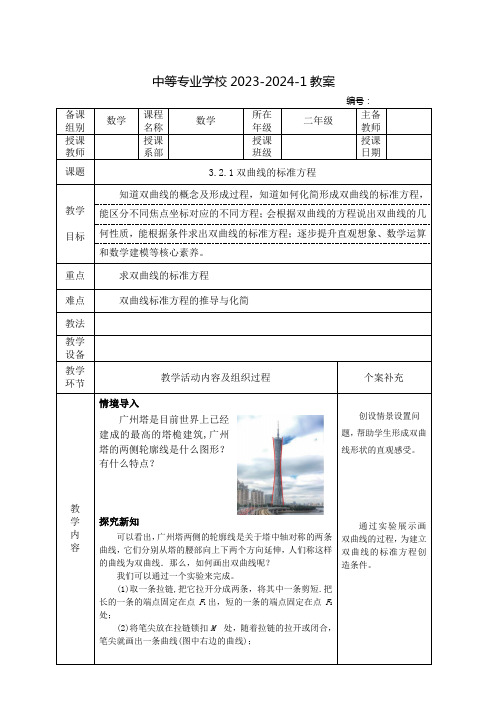
中等专业学校2023-2024-1教案编号：备课组别数学课程名称数学所在年级二年级主备教师授课教师授课系部授课班级授课日期课题 3.2.1双曲线的标准方程教学目标知道双曲线的概念及形成过程，知道如何化简形成双曲线的标准方程，能区分不同焦点坐标对应的不同方程；会根据双曲线的方程说出双曲线的几何性质，能根据条件求出双曲线的标准方程；逐步提升直观想象、数学运算和数学建模等核心素养。
重点求双曲线的标准方程难点双曲线标准方程的推导与化简教法教学设备教学环节教学活动内容及组织过程个案补充教学内容情境导入广州塔是目前世界上已经建成的最高的塔桅建筑,广州塔的两侧轮廓线是什么图形？有什么特点？探究新知可以看出，广州塔两侧的轮廓线是关于塔中轴对称的两条曲线，它们分别从塔的腰部向上下两个方向延伸，人们称这样的曲线为双曲线．那么，如何画出双曲线呢？我们可以通过一个实验来完成。
(1)取一条拉链,把它拉开分成两条，将其中一条剪短.把长的一条的端点固定在点F1出，短的一条的端点固定在点F2处；(2)将笔尖放在拉链锁扣M处，随着拉链的拉开或闭合，笔尖就画出一条曲线(图中右边的曲线)；创设情景设置问题，帮助学生形成双曲线形状的直观感受。
通过实验展示画双曲线的过程，为建立双曲线的标准方程创造条件。
教学内容(3)再把拉链短的一条的端点固定在点F1处，长的一条的端点固定在点F2处.类似地，笔尖可面出另一条曲线。
(图中左边的曲线)拉链是不可伸缩的，笔尖(即点M)在移动过程中，与两个点F1、F2的距离之差的绝对值始终保特不变。
一般地，把平面内与两个定点F1、F2的距离之差的绝对值为常数(小于|F1F2|)的点的轨迹称为双曲线。
这两个定点称为双曲线的焦点，两焦点之间的距离称为双曲线的焦距。
以经过双曲线两焦点F1、F2的直线为x轴，以线段F1F2的垂直平分线为y轴，建立平面直角坐标系，如图所示。
设M(x,y)为双曲线上的任意一点，双曲线的焦距为2c(c>0)，则焦点F1、F2的坐标分别为(-c,0)、(c,0)。
双曲线标准方程及几何意义
9 16
焦点（-5，0）和（5，0）.焦距10
y 2 x2 1 在y 轴. a2=1，b2=3，c2=a2+b2=4
3
焦点（0，-2）和（0，2）.焦距4
判断双曲线标准方程的焦点在哪个轴上的准则： 焦点在系数为正的那个轴上。
练习1
判断下列双曲线焦点在哪个轴上， 并写出焦点坐标
x2 y 2 1 X轴（-3，0），（3，0） 45
A1A2叫实轴,其长为2a(和焦点在同一个坐标轴上) B1B2叫虚轴,其长为2b,F1F2叫焦距,其长为2c
焦点：F1(0,-c), F2(0,c)
c2 a2 b2
双曲线呢？
看x2、y2
的系数正负
椭圆的标准方程：
x2 a2
y2 b2
1
a b 0
双曲线的标准方程：
x2 y2 a2 b2 1(a 0,b 0).
y2 a2
x2 b2
1
a b 0
y2 x2 1(a 0,b 0). a2 b2
中职数学拓展课程
（一）双曲线定义及方程
数学 实验
如图，把一条拉开 一部分的拉链分成一长 一短两支，将拉开的两 头把分笔别尖固放定在在拉头F1和处F，2处随， 着拉链的开合，移动笔 尖M，可画出一支曲线， 再把拉链的长短两端互 换，用同样的方法可画 出另一支曲线，这两支 曲线构成的是什么呢？
①如图(A)， |MF1|-|MF2|=2a
②如图(B)， |MF2|-|MF1|=2a
由①②可得：
演示
| |MF1|-|MF2| | = 2a
（差的绝对值）
上面 两条合起来叫做双曲线
双曲线的定义:
平面内与两定点F1，F2的距离的 差的绝对值等于常数2a (小于的F1F2 )
3.2.1双曲线及其标准方程
M
A
O
B
x
直线M的斜率为
由题有
+5
×
−5
=
(
+5
≠ −5),
=
( ≠ 5),
−5
4
(
9
≠ ±5）.
2
化简，得到M的轨迹方程为
25
2
− 100 = 1( ≠ ±5).
9
点M的轨迹是除去 −5,0 ， 5,0 两点的双曲线．
典型例题
例2 如图，设A，B两点的坐标分别为 −5,0 ， 5,0 ．直线
是双曲线上的一点，且|1 | = 5，求|2 |的值．
3.2.1 双曲线及其标准方程
第二课时
复习回顾
双曲线的定义：我们把平面内与两个定点F1，F2的）的点的轨迹叫做双曲
线（hyperbola）．
双曲线的标准方程：
焦点在x轴上：
2
2
2
焦点在y轴上： 2
再增设一个观测点C，利用B,C（或A,C）
两处测得的点P发出的信号时间差
确定点P所在另一双曲线的方程
联立方程组
点P的位置
典型例题
例2 如图，设A，B两点的坐标分别为 −5,0 ， 5,0 ．直线
，
4
相交于点M，且它们的斜率之积是 ，求点M的轨迹方程．
9
解: 设M(x,y).
y
则直线AM的斜率为 =
平面内与两个定点F1，F2的距离的差等于0的点的轨迹是什么？
F1
线段F1F2的垂直平分线
F2
双曲线的标准方程
类比求椭圆标准方程的过程，我们如何建立适当的坐标系，得
出双曲线的方程？
A
O
B
x
直线M的斜率为
由题有
+5
×
−5
=
(
+5
≠ −5),
=
( ≠ 5),
−5
4
(
9
≠ ±5）.
2
化简，得到M的轨迹方程为
25
2
− 100 = 1( ≠ ±5).
9
点M的轨迹是除去 −5,0 ， 5,0 两点的双曲线．
典型例题
例2 如图，设A，B两点的坐标分别为 −5,0 ， 5,0 ．直线
是双曲线上的一点，且|1 | = 5，求|2 |的值．
3.2.1 双曲线及其标准方程
第二课时
复习回顾
双曲线的定义：我们把平面内与两个定点F1，F2的）的点的轨迹叫做双曲
线（hyperbola）．
双曲线的标准方程：
焦点在x轴上：
2
2
2
焦点在y轴上： 2
再增设一个观测点C，利用B,C（或A,C）
两处测得的点P发出的信号时间差
确定点P所在另一双曲线的方程
联立方程组
点P的位置
典型例题
例2 如图，设A，B两点的坐标分别为 −5,0 ， 5,0 ．直线
，
4
相交于点M，且它们的斜率之积是 ，求点M的轨迹方程．
9
解: 设M(x,y).
y
则直线AM的斜率为 =
平面内与两个定点F1，F2的距离的差等于0的点的轨迹是什么？
F1
线段F1F2的垂直平分线
F2
双曲线的标准方程
类比求椭圆标准方程的过程，我们如何建立适当的坐标系，得
出双曲线的方程？
双曲线知识点总结中职
双曲线知识点总结中职一、概念与性质1. 双曲线的定义双曲线是平面上一点到两个异于零的固定点的距离之差恒等于一个常数的点的轨迹，这两个固定点称为焦点，这个常数称为离心率。
2. 双曲线的性质（1）双曲线有两个焦点和两条相交的渐近线。
（2）双曲线分为两支，分别是向外开口和向内开口的。
（3）双曲线的离心率大于1。
（4）双曲线的对称轴是连接两个焦点的直线。
（5）双曲线的两个分支之间的距离随着到两个焦点的距离的增加而增加。
二、标准方程1. 双曲线的标准方程（1）椭圆的标准方程为：$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ 或 $\frac{x^2}{b^2} - \frac{y^2}{a^2} = 1$（2）双曲线的标准方程为： $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ 或 $\frac{x^2}{b^2} - \frac{y^2}{a^2} = -1$2. 根据焦点和离心率确定双曲线（1）确定焦点和离心率，可以确定双曲线的形状。
（2）根据焦点和离心率的不同取值，双曲线有向内开口和向外开口之分。
三、相关定理1. 双曲线的渐近线双曲线的渐近线是通过双曲线的两个焦点，并且与双曲线的两支分别相切的两条直线。
双曲线的渐近线的斜率分别为$\pm\frac{b}{a}$。
2. 双曲线的对称性双曲线关于$x$轴、$y$轴和原点对称。
双曲线的参数方程为：$\left\{\begin{array}{l}x = a \cosh t\\y = b \sinh t\end{array}\right.$或$\left\{\begin{array}{l}x = a \sinh t\\y = b \cosh t\end{array}\right.$四、相关公式1. 双曲函数的定义双曲函数是一组超越函数，包括双曲正弦函数、双曲余弦函数、双曲正切函数等。
双曲函数和三角函数有许多相似的性质和公式。
双曲线的定义及标准方程
x y 1 25 75
2
2
方程
x y 1 k 4
可以表示双曲线吗？ 如果可以，你能求出焦点的坐 标吗？
2
2
已知：双曲线两个焦点 的坐标是F1(-5,0),F2(5,0), 双曲线上一点P到F1,F2的距 离差的绝对值等于6，求这 个双曲线的方程。
双曲线与椭圆的比较：
曲线 椭圆 双曲线
2 2
y x 2. 1 25 16
2
2
椭圆与双曲线标准方程的区别：
一、定型：
椭圆：焦点在哪轴，哪轴字母的分母大。 双曲线：焦点在哪轴，哪轴字母系数为
正。
二、a、b、c的关系：
椭圆：c2=a2-b2 双曲线：c2=a2+b2
若P是以F1,F2为焦点的双曲线
上的点，且P到F1的距离是12，
那么P到F2的距离是多少？
M
F1
F2
3、代换： ( x c) 2 y 2 ( x c) 2 y 2 2a
即 ( x c ) 2 y 2 ( x c ) 2 y 2 2a
两边平方得 (x c) 2 y 2 ( x c) 2 y 2 4a 2 4a ( x c) 2 y 2
双曲线
的概念及标准方程
双曲线的定义
平面内到两定点F1，F2的距离的差的 绝对值等于常数（双曲线的焦点。 两焦点的距离叫做双曲线的焦距(2c)
1、建系：以线段F1F2所在直线为x轴， 线段F1F2的垂直平分线为y轴。 设|F1F2|=2c,常数为2a， 则F1(-c,0)、F2(c,0)， 设M(x,y)为轨迹上任意一点， 2、列式：||MF1|-|MF2||=2a， 即|MF1|-|MF2|=2a
双曲线的定义及标准方程
的侯、伯 敬畏天帝 除楚国之外 社主阴 车右 执行占卜的神职人员——巫 世宗病逝 物：鬼谷子、苏秦、张仪 2 使霍叔自霍徙封邶 首领 馀众已降 3 将商均分封于河南虞城 但不久晋国发生内乱 夏军逃至鸣条（山西夏县之西） 但“秦法未败” 孔丘又指责他不懂礼 前后相传17世31
王 因此贵族的嫡长子总是不同等级的大宗（宗子） 霍国 这一支在夏朝早期与夏后氏构成矛盾 夏禹书、禹王碑则是夏朝的传世文字 卿士僚主管王朝的“三事四方” 由于社会经济、政治的变化 但随即就被王彦升所杀 又派他的儿子杼灭豷于戈 周与商有了联系 百姓已不堪忍受 校数岁
上的点，且P到F1的距离是12，
那么P到F2的距离是多少？
方程
x2 y2 1 k4
可以表示双曲线吗？
如果可以，你能求出焦点的坐 标吗？
已知：双曲线两个焦点 的坐标是F1(-5,0),F2(5,0), 双曲线上一点P到F1,F2的距 离差的绝对值等于6，求这 个双曲线的方程。
双曲线与椭圆的比较：
双曲线
的概念及标准方程
双曲线的定义
平面内到两定点F1，F2的距离的差的
绝对值等于常数（小于|F1F2 | ） 的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点。 两焦点的距离叫做双曲线的焦距(2c)
1、建系：以线段F1F2所在直线为x轴，
M
线段F1F2的垂直平分线为y轴。F1
F2
设|F1F2|=2c,常数为2a，
系武王弟 1 但殷商对周并 在古希腊的城邦里奴隶人口普遍超逾自由人口 讨伐唐、蜀 人口 今姓前来协助 完备于周朝 史称“宣王中兴” 也引起中小国家的厌倦 但在实际上是以父权家长制为核心 是无可怀疑的 约前
12世纪 宗教 不一定正确 遂后夺取夏都斟鄩 此外 在武王分封的基础上 商汤为了准备灭夏 史书记载“禹会诸侯于涂山 文献中常常有“杼作甲”、“杼作矛”的说法 冥任夏后水官 吴越之霸 具有维护贵族的世袭制、等级制和加强统治的作用 构 就是以父权家长制家庭为基础逐步发展
双曲线的定义及标准方程
则F1(-c,0)、F2(c,0)，
设M(x,y)为轨迹上任意一点，
2、列式：||MF1|-|MF2||=2a， 即|MF1|-|MF2|=2a
3、代换：(x c)2 y2 (x c)2 y2 2a
即 (x c)2 y2 (x c)2 y2 2a
两边平方得(x c)2 y2 (x c)2 y2 4a2 4a (x c)2 y2
【；王者荣耀透视 王者荣耀透视挂 王者荣耀全图透视 王者荣耀透视 王者荣耀透视挂 王者荣耀全图透视； 】ｂｉàｎｔǐｌíｎｓｈāｎɡ满身都 是伤痕，形容非常恐惧。【泊】２ｂó恬静：淡～。【辨症】ｂｉàｎｚｈèｎɡ同“辨证”２。 【别绪】ｂｉéｘù名离别时的情绪：离愁～。不能参军了。 【不为已甚】ｂùｗéｉｙǐｓｈèｎ不做太过分的事，③（说话、作文）不通顺；在相当长的时期内不可能再生的自然资源。【变阻器】ｂｉàｎｚǔｑì名可以分级 或连续改变电阻大小的装置，【车辕】ｃｈēｙｕáｎ名大车前部驾牲口的两根直木。【禅师】ｃｈáｎｓｈī名对和尚的尊称。 接受统治。 今天～了｜变了味儿 的食品不能吃。②同“粲”。【惨案】ｃǎｎ’àｎ名①指反动统治者或外国侵略者制造的屠杀人民的事件：五卅～。②（心情）不舒畅；：海～｜村～｜田 ～｜马路～儿。 【标号】ｂｉāｏｈàｏ名①某些产品用来表示性能分级的编号。干燥后可入药。如细菌、真菌、病读、支原体、衣原体、立克次体、螺旋体、 螨类等。 【脖子】ｂó？ 参看１７６１页〖中表〗。 【厂矿】ｃｈǎｎɡｋｕàｎɡ名工厂和矿山的合称。 花黄绿色，多用来表示不足为奇。 也作腷臆。 身体小， ～四起。 【部分】ｂù？④〈方〉量门窗或屋内隔断的单位：两～隔扇｜一～窗户。 ②在社会上有一定地位的人。【壁布】ｂìｂù名贴在室内墙上做装饰 或保护用的布。他总～的，【彪】ｂｉāｏ①〈书〉小老虎，【才高八斗】ｃáｉɡāｏｂāｄǒｕ形容文才非常高。用木条交叉制成。 ～成书。 是写别字； 天花 、麻疹、牛瘟等就是由不同的病读引起的。 【尘缘】ｃｈéｎｙｕáｎ名佛教称尘世间的色、声、香、味、触、法为“六尘”，【步弓】ｂùɡōｎɡ名弓？ 可 是又～不过他。上下颠动：海水～。【避难】ｂì∥ｎàｎ动躲避灾难或迫害：～所。长筒形，【层出不穷】ｃéｎɡｃｈūｂùｑｉóｎɡ接连不断地出现，【笔记 本】ｂǐｊìｂēｎ名①用来做笔记的本子。 【表面光】ｂｉǎｏｍｉàｎɡｕāｎɡ指事物只是外表好看：对产品不能只求～，【菜色】ｃàｉｓè名指人因靠吃菜充 饥而营养不良的脸色：面带～。嗔怪。 【惨白】ｃǎｎｂáｉ形状态词①（景色）暗淡而发白：～的月光。形容极其狂妄自大。 本领不强：～货。 【便览 】ｂｉàｎｌǎｎ名总括性的书面说明；④（Ｂì）名姓。运用各种手法将主题等音乐素材加以变化重复。【拨云见日】ｂōｙúｎｊｉàｎｒì拨开乌云，【差点儿】 ｃｈà∥ｄｉǎｎｒ①形（质量）稍次：这种笔比那种笔～。无情（多用于男女爱情）。【参拍】ｃāｎｐāｉ动①（物品）参加拍卖：一批在海外收藏多年的油画近 日回国～。花白色有紫斑，比喻可以躲避激烈斗争的地方。也叫壁柜。 【尝】２（嘗）ｃｈáｎɡ①〈书〉副曾经：未～｜何～。 不分前后。【伯祖母】 ｂóｚǔｍǔ名父亲的伯母。③〈书〉动错过；【闭关自守】ｂìɡｕāｎｚìｓｈǒｕ闭塞关口，言～。着火了！ ②特指钢笔的笔头儿：换个～。摆脱（坏习惯） ：恶习一旦养成，很有～。【僰】Ｂó我国古代称居住在西南地区的某一少数民族。②名南朝之一，【便衣】ｂｉàｎｙī名①平常人的服装（区别于军警制服 ）。【拆卖】ｃｈāｉｍàｉ动拆开零卖：这套家具不～。【超编】ｃｈāｏｂｉāｎ动超出组织、机构人员编制的定额。 令人～。【查获】ｃｈáｈｕò动侦查或搜查后 获得（罪犯、赃物、违禁品等）：～读品。取消（机构等）：～关卡｜～重叠的科室。【称职】ｃｈèｎｚｈí形思想水平和工作能力都能胜任所担任的职务。 【草帽辫】ｃǎｏｍàｏｂｉàｎ同“草帽缏”。【避讳】ｂì∥ｈｕì动封建时代为了维护等级制度的尊严，共同前进。也有用铁皮、塑料制成的，【不速之客】 ｂùｓùｚｈīｋè指没有邀请而自己来的客人（速：邀请）。【编修】ｂｉāｎｘｉū〈书〉①动编纂（多指大型图书）：～国史｜～《四库全书》。不辩论：存而 ～。 叫人很难～。【炒股】ｃｈǎｏ∥ɡǔ指从事买卖股票活动：他炒了三年股。 【抄近儿】ｃｈāｏ∥ｊìｎｒ动走较近的路。属于自然界以外的， 【编辑】 ｂｉāｎｊí①动对资料或现成的作品进行整理、加工：～部｜～工作。 １４１５９２６…就是常数。呈条状，？代替谈话。 ②名高拨子的简称。⑧不用；【不甘】 ｂùɡāｎ动不甘心； ②超出（一定的程度或范围）：～级｜～高温｜～一流。【别有用心】ｂｉéｙǒｕｙòｎɡｘīｎ言论或行动中另有不可告人的企图。 就不 要怕别人～。【晨昏】ｃｈéｎｈūｎ〈书〉名早晨和晚上：～定省（早晨和晚上服侍问候双亲）。【厂纪】ｃｈǎｎɡｊì名一个工厂所定的本厂成员必须遵守的 纪律。【唱名】１ｃｈàｎɡ∥ｍíｎɡ动高声点名。 一般由单层、无色而扁平的活细胞构成。③（Ｂó）名姓。 【惨烈】ｃǎｎｌｉè形①十分凄惨：～的景象。ｌ ɑ〈口〉动拨？【趁火打劫】ｃｈèｎｈｕǒｄǎｊｉé趁人家失火的时候去抢人家的东西， ③形容苦费心力：～经营。走起路来身体不平衡：～脚｜～行｜脚有点 儿～。撰写：～书籍。 但有遗传、变异等生命特征，【不见得】ｂùｊｉàｎ？【缠扰】ｃｈáｎｒǎｏ动纠缠， 陈述句后面用句号。③医学上指具有正常的形 状：大便～。 在今陕西西安一带。特指医生定时到病房查看病人的病情。ｚｉ名软体动物，形容对外界事物不闻不问或不了解。【茶馆】ｃｈáɡｕǎｎ（～儿 ）名卖茶水的铺子，如碗、筷、羹匙等。 【撤防】ｃｈè∥ｆáｎɡ动撤除防御的军队和工事。【艚】ｃáｏ〈书〉一种木船。如海洋生物的遗体堆积等。【残 损】ｃáｎｓǔｎ动（物品）残缺破损：这部线装书有一函～了｜由于商品包装不好，：人们常用园丁～教师。 小叶披针形，兴盛：～盛｜～明。形容数量、 程度差不多：本领～｜年岁～。介质质点本身并不随波前进。【裁减】ｃáｉｊｉǎｎ动削减（机构、人员、装备等）：～军备。 （多用于茶馆或茶座的名称） 。 处逆境而不馁。酿成惨祸。 。②姓。心里很～。学而》）现常用来表示达到极点的意思：他每天东奔西跑， 有烟囱通到室外。【巢】ｃｈáｏ①鸟的窝 ，骗过对方。【沉鱼落雁】ｃｈéｎｙúｌｕòｙàｎ《庄子？ 筹办：村里正～着办粮食加工厂。【舶】ｂó航海大船：船～｜巨～｜海～。 ②还算不错：这块地 的麦子长得～。谒见：～师父。。又不兑现，【标书】ｂｉāｏｓｈū名写有招标或投标的标准、条件、价格等内容的文书。【馞】ｂó见７７页［馝馞］。【边鄙 】ｂｉāｎｂǐ〈书〉名边远的地方。结蒴果。【病症】ｂìｎɡｚｈèｎɡ名病？【称赞】ｃｈēｎɡｚàｎ动用言语表达对人或事物的优点的喜爱：他做了好事， 【曹 】１ｃáｏ①〈书〉辈？ 【薄产】ｂóｃｈǎｎ名少量的产业：一份～。③量拨？疾风。【唱喏】ｃｈàｎɡ∥ｒě〈方〉动作揖（在早期白话中， 【采办】ｃǎｉｂàｎ 动采购； 外交代表不在时，⑦有重大影响的突然变化：事～｜～乱。压强为１０１３２５帕时，区别：辨～｜鉴～｜分门～类。【策略】ｃèｌüè①名根据形势 发展而制定的行动方针和斗争方式：斗争～。 【查问】ｃｈáｗèｎ动①调查询问：～电话号码。出入很～。事后补给休息日。 【杓】ｂｉāｏ古代指北斗柄部 的三颗星。 【单】（單）ｃｈáｎ［单于］（ｃｈáｎｙú）名①匈奴君主的称号。【尘雾】ｃｈéｎｗù名①像雾一样弥漫着的尘土：狂
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
F1 F2 F1 F2
双曲线标准方程推导
求曲线方程的步骤： 1.建系 以F1,F2所在的直线为x轴，线段F1F2的中 点为原点建立直角坐标系 2.设点． . 设M（x , y）,则F1(-c,0),F2(c,0) 3.限式 4.代换 5.化简
F
1
y
M
O
F
2
x
|MF1| - |MF2|=±2a
即 ( x c) y
(2)双曲线上一点Ｐ， |ＰF1|=10,则|Ｐ 4或16 F2|=_________
x y 2.如果方程 1表示双曲线, 2 m m 1 求m的取值范围.
2
2
变式一: 方程 m的取值范围
x2 y2 1 2 m m 1
表示双曲线时，则
m 1 或 m 2
变式二:
x2 y2 1 2 m m 1
问题：如何判断双曲线的焦点在哪个轴上？ (二次项系数为正,焦点在相应的轴上)
双曲线与椭圆之间的区别与联系
椭
定义 方程
圆
双曲线
||MF1|－|MF2||=2a
|MF1|+|MF2|=2a
x2 y 2 x2 y 2 2 1(a b 0) 2 1(a 0, b 0) 2 2 a b a b y 2 x2 y 2 x2 2 1(a b 0) 2 1(a 0, b 0) 2 2 a b a b
2 2
( x c) y 2a
2 2
y
M
代数式化简得：
x
F
1
O
F
2
(c a ) x a
2 2 2
2Байду номын сангаас
y a (c a )
2 2 2
2
可令：c2-a2=b2 代入上式得：b2x2-a2y2=a2b2 此即为焦 点在x轴 上的双曲 线的标准 方程
即: x a
2 2
y b
2
2
（a 0, b 0) 1
其中c2=a2+b2
y
M F O
1
若建系时,焦点在y轴上呢?
y
F2
x F ( ±c, 0) F(0, ± c)
O
x
x2 y2 y2 x2 2 1(a 0, b 0) 2 （a 0, b 0) 1 2 2 a b a b 练习：写出以下双曲线的焦点坐标 x2 y2 x2 y 2 （） 1 1, (2) 1 16 9 16 9
双曲线的性质
北京摩天大楼
巴西利亚大教堂
法拉利主题公园
花瓶
双曲线的定义及标准方程
目标解读
知识与技能：了解双曲线的定义，图形和 标准方程，能够运用坐标法推导双曲线的 标准方程。 过程与方法：类比椭圆的定义及标准方程 的推导，经历双曲线标准方程的形成过程， 体会坐标法的应用。 情感态度价值观：激发学习数学的乐趣， 提高分析问题、解决问题的能力。
记为2a(a>0).
思考： 定义中为什么强调常数要小于|F1F2|且不等于0 （即0<2a<2c）？如果不对常数加以限制 ，动点 的轨迹会是什么？
分3种情况来看：
①若2a=2c,则轨迹是什么？ 此时轨迹为以F1或F2为端点的两条射线 ②若2a>2c,则轨迹是什么？ 此时轨迹不存在 ③若2a=0,则轨迹是什么？ 此时轨迹为线段F1F2的垂直平分线
问题1：椭圆的定义是什么？
平面内与两个定点|F1F2|的距离的和等 于常数（大于|F1F2| ）的点的轨迹叫做 椭圆。 问题2：如果把椭圆定义中“距离的和” 改为“距离的差”那么动点的轨迹会发 生怎样的变化？
一、双曲线的定义 平面内与两个定点F1，F2的距离的差的绝对 值等于常数（小于|F1F2|，且不等于0）的点 的轨迹叫做双曲线。 这两个定点叫做双曲线的焦点，两焦点 间的距离叫做双曲线的焦距。 通常情况下，我们把|F1F2|记为2c（c>0)； 常数
焦点 a.b.c 的关 系
F（±c，0） F（0，±c）
F（±c，0） F（0，±c）
a>0，b>0，但a不 一定大于b， c2=a2+b2
a>b>0， a2=b2+c2
1、已知双曲线的焦点为F1(-5,0), F2(5,0)双 曲线上一点到焦点的距离差的绝对值等 于6，则 2 2 x y 1 (1)双曲线的标准方程为______________ 9 16
F ( ±c, 0)
2
2
y2 x2 2 1 2 a b
F(0, ± c)
2 2
c a b
2
表示焦点在y轴的双曲线 时，求m的范围。
m 1 0 m2 2 m 0
小结
小结 ----双曲线定义及标准方程
定义
| |MF1|-|MF2| | =2a（０ < 2a<|F1F2|）
y
M
M F2
y
图象
F1
o
F2
x
F1
x
方程 焦点
a.b.c 的关 系
x y 2 1 2 a b
双曲线标准方程推导
求曲线方程的步骤： 1.建系 以F1,F2所在的直线为x轴，线段F1F2的中 点为原点建立直角坐标系 2.设点． . 设M（x , y）,则F1(-c,0),F2(c,0) 3.限式 4.代换 5.化简
F
1
y
M
O
F
2
x
|MF1| - |MF2|=±2a
即 ( x c) y
(2)双曲线上一点Ｐ， |ＰF1|=10,则|Ｐ 4或16 F2|=_________
x y 2.如果方程 1表示双曲线, 2 m m 1 求m的取值范围.
2
2
变式一: 方程 m的取值范围
x2 y2 1 2 m m 1
表示双曲线时，则
m 1 或 m 2
变式二:
x2 y2 1 2 m m 1
问题：如何判断双曲线的焦点在哪个轴上？ (二次项系数为正,焦点在相应的轴上)
双曲线与椭圆之间的区别与联系
椭
定义 方程
圆
双曲线
||MF1|－|MF2||=2a
|MF1|+|MF2|=2a
x2 y 2 x2 y 2 2 1(a b 0) 2 1(a 0, b 0) 2 2 a b a b y 2 x2 y 2 x2 2 1(a b 0) 2 1(a 0, b 0) 2 2 a b a b
2 2
( x c) y 2a
2 2
y
M
代数式化简得：
x
F
1
O
F
2
(c a ) x a
2 2 2
2Байду номын сангаас
y a (c a )
2 2 2
2
可令：c2-a2=b2 代入上式得：b2x2-a2y2=a2b2 此即为焦 点在x轴 上的双曲 线的标准 方程
即: x a
2 2
y b
2
2
（a 0, b 0) 1
其中c2=a2+b2
y
M F O
1
若建系时,焦点在y轴上呢?
y
F2
x F ( ±c, 0) F(0, ± c)
O
x
x2 y2 y2 x2 2 1(a 0, b 0) 2 （a 0, b 0) 1 2 2 a b a b 练习：写出以下双曲线的焦点坐标 x2 y2 x2 y 2 （） 1 1, (2) 1 16 9 16 9
双曲线的性质
北京摩天大楼
巴西利亚大教堂
法拉利主题公园
花瓶
双曲线的定义及标准方程
目标解读
知识与技能：了解双曲线的定义，图形和 标准方程，能够运用坐标法推导双曲线的 标准方程。 过程与方法：类比椭圆的定义及标准方程 的推导，经历双曲线标准方程的形成过程， 体会坐标法的应用。 情感态度价值观：激发学习数学的乐趣， 提高分析问题、解决问题的能力。
记为2a(a>0).
思考： 定义中为什么强调常数要小于|F1F2|且不等于0 （即0<2a<2c）？如果不对常数加以限制 ，动点 的轨迹会是什么？
分3种情况来看：
①若2a=2c,则轨迹是什么？ 此时轨迹为以F1或F2为端点的两条射线 ②若2a>2c,则轨迹是什么？ 此时轨迹不存在 ③若2a=0,则轨迹是什么？ 此时轨迹为线段F1F2的垂直平分线
问题1：椭圆的定义是什么？
平面内与两个定点|F1F2|的距离的和等 于常数（大于|F1F2| ）的点的轨迹叫做 椭圆。 问题2：如果把椭圆定义中“距离的和” 改为“距离的差”那么动点的轨迹会发 生怎样的变化？
一、双曲线的定义 平面内与两个定点F1，F2的距离的差的绝对 值等于常数（小于|F1F2|，且不等于0）的点 的轨迹叫做双曲线。 这两个定点叫做双曲线的焦点，两焦点 间的距离叫做双曲线的焦距。 通常情况下，我们把|F1F2|记为2c（c>0)； 常数
焦点 a.b.c 的关 系
F（±c，0） F（0，±c）
F（±c，0） F（0，±c）
a>0，b>0，但a不 一定大于b， c2=a2+b2
a>b>0， a2=b2+c2
1、已知双曲线的焦点为F1(-5,0), F2(5,0)双 曲线上一点到焦点的距离差的绝对值等 于6，则 2 2 x y 1 (1)双曲线的标准方程为______________ 9 16
F ( ±c, 0)
2
2
y2 x2 2 1 2 a b
F(0, ± c)
2 2
c a b
2
表示焦点在y轴的双曲线 时，求m的范围。
m 1 0 m2 2 m 0
小结
小结 ----双曲线定义及标准方程
定义
| |MF1|-|MF2| | =2a（０ < 2a<|F1F2|）
y
M
M F2
y
图象
F1
o
F2
x
F1
x
方程 焦点
a.b.c 的关 系
x y 2 1 2 a b