第六章_序列相关
第六章 自相关(序列相关)

2 横截面数据中的自相关:一般来说截面数据不容
易出现自相关,但相邻的观测单位之间也可能存在 “溢出效应”(neighborhood effect)。例如,相邻 省份、国家之间的经济活动相互影响(通过贸易、 投资、劳动力流动等);相邻地区的农业产量受到 类似的天气影响而相关;同一社区内的房屋价格存 在相关性;相邻地区的消费倾向有相关性
图 中 实 线 表 示 真 实 的 总 体 回 归 线 。 假 设 扰 动 项 存 在
正 自 相 关 , 即 E ij X >0 , 若 1>0 ( 图 中 左 边 小 椭 圆 形 ) 由 于 存 在 正 自 相 关 , 则 2 >0 的 可 能 性 也 就 很 大 ; 而 若
n-1<0 ( 图 中 右 边 小 椭 圆 形 ) 则 n <0 的 可 能 性 也 就 很 大
此 检 验 被 称 为 B GB 检 验 ( r e u s c h - G o d f r e y )
3B 、 o x P i e r c e Q 检 验
定义残差的各阶样本自相关系数为
t=j+1 ˆ j n
e e
t=1
n
t t-j
2 e t
(j=1,2, ,p)
d ˆ 且 n 正 态 分 布 , j = 1 , 2 , , p j
3 设 定 误 差 m i s s p e c i f i c a t i o n : 如 果 模 型 设 定 中 遗 漏 会 引 起 扰 动 项 的 自 相 关 。
了 某 个 自 相 关 的 解 释 变 量 , 并 被 纳 入 到 扰 动 项 中 , 则
三 、 自 相 关 的 检 验
X X X X n 1 j ˆ ˆ Q = S+ 1 - etet-j xt x + xt-jx t-j t n j= p+1 1i=j+1 p
第六章时间序列作业试题及答案 (2)

第六章动态数列一、判断题二、1.若将某地区社会商品库存额按时间先后顺序排列,此种动态数列属于时期数列。
()三、2.定基发展速度反映了现象在一定时期内发展的总速度,环比发展速度反映了现象比前一期的增长程度。
()四、3.平均增长速度不是根据各期环比增长速度直接求得的,而是根据平均发展速度计算的。
()五、4.用水平法计算的平均发展速度只取决于最初发展水平和最末发展水平,与中间各期发展水平无关。
()六、5.平均发展速度是环比发展速度的平均数,也是一种序时平均数。
()1、×2、×3、√4、√5、√。
七、单项选择题八、1.根据时期数列计算序时平均数应采用()。
九、 A.几何平均法 B.加权算术平均法 C.简单算术平均法 D.首末折半法十、2.下列数列中哪一个属于动态数列()。
AHA12GAGGAGAGGAFFFFAFAF十一、 A.学生按学习成绩分组形成的数列 B.工业企业按地区分组形成的数列十二、 C.职工按工资水平高低排列形成的数列 D.出口额按时间先后顺序排列形成的数列十三、 3.已知某企业1月、2月、3月、4月的平均职工人数分别为190人、195人、193人和201人。
则该企业一季度的平均职工人数的计算方法为()。
十四、十五、AHA12GAGGAGAGGAFFFFAFAF4.说明现象在较长时期内发展的总速度的指标是()。
A、环比发展速度 B.平均发展速度 C.定基发展速度 D.环比增长速度5.已知各期环比增长速度为2%、5%、8%和7%,则相应的定基增长速度的计算方法为()。
A.(102%×105%×108%×107%)-100%B.102%×105%×108%×107%C.2%×5%×8%×7%D.(2%×5%×8%×7%)-100%6.定基增长速度与环比增长速度的关系是()。
第六章-自相关-答案

第六章 自相关一、判断题1. 模型中的解释变量含有滞后被解释变量的时候可以使用DW 检验法检验自相关。
(F )2. 可以作残差对某个解释变量的散点图来大概判断是否存在自相关。
(F )3. 存在序列相关时, 使用标准公式估计的随机扰动项的方差不再具有无偏性。
(T )4. 杜宾—瓦尔森检验能够检验出任何形式的自相关。
( F )5. 不存在负的自相关关系。
(F )6. LM 检验与DW 检验结果不一致是很有可能的。
(T )二、存在序列相关时, 有可能会高估或者低估随机扰动项的真实方差, 但通常会低估。
(T )三、单项选择题1. 如果模型存在序列相关, 则( D )。
A......B....C......D.2. DW 检验的零假设是(为随机误差项的一阶相关系数)( B )。
A. DW =0B.C. DW =1D.3.下列哪个序列相关可用DW 检验(为具有零均值, 常数方差且不存在序列相关的随机变量)( A )。
A. B.C.4. DW 的取值范围是( D )。
A. -1≤DW ≤0B. -1≤DW ≤1C. -2≤DW ≤2D. 0≤DW ≤45.当DW =4时, 说明( D )。
A. 不存在序列相关B. 不能判断是否存在自相关C. 存在完全的正的自相关D. 存在完全的负的自相关6.根据20个观测值估计的结果, 一元线性回归模型的DW =2.3。
在样本容量n=20,解释变量k=1, 显著性水平为0.05时, 查得dL=1,dU=1.41,则可以决断( A )。
A. 不存在自相关B. 存在正的自相关C. 存在负的自相关D. 无法确定7.当模型存在序列相关现象时, 适宜的参数估计方法是( C )。
A. 加权最小二乘法B. 间接最小二乘法C. 广义差分法D. 工具变量法8.对于原模型, 广义差分模型是指( D )。
A.B.C.D .()()()1t t 1t t 101t t u u x x 1y y ----+-+-=-ρρβρβρ9. 假定某企业的生产决策是由模型描述的(其中为产量, 为价格), 又知: 如果该企业在t -1期生产过剩, 经营人员会削减t 期的产量。
计量第六章习题

自相关性一、单项选择题1、如果模型t t t u X b b Y ++=10存在序列相关,则【 】A cov (t x ,t u )=0B cov (t u ,s u )=0(ts )C cov (t x ,t u )0D cov (t u ,s u )0(ts ) 2、DW 检验的零假设是(为随机项的一阶自相关系数)【 】A DW=0B =0C DW=1D =13、下列哪种形式的序列相关可用DW 统计量来检验(i v 为具有零均值,常数方差,且不存在序列相关的随机变量)【 】A t t t v u u +=-1ρB t t t t v u u u +++=--Λ221ρρC t t v u ρ=D Λ++=-12t t t v v u ρρ4、DW 值的取值范围是【 】A -1DW0B -1DW1C -2DW2D 0 DW4 5、当DW =4是时,说明【 】A 不存在序列相关B 不能判断是否存在一阶自相关C 存在完全的正的一阶自相关D 存在完全的负的一阶自相关6、根据20个观测值估计的结果,一元线性回归模型的DW =。
在样本容量n=20,解释变量k=1,显着性水平=时,查得L d =1,U d =,则可以判断【 】A 不存在一阶自相关B 存在正的一阶自相关C 存在负的一阶自相关D 无法确定 7、当模型存在序列相关现象时,适宜的参数估计方法是【 】A 加权最小二乘法B 间接最小二乘法C 广义差分法D 工具变量法 8、对于原模型t t t u X b b Y ++=10,一阶广义差分模型是指【 】A)()()(1)(1t t t t t t t X f u X f X b X f b X f Y ++=B tt t u X b Y ∆+∆=∆1C t t t u X b b Y ∆+∆+=∆10D )()()1(11101----+-+-=-t t t t t t u u X X b b Y Y ρρρρ9、采用一阶差分模型克服一阶线性自相关问题适用于下列哪种情况【 】 A 0 B 1 C -1<<0 D 0<<110、假定某企业的生产决策由模型t t t u P b b S ++=10描述(其中t S 为产量,t P 为价格),如果该企业在t-1期生产过剩,经济人员会削减t 期的产量。
第六章 序列相关性

一、序列相关性概念
对于模型
Yi=0+1X1i+2X2i+…+kXki+i
随机项互不相关的基本假设表现为
i=1,2, …,n
Cov(i , j)=0
ij, i,j=1,2, …,n
如果对于不同的样本点,随机误差项之间不再
是不相关的,而是存在某种相关性,则认为出现 了序列相关性。
第一节 序列相关性概念
t 是满足以下标准的OLS假定的随机干扰项:
E( t )0
,
E
(
2 t
)
2
且
E( t s )0 (t s,t ,s 1,2,,n)
t ~
N
(0,
2
)
在计量经济学中,具备上述性质的量称为白噪声(white noise)。
第一节 序列相关性概念
二、自相关的分类
(一)一阶自回归形式
如前所述,当 t误差项只与其滞后一期值 t1 有关时,即 t f (t1) t 则称 t 具有一阶自回归形式。
第一节 序列相关性概念
• 相关系数 的取值范围是[-1,1]。
• 当 0 时,称 t 存在正自相关;
• 当 0 时,称 t 存在负自相关;
•当 。
0
时,称
t
不存在自相关或非自相关
第一节 序列相关性概念
一阶自回归模型的图形
ut
ut
o >0
o t
t
<0
•0< <1, 正自相关。
•-1< <0,负自相关。
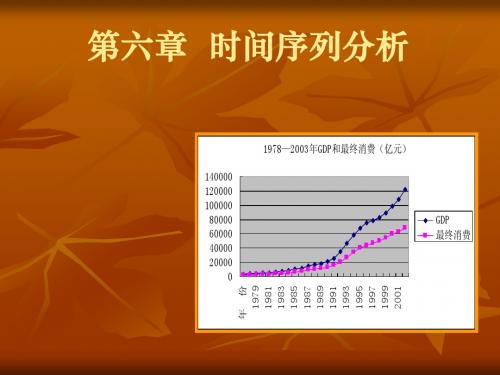
大多数经济时间数据都有一个明显的特点:惯性,表现在时间 序列不同时间的前后关联上。
第六章 时间序列分析

长期趋势 季节变动 循环变动 不规则变动
第二节 时间序列的基本分析指标
一、时间序列的水平指标
发展水平 平均发展水平 增长量 平均增长量
(一)发展水平
(1)概念:在一定时间下的具体指标数值。可以是: 绝对数:02年GDP为102398亿元。 相对数:02年第三产业值占GDP比重为33.7%。 平均数:02年去全国职工年平均工资为12422元。
动态平均数时间序列
三、时间序列编制的原则
(1)同一时间序列。 指标值所属时间长短应一致。
(2)总体范围应一致。 (3)经济内容应一致。 (4)计算口径应一致。
包括计算方法和计量单位。
四、时间序列的分析内容
时间数列分析指标 时间数列构成分析
水平指标
发展水平 增减水平 平均发展水平
速度指标 发展速度
时间数列的作用
(1)进行统计预测。历史数据→模型→预测 (2)进行相关分析。将两组时间数列对比分
析→相关程度
二、时间序列的种类
(一)绝对数时间数列
第一 时期数列 A .概念:绝对数时间数列中的各项指标反映现象在
各个时期发展过程的累计总量。 如:GDP总量时间序列、销售额时间序列、生产量 时间序列 B. 特点: a.可加性 b.指标数值大小与所属时间长短有直接关系。 c.指标值通过连续登记方式获得
a
af f
1028 105 7 10815 106(人) 30
例题
日期
1-9
库存(件)a 245
af
2205
9-16 16-21 21-24 24-31 合计 230 241 257 263 - 1610 1205 771 3941 9732
第六章 时间序列的分析
(二)序时平均数与静态平均数的比较
异同 特点 抽象的反 映内容 依据的数 列 区别 平均的差 异 说明内容 静态平均数 动态平均数
联系
一般水平 变量数列 不同总体单位的 总体一定历史条件下 的一般水平
一般水平 时间数列 不同时间的 现象一定发展阶段 的一般水平
㈢平均发展水平的计算
计算平均发展水平要分不同的情形,根据 不同的情形采取不同的计算方法。即,在 计算平均发展水平时,要注意以下几点: 首先是考虑时间数列种类;对于绝对数时 间数列要分清是时期数列还是时点数列; 对其中的时点数列还要进一步分清是间隔 时点还是连续的时点等等。
职工年平均工 资指数(%) (以1990年为 100) 110.0
124.5 150.5 209.8 255.8
时间序列的作用
可以描述现象在具体时间条件下的发展状 况和结果; 可以进行各种动态对比分析,研究现象发 展变化的方向和程度; 可以分析现象的发展变化趋势及其规律, 如长期趋势、季节趋势等; 根据对现象发展变化趋势与规律的分析, 可以进行动态预测。
循环变动的测定
1、长期趋势(T):主要的、决定性的因 素,例如:经济增长 2、季节变动(S):每年重复出现的有规 律的周期变动,例如:羽绒服和农产品的 销售量 3、循环变动(C):一年以上的周期变动, 例如:经济周期 4、不规则变动(I):偶然因素引起的无规 律不规则变动。
第二节
动态发展水平指标
产 量
6 604
7 057
8 000
8 868
9 153
9 400
逐期增 长量 累计增 长量
----
453
6-蛋白质序列分析

FASTA格式 SWISS-PROT格式 PDB格式
2. 理化特性分析--基于一级结构的预测
理化特性分析
相对分子量、氨基酸组成、等电点、酶切特性、疏水 性等、亲水性,及消光系数等
常用工具
蛋白的功能位点是与其三维结构紧密相关 的,局部区域符合某种pattern不能保证一 定会具有对应的性质,要根据实际情况, 谨慎对待pattern 预测结果。
PROSITE 工具
ScanProsite
搜索蛋白序列是否含PROSITE数据库中存有的模式或是功能位点;搜 索Swiss-Prot中符合某种模式的蛋白以及蛋白三维结构数据库PDB中 含有该模式的蛋白,可察看其三维结构。
2. 蛋白质序列数据库
/
/swissprot/
3. 蛋白质模体及结构域数据库
PROSITE蛋白质家族和结构域数据库 (/prosite/ )
PROSITE数据库收集了有显著生物学意义的蛋白质位点序 列、蛋白质特征序列谱库以及序列模型,
注意问题
不要把所有搜索结果用在比对中 对搜索结果进行手工校正,将显著性不高的序列,非
蛋白质家族的序列剔除掉。
6. 同源建模
如果蛋白质序列有显著的同源序列(相似 性>50%,尤其是与已知结构的蛋白质之间 有显著同源性时,即可进行同源建模
以已知结构的蛋白质为模板进行精确的结构模 型构建
数字表示氨基酸个数。 [AC]-x-V-x(4)-{ED}This pattern is translated as: [Ala or Cys]-any-Val-any-any-any-any-{any but Glu or Asp}
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
负自相关 不能确定的区域, 无自相关 不能确定的区域, 正自相关
杜宾检验失效怎么办?
45
3、拉格朗日乘数检验
杜宾-沃森(Durbin-Waston)检验具有 一定局限性,并有可能会出现无法确定结 果的情况,为此,推出备择检验方法—— 拉格朗日乘数检验
(1)提出假设
H0:=0,即不存在一阶自相关; HA:0,即存在一阶自相关。
这种现象就不能期望误差项是无关的。
5、模型设定的偏误
所谓模型设定偏误(Specification error)是指 所设定的模型“不正确”。主要表现在模型中丢掉 了重要的解释变量或模型函数形式有偏误。 例如,本来应该估计的模型为
Yt=0+1X1t+ 2X2t + 3X3t + t
但在模型设定中做了下述回归:
第六章 序列相关
引子:t检验和F检验一定就可靠吗?
研究居民储蓄存款 Y 与居民收入 X 的关系:
Yt = 1 + 2 X t + ut
用普通最小二乘法估计其参数,结果为
ˆ Yt = 27.9123 + 0.3524 X t
(1.8690) (0.0055)
t = (14.9343) Fra bibliotek64.2069)
4 - d L DW 4
问题: dL与du 如何查?
DW检验的判断准则图
不能检出 不能检出
ýÔàØ Õ ×Ï ¹
Þ Ô à Î ×Ï Ø ¹
ºÔàØ ¸ ×Ï ¹
0
dL
dU
2
4- dU
4- dL
4
例题2 见上例
某地区制造业的库存(KC)与销售情况(XS) 研究,
R2 是辅助 回归的拟合 优度
(2)构造统计量LM
LM (n 1) R 2 ~ (1)
1)估计模型,求出残差ε 2)做辅助方程, 计算LM (辅助方程因变量为ε; 辅助方程自变量为:c, εi-1, 原方程中所有 自变量)
如果大部分落在II,IV象限,存在负相关。
EViews软件实现
A:时间与残差的散点图(ε-t 图)
1.键入 LS y c x 作回归 2.在方程窗口中单击“Resids”按钮, (或者单击“View”→ “Actual, Fitted, Residual” →”Table”),可得到残差分布图
B: t 与 t 1的散点图
1. 键入 LS y c x 作回归,求的残差resid, 2. 用GENR生成序列R,R=resid, 3. 在Quick菜单中选Graph项,键入R R(1),选择Scatter Diogram,得所需残差图
例题1.
某地区制造业的库存(KC)与销售情况(XS)如
例如:季度数据来自月度数据的简单平 均,这种平均的计算减弱了每月数据的波 动性,从而使随机干扰项出现序列相关。 。
4.蛛网现象
许多农产品的供给表现出一种所谓的蛛网现象,
例如:供给对价格的反应要滞后一个时期,今 年的作物种植是受去年流行的价格影响的。因 此,相关的函数形式是:
St 1 2 Pt 1 ut
表(单位:亿元),要求估计模型:
KCi 0 1 XS i i
检验是否存在自相关
(一)用OLS法估计模型
点击New,建立Workfile,输入KC和XS的数据。
点击Procs,选Make Equation,输出结果如下:
(二)自相关检验
1、残差图法
(1)时间与残差的散点图
则称为一阶序列相关;
如果仅仅与它的前两期有关,则称为二阶序
列相关;依此类推,有三阶、四阶……;我们 把二阶以上的统称为高阶序列相关。
(二) 一阶序列相关表现形式
本书只讨论一阶序列相关,且一般假定它是
线性相关,可表示成:
i i 1 i
满足经典假设对随机项的所有要求。
这里:1 1, 称为一阶自相关系数, i 是随机项,
两种散点图
(1)时间与残差的散点图
40 30 20 4 10 2 0 0 -2 -4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Actual Fitted
Residual
t 与 t 1的散点图
2 1 0
R(-1)
-1 -2 -3 -4 -4 -2 0 R 2 4
负自相关
εt
t
O εt随着t 的变化呈锯齿型(一个正接一个负),随时间逐 次改变符号,表明存在负自相关。
B: 绘制 t 与 t 1的散点图
以 t 为纵坐标, t 1为横坐标, 绘制( 1 , 2), ( 2 , 3 )....( n1 , n )的散点图
大部分点落在I,III象限,表明存在正自相关;
2.滞后效应
指某一指标对另一指标的影响不仅限于当期而是 延续若干期。由此带来变量的自相关。
例如,居民当期可支配收入的增加,不会使居民的消费 水平在当期就达到应有水平,而是要经过若干期才能达 到。因为人的消费观念的改变客观上存在自适应期。
3、数据处理造成的相关 在实际经济问题中,有些数据是通过已知数据 生成的。 新生成的数据与原数据间就有了内在 的联系,表现出序列相关性。
(1960-2001) 1.求出DW值 EVIEW软件 dW =1.37 2. 临界值 a=0.05 n=42 k=2 dl=1.46 du=1.55 3. 判断 dW =1.37<dl=1.46 所以存在一阶正序列相关
练习:用DW法检验产品销售收入与研发数据
的序列相关性
1. 求出DW值 EVIEW软件 dW =1.202918 2. 临界值 a=0.05 n=15 k=2 dl=0.81 du=1.07 4-dl=3.19 4-du=2.93 3. 判断 1.07=du<dW =1.2029<4-du=2.93 所以不存在一阶正序列相关
3
模型的假设
1) Eui 0 对任意 i 都成立 2 V ui u 即所有随机误差项的方差都相等 2) 3)不同期的两个随机误差项彼此不相关,即 i j covu i , u j 0
4) 解释变量与随机误差项不相关,即 cov(x j , ui ) 0
正自相关
(2)
t
与 t 1的散点图
在(一)的操作后,得到残差resid,用GENR生成序列R, R=resid, 在Quick菜单中选Graph项,键入R R(-1), 选择Scatter Diogram,得残差图:
正自相关
练习:检验异方差5.31收入与消费例题的数
据的有无序列相关性?
有大于0的倾向,当ut小于0时,随后若干项都有 小于0的倾向,则认为ut具有正序列相关性;
如果两个相继的随机项ut与ut+1具有正负相 反的倾向.则则意味着ut具有负序列相关性
一阶序列相关
二阶序列相关
高阶序列相关
如果 i 仅仅与它的前一期有关,即 i f ( i 1 ),
2. 杜宾-沃森(Durbin-Watson)检验法
A :适用条件
(1)自变量X非随机;
检验什么?
(2)随机误差项i为一阶自回归形式: i=i-1+i (3)回归模型中不应含有滞后应变量作为解释变 量,即不应出现下列形式:
Yi=0+1X1i+kXki+Yi-1+i
(4)回归含有截距项
DW与ρ 的关系
可以证明,在大样本情况下,
ˆ DW 2(1 )
其中
ˆ
i 2 n i i 2
n
i 1
i21
由 DW 2(1 ) ˆ ˆ 可得DW 值与 的对应关系如表所示。
ˆ
-1 (-1,0) 0 (0,1) 1
DW
4 (2,4) 2 (0,2) 0
如果 如果
0, 称为正的序列相关;
0, 称为负的序列相关。
如果 ρ =0, 没有自相关性 当ρ =1或-1时,序列相关性最强
二、序列相关产生的原因
序 列 相 关 产 生 的 原 因
经济系统的惯性 经济活动的滞后效应 数据处理造成的相关 蛛网现象 模型设定偏误
13
1、经济系统的惯性 经济时间数据明显的特点: 惯性,表现在时间序列 不同时间的前后关联上。 如众所周知,GDP、价格指数、生产、就业和 失业等时间序列都呈现周期循环。相继的观测值很 可能是相互依赖的。 例如,绝对收入假设下居民总消费函数模型: Ct=0+1Yt+t t=1,2,…,n 由于消费习惯的影响被包含在随机误差项中,则可 能出现序列相关性(往往是正相关 )
然后,通过分析这些“近似估计量”之间的相关 性,以判断随机误差项是否具有序列相关性。
(二)具体检验方法
● 图示检验法 ● DW检验法 ● 拉格朗日乘数检验
23
1.图示检验法---- 残差图法
A.时间顺序图(以时间t为横轴,残差ε为纵轴,绘制残差对
时间的变化图)
εt
O t
正自相 关
εt 随着t 的变化逐次变化并不频繁地改变符号,而是几个正的, 后面跟着几个 负的 ,表明随机误差项ut存在正自相关。
Yt=0+1X1t+ 1X2t + vt
Vt=3X3t + t,如果X3确实影响Y,则出现序列 相关。
自相关可能出现在横截面数据中,但
更一般出现在时间序列数据中
三、序列相关的后果
1. 最小二乘估计量具有线性、无偏,但非有
效, 即不是最佳线性无偏估计量
