湖北省黄冈市2016-2017学年高二下学期期末考试理科数学试题(word版含答案)
湖北省黄冈市数学高二下学期理数期末考试试卷

湖北省黄冈市数学高二下学期理数期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2017高二下·赤峰期末) 设为虚数单位,则复数()A .B .C .D .2. (2分)已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.6826,则P(X>4)=()A . 0.1588B . 0.1587C . 0.1586D . 0.158583. (2分)用数学归纳法证明:1+x+x2+x3+…+xn+2= (x≠1,n∈N+)成立时,验证n=1的过程中左边的式子是()A . 1B . 1+xC . 1+x+x2D . 1+x+x2+x34. (2分) (2016高二下·辽宁期中) 已知随机变量x服从二项分布x~B(6,),则P(x=2)=()A .B .C .D .5. (2分)甲、乙两人同时从图书馆走向教室,甲一半路程步行,一半路程跑步;乙一半时间步行,一半时间跑步,若两人步行、跑步的速度一样,则先到教室的是A . 甲B . 乙C . 甲、乙同时到达D . 无法确定6. (2分) (2019高二下·吉林月考) 下列表述正确的是()①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.A . ①②③B . ②③④C . ①③⑤D . ②④⑤;7. (2分) (2017高二下·汉中期中) 若f(x)=ax4+bx2+c满足f′(1)=2,则f′(﹣1)=()A . ﹣4B . ﹣2C . 2D . 48. (2分) (2017高二下·钦州港期末) 某班选派6人参加两项公益活动,每项活动最多安排4人,则不同的安排方法有()A . 50种B . 70种C . 35种D . 55种9. (2分) (2016高二下·三门峡期中) 若离散型随机变量X的分布列如图,则常数c的值为()X01P9c2﹣c3﹣8cA . 或B .C .D . 110. (2分)将1枚硬币抛2次,恰好出现1次正面的概率是()A .B .C .D . 011. (2分)当n=1,2,3,4,5,6 时,比较 2n 和 n2 的大小并猜想,则下列猜想中一定正确的是()A . 时,n2>2nB . 时, n2>2nC . 时, 2n>n2D . 时, 2n>n212. (2分)函数f(x)= ,若实数a满足f(f(a))=1,则实数a的所有取值的和为()A . 1B . ﹣C . ﹣﹣D . ﹣2二、填空题 (共4题;共4分)13. (1分)(2019·天津模拟) 已知为虚数单位,复数,则等于________;14. (1分) (2016高三上·杭州期中) 袋中有4只红球3只黑球,从袋中任取4只球,取到1只红球得1分,取到1只黑球得3分,设得分为随机变量ξ,则P(ξ≤7)=________.15. (1分) (2016高二下·天津期末) 将2名教师,4名学生分成两个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师2名学生组成,不同的安排方案共有________种.16. (1分) (2016高三上·沈阳期中) 曲线与直线y=x﹣1及x=4所围成的封闭图形的面积为________.三、解答题 (共7题;共50分)17. (5分)已知(a2+1)n(a≠0)展开式中各项系数之和等于(x2+)5展开式的常数项.(1)求n值;(2)若(a2+1)n展开式的系数最大的项等于54,求a值.18. (10分)已知函数f(x)=lnx+ax.(1)若函数f(x)在x=1处的切线方程为y=2x+m,求实数a和m的值;(2)若函数f(x)在定义域内有两个不同的零点x1,x2,求实数a的取值范围.19. (5分) (2017高一下·南昌期末) 某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:学历35岁以下35~50岁50岁以上本科803020研究生x20y(Ⅰ)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为10的样本,将该样本看成一个总体,从中任取3人,求至少有1人的学历为研究生的概率;(Ⅱ)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取出1人,此人的年龄为50岁以上的概率为,求x、y的值.20. (10分) (2017高一下·沈阳期末) 下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对照数据:34562.534 4.5参考公式:(1)已知产量和能耗呈线性关系,请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;(2)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?21. (10分) (2017高二下·安徽期中) 已知函数f(x)=x﹣﹣2lnx,a∈R.(1)讨论函数f(x)的单调性;(2)若函数f(x)有两个极值点x1,x2,且x1<x2,①求a的取值范围;②证明:f(x2)<x2﹣1.22. (5分) (2018高一上·台州期末) 已知函数.(Ⅰ)求函数的最小正周期和单调递增区间;(Ⅱ)函数的图象向左平移个单位后,得到偶函数的图象,求实数的最小值. 23. (5分) (2018高三上·邹城期中) 已知函数,不等式的解集为 . (Ⅰ)求实数的值;(Ⅱ)若关于的不等式恒成立,求实数的取值范围.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共50分) 17-1、18-1、18-2、19-1、20-1、20-2、21-1、21-2、22-1、23-1、第11 页共11 页。
湖北省三市2016-2017学年高二下期末考试数学试题(理)含解析

2016~2017学年度第二学期期末联考试题高二数学(理科)本试卷共4页,全卷满分150分,考试时间120分钟。
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 已知集合,集合,则A. B. C. D.【答案】C【解析】,所以=2. 已知命题;命题,则下列命题中为真命题的是A. B. C. D.【答案】B【解析】试题分析:∵当时,,∴命题为假命题;∵,图象连续且,∴函数存在零点,即方程有解,∴命题为真命题,由复合命题真值表得:为假命题;为真命题;为假命题;为假命题.选故B.考点:1、复合命题的真假判断;2、指数函数;3、函数与方程.3. 设随机变量x服从正态分布N(2,9),若,则m=A. B. C. D. 2【答案】B【解析】由正态分布性质可得4. 设复数,若,则的概率为A. B. C. D.【答案】D【解析】若则,则的概率为:作出如图,则概率为直线上方与圆的公共部分的面积除以整个圆的面积,即:5. 某几何体的三视图如图所示,则该几何体的体积为A. B. C. D.【答案】B【解析】作出立体图形为:故该几何体的体积为:6. 若双曲线的一条渐近线与圆至多有一个交点,则双曲线的离心率为...A. B. C. D.【答案】C【解析】由题得双曲线的渐近线为:,与圆至多有一个交点,则,由,故选C7. 设x,y满足约束条件则的最大值是A. B. C. D.【答案】B【解析】作出如图:则表示阴影区域点与原点的连线的斜率,故8. 若抛物线上一点到焦点和抛物线对称轴的距离分别为10和6,则抛物线方程为A. B.C. 或D. 或【答案】C【解析】试题分析:,即,代入抛物线中,,所以或.∴或.考点:1.抛物线的焦点;2.抛物线的对称轴;3.抛物线的标准方程.9. 用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有A. 144个B. 120个C. 96个D. 72个【答案】B【解析】试题分析:根据题意,符合条件的五位数首位数字必须是4、5其中1个,末位数字为0、2、4中其中1个;进而对首位数字分2种情况讨论,①首位数字为5时,②首位数字为4时,每种情况下分析首位、末位数字的情况,再安排剩余的三个位置,由分步计数原理可得其情况数目,进而由分类加法原理,计算可得答案.解:根据题意,符合条件的五位数首位数字必须是4、5其中1个,末位数字为0、2、4中其中1个;分两种情况讨论:①首位数字为5时,末位数字有3种情况,在剩余的4个数中任取3个,放在剩余的3个位置上,有A43=24种情况,此时有3×24=72个,②首位数字为4时,末位数字有2种情况,在剩余的4个数中任取3个,放在剩余的3个位置上,有A43=24种情况,此时有2×24=48个,共有72+48=120个.故选:B考点:排列、组合及简单计数问题.10. 公元前300年欧几里得提出一种算法,该算法程序框图如图所示。
湖北省黄冈市2017-2018学年高二下学期期末考试数学(理)试题(图片版)

2018年春季期末高二数学参考答案(理科)一、选择题1—5 DCCCA 6—10 DCADB 11—12 AC二、填空题13、14、15、16、2592三、解答题17、解:若命题p真,则在恒成立.则有…………………………………………3分若命题q真,则……………………………………………………6分由题意知p与q必为一真一假………………………………7分若q真q假若p假q真综合得a的范围为.………………………………12分18.解:(1)有解即可. ………………………………2分有解为“局部奇函数”. ………………………………5分(2)由题意知在上有解…………………6分令则………………………………10分.………………………………12分19. 解:(1)先排前4次,只能正品再排第5和第10的位置上,再排余下4个位置共有种. ………………………………6分(2)第6次为最后一件次品,另2件在前5次中出现,前5次中有3件正品.共有不同测试方法种. (12)20、解:(Ⅰ)依题意,p1=P(40<X<80)=,,,由二项分布,未来4年中,至多有1年的年入流量超过120的概率为=………4分(Ⅱ)记水电站的总利润为Y(单位,万元)(1)安装1台发电机的情形,由于水库年入流总量大于40,故一台发电机运行的概率为1,对应的年利润Y=4000,E(Y)=4000×1=4000,…………………………6分(2)安装2台发电机的情形,依题意,当 40<X<80时,一台发电机运行,此时Y=4000﹣600=3400,因此P(Y=3400)=P(40<X<80)=p1=,当X≥80时,两台发电机运行,此时Y=4000×2=8000,因此,P(Y=10000)=P(X≥80)=P2+P3=0.8,所以E(Y)=3400×0.2+8000×0.8=7080. (9)(3)安装3台发电机的情形,依题意,当 40<X<80时,一台发电机运行,此时Y=4000﹣1200=2800,因此P(Y=2800)=P(40<X<80)=p1=0.2,当80≤X≤120时,两台发电机运行,此时Y=4000×2﹣600=7400,因此,P(Y=7400)=P(80≤X ≤120)=p2=0.7,当X>120时,三台发电机运行,此时Y=4000×3=12000,因此,P(Y=12000)=P(X>120)=p3=0.1,由此得Y的分布列如下×0.7+12000×0.1=6940.综上,欲使水电站年总利润的均值达到最大,应安装发电机2台.…………………12分21、解:⑴由题意得函数的定义域为.∵,∴,……………………2分①当时,恒成立,上单调递增. ………………3分②当时,则当时,,单调递减;当时,,单调递增. ………………………………4分综上,当时,上单调递减,在上单调递增;当时,函数上单调递增;当时,,在上单调递增. ……………5分(2)当时,,∴,∴函数单调递增,………………………………6分又,,所以存在唯一的,使得,………………………8分且当时,,单调递减;当时,,单调递增,所以,………………9分设,则在上单调递减,所以,即.………………………………11分若关于的不等式有解,又为整数,所以.所以存在整数满足题意,且的最小值为0. ………………………………12分(注:只要判断g(x0)在(-1,0)上如,照样给分)22、解:(1)………………………………3分………………………………5分(2)圆心(-2,1)到直线距离………………………………8分最小值为………………………………10分23、(1)当时,………………………………2分当时,…………………………4分当时综上:不等式解集为………………………………5分(2)存在x使得成立………………………………8分………………………………10分。
(全优试卷)湖北省黄冈市高二下学期期末考试理科数学试题Word版含答案

2017学年黄冈市高二(下)期末试题数学(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)1. 设集合S ={x |x >-2},T ={x |x 2+3x -4≤0},则(∁R S )∪T =( ) A .B .(-∞,1]C .2.已知复数201712i z i=-,则复数z 的虚部为( )A. 25-B. 15iC. 15D. 15-3. 随机变量X ~()1,4N ,若()20.2p x ≥=,则()01p x ≤≤为( ) A. 0.2 B. 0.3 C. 0.4 D. 0.64.若4个人报名参加3项体育比赛,每个人限报一项,则不同的报名方法的种数有( ) A. 34A B. 34C C. 34 D. 435. 广告投入对商品的销售额有较大影响.某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如下表(单位:万元)8万元时的销售额约为( )A. 90.8B. 72.4C. 98.2D. 111.26. 从1,2,3,4,5中不放回地依次取2个数,事件A 表示“第1次取到的是奇数”,事件B 表示“第2次取到的是奇数”,则(|)P B A =( )A.15 B.310 C.25 D.127.,()f x '是()f x 的导函数,则()f x '的图象大致是( )8. 如图,长方形的四个顶点坐标为O (0,0),A (4,0),B (4,2),C (0,2),曲线y =B,现将质点随机投入长方形OABCA.23 B. 34 C. 45 D. 569.若,0x y >且2x y +>,则1y x+和1xy +的值满足( )A.1y x +和1x y +都大于2 B. 1y x +和1xy +都小于2C.1y x+和1x y +中至少有一个小于2 D. 以上说法都不对10.2013年8月,考古学家在湖北省随州市叶家山发现了大量的古墓,经过对生物体内碳14含量的测量,估计该古墓群应该形成于公元前850年左右的西周时期,已知碳14的“半衰期”为5730年(即含量大约经过5730年衰减为原来的一半),由此可知,所测生物体内碳14的含量应最接近于( ) A .25﹪ B . 50﹪C . 70﹪D .75﹪11. 对大于1的自然数 m 的三次幂可用奇数进行以下形式的“分裂”:33313731523945171119⎧⎧⎪⎧⎪⎪⎨⎨⎨⎩⎪⎪⎩⎪⎩, , ,....仿此,若3m 的“分裂数”中有一个是2017,则m 的值为( )A. 44B. 45C. 46D.4712. 已知函数()()2ln 2f x a x x a x =+-+恰有两个零点,则实数a 的取值范围是( )A. ()1,-+∞B. ()1,0-C. ()2,0-D. ()2,1-- 二、填空题:(本大题共4小题,每小题5分,共20分)13. 数学老师从6道习题中随机抽3道让同学检测,规定至少要解答正确2道题才能及格。
湖北省黄冈市16-17学年度高二下学期期末考试(图片)—

湖北省黄冈市2016—2017学年度下学期期末考试高二数学文试题2017年春季高二期末考试数学参考答案(文科)一、选择题二、填空题13. 5 14. 10015. [1,5) 16. 72解答题17.解:或; ...................................................................4分或, ...................................................................8分 若为真,则真且真,∴ ...............................................................12分18.解:(1)∵函数h(x)=(m 2-5m +1)xm +1为幂函数,∴m 2-5m +1=1,. ...........2分解得m =0或5 ...................................................4分 又h(x)为奇函数,∴m =0 .............................................................................6分(2)由(1)可知g(x)=x +1-2x ,x ∈⎣⎡⎦⎤0,12, 令1-2x =t ,则x =-12t 2+12,t ∈[0,1], ...................................................................9分 ∴f(t)=-12t 2+t +12=-12(t -1)2+1∈⎣⎡⎦⎤12,1,故g(x)=h(x)+,x ∈⎣⎡⎦⎤0,12的值域为⎣⎡⎦⎤12,1. ..............................................................................................12分19. 解:(1) ........................................................4分(2)根据列联表中的数据,得到..............................6分因此按99.9%的可靠性要求,不能认为“成绩与班级有关系”. .............................8分(3)设“抽到或号”为事件,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y ),所有的基本事件有(1,1), (1,2) (1,3),……(6,6),共36个. ............................ 9分事件包含的基本事件有(3,6),(6,3),(5,4) ,(4,5) (4,6) (6,4), (5,5)共7个 ∴,即抽到9号或10号的概率为736 ...........................................................12分20.解:①当6≤t <9时,y ′=-38t 2-32t +36=-38(t +12)(t -8). .........................................................2分令y ′=0,得t =-12(舍去)或t =8.当6≤t <8时,y ′>0,当8<t<9时,y ′<0,故t =8时,y 有最大值,y max =19. .........................................................5分②当9≤t ≤10时,y =18t +594是增函数,故t =10时,y max =16. .........................................................8分③当10<t ≤12时,y =-3(t -11)2+18,故t =11时,y max =18. .........................................................11分 综上可知,通过该路段用时最多的时刻为上午8点..................................................12分 21.解:(I )由已知得函数的定义域为, ...........................1分函数22)(ln 1ln )(ln 1ln )(x x x x x x x g -=⋅-=', ...........................2分当时,, 所以函数的增区间是; ...........................4分当且时,,所以函数的单调减区间是, .....5分 (II )因f(x)在上为减函数,且.故2ln 1()0(ln )x f x a x -'=-≤在上恒成立. 所以当时,......8分 又()22ln 111()ln ln (ln )x f x a a x x x -'=-=-+-()2111ln 24a x =--+-, 故当,即时,. ...............................8分所以于是,故a 的最小值为. ...............................12分三、选考题 22.解:(1)由曲线C 的极坐标方程为ρsin 2θ=4cos θ,即ρ2sin 2θ=4ρcos θ,可得直角坐标方程:y 2=4x . ...............................5分(2)把直线l 的参数方程(t 为参数)代入曲线C 的直角坐标方程可得:3t 2﹣8t ﹣16=0,∴t 1+t 2=,t 1t 2=﹣. ...............................7分 ∴|t 1﹣t 2|===.∴+===1. ...............................10分23.解:(1)∵函数f (x )=|2x +1|+|2x ﹣a |≥|2x +1﹣(2x ﹣a )|=|a +1|,且f (x )的最小值为2,∴|a +1|=2,∴a=1 或a=﹣3. ...............................5分(2)f (x )≤|2x ﹣4|的解集包含[﹣2,﹣1],即x ∈[﹣2,﹣1]时, f (x )≤|2x ﹣4|恒成立, 即|2x +1|+|2x ﹣a |≤|2x ﹣4|恒成立,即﹣2x ﹣1+|2x ﹣a |≤4﹣2x 恒成立,....................7分 即|2x ﹣a |≤5恒成立,即﹣5+a ≤2x ≤5+a 恒成立,即,∴﹣7≤a ≤1..10分。
湖北省黄冈市高二下学期数学期末考试试卷
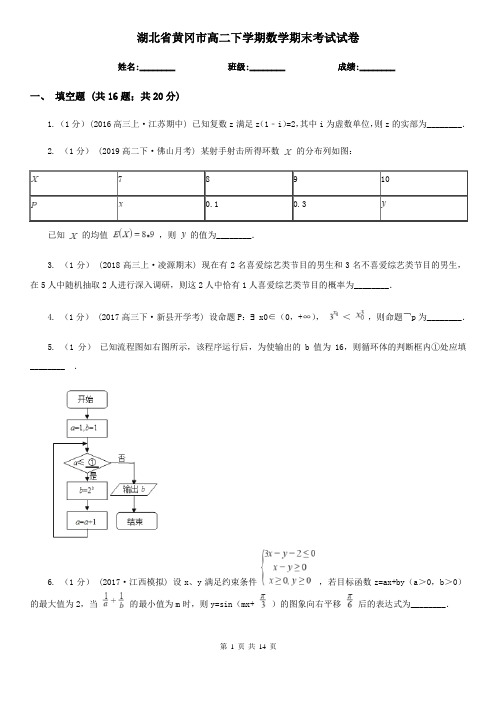
湖北省黄冈市高二下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、填空题 (共16题;共20分)1. (1分) (2016高三上·江苏期中) 已知复数z满足z(1﹣i)=2,其中i为虚数单位,则z的实部为________.2. (1分) (2019高二下·佛山月考) 某射手射击所得环数的分布列如图:789100.10.3已知的均值,则的值为________.3. (1分) (2018高三上·凌源期末) 现在有2名喜爱综艺类节目的男生和3名不喜爱综艺类节目的男生,在5人中随机抽取2人进行深入调研,则这2人中恰有1人喜爱综艺类节目的概率为________.4. (1分) (2017高三下·新县开学考) 设命题P:∃x0∈(0,+∞),<,则命题¬p为________.5. (1分)已知流程图如右图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填________ .6. (1分)(2017·江西模拟) 设x、y满足约束条件,若目标函数z=ax+by(a>0,b>0)的最大值为2,当的最小值为m时,则y=sin(mx+ )的图象向右平移后的表达式为________.7. (1分) (2018高二上·南阳月考) 与双曲线有相同渐近线,且过的双曲线方程是________.8. (5分) (2018高二上·沭阳月考) 已知“过圆上一点的切线方程是”,类比上述结论,则过椭圆上一点的切线方程为________.9. (1分)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是________10. (1分)若函数f(x)=xln(x+)为偶函数,则a= ________ 。
11. (1分)(2017·山东) 已知(1+3x)n的展开式中含有x2的系数是54,则n=________.12. (1分) (2016高一上·黑龙江期中) 若x≥0,y≥0,且x+2y=1,则2x+3y2的最小值是________.13. (1分) (2017高二下·河口期末) 下列命题正确的是________⑴若,则;⑵若,,则是的必要非充分条件;⑶函数的值域是;⑷若奇函数满足,则函数图象关于直线对称.14. (1分) (2016高二下·静海开学考) 过椭圆的左焦点F且倾斜角为60°的直线交椭圆于A、B两点,若,则椭圆的离心率e=________.15. (1分)定义在R上的运算:x*y=x(1﹣y),若不等式(x﹣y)*(x+y)<1对一切实数x恒成立,则实数y的取值范围是________16. (1分) (2016高二下·信阳期末) 已知e是自然对数的底数,实数a,b满足eb=2a﹣3,则|2a﹣b﹣1|的最小值为________.二、解答题 (共9题;共95分)17. (10分)已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,BE=BC=1,AE= ,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点.(1)求证:MN⊥EA;(2)求二面角M﹣NE﹣A的余弦值.18. (10分) (2018高二下·巨鹿期末) 已知函数在处取得极值.(1)求实数的值;(2)若,试讨论的单调性.19. (10分) (2020高二上·青铜峡期末) 有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.(1)将红色卡片和蓝色卡片分别放在两个袋中,然后从两个袋中各取一张卡片,求两张卡片数字之积为偶数的概率(2)将五张卡片放在一个袋子中,从中任取两张,求两张卡片颜色不同的概率20. (10分) (2017高一上·南昌期末) 已知α,β均为锐角,s inα= ,cos(α+β)= ,求(Ⅰ)sinβ,(Ⅱ)tan(2α+β)21. (10分) (2017高二下·惠来期中) 数列{an}满足(1)计算a1,a2,a3,a4(2)猜想an的表达式,并用数学归纳法证明你的结论.22. (10分)(2017·成武模拟) 解答题(Ⅰ)讨论函数f(x)= ex的单调性,并证明当x>0时,(x﹣2)ex+x+2>0;(Ⅱ)证明:当a∈[0,1)时,函数g(x)= (x>0)有最小值.设g(x)的最小值为h(a),求函数h(a)的值域.23. (10分) (2015高二下·广安期中) 已知函数f(x)=alnx+x2 (a为实常数).(1)当a=﹣4时,求函数f(x)的单调区间;(2)当x∈[1,e]时,讨论方程f(x)=0根的个数;(3)若 a>0,且对任意的x1,x2∈[1,e],都有|f(x1)﹣f(x2)| ,求实数a的取值范围.24. (10分) (2019高三上·长春月考) 已知是椭圆的两个焦点, 为坐标原点,离心率为 ,点在椭圆上.(1)求椭圆的标准方程;(2)为椭圆上三个动点, 在第二象限, 关于原点对称,且 ,判断是否存在最小值,若存在,求出该最小值,并求出此时点的坐标,若不存在,说明理由.25. (15分)(2016·山东理) 已知f(x)=a(x﹣lnx)+ ,a∈R.(1)讨论f(x)的单调性;(2)当a=1时,证明f(x)>f′(x)+ 对于任意的x∈[1,2]成立.参考答案一、填空题 (共16题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、二、解答题 (共9题;共95分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、21-1、21-2、22-1、23-1、23-2、23-3、24-1、24-2、25-1、25-2、。
2016-2017学年度第二学期期末考试高二理科数学_最新修正版
2016—2017学年度第二学期教学质量检查 高二理科数学考生注意:本卷共三大题,22小题,满分150分. 考试用时120分钟,不能使用计算器.第Ⅰ卷 选择题一、选择题:本大题共12小题,每小题5分,共60分. 每小题各有四个选择支,仅有一个选择支正确.请把正确选择支号在答题卡中的相应位置涂黑.1.已知i 为虚数单位,则复数21i z i=+的共轭复数z =( ) A. 1i - B. 1i + C. 1i -+ D. 1i --2.函数2()(1)f x x =+的导函数为( )A .1)(+='x x fB .12)(+='x x fC .2)(+='x x fD .22)(+='x x f3.已知随机变量X 服从正态分布即2(,)XN μσ,且()0.6826P X μσμσ-<≤+=,若随机变量(5,1)X N ,则(6)P X ≥=( )A .0.3413B .0.3174C .0.1587D .0.15864.若离散型随机变量ξ的取值分别为,m n ,且3(),(),8P m n P n m E ξξξ=====,则22m n +的值为( )A .14B .516C .58D .13165.'()f x 是()f x 的导函数,'()f x 的图象如右图所示,则()f x 的大致图象只可能是( )A B C D 6.将甲、乙、丙、丁四名学生分配到三个不同的班,每个班至少一名,则不同分法的种数为( )A .18B .24C .36D .727.为直观判断两个分类变量X 和Y 之间是否有关系,若它们的取值分别为{}21,x x 和{}21,y y ,通过抽样得到频数表为:则下列哪两个比值相差越大,可判断两个分类变量之间的关系应该越强( )y 1 y 2 x 1 a b x 2 c d 第5题图A. c a a +与d b b +B. d a a +与c b c +C. d b a +与c a c +D.d c a +与ba c + 8.用数学归纳法证明等式3)12(12)1()1(2122222222+=+++-++-++n n n n n ,当1n k =+时,等式左端应在n k =的基础上加上( )A .222)1(k k ++B .22)1(k k ++C .2)1(+kD .]1)1(2)[1(312+++k k9.五个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币. 若硬币正面朝上, 则这个人站起来; 若硬币正面朝下, 则这个人继续坐着. 那么, 没有相邻的两个人站起来的概率为( )A .516B .1132C .1532D .12 10.由曲线x y =与直线2,0-==x y y 围成封闭图形的面积为( ) A .310 B .4 C .316 D .6 11.已知数列{}n a 满足)(11,21*11N n a a a n n ∈-==+,则使10021<+++k a a a 成立的最大正整数k 的值为( )A .198B .199C .200D .20112.已知函数b ax x x f --=ln )(,若0)(≤x f 对任意0>x 恒成立,则a b +的最小值为( )A .1e -B .0C .1D .e 2第Ⅱ卷 非选择题二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中相应的位置上.13. 已知函数()ln f x x x =,则曲线)(x f y =在点1=x 处切线的倾斜角为__________.14. 若n x )3(-的展开式中所有项的系数和为32,则含3x 项的系数是__________(用数字作答). 15.若随机变量~(,)X B n p ,且52EX =,54DX =,则当(1)P X ==__________(用数字作答). 16.已知)(x f y =为R 上的连续可导函数,且)()()(x f x f x f x '>+',则函数21)()1()(+-=x f x x g 在),1(+∞上的零点个数为___________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.解答过程必须写在答题卡相应题号指定的区域内,超出指定区域的答案无效.)17.(本小题满分10分)已知复数12=2 , =34z a i z i +-(a R ∈,i 为虚数单位).(Ⅰ)若12z z ⋅是纯虚数,求实数a 的值;(Ⅱ)若复数12z z ⋅在复平面上对应的点在第二象限,且1||4z ≤,求实数a 的取值范围.18.(本小题满分 12 分)东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限x (单位:年,*x N ∈)和所支出的维护费用y (单位:万元)厂家提供的统计资料如下:使用年限x (年) 1 2 3 4 5维护费用y (万元) 6 7 7.5 8 9(Ⅰ)请根据以上数据,用最小二乘法原理求出维护费用y 关于x 的线性回归方程a x b yˆˆˆ+=; (Ⅱ)若规定当维护费用y 超过13.1万元时,该批空调必须报废,试根据(1)的结论预测该批空调使用年限的最大值.参考公式:最小二乘估计线性回归方程a x b yˆˆˆ+=中系数计算公式:∑∑∑∑====-⋅-=---=n i in i i i n i i n i i i x n x y x n y x x x y y x x b1221121)())((ˆ,x b y a ˆˆ-=,其中x ,y 表示样本均值. 19.(本小题满分 12 分)甲、乙两人想参加《中国诗词大会》比赛,筹办方要从10首诗词中分别抽出3首让甲、乙背诵,规定至少背出其中2首才算合格;在这10首诗词中,甲只能背出其中的7首,乙只能背出其中的8首.(Ⅰ)求抽到甲能背诵的诗词的数量ξ的分布列及数学期望;(Ⅱ)求甲、乙两人中至少有一人能合格的概率.20.(本小题满分 12 分)已知函数23(),()2x f x x e g x x ==.(Ⅰ)求函数()f x 的单调区间;(Ⅱ)求证:R x ∈∀,()()f x g x ≥.21.(本小题满分 12 分) 已知函数32()(,)f x x mx nx m n R =++∈.(Ⅰ)若()f x 在1x =处取得极大值,求实数m 的取值范围;(Ⅱ)若(1)0f '=,且过点(0,1)P 有且只有两条直线与曲线()y f x =相切,求实数m 的值.22.(本小题满分 12 分)已知函数()R a x a x x f ∈-=ln )(2,()()F x bx b R =∈.(Ⅰ)讨论()f x 的单调性;(Ⅱ)设2,()()()a g x f x F x ==+,若12,x x 12(0)x x <<是)(x g 的两个零点,且1202x x x +=,试问曲线()y g x =在点0x 处的切线能否与x 轴平行?请说明理由.。
2016-2017学年度高二第二学期期末考试理科数学试题及答案
试卷类型:A高二数学(理科)试题2017.7 注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共5页。
2.答题前,考生务必在答题卡上用直径0.5毫米的黑色字迹签字笔将自己的姓名、准考证号填写清楚,并粘好条形码。
请认真核准条形码上的准考证号、姓名和科目。
3.答第Ⅰ卷时,选出每题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在本试卷上无效。
4.答第Ⅱ卷时,请用直径0.5毫米的黑色字迹签字笔在答题卡上各题的答题区域内作答。
答在本试卷上无效。
5.第(22)、(23)小题为选考题,请按题目要求从中任选一题作答,并用2B 铅笔在答题卡上把所选题目题号后的方框涂黑。
6.考试结束后,将本试卷和答题卡一并收回。
附:回归方程ˆˆˆybx a =+中斜率与截距的最小二乘估计公式分别为: ∑∑∑∑====--=---=ni ini ii ni ini iixn xy x n yx x x y yx x b1221121)())((ˆ,x b y aˆˆ-= 第Ⅰ卷一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合 题目要求的。
(1)已知复数iiz +-=122,其中i 是虚数单位,则z 的模等于 (A )2- (B) 3 (C) 4 (D) 2(2)用反证法证明某命题时,对结论:“自然数c b a ,,中恰有一个偶数”正确的反设为 (A) c b a ,,中至少有两个偶数 (B)c b a ,,中至少有两个偶数或都是奇数 (C) c b a ,,都是奇数 (D) c b a ,,都是偶数 (3)用数学归纳法证明:对任意正偶数n ,均有41212111 (41)31211+++=--++-+-n n n n ( )21...n++,在验证2=n 正确后,归纳假设应写成 (A )假设)(*N k k n ∈=时命题成立 (B )假设)(*N k k n ∈≥时命题成立 (C )假设)(2*N k k n ∈=时命题成立 (D )假设))(1(2*N k k n ∈+=时命题成立(4)从3男4女共7人中选出3人,且所选3人有男有女,则不同的选法种数有 (A )30种 (B) 32 种 (C) 34种 (D) 35种 (5)曲线xe y =在点()22e ,处的切线与坐标轴所围三角形的面积为(A)22e (B)2e (C) 22e (D) 492e(6)已知随机变量X 服从正态分布()2,3σN ,且)3(41)1(>=<X P X P ,则)5(<X P 等于(A)81 (B) 85 (C) 43 (D) 87(7)已知⎰≥3sin 2πxdx a ,曲线)1ln(1)(++=ax aax x f 在点())1(,1f 处的切线的斜率为k ,则k 的最小值为 (A)1 (B)23(C)2 (D) 3 (8)甲、乙、丙三人独立参加体育达标测试,已知甲、乙、丙各自通过测试的概率分别为p ,4332,,且他们是否通过测试互不影响.若三人中只有甲通过的概率为161,则甲、丙二人中至少有一人通过测试的概率为 (A)87 (B) 43 (C) 85 (D) 76(9)函数)1(2)(3-'+=f x x x f ,则函数)(x f 在区间[]3,2-上的值域是 (A) ]9,24[- (B) ]24,24[- (C) ]24,4[ (D)[]9,4 (10)设()()5522105)1(...1)1(1x a x a x a a x +++++++=-,则420a a a ++等于(A) 242 (B) 121 (C) 244 (D)122(11)已知函数)()()(2R b x bx x e x f x ∈-=.若存在⎥⎦⎤⎢⎣⎡∈2,21x ,使得0)()(>'+x f x x f ,则实数b 的取值范围是(A) ⎪⎭⎫ ⎝⎛∞-65, (B) ⎪⎭⎫ ⎝⎛∞-38, (C) ⎪⎭⎫⎝⎛-65,23 (D) ⎪⎭⎫⎝⎛∞+,38 (12)中国南北朝时期的著作《孙子算经》中,对同余除法有较深的研究.设)0(,,>m m b a 为整数,若a 和b 被m 除得的余数相同,则称a 和b 对模m 同余,记为)(mod m b a =.如9和21被6除得的余数都是3,则记)6(m o d 219=.若20202022201200202...22⋅++⋅+⋅+=C C C C a ,)10(mod b a =,则b 的值可以是(A) 2011 (B) 2012 (C) 2013 (D) 2014第II 卷本卷包括必考题和选考题两部分。
2016-2017学年湖北省黄冈市高二(下)期末数学试卷(理科)(解析版)
2016-2017学年湖北省黄冈市高二(下)期末数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)1.(5分)设集合S={x|x>﹣2},T={x|x2+3x﹣4≤0},则(∁R S)∪T=()A.[﹣4,﹣2]B.(﹣∞,1]C.[1,+∞)D.(﹣2,1]2.(5分)已知复数z=,则复数z的虚部为()A.﹣B.i C.D.﹣3.(5分)随机变量X~N(1,4),若p(x≥2)=0.2,则p(0≤x≤1)为()A.0.2B.0.6C.0.4D.0.34.(5分)若4个人报名参加3项体育比赛,每个人限报一项,则不同的报名方法的种数有()A.A B.C C.34D.435.(5分)广告投入对商品的销售额有较大影响.某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如下表(单位:万元)由上表可得回归方程为=10.2x+,据此模型,预测广告费为8万元时的销售额约为()A.90.8B.72.4C.98.2D.111.26.(5分)从1,2,3,4,5中不放回地依次取2个数,事件A=“第一次取到的是奇数”,B=“第二次取到的是奇数”,则P(B|A)=()A.B.C.D.7.(5分)已知函数f(x)=x2+cos x,f′(x)是函数f(x)的导函数,则f′(x)的图象大致是()A.B.C.D.8.(5分)如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为()A.B.C.D.9.(5分)若x,y且x+y>2,则和的值满足()A.和都大于2B.和都小于2C.和中至少有一个小于2D.以上说法都不对10.(5分)2013年8月,考古学家在湖北省随州市叶家山发现了大量的古墓,经过对生物体内碳14含量的测量,估计该古墓群应该形成于公元前850年左右的西周时期,已知碳14的“半衰期”为5730年(即含量大约经过5730年衰减为原来的一半),由此可知,所测生物体内碳14的含量应最接近于()A.25%B.50%C.70%D.75%11.(5分)对大于1的自然数m的三次幂可用奇数进行以下形式的“分裂”:23,33,43,….仿此,若m3的“分裂数”中有一个是2017,则m的值为()A.44B.45C.46D.4712.(5分)已知函数f(x)=alnx+x2﹣(a+2)x恰有两个零点,则实数a的取值范围是()A.(﹣1,+∞)B.(﹣2,0)C.(﹣1,0)D.(﹣2,﹣1)二、填空题:(本大题共4小题,每小题5分,共20分)13.(5分)数学老师从6道习题中随机抽3道让同学检测,规定至少要解答正确2道题才能及格.某同学只能求解其中的4道题,则他能及格的概率是.14.(5分)已知函数f(x)=2lnx﹣xf′(1),则曲线y=f(x)在x=1处的切线方程是.15.(5分)设(2﹣x)6=a0+a1(1+x)+a2(1+x)2+…+a6(1+x)6,则a4等于.16.(5分)先阅读下面的文字:“求的值时,采用了如下的方式:令=x,则有x=,两边平方,可解得x=2(负值舍去)”.那么,可用类比的方法,求出2+的值是.三、解答题:(本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(12分)已知定义在R上的函数f(x)=是奇函数.(1)求a,b的值,并判断函数f(x)在定义域中的单调性(不用证明);(2)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求实数k的取值范围.18.(12分)为了增强环保意识,我校从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:(Ⅰ)试判断是否有99%的把握认为环保知识是否优秀与性别有关;(Ⅱ)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X 表示这3人中通过预选赛的人数,求X的分布列与数学期望.附:K2=19.(12分)如图,某段铁路AB长为80公里,BC⊥AB,且BC=10公里,为将货物从A地运往C地,现在AB上的距点B为x的点M处修一公路至点C.已知铁路运费为每公里2元,公路运费为每公里4元.(1)将总运费y表示为x的函数.(2)如何选点M才使总运费最小?20.(12分)已知数列{a n}的前n项和为S n,且a1=1,S n=n2a n(n∈N*).(1)写出S1,S2,S3,S4,并猜想S n的表达式;(2)用数学归纳法证明你的猜想,并求出a n的表达式.21.(12分)设函数f(x)=x﹣(x+1)ln(x+1).(1)求f(x)的极值;(2)当a>b>0时,试证明:(1+a)b<(1+b)a.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修44:坐标系与参数方程]22.(10分)在极坐标系中,曲线C的方程为ρ2cos2θ=9,点P(2,),以极点O为原点,极轴为x轴的正半轴建立直角坐标系.(1)求直线OP的参数方程和曲线C的直角坐标方程;(2)若直线OP与曲线C交于A、B两点,求+的值.[选修45:不等式选讲]23.设函数f(x)=|x﹣a|,不等式f(x)≤2的解集是{x|1≤x≤5}.(1)求实数a的值;(2)若f(2x)+f(x+2)≥m对一切x∈R恒成立,求m的范围.2016-2017学年湖北省黄冈市高二(下)期末数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)1.【解答】解:集合S={x|x>﹣2},T={x|x2+3x﹣4≤0}={x|﹣4≤x≤1},则(∁R S)∪T={x|x≤﹣2}∪{x|﹣4≤x≤1}={x|x≤1}=(﹣∞,1].故选:B.2.【解答】解:复数z====﹣+i,则复数z的虚部为,故选:C.3.【解答】解:P(X≤0)=P(X≥2)=0.2,∴,故选:D.4.【解答】解:根据题意,4个人报名参加3项体育比赛,每个人限报一项,则每人都有3项体育比赛可选,即每人都有3种情况,则不同的报名方法的种数有3×3×3×3=34种;故选:C.5.【解答】解:由题意,计算=×(2+3+4+5+6)=4,=×(29+41+50+59+71)=50;代入回归方程=10.2x+中,解得=50﹣10.2×4=9.2;∴回归方程为=10.2x+9.2,∴当x=8时,=10.2×8+9.2=90.8;据此模型,预测广告费为8万元时的销售额约为90.8万元.故选:A.6.【解答】解:由题意,P(AB)==,P(A)==∴P(B|A)===故选:D.7.【解答】解:由于f(x)=x2+cos x,∴f′(x)=x﹣sin x,∴f′(﹣x)=﹣f′(x),故f′(x)为奇函数,其图象关于原点对称,排除BD,又当x=时,f′()=﹣sin=﹣1<0,排除C,只有A适合,故选:A.8.【解答】解:由已知易得:S长方形=4×2=8,S阴影=∫04()dx==,故质点落在图中阴影区域的概率P==;故选:A.9.【解答】解:假设和都不小于2.因为x>0,y>0,所以1+x≥2y,且1+y≥2x,两式相加得1+x+1+y≥2(x+y),即x+y≤2,这与x+y>2相矛盾,因此1+xy与1+yx中至少有一个小于2.故选:C.10.【解答】解:依题意知,生物体内碳14含量P与死亡年数t的关系为:,而生物体距发掘时有约2863年,故可得.故选:C.11.【解答】解:由题意,从23到m3,正好用去从3开始的连续奇数共2+3+4+…+m=(m+2)(m﹣1)个,∵2n+1=2017,得n=1008,∴2017是从3开始的第1008个奇数,当m=45时,从23到453,用去从3开始的连续奇数共=1034个,当m=46时,从23到463,用去从3开始的连续奇数共=1080个,故m=45.故选:B.12.【解答】解:函数定义域为x>0,且f′(x)=2x﹣(a+2)+=.①当a=0时,f(x)=x2﹣2x,在(0,+∞)上仅有一个零点,不合题意;②当a<0,即<0时,令f'(x)<0,得0<x<1,函数f(x)的单调递减区间为(0,1),令f'(x)>0,得x>1,函数f(x)的单调递增区间为(1,+∞).∴f(x)的极小值也就是f(x)在(0,+∞)上的最小值为f(1)=1﹣a﹣2=﹣a﹣1,∵当x→0时,f(x)→+∞,∴要使函数f(x)=alnx+x2﹣(a+2)x恰有两个零点,则﹣a﹣1<0,即a>﹣1,∴﹣1<a<0;③当0<<1,即0<a<2时,令f'(x)>0,得0<x<或x>1,函数f(x)的单调递增区间为(0,),(1,+∞).令f'(x)<0,得<x<1,函数f(x)的单调递减区间为(,1).f(x)的极大值为f()=<0,极小值为f(1)=1﹣a﹣2=﹣a﹣1<0,∴f(x)在(0,+∞)上仅有一个零点,不合题意;④当=1,即a=2时,f'(x)≥0恒成立,函数f(x)的单调递增区间为(0,+∞),不可能有两个零点,不合题意;⑤当>1,即a>2时,令f'(x)>0,得0<x<1或x>,函数f(x)的单调递增区间为(0,1),(,+∞).令f'(x)<0,得1<x<,函数f(x)的单调递减区间为(1,).f(x)的极大值为f(1)=1﹣a﹣2=﹣a﹣1<0,极小值f()=<0,∴f(x)在(0,+∞)上仅有一个零点,不合题意.综上,函数f(x)=alnx+x2﹣(a+2)x恰有两个零点,则实数a的取值范围是(﹣1,0).故选:C.二、填空题:(本大题共4小题,每小题5分,共20分)13.【解答】解:数学老师从6道习题中随机抽3道让同学检测,基本事件总数n=,规定至少要解答正确2道题才能及格.某同学只能求解其中的4道题,则他能及格包含的基本事件个数m==16,∴他能及格的概率p=.故答案为:.14.【解答】解:f′(x)=2ln x﹣xf′(1),由题意可知,曲线在(1,f(1))处切线方程的斜率k=f′(1),则f′(1)=2﹣f′(1),解得f′(1)=1,则f(1)=﹣1,所以切点(1,﹣1),所以切线方程为:y+1=x﹣1,化简得x﹣y﹣2=0故答案为:x﹣y﹣2=0.15.【解答】解:(2﹣x)6=a0+a1(1+x)+a2(1+x)2+…+a6(1+x)6,将x换为x﹣1,∴(3﹣x)6=a0+a1x+a2x2+…+a6x6,∴通项为T r+1=C6r36﹣r(﹣1)r x r,令r=4,∴a4=C6436﹣4(﹣1)4=135.故答案为:13516.【解答】解:设2+=x,则2+=x∴x2﹣2x﹣1=0∴x=1±,∵x>0,∴x=1+,故答案为:1+.三、解答题:(本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.【解答】解:(1)∵f(x)是定义在R上的奇函数,∴,∴b=1…(1分)∴,∴a•2x+1=a+2x,…(3分)即a(2x﹣1)=2x﹣1对一切实数x都成立.∴a=1,∴a=b=1.…(5分)f(x)是R上的减函数.…(6分)(2)不等式f(t2﹣2t)+f(2t2﹣k)<0,等价于f(t2﹣2t)<f(k﹣2t2),又f(x)是R上的减函数,∴t2﹣2t>k﹣2t2,…(8分)∴对t∈R恒成立,…(10分)∴,即实数k的取值范围是.…(12分)18.【解答】解:(I)由题意:K2≈7.822K2≈7.822>6.635,∴有99%的把握认为环保知识是否优秀与性别有关.(II)由题意X的可能取值为0,1,2,3,,,,,∴X的分布列为:E(X)==2.19.【解答】解:(1)依题意,铁路AM上的运费为2(80﹣x),公路MC上的运费为,则由A到C的总运费为.…(6分)(2),…(8分)令y'=0,解得,或(舍).…(10分)当时,y'≤0;当时,y'≥0;故当时,y取得最小值,即当在距离点B为公里时的点M处修筑公路至C时总运费最省.…(12分)20.【解答】解:(1):∵a1=1,S n=n2a n,∴S1=a1=1,当n=2时,S2=a1+a2=4a2,解得a2=,S2=1+=,当n=3时,S3=a1+a2+a3=9a3,解得a3=,S3=1++==,当n=4时,S4=a1+a2+a3+a4=16a4,解得a4=,S4=,∴S n=(2)下面用数学归纳法证①当n=1时,结论显然成立.②假设当n=k时结论成立,即S k=,则当n=k+1时,则S k+1=(k+1)2a k+1=(k+1)2(S k+1﹣S k),∴(k2+2k)S k+1=(k+1)2S k=(k+1)2,∴S k+1=故当n=k+1时结论也成立.由①、②可知,对于任意的n∈N*,都有S n=,∵S n=n2a n,∴a n===21.【解答】解:(1)函数f(x)定义域为(﹣1,+∞),f'(x)=1﹣[ln(x+1)+1]=﹣ln (x+1)…(2分)当x∈(﹣1,0)时,f'(x)>0,x∈(0,+∞)时,f'(x)<0,…(4分)所以当x=0时,f(x)极大值=f(0)=0.函数f(x)无极小值.…(5分)(2)要证(1+a)b<(1+b)a,只需证bln(1+a)<aln(1+b),…(6分)只需证,…(7分)设,(x>0),则g′(x)=,…(10分)由(1)知f(x)=x﹣(x+1)ln(x+1)在(0,+∞)单调递减,∴x﹣(x+1)ln(x+1)<f(0)=0,即g(x)在(0,+∞)上是减函数,而a>b>0∴g(a)<g(b),故不等式(1+a)b<(1+b)a.成立.…(12分)请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修44:坐标系与参数方程]22.【解答】解:(1)∵点P(2,),∴化为直角坐标得P(3,),,∴直线OP的参数方程为,∵曲线C的方程为ρ2cos2θ=9,即ρ2cos2θ﹣ρ2sin2θ=9,∴曲线C的直角坐标方程为x2﹣y2=9.(2)直线OP的参数方程为代入曲线C,得:t2+4t﹣6=0,∴,∴===.[选修45:不等式选讲]23.【解答】解:(1)由题意可知|x﹣a|≤2,﹣2≤x﹣a≤2,解得a﹣2≤x≤a+2,…(2分)∵不等式f(x)≤2的解集是{x|1≤x≤5},∴解得a=3.…(5分)(2)∵f(x)=|x﹣3|,∴f(2x)+f(x+2)=|2x﹣3|+|x﹣1|…(6分)=,…(8分)当时,,∴.…(10分)或解当时,,∴.。
2016_2017学年度高二第二学期期末考试理科数学试题与答案
试卷类型:A高二数学(理科)试题2017.7 注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共5页。
2.答题前,考生务必在答题卡上用直径0.5毫米的黑色字迹签字笔将自己的、号填写清楚,并粘好条形码。
请认真核准条形码上的号、和科目。
3.答第Ⅰ卷时,选出每题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在本试卷上无效。
4.答第Ⅱ卷时,请用直径0.5毫米的黑色字迹签字笔在答题卡上各题的答题区域作答。
答在本试卷上无效。
5.第(22)、(23)小题为选考题,请按题目要求从中任选一题作答,并用2B 铅笔在答题卡上把所选题目题号后的方框涂黑。
6.考试结束后,将本试卷和答题卡一并收回。
附:回归方程ˆˆˆybx a =+中斜率与截距的最小二乘估计公式分别为: ∑∑∑∑====--=---=ni ini ii ni ini iixn xy x n yx x x y yx x b1221121)())((ˆ,x b y aˆˆ-= 第Ⅰ卷一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合 题目要求的。
(1)已知复数iiz +-=122,其中i 是虚数单位,则z 的模等于 (A )2- (B) 3 (C) 4 (D) 2(2)用反证法证明某命题时,对结论:“自然数c b a ,,中恰有一个偶数”正确的反设为 (A) c b a ,,中至少有两个偶数 (B)c b a ,,中至少有两个偶数或都是奇数 (C) c b a ,,都是奇数 (D) c b a ,,都是偶数 (3)用数学归纳法证明:对任意正偶数n ,均有41212111 (41)31211+++=--++-+-n n n n ( )21...n++,在验证2=n 正确后,归纳假设应写成 (A )假设)(*N k k n ∈=时命题成立 (B )假设)(*N k k n ∈≥时命题成立 (C )假设)(2*N k k n ∈=时命题成立 (D )假设))(1(2*N k k n ∈+=时命题成立(4)从3男4女共7人中选出3人,且所选3人有男有女,则不同的选法种数有 (A )30种 (B) 32 种 (C) 34种 (D) 35种 (5)曲线xe y =在点()22e ,处的切线与坐标轴所围三角形的面积为(A)22e (B)2e (C) 22e (D) 492e(6)已知随机变量X 服从正态分布()2,3σN ,且)3(41)1(>=<X P X P ,则)5(<X P 等于(A)81 (B) 85 (C) 43 (D) 87(7)已知⎰≥3sin 2πxdx a ,曲线)1ln(1)(++=ax aax x f 在点())1(,1f 处的切线的斜率为k ,则k 的最小值为 (A)1 (B)23(C)2 (D) 3 (8)甲、乙、丙三人独立参加体育达标测试,已知甲、乙、丙各自通过测试的概率分别为p ,4332,,且他们是否通过测试互不影响.若三人中只有甲通过的概率为161,则甲、丙二人中至少有一人通过测试的概率为 (A)87 (B) 43 (C) 85 (D) 76(9)函数)1(2)(3-'+=f x x x f ,则函数)(x f 在区间[]3,2-上的值域是 (A) ]9,24[- (B) ]24,24[- (C) ]24,4[ (D)[]9,4 (10)设()()5522105)1(...1)1(1x a x a x a a x +++++++=-,则420a a a ++等于(A) 242 (B) 121 (C) 244 (D)122(11)已知函数)()()(2R b x bx x e x f x ∈-=.若存在⎥⎦⎤⎢⎣⎡∈2,21x ,使得0)()(>'+x f x x f ,则实数b 的取值围是(A) ⎪⎭⎫ ⎝⎛∞-65, (B) ⎪⎭⎫ ⎝⎛∞-38, (C) ⎪⎭⎫⎝⎛-65,23 (D) ⎪⎭⎫⎝⎛∞+,38 (12)中国南北朝时期的著作《子算经》中,对同余除法有较深的研究.设)0(,,>m m b a 为整数,若a 和b 被m 除得的余数相同,则称a 和b 对模m 同余,记为)(mod m b a =.如9和21被6除得的余数都是3,则记)6(mod 219=.若20202022201200202...22⋅++⋅+⋅+=C C C C a ,)10(mod b a =,则b 的值可以是(A) 2011 (B) 2012 (C) 2013 (D) 2014第II 卷本卷包括必考题和选考题两部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017学年黄冈市高二(下)期末试题数学(理科)2017年6月一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)1. 设集合S ={x |x >-2},T ={x |x 2+3x -4≤0},则(∁R S )∪T =( ) A .B .(-∞,1]C .2.已知复数201712i z i=-,则复数z 的虚部为( )A. 25-B. 15iC. 15D. 15-3. 随机变量X ~()1,4N ,若()20.2p x ≥=,则()01p x ≤≤为( ) A. 0.2 B. 0.3 C. 0.4 D. 0.64.若4个人报名参加3项体育比赛,每个人限报一项,则不同的报名方法的种数有( )A. 34A B. 34C C. 34 D. 435. 广告投入对商品的销售额有较大影响.某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如下表(单位:万元)8万元时的销售额约为( )A. 90.8B. 72.4C. 98.2D. 111.26. 从1,2,3,4,5中不放回地依次取2个数,事件A 表示“第1次取到的是奇数”,事件B 表示“第2次取到的是奇数”,则(|)P B A =( )A.15 B.310 C.25 D.127.,()f x '是()f x 的导函数,则()f x '的图象大致是( )8. 如图,长方形的四个顶点坐标为O (0,0),A (4,0),B (4,2),C (0,2),曲线y =B,现将质点随机投入长方形OABC 中,则质点落在图中阴影部分的概率为( ) A.23 B. 34 C. 45 D. 569.若,0x y >且2x y +>,则1y x +和1xy+的值满足( ) A.1y x +和1x y +都大于2 B. 1y x +和1xy +都小于2 C.1y x +和1xy+中至少有一个小于2 D. 以上说法都不对 10.2013年8月,考古学家在湖北省随州市叶家山发现了大量的古墓,经过对生物体内碳14含量的测量,估计该古墓群应该形成于公元前850年左右的西周时期,已知碳14的“半衰期”为5730年(即含量大约经过5730年衰减为原来的一半),由此可知,所测生物体内碳14的含量应最接近于( ) A .25﹪ B . 50﹪C . 70﹪D .75﹪11. 对大于1的自然数 m 的三次幂可用奇数进行以下形式的“分裂”:33313731523945171119⎧⎧⎪⎧⎪⎪⎨⎨⎨⎩⎪⎪⎩⎪⎩, , ,....仿此,若3m 的“分裂数”中有一个是2017,则m 的值为( )A. 44B. 45C. 46D.4712. 已知函数()()2ln 2f x a x x a x =+-+恰有两个零点,则实数a 的取值范围是( )A. ()1,-+∞B. ()1,0-C. ()2,0-D. ()2,1-- 二、填空题:(本大题共4小题,每小题5分,共20分)13. 数学老师从6道习题中随机抽3道让同学检测,规定至少要解答正确2道题才能及格。
某同学只能求解其中的4道题,则他能及格的概率是______________14. 已知函数()()2ln '1f x x x f =-⋅,则曲线()y f x =在1x =处的切线方程是_________ 15.设()()()()62601262111x a a x a x a x -=+++++++ ,则4a 等于______________ 16.先阅读下面的文字:“求的值时,采用了如下的方式:令x =,则有x =x =2(负值舍去)”。
那么,可用类比的方法,求出12122+++⋅⋅⋅的值是 .三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)已知定义在R⑴求a b ,的值,并判断函数()f x 在定义域中的单调性(不用证明);⑵若对任意的t R ∈,不等式()()22220f t t f t k -+-<恒成立,求实数k 的取值范围.18. (本小题满分12分)为了增强环保意识,某社团从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:(2)为参加市举办的环保知识竞赛,学校举办预选赛,现在环保测试优秀的同学中选3人参加预选赛,已知在环保测试中优秀的同学通过预选赛的概率为32,若随机变量X 表示这3人中通过预选赛的人数,求X 的分布列与数学期望. 附:2K =2()()()()()n ad bc a b c d a c b d -++++19. (本小题满分12分)如图,某段铁路AB 长为80公里,BC AB ⊥,且10BC =公里,为将货物从A 地运往C 地,现在AB 上的距点B 为x 的点M 处修一公路至点C.已知铁路运费为每公里2元,公路运费为每公里4元.(1)将总运费y 表示为x 的函数. (2)如何选点M 才使总运费最小?20. (本小题满分12分)已知数列{}n a 的前n 项和为n S ,且()211,n n a S n a n N +==∈(1)试求出1234,,,S S S S ,并猜想n S 的表达式; (2)用数学归纳法证明你的猜想,并求出n a 的表达式。
21.(本小题满分12分)设函数()(1)ln(1)f x x x x =-++. (1)求()f x 的极值;(2)当0a b >>时,试证明:(1)(1)baa b +<+.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
22.(本小题满分10分)选修4-4:坐标系与参数方程在极坐标系中,曲线C 的方程为2cos29ρθ=,点)6P π.以极点O 为原点,极轴为x 轴的正半轴建立直角坐标系.(1)求直线OP 的参数方程和曲线C 的直角坐标方程; (2)若直线OP 与曲线C 交于A 、B 两点,求11||||PA PB +的值.23.(本小题满分10分)选修4-5:不等式选讲设函数()||f x x a =-,不等式()2f x ≤的解集是{}|15x x ≤≤. (1)求实数a 的值;(2)若(2)(2)f x f x m ++≥对一切x R ∈恒成立,求m 的范围.黄冈市2017年春季高二期末试题数学(理科)参考答案及评分标准一、选择题:13.4514. 20x y --= 15. 135 16. 72部分题解析: 9. 【答案】C 【解析】假设1y x +和1xy+都不小于2. 因为x >0,y >0,所以1+x ≥2y ,且1+y ≥2x ,两式相加得1+x+1+y ≥2(x+y), 即x+y ≤2,这与x+y >2相矛盾,因此1+xy 与1+yx 中至少有一个小于2.故选C. 10. 【答案】C【解析】依题意知,生物体内碳14含量P 与死亡年数t 的关系为:57301()2tP =,而生物体距发掘时有约2863年,故可得286357301()0.72P =≈,选C三、解答题:.17. 【答案】⑴1a b ==;⑵13⎛⎫-∞- ⎪⎝⎭,.【解析】⑴∵()f x 是定义在R 上的奇函数, ∴()1001b f a -==+,∴1b = ……………………1分∴212x x a a +=+ , ……………………3分 即()2121x x a -=-对一切实数x 都成立.∴1a =,∴1a b ==. ……………………5分 ()f x 是R 上的减函数。
……………………6分⑵不等式()()22220f t t f t k -+-<等价于()()2222f t t f k t -<-.又()f x 是R 上的减函数,∴2222t t k t ->-. ……………………8分∴221132333k t t t ⎛⎫<-=-- ⎪⎝⎭对t R ∈恒成立, ……………………10分∴13k <-.即实数k 的取值范围是13⎛⎫-∞- ⎪⎝⎭,. ……………………12分18. 【答案】(1)有99%的把握认为环保知识是否优秀与性别有关;(2)分布列见解析,【解析】(1……………………3分因为27.822 6.635K ≈> 2( 6.635)0.01P K >=所以有99%的把握认为环保知识是否优秀与性别有关. ……………………6分 (2)X 的可能取值为0,1,2,3 ……………………7分 271)31()0(3===X P , 92)31)(32()1(213===C X P所以X 的分布列为:……………………10分因为2~(3,)3X B , 所以2()323E X np ==⨯= ……………………12分19. 【答案】(1(2)当在距离点B 里时的点M 处修筑公路至C 时总运费最省.【解析】(1)依题意,铁路AM 上的运费为()280x -,公路MC 上的运费为,则由A 到C ……………………6分(2……………………8分令'0y =,. ……………………10分,'0y ≤ ,'0y ≥ ;,y 取得最小值, 即当在距离点B M 处修筑公路至C 时总运费最省. ……………………12分20. 【答案】(1)21n nS n =+;(2)见解析. 【解析】(1)解: ()()()221112221n n n n n n n n n a S S n S n S S S S n n ---=-≥∴=-∴=≥- 11123443681,1,,,,3245a S a S S S =∴====== ` ……………………3分 猜想21n nS n =+……………………5分(2)证明:(1)当1n =时, 1211,111S ⨯==+等式成立。
假设当()1,n k k k N +=≥∈时,等式成立,即21k kS k =+。
当1n k =+时,()21111211k k k kkkS k aa S ak ++++=+⋅=+=+,∴()()122121212k k a k k k k k +=⋅=++++ ……………………8分 ()()()()()()()2211212121112211k k k k S k a k k k k k ++++∴=+⋅=+⋅==+++++1n k ∴=+时,等式也成立。
综上1)2)知,对于任意n N +∈, 21n nS n =+都成立。
……………………10分 又()()()122121k n a a k k n n +=∴=+++……………………12分21. 【答案】(1)()f x 极大值=(0)0f =;(2)证明见解析. 【解析】(1)函数()f x 定义域为(1,)-+∞,()[]'1ln(1)1ln(1)f x x x =-++=-+ ……………………2分当)0,1(-∈x 时,'()0f x >, (0,+),'()0,x f x ∈∞<时 ……………………4分 所以当0x =时,()f x 极大值=(0)0f =.函数()f x 无极小值。
