用Excel解一元二次方程的探究
excel怎么求一元多次方程x在一定范围内y的最大值

excel怎么求一元多次方程x在一定范围内y的最大值【原创版】目录1.引言:介绍一元多次方程和 Excel 求解问题2.解析:解释一元多次方程在 Excel 中的求解方法3.操作步骤:详细说明在 Excel 中求解一元多次方程 x 在一定范围内 y 的最大值的步骤4.总结:回顾操作过程,强调注意事项正文引言:在数学中,一元多次方程是指包含一个未知数的多项方程。
在实际应用中,我们常常需要求解这类方程在某个特定范围内的极值。
而 Excel 作为一款强大的办公软件,可以协助我们快速解决这类问题。
本文将介绍如何使用 Excel 求解一元多次方程 x 在一定范围内 y 的最大值。
解析:在 Excel 中,求解一元多次方程的问题可以通过使用 Excel 内置的求解器插件来完成。
该插件可以解决线性规划、二次规划等优化问题,进而帮助我们求解一元多次方程在某个范围内的极值。
操作步骤:以下是在 Excel 中求解一元多次方程 x 在一定范围内 y 的最大值的具体操作步骤:1.首先,打开 Excel,创建一个新的工作表,并输入一元多次方程的各个系数和常数项。
例如,如果要求解方程 5x^2 - 3x + 2 = y,将 5、-3、2 输入到 A1、A2、A3 单元格中,将 x 的取值范围(如 1 到 10)输入到 B1 单元格,将 y 的取值范围(如 1 到 100)输入到 B2 单元格。
2.其次,在 Excel 中插入求解器插件。
点击“文件”>“选项”>“加载项”>在“Excel 加载项”中勾选“求解器加载项”,然后点击“确定”。
3.接着,在 Excel 中创建一个新的工作表,并输入求解器的参数。
在第一行输入“=MAX(range1)”,其中 range1 表示 y 的取值范围。
例如,如果 y 的取值范围在 B2:B100,则在第一行输入“=MAX(B2:B100)”。
4.将求解器插件应用于新工作表中的公式。
利用Excel进行主成分分析的具体操作
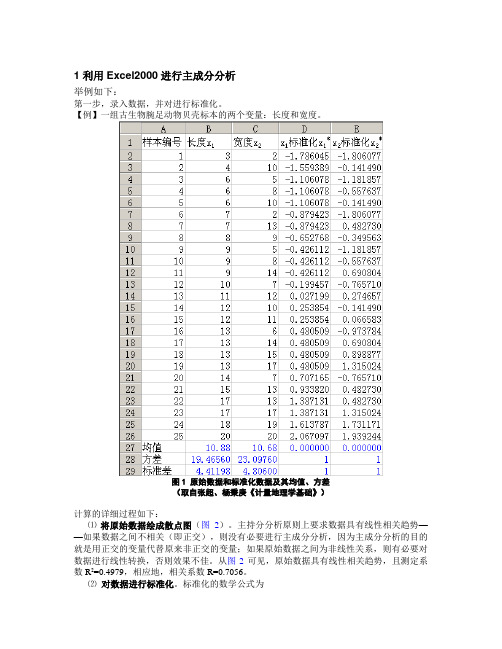
1 利用Excel2000进行主成分分析举例如下:第一步,录入数据,并对进行标准化。
【例】一组古生物腕足动物贝壳标本的两个变量:长度和宽度。
图1 原始数据和标准化数据及其均值、方差(取自张超、杨秉庚《计量地理学基础》)计算的详细过程如下:⑴将原始数据绘成散点图(图2)。
主持分分析原则上要求数据具有线性相关趋势——如果数据之间不相关(即正交),则没有必要进行主成分分析,因为主成分分析的目的就是用正交的变量代替原来非正交的变量;如果原始数据之间为非线性关系,则有必要对数据进行线性转换,否则效果不佳。
从图2可见,原始数据具有线性相关趋势,且测定系数R2=0.4979,相应地,相关系数R=0.7056。
⑵对数据进行标准化。
标准化的数学公式为j jij ij x x x σ-=*这里假定按列标准化,式中∑==ni ij ij x n x 11,)(Var )(12ij n i j ij ij x x x =-=∑=σ 分别为第j 列数据的均值和标准差,ij x 为第i 行(即第i 个样本)、第j 列(即第j 个变量)的数据,*ij x 为相应于ij x 的标准化数据,25=n 为样本数目。
图2 原始数据的散点图图3 标准化数据的散点图对数据标准化的具体步骤如下:① 求出各列数据的均值,命令为average ,语法为:average(起始单元格:终止单元格)。
如图1所示,在单元格B27中输入“=AVERAGE(B1:B26)”,确定或回车,即得第一列数据的均值88.101=x ;然后抓住单元格B27的右下角(光标的十字变细)右拖至C27,便可自动生成第二列数据的均值68.102=x 。
②求各列数据的方差。
命令为varp ,语法同均值。
如图1所示,在单元格B28中输入“=VARP(B2:B26)”,确定或回车,可得第一列数据的方差4656.19)(V ar 1=x ,右拖至C28生成第二列数据的方差0976.23)(V ar 2=x 。
计算机解一元二次方程

计算机解一元二次方程一元二次方程是指形如ax^2 + bx + c = 0的方程,其中a、b、c是已知的常数,x是未知数。
解一元二次方程是求出方程的根,即方程等号两边相等时的x的取值。
在计算机中,可以使用数值计算的方法来解一元二次方程。
下面将介绍一种简单而常用的计算机解一元二次方程的方法。
首先,我们需要从用户那里获取方程的系数a、b、c的值。
可以通过输入框或者命令行参数的形式获取用户输入的值。
假设我们获取到的系数分别是a_val、b_val、c_val。
接下来,我们需要计算一元二次方程的判别式delta = b_val^2 - 4*a_val*c_val。
判别式的值可以用来判断方程的根的情况。
若delta大于0,则方程有两个不相等的实根;若delta等于0,则方程有两个相等的实根;若delta小于0,则方程没有实根。
根据判别式的值,我们可以分别处理这三种情况。
若delta大于0,则方程有两个不相等的实根。
我们可以使用求根公式x1 = (-b_val + sqrt(delta)) / (2*a_val)和x2 = (-b_val - sqrt(delta)) / (2*a_val)来求出方程的两个根x1和x2。
若delta等于0,则方程有两个相等的实根。
我们可以使用求根公式x = -b_val / (2*a_val)来求出方程的根。
若delta小于0,则方程没有实根。
可以输出“该方程无实根”。
最后,我们将求得的方程根输出给用户。
可以使用命令行输出结果,或者将结果显示在网页上。
使用计算机解一元二次方程可以方便、快捷地得到方程的根。
计算机的高精度计算和快速运算能力可以帮助我们处理各种复杂的方程,解决实际问题。
以上是一种简单而常用的计算机解一元二次方程的方法。
当然,还有其他更复杂的算法和工具可以使用,但基本的原理仍然是计算方程的判别式,根据判别式的值求解方程的根。
这种计算机解方程的方法不仅可以应用于一元二次方程,还可以推广到解其他类型的方程,如高次方程、多元方程等。
excel解方程二元一次方程组

方法
1/9
在excel的两个单元格输入两个公式,构成二元一次方程。
2/9
将下面这个公式转换一下形式,变成等号左边是变量,等号右边是一个数值,这个数值也可以是0
3/9
c4单元格输入:x+2Y,上面的公式中的等号的左边的算式。
4/9
在B5单元格,输入公式=9+A5 。
5/9
C5单元格填入公式:=A5+2*B5 。
6/9
在菜单栏上选择数据,点击假设分析,选择单变量求解。
7/9
单元格为C5,也就是X+2Y,目标值就是X+2Y的值,值是5;可变单元格指的是自变量X,用A5单元格代表的,输入A5,然后点击确定。
8/9
弹出了一个对话框,求解成功,点击确定。
9/9
即可看到最终的解。
Excel解多元一次方程组的几种方法

Excel解多元一次方程组的几种方法本文列出了在Excel中解多元一次方程组的三种方法:矩阵解法、用克莱姆法则和用规划求解的方法,供参考。
单击右侧链接打开示例文件下载页面:示例文件。
方法一:矩阵解法原理:对于由n个未知数,n个方程组成的多元一次方程组:写成矩阵形式为Ax=b,其中A为系数n*n方阵,x为n个变量构成列向量,b为n个常数项构成列向量。
当它的系数矩阵可逆,或者说对应的行列式|A|不等于0的时候,由Ax=b可得:x=b*A^(-1) ,A^(-1)为A的逆矩阵。
利用Excel提供的MDETERM、MINVERSE和MMULT等函数即可求解多元一次方程组。
MDETERM函数返回一个数组的矩阵行列式的值,可用其判断矩阵是否可逆;MINVERSE函数返回矩阵的逆矩阵;MMULT函数返回两个数组的矩阵乘积。
有关MMULT函数的用法可参考《用公式进行多条件求和》一文中的方法三。
示例及步骤:假如在Excel的A2:N5区域中以下图方法输入了一个四元一次方程组。
在P2:S5区域用公式得到其系数矩阵,T2:T5的返回值为常数项向量。
如P2单元格中的公式为:=OFFSET($B$1,ROW(A1),COLUMN(A1)*3-3)*IF(OFFSET($A$1,ROW(A1),CO LUMN(A1)*3-3)="-",-1,1)由于“=MDETERM(P2:S5)”的值不等于“0”,可知系数矩阵可逆。
选择某列中的四个连续单元格,如Q11:Q14,输入数组公式:=MMULT(MINVERSE(P2:S5),T2:T5)公式输入完毕按Ctrl+Shift+Enter结束,即可在Q11:Q14得到方程组的解。
方法二:用克莱姆法则原理:参考克莱姆法则。
示例及步骤:对于上述四元一次方程组,复制P2:S5区域,将其粘贴到其他区域,如本例有4个未知数,用“选择性粘贴——粘贴链接”的方法将其粘贴到4个不同的区域。
利用Excel表格解决二分法求方程的近似解问题 课件

一 问题引入
中央电视台 “幸运52”录制现场
有奖竞猜
问题1:主持人给出高了、低了的提示有什 么用?
问题2:参赛者如何才能最快的猜出价格?
智力游戏
数字
竞猜
(老师从1-100中选一个整数,看谁猜的 又快又准)
复习回顾
函数f (x) ln x 2x 6在下列哪个区间内有零点? A.(0,1) B(. 1,2) C(. 2,3) D(. 3,4)
求 ln x 2x 6=0的解 求函数y ln x 2x 6的零点.
问题2:该方程有几个解?
初始 区间
由函数的单调性知:有且仅有一个零点x0 , x0 (2, 3).
问题3:如何求该方程的解?
问题:怎样理解 a b ,则方程的近似解达到 精确度要求?
设函数的零点为x0 ,则a x0 b. 作出数轴,在数轴上标出a,b, x0对应的点.
如果函数y=f(x)在区间[a,b]上的图象是连续不断的 一条曲线,并且有f(a).f(b)<0,那么,函数y=f(x)在区
间(a,b)内有零点。 ——零点存在定理
合作探究: 运用excel进行有关计算
几何画板
如何求 ln x 2x 6=0的近似解?(精确度0.1)
问题1:该方程有没有解?怎么判断
a
x0
b
x
所以0 x0 a b a, a b x0 b 0.
由于 a b ,所以 x0 a b a , x0 b a b , 即a或b作为函数的零点x0的近似值都达到给定的精确度 .
二分法概念
口诀
定区间,找中点,中值计算两边看; 同号去,异号算,零点落在异号间. 周而复始怎么办?精确度上来判断.
excel解方程一元三次方程
excel解方程一元三次方程
Excel可以使用“求根函数”来求解一元三次方程,方法如下:
1. 打开Excel,在一个单元格中输入=ROOT(,然后按Tab键或单击函数框中的“求根函数”以打开函数对话框。
2. 在函数对话框中,选择“函数”下拉菜单,并选择“三次方程”的“根号”。
然后在“值”框中输入a、b、c和d的值,分别对应于方程ax³+bx²+cx+d=0中的系数。
3. 输入小数点和精度所需的数字位数。
如需尝试不同值,请复制并粘贴公式到其他单元格中。
例如,要解方程4x³+8x²-7x-9=0,可以在单元格中输入以下公式:
=ROOT(4,8,-7,-9)
然后按Enter键,Excel将给出三个根,每个根以及相关的精度。
选择精度最接近所需答案的根,并将其复制到另一个单元格中以获得最终答案。
使用Excel解多元一次方程组的三种方法
使用Excel解多元一次方程组的三种方法本文列出了使用Excel中解多元一次方程组的三种方法:矩阵解法、用克莱姆法则和用规划求解的方法。
方法一:矩阵解法原理:对于由n个未知数,n个方程组成的多元一次方程组:写成矩阵形式为Ax=b,其中A为系数n*n方阵,x为n个变量构成列向量,b为n个常数项构成列向量。
当它的系数矩阵可逆,或者说对应的行列式|A|不等于0的时候,由Ax=b可得:x=b*A^(-1) ,A^(-1)为A的逆矩阵。
利用Excel提供的MDETERM、MINVERSE和MMULT等函数即可求解多元一次方程组。
MDETERM函数返回一个数组的矩阵行列式的值,可用其判断矩阵是否可逆;MINVERSE函数返回矩阵的逆矩阵;MMULT函数返回两个数组的矩阵乘积。
示例及步骤:假如在Excel的A2:N5区域中以下图方法输入了一个四元一次方程组。
在P2:S5区域用公式得到其系数矩阵,T2:T5的返回值为常数项向量。
如P2单元格中的公式为:=OFFSET($B$1,ROW(A1),COLUMN(A1)*3-3)*IF(OFFSET($A$1,ROW(A1),COLUMN(A1)*3-3)="-",-1,1)由于“=MDETERM(P2:S5)”的值不等于“0”,可知系数矩阵可逆。
选择某列中的四个连续单元格,如Q11:Q14,输入数组公式:=MMULT(MINVERSE(P2:S5),T2:T5)公式输入完毕按Ctrl+Shift+Enter结束,即可在Q11:Q14得到方程组的解。
方法二:用克莱姆法则示例及步骤:对于上述四元一次方程组,复制P2:S5区域,将其粘贴到其他区域,如本例有4个未知数,用“选择性粘贴——粘贴链接”的方法将其粘贴到4个不同的区域。
然后复制T2:T5常数项的列向量,用“选择性粘贴——粘贴链接”的方法分别将其粘贴到上述四个区域中的各列,依次得到矩阵A1、A2、A3、A4,再用MDETERM函数计算各矩阵行列式的值,分别除以系数矩阵A的行列式的值,即可得到方程组的解。
线性方程组解的EXCEL制作方法
线性方程组解的EXCEL制作方法摘要:本文主要介绍了EXCEL在数学中的一个应用,可以快速求解线性方程组,所以解决了求解方程组繁琐的问题。
同时也解决了在建筑工程中求解方程组繁琐的问题,在实际中有一定的应用价值,但这个操作(可求解二次到五次方程组),只能解决方程组有一种解的情况,解决方程组多种解的情况还需后人多多努力。
0 引言求解方程组一般来说都是通过草纸,一步一步的求出解,不但速度慢,费脑力,而且一不小心就算错结果,如何快速求解方程组是一个热点,所以如何利用EXCEL快速求解方程组是一个新的话题。
1、求解多次方程组,一般都是通过矩阵的知识,应用到矩阵的逆矩阵,矩阵的相乘等,求解的步骤麻烦,计算量很大,很费时间与脑力。
2、利用EXCEL中矩阵的知识求解方程组,设计好程序,只需改变未知数前的系数即可得到相应的答案,简单快捷。
制作方法如下所示:2.1 设计工作表①首先新建两个工作表,由左至右分别命名为目录、二次、三次、四次、五次。
②单击“工具——选项”选中视图,将网格线前的对号去掉。
这样就把工作表中的网格线去除掉了。
③单击“格式——工作表——背景”分别为每个工作表添加来自文件的背景图片。
这样可以美化工作表,使我们使用时感觉更加轻松。
④在目录工作表,输入的文字,并为其中一些文字设置超链接,分别连接到相应的“次数”工作表上,并在工作表最下方添加“注”(用来说明该EXCEL文件的使用方法),分别设计字体的样式,达到美化的效果。
最终效果如下图所示:⑤后在在其余工作表中,根据名字分别输入相应次数的方程组(未知数前的系数任意输入),和“x=”,并且为它们所在的单元格设置属性,添加图案,填充颜色等。
最后在工作表的右下角选中一个单元格输入“返回”,设置超链接到目录。
例如名为“五次”的工作表中输入五次方程组,得到的效果如下图所示:2.2 利用公式,求解方程组的解。
只举例说明“五次”工作表中的操作方法,其它工作表与该工作表的操作方法类似。
Excel2013中怎么求解一元N次方程式
Excel2013中怎么求解一元N次方程式
Excel2013中怎么求解一元N次方程式?我们都学过方程式,最为简单的就是一元一次方程式了,元,表示未知数的个数,次,则表示未知数的次幂。
下面店铺就教你Excel2013中求解一元N次方程式的方法。
Excel2013中求解一元N次方程式的方法:
①如下表所示,我们现在要求出满足一元3次方程式x³+x²+x+2=586,X的根为多少。
初学者可能一时想不到用什么来求。
下面听我一一道来。
②在A3单元格输入公式: =A2^3+A2^2+A2+2 ,意思是将A2单元格模拟为方程式中的X,在Excel中,N次方的表示方法为^N,所以A2的三次方可以表示为A2^3。
③输入完公式回车,得到2,然后单击菜单栏--数据--模拟分析--单变量求解。
④弹出对话框,在目标单元格中单击A3单元格,会自动变为绝对引用格式,目标值填入586,可变单元格为A2,确定。
⑤开始计算,Excel自动匹配满足条件的值。
由于只是一个分析功能,得到的是个近似的值。
这里称之为误差。
⑥选中A2、A3单元格,右击设置单元格格式。
⑦在数字--数值标签中,将小数位设为0,确定。
⑧这样就得到了满足方程式的值,X等于8.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
27
探究
实践
Inquiry
学科探究
探究教与学
性 。
学生打开Ex单元格中输入公式的方法,再次熟悉求和函数
SUM()、求算术平均值函数中练习求 和 在Excel输入“系数一、设计思想
本案例的选题内容取材于学生学习生活中最熟悉的教材,通过运用电子表格中的函数知识,创造性地解决初中数学教材中的一元二次方程,进而实现信息技术与学科教学的有机整合。
根据学生现有的认知水平,整个活动过程将不断出现新问题,激励学生不断探求新方法,获得新知识。
二、案例设计
(一)探究主题:用Excel解一元二次方程。
(二)学习内容:对一元二次方程的解题方法作深度学习,在Excel中进一步熟练公式的编辑方法,扩展函数知识。
(三)学习方式:在教师指导下的自主探究学习活动。
(四)活动过程设计见下表:
■ 陈春兴
图1
解一元二次方程的探究
用Excel
28
探究
实践
Nettime
(续表
图2
图3
图4
29
探究
实践
Nettime
三、案例反思
通过本案例的实践活动,多数学生对自主探究学习表示具有成就感。
学生通过探究学习活动,既加深了已掌握的课本知识,又可以在已有知识的基础上深度研究学习,获取新的知识。
实现了学生的思维创新、方法创新和手段创新,培养了学生综合运用知识的能力。
(作者单位:福建省顺昌县教师进修学校)
专家点评
从现行教材内容中挖掘适合探究性学习的题材,设计研究性学习案例是开展探究性学习活动的有效途径。
《用Excel解一元二次方程的探究》案例就是一个很好的
尝试。
该案例设计科学,体现了信息技术与学科教学整合的理念,符合探究学习的一般规律。
选题新颖,用Excel中的函数知识去解决数学中的问题,并设计出一个解题程序,能使学生的创新思维得到提高,起到激趣、引思、促动和求异的作用。
实施方案可行,在信息技术支持下的学科探究学习活动,既可个别化自主学习,也可小组合作学习。
相信通过本案例的活动,能够激发学生学习信息技术的兴趣,为数学学科开展探究学习提供一定的借鉴作用。
(福建教育学院 邹开煌)
图5。
