运筹学第七章动态规划PPT课件
合集下载
运筹学动态规划
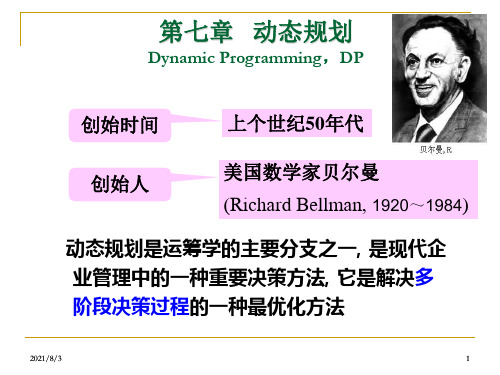
第三节 动态规划应用举例
例1 生产与存储问题 一个工厂生产的某种产品，在一定的时期
内，增大生产批量，能够降低产品的单位成本，但若超过市场的需 求量，就会造成产品的积压而增加存储的费用。因此如何正确地制 定生产计划，使得在整个计划期内，生产和存储的总费用最小，这 就是生产与存储问题。
第三节 动态规划应用举例
第七章 动态规划
第一节 最短线路问题
第二节 动态规划的基本概念和原理 第三节 动态规划应用举例 第四节 决策变量连续的动态规划问题 第五节 乘积形式的目标函数 第六节 随机型动态规划问题
第一节 最短线路问题
一、最短线路问题及其解法
图7-1是一个线路网络图。从A到E要修建一条石 油管道。管道必须在B、C、D三处设立加压站。 在B处有B1，B2，B3三个不同地址可供选择作为 建站点。当然，从A到这3个点的距离是不同的； 同样，C和D处也都有不同的地址可供选择。图 上的圆圈称为节点，表示地址，两个节点之间的 箭线称为线或边，表示可以修建管道，线上的数 字表示两个地址之间的距离。现在的问题是在许 多条从A到E的线路中，找出一条最短的，称为最 短线路问题。
三、最优化原理与动态规划方程
基本步骤为：
(1)将问题的求解过程恰当地分成若干阶段，一般可按问题所处的空间或时间 进行划分，并确定阶段变量，对n个阶段问题来说，k=1,2,…,n。 (2)正确地选择状态变量sk，它应当满足无后效性等三个条件，并确定状态集
合Sk。
(3)确定决策变量xk(sk)及阶段的允许决策集合Dk(sk)。 (4)写出状态转移函数 (5)根据题意，列出指标函数Fk,n,fk(sk),F1,n,f1(s1)。
三、最优化原理与动态规划方程
•最优化原理 对于多阶段决策问题，作为整个 过程的最优策略具有这样的性质：无论过去的状 态和决策如何，就前面决策所形成的状态而言， 余下的诸决策必然构成一个最优子策略。
运筹学-第七章-动态规划
6
5
7
f2(D)=8 3
D
4
f3(E)=3
E 3
f3(F)=5
5
F
f3(G)=8 8
G
f2(D )m d d i((n D D ,,G F )) ff3 3((G F )) m 3 4 i n 5 8 8 u22(0D 21/)8/ 3 DF
f4(H)=0
H
14
f1(A)=14
A
f2(B)=13
2021/8/3
20
逆推公式
fk(sk)＝OPT {v(sk,uk)+ fk+1(sk+1)} k =n, …1
fn+1(sn+1)＝0 或
Max 或 Min
fk(sk)＝OPT{v(sk ,uk)+ fk+1(sk+1)} k =n-1, …1 fn(sn)＝ OPT{v(sn ,un)}
多阶段决策问题中，常见的目标函数形式之一是取各阶段效 益之和的形式。有些问题，如系统可靠性问题，其目标函数 是取各阶段效益的连乘积形式。总之，具体问题的目标函数 表达形式需要视具体问题而定
2021/8/3
19
(4) 状态转移方程 sk＋1 ＝T (sk, uk)：描述第 k 阶段与第 k+1 阶段的状态变量的关系
(5) 指标 v (sk ,uk) ：第 k 阶段在状态 sk 下采取决策 uk 得到的 结果（距离、得益、成本等）
指标函数是指各阶段指标的累计。即 V (sk,uk, …, sn,un, sn+1)=vk(sk,uk)*vk+1(sk+1,uk+1)…*vn(sn,un)
30
k=2, S2 = {0,1,2,3,4,5}, f2(s2)＝0mua2x{sg22(u2)+ f3(s3)}
第七章 动态规划法1(算法分析与设计课件)
第七章 动态规划法
计算机科学与技术学院
通过应用范例学习动态规划算法设计策略。
（1）矩阵连乘问题； （2）最长公共子序列； （3）0/1背包问题； （4）流水作业调度；
第七章 动态规划法
是另一种求解最优化问题的算法设计策略 适合求解的问题(多阶段决策问题):
问题的活动过程可以分成若干个阶段,每个阶段包含一 个或多个状态，在任一阶段的决策仅依赖与该阶段的状 态，与该阶段之前的过程如何达到这种状态的方式无关， 这类问题的解决是多阶段的决策过程.
}
7.3 矩阵连乘
穷举法 动态规划法
分析最优解的结构 递归定义最优解的值 自底向上计算最优解的值
对于1≤i≤j≤n不同的有序对(i,j)对应于不同的子问题。因此，不同
子 在递问归题计的算个时数，最许多多只有子问题n2被 重n 复 计(n算2)。多次。这也是该问题可用动
m[4][m5][=3]m[4[4]+][m4][+5]m[5[5]+][5P]3+P5PP46P=5P56*=1100**2200=*12050=05}000
m=
0 15750 7875 9735 11875 15125
0 2625 4375 712510500
0 750 2500 5375 0 1000 3500
所以，不能在某个阶段直接做出决策
再看一例：
最优子结构：
如果ABEG是A 到G的最短路径，那 么ABE也是A到E的 最短路径。
第七章 动态规划法
例2.数塔问题:设有一个三角形数塔，求一自塔顶到塔底的 路径,且该路径上结点的值的和最大.择12方向还是选择 15方向,取决于分别从12和15出发的两 条子路径上的最大路径值，设他们分别
计算机科学与技术学院
通过应用范例学习动态规划算法设计策略。
（1）矩阵连乘问题； （2）最长公共子序列； （3）0/1背包问题； （4）流水作业调度；
第七章 动态规划法
是另一种求解最优化问题的算法设计策略 适合求解的问题(多阶段决策问题):
问题的活动过程可以分成若干个阶段,每个阶段包含一 个或多个状态，在任一阶段的决策仅依赖与该阶段的状 态，与该阶段之前的过程如何达到这种状态的方式无关， 这类问题的解决是多阶段的决策过程.
}
7.3 矩阵连乘
穷举法 动态规划法
分析最优解的结构 递归定义最优解的值 自底向上计算最优解的值
对于1≤i≤j≤n不同的有序对(i,j)对应于不同的子问题。因此，不同
子 在递问归题计的算个时数，最许多多只有子问题n2被 重n 复 计(n算2)。多次。这也是该问题可用动
m[4][m5][=3]m[4[4]+][m4][+5]m[5[5]+][5P]3+P5PP46P=5P56*=1100**2200=*12050=05}000
m=
0 15750 7875 9735 11875 15125
0 2625 4375 712510500
0 750 2500 5375 0 1000 3500
所以，不能在某个阶段直接做出决策
再看一例：
最优子结构：
如果ABEG是A 到G的最短路径，那 么ABE也是A到E的 最短路径。
第七章 动态规划法
例2.数塔问题:设有一个三角形数塔，求一自塔顶到塔底的 路径,且该路径上结点的值的和最大.择12方向还是选择 15方向,取决于分别从12和15出发的两 条子路径上的最大路径值，设他们分别
[管理学]运筹学 动态规划
![[管理学]运筹学 动态规划](https://img.taocdn.com/s3/m/25633974f7ec4afe04a1dfe5.png)
多阶段决策过程图示
决策 决策
决策
第第
第
1
2
n
阶阶
阶
段段
段
动态规划的基本概念
C1 5
2
8 D1 3
4
A
B1 3
4
6
C2
5
58
3
5 6 D2 2
E1 4 3
F
B2 7 C3 4
1
E2
7
8
D3 3
C4 4
1
2
3
4
5
阶段: k=1,2,3,4,5
基本概念（续一）
C1 5
2
8 D1 3
B1 3
4
4
A
6
C2
第七章 动态规划
动态规划简介
多阶段决策过程最优化
多阶段决策过程，是指一类特殊的过程， 它们可以按时间顺序分解成若干个相互联 系的阶段，称为“时段”，在每个时段都 要做决策，全部过程的决策是一个决策序 列。多阶段决策问题也称为序贯决策问题。 多阶段决策问题的目标是要达到整个活动 过程的总体最优。在每个阶段进行决策时 不应仅考虑本阶段最优，尤其应考虑对最 终目标的影响，从而做出对全局来说最优 的决策。 动态规划是符合这种要求的一种决策方法。
C1 5
2
8 D1 3
4
A
B1 3
4
6
C2
5
58
3
5 6
D2
2
E1 4 3
F
B2 7 C3 4
1
E2
7
8
D3 3
C4 4
第二步，k=4，状态变量s4可以取三个值D1，D2，D3。于是
f
运筹学-动态规划
例７.1是一个四阶段决策问题,一般可分为四步：
运筹学-动态规划
●逆序法求解最短路问题
第一步,从K=4开始
状态变量S4可取两种状态D1, D2,它们到E点的距离 分别为4和3,这也就是由D1和D2到终点E 的最短距离， 即
f4(D1)=4, f4(D2)=3.
1 S1
2
3
4
Байду номын сангаас
S2
S3
S4
运筹学-动态规划
1
2
3
4
2）、状态 ( state) 各阶段开始时的出发点称作状态。
描述各阶段状态的变量，称作状态变量，用sk 表示。
在例７.1 中，第一阶段的状态为 A ，第二阶段的状态为城市 B1，B2 和 B3。所以状态变量 S1 的集合 S1={A},S2 的集合是 S2={B1,B2,B3}, 依次有 S3={C1,C2,C3}, S4={D1,D2} 。
C3 ，如果我们选择，从C2走，则此时的决策变量可表示x2(B1)=C2。
1
2
3
4
4）、策略（ Policy）
在各阶段决策确定以后，整个问题的决策序列就构成了一个策略,
用P1n(s1)表示。
如对于例７.1总共可有18个策略，但最优策略只有一个。
1
2
3
4
运筹学-动态规划
5）、目标函数
用于衡量所选定策略优劣的数量指标称作目标函数。
第七章 动态规划
７.1 动态规划问题和基本概念 ７.2 动态规划的基本原理 ７.3 动态规划的应用
引言
动态规划与多阶段决策：
多阶段决策是指这样一类特殊的活动过程, 它们可以按时间顺序分 解成若干相互联系的阶段, 每个阶段都要作出决策, 全部过程的决策是 一个决策序列, 所以多阶段决策问题又称为序贯决策问题。
运筹学-动态规划
●逆序法求解最短路问题
第一步,从K=4开始
状态变量S4可取两种状态D1, D2,它们到E点的距离 分别为4和3,这也就是由D1和D2到终点E 的最短距离， 即
f4(D1)=4, f4(D2)=3.
1 S1
2
3
4
Байду номын сангаас
S2
S3
S4
运筹学-动态规划
1
2
3
4
2）、状态 ( state) 各阶段开始时的出发点称作状态。
描述各阶段状态的变量，称作状态变量，用sk 表示。
在例７.1 中，第一阶段的状态为 A ，第二阶段的状态为城市 B1，B2 和 B3。所以状态变量 S1 的集合 S1={A},S2 的集合是 S2={B1,B2,B3}, 依次有 S3={C1,C2,C3}, S4={D1,D2} 。
C3 ，如果我们选择，从C2走，则此时的决策变量可表示x2(B1)=C2。
1
2
3
4
4）、策略（ Policy）
在各阶段决策确定以后，整个问题的决策序列就构成了一个策略,
用P1n(s1)表示。
如对于例７.1总共可有18个策略，但最优策略只有一个。
1
2
3
4
运筹学-动态规划
5）、目标函数
用于衡量所选定策略优劣的数量指标称作目标函数。
第七章 动态规划
７.1 动态规划问题和基本概念 ７.2 动态规划的基本原理 ７.3 动态规划的应用
引言
动态规划与多阶段决策：
多阶段决策是指这样一类特殊的活动过程, 它们可以按时间顺序分 解成若干相互联系的阶段, 每个阶段都要作出决策, 全部过程的决策是 一个决策序列, 所以多阶段决策问题又称为序贯决策问题。
运筹与优化--动态规划.ppt
2.2. 动态 规划的基本思想和基本方程
最短路线有一个重要特性：如果L是允许策略集
合P中从始点A到终点E的最短路线,M是L中的一点,则
从M沿L到E的路是从M到E的最短路线.
寻找最短路线的方法,可以从最后一段开始,由后
向前逐步递推,求出各点到后一点的最短路线,最后求
得始点到终点的最短路线.所以,动态规划的方法是从
终点逐段向始点方向寻找最短路线的一种方法. 如图
所示:
行进方向
始点 1 2 3
n 终点
寻优途径
例1、最短路径问题
2
A5
1
B1
12 14
10
6
B2 10
4 13
B3
12 11
C1
3
9
6
C2
5 8
C3
10
求从A到E的最短路径
D1
5
E
D2 2
2
A5
1
B1
12 14
10
6
B2 10
4 13
B3
12 11
B1 12 14
2 f2(B2)=110 4
6
5
B2 10
4
1
13
B3
12 11
f2(B3)=19
f3(C1)=8
C1
3
9
f3(C2)=7
6
C2
5 8
C3
10
f3(C3)=12
f4(D1)=5
D1
5 f5(E)=0
E
D2 2
f4(D2)=2
状态 最优决策 状态 最优决策 状态 最优决策 状态 最优决策 状态 A （ A，B2） B2 （B2，C1） C1 （C1，D1） D1
管理运筹学07动态规划
生产计划、库存管理、路径规划 等。
连续时间动态规划
定义
连续时间动态规划是指时间连续变化，状态 和决策也连续变化，状态转移和决策可以发 生在任意时刻。
解决思路
通过将时间连续化，将连续的时间动态问题转化为 离散的时间动态问题，然后应用动态规划的方法进 行求解。
应用场景
控制系统优化、金融衍生品定价、物流优化 等。
状态转移
指从一个状态转移到另一个状态的过程，是动态规划的基本要素 之一。
状态转移方程
描述了状态转移的数学表达式，是动态规划算法的核心。
最优化原理
最优化原理
在多阶段决策问题中，如果每个阶段 都按照最优策略进行选择，则整个问 题的最优解一定是最优的。
最优子结构
如果一个问题的最优解可以由其子问 题的最优解推导出来，则称该问题具 有最优子结构。
解决方案
采用启发式搜索策略， 如模拟退火、遗传算法 等，来引导算法跳出局 部最优解。
案例
在旅行商问题中，采用 模拟退火算法结合动态 规划，在局部搜索和全 局搜索之间取得平衡， 得到全局最优解。
06 动态规划案例研究
案例一：生产与存储问题的动态规划解决方案
总结词
该案例研究探讨了如何利用动态规划解决生 产与存储问题，通过合理安排生产和存储策 略，降低总成本。
管理运筹学07动态规划
contents
目录
• 动态规划概述 • 动态规划的基本概念 • 动态规划的应用 • 动态规划的扩展 • 动态规划的挑战与解决方案 • 动态规划案例研究
01 动态规划概述
定义与特点
定义
动态规划是一种通过将原问题分解为 相互重叠的子问题，并存储子问题的 解以避免重复计算的方法，从而有效 地解决最优化问题的方法。
连续时间动态规划
定义
连续时间动态规划是指时间连续变化，状态 和决策也连续变化，状态转移和决策可以发 生在任意时刻。
解决思路
通过将时间连续化，将连续的时间动态问题转化为 离散的时间动态问题，然后应用动态规划的方法进 行求解。
应用场景
控制系统优化、金融衍生品定价、物流优化 等。
状态转移
指从一个状态转移到另一个状态的过程，是动态规划的基本要素 之一。
状态转移方程
描述了状态转移的数学表达式，是动态规划算法的核心。
最优化原理
最优化原理
在多阶段决策问题中，如果每个阶段 都按照最优策略进行选择，则整个问 题的最优解一定是最优的。
最优子结构
如果一个问题的最优解可以由其子问 题的最优解推导出来，则称该问题具 有最优子结构。
解决方案
采用启发式搜索策略， 如模拟退火、遗传算法 等，来引导算法跳出局 部最优解。
案例
在旅行商问题中，采用 模拟退火算法结合动态 规划，在局部搜索和全 局搜索之间取得平衡， 得到全局最优解。
06 动态规划案例研究
案例一：生产与存储问题的动态规划解决方案
总结词
该案例研究探讨了如何利用动态规划解决生 产与存储问题，通过合理安排生产和存储策 略，降低总成本。
管理运筹学07动态规划
contents
目录
• 动态规划概述 • 动态规划的基本概念 • 动态规划的应用 • 动态规划的扩展 • 动态规划的挑战与解决方案 • 动态规划案例研究
01 动态规划概述
定义与特点
定义
动态规划是一种通过将原问题分解为 相互重叠的子问题，并存储子问题的 解以避免重复计算的方法，从而有效 地解决最优化问题的方法。
运筹学 动态规划
max
3x1 4 x2 5 x3
max 3 x1 max 4 x2 5 x3 5 x2 6 x3 10 4 x1 10 0 x1 max 3 x1 f 2 10 4 x1
10 0 x1 4 4
，则有：
N 1 J x0 max L xk , u k u 0 ,u 1,,u N 1 k 0
* N N 1 max L x0 , u 0 L xk , u k u 0 ,u 1,,u N 1 k 1
（5）
（5）式表明，多阶段决策的最优策略只依赖于系统的初始状态 x 0 。
Байду номын сангаас
多阶段决策问题的最优性原理 多阶段决策问题的最优性原理可表述为： 如果 u * 0, u * 1,, u * N 1 是最优 策略序列，那么它的一部分 u * 1, u * 2,, u * N 1 也是一个最优策略序列。其反 证法的证明是无须赘述的[8,9]。 简单说， “最优策略的子策略必为最优子策略”
4 x2 5 x3
max 4 x2 max 5 x3 6 x3 2 5 x2 2 0 x2 max 4 x2 f 3 2 5 x2
2 0 x2 5 5
max 4 x2 max 5 x3 6 x3 105 x2 10 0 x2 max 4 x2 f 3 10 5 x2
k 1:
f1 10
4 x1 5 x2 6 x3 10
max
3 x1 4 x2 5 x3
Max z 3 x1 4 x2 5 x3 s.t. 3 x1 4 x2 5 x3 10 var iable positive, I