圆的方程习题精讲,附有详细答案
2.4 圆的方程(精讲)高二数学上学期同步讲与练(人教A版2019选择性必修第一册)(解析版)

2.4圆的方程一、圆的标准方程1、圆的定义:平面内到定点的距离等于定长的点的集合叫做圆,定点称为圆心,定长称为圆的半径。
2、确定圆的基本要素是:圆心和半径3、圆的方程:圆心为(),A a b ,半径长为r 的圆的标准方程为()()222-+-=x a y b r 4、几种特殊位置的圆的标准方程条件方程的标准形式圆心在原点()2220+=≠r x y r 圆过原点()()()2222220-+-=++>x a y b a b a b 圆心在x 轴()()2220-+=≠x a y r r 圆心在y 轴()()2220+-=≠x y b r r 圆心在x 轴上且过原点()()2220-+=≠x a y a a 圆心在y 轴上且过原点()()2220+-=≠x y b b b 圆与x 轴相切()()()2220+-=≠-y b b b x a 圆与y 轴相切()()()2220+-=≠-y b a a x a 圆与两坐标轴都相切()()()2220+-==-≠y b a a b x a 二、点和圆的位置关系圆的标准方程为()()222-+-=x a y b r ,圆心(),A a b ,半径为r .设所给点为()00,M x y ,则()()22200-+-=x a y b r位置关系判断方法几何法代数法点在圆上=MA r ⇔点M 在圆A 上点M 在圆上⇔()()22200-+-=x a y b r 点在圆内<MA r ⇔点M 在圆A 内点M 在圆内⇔()()22200-<+-x a y b r 点在圆外>MA r ⇔点M 在圆A 外点M 在圆外⇔()()22200->+-x a y b r三、圆的一般方程1、定义:当2240D E F +->时,方程220x y Dx Ey F ++++=叫做圆的一般方程.其中,22D E ⎛⎫-- ⎪⎝⎭为圆心,为半径.2、一般方程与标准方程关系:由方程220x y Dx Ey F ++++=得22224224D E D E F x y +-⎛⎫⎛⎫+++=⎪ ⎪⎝⎭⎝⎭(1)当2240D E F +-=时,方程只有实数解,22D E x y =-=-.它表示一个点(,)22D E --.(2)当2240D E F +-<时,方程没有实数解,因而它不表示任何图形.(3)当2240D E F +->时,可以看出方程表示以,22D E ⎛⎫-- ⎪⎝⎭为半径的圆.四、用待定系数法求圆的方程的步骤求圆的方程常用“待定系数法”,大致步骤是:(1)根据题意,选择标准方程或一般方程.(2)根据已知条件,建立关于a b r 、、或D E F 、、的方程组.(3)解方程组,求出a b r 、、或D E F 、、的值,并把它们代入所设的方程中去,就得到所求圆的方程.题型一由圆的标准方程确定圆心与半径【例1】圆22(1)4x y -+=的圆心为()A.(1,0)B.(1,0)-C.(0,1)D.(0,1)-【答案】A【解析】由圆的方程22(1)4x y -+=得圆心(1,0),故选:A【变式1-1】圆()()22111x y -+-=的半径长等于()A.13B.1D.4【答案】B【解析】圆()()22111x y -+-=的半径长1,故选:B.【变式1-2】已知圆M 的方程为22(1)(2)4x y ++-=,则圆心M 的坐标是()A.(1-,2)B.(1,2)C.(1,2-)D.(1-,2-)【答案】A 【解析】222()()x a y b r -+-=的圆心坐标为(),a b ;∴22(1)(2)4x y ++-=的圆心坐标为()1,2-;故选:A.【变式1-3】圆2220x x y ++=的圆心到直线30x y -+=的距离为()A.1B.2D.【答案】C【解析】圆的标准方程为()2211x y ++=,圆心坐标为()1,0-,因此,圆心到直线30x y -+=的距离为d 题型二求圆的标准方程【例2】以点()2,3为圆心,2为半径的圆的标准方程为()A.()()22232x y +++=B.()()22232x y -+-=C.()()22234x y +++=D.()()22234x y -+-=【答案】D【解析】以点()2,3为圆心,2为半径的圆的标准方程为()()222232x y -+-=,即()()22234x y -+-=,故选:D.【变式2-1】圆心在直线2x -3y -1=0上的圆与x 轴交于A (1,0)、B (3,0)两点,则圆的方程为________.【答案】22(2)(1)x y -+-=2【解析】由题意得:圆心在直线2x =上,又圆心在直线2310x y --=上,令2x =,得1y =∴圆心M 的坐标为(2,1),又(1,0)A ,半径||AM ,则圆的方程为22(2)(1)2x y -+-=.故答案为:22(2)(1)2x y -+-=【变式2-2】已知(1,1),(1,1)P Q --,则以,P Q 为直径的圆的方程为________.【答案】222x y +=【解析】因为(1,1),(1,1)P Q --,所以线段PQ 的中点为(0,0),4PQ ==,所以以,P Q 为直径的圆的方程为222x y +=,故答案为:222x y +=【变式2-3】已知一圆经过点(4,3)P -,圆心在直线210x y -+=上,且半径为5,求该圆的标准方程.【答案】22(1)(3)25x y -+-=或22(1)(1)25x y +++=【解析】设圆的方程22()()25x a y b -+-=,由圆心在直线210x y -+=上,且圆经过点(4,3)P -,得()()222104325a b a b -+=⎧⎪⎨--+-=⎪⎩,解得13a b =⎧⎨=⎩或11a b =-⎧⎨=-⎩,故圆的标准方程为22(1)(3)25x y -+-=或22(1)(1)25x y +++=.题型三点和圆的位置关系判断【例3】已知圆C 的标准方程是()()22234x y -+-=,则点()3,2P ()A.在圆C 外B.在圆C 内C.在圆C 上D.不能确定【答案】B 【解析】圆C()()22234x y -+-=的圆心为(2,3)C ,半径为2,因为2PC =<,所以点P 在圆内.故选:B【变式3-1】点P (m ,3)与圆(x -2)2+(y -1)2=2的位置关系为()A.点在圆外B.点在圆内C.点在圆上D.与m 的值有关【答案】A【解析】将点P (m ,3)坐标代入(x -2)2+(y -1)2=2中,有:2(2)42m -+>恒成立,故点P 在圆外,故选:A.【变式3-2】点()2,1a a -在圆222120x y y +--=的内部,则实数a 的取值范围是()A.195a -<<B.915a -<<C.915a -<<D.195a -<<【答案】B【解析】因为222120x y y +--=,所以()22113x y +-=,由于点()21a a -,在圆内所以()()222213a a +-<,所以()()25495910a a a a --=-+<,所以915a -<<,故选:B【变式3-3】若点()41,32a a -+不在圆()()221225x y ++-=的外部,则a 的取值范围是()A.a <B.11a -<<C.a ≤≤D.11a -≤≤【答案】D【解析】由已知得()()224325a a +≤,解得21a ≤,∴1a ≤,即11a -≤≤,故选:D .题型四圆的一般方程与标准方程互化【例4】已知圆方程222410+-+-=x y x y 的圆心为()A.()2,4-B.()1,2-C.()1,2-D.()2,4-【答案】C【解析】因为222410+-+-=x y x y ,即()()22126x y -++=,所以圆心坐标为()1,2-;故选:C【变式4-1】圆222460x y x y ++--=的圆心和半径分别是()A.()1,2--,11B.()1,2-,11C.()1,2--D.()1,2-【答案】D【解析】先化为标准方程可得()()221211x y ++-=,故圆心为()1,2-【变式4-2】已知圆22620x y x y ++-=,则该圆的圆心和半径分别是().A.()3,1--B.()3,1-,10C.()3,1-D.()3,1-,10【答案】C【解析】将圆的一般式方程22620x y x y ++-=化为标准方程得()()223110x y ++-=,所以圆心为()3,1-,故选:C【变式4-3】已知实数,x y 满足2284160x y x y ++-+=,则y 的最大值是()A.3B.2C.1-D.4【答案】D【解析】2284160x y x y ++-+=可化为:()()22424x y ++-=,所以()224y -≤,解得:04y ≤≤,即y 的最大值是4,故选:D【变式4-4】已知实数,x y 满足方程2284160x y x y ++-+=,则x 的最大值为()A.3B.2C.1-D.2-【答案】D【解析】将方程变形为()()22424x y ++-=,则圆心坐标为()4,2-,半径2r =,则圆上的点的横坐标的范围为:62x -≤≤-则x 的最大值是2-,故选:D.题型五求圆的一般方程【例5】ABC 三个顶点的坐标分别是()1,1A ,()4,2B ,()3,0C ,则ABC 外接圆方程是()A.223560x y x y +--+=B.225360x y x y +--+=C.223560x y x y +---=D.225360x y x y +---=【答案】B【解析】设圆的一般方程为2222040x y Dx Ey F D E F ++++=+->,,因为()1,1A ,()4,2B ,()3,0C 在这个圆上,所以有222222110542420330306D E F D D E F E D F F ⎧++++==-⎧⎪⎪++++=⇒=-⎨⎨⎪⎪+++==⎩⎩,故选:B【变式5-1】过四点()1,0-,()4,4-,()0,1,()1,0中的三点的一个圆的方程为______.【答案】223131240777x y x y ++-+=或2231104x y y +--=或2210x y +-=或223131320x y x y +++-=【解析】设圆的一般方程为220x y Dx Ey F ++++=,若圆过(1,0)(4,4)(0,1)--,,三点,则103244010D F DEF E F -+=⎧⎪-++=⎨⎪++=⎩,解得313124777D E F ==-=,,,此时圆的一般方程为223131240777x y x y ++-+=;若圆过(1,0)(4,4)(1,0)--,,三点,则103244010D F DEF D F -+=⎧⎪-++=⎨⎪++=⎩,解得31014D E F ==-=-,,,此时圆的一般方程为2231104x y y +--=;若圆过(1,0)(0,1)(1,0)-,,三点,则101010D F E F D F -+=⎧⎪++=⎨⎪++=⎩,解得001D E F ===-,,,此时圆的一般方程为2210x y +-=;若圆过(4,4)(0,1)(1,0)-,,三点,则324401010D E F E F D F -++=⎧⎪++=⎨⎪++=⎩,解得313132D E F ===-,,,此时圆的一般方程为223131320x y x y +++-=.【变式5-2】已知一个等腰三角形底边上的高等于5,底边两端点的坐标分别是()4,0-、(4,0),求它的外接圆的方程.【答案】2291605x y y +--=或2291605x y y ++-=.【解析】由题意得,等腰三角形顶点的坐标为(0,5)或(0,5)-.当顶点坐标为(0,5)时,设三角形外接圆的方程为220x y Dx Ey F ++++=,则2550,1640,1640,E F D F D F ++=⎧⎪-+=⎨⎪++=⎩解得0,9,516.D E F =⎧⎪⎪=-⎨⎪=-⎪⎩所以圆的方程为2291605x y y +--=.当顶点坐标是(0,5)-时,同理可得圆的方程为2291605x y y ++-=.综上,它的外接圆的方程为2291605x y y +--=或2291605x y y ++-=.【变式5-3】过三点()1,5A -、()5,5B 、()6,2C -的圆的方程为____________________.【答案】2242200x y x y +---=.【解析】点()1,5A -、()5,5B 的中点为(2,5),0AB k =,中垂线为x=2.点()5,5B 、()6,2C -的中点为113(,)22,7BC k =-,所以17k =,中垂线为x-7y+5=0.两直线交点为圆心D(2,1),r=AD=5.所以圆的方程为22(2)(1)25x y -+-=,也即2242200x y x y +---=.填2242200x y x y +---=.题型六二元二次方程与圆的关系【例6】若曲线22220x y x my ++++=表示圆,则m 的取值范围是()A.()2,+∞B.[)2,+∞C.()(),22,∞∞--⋃+D.(][),22,-∞-+∞U 【答案】C【解析】22280,2m m +-><-或2m >.故选:C.【变式6-1】已知方程()()2224232141690x y m x my m+-++++=─表示一个圆,则实数m 的取值范围为()A.1(,1)7-B.1(,1)7-C.1(,)(1,)7-∞-⋃+∞D.1(,1)(,)7-∞-⋃+∞【答案】B【解析】由题意可得()()()22244341441690m m m ++⨯--+>,所以()()7110m m +-<,解得117m -<<.故选:B.【变式6-2】若方程2222210x y ax a a +++-+=表示圆,则a 的取值范围为()A.0a ≠B.0a >C.1a >D.12a >【答案】D【解析】因为方程2222210x y ax a a +++-+=表示圆,所以()()2222424021a a D E F a +--+-=>,即840a ->,解得12a >;故选:D【变式6-3】已知“m t ≤”是“220x y m ++=”表示圆的必要不充分条件,则实数t 的取值范围是()A.()1,-+∞B.[)1,+∞C.(),1-∞D.(),1-∞-【答案】B【解析】若表示圆,则22(40+->m ,解得1m <.“m t ≤”是“220x y m ++=”表示圆的必要不充分条件,所以实数t 的取值范围是[1,)+∞.故选:B题型七与圆有关的对称问题【例7】圆()()22112x y -+-=关于直线3y kx =+对称,则k 的值是()A.2B.2-C.1D.1-【答案】B【解析】圆()()22112x y -+-=关于直线3y kx =+对称,所以圆心(1,1)在直线3y kx =+上,得132k =-=-,故选B.【变式7-1】如果圆220x y Dx Ey F ++++=(2240D E F +->)关于直线y x =对称,则有().A.0D E F ++=B.D E=C.D F=D.E F=【答案】B【解析】由220x y Dx Ey F ++++=可得圆心坐标为,22D E ⎛⎫-- ⎪⎝⎭,因为圆关于直线y x =对称,所以圆心在直线y x =上,即22E D-=-,可得D E =,故选:B.【变式7-2】圆:C ()()22439x y -++=关于直线:l 30x y +-=对称的圆的标准方程是()A.()()22619x y -++=B.()()22619x y ++-=C.()()22619x y -+-=D.()()22619x y +++=【答案】A【解析】由题意有,圆C 的圆心C ()4,3-,半径为3,设所求圆的圆心为'(,)C a b ,由圆C 和圆C’关于直线l 对称得,点C 和点C ’关于直线l 对称,则4330223·(1)14a bb a +-+⎧+-=⎪⎪⎨+⎪-=-⎪-⎩,解得61a b =⎧⎨=-⎩,则所求圆的标准方程是()()22619x y -++=.故选:A.【变式7-3】求圆22:8280C x y x y +-+-=关于点()2,1-对称的圆的方程为___________.【答案】()22125x y ++=【解析】圆22:8280C x y x y +-+-=化为标准方程为:()()224125x y -++=.所以()4,1C -,半径=5r .故圆C 关于点()2,1-对称的圆的半径5,圆心设为D .由中点坐标公式求得:()0,1D -,所以对称圆的方程为:()22125x y ++=.故答案为:()22125x y ++=.。
圆的方程 习题含答案

圆的方程习题(含答案)一、单选题1.以点P(2,-3)为圆心,并且与y轴相切的圆的方程是( )A.(x+2)2+(y-3)2=4B.(x+2)2+(y-3)2=9C.(x-2)2+(y+3)2=4D.(x-2)2+(y+3)2=92.当点在圆上运动时,连接它与定点,线段的中点的轨迹方程是()A.B.C.D.3.圆x2+y2-(4m+2)x-2my+4m2+4m+1=0的圆心在直线x+y-4=0上,那么圆的面积为( )A.9πB.πC.2πD.由m的值而定4.圆的半径是()A.B.2C.D.45.已知圆与圆相交于A、B两点,则线段AB的垂直平分线的方程为A.B.C.D.6.若点为圆上的一个动点,点,为两个定点,则的最大值为()A.B.C.D.7.已知直线:是圆的对称轴.过点作圆的一条切线,切点为,则()A.2B.C.6D.8.若直线l:ax+by+1=0经过圆M:的圆心则的最小值为A.B.5C.D.109.若均为任意实数,且,则的最小值为()A.B.C.D.二、填空题10.如图,扇形的圆心角为90°,半径为1,点是圆弧上的动点,作点关于弦的对称点,则的取值范围为____.11.已知x,y满足-4-4+=0, 则的最大值为____12.若直线l:与x轴相交于点A,与y轴相交于B,被圆截得的弦长为4,则为坐标原点的最小值为______.13.设直线与圆相交于两点,若,则圆的面积为________.14.已知圆的圆心在曲线上,且与直线相切,当圆的面积最小时,其标准方程为_______.15.在平面直角坐标系xOy中,已知过点的圆和直线相切,且圆心在直线上,则圆C的标准方程为______.16.已知圆的圆心在直线上,且经过,两点,则圆的标准方程是__________.17.在平面直角坐标系中,三点,,,则三角形的外接圆方程是__________.18.如图,O是坐标原点,圆O的半径为1,点A(-1,0),B(1,0),点P,Q分别从点A ,B 同时出发,圆O 上按逆时针方向运动.若点P 的速度大小是点Q 的两倍,则在点P 运动一周的过程中,的最大值是_______.三、解答题 19.设抛物线的焦点为,过且斜率为的直线与交于,两点,.(1)求的方程;(2)求过点,且与的准线相切的圆的方程. 20.已知圆内一点,直线过点且与圆交于,两点.(1)求圆的圆心坐标和面积; (2)若直线的斜率为,求弦的长;(3)若圆上恰有三点到直线的距离等于,求直线的方程.21.已知点在圆上运动,且存在一定点,点为线段的中点.(1)求点的轨迹的方程; (2)过且斜率为的直线与点的轨迹交于不同的两点,是否存在实数使得,并说明理由.22.已知圆经过()()2,5,2,1-两点,并且圆心在直线12y x =上。
圆方程的应用(讲义及答案)
B. (19,23) 55
D. (11,17) 55
10. 已知圆 C1:(x 2)2 ( y 3)2 1 ,圆 C2:(x 3)2 ( y 4)2 9 , M,N 分别是圆 C1,C2 上的动点,P 是 x 轴上的动点,则 PM PN 的最小值为( )
A. 5 2 4 C. 6 2 2
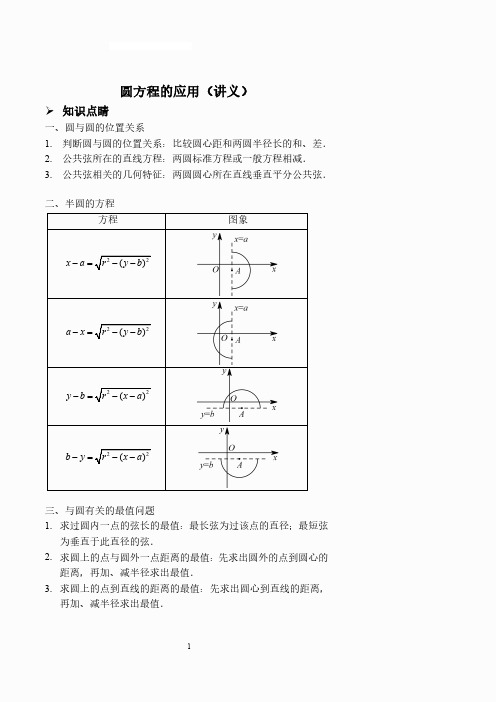
y b r2 (x a)2
b y r2 (x a)2
三、与圆有关的最值问题 1. 求过圆内一点的弦长的最值:最长弦为过该点的直径;最短弦
为垂直于此直径的弦. 2. 求圆上的点与圆外一点距离的最值:先求出圆外的点到圆心的
距离,再加、减半径求出最值. 3. 求圆上的点到直线的距离的最值:先求出圆心到直线的距离,
6
弦分别是 AC 和 BD,则四边形 ABCD 的面积为( )
A. 4 6
B. 8 6
C.12 6
D.16 6
3
9. 已知圆 C :(x 3)2 ( y 4)2 1 ,点 A(0,-1),B(0,1),P 是 圆 C 上的动点,当 PA 2 PB 2 取最大值时,点 P 的坐标为
()
A. (12,16) 55
2. 圆 C1:x2 y2 50 与 圆 C2:x2 y2 12x 6 y 40 0 的 公 共 弦 AB 的长为( )
A. 5
B. 6
C. 2 5
D. 2 6
3. 若圆 C:(x a)2 ( y a)2 4 上,总存在不同的两点到原点的
距离为 1,则实数 a 的取值范围是( )
点,则实数 k 的取值范围是( )
A. (0, 5 ) 12
C. (1,3) 34
B. ( 5 , ) 12
第04讲_圆的方程(解析版)

高中数学辅导讲义[解析版]知识图谱圆的方程知识精讲一. 圆的定义平面内到一定点距离等于定长的点的轨迹是圆. 定点是圆心,定长是圆的半径.当圆心位置与半径大小确定后,圆就唯一确定了. 因此圆心和半径是一个圆最基本的要素.二.圆的标准方程1. 以点(,)C a b 为圆心,r 为半径的圆的标准方程为:222()()x a y b r -+-=圆心在原点的圆的标准方程:222x y r +=2. 如何根据条件求圆的标准方程:圆的标准方程222()()x a y b r -+-=中,有三个参数a b r 、、,只要求出a b r 、、,这时圆的方程就确定了. 因此确定圆的方程需三个独立条件,其中圆心是圆的定位条件,半径是圆的定形条件.一般步骤为: (1)根据题意,设所求的圆的标准方程为:222()()x a y b r -+-=;(2)根据已知条件,建立关于a b r 、、的方程组;(3)解方程组,代入所设方程,即得所求圆的标准方程. 3. 圆心的三个重要几何性质:(1)圆心在过切点且与切线垂直的直线上; (2)圆心在弦的中垂线上;(3)两圆内切或外切时,切点与两圆圆心三点共线. 三.圆的一般方程1. 将圆的标准方程222()()x a y b r -+-=展开,得22222220x y ax by a b r +--++-=,令2222, 2, D a E b F a b r =-=-=+- ,则这个方程可表示成:220x y Dx Ey F ++++=,配方得:22224224D E E F F x y +-⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭ .(1)当2240D E F +->时,方程220x y Dx Ey F ++++=叫做圆的一般方程,圆心为(,)22D E --22142D E F +-(2)当2240D E F +-=时,方程表示一个点(,)22D E --; (3)当2240D E F +-<时,方程没有实数解,它不表示任何图形(没有轨迹). 2. 圆的一般方程特征:(1)没有xy 这样的二次项;(2)表示以(,)22D E --22142D E F +-三点剖析一.方法点拨1. 求圆的标准方程,需要确定圆心的坐标和圆的半径;而求圆的一般方程,则需要确定一般方程中的三个系数,,D E F .2. 圆的标准方程明确指出了圆的圆心和半径;而圆的一般方程表明了方程形式上的特点.3. 如何选用圆的方程:一般来说,如果根据已知条件容易求得圆心坐标、半径,或需要利用圆心的坐标或半径来列方程的问题,一般采用圆的标准方程,再用待定系数法求出a b r 、、.如果已知条件与圆心和半径都无直接联系,一般采用圆的一般方程,再利用待定系数法求出常数,,D E F . 4. 解决与圆有关的轨迹方程问题,步骤如下: (1)设动点坐标为(),x y ;(2)找出动点满足的条件;(3)用等式表示此条件. 化简后得到的,x y 的关系式即为轨迹方程.圆的标准方程例题1、 写出下列各圆的标准方程: (1)圆心在原点,半径为8 (2)圆心在()2,3,半径为2 (3)圆心在()2,1-且过原点例题2、 已知圆C :22()()12x a y a -++=过点(3,1)A ,那么圆心坐标为( ) A.(1,1) B.(1,1)- C.(21,21)-或(221)D.(21,21)+-或(12,21)--例题3、 方程211(1)x y -=-- )A.一条直线B.一条抛物线C.圆D.半圆随练1、 圆()()222x a y b r -+-=过原点,且与y 轴相切,则a b r 、、满足的条件为( ) A.,0a r b ==B.0,0b r a =≠=C.,0a b r =≠D.0,0a r b =≠=随练2、 圆222450x y x y +++-=的半径为( )A.10 5 C.5 10随练3、 求圆222690x y x y +--+=关于直线250x y ++=对称的圆的方程 随练4、 若实数满足,求的最小值.圆的一般方程例题1、 下列方程能否表示圆?若能表示圆,求出圆心和半径. (1)222750;x y x +-+= (2)22670;x xy y x y -+++=x y 、22(2)(1)1x y ++-=22x y +(3)2224100;x y x y +--+= (4)222240;x y x +-=(5)222360;x y x +++=例题2、 已知点(1,3)A ,(2,4)B -,(0,2)C ,求过这三点的圆方程.例题3、 已知点(0,1)A -,(0,0)B ,(2,1)C -,(1,1)D ,则这四点是否在同一个圆上?请说明理由 随练1、 已知点(6,5)M -,(1,7)N ,求以线段MN 为直径的圆方程.圆的简单应用例题1、 已知圆22240x y x y a ++-+=关于直线2y x b =+成轴对称,则a b -的取值范围是________ 例题2、 已知动点A 在圆221x y +=上移动时,定点(3,0)B ,求线段AB 中点的轨迹方程.拓展1、 圆()()224325x y -++=关于原点对称的圆的方程为( ) A.()()224325x y -+-= B.()()224325x y +++= C.()()224325x y ++-=D.()()223425x y ++-=2、 已知圆关于直线对称,则的取值范围是(). A. B. C.D. 3、 若实数满足,则的最大值为_________.4、 若22(1)20x y x y λλλ++-++=表示圆,则λ的取值范围是( )A.()0,+∞B.1,14⎡⎤⎢⎥⎣⎦C.()11,,5⎛⎫+∞-∞ ⎪⎝⎭ D.R5、 已知点(2,2)A ,(0,3)B ,(1,)C m ,(0,4)D 四点共圆,则m =________222410x y x y ++-+=220(,)ax by a b R -+=∈ab (1,4⎤-∞⎥⎦10,4⎛⎫ ⎪⎝⎭1,04⎛⎫- ⎪⎝⎭1,4⎡⎫-+∞⎪⎢⎣⎭x y 、22(2)3x y -+=y x答案解析圆的方程圆的标准方程例题1、【答案】 (1)2264x y +=(2)()()22234x y -+-=(3)()()22215x y -++= 【解析】 以点(,)C a b 为圆心,r 为半径的圆的方程:222()()x a y b r -+-= (1)2264.x y +=(2)()()2223 4.x y -+-=(3)()()2221 5.x y -++= 例题2、 【答案】 D【解析】 将(3,1)A 代入圆C 的方程.可得:()()223112a a -++= 化简得22420a a --=即2210a a --=, ∴12a =(),a a -. 例题3、 【答案】 D【解析】 由圆的标准方程()()222x a y b r -+-=得()()222x a r y b -=--, 所以a x a r ≤≤+时,有()22x a r y b -=--表示半圆;所以a r x a -≤≤时, 有()22x a r y b -=--则表示另一半圆. 随练1、 【答案】 D【解析】 由题可知()()22200a b r -+-=,与y 轴相切,则0,0r a b =≠∴= 随练2、 【答案】 D【解析】 半径为224D E Fr +-=()222451022⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭随练3、【答案】 圆的方程为()()22471x y +++=【解析】 两圆关于直线对称,两圆的半径相等,两圆心关于直线对称圆222690x y x y +--+=的圆心为()1,3,半径为1,设点()1,3关于直线250x y ++=对称的点为(),m n ,则有()32111325022n m m n -⎧⋅-=-⎪⎪-⎨++⎪⋅++=⎪⎩解得71m n =-⎧⎨=-⎩即所求圆的圆心为()7,1--,故圆的方程为()()22711x y +++= 随练4、【答案】 65-【解析】 根据两点之间距离公式,可转化为在约束条件下的点到点的距离或距离的平方.点到圆的距离的最大值等于点到圆心的距离加上半径,点到圆的距离的最小值等于点到圆心距离和半径的差的绝对值.表示圆上的点到原点的距离的平方,圆的圆心为,半径,圆心到原点的距离圆的一般方程例题1、【答案】 (1)(2)(3)(5)不能表示圆;(4)能,圆心()1,0,半径为1 【解析】 圆的一般方程为220x y Dx Ey F ++++=,(2240D E F +->), (1)(2)(3)(5)不满足圆的一般方程形式,故不能表示为圆 例题2、【答案】 所求圆的方程为221315022x y x y +-+-=【解析】 解法一:设所求圆的方程为220x y Dx Ey F ++++=,则 ()22222133024240220D E F D E F E F ⎧++++=⎪⎪+-+-+=⎨⎪++=⎪⎩解得132125D E F ⎧=-⎪⎪⎪=⎨⎪=-⎪⎪⎩, 所以所求圆的方程为221315022x y x y +-+-=解法二:线段AB ,BC 的中点分别为31,22M ⎛⎫- ⎪⎝⎭,()1,1N -,直线AB ,BC 的斜率分别为34712AB k +==--,24302BC k +==--,所以线段AB 的中垂线为113272y x ⎛⎫+=- ⎪⎝⎭,即750x y --=线段BC 的中垂线为()1113y x +=-,即340x y --=,联立方程750340x y x y --=⎧⎨--=⎩解得13414x y ⎧=⎪⎪⎨⎪=-⎪⎩即圆心坐标为131,44⎛⎫- ⎪⎝⎭,到点(1,3)A 的距离即半径221315101344r ⎛⎫⎛⎫⎛⎫=-+-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭例题3、【答案】 见解析【解析】 不共线的三点必共圆,任意共圆的点必满足同一个圆的方程.要判断四点是否共圆,可以先解出过其中三点的圆的方程,将第四个点代入所求方程验证是否满足.或者找到一个到各点距离相等的点,则它们共圆. 在平面直角坐标系中,容易得知ABC ∆是直角三角形,其中90BAC ∠=.所以,ABC ∆的外接圆圆心为线段BC 的中点1(1,)2M -,易求得32MD =22151(0)2MB =++=MD MB ≠所以这四点不在同一个圆上.随练1、()()22x m y n -+-()()22x m y n -+-(),x y (),m n ()()222200x y x y +=-+-()()22211x y ++-=(),x y ()0,0()2,1-1r =()22215d =-+())2251625d r ∴-==-【答案】 ()227169124x y ⎛⎫-+-= ⎪⎝⎭【解析】 解法一:设所求圆上任意点为(),P x y ,当点P 与点M ,N 不重合即1x ≠且6x ≠时, 因为MN 为直径,所以90MPN ∠= ∴()57161y y x x ---⋅=---∴()()()()16570x x y y --++-=,当点P 与点M 或N 重合即1x =或6x =时,将点M ,N 代入上式 ()()()()16570x x y y --++-=成立. 解法二: ()()22615713MN =-+--,所以圆的半径1322MN r == 线段MN 中点即圆心为7,12⎛⎫⎪⎝⎭,所以所圆的方程为()227169124x y ⎛⎫-+-= ⎪⎝⎭圆的简单应用例题1、【答案】 (),1-∞【解析】 圆是轴对称图形,圆关于直线对称,则直线经过圆心.依题意,可知圆22240x y x y a ++-+=的圆心()1,2-经过直线2y x b =+∴22b =-+ 解得4b =,又22240x y x y a ++-+=的半径22245022r a a ⎛⎫⎛⎫=+-=- ⎪ ⎪⎝⎭⎝⎭>解得a <5∴41a b a -=-<例题2、【答案】 圆的方程为223124x y ⎛⎫-+= ⎪⎝⎭【解析】 求点的轨迹方程常设所求点坐标为(),x y ,再根据题意代入已知或可求得式子中求的轨迹方程.设线段AB 中点为(),x y ,因为点(3,0)B ,则点()23,2A x y -, 又点A 在圆221x y +=上,故圆的方程为223124x y ⎛⎫-+= ⎪⎝⎭拓展1、【答案】 C【解析】 圆心(4,3)-关于原点对称的点为(4,3)-,故圆的方程为()()224325x y ++-=2、【答案】 A【解析】 依题意,可知圆的圆心经过直线∴,化简得, ∴222410x y x y ++-+=()1,2-220(,)ax by a b R -+=∈2220a b --+=1a b +=1b a =-()221111244ab a a a a a ⎛⎫=-=-+=--+≤⎪⎝⎭3、【答案】【解析】 可看作点和点连线的斜率,其中点在圆上故当取得最大值时,直线与圆相切,由几何意义和斜率的定义,可得4、【答案】 C【解析】 依题意,得()()221240λλλ-+->即25610λλ-+>,解得15λ<或1λ>5、【答案】 2m =或5m =【解析】 设过A ,B ,C ,D 的圆方程为220x y Dx Ey F ++++= 则2222222222033044010D E F E F E F m D mE F ⎧++++=⎪++=⎪⎨++=⎪⎪++++=⎩,解得2m =或5m = y x(),x y ()0,0l (),x y 22(2)3x y -+=y x l 22(2)3x y -+=maxyx ==。
数学圆的方程讲义含答案解析

数学课程讲义 学科:数学专题:圆的方程考点梳理一、圆的标准方程设圆心的坐标为(,)C a b ,半径为r ,222()()x a y b r -+-=特别地,当圆心为坐标原点(0,0)O 时,半径为r 的圆的标准方程为222x y r +=二、圆的一般方程220x y Dx Ey F ++++=. (2240D E F +->)问题:此圆的圆心和半径分别是多少?将方程配方整理得22224224D E D E Fx y +-⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭其圆心在(,)22D E --224D E F+-. 金题精讲题一题面:圆心在y 轴上,半径为1,且过点(1,2)的圆的方程为()A .22(2)1x y +-=B .22(2)1x y ++=C .22(1)(3)1x y -+-=D .22(3)1x y +-=题二题面:根据下面所给的条件,分别求出圆的方程:(1) 以点(2,5)-为圆心,并且过点(3,7)-;(2) 设点(4,3)A 、(6,1)B -,以线段AB 为直径;(3) 经过点(2,4)P -和点(0,2)Q ,并且圆心在直线0x y +=上.题三题面:以点(2,-1)为圆心且与直线3450x y -+=相切的圆的方程为 ( )A .22(2)(1)3x y -++=B .22(2)(1)3x y ++-=C .22(2)(1)9x y -++=D .22(2)(1)9x y ++-=题四题面:圆01222=--+x y x 关于直线032=+-y x 对称的圆的方程是( )A.21)2()3(22=-++y x B.21)2()3(22=++-y x C.2)2()3(22=-++y x D.2)2()3(22=++-y x题五题面:在圆06222=--+y x y x 内,过点E (0,1)的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积为( )A .25B .210C .D .220题六题面:已知圆C 与直线x -y =0 及x -y -4=0都相切,圆心在直线x +y =0上,则圆C 的方程为_____________.题七题面:点P (4,-2)与圆224x y +=上任一点连线的中点轨迹方程是________课后练习注:此部分为老师根据本讲课程内容为大家精选的课下拓展题目,故不在课堂中讲解,请同学们课下自己练习并对照详解进行自测.题一题面:若P (2,-1)为圆(x -1)2+y 2=25的弦AB 的中点,则直线AB 的方程是( )A. x -y -3=0B.2x +y -3=0C. x +y -1=0D.2x -y -5=0题二题面:以点(2,1-)为圆心且与直线6x y +=相切的圆的方程是 .题三题面:圆心为(1,1)且与直线x+y=4相切的圆的方程是.讲义参考答案金题精讲题一答案:A题二答案:(1)22 (2)(5)169 x y++-=(2)22 (5)(1)5 x y-+-=(3)22 (2)(2)4 x y++-=题三答案:C 题四答案:C 题五答案:B题六答案:22(1)(1)2x y -++=题七 答案:22(2)(1)1x y -++= 课后练习题一答案:A详解:由(x -1)2+y 2=25知圆心为Q (1,0). 据k QP ·k AB =-1, ∴k AB =-QP k 1=1(其中k QP =1201---=-1). ∴AB 的方程为y =(x -2)-1=x -3,即x -y -3=0.题二答案:2225(2)(1)2x y -++=详解:将直线6x y +=化为60x y +-=,圆的半径|216|5112r --==+, 所以圆的方程为2225(2)(1)2x y -++=题三答案:(x -1)2+(y -1)2=2详解:设圆的方程为()()22211r y x =-+- , ∵直线x +y =4与圆相切,∴21141122=+-+==d r ,∴所求圆的方程为(x -1)2+(y -1)2=2.。
高中圆的方程基础练习题及讲解

高中圆的方程基础练习题及讲解### 高中圆的方程基础练习题及讲解#### 练习题一题目:已知圆心在原点的圆的方程为 \(x^2 + y^2 = r^2\),求半径为3的圆的方程。
解答:将 \(r = 3\) 代入圆的标准方程,我们得到:\[ x^2 + y^2 = 3^2 \]\[ x^2 + y^2 = 9 \]这就是半径为3的圆的方程。
#### 练习题二题目:圆 \(x^2 + y^2 + 6x - 8y + 20 = 0\) 与直线 \(x + y - 1 = 0\) 相切。
求圆的半径。
解答:首先,将圆的方程化为标准形式:\[ (x + 3)^2 + (y - 4)^2 = r^2 \]\[ x^2 + 6x + y^2 - 8y + 20 = r^2 \]\[ x^2 + y^2 + 6x - 8y = r^2 - 20 \]由于圆与直线相切,圆心到直线的距离等于圆的半径。
圆心坐标为\((-3, 4)\),直线方程可以写成 \(y = -x + 1\)。
使用点到直线距离公式:\[ \text{距离} = \frac{|-3 + 4 - 1|}{\sqrt{2}} \]将距离等于半径代入:\[ r = \frac{|-3 + 4 - 1|}{\sqrt{2}} \]\[ r = \frac{1}{\sqrt{2}} \]#### 练习题三题目:已知圆 \(x^2 + y^2 = 1\) 与直线 \(y = x + b\) 相切,求\(b\) 的值。
解答:由于圆与直线相切,圆心到直线的距离等于圆的半径,即1。
圆心坐标为 \((0, 0)\),直线方程可以写成 \(x - y + b = 0\)。
使用点到直线距离公式:\[ 1 = \frac{|0 - 0 + b|}{\sqrt{1^2 + (-1)^2}} \]\[ 1 = \frac{|b|}{\sqrt{2}} \]解得:\[ b = \pm \sqrt{2} \]#### 练习题四题目:求圆 \(x^2 + y^2 - 4x - 6y + 9 = 0\) 的圆心坐标和半径。
圆的方程 习题(含答案)#(优选.)
圆的方程习题(含答案)一、单选题1.以点P(2,-3)为圆心,并且与y轴相切的圆的方程是( )A.(x+2)2+(y-3)2=4B.(x+2)2+(y-3)2=9C.(x-2)2+(y+3)2=4D.(x-2)2+(y+3)2=92.当点在圆上运动时,连接它与定点,线段的中点的轨迹方程是()A.B.C.D.3.圆x2+y2-(4m+2)x-2my+4m2+4m+1=0的圆心在直线x+y-4=0上,那么圆的面积为( )A.9πB.πC.2πD.由m的值而定4.圆的半径是()A.B.2C.D.45.已知圆与圆相交于A、B两点,则线段AB的垂直平分线的方程为A.B.C.D.6.若点为圆上的一个动点,点,为两个定点,则的最大值为()A.B.C.D.7.已知直线:是圆的对称轴.过点作圆的一条切线,切点为,则()A.2B.C.6D.8.若直线l:ax+by+1=0经过圆M:的圆心则的最小值为A.B.5C.D.109.若均为任意实数,且,则的最小值为()A.B.C.D.二、填空题10.如图,扇形的圆心角为90°,半径为1,点是圆弧上的动点,作点关于弦的对称点,则的取值范围为____.11.已知x,y满足-4-4+=0, 则的最大值为____12.若直线l:与x轴相交于点A,与y轴相交于B,被圆截得的弦长为4,则为坐标原点的最小值为______.13.设直线与圆相交于两点,若,则圆的面积为________.14.已知圆的圆心在曲线上,且与直线相切,当圆的面积最小时,其标准方程为_______.15.在平面直角坐标系xOy中,已知过点的圆和直线相切,且圆心在直线上,则圆C的标准方程为______.16.已知圆的圆心在直线上,且经过,两点,则圆的标准方程是__________.17.在平面直角坐标系中,三点,,,则三角形的外接圆方程是__________.18.如图,O是坐标原点,圆O的半径为1,点A(-1,0),B(1,0),点P,Q分别从点A ,B 同时出发,圆O 上按逆时针方向运动.若点P 的速度大小是点Q 的两倍,则在点P 运动一周的过程中,的最大值是_______.三、解答题 19.设抛物线的焦点为,过且斜率为的直线与交于,两点,.(1)求的方程;(2)求过点,且与的准线相切的圆的方程. 20.已知圆内一点,直线过点且与圆交于,两点.(1)求圆的圆心坐标和面积; (2)若直线的斜率为,求弦的长;(3)若圆上恰有三点到直线的距离等于,求直线的方程.21.已知点在圆上运动,且存在一定点,点为线段的中点.(1)求点的轨迹的方程; (2)过且斜率为的直线与点的轨迹交于不同的两点,是否存在实数使得,并说明理由.22.已知圆经过()()2,5,2,1-两点,并且圆心在直线12y x =上。
2023版高中数学新同步精讲精炼(选择性必修第一册) 2
2.4 圆的方程(精讲)考点一 圆的方程【例1-1】(1)(2021·浙江高二期末)圆22(1)3x y -+=的圆心坐标和半径分别是( ) A .(-1,0),3 B .(1,0),3C .()1,0-D .()1,0(2).(2021·北京高二期末)圆22:210C x x y ++-=的圆心C 的坐标为( ) A .(1,0) B .(-1,0) C .(2,0) D .(-2,0)【答案】(1)D(2)B【解析】(1)根据圆的标准方程可得,22(1)3x y -+=的圆心坐标为(1,0) D. (2)由圆22:210C x x y ++-=可得22(1)2x y ++=,故圆心坐标为(1,0)-,故选:B【例1-2】(1)(2021·广东肇庆市)在平面直角坐标系中,经过三点(0,1),(0,2),(1,3)的圆的方程为________. (2)(2021·新疆乌苏市第一中学)过点(1,1),(1,1)A B --,且圆心在直线20x y +-=上的圆的方程 。
(3)(2021·全国高二专题练习)若圆C 与圆(x +2)2+(y -1)2=1关于原点对称,则圆C 的方程是________(4)(2021·青铜峡市高级中学 )经过圆2220x x y -+=的圆心且与直线20x y +=平行的直线方程是 。
【答案】(1)223320x y x y +--+=(2)()()22114x y -+-=(3)()()22211x y -++=(4)210x y +-=【解析】(1)设圆的方程为220x y Dx Ey F ++++=,因为圆过(0,1),(0,2),(1,3)三点,所以10,420,1930,E F E F D E F ++=⎧⎪++=⎨⎪++++=⎩得3,3,2,D E F =-⎧⎪=-⎨⎪=⎩所以圆的方程为223320x y x y +--+=.故答案为:223320x y x y +--+= (2)因为过点()1,1A -,()1,1B -,所以线段AB 的中点坐标为()0,0,()11111AB k --==---,所以线段AB 的中垂线的斜率为1k =,所以线段AB 的中垂线的方程为y x =, 又因为圆心在直线20x y +-=上,所以20x y y x+-=⎧⎨=⎩,解得11x y =⎧⎨=⎩,所以圆心为()1,1,2r ==所以圆的方程为()()22114x y -+-=.故选:C(3)已知圆圆心为(2,1)-,∴(2,1)C -,∴圆C 方程为22(2)(1)1x y -++=. (4)圆的方程化简为()2211x y -+=,圆心()1,0,半径1r =,由条件可知设直线方程:20x y c ++=,直线过点()1,0,代入直线方程101c c +=⇒=-,所以直线方程是210x y +-=.故选:B 【一隅三反】1.(2021·全国高二专题练习)圆的方程为222100x y x y +++-=,则圆心坐标为( ) A .(1,1)- B .1(,1)2-C .(1,2)-D .1(,1)2-- 【答案】D【解析】由222100x y x y +++-=可知1D =,2E =,所以122D -=-,12E -=-,所以圆心为1(,1)2--. 故选:D.2.(2021·福建漳州市·高二期末)圆心在y ,且过点(1,2)-的圆的方程为( ) A .22(1)2x y ++= B .22(3)2x y +-=C .22(1)2x y ++=或22(3)2x y ++= D .22(1)2x y +-=或22(3)2x y +-= 【答案】C【解析】设圆心为(0,)a ,则圆方程为22()2x y a +-=,将点(1,2)-代入圆方程得221(2)2+--=a 解得1a =-或3a =-所以圆方程为22(1)2x y ++=或22(3)2x y ++=故选:C3.(2021·内蒙古包头市·高二月考(理))AOB 顶点坐标分别为()2,0A ,()0,4B ,()0,0O .则AOB 外接圆的标准方程为______. 【答案】()()22125x y -+-=【解析】设圆的标准方程为()()222x a y b r -+-=,因为过点()2,0A ,()0,4B ,()0,0O所以()()()()()()222222222200400a b r a b r a b r ⎧-+-=⎪⎪-+-=⎨⎪-+-=⎪⎩解得2125a b r =⎧⎪=⎨⎪=⎩则圆的标准方程为()()22125x y -+-= 故答案为:()()22125x y -+-=4.(2021·安徽省肥东县第二中学高二期末(文))圆22(2)5x y ++=关于直线10x y -+=对称的圆的方程为____________.【答案】22(1)(1)5x y +++=【解析】由圆22(2)5x y ++=可知,圆心(2,0)-,半径r =,设点(2,0)-关于直线10x y -+=对称的点为(,)x y ,则1221022yx x y ⎧=-⎪⎪+⎨-⎪-+=⎪⎩,解得11x y =-⎧⎨=-⎩,∴所求圆的圆心为(1,1)--,半径为r =,∴圆22(2)5x y ++=关于直线10x y -+=对称的圆的方程为22(1)(1)5x y +++=,故答案为:22(1)(1)5x y +++=. 5.(2021·广东)求下列各圆的方程 (1)圆心为点()8,3C -,且过点()5,1A ;(2)过()1,5A -,()5,5B ,()6,2C -三点. (3)圆心为()3,4C -(4)圆心为()8,3C -,且经过点()5,1M --(5)已知AOB 的三个顶点分别是点()4,0A ,()0,0O ,()0,3B ,求AOB 的外接圆的标准方程. 【答案】(1)22(8)(3)25x y -++=(2)2242200x y x y +---=(3)(x +3)2+(y ﹣4)2=5.(4)(x +8)2+(y ﹣3)2=25(5)()22325224x y ⎛⎫-+-= ⎪⎝⎭ 【解析】(1)由题意知半径5r ==,所以圆的方程为:22(8)(3)25x y -++=. (2)设圆的一般方程为:220x y Dx Ey F ++++=.将()1,5A -,()5,5B ,()6,2C -代入得:1+255042525550236462020D E F D D E F E D E F F -++==-⎧⎧⎪⎪++++=⇒=-⎨⎨⎪⎪++-+==-⎩⎩所以圆的方程为:2242200x y x y +---=. (3)∵圆心在C (﹣3,4),故圆的标准方程为(x +3)2+(y ﹣4)2=5. (4)∵圆心在C (﹣8,3),且经过点M (﹣5,﹣1),故半径为MC==5,故圆的标准方程为 (x +8)2+(y ﹣3)2=25.(5)由题意知,AB 为圆的直径,设圆心为()C a b ,,则AB 中点即为3(2)2C ,,所以半径为52OC =,故外接圆的标准方程为:22325(2)()24x y -+-=.考点二 圆的定义及方程求参【例2】(1)(2021·全国高二专题练习)已知方程x 2+y 2-2x +2k +3=0表示圆,则k 的取值范围是( ) A .(-∞,-1)B .(3,+∞)C .(-∞,-1)∪(3,+∞)D .3(,)2-+∞(2)(2)(2021·青海西宁市·高二期末(文))若直线()2200,0ax by a b -+=>>经过圆222410x y x y ++-+=的圆心,则14a b+的最小值是( ). A .16B .12C .9D .8(3)(2021·全国高二单元测试)当方程22220x y ax y a ++++=所表示的圆的面积最大时,直线(1)2y a x =-+的倾斜角为( ).A .4π B .34π C .32π D .54π 【答案】(1)A(2)C(3)B【解析】(1)方程可化为(x -1)2+y 2=-2k -2,只有-2k -2>0,即k <-1时才能表示圆.故选:A. (2)222410x y x y ++-+=化为标准方程为:()()22124x y ++-=, 圆心坐标为()1,2-,带入直线方程,得1a b +=,所以()14144559b a a b a b a b a b ⎛⎫+=++=++≥= ⎪⎝⎭,故选C. (3)方程22220x y ax y a ++++=可化为2223(1)124a x y a ⎛⎫+++=-+ ⎪⎝⎭,设圆的半径为()0r r >,则22314r a =-, ∴当0a =时,2r 取得最大值,从而圆的面积最大. 此时,直线方程为2y x =-+,斜率1k =-,倾斜角为34π,故选:B 【一隅三反】1.(2021·山西省沁源县第一中学高二开学考试(文))若方程220x y x y k +-++=表示一个圆,则实数k 的取值范围为( ) A .12k ≤B .12k =C .12k ≥D .12k <【答案】D【解析】由题意得:()221140k -+->,即12k <,故选:D.2.(2021·中国农业大学附属中学高二期末)已知圆22:2C x y ax +=,若直线21y x =+过圆心,则实数a =( ) A .0B .12-C .12D .1【答案】B【解析】将圆的一般式方程化为标准方程得:()222:C x a y a -+=, 所以圆心的坐标为:(),0C a ,由于直线21y x =+过圆心, 所以210a +=,解得12a =-.故选:B. 3.(2021·全国高二课时练习)当a 取不同的实数时,由方程222210x y ax ay +++-=可以得到不同的圆,则( )A .这些圆的圆心都在直线y x =上B .这些圆的圆心都在直线y x =-上C .这些圆的圆心都在直线y x =或y x =-上D .这些圆的圆心不在同一条直线上 【答案】A【解析】由题意知,圆的标准方程:()()22221x a y a a +++=+,圆心(),a a --,圆心都在直线y x =上.故选: A4.(2021·全国高二专题练习)已知圆C:22(2)(4)1x y m -++-=,当m 变化时,圆C 上的点与原点的最短距离是_________. 【答案】1【解析】圆C :(x ﹣2)2+(y +m ﹣4)2=1表示圆心为C (﹣2,﹣m +4),半径R =1的圆,求得|OC |=∴m =4时,|OC |的最小值为2故当m 变化时,圆C 上的点与原点的最短距离是()OC 的最小值﹣R =2﹣1=1, 故答案为1.5.(2021·全国高二专题练习)已知方程22224230x y mx y m m ++++-=表示一个圆. (1)求实数m 的取值范围; (2)求半径R 的最大值.【答案】(1)()1,4-;(2)52. 【解析】(1)()()222234014x m y m m m +++=-++>⇒-<<,即实数m 的取值范围是()1,4-;(2)2223252534244R m m m ⎛⎫=-++=--+ ⎪⎝⎭≤,当且仅当32m =时,半径R 取得最大值52.考点三 点与圆的位置关系【例3】(1)(2021·全国高二专题练习)两个点()2,4M -、()2,1N -与圆22:2440C x y x y +-+-=的位置关系是( )A .点M 在圆C 外,点N 在圆C 外B .点M 在圆C 内,点N 在圆C 内 C .点M 在圆C 外,点N 在圆C 内D .点M 在圆C 内,点N 在圆C 外(2)(2021·全国高二课时练习)若坐标原点在圆22222240x y mx my m +-++-=的内部,则实数m 的取值范围是( )A .(1,1)-B .(22-C .(D .(【答案】(1)D(2)D【解析】(1)将()2,4M -代入方程左边得22242244440,则点M 在圆C 内,将()2,1N -代入方程左边得2221224490,则点N 在圆C 外,故选:D.(2)22222240x y mx my m +-++-=化为标准方程为:22()()4x m y m -++=把原点坐标代入圆的方程得: 22(0)(0)4m m -++<,解得:m ,故选:D. 【一隅三反】1.(2021·全国高二课时练习)点()1,1在圆()2211x y +-=的( )A .圆上B .圆内C .圆外D .无法判定【答案】A【解析】将点()1,1的坐标代入圆()2211x y +-=的方程即()221111+-=,∴点()1,1在圆()2211x y +-=上,故选:A2.(2021·全国高二专题练习)点()sin30,cos30︒︒与圆2212xy +=的位置关系是( ). A .点在圆上 B .点在圆内 C .点在圆外 D .不能确定【答案】C1==> C 3.(2021·全国高二课时练习)点2(,5)m 与圆2224x y +=的位置关系是( ). A .点在圆外 B .点在圆内 C .点在圆上 D .不能确定【答案】A【解析】将点2(,5)m 代入圆方程,得42524m +>.故点在圆外,选A .4.(2021·全国高二课时练习)(多选)点()1,1在圆()()224x a y a -++=的内部,则a 的取值不可能是( ) A .2- B .12-C .12D .2【答案】AD【解析】由已知条件可得()()22114a a -++<,即2224a +<,解得11a -<<.故选:AD.考点四 有关圆的轨迹方程【例4-1】(2021·广东)已知动点M 与两个定点()0,0O ,()3,0A 的距离的比为12,求动点M 的轨迹方程,并说明轨迹的形状.【答案】22(1)4x y ++=,以(1,0)-为圆心2为半径的圆 【解析】设点(,)M x y .则12MO MA==,化简得:2222230(1)4x y x x y ++-=⇒++=为以(1,0)-为圆心2为半径的圆.【例4-2】(2021年云南)已知Rt△ABC 的斜边为AB ,且A (-1,0),B (3,0).求:(1)直角顶点C 的轨迹方程; (2)直角边BC 的中点M 的轨迹方程.【答案】(1)x 2+y 2-2x -3=0(y ≠0)(2)(x -2)2+y 2=1(y ≠0)【解析】(1)方法一 设C (x ,y ),因为A ,B ,C 三点不共线,所以y ≠0. 因为AC △BC ,且BC ,AC 斜率均存在,所以k AC ·k BC =-1,又k AC =y x +1,k BC =y x -3,所以y x +1·yx -3=-1,化简得x 2+y 2-2x -3=0.因此,直角顶点C 的轨迹方程为x 2+y 2-2x -3=0(y ≠0).方法二 设AB 的中点为D ,由中点坐标公式得D (1,0),由直角三角形的性质知|CD |=12|AB |=2.由圆的定义知,动点C 的轨迹是以D (1,0)为圆心,2为半径的圆(由于A ,B ,C 三点不共线,所以应除去与x 轴的交点). 所以直角顶点C 的轨迹方程为(x -1)2+y 2=4(y ≠0).(2)设M (x ,y ),C (x 0,y 0),因为B (3,0),M 是线段BC 的中点,由中点坐标公式得x =x 0+32,y =y 0+02,所以x 0=2x -3,y 0=2y .由(1)知,点C 的轨迹方程为(x -1)2+y 2=4(y ≠0),将x 0=2x -3,y 0=2y 代入得(2x -4)2+(2y )2=4, 即(x -2)2+y 2=1.因此动点M 的轨迹方程为(x -2)2+y 2=1(y ≠0). 【一隅三反】1.(2021·全国高二课时练习)方程y( ) A .一个圆 B .两条射线 C .半个圆 D .一条射线【答案】C【解析】由y =得2236y x =-,即2236(0)x y y +=≥,∴曲线表示圆x 2+y 2=36在x 轴上方的半圆.故选:C.2.(2021·上海高二专题练习)已知圆C 过三个点(1,0)M ,(3,2)N , (5,0)R . (1)求圆C 的方程;(2)过原点O 的动直线l 与圆C 相交于不同的A 、B 两点,求线段AB 的中点 Q 的轨迹.【答案】(1)22(3)4x y -+=;(2)M 的轨迹是以3(,0)2为圆心,32为半径的圆(点M 在圆C 内,不与边界重合).【解析】(1)设圆方程为220x y Dx Ey F ++++=,则10943202550D F D E F D F ++=⎧⎪++++=⎨⎪++=⎩,解得 605D E F =-⎧⎪=⎨⎪=⎩, 所以圆方程为22650x x y -++=,即22(3)4x y -+=;(2)由(1)(3,0)C ,设(),Q x y ,则由 OQ QC ⊥得,0OQ CQ ⋅=,即 (,)(3,)0x y x y ⋅-=,2230x x y -+=,2239()24x y -+=. 又Q 在圆C 内部,所以Q 的轨迹是以3(,0)2为圆心, 32为半径的圆(点Q 在圆C 内部).3.(2021·上海)圆C 过点()60A ,,()1,5B ,且圆心在直线:2780l x y -+=上.(1)求圆C 的方程;(2)P 为圆C 上的任意一点,定点()8,0Q ,求线段PQ 中点M 的轨迹方程.【答案】(1)22(3)(2)13x y -+-=;(2)221113(1)24x y ⎛⎫-+-= ⎪⎝⎭.【解析】(1)直线AB 的斜率50116k -==--, 所以AB 的垂直平分线m 的斜率为1.AB 的中点的横坐标和纵坐标分别为61722x +==,95522y +==. 因此,直线m 的方程为57122y x ⎛⎫-=- ⎪⎝⎭.即10x y --=. 又圆心在直线l 上,所以圆心是直线m 与直线l 的交点.联立方程组102780x y x y --=⎧⎨-+=⎩,解得32x y =⎧⎨=⎩所以圆心坐标为()3,2C,又半径r CA == 则所求圆的方程是22(3)(2)13x y -+-=. (2)设线段PQ 的中点(),M x y ,()00,P x yM 为线段PQ 的中点,则008202x x y y +⎧=⎪⎪⎨+⎪=⎪⎩,解得00282x x y y =-⎧⎨=⎩()28,2P x y -代入圆C 中得22(283)(22)13x y --+-=,即线段PQ 中点M 的轨迹方程为221113(1)24x y ⎛⎫-+-= ⎪⎝⎭.4.(2021·江苏)在半面直角坐标系中,如果点P 的坐标(),x y 满足cos sin x a r y b r θθ=+⎧⎨=+⎩,其中θ为参数,0r >.证明:点P 的轨迹是圆心为(),a b ,半径为r 的圆. 【答案】证明见解析. 【解析】由cos sin x a r y b r θθ=+⎧⎨=+⎩可得222()()x a y b r -+-=,所以点P 的轨迹是圆心为(,)a b ,半径为r 的圆.考点五 与圆有关的最值【例5】(2021年广东湛江)已知实数x ,y 满足方程x 2+y 2-4x +1=0,则 (1)y x的最大值和最小值分别为________和________; (2)y -x 的最大值和最小值分别为________和________; (3)x 2+y 2的最大值和最小值分别为_______和_______.【答案】(1) 3 - 3 (2)-2+6,-2- 6.(3)7+4 3 7-4 3【解析】原方程可化为(x -2)2+y 2=3,表示以(2,0)为圆心, 3为半径的圆.(1)y x 的几何意义是圆上一点与原点连线的斜率,所以设y x=k ,即y =kx .当直线y =kx 与圆相切时(如图),斜率k 取最大值或最小值,此时|2k -0|k 2+1=3,解得k =± 3.所以yx 的最大值为3,最小值为- 3.(2)y -x 可看作是直线y =x +b 在y 轴上的截距.如图所示,当直线y =x +b 与圆相切时,纵截距b 取得最大值或最小值,此时|2-0+b |2=3,解得b =-2±6,所以y -x 的最大值为-2+6,最小值为-2- 6.(3)x 2+y 2表示圆上的一点与原点距离的平方.由平面几何知识知,在原点和圆心连线与圆的两个交点处取得最大值和最小值.又圆心到原点的距离为2,所以x 2+y 2的最大值是(2+3)2=7+43,x 2+y 2的最小值是(2-3)2=7-4 3.(1) (3)【一隅三反】1.(2021·全国高二课时练习)若0x =,则2yx -的取值范围为 【答案】11[,]22-【解析】因为0x =x =-所以()2210x y x +=≤如图,此方程表示的是圆心在原点,半径为1的半圆,2yx -的几何意义是点(),x y 与点()2,0连线的斜率 如图,()()0,1,0,1A B -,()2,0P101022PA k -==--,101022PB k --==- 所以2y x -的取值范围为11[,]22-故选:D2.(2021·保定质检)已知A (0,2),点P 在直线x +y +2=0上,点Q 在圆C :x 2+y 2-4x -2y =0上,则|PA |+|PQ |的最小值是________. 【答案】 2 5【解析】因为圆C :x 2+y 2-4x -2y =0, 故圆C 是以C (2,1)为圆心,半径r =5的圆.设点A (0,2)关于直线x +y +2=0的对称点为A ′(m ,n ),故⎩⎪⎨⎪⎧m +02+n +22+2=0,n -2m -0=1,解得⎩⎪⎨⎪⎧m =-4,n =-2,故A ′(-4,-2).连接A ′C 交圆C 于Q ,由对称性可知|PA |+|PQ |=|A ′P |+|PQ |≥|A ′Q |=|A ′C |-r =2 5.3.已知M (x ,y )为圆C :x 2+y 2-4x -14y +45=0上任意一点,且点Q (-2,3). (1)求|MQ |的最大值和最小值;(2)求y -3x +2的最大值和最小值. 【答案】(1)6 2 22(2)2+3,2- 3.【解析】(1)由圆C :x 2+y 2-4x -14y +45=0,可得(x -2)2+(y -7)2=8, ∴圆心C 的坐标为(2,7),半径r =2 2. 又|QC |=2+22+7-32=42,∴|MQ |max =42+22=62,|MQ |min =42-22=2 2. (2)可知y -3x +2表示直线MQ 的斜率k . 设直线MQ 的方程为y -3=k (x +2), 即kx -y +2k +3=0. ∵直线MQ 与圆C 有交点, ∴|2k -7+2k +3|1+k2≤22, 可得2-3≤k ≤2+3, ∴y -3x +2的最大值为2+3,最小值为2- 3.。
圆的标准方程(经典练习及答案详解)
2.4 圆的方程 2.4.1 圆的标准方程1.已知圆的方程是(x-2)2+(y-3)2=4,则点P (3,2)( )A.是圆心B.在圆上C.在圆内D.在圆外(3-2)2+(2-3)2=2<4,∴点P 在圆内.2.已知点A (-4,-5),B (6,-1),则以线段AB 为直径的圆的方程是( ) A.(x+1)2+(y-3)2=29 B.(x+1)2+(y-3)2=116 C.(x-1)2+(y+3)2=29D.(x-1)2+(y+3)2=116A (-4,-5),B (6,-1),所以线段AB 的中点为C (1,-3),所求圆的半径r=12|AB|=12√102+42=√29,所以以线段AB 为直径的圆的方程是(x-1)2+(y+3)2=29,故选C .3.方程x=√1-y 2表示的图形是( ) A.两个半圆 B.两个圆 C.圆D.半圆x ≥0,方程两边同时平方并整理得x 2+y 2=1,由此确定图形为半圆,故选D .4.一个动点在圆x 2+y 2=1上移动时,它与定点A (3,0)的连线中点的轨迹方程是( ) A.(x+3)2+y 2=4 B.(x-3)2+y 2=1 C.(2x-3)2+4y 2=1D.x+322+y 2=12M (x 0,y 0)为圆上的动点,则有x 02+y 02=1,设线段MA 的中点为P (x ,y ),则x=x 0+32,y=y 0+02,则x 0=2x-3,y 0=2y ,代入x 02+y 02=1,得(2x-3)2+(2y )2=1,即(2x-3)2+4y 2=1.5.圆(x-2)2+(y+3)2=2的圆心是 ,半径是 .-3) √26.圆(x+1)2+y 2=5关于直线y=x 对称的圆的标准方程为 .(x+1)2+y 2=5的圆心坐标为(-1,0),它关于直线y=x 的对称点坐标为(0,-1),即所求圆的圆心坐标为(0,-1),所以所求圆的标准方程为x 2+(y+1)2=5.2+(y+1)2=57.若直线3x-4y+12=0与两坐标轴交点为A ,B ,则以线段AB 为直径的圆的方程是 .解析由题意得A (0,3),B (-4,0),AB 的中点-2,32为圆的圆心,直径AB=5,以线段AB 为直径的圆的标准方程为(x+2)2+y-322=254. 答案(x+2)2+y-322=2548.已知圆M 过A (1,-1),B (-1,1)两点,且圆心M 在直线x+y-2=0上. (1)求圆M 的方程;(2)若圆M 上存在点P ,使|OP|=m (m>0),其中O 为坐标原点,求实数m 的取值范围.设圆M 的方程为(x-a )2+(y-b )2=r 2(r>0),根据题意得{a +b -2=0,(1-a )2+(-1-b )2=r 2,(-1-a )2+(1-b )2=r 2,解得{a =1,b =1,r =2,所以圆M 的方程为(x-1)2+(y-1)2=4. (2)如图,m=|OP|∈[2-√2,2+√2].关键能力提升练9.若直线y=kx 与圆(x-2)2+y 2=1的两个交点关于直线2x+y+b=0对称,则k ,b 的值分别为( ) A.12,-4B.-12,4C.12,4D.-12,-4y=kx与圆(x-2)2+y2=1的两个交点关于直线2x+y+b=0对称,直线2x+y+b=0的斜率为-2,所以k=12,并且直线2x+y+b=0经过已知圆的圆心,所以圆心(2,0)在直线2x+y+b=0上,所以4+0+b=0,所以b=-4.故选A.10.已知圆O:x2+y2=1,点A(-2,0)及点B(2,a),从A点观察B点,要使视线不被圆O挡住,则实数a的取值范围是()A.(-∞,-1)∪(-1,+∞)B.(-∞,-2)∪(2,+∞)C.-∞,-4√33∪4√33,+∞D.(-∞,-4)∪(4,+∞)方法1)(直接法)写出直线方程,将直线与圆相切转化为点到直线的距离来解决.过A,B两点的直线方程为y=a4x+a2,即ax-4y+2a=0,令d=√a2+16=1,化简后,得3a2=16,解得a=±4√33.再进一步判断便可得到正确答案为C.(方法2)(数形结合法)如图,设直线AB切圆O于点C在Rt△AOC中,由|OC|=1,|AO|=2,可求出∠CAO=30°.在Rt△BAD中,由|AD|=4,∠BAD=30°,可求得BD=4√33,再由图直观判断,故选C.11.(2020四川成都石室中学高二上期中)已知实数x,y满足x2+y2=1,则√3x+y的取值范围是()A.(-2,2)B.(-∞,2]C.[-2,2]D.(-2,+∞)解析因为x2+y2=1,所以设x=sin α,y=cos α,则√3x+y=√3sin α+cos α=2sinα+π6,所以√3x+y的取值范围是[-2,2].故选C.12.(多选题)若经过点P(5m+1,12m)可以作出圆(x-1)2+y2=1的两条切线,则实数m的取值可能是()A.110B.113C.-113D.-12P 可作圆的两条切线,说明点P 在圆的外部,所以(5m+1-1)2+(12m )2>1,解得m>113或m<-113,对照选项知AD 可能.13.(多选题)设有一组圆C k :(x-k )2+(y-k )2=4(k ∈R ),下列命题正确的是( ) A.不论k 如何变化,圆心C 始终在一条直线上 B.所有圆C k 均不经过点(3,0) C.经过点(2,2)的圆C k 有且只有一个 D.所有圆的面积均为4π(k ,k ),在直线y=x 上,故A 正确;令(3-k )2+(0-k )2=4,化简得2k 2-6k+5=0,∵Δ=36-40=-4<0,∴2k 2-6k+5=0无实数根,故B 正确;由(2-k )2+(2-k )2=4,化简得k 2-4k+2=0,∵Δ=16-8=8>0,有两个不等实根,∴经过点(2,2)的圆C k 有两个,故C 错误;由圆的半径为2,得圆的面积为4π,故D 正确.故选ABD .14.已知点A (8,-6)与圆C :x 2+y 2=25,P 是圆C 上任意一点,则|AP|的最小值是 .82+(-6)2=100>25,故点A 在圆外,从而|AP|的最小值为√82+(-6)2-5=10-5=5.15.已知圆C 的半径为2,圆心在x 轴的正半轴上,且圆心到直线3x+4y+4=0的距离等于半径长,则圆C 的标准方程为 .(a ,0),且a>0,则点(a ,0)到直线3x+4y+4=0的距离为2,即√32+42=2,所以3a+4=±10,解得a=2或a=-143(舍去),则圆C 的标准方程为(x-2)2+y 2=4.x-2)2+y 2=416.矩形ABCD 的两条对角线相交于点M (2,1),AB 边所在直线的方程为x-2y-4=0,点T (-1,0)在AD 边所在直线上. (1)求AD 边所在直线的方程; (2)求矩形ABCD 外接圆的方程.因为AB 边所在直线的方程为x-2y-4=0,且AD 与AB 垂直,所以直线AD 的斜率为-2.又因为点T (-1,0)在直线AD 上,所以AD 边所在直线的方程为y-0=-2(x+1),即2x+y+2=0.(2)由{x -2y -4=0,2x +y +2=0,解得{x =0,y =-2,所以点A 的坐标为(0,-2),因为矩形ABCD 两条对角线的交点为M (2,1),所以M 为矩形外接圆的圆心.又|AM|=√(2-0)2+(1+2)2=√13,从而矩形ABCD 外接圆的方程为(x-2)2+(y-1)2=13.学科素养创新练17.设A(x A,y A),B(x B,y B)为平面直角坐标系内的两点,其中x A,y A,x B,y B∈Z.令Δx=x B-x A,Δy=y B-y A,若|Δx|+|Δy|=3,且|Δx|·|Δy|≠0,则称点B为点A的“相关点”,记作B=τ(A).(1)求点(0,0)的“相关点”的个数.(2)点(0,0)的所有“相关点”是否在同一个圆上?若在,写出圆的方程;若不在,请说明理由.因为|Δx|+|Δy|=3(Δx,Δy为非零整数),所以|Δx|=1,|Δy|=2或|Δx|=2,|Δy|=1,所以点(0,0)的“相关点”有8个.(2)是.设点(0,0)的“相关点”的坐标为(x,y).由(1)知|Δx|2+|Δy|2=5,即(x-0)2+(y-0)2=5,所以所有“相关点”都在以(0,0)为圆心,√5为半径的圆上,所求圆的方程为x2+y2=5.。
(完整版)圆的方程 习题(含答案)
一、单选题
1.以点P(2,-3)为圆心,并且与y轴相切的圆的方程是( )
A.(x+2)2+(y-3)2=4
B.(x+2)2+(y-3)2=9
C.(x-2)2+(y+3)2=4
D.(x-2)2+(y+3)2=9
2.当点 在圆 上运动时,连接它与定点 ,线段 的中点 的轨迹方程是( )
6.若点 为圆 上的一个动点,点 , 为两个定点,则 的最大值为( )
A. B. C. D.
7.已知直线 : 是圆 的对称轴.过点 作圆 的一条切线,切点为 ,则 ( )
A.2B. C.6D.
8.若直线l:ax+by+1=0经过圆M: 的圆心则 的最小值为
A. B.5C. D.10
9.若 均为任意实数,且 ,则 的最小值为( )
21.已知点 在圆 上运动,且存在一定点 ,点 为线段 的中点.
(1)求点 的轨迹 的方程;
(2)过 且斜率为 的直线 与点 的轨迹 交于不同的两点 ,是否存在实数 使得 ,并说明理由.
22.已知圆经过 两点,并且圆心在直线 上。
(1)求圆的方程;
(2)求圆上的点到直线 的最小距离。
23.在平面直角坐标系 中,曲线 与坐标轴的交点都在圆 上.
A. B.
C. D.
3.圆x2+y2-(4m+2)x-2my+4m2+4m+1=0的圆心在直线x+y-4=0上,那么圆的面积为( )
A.9πB.πC.2πD.由m的值而定
4.圆 的半径是( )
A. B.2C. D.4
5.已知圆 与圆 相交于A、B两点,则线段AB的垂直平分线的方程为
A. B. C. D.
A. B. C. D.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求证:不论 为何值,所给圆必经过两个定点。
证明:把所给方程写为:
这是经过以下两个圆的交点的圆系的方程:
所以,不论 为何值,所给圆必经过这两个圆的两个交点
轴对称
轴对称是解析几何的一个重要内容,利用它不仅可以解决点、线、曲线等关于直线的对称问题,而且还可以解决诸如最值、光线反射、角平分线等问题,并且常得到意想不到的效果。本文将以数例来谈谈它的应用。
点评:一般通过线心距 与圆半径 相等和待定系数法,或切线垂直于经过切点的半径来处理切线问题.
四、弦长问题
例4 (06天津卷理)设直线 与圆 相交于 两点,且弦 的长为 ,则 .
解由已知圆 ,即得圆心 和半径 .
∵线心距 ,且 ,∴ ,即 ,解得 .
点评:一般在线心距 、弦长 的一半和圆半径 所组成的直角三角形中处理弦长问题: .
∵圆上至少有三个不同的点到直线l:ax+by=0的距离为2 ,
∴圆心到直线的距离小于或等于 .
即 ,亦即 .故
∴15°
故所求角的范围为[15°,75°].
【点评】解析1采用几何法来处理直线与圆的位置关系问题,而解析2是通过代数的方法来处理.
(4)圆与圆的位置关系——由心心距和半径长确定
【例4】已知两圆 和 ,求:
即x2+y2+4x的最大值为7+2 ,最小值为
习题精选精讲圆标准方程
已知圆心 和半径 ,即得圆的标准方程 ;已知圆的标准方程 ,即得圆心 和半径 ,进而可解得与圆有关的任何问题.
一、求圆的方程
例1 (06重庆卷文)以点 为圆心且与直线 相切的圆的方程为( )
(A) (B)
(C) (D)
解已知圆心为 ,且由题意知线心距等于圆半径,即 ,∴所求的圆方程为 ,故选(C).
为何值所给圆必经过这两个圆的两个交点轴对称轴对称是解析几何的一个重要内容利用它不仅可以解决点线曲线等关于直线的对称问题而且还可以解决诸如最值光线反射角平分线等问题并且常得到意想不到的效果
圆的方程习题精选精讲
(1)标准方程——请看圆心和半径
从圆的标准方程(x-a)2+(y-b)2=r2(r>0)中,我们能看见它的图形特征:圆心即定点(a,b),半径即定长r.a,b确定了圆的位置,r确定了圆的大小.
当A到l的距离d= 时,圆上恰有三个点到l的距离为2 ;
当d< 时,圆上有四点到直线l的距离为2 ;
当d> 时,圆上有两点到l的距离为2 .
如右图,当d=AC= 时,OA=2 , AOC=30°,
∴ COx=15°.
在另一极端位置l′时,其倾斜角为75°.
∴所求角的范围为[15°,75°]
【解析2】圆 的圆心为(2,2),半径为3 .
∴Q分PA的比为 .
∴
又因 =1,且y0>0,∴ .
∴Q的轨迹方程为 .
【法二】设∠AOP=α,α∈(0,π),则P(cosα,sinα),∠AOQ= ,则OQ直线方程为y=x·tan =kx①
kPA= ∴直线PA方程为y= (x-3)②
由Q满足①②且k=tan .由②得y= .消去k有y= ∴x2+y2- ,由图知y>0.
八、综合问题
例8 (06湖南卷理)若圆 上至少有三个不同的点到直线 的距离为 ,则直线 的倾斜角的取值范围是( )
(A) (B) (C) (D)
解已知圆化为 ,即得圆心 和半径 .
∵圆上至少有三个不同的点到直线 的距离为 ,∴ ,即 ,由直线 的斜率 代入得 ,解得 ,又 , ,∴直线 的倾斜角的取值范围是 ,故选(B).
故所求Q点轨迹方程为x2+y2- x=0(y>0).
【点评】上述两种方程为求轨迹的基本方法:相关点及参数法.
(2)待定系数法——把方程(组)带进几何
当已知动点的轨迹是所学过的曲线方程时,则可设出含有待定系数的方程,再根据动点满足的条件,确定待定系数,从而求得动点的轨迹方程.其基本思路是:先定性,再定型,最后定量.
(3)几何法——与向量或三角沟通
直线被圆截得的弦长计算,运用弦心距(即圆心到直线的距离)、弦半径及半径构成直角三角形计算,此公式是
半径2=弦心距2+半弦长2.
【例7】在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量 的坐标;(2)求圆 关于直线OB对称的圆的方程;
判断直线与圆的位置关系有两种方法:
①几何法:利用圆心到直线的距离d与半径r的大小判断
②代数法:联立直线与圆的方程,转化为一元二次方程,利用判别式“Δ”进行判断:
【例3】若圆 上至少有三个不同的点到直线l:ax+by=0的距离为2 ,求直线l的倾斜角的取值范围.
【解析1】圆(x-2)2+(y-2)2=18的圆心为A(2,2),半径为r= .
点评:一般通过比较线心距 与圆半径 的大小来处理直线与圆的位置关系: 线圆相离; 线圆相切; 线圆相交.
三、切线问题
例3 (06重庆卷理)过坐标原点且与圆 相切的直线方程为( )
(A) 或 (B) 或
(C) 或 (D) 或
解化为标准方程 ,即得圆心 和半径 .
设过坐标原点的切线方程为 ,即 ,∴线心距 ,平方去分母得 ,解得 或 ,∴所求的切线方程为 或 ,故选(A).
确定一个圆需要三个条件,1个圆心相当2个条件,而半径只相当1个条件.
【例1】求过点A(5,2)和点B(3,-2),圆心在直线2x-y=3上的圆的方程.
【分析】点A和点B已知相当2个条件,圆心在已知直线上只相当1个条件.三个条件已知,圆的方程可定.
【解析】设圆心为(a,b),则有
解得
即圆心为(2,1).
(3)当 ,①不表示任何图形.
【例2】已知方程x2+y2-2(m+3)x+2·(1-4m2)·y+16m4+9=0表示一个圆.
(1)求实数m的取值范围;(2)求该圆半径r的取值范围;(3)求圆心的轨迹方程.
【解析】(1)方程表示圆的充要条件是D2+E2-4F>0,即:4(m+3)2+4(1-4m2)2-4(16m4+9)>0,解之得- <m<1.
【解析】∵
∴ =
设x2+y2+4x=k,即(x+2)2+y2=4+k,视为以K(-2,0)为圆心, 为半径.
(问题转化为求半径的取值范围)
∵x、y在圆 上运动,而点K(-2,0)在圆C外,
又两圆心距为
当圆K与圆C内切时 取最大值,最大值为 +1,此时k=( +1)2-4=7+2 .
当圆K与圆C外切时 取最小值,此时有 +1= ,
(4)参数法——与函数或不等式接轨
当动点P(x,y)直接找不出坐标x,y之间的关系时,可设动点P(x,y)满足关于参数t的方程 (t是参数)③
则由方程组③消去参数t,即求得动点P(x,y)的普通方程:f(x,y)=0.
【例8】点P(x,y)在圆C:x2+y2-2x-2y+1=0上运动,点A(2,2),B(2,-2)是平面上两点,求 的最值.
由距离公式得半径r2=
因此所求圆的方程为 .
【点评】具备三个独立条件方能确定圆的三个参数值,即确定圆的方程.如果还有某个条件未能确定,则得到的是“圆系”(圆的集合)方程.当题设中有条件很隐晦时,可先按“显形条件”求出圆系方程,再让圆系方程满足隐晦条件而把圆方程最后确定.
(2)一般方程——看圆的代数式特征
当两圆外切时, 解得 .
(2)当两圆内切时,因定圆的半径 小于两圆圆心距离5,故只有
解得 又∵ ∴两圆公切线的斜率为 .
设所求公切线方程为
解得 易验证当 时,直线与后一圆相交.
故所求公切线方程为 ,即
(3)当m=45时,两圆公共弦所在直线方程为4x+3y-23=0.由圆的半径、弦长、弦心距间的关系,不难求得公共弦的长为
【解析】(1)设 得
所以v-3>0,得v=8,故 ={6,8}.
(2)由 ={10,5},得B(10,5),于是直线OB方程:
由条件可知圆的标准方程为:(x-3)2+y(y+1)2=10,得圆心(3,-1),半径为 .设圆心(3,-1)关于直线OB的对称点为(x,y)则
故所求圆的方程为(x-1)2+(y-3)2=10.
①
则关于α、β反解方程组①,得 ②
代入曲线方程f1(x,y)=0,即可求得动点P的轨迹方程C:f(x,y)=0.
【例5】已知点A(3,0),点P在圆x2+y2=1的上半圆周上,∠AOP的平分线交PA于Q,求点Q的轨迹方程.
【法一】如图所示,设P(x0,y0)(y0>0),Q(x,y).
∵OQ为∠AOP的平分线,∴ ,
(1)m取何值时两圆外切;(2)m取何值时两圆内切,此时内切线方程是什么?
(3)求m=45时两圆的公共弦长.
【分析】先将两圆方程变为标准方程,利用外切和内切的条件求m的值,特别是两圆内切时,还应分析两圆半径大小关系再准确求解.
【解析】(1)两圆的标准方程分别为:
圆心分别为M(1,3),N(5,6),半径分别为 和 .
【例6】求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点,并且圆心在直线x-y-4=0上的圆的方程.
【法一】解方程组 得 或
∴两圆交点为(-1,3),(-6,-2).
设所求圆方程为:x2+y2+dx+ey+f=0
∴所求圆方程为:x2+y2-x+7y-32=0 .
【法二】解方程组 得 或
如果把圆的标准方程称作圆方程的“几何式”,而圆的一般方程则可称作圆方程的“代数式”.
